A&A 456, 941-952 (2006)
DOI: 10.1051/0004-6361:20054727
C. Möllenhoff 1 - C. C. Popescu2,3,4 - R. J. Tuffs2,3
1 - Zentrum für Astronomie der Universität Heidelberg,
Landessternwarte, Königstuhl 12, 69117 Heidelberg, Germany
2 -
Max-Planck-Institut für Kernphysik, Saupfercheckweg 1,
69117 Heidelberg, Germany
3 -
The Observatories of the Carnegie Institution of Washington, 813 Santa Barbara
St., Pasadena, CA 91101, USA
4 -
Research Associate, The Astronomical Institute of the Romanian
Academy, Str. Cutitul de Argint 5, Bucharest, Romania
Received 20 December 2005 / Accepted 16 June 2006
Abstract
We present corrections for the change in the apparent scalelengths,
central surface brightnesses and axis ratios due to the presence of dust in
pure disk galaxies, as a function of inclination, central face-on opacity in
the B-band (
![]() )
and
wavelength. The correction factors were derived from simulated images of disk
galaxies created using geometries for stars and dust which can reproduce the
entire spectral energy distribution from the ultraviolet (UV) to the
Far-infrared (FIR)/submillimeter (submm) and can also account for the
observed surface-brightness distributions in both the optical/Near-infrared
and FIR/submm. We found that dust can significantly affect both the scalelength
and central surface brightness, inducing variations in the apparent to
intrinsic
quantities of up to 50
)
and
wavelength. The correction factors were derived from simulated images of disk
galaxies created using geometries for stars and dust which can reproduce the
entire spectral energy distribution from the ultraviolet (UV) to the
Far-infrared (FIR)/submillimeter (submm) and can also account for the
observed surface-brightness distributions in both the optical/Near-infrared
and FIR/submm. We found that dust can significantly affect both the scalelength
and central surface brightness, inducing variations in the apparent to
intrinsic
quantities of up to 50![]() in scalelength and up to 1.5 mag in
central surface brightness. We also identified some astrophysical effects for
which, although the absolute effect of dust is non-negligible,
the predicted variation over a likely range in opacity is relatively small,
such that
an exact knowledge of opacity is not needed. Thus, for a
galaxy
at a typical inclination of
in scalelength and up to 1.5 mag in
central surface brightness. We also identified some astrophysical effects for
which, although the absolute effect of dust is non-negligible,
the predicted variation over a likely range in opacity is relatively small,
such that
an exact knowledge of opacity is not needed. Thus, for a
galaxy
at a typical inclination of
![]() and having any
and having any
![]() ,
the
effect of dust is to increase the scalelength in B relative to that in I by a
factor of
,
the
effect of dust is to increase the scalelength in B relative to that in I by a
factor of
![]() and to change the B-I central colour by
and to change the B-I central colour by
![]() mag. Finally we use the model to analyse the observed
scalelength ratios between B and I for a sample of disk-dominated spiral
galaxies, finding that the tendency for apparent scalelength to increase with
decreasing wavelength is primarily due to the effects of dust.
mag. Finally we use the model to analyse the observed
scalelength ratios between B and I for a sample of disk-dominated spiral
galaxies, finding that the tendency for apparent scalelength to increase with
decreasing wavelength is primarily due to the effects of dust.
Key words: galaxies: spiral - galaxies: structure - galaxies: photometry - galaxies: fundamental parameters - ISM: dust, extinction - radiative transfer
A primary goal of modern studies of star-forming galaxies is to understand how these systems were assembled over cosmic time. If the disks of spiral galaxies grow from the inside out, as predicted by semi-analytical hierarchical models for galaxy formation (e.g. Mo et al. 1998), one would predict the stellar populations to be younger and have lower metallicity in the outer disk than in the inner disk, such that local universe galaxies should be intrinsically larger at the shorter wavelengths where light from the young stellar population is more prominent. For the same reason one would expect the intrinsic sizes of spiral disks to be larger at the current epoch than at higher redshift. Observationally, such predictions can be tested in two ways. One way is to compare the spatial distribution of the constituent stellar populations at different wavelengths, for local universe galaxies. Another way is to look for structural differences in galaxies observed at different cosmological epochs, at the same rest frame wavelength. Both methods require an analysis of the surface-brightness distribution of spiral galaxies in the optical and near-infrared (NIR) to quantify the distribution of starlight, for example by deriving the scalelength of the disk. This is done by fitting observed images with models for the surface-brightness distribution of stellar light, whereby the disk component is usually specified by an exponential distribution. The derived exponential scalelengths can either be intercompared between different wavelengths for local universe galaxies (Elmegreen & Elmegreen 1984; Peletier et al. 1994; Evans 1994; De Jong 1996a,b; de Grijs 1998; Cunow 1998, 2001, 2004; MacArthur et al. 2003; Möllenhoff 2004), or between galaxies at different redshifts at a given wavelength (Lilly et al. 1998; Simard et al. 1999; Ravindranath et al. 2004; Trujillo & Aguerri 2004; Trujillo et al. 2005; Barden et al. 2005). However, the appearance of disk galaxies is strongly affected by dust and this effect is different at different wavelengths and for different opacities. This has consequences not only for the derivation of the variation of intrinsic scalelength with wavelength, but also for the variation of intrinsic scalelength with cosmological epoch, since the opacity of disk galaxies is expected to have been systematically higher in the past (e.g. Dwek 1998; Pei et al. 1999).
The effect of dust on the observed scalelengths and central
surface brightnesses of disk galaxies has been previously modelled by
Byun et al. (1994), Evans (1994) and Cunow (2001). By means of radiative
transfer calculations these works investigated the dependence of this effect
on star/dust geometry, opacity, inclination and wavelength. Recently, a better
knowledge of the star/dust geometry has been obtained through a joint
consideration of the direct starlight, emitted in the ultraviolet
(UV)/optical/NIR, and of the starlight which is re-radiated
in the Far-infrared (FIR)/submillimeter (submm).
In a series of papers devoted
to modelling the spectral energy distributions (SEDs) we derived geometries
of the distribution of stellar light and dust that are
successful in reproducing not only the observed integrated SEDs, but also the
observed radial profiles both in the optical/NIR
and
FIR/submm (Popescu et al. 2000, hereafter Paper I; Misiriotis et al. 2001,
hereafter Paper II; Popescu et al. 2004; see also Popescu & Tuffs 2005![]() ).
).
In this paper, the fourth in this series, we use
these derived distributions of stars and dust to obtain a new
quantitative measure of the effect of dust on the observed photometric
parameters in the optical wavebands. Furthermore, because it is no longer
necessary to explore a wide
range of star/dust geometries, we are also able to
systematically explore the full parameter space in opacity, inclination and
wavelength, and tabulate the results in a form convenient for the use of the
community.
We give quantitative measures of the change in the
apparent scalelength, central surface brightnesses and inclination of disk
galaxies due to the presence of dust![]() . All these changes
are expressed as
the ratio of the apparent quantity (i.e. that obtained by fitting images of
dusty disks with pure exponential disks) to the intrinsic quantity (i.e. that
which would be obtained in the absence of dust). These corrections have been
derived from a subset of the simulated images (those in the optical bands)
presented in Tuffs et al. (2004, hereafter Paper III).
. All these changes
are expressed as
the ratio of the apparent quantity (i.e. that obtained by fitting images of
dusty disks with pure exponential disks) to the intrinsic quantity (i.e. that
which would be obtained in the absence of dust). These corrections have been
derived from a subset of the simulated images (those in the optical bands)
presented in Tuffs et al. (2004, hereafter Paper III).
In Sect. 2 we give a brief description of the distributions of stars and dust used in the simulated images. In Sect. 3 we specify the fitting procedure used to extract apparent scalelengths, central surface brightnesses and axis ratios from the simulated images. These quantities are tabulated in Sect. 4, where we also describe and explain their dependence on opacity, inclination and wavelength due to the effect of dust. In Sect. 5 we examine the impact of these new results on our ability to derive quantities of astrophysical interest from optical observations and give in Sect. 6 a specific example of the determination of the variation of intrinsic scalelength with wavelength for local universe galaxies. A summary of the paper is given in Sect. 7.
In Paper III we presented simulated images for the diffuse component of a
spiral galaxy. This diffuse component is comprised of a diffuse old stellar
population and associated dust and a
diffuse young stellar population and associated dust.
Direct evidence for the existence of the diffuse dust disk is provided by
images of FIR emission in spiral galaxies (for example in M 31 by
Haas et al. 1998 and in M 33 by Hippelein et al. 2003), which clearly show a
diffuse disk of cold dust emission prominent at 170 ![]() m.
FIR measurements of a statistically unbiased optically selected sample
of gas-rich galaxies (Tuffs et al. 2002a,b) have shown that this
diffuse cold dust emission component is ubiquitous along
the Hubble sequence of late-type galaxies, and carries the bulk of
the dust luminosity for most of these systems (Popescu et al. 2002). It is thus
responsible for most of the attenuation of the stellar light and the associated
modification of disk brightness and scalelength measured in the optical, which
is the subject of this paper.
m.
FIR measurements of a statistically unbiased optically selected sample
of gas-rich galaxies (Tuffs et al. 2002a,b) have shown that this
diffuse cold dust emission component is ubiquitous along
the Hubble sequence of late-type galaxies, and carries the bulk of
the dust luminosity for most of these systems (Popescu et al. 2002). It is thus
responsible for most of the attenuation of the stellar light and the associated
modification of disk brightness and scalelength measured in the optical, which
is the subject of this paper.
We know that in reality the apparently diffuse
dust component may itself have some structure, and that some fraction
(currently
unconstrained by direct observation) may be contained in clumps which are
externally heated and have no embedded sources, the so-called "passive
clumps'' (Popescu & Tuffs 2005). However,
providing these passive clumps are optically thin, the attenuation
characteristics
will be almost identical to those of a completely homogeneous distribution
(Kuchinski et al. 1998; Pierini et al. 2004). If the passive clumps are
considered to be optically thick, then the overall attenuation of a galaxy
can be reduced by up
to ![]() (Bianchi et al. 2000a; Misiriotis & Bianchi 2002). But, once UV
photons can no longer penetrate a clump, the photoelectric heating of the gas
is lost and there is nothing to prevent the clump collapsing to form
stars. This means that in practice optically thick passive clumps should not
exist as stable long-lived structures, but rather as transient precursors of
star-forming clouds. Once the star-formation is underway, the clumps will start
to contain embedded sources, becoming "active'' clumps
(Popescu & Tuffs 2005). In terms of the global attenuation of stellar light in
galaxies, the main effect of active clumps is to locally absorb a fraction of
the UV output from the embedded massive stars and transform it into warm dust
emission. This is taken into account by the model of Popescu et al. (2000) used
in this series of papers. Active clumps have such a small filling
factor in normal spiral galaxies that their effect on the propagation of the
long-range optical/NIR photons in galaxy disks is negligible. Since in this
paper we only consider the optical/NIR spectral range, it is only necessary
here to take into account the diffuse dust distribution.
(Bianchi et al. 2000a; Misiriotis & Bianchi 2002). But, once UV
photons can no longer penetrate a clump, the photoelectric heating of the gas
is lost and there is nothing to prevent the clump collapsing to form
stars. This means that in practice optically thick passive clumps should not
exist as stable long-lived structures, but rather as transient precursors of
star-forming clouds. Once the star-formation is underway, the clumps will start
to contain embedded sources, becoming "active'' clumps
(Popescu & Tuffs 2005). In terms of the global attenuation of stellar light in
galaxies, the main effect of active clumps is to locally absorb a fraction of
the UV output from the embedded massive stars and transform it into warm dust
emission. This is taken into account by the model of Popescu et al. (2000) used
in this series of papers. Active clumps have such a small filling
factor in normal spiral galaxies that their effect on the propagation of the
long-range optical/NIR photons in galaxy disks is negligible. Since in this
paper we only consider the optical/NIR spectral range, it is only necessary
here to take into account the diffuse dust distribution.
The diffuse old stellar
population has both a "bulge'' and a "disk'' component, whereas the
diffuse young stellar population resides only in a "thin disk''.
Here we only use the disk component,
since in this paper we are only concerned with the appearance of the disk in the
optical/NIR range.
The simulations for the disk were performed taking the geometry of
the diffuse dust to be the superposition of the dust in the disk and the dust
in the thin disk. In other words the attenuated images represent the appearance
of the stellar populations in the disk as seen through the dust in the disk
and thin disk.
The stellar emissivity of the disk ![]() and the extinction coefficients of
the dust associated with the disk,
and the extinction coefficients of
the dust associated with the disk,
![]() ,
and with the
thin disk,
,
and with the
thin disk,
![]() ,
are described by exponentials:
,
are described by exponentials:
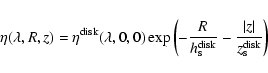 |
(1) |
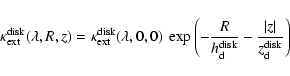 |
(2) |
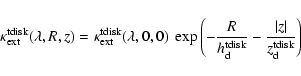 |
(3) |
The simulated images of the disk were calculated
using the radiative transfer code of Kylafis & Bahcall (1987), which includes
anisotropic multiple scattering in which the higher orders of scattered light
are calculated using the method of "scattered intensities'' (see also
Kylafis & Xilouris 2005). The images have a pixel size (equal to the
resolution) of 0.0066 of the B-band scalelength
![]() and
were sampled every 5 and 10 pixels in the inner and outer disk,
respectively. They
extend out to a radius of 4.63 B-band scalelengths
and
were sampled every 5 and 10 pixels in the inner and outer disk,
respectively. They
extend out to a radius of 4.63 B-band scalelengths
![]() ,
which is equivalent to 3.31 dust scalelengths
,
which is equivalent to 3.31 dust scalelengths
![]() .
Examples
of simulated disk images are shown in Fig. 1 from Paper III.
.
Examples
of simulated disk images are shown in Fig. 1 from Paper III.
Here we make use of a subset of 280 of the simulated disk images presented in
Paper III, spanning 7 values of total central face-on optical depth in B band
![]() ,
8 inclinations i and 5 wavelengths.
For the sampling in
,
8 inclinations i and 5 wavelengths.
For the sampling in
![]() we chose the set of values
0.1,0.3,0.5,1.0,2.0,4.0,8.0, which range from extremely optically thin to
moderately optically thick cases.
For the sampling in inclination we used
we chose the set of values
0.1,0.3,0.5,1.0,2.0,4.0,8.0, which range from extremely optically thin to
moderately optically thick cases.
For the sampling in inclination we used
![]() ,
and
,
and
![]() ,
which correspond to
,
which correspond to
![]() .
The limit of
.
The limit of
![]() in i was imposed since standard methods to
derive apparent exponential scalelength from observed
images are no longer applicable for higher inclinations.
The simulations were performed in the standard optical/NIR bands B, V, I, J,
and K.
We also used the corresponding intrinsic images of the stellar emissivity
(as would be observed in the absence of dust).
in i was imposed since standard methods to
derive apparent exponential scalelength from observed
images are no longer applicable for higher inclinations.
The simulations were performed in the standard optical/NIR bands B, V, I, J,
and K.
We also used the corresponding intrinsic images of the stellar emissivity
(as would be observed in the absence of dust).
When extracting apparent scalelengths, central surface brightnesses and axis ratios from observed (dust attenuated) images of galaxy disks, the common procedure is to fit the observed surface-brightness distribution with the brightness distributioncorresponding to the projection of an inclined thin axisymmetric exponential disk. This brightness distribution takes the form:
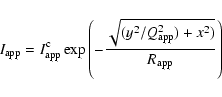 |
(4) |
The strategy we adopt in this paper is to use the same fitting procedure as
used to fit real observations to derive
![]() ,
,
![]() and
and
![]() from our simulated dust attenuated disk images. These quantities
can then be compared with the corresponding intrinsic quantities
from our simulated dust attenuated disk images. These quantities
can then be compared with the corresponding intrinsic quantities
![]() ,
,
![]() ,
and Q0,
where
,
and Q0,
where
![]() is the
intrinsic face-on surface brightness,
is the
intrinsic face-on surface brightness, ![]() is the intrinsic exponential
scalelength, and Q0 is the intrinsic inclination of the disk.
The intrinsic quantities are known as input to our simulations or can be
derived from the simulated dustless face-on images:
is the intrinsic exponential
scalelength, and Q0 is the intrinsic inclination of the disk.
The intrinsic quantities are known as input to our simulations or can be
derived from the simulated dustless face-on images:
![]() is equal to the value of the scalelength of the stellar
emissivity
is equal to the value of the scalelength of the stellar
emissivity
![]() ,
Q0 is
,
Q0 is ![]() for
a simulation made with inclination i, and
for
a simulation made with inclination i, and
![]() is the
brightness of the central pixel of the simulated dustless face-on image.
The ratios
is the
brightness of the central pixel of the simulated dustless face-on image.
The ratios
![]() /
/
![]() ,
,
![]() /
/![]() ,
and
,
and
![]() /Q0 can then be used to quantify the discrepancy
between intrinsic and perceived quantities arising from the presence of dust.
/Q0 can then be used to quantify the discrepancy
between intrinsic and perceived quantities arising from the presence of dust.
The simulated disk images containing
![]() pixels and covering half a
galaxy were first converted into full images of galaxies containing
pixels and covering half a
galaxy were first converted into full images of galaxies containing
![]() pixels. The sky-value was zero by construction. The maximum of the light
distribution was determined and was used as the centre of the disk fit.
pixels. The sky-value was zero by construction. The maximum of the light
distribution was determined and was used as the centre of the disk fit.
The two-dimensional surface-brightness function from Eq. (4)
was fitted to the brightness distribution of the simulated images following
Möllenhoff & Heidt (2001).
Fitting
![]() to the two-dimensional surface-brightness distribution results in a
nonlinear system of equations for the 3 free parameters
to the two-dimensional surface-brightness distribution results in a
nonlinear system of equations for the 3 free parameters
![]() ,
,
![]() and
and
![]() .
A Levenberg-Marquardt algorithm was used for the solution of this system
(e.g. Bevington & Robinson 1992).
.
A Levenberg-Marquardt algorithm was used for the solution of this system
(e.g. Bevington & Robinson 1992).
Several technical steps were necessary as prerequisites for the fit:
The centre of the galaxy was determined in each image and the
function from Eq. (4) was fitted to the whole image.
Since there were 280 images to fit, a systematic procedure
was necessary. We started in K with the face-on image and the lowest optical
depth (
![]() ,
,
![]() ).
A rough guess for the start values of the parameters in the initial
Levenberg-Marquardt fit was sufficient. The resulting parameters
).
A rough guess for the start values of the parameters in the initial
Levenberg-Marquardt fit was sufficient. The resulting parameters
![]() ,
,
![]() and
and
![]() were used as start values for the next fits
(
were used as start values for the next fits
(
![]() ,
,
![]() ).
Then the same procedure was repeated with the inclinations
).
Then the same procedure was repeated with the inclinations
![]() until
until
![]() .
Afterwards we proceeded in the same manner for the other filters J, I, V, B.
.
Afterwards we proceeded in the same manner for the other filters J, I, V, B.
Figure 1 shows two examples of simulated disks and of residua after subtraction of our photometric fits to these simulated disks. For face-on galaxies the fit is perfect and the residuum is practically zero. For inclined galaxies the stronger forward scattering induces a relative brightening of the near side of the disk, leading to an asymmetry around the horizontal axis. Such an asymmetry is not considered by our fitting function, therefore the fit to the inclined galaxies will be imperfect.
To show the details of the photometric fits and of the residua between the
simulated disks and the fits, we plot in Fig. 2 cuts parallel
and perpendicular to the major axis. This is shown for simulations done in the
B band, for
![]() and for three different inclinations,
and for three different inclinations,
![]() .
Due to the central opacity the disk models are somewhat rounder in the
centre than the corresponding exponential fits. This effect is reflected
in the central cusp of the residuum (solid bottom line) and increases with
increasing inclination. Nevertheless the exponential fit is a good
representation of the simulated brightness distribution. The above mentioned
asymmetry
due to dust scattering is especially prominent at high inclination in
the cuts perpendicular to the major axis (bottom right panel of Fig. 2).
.
Due to the central opacity the disk models are somewhat rounder in the
centre than the corresponding exponential fits. This effect is reflected
in the central cusp of the residuum (solid bottom line) and increases with
increasing inclination. Nevertheless the exponential fit is a good
representation of the simulated brightness distribution. The above mentioned
asymmetry
due to dust scattering is especially prominent at high inclination in
the cuts perpendicular to the major axis (bottom right panel of Fig. 2).
![\begin{figure}
\par\mbox{\includegraphics[width=4cm,clip]{4727fig1a.eps} \hspace...
...} \hspace*{0.3cm}
\includegraphics[width=4cm,clip]{4727fig1d.eps} }
\end{figure}](/articles/aa/full/2006/36/aa4727-05/Timg58.gif) |
Figure 1:
Top: B image of the dusty disk model
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{4727fig2.ps}\end{figure}](/articles/aa/full/2006/36/aa4727-05/Timg59.gif) |
Figure 2:
Behaviour of two-dimensional fits and residua for simulations done
in the B band, for
|
| Open with DEXTER | |
Tables 1 to 5 show the results of the fitting procedure for the
B, V, I, J, and K bands. For each table the first two columns contain
the input parameters inclination i and central face-on central optical
depth in the B band
![]() and the last
four columns
contain the output parameters
and the last
four columns
contain the output parameters
![]() ,
,
![]() /
/![]() ,
,
![]() /
/
![]() (as defined in Sect. 3.1) and
(as defined in Sect. 3.1) and
![]() .
.
![]() is the ratio of the apparent average
central surface brightness F to the intrinsic average
central face-on surface brightness F0, expressed in magnitudes.
Fis an average taken over an elliptical aperture
is the ratio of the apparent average
central surface brightness F to the intrinsic average
central face-on surface brightness F0, expressed in magnitudes.
Fis an average taken over an elliptical aperture![]() centred on the position of peak
brightness in the simulated dusty image, with a semi-major axis of
centred on the position of peak
brightness in the simulated dusty image, with a semi-major axis of
![]() and an axis ratio of
and an axis ratio of ![]() .
F0 is an average taken over a circular aperture
centred on the position of peak
brightness of the face-on dustless simulated image,
with a radius
.
F0 is an average taken over a circular aperture
centred on the position of peak
brightness of the face-on dustless simulated image,
with a radius
![]() .
.
Here we should mention that the results given here are, as described in
Sect. 3.2, obtained by fixing the coordinates of the centre of the fit to the
position of maximum observed brightness. Other fitting procedures
such as GIM2D (Simard 1998; Marleau & Simard 1999) or GALFIT (Peng et
al. 2002) constrain
the coordinates of the centre from the moments of the two-dimensional
intensity distribution, which result in a small shift along the minor axis
of the fitted centre
for opaque high-inclination disks. The effect of this shift on the derivation
of the central brightness is at most ![]() .
The effect on the derivation of
the scalelength is negligible, since it depends only to second
order on the shift.
.
The effect on the derivation of
the scalelength is negligible, since it depends only to second
order on the shift.
In the following subsections we describe the general behaviour of the
structural parameters listed in Tables 1-5 as a function of
![]() ,
i and wavelength.
,
i and wavelength.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{4727fig3.ps}\end{figure}](/articles/aa/full/2006/36/aa4727-05/Timg64.gif) |
Figure 3:
The ratio of the apparent to intrinsic scalelengths
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4727fig4.ps}\end{figure}](/articles/aa/full/2006/36/aa4727-05/Timg66.gif) |
Figure 4:
The ratio of the apparent to intrinsic scalelengths
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{4727fig5.ps}\end{figure}](/articles/aa/full/2006/36/aa4727-05/Timg67.gif) |
Figure 5:
The ratio of the apparent to intrinsic scalelengths
|
| Open with DEXTER | |
In Fig. 3 we show the dependence of
![]() on
on
![]() ,
for different
inclinations and wavelengths. Because disks are always more attenuated in
their central regions than in their outer regions,
,
for different
inclinations and wavelengths. Because disks are always more attenuated in
their central regions than in their outer regions,
![]() is
always greater than unity and increases monotonically with
is
always greater than unity and increases monotonically with
![]() .
In some cases this increase is linear, whereas in others the increase flattens
off towards higher values of
.
In some cases this increase is linear, whereas in others the increase flattens
off towards higher values of
![]() .
The linear behaviour
happens when the disk is optically thin
along the lines of sight towards most of the projected radii. As
.
The linear behaviour
happens when the disk is optically thin
along the lines of sight towards most of the projected radii. As
![]() increases, an increasing area of the inner disk becomes
optically thick, producing a slowing-down in the increase with
increases, an increasing area of the inner disk becomes
optically thick, producing a slowing-down in the increase with
![]() ,
until an asymptote is approached when the disk becomes optically thick
along the lines of sight over the whole extent of the disk. At longer
wavelengths, e.g. in the K band, such an asymptote is never reached and the
behaviour of the curves remains in the linear regime, since
even at the highest
,
until an asymptote is approached when the disk becomes optically thick
along the lines of sight over the whole extent of the disk. At longer
wavelengths, e.g. in the K band, such an asymptote is never reached and the
behaviour of the curves remains in the linear regime, since
even at the highest
![]() and inclinations considered, the disk
remains optically thin along most of the lines of sight. By contrast, at the
shorter wavelengths, for instance in the B band, the asymptote is approached
for high
and inclinations considered, the disk
remains optically thin along most of the lines of sight. By contrast, at the
shorter wavelengths, for instance in the B band, the asymptote is approached
for high
![]() and inclinations, as the disk becomes optically thick
along most of the lines of sight. Furthermore, at these wavelengths the curves
enter the non-linear regime at all inclinations, since some
part of the disk is always optically thick along the line of sight. At
intermediate wavelengths, such as in the I band, the variation with
and inclinations, as the disk becomes optically thick
along most of the lines of sight. Furthermore, at these wavelengths the curves
enter the non-linear regime at all inclinations, since some
part of the disk is always optically thick along the line of sight. At
intermediate wavelengths, such as in the I band, the variation with
![]() remains in the linear regime at lower inclinations, and
only at high inclination is a non-linear behaviour seen, though without getting
near the asymptote. Another consequence of the existence of the
asymptote
is that the curves for different inclinations tend to bunch together at high
remains in the linear regime at lower inclinations, and
only at high inclination is a non-linear behaviour seen, though without getting
near the asymptote. Another consequence of the existence of the
asymptote
is that the curves for different inclinations tend to bunch together at high
![]() and shorter wavelengths, as the asymptote is
approached. Thus, in B, V and I bands, the highest spread between the
curves at different inclinations is reached at intermediate
and shorter wavelengths, as the asymptote is
approached. Thus, in B, V and I bands, the highest spread between the
curves at different inclinations is reached at intermediate
![]() ,
since, by necessity, the curves must also be bunched together at low
,
since, by necessity, the curves must also be bunched together at low
![]() .
In K band the curves never enter the non-linear
regime so the maximum spread happens at the highest
.
In K band the curves never enter the non-linear
regime so the maximum spread happens at the highest
![]() .
.
In Fig. 4 we plot the same information as in Fig. 3, but as the
variation of
![]() with inclination, for different
with inclination, for different
![]() and wavelengths. The curves appear flat when the disk is
either predominantly optically thin at all inclinations (for example in K band at
and wavelengths. The curves appear flat when the disk is
either predominantly optically thin at all inclinations (for example in K band at
![]() ,
where
,
where
![]() is close to unity)
or when the disk is predominantly optically thick at all inclinations
(for example in B band at
is close to unity)
or when the disk is predominantly optically thick at all inclinations
(for example in B band at
![]() ,
where
,
where
![]() approaches the asymptote of 1.5).
approaches the asymptote of 1.5).
In Fig. 5 we plot
![]() versus wavelength, for
different
versus wavelength, for
different
![]() and inclinations. The variation with wavelength
also shows a transition between a linear behaviour in an optically thin
regime (for
and inclinations. The variation with wavelength
also shows a transition between a linear behaviour in an optically thin
regime (for
![]() )
and a non-linear approach to an
asymptote at
)
and a non-linear approach to an
asymptote at
![]() .
.
In order to see what is the relative change in the scalelength between
different wavelengths just due to the effect of dust, one can look at the
variation of the quantity
![]() with
with
![]() .
As an
example, we plot in Fig. 6 this quantity for the wavelengths B and I. At all
inclinations, the curves show a similar basic shape. The curves rise steeply at
low
.
As an
example, we plot in Fig. 6 this quantity for the wavelengths B and I. At all
inclinations, the curves show a similar basic shape. The curves rise steeply at
low
![]() ,
reach a maximum and then decline slowly. This
behaviour is compressed over a smaller range of
,
reach a maximum and then decline slowly. This
behaviour is compressed over a smaller range of
![]() for higher
inclinations. Because of this,
for higher
inclinations. Because of this,
![]() increases with inclination at low
increases with inclination at low
![]() ,
but decreases with inclination at high
,
but decreases with inclination at high
![]() ,
with the curves crossing at intermediate
,
with the curves crossing at intermediate
![]() .
In other
words, for a low
.
In other
words, for a low
![]() ,
in order to convert the ratio between
the apparent scalelength in B and I to the corresponding intrinsic ratio, one
needs to apply a correction factor which is larger for high inclinations than
for low inclinations, whereas at high
,
in order to convert the ratio between
the apparent scalelength in B and I to the corresponding intrinsic ratio, one
needs to apply a correction factor which is larger for high inclinations than
for low inclinations, whereas at high
![]() the opposite
is true. An interesting feature of these curves is that they are relatively
flat for
the opposite
is true. An interesting feature of these curves is that they are relatively
flat for
![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4727fig6.ps}\end{figure}](/articles/aa/full/2006/36/aa4727-05/Timg73.gif) |
Figure 6:
The change in the ratio of the scalelengths in B and I bands due
to the effects of dust, plotted as
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4727fig7.ps}\end{figure}](/articles/aa/full/2006/36/aa4727-05/Timg74.gif) |
Figure 7:
Comparison between the apparent ratios of scalelength in B and I predicted by our work (solid lines) and by the work of Cunow et al. (2001)
(dashed lines).
The curves are for
|
| Open with DEXTER | |
Simulations of the observed ratios of scalelength in B and I as a function of
inclination and
![]() have also been performed by Cunow et
al. (2001). The closest comparison possible is that with model (k) of Cunow,
which differs from our model only through the absence of the dust disk
associated with the young stellar population. In Fig. 7 we have plotted the
ratios of apparent scalelength in B and I as a function of apparent ellipticity
(1-b/a) for both our model and the model from Fig. 7 of Cunow et al. (2001),
where the ratios from Cunow have been interpolated to match the opacities
given in our tables. Overall the curves of Cunow behave as if their model is
more optically thin for the same
have also been performed by Cunow et
al. (2001). The closest comparison possible is that with model (k) of Cunow,
which differs from our model only through the absence of the dust disk
associated with the young stellar population. In Fig. 7 we have plotted the
ratios of apparent scalelength in B and I as a function of apparent ellipticity
(1-b/a) for both our model and the model from Fig. 7 of Cunow et al. (2001),
where the ratios from Cunow have been interpolated to match the opacities
given in our tables. Overall the curves of Cunow behave as if their model is
more optically thin for the same
![]() ,
which is the opposite
behaviour one would expect from the differences in the geometrical
distributions between the models. However the procedure to derive scalelength
followed by Cunow et al. only uses data from the outer parts of the disk having
a linear profile, whereas our method uses data from the whole disk. This
obviously biases the results from Cunow towards more optically thin solutions
and this effect dominates over the differences induced by the different
geometrical distributions.
,
which is the opposite
behaviour one would expect from the differences in the geometrical
distributions between the models. However the procedure to derive scalelength
followed by Cunow et al. only uses data from the outer parts of the disk having
a linear profile, whereas our method uses data from the whole disk. This
obviously biases the results from Cunow towards more optically thin solutions
and this effect dominates over the differences induced by the different
geometrical distributions.
Another work on predicting apparent scalelength ratios between B and I is that of Byun et al. (1994). These results are very similar to those of Cunow et al. (2001) (see Fig. 8 of Cunow et al.), which may reflect the fact that Byun et al. also use extrapolation from the outer disk in deriving photometric parameters.
In Fig. 8 we show the dependence of
![]() on
on
![]() ,
for
different inclinations and wavelengths.
An interesting feature of these curves is that they pass through both positive
and negative values of
,
for
different inclinations and wavelengths.
An interesting feature of these curves is that they pass through both positive
and negative values of
![]() :
the centre of the disk can appear either
dimmer or brighter than the face-on dustless disk. This is because the
projected surface density of stars visible along the line of sight can be
either greater or smaller than the surface density of stars seen towards the
centre of a face-on dustless disk. The projected surface density of stars can
be increased by viewing the disk at higher inclinations and can be decreased by
attenuating the stellar light with dust. In the K band the central part of the
disk appears brighter than the centre of the face-on dustless disk at
almost all inclinations and
:
the centre of the disk can appear either
dimmer or brighter than the face-on dustless disk. This is because the
projected surface density of stars visible along the line of sight can be
either greater or smaller than the surface density of stars seen towards the
centre of a face-on dustless disk. The projected surface density of stars can
be increased by viewing the disk at higher inclinations and can be decreased by
attenuating the stellar light with dust. In the K band the central part of the
disk appears brighter than the centre of the face-on dustless disk at
almost all inclinations and
![]() ,
because the line of sight
through the centre is almost always transparent. On the contrary, in the B band
the opposite is true, since the line of sight through the centre is almost
always opaque.
,
because the line of sight
through the centre is almost always transparent. On the contrary, in the B band
the opposite is true, since the line of sight through the centre is almost
always opaque.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4727fig8.ps}\end{figure}](/articles/aa/full/2006/36/aa4727-05/Timg75.gif) |
Figure 8:
The ratio of the apparent average central surface brightness to
the intrinsic average central face-on surface brightness expressed in
magnitudes,
|
| Open with DEXTER | |
The form of the curves in Fig. 8 can be explained in terms of the two
competing factors viewing angle and opacity:
the brightening of the
![]() with increasing inclination
and the dimming of the
with increasing inclination
and the dimming of the
![]() with increasing
with increasing
![]() .
The former effect is
independent of wavelength, since the line of sight of stars is always the same
for a certain inclination
.
The former effect is
independent of wavelength, since the line of sight of stars is always the same
for a certain inclination![]() This can be seen
from the wavelength independence of the spread in
This can be seen
from the wavelength independence of the spread in
![]() from 0 to -1 mag for
from 0 to -1 mag for
![]() .
The latter effect (the dimming due to
opacity) is strongly dependent
on wavelength, since, for a certain
.
The latter effect (the dimming due to
opacity) is strongly dependent
on wavelength, since, for a certain
![]() ,
the depth into
which stars can be seen along the line of sight decreases withdecreasing
wavelength. The dimming of
,
the depth into
which stars can be seen along the line of sight decreases withdecreasing
wavelength. The dimming of
![]() with increasing
with increasing
![]() is almost negligible in the K band at inclinations
close to face-on, when the line of sight through the centre is almost
transparent. On the contrary, in the B band this effect becomes strong at all inclinations.
is almost negligible in the K band at inclinations
close to face-on, when the line of sight through the centre is almost
transparent. On the contrary, in the B band this effect becomes strong at all inclinations.
Another feature of these curves is the transition between a linear dependence
of
![]() on
on
![]() when the lines of sight through the
centre are optically thin (e.g. in the K band at all inclinations), to a
non-linear regime for optically thick lines of sight (e.g. in the B band at
all
inclinations). At intermediate wavelengths (e.g. in the J band) one sees a
transition between these two regimes: the upper curves (close to face-on) are
in the linear regime, whereas the lower curves (high inclinations) are
non-linear.
when the lines of sight through the
centre are optically thin (e.g. in the K band at all inclinations), to a
non-linear regime for optically thick lines of sight (e.g. in the B band at
all
inclinations). At intermediate wavelengths (e.g. in the J band) one sees a
transition between these two regimes: the upper curves (close to face-on) are
in the linear regime, whereas the lower curves (high inclinations) are
non-linear.
For a given (non-zero)
![]() ,
the dispersion between the
curves in Fig. 8 for low and high inclinations varies systematically with
wavelength. For the case of
,
the dispersion between the
curves in Fig. 8 for low and high inclinations varies systematically with
wavelength. For the case of
![]() one can see that the
dispersion has a maximum in the K band, then it decreases towards I band, after
which it increases again towards B band. At first glance this behaviour is not
very intuitive. If the stars and dust had an
identical distribution, then one
would expect a monotonic decrease in dispersion when moving from
transparent central disks to opaque central disks, until the lines of
sight would become completely opaque at all inclinations and the
dispersion would tend to zero (since the brightness of an optically thick
body is independent of the viewing angle). The fact that the behaviour is
more complex than this is a consequence of the non-identical distribution of
stars and dust in the vertical direction. In our model the stars and
dust are distributed in exponential disks, with the stars having
scaleheights larger than those of the dust. As already remarked by Disney et
al. (1989), "even in a highly obscured galaxy, the upper layers of unobscured
stars will apparently increase its mean surface brightness as it is
inclined, mimicking the behaviour of an optically thin system''. Thus, at the
extreme of very high
optical depth one approaches the same dispersion as for the very low optical
depth,
since the variation in the surface brightness between low and high inclination
is only produced by the stars above the (exponential) dust layer.
At intermediate optical depths the dispersion over inclination is lower,
because a larger fraction of this dispersion comes from stars well mixed
with the dust which have a smaller variation in the surface brightness
between low and high inclination. In our model, there will always be an
increase in the surface brightness with increasing inclination, even for
optically thick disks. This can be seen even better in Fig. 9, where we plot
the same information as in Fig. 8, but as the variation of
one can see that the
dispersion has a maximum in the K band, then it decreases towards I band, after
which it increases again towards B band. At first glance this behaviour is not
very intuitive. If the stars and dust had an
identical distribution, then one
would expect a monotonic decrease in dispersion when moving from
transparent central disks to opaque central disks, until the lines of
sight would become completely opaque at all inclinations and the
dispersion would tend to zero (since the brightness of an optically thick
body is independent of the viewing angle). The fact that the behaviour is
more complex than this is a consequence of the non-identical distribution of
stars and dust in the vertical direction. In our model the stars and
dust are distributed in exponential disks, with the stars having
scaleheights larger than those of the dust. As already remarked by Disney et
al. (1989), "even in a highly obscured galaxy, the upper layers of unobscured
stars will apparently increase its mean surface brightness as it is
inclined, mimicking the behaviour of an optically thin system''. Thus, at the
extreme of very high
optical depth one approaches the same dispersion as for the very low optical
depth,
since the variation in the surface brightness between low and high inclination
is only produced by the stars above the (exponential) dust layer.
At intermediate optical depths the dispersion over inclination is lower,
because a larger fraction of this dispersion comes from stars well mixed
with the dust which have a smaller variation in the surface brightness
between low and high inclination. In our model, there will always be an
increase in the surface brightness with increasing inclination, even for
optically thick disks. This can be seen even better in Fig. 9, where we plot
the same information as in Fig. 8, but as the variation of
![]() with
inclination, for different
with
inclination, for different
![]() and wavelengths. We also
plotted the variation
and wavelengths. We also
plotted the variation
![]() with wavelength (Fig. 10), for
different
with wavelength (Fig. 10), for
different
![]() and inclinations, to better capture the
transition between the almost independence of
and inclinations, to better capture the
transition between the almost independence of
![]() on wavelength at
low
on wavelength at
low
![]() to a strong dependence on wavelength at high
to a strong dependence on wavelength at high
![]() .
In order to see what is the change in the central colour of the disk due to
dust, one can look at the variation of
.
In order to see what is the change in the central colour of the disk due to
dust, one can look at the variation of
![]() with
with
![]() .
As for the analogous plot for the variation of scalelength, we plot in
Fig. 11 this quantity for the wavebands B and I,
.
As for the analogous plot for the variation of scalelength, we plot in
Fig. 11 this quantity for the wavebands B and I,
![]() ,
which is equivalent to a plot of
,
which is equivalent to a plot of
![]() shifted by a constant value,
such that the curves go through the origin. These curves, therefore, give the
colour correction that needs to be applied to correct apparent colour to
intrinsic colour at the centre of the disk. The curves show the same
qualitative behaviour as those for the relative change in scalelength, namely
that they rise steeply at
low
shifted by a constant value,
such that the curves go through the origin. These curves, therefore, give the
colour correction that needs to be applied to correct apparent colour to
intrinsic colour at the centre of the disk. The curves show the same
qualitative behaviour as those for the relative change in scalelength, namely
that they rise steeply at
low
![]() ,
reach a maximum and then decline slowly.
We note again the relatively flat behaviour of the curves for
,
reach a maximum and then decline slowly.
We note again the relatively flat behaviour of the curves for
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{4727fig9.ps}\end{figure}](/articles/aa/full/2006/36/aa4727-05/Timg82.gif) |
Figure 9:
The ratio of the apparent average central surface brightness to
the intrinsic average central face-on surface brightness expressed in
magnitudes,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4727fig10.ps}\end{figure}](/articles/aa/full/2006/36/aa4727-05/Timg83.gif) |
Figure 10:
The ratio of the apparent average central surface brightness to
the intrinsic average central face-on surface brightness expressed in
magnitudes,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4727fig11.ps}\end{figure}](/articles/aa/full/2006/36/aa4727-05/Timg84.gif) |
Figure 11:
The change in the B-I central colour due to the effects of dust,
plotted as
|
| Open with DEXTER | |
In Fig. 12 we show the dependence of the ratio of the apparent to the intrinsic
axis ratio,
![]() /Q0 on
/Q0 on
![]() ,
for different
inclinations and wavelengths. One can see that this ratio can be either greater
or less than one, which means that the galaxy can appear less or more inclined
than it is in reality. In other words the galaxy can appear rounder or
flatter than the shape of an infinitely thin dustless disk at the true
inclination of the galaxy.
This behaviour is attributed to two effects that act in the opposite sense.
Firstly, the vertical distribution of stars makes the galaxy appear rounder
than an infinitely thin dustless disk. Secondly,
the presence of dust makes the galaxy appear flatter than an infinitely thin
dustless disk. The first effect is obvious, but the second needs some
explaining. As one increases the line of sight optical depth, either by
increasing the inclination or the
,
for different
inclinations and wavelengths. One can see that this ratio can be either greater
or less than one, which means that the galaxy can appear less or more inclined
than it is in reality. In other words the galaxy can appear rounder or
flatter than the shape of an infinitely thin dustless disk at the true
inclination of the galaxy.
This behaviour is attributed to two effects that act in the opposite sense.
Firstly, the vertical distribution of stars makes the galaxy appear rounder
than an infinitely thin dustless disk. Secondly,
the presence of dust makes the galaxy appear flatter than an infinitely thin
dustless disk. The first effect is obvious, but the second needs some
explaining. As one increases the line of sight optical depth, either by
increasing the inclination or the
![]() ,
the
observed light becomes dominated by photons originating
from an increasingly thin stellar layer on the side of the dust disk nearest to
the observer, due to absorption by dust of photons originating
from below this layer.
,
the
observed light becomes dominated by photons originating
from an increasingly thin stellar layer on the side of the dust disk nearest to
the observer, due to absorption by dust of photons originating
from below this layer.
The effect of the vertical distribution of stars is best seen by looking at the
inclination dependence of
![]() /Q0 for
/Q0 for
![]() close to
zero. For example in the K band,
close to
zero. For example in the K band,
![]() /Q0 increases monotonically with
inclination up to
/Q0 increases monotonically with
inclination up to ![]() 1.13 for
1.13 for
![]() .
.
The effect of opacity is more complex. One feature is the decrease of
![]() /Q0 with increasing
/Q0 with increasing
![]() ,
for all inclinations
and wavelengths. This effect is weak in the K band where opacity is small, and
is strong in the B band where opacity is large. A further aspect
of the effect of dust is that at high opacity, and except for inclinations
near to edge-on, the dependence of
,
for all inclinations
and wavelengths. This effect is weak in the K band where opacity is small, and
is strong in the B band where opacity is large. A further aspect
of the effect of dust is that at high opacity, and except for inclinations
near to edge-on, the dependence of
![]() /Q0 on inclination is
the opposite of that predicted by the model at low opacity. Thus, in B-band at
/Q0 on inclination is
the opposite of that predicted by the model at low opacity. Thus, in B-band at
![]() ,
the general trend is for
,
the general trend is for
![]() /Q0 to
decrease with increasing inclination
/Q0 to
decrease with increasing inclination![]() over the range i=0 to i=66,
as one progressively sees a
thinner and thinner layer of stars above the dust layer, making the galaxy
appear flatter with increasing inclination.
Suddenly, at i=73,
this trend is reversed, as one starts to see stars both above and below the
dust layer, and a big step is made to a rounder shape. The different behaviour
of
over the range i=0 to i=66,
as one progressively sees a
thinner and thinner layer of stars above the dust layer, making the galaxy
appear flatter with increasing inclination.
Suddenly, at i=73,
this trend is reversed, as one starts to see stars both above and below the
dust layer, and a big step is made to a rounder shape. The different behaviour
of
![]() /Q0 on inclination at low and high
/Q0 on inclination at low and high
![]() means that the curves cross at intermediate
means that the curves cross at intermediate
![]() .
.
Having established the dependence on inclination, face-on opacity and wavelength of the corrections needed to convert the apparent photometric parameters scalelength, central surface brightness and axis ratios into the corresponding intrinsic quantities, we can now discuss the implications of these findings. But before doing this, we caution that the corrections given in this paper are valid only for disk-dominated galaxies. In reality, many galaxies have prominent bulges and therefore the apparent photometric parameters of the disk (including scalelength, central surface brightness and total magnitudes) have to be found in a simultaneous fit of geometrical functions for the bulge and the disk. However, the apparent photometric parameters derived from this bulge-to-disk decomposition will be a function of both opacity and bulge-to-disk ratio. In other words, the apparent scalelength and central surface brightness that one derives for a disk galaxy with a given opacity and inclination in the presence of a bulge will in general be different from the apparent scalelength that one derives for the same disk (with the same opacity and inclination) without a bulge. Therefore one should restrict the analysis to galaxies having small bulges, where such effects can be ignored.
One should also caution that the corrections for dust given in
this paper are calculated assuming a small wavelength dependence of the ratio
of the intrinsic scalelength of the stars to that of the dust, as specified
in Tuffs et al. (2004). Thus, strictly speaking, the tabulated corrections
are valid only for this geometry. In practice, however, these corrections can
be used also for systems having a different variation in the ratio of the
intrinsic scalelengths. Comparison
between Figs. 7b and h from Cunow et al. (2001) show that, if one were to make
an error of ![]() in the assumed intrinsic scalelength of stars relative to
the dust, the corresponding error in the effect of dust would be at most a
few percent for typical opacities and inclinations less than
in the assumed intrinsic scalelength of stars relative to
the dust, the corresponding error in the effect of dust would be at most a
few percent for typical opacities and inclinations less than
![]() .
Only
for
.
Only
for
![]() and inclination greater than
and inclination greater than
![]() does the error exceed
does the error exceed ![]() .
.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{4727fig12.ps}\end{figure}](/articles/aa/full/2006/36/aa4727-05/Timg90.gif) |
Figure 12:
The ratio of the apparent to intrinsic axis ratio
|
| Open with DEXTER | |
After these words of caution we can now examine the impact of these new results on our ability to derive quantities of astrophysical interest from optical observations of disk-dominated galaxies. In principle, if one knew the face-on opacity, one could use the correction factors to analyse the intrinsic properties of galaxies on an object to object basis. In practice, however, the face-on opacity of an individual galaxy can only be reliably determined by self-consistently modelling its combined UV/optical/FIR/submm output, which is at present only rarely possible, since the vast majority of galaxies has not yet been measured in the FIR/submm regime. For large statistical samples, though, one can derive a characteristic value for the face-on opacity of a population of systems from the optical measurements themselves by analysing the inclination dependence of the photometric parameters described here.
One can also use our tabulated corrections for the investigation of
astrophysical effects for which, although the absolute effect of dust is
non-negligible,
the predicted variation over a likely range in opacity is relatively small,
such that
an exact knowledge of opacity is not needed. An example is the variation of the
scalelength between B and I due to dust, which is small, provided
that
![]() (galaxies are not too
optically thin)
(galaxies are not too
optically thin)![]() .
Indeed, inspection of Fig. 6 shows that for a galaxy at a typical
inclination of
.
Indeed, inspection of Fig. 6 shows that for a galaxy at a typical
inclination of
![]() and having any
and having any
![]() ,
the effect of dust is to increase the
scalelength in B relative to that in I by a factor of
,
the effect of dust is to increase the
scalelength in B relative to that in I by a factor of
![]() .
The
scatter in this ratio is so small that one can compare the intrinsic
scalelength of the stellar populations in B and I by simply applying a
single correction factor for dust for any spiral galaxy at this
inclination. Similarly, other correction factors can be derived from our tables
for other inclinations and other waveband combinations.
.
The
scatter in this ratio is so small that one can compare the intrinsic
scalelength of the stellar populations in B and I by simply applying a
single correction factor for dust for any spiral galaxy at this
inclination. Similarly, other correction factors can be derived from our tables
for other inclinations and other waveband combinations.
Correspondingly, one can also compare the surface brightnesses between B and I to get
information about the intrinsic colour of the central and most dust affected
regions of the disks, even without detailed knowledge of
![]() .
Inspection of Fig. 11 shows that for a galaxy at an
inclination of
.
Inspection of Fig. 11 shows that for a galaxy at an
inclination of
![]() and for
and for
![]() ,
the change in B-Icentral colour due to dust is
,
the change in B-Icentral colour due to dust is
![]() mag. Again, the scatter in
the central colour is small enough that one can look at the intrinsic central
colour between B and I by simply applying a single correction factor for dust
for any spiral galaxy at this inclination.
mag. Again, the scatter in
the central colour is small enough that one can look at the intrinsic central
colour between B and I by simply applying a single correction factor for dust
for any spiral galaxy at this inclination.
Lack of knowledge of opacity may be somewhat more problematic when one
attempts to compare the properties of dusty galaxies in the local and distant
universe at a fixed restwavelength.
When studying the evolution of disk sizes with redshift (e.g. by comparing
the scalelength of low (![]() )
and high (
)
and high (![]() )
redshifted galaxies
at a common restwavelength)
one must correct for the increase in the apparent disk scalelength with
increasing redshift, stemming from the expected increase in opacity.
If, for example, the opacity increased from 4 at z=0 to 8 or more at
z=1, the apparent scalelength in the B band of a galaxy seen at
)
redshifted galaxies
at a common restwavelength)
one must correct for the increase in the apparent disk scalelength with
increasing redshift, stemming from the expected increase in opacity.
If, for example, the opacity increased from 4 at z=0 to 8 or more at
z=1, the apparent scalelength in the B band of a galaxy seen at
![]() would increase by a factor of at least 1.10 due to dust.
This factor would rise to at least 1.24 for an increase in opacity from 2
to 8 or more. The increase in the apparent scalelength with increasing
redshift due to the
effect of dust goes in the opposite direction to the
predicted evolution in intrinsic disk size, and in general would need to
be taken into account in quantitative analyses. Ultimately one would
need to refine the technique to
take into account the possible evolution of the dust/star geometry
would increase by a factor of at least 1.10 due to dust.
This factor would rise to at least 1.24 for an increase in opacity from 2
to 8 or more. The increase in the apparent scalelength with increasing
redshift due to the
effect of dust goes in the opposite direction to the
predicted evolution in intrinsic disk size, and in general would need to
be taken into account in quantitative analyses. Ultimately one would
need to refine the technique to
take into account the possible evolution of the dust/star geometry![]() when making
corrections for high-redshifted galaxies. This will become possible when
spatially resolved dust emission data from the rest-frame far-infrared is
available for such systems, thereby permitting an analysis of the
star/dust geometry to be performed analogous to that performed for local
universe galaxies.
when making
corrections for high-redshifted galaxies. This will become possible when
spatially resolved dust emission data from the rest-frame far-infrared is
available for such systems, thereby permitting an analysis of the
star/dust geometry to be performed analogous to that performed for local
universe galaxies.
Our tabulated corrections for dust will also allow the analysis of the
correlation between the central face-on surface brightness versus scalelength,
as investigated by Graham (2001) in the K band where the galaxies are optically
thin, to be extended to the shorter wavebands where the galaxies may be
optically thick. As a by-product of such an investigation, we note that one
could obtain a statistical determination of
![]() from the
inclination dependence of both central surface-brightness and scalelength.
As previously cautioned, however, this analysis has for the moment to be
restricted to disk-dominated galaxies.
from the
inclination dependence of both central surface-brightness and scalelength.
As previously cautioned, however, this analysis has for the moment to be
restricted to disk-dominated galaxies.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4727fig13.ps}\end{figure}](/articles/aa/full/2006/36/aa4727-05/Timg95.gif) |
Figure 13:
Observed scalelength ratios between B and I,
|
| Open with DEXTER | |
As mentioned in the introduction, one of the motivations of this work is to
quantify the change in the intrinsic scalelength of different stellar
populations in local universe disk galaxies. Here we give an example of the
application of our model to such an
investigation. For this we used published apparent disk scalelengths in
B and I, restricting the data to galaxies which have measured bulge-to-disk
ratios of less than 0.2. There are
two reasons for this selection criterion. Firstly, as mentioned in the
discussion, one needs to restrict the analysis to disks with small
bulges, since the apparent scalelength derived for dusty disks with large
bulges will diverge from the apparent scalelength of pure
dusty disks.
Secondly, for systems with small bulges MacArthur et al. (2003) showed that
results from one-dimensional
photometry are equivalent to those derived from two-dimensional fits (as
required by this work). The
resulting sample is comprised of 61 galaxies taken
from Möllenhoff (2004), MacArthur et al. (2003), Prieto et al. (2001) and
Pompei & Natali (1997). Since MacArthur et al. had measurements in B V R H,
their R band scalelengths were converted to I band scalelengths
by multiplying them by a factor of 0.981. This factor was obtained by linearly
interpolating between the average scalelength in R and H, as given in Table 3
of MacArthur et al.
Despite our selection of disk-dominated galaxies and the known tendency
of such
systems to preferentially populate the intermediate- and low-mass end of the
mass distribution of nearby, late-type galaxies (e.g. Pierini & Tuffs 1999),
the galaxies used in this sample are all bright spiral galaxies with absolute
magnitudes
![]() to -22.3. Thus they have geometries of stars
and dust appropriate to giant spirals, which are well described by our model.
to -22.3. Thus they have geometries of stars
and dust appropriate to giant spirals, which are well described by our model.
In Fig. 13 we plot observed scalelength ratios between B and I,
![]() ,
versus axis ratios 1-b/a.
All but three of the 61 data points lie above unity, which means that almost
all galaxies have apparent scalelengths which are larger in B than in I. The
data also show a scatter, which is consistent with the
random errors estimated for the measurements
,
versus axis ratios 1-b/a.
All but three of the 61 data points lie above unity, which means that almost
all galaxies have apparent scalelengths which are larger in B than in I. The
data also show a scatter, which is consistent with the
random errors estimated for the measurements![]() .
The mean and the standard deviation in
.
The mean and the standard deviation in
![]() is 1.156 and 0.094, respectively.
In order to see whether these observed values can be accounted
for by the effect of dust alone, we compare them with model predictions for
is 1.156 and 0.094, respectively.
In order to see whether these observed values can be accounted
for by the effect of dust alone, we compare them with model predictions for
![]() (see Fig. 13) which is a reasonable range in
(see Fig. 13) which is a reasonable range in
![]() to expect for
disk galaxies.
For each of the model predictions we calculated the corresponding ratio of intrinsic scalelengths at B and Iwhich best fit the data by shifting the lines vertically in the figure
until an equal number of data points appeared above and below the line.
This process yielded
average ratios of intrinsic scalelengths
of 1.057, 1.019 and 1.037, for
to expect for
disk galaxies.
For each of the model predictions we calculated the corresponding ratio of intrinsic scalelengths at B and Iwhich best fit the data by shifting the lines vertically in the figure
until an equal number of data points appeared above and below the line.
This process yielded
average ratios of intrinsic scalelengths
of 1.057, 1.019 and 1.037, for
![]() ,
respectively,
and an overall range (
,
respectively,
and an overall range (
![]() for the sample) of intrinsic scalelength
ratios from 0.93 to 1.15. Because the deviation from unity of the averaged
ratios is so much less than the spread in the individual data points, we
conclude that, on average, and within the available
statistics,
there is almost no systematic increase in the intrinsic scalelength
with decreasing wavelength and that the observed predominance of
galaxies with ratios of apparent scalelengths greater than unity is mainly
due to the effects of dust. The data would only admit a small
variation of the intrinsic stellar scalelength between B and I (less than 1.15)
if
for the sample) of intrinsic scalelength
ratios from 0.93 to 1.15. Because the deviation from unity of the averaged
ratios is so much less than the spread in the individual data points, we
conclude that, on average, and within the available
statistics,
there is almost no systematic increase in the intrinsic scalelength
with decreasing wavelength and that the observed predominance of
galaxies with ratios of apparent scalelengths greater than unity is mainly
due to the effects of dust. The data would only admit a small
variation of the intrinsic stellar scalelength between B and I (less than 1.15)
if
![]() .
However combined analysis of the UV/optical and
FIR/submm have generally yielded
.
However combined analysis of the UV/optical and
FIR/submm have generally yielded
![]() (Bianchi et al. 2000b; Papers I, II; Misiriotis et al. 2004; Meijerink et al. 2005).
(Bianchi et al. 2000b; Papers I, II; Misiriotis et al. 2004; Meijerink et al. 2005).
Much bigger statistical samples will be needed
to measure systematic trends in intrinsic scalelengths with wavelength,
if they exist. Finally we note that the scatter in the observed ratio of
scalelengths between B and I (with
![]() )
is comparable to the
estimated errors in this quantity for individual galaxies and can therefore
primarily be ascribed to measurement errors.
)
is comparable to the
estimated errors in this quantity for individual galaxies and can therefore
primarily be ascribed to measurement errors.
Our conclusion that dust is mainly responsible for the larger scalelength observed in the B band compared to I band can be contrasted with the results from Cunow (2001, 2004), who deduced that dust alone was not sufficient to explain this effect. Here we note that the different conclusions can primarily be attributed to differences in the data rather than differences in the model. In fact, as noted by Cunow (2004), her data for normal galaxies, both in terms of the absolute values of the scalelength ratios and the variation of these ratios with inclination, cannot be fitted by any model. As shown in Fig. 13, our data is reasonably well fitted by our model in both these respects.
Another study in the literature that has addressed the wavelength dependence of scalelength (this time between B and K bands) is that of Peletier et al. (1994). Here again, on average, the scalelength ratios have much larger values than in our sample, even taken into account the different wavelength used. Although Peletier et al. interpreted their results as being due to the effect of dust on the apparent scalelengths, such large effects are not predicted by any dust model. Bearing in mind the inclusion of galaxies with bulges in the sample of Peletier et al., such effects are, in our view, more likely to be produced by the effect of dust on the bulge-disk decomposition itself. This is because the use of simple templates for dustless bulge and disk in bulge-disk decomposition would lead to systematic bias in the derived photometric parameters, including apparent disk scalelength.
The apparent to intrinsic scalelength ratio is always greater than unity and
can vary up to 50![]() .
The apparent to intrinsic central surface-brightness
ratio expressed in magnitudes can be either positive or negative, depending on
whether the dimming due to dust is more or less important than the brightening
due to the increase in the column density of stars induced by inclining the
disk. This ratio can change up to 1.5 mag due to the effect of dust.
The ratio of the apparent to intrinsic axis ratio is not strongly affected by
dust, but has an opposite dependence on inclination according to whether the
lines of sight through the disk are predominantly optically thin or optically
thick. In the former case the vertical distribution of stars makes the galaxy
appear progressively rounder with increasing inclination than an infinitely
thin disk, whereas in the latter case the opposite trend is seen, because an
increasing proportion of the
observed light originates from a thin layer of stars above the dust.
.
The apparent to intrinsic central surface-brightness
ratio expressed in magnitudes can be either positive or negative, depending on
whether the dimming due to dust is more or less important than the brightening
due to the increase in the column density of stars induced by inclining the
disk. This ratio can change up to 1.5 mag due to the effect of dust.
The ratio of the apparent to intrinsic axis ratio is not strongly affected by
dust, but has an opposite dependence on inclination according to whether the
lines of sight through the disk are predominantly optically thin or optically
thick. In the former case the vertical distribution of stars makes the galaxy
appear progressively rounder with increasing inclination than an infinitely
thin disk, whereas in the latter case the opposite trend is seen, because an
increasing proportion of the
observed light originates from a thin layer of stars above the dust.
Assuming that the basic geometry of dust and stars in local universe
spiral galaxies also applies for higher redshift spiral galaxies, our
tabulated corrections can be used to correct for the increase in the
apparent disk scalelength with increasing redshift due to the expected
increase in opacity. This will allow the intrinsic evolution of
disk sizes with cosmological epoch to be investigated. As an example, we show
that for a possible
variation in opacity between 2 at z=0 to 8 or more at
z=1, the apparent scalelength in the B band of a galaxy seen at
![]() would increase by a factor of at least 1.24 due to dust.
would increase by a factor of at least 1.24 due to dust.
We used our model to analyse the distribution of observed scalelength ratios between B and I for a sample of disk-dominated spiral galaxies. We found that the predominance of galaxies with larger apparent scalelength in B than in I is primarily due to the effects of dust.
Acknowledgements
We would like to acknowledge the anonymous referee for his/her perceptive and constructive criticism which helped us to improve the manuscript.
Table 1: Structural parameters of the disks in B.
Table 2: Structural parameters of the disks in V.
Table 3: Structural parameters of the disks in I.
Table 4: Structural parameters of the disks in J.
Table 5: Structural parameters of the disks in K.