- ... wavelengths
![[*]](/icons/foot_motif.gif)
- Tables 1 to 5 are only available in electronic form at http://www.edpsciences.org
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...2005
![[*]](/icons/foot_motif.gif)
- A simplified version of this geometrical prescription
has been applied by Misiriotis et al. (2004) to fit the FIR SEDs of
bright IRAS galaxies.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... dust
![[*]](/icons/foot_motif.gif)
- These corrections are only valid
for normal disk galaxies and are not applicable to systems with different
star/dust geometries such as starburst or dwarf galaxies.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... aperture
![[*]](/icons/foot_motif.gif)
- We give the average surface brightness in an aperture (in addition
to the surface brightness at the centre position of the fitted template)
because in practice the brightness is blurred over a point spread function.
Therefore it is useful to include a reference aperture which is larger than
typical point spread functions, but smaller than the scalelength of the disk.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... inclination
![[*]](/icons/foot_motif.gif)
- Formally there is a very small dependence on
wavelength due to the fact that the scalelength of the stars varies with
wavelength in our model. In practice, however, this effect is negligible over
the range of inclinations considered here and cannot be seen in the plot.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... inclination
![[*]](/icons/foot_motif.gif)
- Within the numerical noise
induced by the finite numbers of directions for which scattered light is
calculated.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... thin)
![[*]](/icons/foot_motif.gif)
- In our detailed SED modelling of
individual galaxies given in Papers I and II we showed that this range in
opacity is quite likely to characterise spiral galaxies.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... geometry
![[*]](/icons/foot_motif.gif)
- For
example, depending on the assumed star-formation history, it may be
necessary to
invoke different star/dust geometries to explain the observed colours of
distant disk galaxies (Pierini et al. 2005).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... measurements
![[*]](/icons/foot_motif.gif)
- The errors of a single scalelength determination
were estimated to be
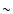 5% in Möllenhoff,
5% in Möllenhoff, 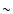 3% in Cunow and
3% in Cunow and
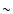 5% in MacArthur et al. Thus the error of the quotients in
Fig. 13 can be estimated to be
5% in MacArthur et al. Thus the error of the quotients in
Fig. 13 can be estimated to be 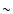 7%. A corresponding error bar is
plotted there.
7%. A corresponding error bar is
plotted there.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.