A&A 456, 1045-1068 (2006)
DOI: 10.1051/0004-6361:20040269
Modeling of PMS Ae/Fe stars using UV spectra![[*]](/icons/foot_motif.gif) ,
,![[*]](/icons/foot_motif.gif)
P. F. C. Blondel1,2 - H. R. E. TjinADjie1
1 - Astronomical Institute "Anton Pannekoek'', University
of Amsterdam, Kruislaan 403, 1098 SJ Amsterdam, The Netherlands
2 - SARA, Kruislaan 415, 1098 SJ Amsterdam, The Netherlands
Received 13 February 2004 / Accepted 13 October 2005
Abstract
Context. Spectral classification of PMS Ae/Fe stars, based on visual observations, may lead to ambiguous conclusions.
Aims. We aim to reduce these ambiguities by using UV spectra for the classification of these stars, because the rise of the continuum in the UV is highly sensitive to the stellar spectral type of A/F-type stars.
Methods. We analyse the low-resolution UV spectra in terms of a 3-component model, that consists of spectra of a central star, of an optically-thick accretion disc, and of a boundary-layer between the disc and star. The disc-component was calculated as a juxtaposition of Planck spectra, while the 2 other components were simulated by the low-resolution UV spectra of well-classified standard stars (taken from the IUE spectral atlases). The hot boundary-layer shows strong similarities to the spectra of late-B type supergiants (see Appendix A).
Results. We modeled the low-resolution UV spectra of 37 PMS Ae/Fe stars. Each spectral match provides 8 model parameters: spectral type and luminosity-class of photosphere and boundary-layer, temperature and width of the boundary-layer, disc-inclination and circumstellar extinction. From the results of these analyses, combined with available theoretical PMS evolutionary tracks, we could estimate their masses and ages and derive their mass-accretion rates. For a number of analysed PMS stars we calculated the corresponding SEDs and compared these with the observed SEDs.
Conclusions. All stars (except 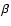 Pic) show indications of accretion, that affect the resulting spectral type of the stellar photosphere. Formerly this led to ambiguities in classificaton of PMS stars as the boundary-layer was not taken into consideration. We give evidence for an increase of the mass-accretion rate with stellar mass and for a decreases of this rate with stellar age.
Pic) show indications of accretion, that affect the resulting spectral type of the stellar photosphere. Formerly this led to ambiguities in classificaton of PMS stars as the boundary-layer was not taken into consideration. We give evidence for an increase of the mass-accretion rate with stellar mass and for a decreases of this rate with stellar age.
Key words: stars: pre-main sequence - accretion, accretion disks
During the past decades it has become clear that low-mass stars
(
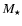 <1.0
<1.0
 )
in their PMS evolutionary stage, known as
"classical'' T Tauri stars (cTTs), are generally surrounded by accretion
discs, which the contraction models of a rotating protostar predict.
This has raised the question of whether more massive stars
(1.0
)
in their PMS evolutionary stage, known as
"classical'' T Tauri stars (cTTs), are generally surrounded by accretion
discs, which the contraction models of a rotating protostar predict.
This has raised the question of whether more massive stars
(1.0
 <
<
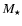 <4.0
<4.0
 )
that radiate strongly in the UV and thus are able to
ionise the infalling material and even reverse the infall of material, have a
similar PMS evolutionary phase, in particular, if Herbig Ae/Be stars also feature
an accretion disc.
)
that radiate strongly in the UV and thus are able to
ionise the infalling material and even reverse the infall of material, have a
similar PMS evolutionary phase, in particular, if Herbig Ae/Be stars also feature
an accretion disc.
Herbig stars are usually intrinsically brighter than T Tauri stars, which
makes them observable at larger distances and larger foreground extinction.
However, because of their higher masses and therefore faster evolution,
they are less numerous than the T Tauri stars.
So far, various indications of matter falling towards a Herbig Ae/Be star have been
found from high-resolution spectroscopy in the visual (Hamann & Persson 1992;
Graham 1992; Tambotseva et al. 2001) and in the UV (Blondel et al. 1993;
Pérez et al. 1993; Brown et al. 1997; TjinADjie et al. 1998; Valenti et al. 2000).
Hillenbrand et al. (1992) have successfully fitted the visual and near-infrared
(NIR) spectral energy distributions (SEDs) of a large sample
of Herbig Ae/Be stars with a model consisting of a stellar photosphere and a flat,
optically-thick accretion disc with an optically-thin circular central hole.
These authors did not include the contribution of an accreting boundary-layer
to the calculated SED.
The larger brightness of the PMS Ae/Fe stars makes it easier to obtain
well-exposed (UV) spectra than for T Tauri stars.
We analysed the low-resolution UV spectra, obtained with IUE in both the
short (SW) and long (LW) wavelength range (Appendix F),
of a sample of PMS Be/Ae/Fe stars
(TWP94) in terms of a 3-component model (UV3C hereafter) that consists of
a star, an accretion disc, and a boundary-layer (BL hereafter), through which
the disc interacts with the star.
The formalism of the model is given in Sect. 2,
and in Sect. 3 we discuss the normalisation and the
extinction corrections needed before we can compare the model spectrum to the
observed spectrum.
In Sect. 4 we describe the procedure for matching the model
spectrum to the observed spectrum and thus of determining the model parameters.
Input values for these parameters were obtained from Appendices B-D and from Table 1.
In this section we also show the sensitivity of the model spectrum to
variations in the various model parameters.
An important result is that in the IUE range the model spectrum receives no
significant direct contributions from the disc component, so that our analysis
only models the photosphere and the BL.
Indirectly, however, the disc plays a role by shadowing the photospheric
contribution, which justifies the use of the name UV3C.
Section 5 presents the results of the UV spectral analysis of
35 PMS Be/Ae/Fe stars and 2 cTTs.
All stars (with the possible exception of 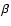 Pic and
Pic and
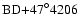 )
are well-known young
emission-line stars.
Our choice of stars is restricted by the availability of low-resolution UV
spectra (both IUE SW and LW).
A second restriction was made based on the quality of the observed spectra,
which eliminates the following 6 stars from Table 1:
WW Vul,
)
are well-known young
emission-line stars.
Our choice of stars is restricted by the availability of low-resolution UV
spectra (both IUE SW and LW).
A second restriction was made based on the quality of the observed spectra,
which eliminates the following 6 stars from Table 1:
WW Vul,
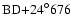 ,
V350 Ori, R CrA, RR Tau, and RY Tau.
The main conclusion from our analysis is that the BL contribution to
the spectra in our sample can be simulated by spectra of type B5 I-A0 I,
most frequently B9 Iab.
In several cases the BL component in the UV spectrum is so strong that it
influences the photometric bands in the near-UV and, therefore, the spectral
classification based on photometry (e.g. NX Pup,
,
V350 Ori, R CrA, RR Tau, and RY Tau.
The main conclusion from our analysis is that the BL contribution to
the spectra in our sample can be simulated by spectra of type B5 I-A0 I,
most frequently B9 Iab.
In several cases the BL component in the UV spectrum is so strong that it
influences the photometric bands in the near-UV and, therefore, the spectral
classification based on photometry (e.g. NX Pup,
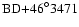 ,
HK Ori, V380 Ori,
and KK Oph).
We also calculated the SEDs of the program stars in the visual and NIR.
Some of these stars - NX Pup, V380 Ori, HK Ori, and HD 139614 - are observed at low
inclinations (almost pole-on), which implies that their BL may also contribute
significantly to the UBV-fluxes.
The presence of this BL contribution may be an important reason why spectral
classifications of the stars based on different distinct features of the
spectrum have led to different spectral types.
,
HK Ori, V380 Ori,
and KK Oph).
We also calculated the SEDs of the program stars in the visual and NIR.
Some of these stars - NX Pup, V380 Ori, HK Ori, and HD 139614 - are observed at low
inclinations (almost pole-on), which implies that their BL may also contribute
significantly to the UBV-fluxes.
The presence of this BL contribution may be an important reason why spectral
classifications of the stars based on different distinct features of the
spectrum have led to different spectral types.
In Sect. 6 we use the UV3C-model parameters to determine the
position of the PMS stars in the HRD and to look for correlations between
the evolutionary status of the star-disc-system, and its mass and c.s.
extinction. And finally in Appendix A we discuss alternative
interpretations of the spectral features of PMS Ae/Fe stars in the UV and compare
our results with those of a few theoretical models.
2 The UV3C-model
Our way of analysing the low-resolution UV spectra of PMS Ae/Fe stars is
similar to that developed by Bertout et al. (1988; BBB88 hereafter) for modeling
the spectra and SEDs of T Tauri stars from the UV to the NIR.
Arguments for the applicability of the model are given and fully discussed in
that paper.
We only summarise the main points.
The UV spectra are analysed in terms of 3 spectral components: a contribution
from the stellar photosphere; a contribution from an extended, geometrically
thin, optically-thick, dusty accretion disc; and a contribution from the hot BL
between the disc and photosphere.
We show that with the parameters determined from IUE spectral analyses we obtain
SEDs that reasonably agree with the photometric data in the visual and NIR,
provided that the photometric V-magnitude is close to the V-magnitude during
the IUE observation.
Eventually, the remaining deviations in the IR regions can be partly removed by
using more sophisticated disc models, but this does not affect the BL
parameters, which are determined from the spectrum shortward of 1800 Å where
the BL component dominates.
The photospheric component gives the spectral distribution of the stellar
photosphere for a given set of parameters (
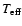 ,
,
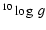 and
and
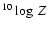 ).
We simulate this component with a de-reddened low-resolution UV spectrum from
the IUE spectral atlases (Appendix G)
because these well-classified spectra have the same resolution as the observed
spectra of the PMS stars.
Comparison with spectra from computed model atmospheres (e.g. Kurucz models,
Kurucz 1979, 1991)
would be more elaborate and less accurate (because these models lack peculiar
absorption lines that may still be unexplained).
After we know the spectral type (ST) and luminosity class (LC) of the
photosphere from the UV classification, we use Kurucz model fluxes to calculate
the photospheric contributions in the visual and NIR photometric bands.
).
We simulate this component with a de-reddened low-resolution UV spectrum from
the IUE spectral atlases (Appendix G)
because these well-classified spectra have the same resolution as the observed
spectra of the PMS stars.
Comparison with spectra from computed model atmospheres (e.g. Kurucz models,
Kurucz 1979, 1991)
would be more elaborate and less accurate (because these models lack peculiar
absorption lines that may still be unexplained).
After we know the spectral type (ST) and luminosity class (LC) of the
photosphere from the UV classification, we use Kurucz model fluxes to calculate
the photospheric contributions in the visual and NIR photometric bands.
Following BBB88 we assume that the disc is a flat, optically-thick, region with
a continuum spectrum that can be simulated by the summation of a sequence of
concentric, isothermal rings with Planck spectra.
The local temperature
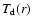 of each ring can be derived from the
sum of the local rate of viscous heating from accretion
of each ring can be derived from the
sum of the local rate of viscous heating from accretion
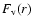 and the local rate of absorption of radiation from the stellar photosphere
and the local rate of absorption of radiation from the stellar photosphere
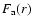 :
:
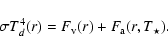 |
(1) |
The absorption from the stellar photosphere
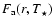 has been evaluated by Adams & Shu (1986):
has been evaluated by Adams & Shu (1986):
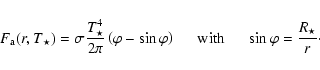 |
(2) |
If in addition the disc is in Kepler rotation and the star rotates slowly, then
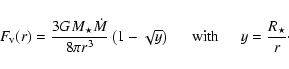 |
(3) |
In this case the integrated dissipated energy in the disc is half of the total
accretion luminosity G
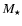

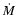 ,
where
,
where
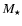 and
and
 are the stellar mass and
radius and
are the stellar mass and
radius and 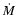 is the accretion rate through the disc (Adams et al. 1987).
The other half of this luminosity is dissipated in the BL, which we assume to be
radiating as an optically-thick ring with radial thickness
is the accretion rate through the disc (Adams et al. 1987).
The other half of this luminosity is dissipated in the BL, which we assume to be
radiating as an optically-thick ring with radial thickness 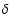 (see Sect. 2.4).
We then can write:
(see Sect. 2.4).
We then can write:
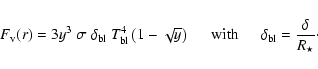 |
(4) |
The flux of each disc ring can now be calculated from Eq. (1)
and the disc contribution is evaluated by integrating over r from
(1+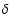 )
to
)
to
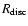 .
.
2.4 The boundary-layer component
Half of the total accretion luminosity G
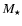

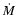 is radiated away by the disc.
The other half of this accretion luminosity is assumed to be spent in heating the
BL, and with BBB88, we assume that the BL is radiating as an annular,
optically-thick layer around the star with radial thickness
is radiated away by the disc.
The other half of this accretion luminosity is assumed to be spent in heating the
BL, and with BBB88, we assume that the BL is radiating as an annular,
optically-thick layer around the star with radial thickness 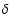 :
:
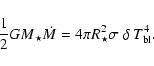 |
(5) |
From an estimate of
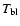 (from spectral shape in SW) and
(from spectral shape in SW) and
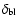 (from the
SW flux), we then can estimate the accretion rate
(from the
SW flux), we then can estimate the accretion rate 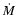 from the stellar mass
from the stellar mass
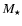 and radius
and radius
 .
For fast rotating stars see Eq. (14) (Sect. 6).
.
For fast rotating stars see Eq. (14) (Sect. 6).
3 The construction of the spectrum
The intrinsic spectra of photosphere and BL of the observed star for given
spectral types and luminosity classes of the components were obtained from the
standard spectra with the corresponding spectral and luminosity classes in the
IUE spectral atlases of Heck & Wu (Table G.6) by dividing their
archived spectral fluxes by the ratio of their de-reddened flux
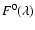 in the Johnson V-band (
in the Johnson V-band ( hereafter) and the flux
at 5500 Å of the Kurucz model (
hereafter) and the flux
at 5500 Å of the Kurucz model (
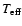 ,
g) for solar abundance and
corresponding ST and LC:
,
g) for solar abundance and
corresponding ST and LC:
where
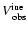 is the observed V-band magnitude of the standard star
with corresponding flux
is the observed V-band magnitude of the standard star
with corresponding flux
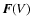 ,
,
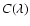 gives the correction
for the foreground extinction of the standard star, and
gives the correction
for the foreground extinction of the standard star, and
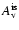 is the
interstellar extinction in
is the
interstellar extinction in  :
:
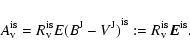 |
(8) |
Equation (7) was derived from the flux calibration of the Johnson
photometric system by Heber et al. (1984).
The intrinsic spectrum of the accretion disc for given
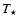 ,
,
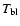 ,
and
,
and
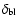 was calculated from Eqs. (1)-(4), using the approximations
of BBB88.
The disc contribution is integrated outward up to 3.5
was calculated from Eqs. (1)-(4), using the approximations
of BBB88.
The disc contribution is integrated outward up to 3.5
 ,
which has proved
to be sufficient for the disc-contribution in the UV.
The disc inclination angle i enters into the contributions of the 3
components; in the photospheric component it is due to shadowing by the disc;
in the BL and disc components it results from screening by the star.
,
which has proved
to be sufficient for the disc-contribution in the UV.
The disc inclination angle i enters into the contributions of the 3
components; in the photospheric component it is due to shadowing by the disc;
in the BL and disc components it results from screening by the star.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{0269f001.ps} %
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg129.gif) |
Figure 1:
From top to bottom: the observed UV spectrum of NX Pup (26-01),
the 3 intrinsic components used in the UV3C model:
F2 III photosphere (HD 89025)
+ B9 Iab BL (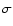 Cyg)
+ disc,
the sum spectrum and the ratio of Calculated/Observed flux.
For each component the flux normalisation factor is shown in the lower right
corner (power of ten).
See Table 2 for the model parameters and also Figs. 2
and 93. Cyg)
+ disc,
the sum spectrum and the ratio of Calculated/Observed flux.
For each component the flux normalisation factor is shown in the lower right
corner (power of ten).
See Table 2 for the model parameters and also Figs. 2
and 93.
|
| Open with DEXTER |
Figure 1 illustrates the 3 intrinsic UV spectral components for
the case of NX Pup, together with their sum and the observed UV spectrum.
The corresponding temperature distribution in the disc is given in
Fig. 2.
In order to compare this intrinsic sum spectrum with the observed UV spectrum,
we have to normalise the intrinsic flux at a chosen wavelength (e.g. 5500 Å)
and to de-redden the intrinsic spectrum with interstellar
extinction, which should give it the observed spectral shape.
![\begin{figure}
\par\includegraphics[angle=270,width=8.4cm,clip]{0269f002.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg130.gif) |
Figure 2:
Temperature distribution of the disc in the UV3C
model (Eq. (1)) for NX Pup as used in Figs. 1 and 93. |
| Open with DEXTER |
If for values of the disc inclination angle (i) (Sect. B.5) and BL
width (
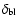 )
(BBB88 Eqs. (5), (9), (11)) we indicate the intrinsic (Kurucz model)
)
(BBB88 Eqs. (5), (9), (11)) we indicate the intrinsic (Kurucz model)
 fluxes of the star, BL and disc by
fluxes of the star, BL and disc by
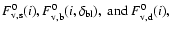 respectively, we can normalise the sum of these fluxes to the "intrinsic
observed flux of the system'': the de-reddened observed flux
(
respectively, we can normalise the sum of these fluxes to the "intrinsic
observed flux of the system'': the de-reddened observed flux
(
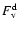 )
in
)
in  (
(
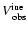 )
after additional
correction for the (yet unknown) circumstellar absorption
)
after additional
correction for the (yet unknown) circumstellar absorption
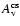 in
in  :
:
where
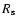 is an (yet unknown) effective radius of the
system (star+BL+disc) and d the distance to the system.
The stellar (photospheric) radius (
is an (yet unknown) effective radius of the
system (star+BL+disc) and d the distance to the system.
The stellar (photospheric) radius (
 )
can be calculated from
the ratio of the expected stellar flux at earth
)
can be calculated from
the ratio of the expected stellar flux at earth
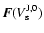 with
with
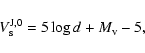 |
(10) |
in which the absolute magnitude  for the star is taken from SK82 for
the chosen ST and LC,
and the intrinsic stellar flux
for the star is taken from SK82 for
the chosen ST and LC,
and the intrinsic stellar flux
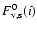 (Eq. (9))
(Eq. (9))
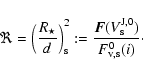 |
(11) |
The circumstellar extinction
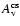 can be determined from
can be determined from
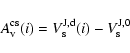 |
(12) |
with
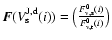
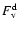 and
and
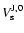 from Eq. (10).
from Eq. (10).
In order to compare the calculated UV3C-model spectrum with the de-reddened
observed spectrum, we need a circumstellar extinction law
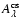 /
/
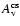 and
the normalisation factor in Eq. (9):
and
the normalisation factor in Eq. (9):
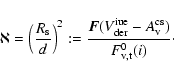 |
(13) |
3.2 Circumstellar extinction
Since little is known about the extinction properties of the circumstellar dust
around PMS Ae/Fe stars, we have assumed that the circumstellar extinction relation
can be approximated by the same analytical expression as obtained by
Cardelli et al. (1988, 1989) for the optical and UV extinction of the
interstellar medium in various directions and parametrized by Eq. (8)
for values of [2.5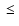
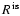
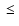 6.5].
For
6.5].
For
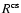 we also use this range
we also use this range![[*]](/icons/foot_motif.gif) .
.
The corresponding extinction curves are shown in Fig. 3.
These extinction laws were not designed for circumstellar dust, but they
generally appear to give satisfactory shapes of the UV3C-model spectra, although
a good comparison of the simulated spectrum with the observed spectrum between
1800 and 2300 Å (where
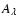 /
/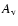 reaches a maximum) is difficult, because of
the high noise level in most of the observed spectra due to the low sensitivity
of the IUE-LW cameras in that interval.
reaches a maximum) is difficult, because of
the high noise level in most of the observed spectra due to the low sensitivity
of the IUE-LW cameras in that interval.
The method of parametrization with circumstellar dust parameters seems supported
by how the large irregular brightness variations for HR 5999 and for
the class of the UXORs![[*]](/icons/foot_motif.gif) correspond to variations in their UV spectra that can be approximated mainly by
variations in
correspond to variations in their UV spectra that can be approximated mainly by
variations in
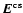 and
and
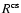 (Tables 3-5).
Deviations in the spectra, which occur for high values of
(Tables 3-5).
Deviations in the spectra, which occur for high values of
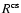 ,
could
be due to the changes in size or orientation of non-spherical circumstellar dust
grains (Sects. 5.2 and 5.6).
,
could
be due to the changes in size or orientation of non-spherical circumstellar dust
grains (Sects. 5.2 and 5.6).
4 The IUE spectral analysis
Table 1:
Observational data of the PMS stars. The spectral classifications based on
different criteria are separated by (/) to distinguish them from the given
spectral ranges (-).
Additional information on the double stars (denoted by in Col. 2) is
given in Table B.1. Uncertain values are indicated with (:).
The foreground colour-excess
 is labelled with (*) if
is labelled with (*) if
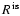
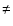 3.1
(Appendix B.4).
The h in Col. 7 denotes Hipparcos values (ESA 1997),
see Appendix C for supplementary information on each star.
Column 9 indicates if Walraven photometry was obtained for the star.
The inclination is indicated with E or P based on the methods (X, Y, Z)
described in Appendices B.5 and D.
3.1
(Appendix B.4).
The h in Col. 7 denotes Hipparcos values (ESA 1997),
see Appendix C for supplementary information on each star.
Column 9 indicates if Walraven photometry was obtained for the star.
The inclination is indicated with E or P based on the methods (X, Y, Z)
described in Appendices B.5 and D.
Table 2:
Data of the analysed stars (Part 1),
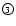 see Table 3,
see Table 3, 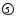 see Table 5.
see Table 5.
In order to match an UV3C model to an observed UV stellar spectrum and the flux
in the photometric  -band during the IUE spectral observation, we may vary 6
parameters:
(1) the ST and LC of the photosphere,
(2) the ST and LC of the BL,
(3) the stellar distance d,
(4) the width
-band during the IUE spectral observation, we may vary 6
parameters:
(1) the ST and LC of the photosphere,
(2) the ST and LC of the BL,
(3) the stellar distance d,
(4) the width 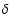 of the BL,
(5) the disc inclination angle i, and
of the BL,
(5) the disc inclination angle i, and
(6)
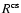 =
=
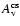 /
/
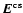 ,
which specifies the extinction law for the
circumstellar dust.
With such a number of parameters we cannot claim to determine these parameters
uniquely from the observed spectrum.
However, the various parameters fortunately have different effects on specific
wavelength regions in the calculated spectrum.
We show these effects here for the case of NX Pup:
,
which specifies the extinction law for the
circumstellar dust.
With such a number of parameters we cannot claim to determine these parameters
uniquely from the observed spectrum.
However, the various parameters fortunately have different effects on specific
wavelength regions in the calculated spectrum.
We show these effects here for the case of NX Pup:
- (a)
- For Ae and Fe stars, the wavelength interval where the continuum drops at
shorter wavelength is especially sensitive to the ST and LC of the photosphere
of the star (Fig. 4).
In general the spectral type can be determined within 2 subtypes by comparing
the observed UV spectrum (including the absorption features) with those of
the well-classified standard stars in the IUE spectral atlases.
The LC leads to a range of
 -values (especially for LC IV, III, II,
and I) that we take from SK82.
-values (especially for LC IV, III, II,
and I) that we take from SK82.
- (b)
- This range in
 is further constrained by d and the requirement
that
is further constrained by d and the requirement
that
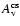 should not be negative.
Figure 5 shows calculated spectra for 4 different distances and
should not be negative.
Figure 5 shows calculated spectra for 4 different distances and
 -values, all of which give comparable agreement to the SW-part
of the observed spectrum of NX Pup.
For the two smaller distances the required
-values, all of which give comparable agreement to the SW-part
of the observed spectrum of NX Pup.
For the two smaller distances the required  -value was closer to that of an
F2 IV star so we used the F2 V star from the list, causing the calculated
spectrum to deviate more from the observed spectrum at longer wavelengths.
Since NX Pup is probably associated with the Gum nebula; the distance
is constrained to values around 500
-value was closer to that of an
F2 IV star so we used the F2 V star from the list, causing the calculated
spectrum to deviate more from the observed spectrum at longer wavelengths.
Since NX Pup is probably associated with the Gum nebula; the distance
is constrained to values around 500 ,
so that
,
so that  must be close to +1
must be close to +1
 60.
60.
- (c)
- In general the shape of the spectrum shortward of
 1800 Å is
dominated by the spectral (late-B) type and LC ( I or II) of the BL,
together with its width
1800 Å is
dominated by the spectral (late-B) type and LC ( I or II) of the BL,
together with its width
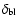 .
The spectral type and LC of the BL can be chosen from the IUE spectral atlases
and estimated with an uncertainty of one subtype.
In several cases (HD 163296, NX Pup,
.
The spectral type and LC of the BL can be chosen from the IUE spectral atlases
and estimated with an uncertainty of one subtype.
In several cases (HD 163296, NX Pup,
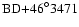 ,
Z CMa, V380 Ori, and KK Oph), the flux
at
,
Z CMa, V380 Ori, and KK Oph), the flux
at 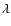 <1800 Å is receiving a considerable contribution from a BL;
see the difference between the solid and dotted lines in Fig. 6,
where the dotted lines give the calculated fluxes without the BL contribution.
To some extent a hotter BL requires a smaller
<1800 Å is receiving a considerable contribution from a BL;
see the difference between the solid and dotted lines in Fig. 6,
where the dotted lines give the calculated fluxes without the BL contribution.
To some extent a hotter BL requires a smaller
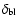 to obtain the same flux
in this spectral range.
Figure 6 shows the model calculations with 4 different BL-types
and sizes applied to the spectrum of NX Pup, and illustrates our preference for
a B9 Iab -type BL (e.g.
to obtain the same flux
in this spectral range.
Figure 6 shows the model calculations with 4 different BL-types
and sizes applied to the spectrum of NX Pup, and illustrates our preference for
a B9 Iab -type BL (e.g. 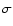 Cyg).
In addition we find comparable matches to the spectrum of SU Aur with a
B9 Iab type (Fig. 19) and a F0 Ib type BL
(Fig. 20).
Cyg).
In addition we find comparable matches to the spectrum of SU Aur with a
B9 Iab type (Fig. 19) and a F0 Ib type BL
(Fig. 20).
- (d)
- The disc flux only contributes significantly to the total flux at
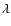 >2900 Å.
However, due to its shadowing effect on the star and the BL, the disc
inclination angle i affects the slope of the calculated spectrum, especially
for
>2900 Å.
However, due to its shadowing effect on the star and the BL, the disc
inclination angle i affects the slope of the calculated spectrum, especially
for 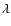 <2300 Å (Fig. 7).
<2300 Å (Fig. 7).
- (e)
- Figure 8 shows the effect of varying
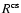 from 2.5 to 6.5
for
from 2.5 to 6.5
for  =1
=1
 70, which is mainly shortward of 2200 Å.
70, which is mainly shortward of 2200 Å.
After an initial choice of the parameter set based on information from the
visual spectral regions (Appendices B and C), we made a
progressive match to the observed UV spectrum by varying the parameters in a
certain order.
First we made a rough match by varying the ST and LC (in particular  )
of the photosphere, the BL, and width
)
of the photosphere, the BL, and width
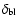 .
Then the distance of the star could be varied within the margins of its
uncertainty, implying a corresponding variation of
.
Then the distance of the star could be varied within the margins of its
uncertainty, implying a corresponding variation of
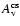 ,
which should be
limited to positive values.
We then varied the inclination angle i of the disc and the extinction law
,
which should be
limited to positive values.
We then varied the inclination angle i of the disc and the extinction law
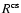 in order to improve the agreement in the LW (
in order to improve the agreement in the LW (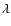 >2000 Å)
spectral range.
After that
>2000 Å)
spectral range.
After that  ,
,
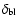 ,
and
,
and
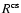 were slightly adjusted until the match was
optimal.
were slightly adjusted until the match was
optimal.
We note that it sometimes occurred that matches of comparable quality could be
obtained for distinctly different spectral types.
In such cases it was necessary to compensate for the difference in  by a
change in
by a
change in
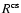 .
Also for a change in distance (in cases where the distance is not well known),
a change in
.
Also for a change in distance (in cases where the distance is not well known),
a change in  and
and
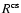 sometimes produced equally good matches to the
observed spectrum.
Examples of such multiple solutions can be found in Table 2
and are discussed in the next section.
sometimes produced equally good matches to the
observed spectrum.
Examples of such multiple solutions can be found in Table 2
and are discussed in the next section.
5 Results of the analysis
The observational information on the stars analysed here is contained in
Appendix B.
Table 1 gives a summary of the most important parameters as
obtained from visual observations.
The selection of input data for the UV3C model analysis is discussed in
Appendix C, and the final model parameters are listed in
Tables 2-6![[*]](/icons/foot_motif.gif) .
In Figs. 10-17 and 45-110 the corresponding UV3C spectra are compared with the
observed spectra.
Fluxes at 3236 Å, obtained from ground-based photometric observations in the
Walraven W pass-band are indicated by w.
A dotted line indicates the model spectrum without the BL contribution, but
this line is not always shown, e.g. when the difference is not large enough
on the plotted scale.
.
In Figs. 10-17 and 45-110 the corresponding UV3C spectra are compared with the
observed spectra.
Fluxes at 3236 Å, obtained from ground-based photometric observations in the
Walraven W pass-band are indicated by w.
A dotted line indicates the model spectrum without the BL contribution, but
this line is not always shown, e.g. when the difference is not large enough
on the plotted scale.
Also shown for all the individual low-resolution spectra
(top - observed (PMS) star,
bottom-upper - comparison star and
bottom-lower - boundary-layer)
are the quality flags as used in ULDA (Wamsteker et al. 1989):
extrapolated ITF (+),
microphonics ( ),
filtered bright spot (
),
filtered bright spot ( ),
unfiltered bright spot (
),
unfiltered bright spot ( ),
resau mark (
),
resau mark ( ),
saturated (
),
saturated ( ),
outside PHOT region (
),
outside PHOT region (
 ),
other flag values i.e. MXLO-files (
),
other flag values i.e. MXLO-files (
![\framebox[2mm]{ }](/articles/aa/full/2006/36/aa0269-04/img170.gif) ).
).
In the following sections we discuss the various groups of related stars
separately, as well as some individual stars.
Although there is general agreement between UV and visual spectral type, we
could match the UV spectra of some stars with more than one ST or LC.
Very remarkable cases are HK Ori (A4 - F9), V380 Ori (A4 - F9), and KK Oph
(A5 - F6).
From Table 2 and Figs. 10-17 and 45-110, it may be noted that in the
first two cases the relative contribution of the BL in the photometric V-band
has strongly increased from  20% for the early A-types to
20% for the early A-types to  45% for
the F-type solutions.
The UV3C calculations suggest that in these cases the later type solutions
should be preferred, because they are capable of giving better agreement with the
observed spectrum in the long wavelength range of the UV spectrum.
More or less the same can be noted for KK Oph, although in this case the
increase in the BL contribution for the F-type solutions is not clear.
Another example is NX Pup, which was previously classified as B9, but from our
UV3C analysis should have an F2 III photosphere (Fig. 9).
Also for this star the increase in the contribution of the BL (
45% for
the F-type solutions.
The UV3C calculations suggest that in these cases the later type solutions
should be preferred, because they are capable of giving better agreement with the
observed spectrum in the long wavelength range of the UV spectrum.
More or less the same can be noted for KK Oph, although in this case the
increase in the BL contribution for the F-type solutions is not clear.
Another example is NX Pup, which was previously classified as B9, but from our
UV3C analysis should have an F2 III photosphere (Fig. 9).
Also for this star the increase in the contribution of the BL ( 25%) is
significant.
The relatively large BL contributions for NX Pup, HK Ori, and V380 Ori are
probably favoured by the small inclination angles of their discs.
This also explains the presence of many strong emission lines in the
LW-range (hires IUE) of NX Pup and V380 Ori.
25%) is
significant.
The relatively large BL contributions for NX Pup, HK Ori, and V380 Ori are
probably favoured by the small inclination angles of their discs.
This also explains the presence of many strong emission lines in the
LW-range (hires IUE) of NX Pup and V380 Ori.
In high-resolution optical spectra of V380 Ori, many strong emission-lines of
Fe II, [Fe II], Ti II, Cr II, and Ni II have been identified
(Shevchenko 1994; Rossi et al. 1999).
The origin of these lines is still unknown: they could be formed in the
(bipolar) outflow or close to the BL.
In the case of KK Oph (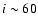
 )
the emission-lines could be contributed
by a nearby nebula.
)
the emission-lines could be contributed
by a nearby nebula.
![\begin{figure}
\par\includegraphics[angle=270,width=16.2cm,clip]{0269f018.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg180.gif) |
Figure 18:
Enlarged part of the SW-range of 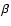 Pic solutions
for d=19.3 Pic solutions
for d=19.3 .
The .
The  -values are based on agreement of the whole spectrum,
except for A6 IV where -values are based on agreement of the whole spectrum,
except for A6 IV where  should be 2
should be 2
 50, but then 50, but then 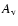 <0.
The <0.
The  ZAMS-values listed by SK82 are 2.1 (A5), 2.25 (A6), and 2.40 (A7).
ZAMS-values listed by SK82 are 2.1 (A5), 2.25 (A6), and 2.40 (A7). |
| Open with DEXTER |
5.2 UXORs
Our model fails to match the spectra of the UXOR-type stars: UX Ori,
BF Ori, and CQ Tau over the whole wavelength range of IUE.
At maximum brightness the model spectrum agrees well with the observed spectrum,
except in the interval 1800-2300 Å, where the model fluxes are too low.
This disagreement seems to increase with lower brightness of the three stars.
The parameters of the best matches to the spectra of BF Ori and UX Ori are
given in Tables 3 and 4.
The very high values needed for
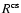 suggest that the employed c.s.
extinction laws are very different from the usual interstellar extinction.
This is an indication that UXORs have a peculiar environment of c.s. dust.
This problem was studied earlier by Grady et al. (1995), who point to the
computations by Voshchinnikov & Karjukin (1994),
which indicate that in order to explain the observed "blueing'' of the
photometric colours (Fig. D.2) and the simultaneous rise in
polarization during the approach to a brightness minimum of UX Ori, one needs
a disc (q = 2) with (possibly) obsidian grains of a size at least 30 times
those of the interstellar medium.
The passing of clouds with such large grains through the line of sight may
result in strong deviations from the i.s. extinction laws during a phase
of low brightness for a UXOR.
suggest that the employed c.s.
extinction laws are very different from the usual interstellar extinction.
This is an indication that UXORs have a peculiar environment of c.s. dust.
This problem was studied earlier by Grady et al. (1995), who point to the
computations by Voshchinnikov & Karjukin (1994),
which indicate that in order to explain the observed "blueing'' of the
photometric colours (Fig. D.2) and the simultaneous rise in
polarization during the approach to a brightness minimum of UX Ori, one needs
a disc (q = 2) with (possibly) obsidian grains of a size at least 30 times
those of the interstellar medium.
The passing of clouds with such large grains through the line of sight may
result in strong deviations from the i.s. extinction laws during a phase
of low brightness for a UXOR.
Table 3:
Additional extinction data of BF Ori; (07-01 top) and
(07-02 bot).
See Table 2 for the other parameters.
For dwarf stars with ST earlier than F2 V, the values of  for ZAMS and MS
stars are somewhat different (SK82).
For sufficiently accurate distances it is then possible to find out from the UV3C
match whether the star is on the ZAMS or on the MS.
We find ZAMS positions for: HD 31648,
for ZAMS and MS
stars are somewhat different (SK82).
For sufficiently accurate distances it is then possible to find out from the UV3C
match whether the star is on the ZAMS or on the MS.
We find ZAMS positions for: HD 31648, 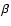 Pic, HD 169142, and HD 139614.
Pic, HD 169142, and HD 139614.
In the case of 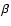 Pic, the photospheric component clearly agrees better
with that of an A7 Vz star (Blondel & TjinADjie 1994) than
with that of an A5 Vz star (Kondo & Bruhweiler 1985),
see Fig. 18.
For an A8 Vz star (as proposed by Crifo et al. 1997),
with
Pic, the photospheric component clearly agrees better
with that of an A7 Vz star (Blondel & TjinADjie 1994) than
with that of an A5 Vz star (Kondo & Bruhweiler 1985),
see Fig. 18.
For an A8 Vz star (as proposed by Crifo et al. 1997),
with  =2
=2
 55 the agreement is very bad, even for d=18.2
55 the agreement is very bad, even for d=18.2 ,
which is the maximum possible (
,
which is the maximum possible (
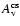 =0
=0
 0).
Barrado y Navascués et al. (1999) derived
0).
Barrado y Navascués et al. (1999) derived
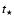 =
=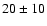
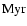 for
for 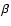 Pic.
Pic.
We do not find any contribution from a boundary-layer to the spectrum of 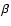 Pic,
which is consistent with the image of the star, showing that the c.s. dust
disc is seen edge on (Smith & Terrile 1984).
However, variable red-shifted absorption components in several lines of ionised
metals were observed in the visual (Vidal-Majar et al. 1994), which points to
episodic infall of matter probably indicating that the accretion disc in
Pic,
which is consistent with the image of the star, showing that the c.s. dust
disc is seen edge on (Smith & Terrile 1984).
However, variable red-shifted absorption components in several lines of ionised
metals were observed in the visual (Vidal-Majar et al. 1994), which points to
episodic infall of matter probably indicating that the accretion disc in 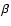 Pic
has already disappeared.
Pic
has already disappeared.
The A7 stars HD 139614 and HD 169142 appear to have similar mass and age as 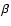 Pic,
and therefore are also classified as A7 Vz stars.
Pic,
and therefore are also classified as A7 Vz stars.
Table 4:
Extinction parameters for 11 observed brightness stages of UX Ori with a
photospheric spectral type of A2 III.
See Table 2 for the other parameters.
5.4 T Tauri stars
Two T Tauri stars have been included in our sample: SU Aur and HD 283572.
The spectrum of SU Aur has been analysed in order to check if we find results
that are comparable with those of BBB88.
Figure 20 shows that for parameters similar to those of
Bertout et al. (BBB88-Table 4a), we find a good match to the UV spectrum of
this star.
For d=160 and i=40
and i=40 we derive the following from our UV3C-model
calculation with a G2 IV star and an F0 I-type BL (
we derive the following from our UV3C-model
calculation with a G2 IV star and an F0 I-type BL (
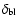 =0.02):
=0.02):
 =2.70
=2.70
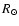 ,
,
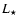 =6.68
=6.68
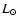 for
for 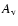 =0
=0
 43, so
43, so
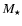 =1.97
=1.97
 .
With
.
With 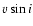 =66
=66
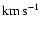 ,
we then obtain an accretion rate of 5.1
,
we then obtain an accretion rate of 5.1 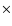 10-8
10-8
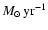 ,
which is about the same as derived by BBB88.
However, the SW-spectrum of SU Aur is very faint and does not permit us to
discriminate between various spectral types for the BL.
Furthermore, we have no clear argument for choosing a cooler BL
(as done by BBB88 for
,
which is about the same as derived by BBB88.
However, the SW-spectrum of SU Aur is very faint and does not permit us to
discriminate between various spectral types for the BL.
Furthermore, we have no clear argument for choosing a cooler BL
(as done by BBB88 for
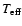 =7940 K, which is much lower than for
all the other cases in our sample); so if we use a B9 Iab BL of 0.0005
=7940 K, which is much lower than for
all the other cases in our sample); so if we use a B9 Iab BL of 0.0005
 (Fig. 19, Table 2), then the mass accretion
rate decreases to 6.5
(Fig. 19, Table 2), then the mass accretion
rate decreases to 6.5 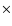 10-9
10-9
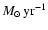 .
The i=62
.
The i=62
 determined by Akeson et al. (2002) does not change
our result significantly if we use
determined by Akeson et al. (2002) does not change
our result significantly if we use  =2
=2
 70 instead of 2
70 instead of 2
 72.
Note that a photospheric type G5 IV improves the calculated spectrum
at
72.
Note that a photospheric type G5 IV improves the calculated spectrum
at 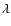 >2900 Å (Fig. 75) and that a B9 Iab BL
gives a better result at
>2900 Å (Fig. 75) and that a B9 Iab BL
gives a better result at 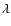 <1800 Å (Fig. 79).
The SED calculated from these parameters is shown in Sect. 5.10
and appears to agree with the (dereddened) observed SED.
<1800 Å (Fig. 79).
The SED calculated from these parameters is shown in Sect. 5.10
and appears to agree with the (dereddened) observed SED.
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{0269f020.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg184.gif) |
Figure 20:
SU Aur "solution'' (G2 IV+ F0 Ib) for
parameters close to those of BBB88. |
| Open with DEXTER |
For the other T Tauri star HD 283572, we could not find comparable previous UV
spectral analyses.
This nTT star has a smaller radius and about half the luminosity, and it should
be less evolved than SU Aur (Walter et al. 1987).
We estimate that the width of its (cooler) BL is about half the width of the BL
of SU Aur, which implies that the accretion rate (after accounting for the
rotation of this star) may be  5 times smaller than that of SU Aur.
5 times smaller than that of SU Aur.
In contrast to the results in Sect. 5.4, the application of our
analysis to the UV spectra of FU Ori and Z CMa leads to very high mass
accretion rates.
Kenyon et al. (1988) and Hartmann et al. (1989) have convincingly argued
that the energy distributions of these stars in the red and IR are dominated
by the contributions of a thick rotating accretion disc.
In the UV, several absorption features in the LW-range suggest a spectral type
F0-5 I for the central star or inner disc (Kenyon et al. 1989).
We modeled the complete UV (SW+LW) spectra of FU Ori and Z CMa with a
stellar spectrum of type F0-5 I with

 7
7
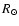 for FU Ori and
for FU Ori and

 14
14
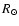 for Z CMa (as estimated from the SEDs by Kenyon et al. 1988
and Hartmann et al. 1989).
In order to obtain such radii, we had to increase the
for Z CMa (as estimated from the SEDs by Kenyon et al. 1988
and Hartmann et al. 1989).
In order to obtain such radii, we had to increase the  -values from -5.1
(SK82) up to -2.0.
Good agreement with the observed spectra could be obtained with a B7-9 I type BL of
-values from -5.1
(SK82) up to -2.0.
Good agreement with the observed spectra could be obtained with a B7-9 I type BL of  0.02
0.02
 .
Because the positions of the stars in the HRD are above the birthline
(Fig. 41), we cannot estimate their masses or ages.
Assuming
.
Because the positions of the stars in the HRD are above the birthline
(Fig. 41), we cannot estimate their masses or ages.
Assuming
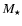
 0.5
0.5
 for FU Ori (a former T Tauri star) and 1.7
for FU Ori (a former T Tauri star) and 1.7
 for Z CMa (Hartmann et al. 1989), we then obtain accretion rates of
6
for Z CMa (Hartmann et al. 1989), we then obtain accretion rates of
6 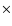 10-6
10-6
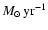 for FU Ori and
for FU Ori and  3
3 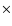 10-5
10-5
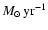 for Z CMa.
However, taking the inclinations into account, the mass accretion rates
become 6
for Z CMa.
However, taking the inclinations into account, the mass accretion rates
become 6 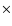 10-4 and 8
10-4 and 8 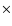 10-4
10-4
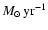 .
Z CMa is a double star, probably consisting of a
.
Z CMa is a double star, probably consisting of a  16
16
 B0 III primary
and a
B0 III primary
and a  3
3
 FUOR secondary (vandenAncker et al. 1904).
Since the UV spectrum is dominated by the FUOR component we neglected
the contribution of the embedded B0-component that only contributes in the
far IR.
FUOR secondary (vandenAncker et al. 1904).
Since the UV spectrum is dominated by the FUOR component we neglected
the contribution of the embedded B0-component that only contributes in the
far IR.
Table 5:
Additional data of HR 5999. The
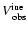 -value marked with () is uncertain, as
the brightness is underestimated due to the degradation of the FES counter
after 1990 (Sect. B.1).
See Table 2 for the other input parameters.
The apparently good agreement of the 3 faint spectra (#10-12) at the long
wavelength is caused by the fact that we used the same (overexposed) image
LWR14027 in these cases.
-value marked with () is uncertain, as
the brightness is underestimated due to the degradation of the FES counter
after 1990 (Sect. B.1).
See Table 2 for the other input parameters.
The apparently good agreement of the 3 faint spectra (#10-12) at the long
wavelength is caused by the fact that we used the same (overexposed) image
LWR14027 in these cases.
Table 6:
Data of the double stars, p for
primary, s for secondary, 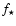 is the relative V-flux of the component.
is the relative V-flux of the component.
5.6 HR 5999
In Table 2 the parameters of this variable star are given for
its phase of maximum visual brightness.
The UV3C calculations give the best match for a photospheric spectral type
A6 IV-III, but A5 III and A7 III also give satisfactory results.
The c.s. extinction is close to the average i.s. extinction law with R=3.1.
Apart from a low amplitude (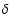 Scuti) oscillation in brightness, the star varies
strongly (
Scuti) oscillation in brightness, the star varies
strongly (
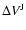

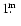 )
and irregularly on time-scales of several
weeks (see e.g. Baade & Stahl 1989a; TjinADjie et al. 1989).
)
and irregularly on time-scales of several
weeks (see e.g. Baade & Stahl 1989a; TjinADjie et al. 1989).
We tried to match the UV spectra of 12 phases of lower brightness
with our model.
In order to match the decreasing slope of the spectrum longward of 2500 Å, we
have to raise the value of
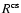 .
The values of
.
The values of
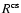 and
and
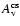 for fixed values (Table 2) of
the other parameters are listed in Table 5.
The rise in
for fixed values (Table 2) of
the other parameters are listed in Table 5.
The rise in
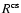 can be interpreted roughly as an increase in the average size
of the obscuring c.s. dust grains.
This may be expected as a result of the passage of c.s. dust clouds with large
dust grains through the line of sight.
However, the UV spectra longward of 2500 Å for photometric phases with
can be interpreted roughly as an increase in the average size
of the obscuring c.s. dust grains.
This may be expected as a result of the passage of c.s. dust clouds with large
dust grains through the line of sight.
However, the UV spectra longward of 2500 Å for photometric phases with
 >6
>6
 7 cannot completely be matched by an increase of
7 cannot completely be matched by an increase of
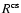 only.
Apparently the shape of the extinction law also has to be changed.
only.
Apparently the shape of the extinction law also has to be changed.
A quantitative evaluation of the variation in the extinction law has been
made through multiple scattering calculations (Monte Carlo method) for
the c.s. dust region by Voshchinnikov & Karjukin (1994).
The results for HR 5999 have been given by Thé et al. (1996).
For the brightest phase (

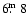 )
the extinction law is produced by
scattering from grains with sizes between 0.01
)
the extinction law is produced by
scattering from grains with sizes between 0.01 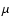 m and 0.25
m and 0.25 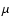 m with
m with
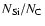 =0.75, which is close to the standard composition of i.s.
grains.
For the fainter phases, however, the observed extinction law requires that
=0.75, which is close to the standard composition of i.s.
grains.
For the fainter phases, however, the observed extinction law requires that
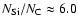 ,
and the sizes range from 0.1
,
and the sizes range from 0.1 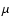 m to 0.13
m to 0.13 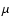 m,
which means that the small grains are depleted, and that
m,
which means that the small grains are depleted, and that
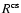
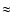 2.5.
The depletion of small grains has been interpreted as the sweeping effect of
the stellar radiation (Thé et al. 1996).
At the same time, the EWs of the Fe II, Mn II, and Cr II resonance
absorption lines in the inner shell decrease when the star grows fainter
(Blondel et al. 1989).
2.5.
The depletion of small grains has been interpreted as the sweeping effect of
the stellar radiation (Thé et al. 1996).
At the same time, the EWs of the Fe II, Mn II, and Cr II resonance
absorption lines in the inner shell decrease when the star grows fainter
(Blondel et al. 1989).
The UV spectra of HD 163296 can be matched with an ST A3-4 IV for
d=122 (ESA 1997).
In order to obtain a good match with A4 Vz (
(ESA 1997).
In order to obtain a good match with A4 Vz ( =1
=1
 85),
however, we are limited to
85),
however, we are limited to 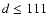
 (when using an A0 Ib BL of
0.06
(when using an A0 Ib BL of
0.06
 ), close to the Hipparcos catalogue lower limit.
), close to the Hipparcos catalogue lower limit.
The parameters obtained by matching the spectra of five B9/A1 stars are given in
Table 2.
Because of the large photospheric contribution in the 1200-1500 Å spectral range of these stars, these spectra are less sensitive to the
contribution of their BL, which results in an increasing uncertainty in the BL
spectral type and accretion mass rate for spectral types earlier than A0.
In fact this problem hampers the application of the UV3C matching procedure to
the spectra of Herbig stars with type earler than B9.
5.9 Double star spectra
Table B.1 collects the parameters for 13 (out of 15) stars of our
sample, which are known to be double.
It is important to check whether the model parameters of the primary component
are different from those of the system determined above
(Table 2).
The results of the attempts to match the spectra of 5 of these systems - XY Per,
NX Pup,
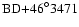 ,
AK Sco, and KK Oph - are given in Table 6.
In most cases we assume that the difference in
,
AK Sco, and KK Oph - are given in Table 6.
In most cases we assume that the difference in  -magnitude of the components
at the time of the IUE observation is the same as the literature value of
Table B.1 and subtract the relative spectral contribution of the
primary component
-magnitude of the components
at the time of the IUE observation is the same as the literature value of
Table B.1 and subtract the relative spectral contribution of the
primary component
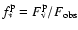 (derived from its
total visual magnitude, the difference in magnitude, and the model parameters of
the star in Table B.1) from the observed spectrum.
The remaining spectrum is assumed to be that of the secondary and is matched
separately.
These 6 double stars are the ones with the smallest magnitude differences between
their components.
For the other stars, the differences in
(derived from its
total visual magnitude, the difference in magnitude, and the model parameters of
the star in Table B.1) from the observed spectrum.
The remaining spectrum is assumed to be that of the secondary and is matched
separately.
These 6 double stars are the ones with the smallest magnitude differences between
their components.
For the other stars, the differences in  are too large to expect a
significant contribution in the UV from the secondary.
are too large to expect a
significant contribution in the UV from the secondary.
For XY Per we tried two values for the distance: 350 and 120
and 120 (Sect. C.1).
The first value was taken from RSF Per B to which the star seems to
belong, while the second is a very uncertain determination by the Hipparcos
program.
It appears that we can only find a double-star solution for d=350
(Sect. C.1).
The first value was taken from RSF Per B to which the star seems to
belong, while the second is a very uncertain determination by the Hipparcos
program.
It appears that we can only find a double-star solution for d=350 .
.
Only in the case of the spectroscopic binary AK Sco could we derive the
magnitudes of the components at the times of the IUE spectral exposures.
These observations were made at apastron (April 1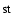 1988:
1988:
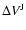 =0
=0
 42)
and at periastron (April 9
42)
and at periastron (April 9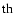 1988:
1988:
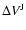 =0
=0
 09).
The magnitudes could be derived from the relative contributions of the two
high-resolution Mg II resonance line profiles of the components, taken on
the same dates.
We assumed that the primary has spectral type F5 V and then matched the
remaining spectrum of the secondary with the same spectral type F5 V (Sect. C.29).
09).
The magnitudes could be derived from the relative contributions of the two
high-resolution Mg II resonance line profiles of the components, taken on
the same dates.
We assumed that the primary has spectral type F5 V and then matched the
remaining spectrum of the secondary with the same spectral type F5 V (Sect. C.29).
From a comparison between Tables 2 and 6 we note
that the parameters for those stars where the primary component dominates the
UV and Visual (XY Per, NX Pup, and KK Oph;
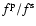 >1.6) are almost the
same.
But for AK Sco and
>1.6) are almost the
same.
But for AK Sco and
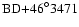 (1.0 <
(1.0 <
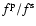 <1.5), we find smaller
<1.5), we find smaller
 ,
,
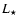 ,
,
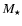 ,
and
,
and 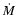 -values than in Table 2, where these
stars were assumed to be single.
-values than in Table 2, where these
stars were assumed to be single.
These results are important for the understanding of the individual components
of the double stars.
Table 7:
Data used for the SED-calculations,
V-magnitude with references for each photometric observation.
Observations on the WULBV (Walraven) photometric system can be found in
deWinter et al. (2001) with the exception of HD 139614 and SU Aur.
Observations in the 4 IRAS bands (11.8, 24.4, 58.6 and 101 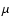 m) can be
found in NASA RP-1190 (1988).
m) can be
found in NASA RP-1190 (1988).
5.10 The SEDs
In the visual and near-infraredi, a large amount of photometric observations of
the stars in our sample has been made and published (references of compilations:
deWinter et al. 2001; Eiroa et al. 2002; Kilkenny et al. 1985;
Sylvester et al. 1996).
Most of the stars are photometrically variable on time-scales of days or weeks.
Only for a few stars (HD 163296, HR 5999, BF Ori, BN Ori, CQ Tau, and AK Sco) do
we have simultaneous IUE and
 photometric observations.
However, in many cases we can find Walraven
photometric observations.
However, in many cases we can find Walraven
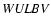 ,
,
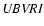 ,
and
,
and
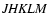 photometry in which the observed
photometry in which the observed  -magnitude is close to the
-magnitude is close to the
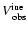 measured
with the FES during the IUE exposure of the star.
In addition we found ANS data for NX Pup and HD 163296.
We assumed that the IRAS PS photometry is not variable.
Table 7 gives the references to the photometry.
We dereddened the observed photometric data for foreground and
circumstellar extinction, given in Table 2 (using
measured
with the FES during the IUE exposure of the star.
In addition we found ANS data for NX Pup and HD 163296.
We assumed that the IRAS PS photometry is not variable.
Table 7 gives the references to the photometry.
We dereddened the observed photometric data for foreground and
circumstellar extinction, given in Table 2 (using
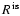 and
and
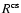 and the extinction laws of Steenman & Thé 1989) and compared these
dereddened SEDs with the sum (Eq. (9)) of the intrinsic SEDs of
photosphere, disc (for which we used
and the extinction laws of Steenman & Thé 1989) and compared these
dereddened SEDs with the sum (Eq. (9)) of the intrinsic SEDs of
photosphere, disc (for which we used
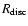 =500
=500
 in this special
case), and BL as specified by the parameters in Table 2.
The results for 16 stars of various spectral types are shown in Figs. 21-40.
Different spectral types that match the UV spectrum of a star equally well
(e.g. KK Oph A5 V and F6 IV) give very similar SEDs.
We also give these for the primary components of AK Sco and NX Pup separately.
All our stars have SEDs of type I in the classification of Hillenbrand et
al. (1992, Hil92 herafter).
It may be noted that, apart from the cases with strong NIR excess (NX Pup,
KK Oph, V380 Ori, HK Ori), most cases (except HD 104237, SU Aur
in this special
case), and BL as specified by the parameters in Table 2.
The results for 16 stars of various spectral types are shown in Figs. 21-40.
Different spectral types that match the UV spectrum of a star equally well
(e.g. KK Oph A5 V and F6 IV) give very similar SEDs.
We also give these for the primary components of AK Sco and NX Pup separately.
All our stars have SEDs of type I in the classification of Hillenbrand et
al. (1992, Hil92 herafter).
It may be noted that, apart from the cases with strong NIR excess (NX Pup,
KK Oph, V380 Ori, HK Ori), most cases (except HD 104237, SU Aur![[*]](/icons/foot_motif.gif) ,
V380 Ori, BN Ori, and perhaps HD 163296) show a flux contribution,
which is higher than the observed flux distribution between the
,
V380 Ori, BN Ori, and perhaps HD 163296) show a flux contribution,
which is higher than the observed flux distribution between the 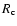 and i
K pass-bands.
It was shown by Hil92 that such excesses can be removed by introducing a
circular optically-thin region ("hole'') in the centre of the optically-thick disc
around the star.
The result for HD 97048 is shown there (Fig. 2a) for a central region
with a radius of
and i
K pass-bands.
It was shown by Hil92 that such excesses can be removed by introducing a
circular optically-thin region ("hole'') in the centre of the optically-thick disc
around the star.
The result for HD 97048 is shown there (Fig. 2a) for a central region
with a radius of  8
8
 .
In this case the photospheric classification (B9 V) and the stellar radius are
the same as in Table 2.
In Hil92-Fig. 2a, it was assumed that the star is observed pole-on.
For an inclination near 60
.
In this case the photospheric classification (B9 V) and the stellar radius are
the same as in Table 2.
In Hil92-Fig. 2a, it was assumed that the star is observed pole-on.
For an inclination near 60 ,
the "hole'' radius that fits the SED should be
larger by
,
the "hole'' radius that fits the SED should be
larger by  30% i.e.
30% i.e.  10
10
 .
.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{0269f041.eps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg210.gif) |
Figure 41:
HRD with - mass-labeled - (0.9-5.0) tracks of Bernasconi (1996) with the
modeled stars ( ), where ), where  is the Sun.
The - upper grey - line is the 10-5
is the Sun.
The - upper grey - line is the 10-5
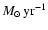 birthline with Z=0.020 and
the - lower grey - line is the ZAMS as given in Table E.1.
The dotted lines are the canonical evolutionary tracks.
Star-labels are from Table 2.
birthline with Z=0.020 and
the - lower grey - line is the ZAMS as given in Table E.1.
The dotted lines are the canonical evolutionary tracks.
Star-labels are from Table 2.
|
| Open with DEXTER |
Hil92-Fig. 6b indicates the effect of the introduction of the optically-thin
central region.
The flux contribution of the disc to the SED is reduced between the 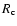 and
M-bands, with the strongest reduction near the J-band.
This is the main difference between the observed and the calculated SED
(Fig. 21) of HD 97048.
Similar improvements of predicted SEDs are shown in Hil92-Fig. 2 for UX Ori,
BF Ori, HD 150193, HR 5999, NX Pup, V380 Ori, HK Ori, KK Ori,
and
M-bands, with the strongest reduction near the J-band.
This is the main difference between the observed and the calculated SED
(Fig. 21) of HD 97048.
Similar improvements of predicted SEDs are shown in Hil92-Fig. 2 for UX Ori,
BF Ori, HD 150193, HR 5999, NX Pup, V380 Ori, HK Ori, KK Ori,
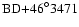 ,
and
,
and
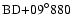 in our program.
in our program.
The resulting "hole radii'' may be expected to be different from those obtained
by Hil92, because the photospheric spectral types adopted by them are
different from our estimates in general and, as a result of this, possible existing
IR excesses (e.g. in NX Pup, KK Oph, HK Ori, and V380 Ori) may be masked in
their fits.
In our paper, however, we are mainly concerned with the components that
dominate the UV spectrum: the photosphere and the BL.
Although interesting in itself, the details of the disc model have no influence
on the match to the observed UV spectrum, and will be ignored in the rest of
this paper.
5.11 UV variability
Among the various space instruments (TD1, Copernicus, ANS, IUE, HST) for
observation of the near UV (1200-3600 Å), IUE is the only one that was
well-suited for repeat observations.
Most of the stars in our sample have been observed at least twice and spectral
changes have been noted (Valenti et al. 2000), but usually time-scales of
such variability cannot be established from these data.
One type of variability mentioned above may be correlated with changes in
circumstellar extinction (UX Ori, BF Ori, HR 5999, CQ Tau).
For this type time-scales of days or weeks have been found from observations
in the visual.
On smaller time-scales only the brightest PMS stars have been observed:
HD 104237 (V=6
 60), HR 5999 (V>6
60), HR 5999 (V>6
 7), HD 163296 (V=6
7), HD 163296 (V=6
 9),
HD 199143 (V=7
9),
HD 199143 (V=7
 1), AB Aur (V>7
1), AB Aur (V>7
 2) and AK Sco (V=8
2) and AK Sco (V=8
 9).
9).
HD 163296 was observed with time intervals of several hours during two weeks
in 1986 and 1987 (Table F.5).
The conclusions from the low-resolution observations of HD 163296 are described
in Sect. A.2.
No periodicity was found in these data thus far.
However, small variations may occur irregularly, which could be indications of
low amplitude activity.
Among the high-resolution results, the Mg II-profile variations have been
interpreted as due to a rotating wind structure coupled to the star, similar
to the situation for AB Aur (Catala et al. 1989).
HD 163296, HD 104237, HD 199143, and HR 5999 were observed in 5 sequences of
IUE observations in 1986 and 1987, 1993, 1995, and 1996 respectively.
From the observed values of 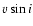 (Table 1), the estimated
inclinations and the derived stellar radii (Table 2) we expect
rotation periods of 14
(Table 1), the estimated
inclinations and the derived stellar radii (Table 2) we expect
rotation periods of 14
 ,
21
,
21
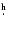 ,
11
,
11
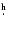 ,
and 36
,
and 36
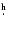 ,
respectively.
In the five sequences the observations were spread over several phases
of the stellar rotations.
We noted variations in the emission-line fluxes, and variations in the
continuum may also be present.
The results of these analyses and alternative interpretations will be
discussed in Paper II.
,
respectively.
In the five sequences the observations were spread over several phases
of the stellar rotations.
We noted variations in the emission-line fluxes, and variations in the
continuum may also be present.
The results of these analyses and alternative interpretations will be
discussed in Paper II.
AK Sco is a spectroscopic binary star with an accurately known
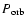 =13
=13
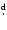 6
(Andersen et al. 1989).
We took low and high-resolution UV spectra of successive apastron and
periastron phases in 1988
6
(Andersen et al. 1989).
We took low and high-resolution UV spectra of successive apastron and
periastron phases in 1988![[*]](/icons/foot_motif.gif) .
Variations in emission-line fluxes and continuum fluxes were noted,
which is confirmed by visual spectroscopy (Alencar et al. 2003).
The variations in the visual spectra were interpreted in terms of inhomogeneities
in the common dust disc of the components.
However, UV-emission flux variability may point to stellar emission variability
and/or to uneven distribution of the emission regions on the surface of the binary
components.
(The estimated rotation period of the (equal) components is 17
.
Variations in emission-line fluxes and continuum fluxes were noted,
which is confirmed by visual spectroscopy (Alencar et al. 2003).
The variations in the visual spectra were interpreted in terms of inhomogeneities
in the common dust disc of the components.
However, UV-emission flux variability may point to stellar emission variability
and/or to uneven distribution of the emission regions on the surface of the binary
components.
(The estimated rotation period of the (equal) components is 17
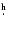 ,
which means
,
which means
 11 rotations between apastron and periastron, e.g. between the observations
in April 1988: 7
11 rotations between apastron and periastron, e.g. between the observations
in April 1988: 7
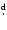 778 (=0.56
778 (=0.56
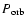 ).)
We will discuss these results in Paper II.
).)
We will discuss these results in Paper II.
5.12 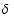 Scuti pulsations
Scuti pulsations
Recently high time resolution photometry of at least 7 of the stars
in our sample: HR 5999, 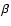 Pic, HD 104237, HD 142666, V346 Ori, V351 Ori, and HD 35929,
have revealed that these stars show
Pic, HD 104237, HD 142666, V346 Ori, V351 Ori, and HD 35929,
have revealed that these stars show 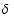 Scuti-type pulsations.
With the stellar parameters in Table 2, we can determine the
location of the stars in the HRD and also derive the instability modes
corresponding to the observed pulsation periods.
The results will be given and discussed in a research note.
Scuti-type pulsations.
With the stellar parameters in Table 2, we can determine the
location of the stars in the HRD and also derive the instability modes
corresponding to the observed pulsation periods.
The results will be given and discussed in a research note.
In the SW-range of many spectra we observe the presence of emission-lines of
O I, C II, Si II, Si III, Si IV, C II, and C IV (TjinADjie et al. 1998).
In the LW-range we often observe emission-lines of Mg II and Fe II.
We shall discuss the emission fluxes of these lines in a separate paper
(Paper II).
6 Mass accretion rates
The UV3C analysis of each low-resolution UV spectrum of a star with known d and
 gives us (for chosen ST and LC of stellar photosphere and BL)
the
gives us (for chosen ST and LC of stellar photosphere and BL)
the
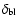 and the circumstellar extinction parameters
and the circumstellar extinction parameters
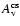 and
and
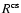 .
Fortunately the value of the distance strongly affects the UV3C model spectrum,
so that d can usually be constrained within
.
Fortunately the value of the distance strongly affects the UV3C model spectrum,
so that d can usually be constrained within 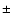 15%.
From the distance and the observed
15%.
From the distance and the observed  -flux (corrected for foreground
extinction), we obtained in each case a value for the photospheric radius;
and with the additional knowledge of
-flux (corrected for foreground
extinction), we obtained in each case a value for the photospheric radius;
and with the additional knowledge of
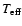 (from adjusting ST and LC), we
calculated
(from adjusting ST and LC), we
calculated
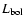 ,
so that we can locate the star in the HRD
(Fig. 41).
With the help of the PMS evolutionary tracks for models of 0.5-7
,
so that we can locate the star in the HRD
(Fig. 41).
With the help of the PMS evolutionary tracks for models of 0.5-7
 stars, calculated by PS93, Bernasconi (1996), and Siess et al. (1999, 2000),
we then interpolated values for
stars, calculated by PS93, Bernasconi (1996), and Siess et al. (1999, 2000),
we then interpolated values for
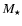 and
and
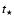 .
The results of the interpolation of the Bernasconi tracks are given in
Tables 2 and 6.
.
The results of the interpolation of the Bernasconi tracks are given in
Tables 2 and 6.
The mass accretion rates (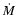 )
were derived from the energy balance
between the viscous energy produced in the disc and BL and the energy radiated
by the BL (Eq. (5)),
where the stellar influx on the inner layers of the disc (less than a few
percent) has been neglected.
Here we approximate the BL flux by that of the Planck spectrum
of the same
)
were derived from the energy balance
between the viscous energy produced in the disc and BL and the energy radiated
by the BL (Eq. (5)),
where the stellar influx on the inner layers of the disc (less than a few
percent) has been neglected.
Here we approximate the BL flux by that of the Planck spectrum
of the same
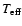 as listed for the supergiant spectral type B8 I or
B9 I (SK82).
For the integrated spectral flux, this approximation is correct within a few
percent.
In the case of a co-rotating star, part of the viscous energy is used to
spin-up the star (see e.g. Kley & Lin 1996), so that the energy available
for BL radiation becomes less.
In order to observe the same radiation flux from the BL as in the non-rotating
situation (as calculated by the UV3C-model), we have to raise the viscous
dissipation, i.e. the accretion rate.
However, this correction could only be made by us for objects for which the
as listed for the supergiant spectral type B8 I or
B9 I (SK82).
For the integrated spectral flux, this approximation is correct within a few
percent.
In the case of a co-rotating star, part of the viscous energy is used to
spin-up the star (see e.g. Kley & Lin 1996), so that the energy available
for BL radiation becomes less.
In order to observe the same radiation flux from the BL as in the non-rotating
situation (as calculated by the UV3C-model), we have to raise the viscous
dissipation, i.e. the accretion rate.
However, this correction could only be made by us for objects for which the
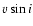 -value and the inclination angle i are known
(Table 1).
Then for a radially thin BL the integrated flux can be obtained from:
-value and the inclination angle i are known
(Table 1).
Then for a radially thin BL the integrated flux can be obtained from:
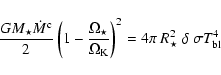 |
(14) |
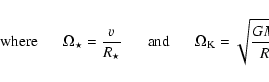 |
(15) |
The mass accretion rates (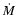 and
and
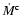 )
derived from Eqs. (5)
and (14) are listed in Tables 2 and 6.
)
derived from Eqs. (5)
and (14) are listed in Tables 2 and 6.
Several authors (see Muzerolle et al. 2005) have reviewed the accretion rates
for T Tauri stars and brown dwarfs, which results in
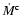
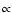
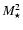 .
Figure 42 shows that our data for more massive stars roughly
follow the same relation, although the
.
Figure 42 shows that our data for more massive stars roughly
follow the same relation, although the
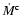 is determined in a different way.
is determined in a different way.
Recently Padoan et al. (2005) re-examined the source of accretion on young
stars.
It has been realised that without influx the circumstellar discs of PMS-stars
do not contain sufficient mass to support the observed mass-accretion rate by
self-gravity or turbulence for more than a few Myr.
However, PMS-stars can in general be associated with the molecular cloud
complexes (in particular dense filaments) in which they were born.
It seems natural to assume that a few Myr after the disc formation, the parent
cloud will become the main supply of accretion.
In this case the accretion rate will only depend on the stellar mass and the
conditions in the cloud.
Padoan et al. used the Bondi-Hoyle (1944) fluid dynamical accretion rate for
a mass
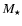 moving supersonically with velocity v through a uniform cloud
medium of density
moving supersonically with velocity v through a uniform cloud
medium of density 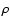 as an estimate of the accretion on the star-disc system:
as an estimate of the accretion on the star-disc system:
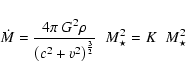 |
(16) |
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{0269f042.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg223.gif) |
Figure 42:
Corrected mass-accretion rate versus stellar
mass.
The solid and dashed lines are from Padoan et al. (2005).
Numbers indicate the
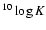 -values and the dotted line is the detection
limit.
See Fig. 44 for the mass-symbols. -values and the dotted line is the detection
limit.
See Fig. 44 for the mass-symbols. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=270,width=14cm,clip]{0269f043.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg224.gif) |
Figure 43:
Mass-accretion rate (Table 2)
versus relative age (Table 8).
The arrow indicates the age of  Pic.
See Fig. 44 for the mass-symbols. Pic.
See Fig. 44 for the mass-symbols. |
| Open with DEXTER |
where  ,
c, and v are gas density, sound speed, and relative velocity
of the gas averaged over some distance (e.g.
,
c, and v are gas density, sound speed, and relative velocity
of the gas averaged over some distance (e.g.  500 AU) in the large-scale
cloud.
Numerical simulations of star formation in self-gravitating turbulent clouds
have supplied values for the three quantities and enabled the authors to estimate
the coefficient K from Eq. (16).
For 104>
500 AU) in the large-scale
cloud.
Numerical simulations of star formation in self-gravitating turbulent clouds
have supplied values for the three quantities and enabled the authors to estimate
the coefficient K from Eq. (16).
For 104>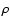 >103
>103
 ,
they find K=
,
they find K=
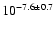 (Fig. 42 dashed lines), while for
(Fig. 42 dashed lines), while for
 >104
>104
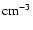 the result is K=
the result is K=
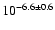 (Fig. 42 solid lines).
These K-values give a good account of the accretion rates that are found
in PMS objects of various masses.
Even accretion rates of 10-11
(Fig. 42 solid lines).
These K-values give a good account of the accretion rates that are found
in PMS objects of various masses.
Even accretion rates of 10-11
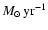 are correctly predicted for brown dwarfs
of 0.03
are correctly predicted for brown dwarfs
of 0.03
 if K
if K  10-8.
Figure 42 may be compared with Muzerolle et al. (2005) Fig. 5.
The young PMS Be/Ae/Fe stars analysed in this paper have masses of 1.8-4.0
10-8.
Figure 42 may be compared with Muzerolle et al. (2005) Fig. 5.
The young PMS Be/Ae/Fe stars analysed in this paper have masses of 1.8-4.0
 .
A group of 14 stars is situated above the K=10-7.2 line and 11 below.
We note that 6 out of these 14 are associated with dark clouds
(Appendix C), while the second group of stars has only associations
with well-known regions of star formation.
Therefore, this second group follow the same trend as the T Tauri stars and seem
to be associated with clouds of similar densities, but higher than those of
brown dwarfs.
We conclude that the accretion rates that we measured for the PMS Be/Ae/Fe stars
are an extrapolation of the accretion rates obtained for T Tauri stars.
We note, however, that HD 163296 belongs to the "high rate group'' in spite of
the fact that it seems to be an "isolated'' star (e.g. no association with
clouds).
It is also not clear if the high rates for FU Ori and Z CMa are constant rates
in time (not related to the outbursts of these objects).
It could mean that they are associated with particularly dense parent cloud filaments.
The molecular parent cloud connection gives a good overall account of the mass
dependence of the derived accretion rates in terms of assumed differences in stellar
mass and gas densities of the associated filaments in the parent cloud.
However, the model is a static one and does not account for the further evolution
of the accretion in the star-disc systems of various mass.
It also ignores the role of the disc replenishment process played by the
nearby material, ejected in (bipolar) outflow by the star.
We shall now briefly discuss these points.
.
A group of 14 stars is situated above the K=10-7.2 line and 11 below.
We note that 6 out of these 14 are associated with dark clouds
(Appendix C), while the second group of stars has only associations
with well-known regions of star formation.
Therefore, this second group follow the same trend as the T Tauri stars and seem
to be associated with clouds of similar densities, but higher than those of
brown dwarfs.
We conclude that the accretion rates that we measured for the PMS Be/Ae/Fe stars
are an extrapolation of the accretion rates obtained for T Tauri stars.
We note, however, that HD 163296 belongs to the "high rate group'' in spite of
the fact that it seems to be an "isolated'' star (e.g. no association with
clouds).
It is also not clear if the high rates for FU Ori and Z CMa are constant rates
in time (not related to the outbursts of these objects).
It could mean that they are associated with particularly dense parent cloud filaments.
The molecular parent cloud connection gives a good overall account of the mass
dependence of the derived accretion rates in terms of assumed differences in stellar
mass and gas densities of the associated filaments in the parent cloud.
However, the model is a static one and does not account for the further evolution
of the accretion in the star-disc systems of various mass.
It also ignores the role of the disc replenishment process played by the
nearby material, ejected in (bipolar) outflow by the star.
We shall now briefly discuss these points.
6.2 Evolutionary trends
Since the mass values derived from the models of Bernasconi (1996) and Siess et al.
(2000) do not differ very much (Table 8) and the rates are not
very sensitive to the mass values, the rates from the various models are very
similar.
In order to search for evolutionary trends in the rates we have to determine
the ages of the stars ( )
from the calculated models.
In contrast to the masses, the ages derived from the three models, are in
general very different.
This is mainly because small differences in mass from the various models lead
to large differences in age.
We expect higher ages from the models of Siess that include accretion, because
these models start with lower mass and therefore evolve more slowly than the
models with fixed mass.
Although this seems to be true if we compare the ages resulting from the
accretion-included models of Siess et al. (1999) and the fixed-mass models
of Bernasconi, it is less clear and often reversed if we compare the
accretion-included models of Siess et al. (1999) with the fixed-mass models
of Siess et al. (2000).
We find, however, that the differences in relative age (absolute age divided
by ZAMS age (Appendix E) for the same mass):
)
from the calculated models.
In contrast to the masses, the ages derived from the three models, are in
general very different.
This is mainly because small differences in mass from the various models lead
to large differences in age.
We expect higher ages from the models of Siess that include accretion, because
these models start with lower mass and therefore evolve more slowly than the
models with fixed mass.
Although this seems to be true if we compare the ages resulting from the
accretion-included models of Siess et al. (1999) and the fixed-mass models
of Bernasconi, it is less clear and often reversed if we compare the
accretion-included models of Siess et al. (1999) with the fixed-mass models
of Siess et al. (2000).
We find, however, that the differences in relative age (absolute age divided
by ZAMS age (Appendix E) for the same mass):
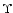 =
=
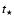 /
/
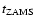 are much smaller.
are much smaller.
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{0269f044.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg228.gif) |
Figure 44:
Mass-accretion versus circumstellar extinction
(Table 2), with a linear-least-square line of the points
with 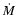 >10-8 >10-8
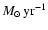 and without CQ Tau.
The arrow indicates the
and without CQ Tau.
The arrow indicates the
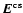 -value of -value of 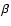 Pic. Pic. |
| Open with DEXTER |
Table 8:
Comparison of the determined stellar masses (
 )
and relative ages,
spectral type z indicates ZAMS.
)
and relative ages,
spectral type z indicates ZAMS.
In Table 8 we compare the masses and 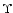 resulting from the
interpolation of the 3 sets of tracks.
In the latter case accretion during the evolution is taken into account.
The mass accretion rate was assumed to decrease exponentially after 4.5
resulting from the
interpolation of the 3 sets of tracks.
In the latter case accretion during the evolution is taken into account.
The mass accretion rate was assumed to decrease exponentially after 4.5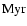 .
It should be noted that the relative ages obtained with the Case-B
grid are not systematically different from those obtained with the other 2
grids, although in Case-B the initial mass is lower and the initial evolution
slower than in the other models.
.
It should be noted that the relative ages obtained with the Case-B
grid are not systematically different from those obtained with the other 2
grids, although in Case-B the initial mass is lower and the initial evolution
slower than in the other models.
Figure 43 shows the distribution of the accretion rates
(derived above from the UV spectra) with the relative age of the stars in
our sample.
We note that the higher rates occur for 0.45<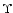 <0.80
and that outside this range we only find lower rates.
Rates of <10-7
<0.80
and that outside this range we only find lower rates.
Rates of <10-7
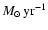 ,
which occur for 0.55<
,
which occur for 0.55<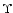 <0.70,
appear to correspond to a group of non-variable stars, among which are the
formerly variable stars BN Ori and V351 Ori.
The stars in the trapezium shaped region labelled non-variable stars
mainly contains stars that are not photometrically variable
(details in Tables 2 and 8).
CQ Tau also appears in this region, presumably because its rate is derived from
spectra obtained at high brightness, in which the accretion activity is low
(Kozlova et al. 2000). Figure 43 suggests that:
<0.70,
appear to correspond to a group of non-variable stars, among which are the
formerly variable stars BN Ori and V351 Ori.
The stars in the trapezium shaped region labelled non-variable stars
mainly contains stars that are not photometrically variable
(details in Tables 2 and 8).
CQ Tau also appears in this region, presumably because its rate is derived from
spectra obtained at high brightness, in which the accretion activity is low
(Kozlova et al. 2000). Figure 43 suggests that:
- (1)
- during the approach to the ZAMS
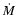
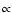
 .
.
Although the decrease is to be expected, the mechanism for this
behaviour is not yet clear; and
- (2)
- during the early evolution
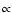
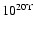 .
.
If this is true, the young (
 2.25
2.25 ,
,
 =0.39)
2
=0.39)
2
 star, SU Auri, can be the precursor of a 2.4
star, SU Auri, can be the precursor of a 2.4
 star
(with
star
(with
 3.25
3.25 ,
,
 =0.58), if the average mass accretion rate
becomes 4
=0.58), if the average mass accretion rate
becomes 4  10-7
10-7
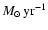 and if there is negligible mass loss from the sytem
during this phase (b
and if there is negligible mass loss from the sytem
during this phase (b
 B, Fig. 43).
In the same way the 1.7
B, Fig. 43).
In the same way the 1.7
 star HD 283572 (with
star HD 283572 (with
 6.7
6.7 ,
,
 =0.41) can become a 1.77
=0.41) can become a 1.77
 star with
star with
 =10
=10 (
(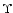 =0.60), if its present rate of
=0.60), if its present rate of  10-9
10-9
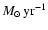 is increasing
by a factor 20 (a
is increasing
by a factor 20 (a
 A, Fig. 43).
A, Fig. 43).
6.3 Circumstellar extinction
The other products of the UV3C analysis are
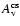 and
and
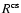 ,
or
,
or
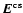 (Table 2).
The relation between
(Table 2).
The relation between
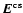 and
and 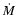 (Fig. 44) is not completely
clear.
The figure may suggest that significant
(Fig. 44) is not completely
clear.
The figure may suggest that significant
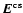 dust excesses only occur for
sufficiently high accretion rates as expected for bipolar outflow during
accretion.
However, the number of stars in our sample with a low accretion rate is too low
to be statistically significant, which does not permit us to draw a definite
conclusion.
In addition, for the points with
dust excesses only occur for
sufficiently high accretion rates as expected for bipolar outflow during
accretion.
However, the number of stars in our sample with a low accretion rate is too low
to be statistically significant, which does not permit us to draw a definite
conclusion.
In addition, for the points with 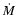 >10-8
>10-8
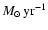 ,
the
,
the
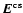 is correlated
neither with accretion rate (as suggested by the dispersion around the linear
least-square line in the figure) nor with the stellar mass.
is correlated
neither with accretion rate (as suggested by the dispersion around the linear
least-square line in the figure) nor with the stellar mass.
With the IUE a large collection of PMS Ae/Fe stars has been observed.
This invites us to look for common properties and for variation of properties
with spectral type and visual brightness.
For this purpose we decided to analyse the low-resolution UV spectra in
terms of a simple model with 3 components: a photosphere, an accretion disc, and
a boundary-layer (BL) between star and disc![[*]](/icons/foot_motif.gif) .
As a result we often find spectral types that are different from the types
quoted in the literature (as e.g. used by Valenti et al. 2000), which are
generally derived from visual spectroscopy.
.
As a result we often find spectral types that are different from the types
quoted in the literature (as e.g. used by Valenti et al. 2000), which are
generally derived from visual spectroscopy.
Some of the classification tools in the visual may not be reliable for
estimating the spectral type of PMS Ae/Fe stars.
In particular the presence of He I absorption lines at 5876 Å and
6678 Å has often been used as an indicator that a star has a hot
photosphere and that the star should be classified as B9 or earlier.
However, we find these absorption lines in the spectra of many Herbig stars,
which we classify from their UV continuum as types A2e up to F8.
Examples are
WW Vul, UX Ori (A2-3e), BF Ori (A4-7e), CQ Tau (F2e) (Grinin et al. 2001),
HD 150193 (A4e) (Catala et al. 1986),
HR 5999 (A7e), NX Pup (F2e), NV Ori (F6e) (Böhm & Catala 1995),
HD 142666 (A8e) (Dunkin et al. 1997b),
HD 163296 (A3-4e), HD 104237 (A7e) (Morrison 1997),
HD 36112 (A7e) (Beskrovnaya et al. 1999),
R CrA (A5-F2e) (Graham 1992),
AK Sco (F5e), CO Ori (F8e) (deWinter 1998), and
SU Aur (G2-5e) (Petrov 1996).
In many cases the strength of the He I lines is highly variable on time
scales of days and in such cases the absorption component sometimes disappears
completely (e.g. RR Tau and CQ Tau, Kozlova et al. 2000; Grinin et al. 2001).
Because of the high excitation energy, the large width, and the variability of
the lines we suspect that they are formed in a hot part of the accretion disc
or its turbulent atmosphere.
In cases where the He I lines are in emission they could be formed in a
chromosphere around the star for spectral types later than F2, and for earlier
spectral types in a layer around the accretion disc.
For certain Herbig stars there may be evidence of accretion guided by
magnetic channelling from the disc (e.g. HD 104237), but so far such cases are
rare in comparison with the many cases of evidence for such processes in
T Tauri stars.
In the simple UV3C model the emission from nearby dust is also ignored.
We simulated the UV spectra of the stellar and BL components by
low-resolution UV spectra of standard stars and that of the disc by a Planck
spectrum.
The BL spectral types B8 I and B9 I have effective temperatures that
agree with those predicted by the theoretical 1-D BL models.
After adoption of a value for the distance and the foreground colour excess
from the literature and the disc inclination from various arguments, we matched
the low-resolution UV spectral flux between 1200 and 3200 Å for each star
together with the flux in the  -band, by varying the spectral and
luminosity types of photosphere and BL, the width of the BL,
and the ratio of total to specific absorption for circumstellar dust
-band, by varying the spectral and
luminosity types of photosphere and BL, the width of the BL,
and the ratio of total to specific absorption for circumstellar dust
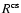 .
From the UV3C-model parameters we obtained values for radius and luminosity
of the photosphere (which locates the star in the HRD), the circumstellar excess,
and values of the width and temperature of the BL, all of which allowed us
to estimate the accretion rate.
In the case of double stars the brightness ratio of the components gives an
additional constraint.
Two kinds of comparisons have been made:
.
From the UV3C-model parameters we obtained values for radius and luminosity
of the photosphere (which locates the star in the HRD), the circumstellar excess,
and values of the width and temperature of the BL, all of which allowed us
to estimate the accretion rate.
In the case of double stars the brightness ratio of the components gives an
additional constraint.
Two kinds of comparisons have been made:
[A] Time variation of individual stars
- (1)
- HD 163296, HD 104237, HD 199143, HR 5999, and AK Sco were observed
with IUE during several days with time intervals of several hours.
From the rotation rates we can derive the succesive parts of the surface
we are observing during each exposure.
Small variations in continuum flux and in emission-line fluxes were
noted.
Only HD 163296 (Sects. 5.11 and A.2) and AK Sco
(Sects. 5.9 and 5.11) have been discussed shortly
here.
- (2)
- for UX Ori, BF Ori, HR 5999, and CQ Tau we have spectra at various
phases of visual brightness, but separated in time by months or years.
The parameter that mainly varies is
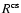 ,
but for fainter phases of the
stars the agreement between model spectrum and observed spectrum becomes
less satisfactory in the wavelength range 1800-2300 Å.
This suggests that the assumed c.s. dust extinction laws are not adequate
for increasing obscuration of the stars.
,
but for fainter phases of the
stars the agreement between model spectrum and observed spectrum becomes
less satisfactory in the wavelength range 1800-2300 Å.
This suggests that the assumed c.s. dust extinction laws are not adequate
for increasing obscuration of the stars.
[B] Evolutionary trends
We have obtained the positions of the stars in the HRD.
From the evolutionary calculations of Palla, Bernasconi, and Siess
we estimated values for the mass and age of each star.
Table 8 shows that the differences between the results of
the estimates from the models of Bernasconi and Siess are in general
small.
On the other hand, the spectral matching also provides us with the accretion
rate and the c.s. dust colour excess of each star.
The rates appear to have the same dependence on mass as T Tauri stars.
This may suggest that these rates have the same origin; i.e. they are
controlled by the conditions in the molecular clouds in which they were formed.
However, we expect that the intrinsic evolution of the star-disc systems will
have a significant influence on the presently obtained accretion rates.
Figure 43 suggests an increase in the accretion rate during
early phases of the contraction towards the MS and a decrease during the
approach to the ZAMS.
It is curious that the non-variable stars seem to have lower accretion rates
than the variable stars of the same relative age between 0.5 and 0.7.
Finally we applied the UV3C parameters to predict the SEDs of the stars
in the visual and NIR.
For B- and A-type stars the flux contribution of the BL is only significant
in the U and B-photometric bands.
The relative flux contribution of the disc increases with increasing wavelength.
In several cases the observed fluxes show an NIR excess with respect to the
calculated model fluxes, which can be interpreted by the presence of dust
in the neighbourhood of the star.
There are also a number of cases where the contribution of the disc seems
larger than observed.
In these cases the introduction of an optically-thin hole in the inner part
of the optical thick disc improves the agreement of the model with the observed
SED (see Hil92), while the other parameters of the UV3C model retain their
values.
In Appendix A we give several observations and theoretical
arguments that seem to support the UV3C-model.
Acknowledgements
The authors are grateful to F. Palla, P. Bernasconi, and L. Siess
for providing us with the files of their models for the PMS evolution
of intermediate mass stars.
Along with the support by the VILSPA and GSFC Operational staff during
the IUE observations, we are also indebted to the staff at the IUE spectral
archives ULDA, INES, and NEWSIPS.
We also thank the contributors to the photometric archive of Wesleyan Observatory,
that of the ROTOR group at Maidanak Observatory (Uzb.), the LTPV-group of ESO
observers (Sterken 1983), and the observations of deWinter et al.
Photometry on the Walraven system was obtained at ESO.
Most of the stellar distances were supplied by the Hipparcos Catalogue.
The authors wish to thank the referee for valuable suggestions for improving
this paper.
- Adams, F. C., &
Shu, F. H. 1986, ApJ, 308, 836 [NASA ADS] [CrossRef] (In the text)
- Adams, F. C., Lada,
C. J., & Shu, F. H. 1987, ApJ, 312, 788 [NASA ADS] [CrossRef] (In the text)
- Adams, W. S., Joy, A.
H., Humason, M. L., & Brayton, A. M. 1935, ApJ, 81, 187 [NASA ADS] [CrossRef] (In the text)
- Akeson, R. L.,
Ciardi, D. R., van Belle, G. T., & Creech-Eakman, M. J. 2002,
ApJ, 566, 1124 [NASA ADS] [CrossRef] (In the text)
- Alencar, S. H.
P., Melo, C. H. F., Dullemond, C. P., et al. 2003, A&A, 409,
1037 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- vandenAncker, M. E.
1996, Master's Thesis University of Amsterdam The Evolutionary
Status of Herbig Ae/Be Stars
- vandenAncker, M. E.,
Thé, P. S., & deWinter, D. 1996, A&A, 309, 809 [NASA ADS] (In the text)
- vandenAncker, M. E.,
Thé, P. S., TjinADjie, H. R. E., et al. 1997, A&A, 324,
L33 [NASA ADS] (ATT97)
- vandenAncker, M. E.,
deWinter, D., & TjinADjie, H. R. E. 1998, A&A, 330, 145 [NASA ADS]
(AWT98)
- vandenAncker, M. E.,
Pérez, M. R., deWinter, D., & McCollum, B. 2000, A&A,
363, L25 [NASA ADS] (In the text)
- vandenAncker, M. E.,
Blondel, P. F. C., TjinADjie, H. R. E., et al. 2004, MNRAS, 349,
1516 [NASA ADS] [CrossRef] (In the text)
- Andersen, J.,
Lindgren, H., Hazen, M. L., & Mayor, M. 1989, A&A, 299, 933
(And89)
(In the text)
- Armitage, P.
J., & Clarke, C. J. 1996, MNRAS, 280, 458 [NASA ADS] (In the text)
- Artyukhina,
N. M. 1959, AZh, 36, 832 [NASA ADS] (SvA, 3, 808)
(In the text)
-
Artyukhina, N. M. 1960, AZh, 37, 95 [NASA ADS] (SvA, 4, 91)
(In the text)
- Augereau, J.
C., Langrange, A. M., Mouillet, D., & Ménard, F. 2001,
A&A, 365, 78 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Aveni, A. F., &
Hunter, J. H. 1969, AJ, 74, 1021 [NASA ADS] [CrossRef] (In the text)
- Baade, D., &
Stahl, O. 1989a, A&A, 209, 255 [NASA ADS] (In the text)
- Baade, D., &
Stahl, O. 1989b, A&A, 209, 268 [NASA ADS] (In the text)
- Barrado y
Navascués, D., Stauffer, J. R., Song, I., & Caillault,
J.-P. 1999, ApJ, 520, L123 [NASA ADS] [CrossRef] (In the text)
- Barth, W., Weigelt,
G., & Zinnecker, H. 1994, A&A, 291, 500 [NASA ADS] (In the text)
- Barylak, M. 1989,
IUE ESA Newsletter, 33, 20 (In the text)
- Basri, G., &
Bertout, C. 1989, ApJ, 341, 340 [NASA ADS] [CrossRef] (In the text)
- Berdyugin, A.
V., Berdyugina, S. V., Grinin, V. P., & Minikulov, N. Kh. 1990,
AZh, 67, 812 [NASA ADS] (SvA, 34, 408)
(In the text)
- Berdyugin, A.
V., Grinin, V. P., & Minikulov, N. Kh. 1992, Izvestiya Krimskoi
Astr. Obs., 86, 69 [NASA ADS]
- Bernacca, P.
L., Lattanzi, M. G., Bucciarelli, B., et al. 1993, A&A, 278,
L47 [NASA ADS] (In the text)
- Bernacca, P.
L., Lattanzi, M. G., Porro, I., Neuhäuser, R., &
Bucciarelli, B. 1995, A&A, 299, 933 [NASA ADS] (In the text)
- Bernasconi,
P. A. 1996, A&AS, 120, 57 [EDP Sciences] [NASA ADS] (In the text)
- Bertout, C.,
Basri, G., & Bouvier, J. 1988, ApJ, 330, 350 [NASA ADS] [CrossRef] (BBB88)
(In the text)
- Bertout, C.,
& Regev, O. 1992, ApJ, 399, L163 [NASA ADS] [CrossRef] (In the text)
- Bertout, C.,
Robichon, N., & Arenou, F. 1999, A&A, 352, 574 [NASA ADS] (In the text)
-
Beskrovnaya, N. G., & Pogodin, M. A. 1996, Astro. Lett., &
Comm., 34, 321, Adv. Study Inst. on Solar and Astrop. MHD flows,
Heraklion, Greece 1995
(In the text)
-
Beskrovnaya, N. G., Pogodin, M. A., Miroshnichenko, A. S., et al.
1999, A&A, 343, 163 [NASA ADS] (In the text)
- Bessel, M. S.,
& Eggen, O. J. 1972, ApJ, 177, 209 [NASA ADS] [CrossRef] (In the text)
- Bibo, E. A., &
Thé, P. S. 1990, A&A, 236, 155 [NASA ADS] (In the text)
- Blondel, P. F.
C., & TjinADjie, H. R. E. 1994, ASP Conf. Ser., 62, 211 [NASA ADS]
(In the text)
- Blondel, P. F.
C., & TjinADjie, H. R. E. 1996, Lecture Notes in Physics, 465
(Heidelberg: Springer-Verlag), Proceedings Disks and Outflows
around Young Stars, Heidelberg 5-9 september 1994, ed. S. V. W.
Beckwith, J. Staude, A. Quetz, & A. Natta
- Blondel, P. F.
C., TjinADjie, H. R. E., & Thé, P. S. 1989, A&A, 80,
115 (In the text)
- Blondel, P. F.
C., Talavera, A., & TjinADjie, H. R. E. 1993, A&A, 268,
624 [NASA ADS] (In the text)
- de Boer, K. S. 1977,
A&A, 61, 605 [NASA ADS]
- Böhm, T., &
Catala, C. 1995, A&A, 301, 155 [NASA ADS] (In the text)
- Bond, H. E. 1970, PASP,
82, 1065 [NASA ADS] [CrossRef] (In the text)
- Bondi, H., &
Hoyle, F. 1944, MNRAS, 104, 273 [NASA ADS]
- Boyd, C. D. 1936,
Harvard Bull., 904, 18 (In the text)
- Brand, P. W. J. L.,
Hawarden, T. G., Longmore, A. J., Williams, P. M., & Caldwell,
J. A. R. 1983, MNRAS, 203, 215 [NASA ADS] (In the text)
- Brandner, W.,
Bouvier, J., Grebel, E. K., et al. 1995, A&A, 298, 818 [NASA ADS] (In the text)
- Brandner, W.,
Lehman, T., Schöller, M., Weigelt, G., & Zinnecker, H.
1996, ESO Mess., 83, 43 [NASA ADS] (In the text)
- Brown, A., TjinADjie,
H. R. E., Blondel, P. F. C., et al. 1997, ASP Conf. Ser., 121 (IAU
Coll., 163), Accretion Phenomena and Related Outflow, Port Douglas,
Queensland, 1996, ed. D. T. Wickramasinghe, L. Ferrario, & G.
V. Bicknell
(In the text)
- Brunini, A.,
& Benvenuto, O. G. 1996, MNRAS, 283, L84 [NASA ADS] (In the text)
- Burbidge, E.
M., & Burbidge, O. J. 1954, ApJ, 119, 501 [NASA ADS] [CrossRef] (In the text)
- Cameron, A. C.,
& Campbell, C. G. 1993, A&A, 274, 309 [NASA ADS] (In the text)
- Cameron, A. C.,
Campbell, C. G., & Quaintrell, H. 1995, A&A, 298, 133 [NASA ADS] (In the text)
- Cannon, A. J. 1931,
Harvard Ann., 100, 87 (In the text)
- Cantó, J.,
D'Alessio, P., & Lizano, S. 1995, RevMexAASC, 1, 217 [NASA ADS] (In the text)
- Cardelli, J.
A., Clayton, G. C., & Mathis, J. S. 1988, ApJ, 329, L33 [NASA ADS] [CrossRef] (In the text)
- Cardelli, J.
A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] (In the text)
- Catala, C., Czarny,
J., Felenbok, P., & Praderie, F. 1986, A&A, 154, 103 [NASA ADS] (In the text)
- Catala, C., Simon,
T., Praderie, F., et al. 1989, A&A, 221, 273 [NASA ADS] (In the text)
- Chauvin, G.,
Fusco, T., Lagrange, A.-M., et al. 2002, A&A, 394, 223 (In the text)
- Cincotta, P.
M., Méndez, N., & Núñes, J. A. 1995, ApJ, 449,
231 [NASA ADS] [CrossRef] (In the text)
- Claria, J. J. 1974,
A&A, 37, 229 [NASA ADS] (In the text)
- Cohen, M., &
Schwartz, R. D. 1976, MNRAS, 174, 137 [NASA ADS]
- Cohen, M., &
Kuhi, L. V. 1979, ApJS, 41, 743 [NASA ADS] [CrossRef] (CK79)
- Corcoran, M.,
& Ray, T. P. 1995, A&A, 301, 729 [NASA ADS] (In the text)
- Corporan, P.,
& Lagrange, A.-M. 1999, A&AS, 136, 429 [EDP Sciences] [NASA ADS]
- Covino, E.,
Terranegra, L. V., Vittone, A. A., & Russo, G. 1984, AJ, 89,
12 (In the text)
- Crifo, F.,
Vidal-Madjar, A., Lallement, R., Ferlet, R., & Gerbaldi, M.
1997, A&A, 320, L29 [NASA ADS] (In the text)
- Devine, D., Grady,
C. A., Kimble, R. A., et al. 2000, ApJ, 542, L115 [NASA ADS] [CrossRef] (In the text)
- Donati, J.-F.,
Semel, M., Carter, B. D., Rees, D. E., & Cameron, A. C. 1997,
MNRAS, 291, 658 [NASA ADS] (In the text)
-
Dragomiretskaya, B. A. 1965, Afz., 1, 455 (Astroph., 1, 241)
(In the text)
- Dunkin, S. K.,
Barlow, M. J., & Ryan, S. G. 1997a, MNRAS, 286, 604 [NASA ADS] (In the text)
- Dunkin, S. K.,
Barlow, M. J., & Ryan, S. G. 1997b, MNRAS, 290, 165 [NASA ADS] (In the text)
- Dutrey, A. 2000,
Workshop Herbig Ae/Be stars Amsterdam 25-27 Oct. 2000
(In the text)
- Eaton, N. L., &
Herbst, W. 1995, AJ, 110, 2369 [NASA ADS] [CrossRef]
- Eggen, O. J. 1998,
AJ, 116, 1322 [NASA ADS] (In the text)
- Eiroa, C., Oudmaijer,
R. D., Davies, J. K., et al. 2002, A&A, 384, 1038 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Elias, J. H. 1978a,
ApJ, 224, 453 [NASA ADS] [CrossRef] (In the text)
- Elias, J. H. 1978b,
ApJ, 223, 859 [NASA ADS] [CrossRef]
- Eugenio, M.,
& Mendoza, V. 1966, ApJ, 143, L1010 [CrossRef]
- Evans, A., Davies, J.
K., Kilkenny, D., & Bode, M. F. 1989, MNRAS, 237, 695 [NASA ADS] (In the text)
- ESA 1997, The Hipparcos
and Tycho Catalogues, ESA SP-1200
- ESO Scientific Reports 8
(1991), 12 (1993), 14 (1994) & 16 (1995)
- Felenbok, P.,
Praderie, F., & Talavera, A. 1983, A&A, 128, 74 [NASA ADS] (In the text)
- Fernández, M.,
& Eiroa, C. 1995, A&A, 310, 143 [NASA ADS] (In the text)
- Fernández, M.,
Ortiz, E., Eiroa, C., & Miranda, L. F. 1995, A&AS, 114,
439 [NASA ADS]
-
Finkenzeller, U. 1985, A&A, 151, 340 [NASA ADS] (Fz85)
-
Finkenzeller, U., & Jankovics, I. 1984, A&AS, 57, 285 [NASA ADS]
(FJ84)
-
Finkenzeller, U., & Mundt, R. 1984, A&AS, 55, 109 [NASA ADS]
- Friedemann,
C., Reimann, H. G., Gürtler, J., & Tóth, V. 1993,
A&A, 277, 184 [NASA ADS]
- Garrison, L. M.
jr. 1978, ApJ, 224, 535 [NASA ADS] [CrossRef] (In the text)
-
Glagolevskii, Y. V., & Choutonov, G. A. 1998, Bull. Spec.
Astrop. Obs., 45, 105 [NASA ADS]
- Godon, P. P. 1996,
ApJ, 463, 674 [NASA ADS] [CrossRef] (In the text)
- Gómez de Castro, A.
I., & Fernández, M. 1996, MNRAS, 283, 55 [NASA ADS] (In the text)
- Götz, W., &
Wenzel, W. 1968, Mit. Ver. St., 5, 13 (In the text)
- Grady, C. A.,
Pérez, M. R., Thé, P. S., et al. 1995, A&A, 302,
472 [NASA ADS] (In the text)
- Grady, C. A.,
Pérez, M. R., Talavera, A., et al. 1996, A&AS, 120,
157 [EDP Sciences] [NASA ADS] (In the text)
- Grady, C. A., Devine
D., Woodgate B., et al. 2000, ApJ, 544, 895 [NASA ADS] [CrossRef] (In the text)
- Grinin, V. P. 1988,
Pis'ma AZh, 14, 65 (SvA Lett., 14, 27)
(In the text)
- Grinin, V. P.,
& Rostopchina, A. N. 1996, AZh, 73, 194 (Astr. Rep., 40,
171)
(In the text)
- Grinin, V. P.,
Kiselev, N. N., Minikulov, N. Kh., & Chernova, G. P. 1988,
Pis'ma AZh, 14, 514 (SvA Lett., 34, 84)
- Grinin, V. P.,
Kozlova, O. V., Natta, A., et al. 2001, A&A, 379, 482 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- de Groot, M. 1971,
ESO Ann. Rep., 32
(In the text)
- Gurzadyan, G.
A., & Rustambekova, S. S. 1980, Ap&SS, 69, 295 [NASA ADS] (In the text)
- Haas, M., Christov, J.
C., Zinnecker, H., Ridgway, S. T., & Leinert, Ch. 1993,
A&A, 269, 282 [NASA ADS] (In the text)
- Hamann, F., &
Persson, S. E. 1992, ApJS, 82, 285 [NASA ADS] [CrossRef] (In the text)
- Hartigan, P.,
& Graham, J. H. 1987, ApJ, 93, 913 [NASA ADS]
- Hartmann, L.,
Kenyon, S. J., Hewett, R., et al. 1989, ApJ, 338, 1001 [NASA ADS] [CrossRef] (In the text)
- Hartmann, L.
W., Kenyon, S. J., & Calvet, N. 1993, ApJ, 407, 219 [NASA ADS] [CrossRef]
- Heber, U., Hunger,
K., Jonas, G., & Kudritski, R. P. 1984, A&A, 130, 119 [NASA ADS] (In the text)
- Herbertz, R.,
Ungerechts, H., & Winnewasser, G. 1991, A&A, 249, 483 [NASA ADS]
- Herbig, G. H. 1954,
Trans. IAU, 8, 805 (Hb54)
- Herbig, G. H.
1960a, ApJS, 43, 337 [NASA ADS] [CrossRef] (Hb60a)
- Herbig, G. H.
1960b, ApJ, 131, 632 [NASA ADS] [CrossRef] (Hb60b)
- Herbig, G. H. 1966,
Vistas Astron., 8, 109 [NASA ADS] [CrossRef] (Hb66)
- Herbig, G. H.,
& Bell, K. R. 1988, Lick Obs. Bull., 1111 (HB88)
- Herbst, W. 1994,
ASP Conf. Ser., 62, 35 [NASA ADS]
(In the text)
- Herbst, W., &
Shevchenko, V. S. 1999, AJ, 118, 1043 [NASA ADS] [CrossRef] (In the text)
- Herbst, W., Booth,
J. F., Koret, D. L., et al. 1987, AJ, 94, 137 [NASA ADS] [CrossRef] (In the text)
- Herbst, W.,
Herbst, D. K., Grossman, E. J., & Weinstein, D. 1994, AJ, 108,
1906 [NASA ADS] [CrossRef]
- Hessman, F. V.,
Eislöffel, J., Mundt, R., et al. 1991, ApJ, 370, 384 [NASA ADS] [CrossRef] (In the text)
-
Hillenbrand, L. A., Strom, S. E., Vrba, F. J., & Keene, J.
1992, ApJ, 397, 613 [NASA ADS] [CrossRef] (Hil92)
(In the text)
- Hobbs, L. M. 1974,
ApJ, 191, 381 [NASA ADS] [CrossRef] (In the text)
- Hu, J. Y., Thé, P. S.,
& deWinter, D. 1989, A&A, 208, 213 [NASA ADS] (In the text)
- Hu, J. Y., Blondel, P. F.
C., Catala, C., et al. 1991, A&A, 248, 150 [NASA ADS] (In the text)
- Hughes, J.,
Hartigan, P., & Clampitt, L. 1993, AJ, 105, 571 [NASA ADS] [CrossRef] (In the text)
- Hutchinson,
M. G., Albinson, J. S., Barrett, P., et al. 1994, A&A, 285,
883 [NASA ADS] (In the text)
- Imhoff, C., &
Wasatonic, R. 1986, IUE NASA Newsletter, 29, 45 (In the text)
- Irvine, N. J. 1975,
PASP, 87, 78 [NASA ADS] (In the text)
- Jaschek, M.,
Jaschek, C., & Andrillat, Y. 1988, A&AS, 72, 505 [NASA ADS] (In the text)
-
Jayawardhana, R., & Brandeker, A. 2001, ApJ, 561, L111 [NASA ADS] [CrossRef]
- Johnson, H. M.
1964, ApJ, 142, 964 [NASA ADS] [CrossRef] (In the text)
- Joncour, I.,
Bertout, C., & Bouvier, J. 1994, A&A, 291, L19 [NASA ADS]
- Joy, A. H. 1949, ApJ,
110, 424 [NASA ADS] [CrossRef] (In the text)
- Kenyon, S. J.,
Hartmann, L. W., & Hewitt, R. 1988, ApJ, 325, 231 [NASA ADS] [CrossRef] (In the text)
- Kenyon, S. J.,
Hartmann, L. W., Imhoff, C., & Cassatella, A. 1989, ApJ, 344,
925 [NASA ADS] [CrossRef] (In the text)
- Kholopov, P. N.
1959, AZh, 36, 295 [NASA ADS] (SvA, 3, 291) (Kh59)
- Kholopov, P. N.
1985, Gen. Cat. of Var. Stars 4
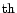 Ed. (Moscow: Nauka Pub.) (Kh85)
Ed. (Moscow: Nauka Pub.) (Kh85)
- Kilkenny, D.,
Whittet, D. C. B., Davies, J. K., et al. 1985, South Afr. Obs.
Circ., 9, 55 [NASA ADS] (In the text)
- Kley, W., & Lin, D.
N. C. 1996, ApJ, 461, 933 [NASA ADS] [CrossRef] (In the text)
- Knee, L. B. G., &
Prusti, T. 1996, A&A, 312, 455 [NASA ADS] (In the text)
- Koen, C. 2003, MNRAS,
341, 1385 [NASA ADS] [CrossRef] (In the text)
- Kolotilov, E.
A., & Zajtseva, G. V. 1974, Afz, 10, 365 (Astroph., 10,
228)
- Kondo, Y., &
Bruhweiler, F. C. 1985, ApJ, 291, L1 [NASA ADS] [CrossRef] (In the text)
- Koresko, C. D.,
Beckwith, S. V. W., Ghez, A. M., Matthews, K., & Neugebauer, G.
1991, AJ, 102, 2073 [NASA ADS] [CrossRef] (In the text)
- Koval'chuk, G. H.
1984, IBVS, 248, 2 [NASA ADS] (Konkoly Obs. Budapest)
(In the text)
- Koval'chuk, G. H.
1985, Afz, 23, 255 [NASA ADS] (Astroph., 23, 514)
(In the text)
- Koval'chuk, G. H.
1986, Afz, 24, 213 [NASA ADS] (Astroph., 24, 213)
(In the text)
- Kozlova, O. V.,
Grinin, V. P., & Rostopchina, A. N. 2000, AZh, 77, 1 (Astron.
Rep., 44, 1)
(In the text)
- Krautter, J.
1980, A&A, 89, 74 [NASA ADS] (In the text)
- Krautter, J.
1991, Low Mass Star Formation in Southern Molecular Clouds, ESO
Rep., 11, 127
- Kurtz, D. W., &
Marang, F. 1995, MNRAS, 276, 191 [NASA ADS] (In the text)
- Kurtz, D. W., &
Müller, M. 1999, MNRAS, 310, 1071 [NASA ADS] [CrossRef] (In the text)
- Kurtz, D. W., &
Müller, M. 2001, MNRAS, 325, 1341 [NASA ADS] [CrossRef] (In the text)
- Kurucz, R. L. 1979,
ApJS, 40, 1 [NASA ADS] [CrossRef] (In the text)
- Kurucz, R. L. 1991,
in Precision Photometry: Astrophysics of the Galaxy, ed. A. G.
Davis Philip, A. R. Upgren, & K. A. Janes (Schenectady, New
York: L. Davis press)
(In the text)
- Lanz, T., Heap, S. R.,
& Hubeny, I. 1995, ApJ, 447, L41 [NASA ADS] (In the text)
- Leinert, Ch.,
Richichi, A., Weitzel, N., & Haas, M. 1994, ASP Conf. Ser., 62,
155 [NASA ADS]
(In the text)
- Leinert, Ch.,
Richichi, A., & Haas, M. 1997, A&A, 318, 472 [NASA ADS] (In the text)
- Lioure, A., &
Le Contel, O. 1994, A&A, 285, 185 [NASA ADS] (In the text)
- Lub, J., & Pel, J. W.
1977, A&A, 54, 137 [NASA ADS] (In the text)
- Makarov, V.,
Bastian, U., Hoeg, E., Grossmann, V., & Wicenec, A. 1994, IAU
IBVS, 4118, 1 [NASA ADS] (In the text)
- Mannings, V.,
& Sargent, A. I. 1997, ApJ, 490, 792 [NASA ADS] [CrossRef] (In the text)
- Malfait, K.,
Bogaert, E., & Waelkens, C. 1998, A&A, 331, 211 [NASA ADS]
(MBW98)
- Marconi, M.,
Ripepi, V., Alcalá, J. M., et al. 2000, A&A, 355, L35 [NASA ADS] (In the text)
- Martin, E. L. 1993,
PASP, 105, 277 [NASA ADS] [CrossRef]
- Merrill, P. W.,
Burwell, C. G., & Miller, W. C. 1942, ApJ, 96, 15 [NASA ADS] [CrossRef] (In the text)
- Meeus, G., Waelkens,
C., & Malfait, K. 1998, A&A, 329, 131 [NASA ADS] (MWM98)
- Mihalas, D. 1966,
ApJS, 13, 1 [NASA ADS] [CrossRef]
-
Miroshnichenko, A. S., Bergner, Yu. K., & Kuratov, K. S. 1997,
Pis'ma AZh, 23,118 (SvA Lett., 23, 97)
- Mora, A., Merin, B.,
Solano, E., et al. 2001, A&A, 378, 116 [EDP Sciences] [NASA ADS] [CrossRef]
- Morrison, N. D.
1997 (priv. comm.)
(In the text)
- Murdin, P., &
Penston, M. V. 1977, MNRAS, 181, 657 [NASA ADS] (In the text)
- Muzerolle,
J., Luhman, K. L., Briceño, C., Hartman, L., & Calvet, N.
2005, ApJ, 625, 906 [NASA ADS] [CrossRef] (In the text)
- NASA RP-1190 1988, IRAS
Catalogs and Atlases Explanatory Supplement, ed. C. Beichman, G.
Neugebauer, H. J. Habing, P. E. Clegg, & T. J. Chester
(Washington, DC: GPO), Vol. 1
(In the text)
- Neuhäuser, R.,
Guenther, E., Mugrauer, M., Ott, Th., & Eckart, A. 2002,
A&A, 395, 877 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Ng, Y. K. 1986 (priv.
comm.)
(In the text)
- Olsen, E. H. 1979,
A&AS, 37, 367 [NASA ADS]
- Oudmaijer, R.
D., van der Veen, W. E. C. J., Waters, L. B. F. M., et al. 1992,
A&AS, 96, 625 [NASA ADS] (Oud92)
- Padoan, P.,
Kritsuk, A., & Norman, M. L. 2005, ApJ, 662, L61 [NASA ADS] [CrossRef] (In the text)
- Palla, F. 1997 (priv.
comm.)
- Palla, F., &
Stahler, S. W. 1993, ApJ, 418, 414 [NASA ADS] [CrossRef] (PS93)
- Palla, F., &
Stahler, S. W. 1999, ApJ, 525, 772 [NASA ADS] [CrossRef] (In the text)
- Paresce, F. 1991,
A&A, 247, L25 [NASA ADS] (In the text)
- Penston, M. V.,
Allen, D. A., & Lloyd, Ch. 1976, The Observatory, 96, 22 [NASA ADS] (In the text)
- Petrov, P. P.,
Gullbring, E., Ilyin, I., et al. 1996, A&A, 314, 821 [NASA ADS] (In the text)
- Pérez, M. R.
1991, IUE NASA Newsletter, 38, 27 (In the text)
- Pérez, M. R.,
Grady, C. A., & Thé, P. S. 1993, A&A, 274, 381 [NASA ADS] (In the text)
- Pérez, M. R.,
vandenAncker, M. E., deWinter, D., & Bopp, B. W. 2004, A&A,
416, 647 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Pinheiro, F. J.
G., Folha, D. F. M., Marconi, M., et al. 2003, A&A, 399,
271 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Pirzkal, N.,
Spillar, E. J., & Dyck, H. M. 1997, ApJ, 481, 392 [NASA ADS] [CrossRef] (In the text)
- Plavec, M. J.,
Weiland, J. L., & Koch, R. H. 1982, ApJ, 256, 206 [NASA ADS] [CrossRef] (In the text)
- Plavec, M. J. 1983,
ApJ, 275, 251 [NASA ADS] [CrossRef] (In the text)
- Pogodin, M. A.
1987, Pis'ma AZh, 13, 695 (SvA Lett., 13, 293)
(In the text)
- Pogodin, M. A.
1995, Ap&SS, 224, 539 [NASA ADS]
- Popham, R.,
Narayan, R., Hartmann, L. W., & Kenyon, S. J. 1993, ApJ, 415,
L127 [NASA ADS] [CrossRef] (In the text)
- Regev, A., &
Bertout, C. 1995, MNRAS, 272, 71 [NASA ADS] (In the text)
- Remijn, L. 1980,
Master's Thesis University of Amsterdam, Herbig Ae/Be stars
- Reipurth, B.
1983, A&A, 117, 183 [NASA ADS] (In the text)
- Reipurth, B.,
Pedrosa, A., & Lago, M. T. V. T. 1996, A&AS, 120, 229 [EDP Sciences] [NASA ADS] (In the text)
- Rossi, C., Errico,
L., Friedjung, M., et al. 1999, A&AS, 136, 95 [EDP Sciences] [NASA ADS] (In the text)
- Rydgren, A. E.
1980, AJ, 85, 444 [NASA ADS] [CrossRef] (In the text)
- Rydgren, A. E.,
Strom, S. E., & Strom, K. M. 1976, ApJS, 30, 307 [NASA ADS] [CrossRef]
- Schmidt-Kaler,
Th. 1982, in Landolt-Börnstein Tables, Vol. VI/2b,
Springer-Verlag (SK82)
- Schöller, M.,
Brandner, W., Lehman, T., Weigelt, G., & Zinnecker, H. 1996,
A&A, 315, 445 [NASA ADS] (In the text)
- Shevchenko
1989, Herbig Ae/Be stars, Tashkent Ed. FAN
Academic Sciences Uzbekistan (in Russian)
- Shevchenko,
V. S. 1994, AZh, 71, 572 [NASA ADS] (Astron. Rep., 38, 505)
(In the text)
- Shevchenko,
V. S. 1998, AZh, 76, 289 (Astron. Rep., 43, 246)
(In the text)
- Shevchenko,
V. S., Grankin, K. N., Ibrahimov, M. A., Melnikov, S. Yu., &
Yakubov, S. O. 1993, Ap&SS, 202, 121 [NASA ADS]
- Shevchenko,
V. S., Ezhkova, O. V., TjinADjie, H. R. E., et al. 1997, A&AS,
124, 33 [EDP Sciences] [NASA ADS] (In the text)
- Shevchenko,
V. S., Ezhkova, O. V., Ibrahimov, M. A., van den Ancker, M. E.,
& TjinADjie, H. R. E. 1999, MNRAS, 310, 210 [NASA ADS] [CrossRef] (In the text)
- Shore, S. N., &
King, A. R. 1986, A&A, 154, 263 [NASA ADS] (In the text)
- Siess, L., Forestini,
M., & Bertout, C. 1999, A&A, 342, 480 [NASA ADS] (In the text)
- Siess, L., Dufour,
M., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS] (In the text)
- Slettebak, A.
1982, ApJS, 50, 55 [NASA ADS] [CrossRef]
- Smith, B. A., &
Terrile, R. J. 1984, Science, 226, 1421 [NASA ADS] (In the text)
- Stecklum, B.,
Eckart, A., Henning, T., & Loewe, M. 1995, A&A, 296,
463 [NASA ADS]
- Steenman, H.,
& Thé, P. S. 1989, Ap&SS, 159, 189 [NASA ADS] (In the text)
- Sterken, C. 1983,
ESO Mess., 33, 10 [NASA ADS] (In the text)
- Strand, K. A. 1958,
ApJ, 128, 14 [NASA ADS] [CrossRef] (In the text)
- Strom, S. E., Strom,
K. M., Yost J., Carrasco L., & Grasdalen, G. 1972, ApJ, 173,
353 [NASA ADS] [CrossRef] (Str72)
- Strom, K. M., Strom,
S. E., Carrasco L., & Vrba, F. J. 1975, ApJ, 196, 489 [NASA ADS] [CrossRef] (In the text)
- Strömgren, B. 1948,
ApJ, 108, 242 [NASA ADS] [CrossRef] (In the text)
- Sylvester, R.
J., Barlow,, M. J., & Skinner, C. J. 1994, Ap&SS, 212,
261 [NASA ADS] (In the text)
- Sylvester, R.
J., Skinner, C. J., Barlow, M. J., & Mannings, V. 1996, MNRAS,
279, 915 [NASA ADS] (In the text)
- Talavera, A.,
Blondel, P. F. C., & TjinADjie, H. R. E. 1994, ASP Conf. Ser.,
62, 115 [NASA ADS]
(In the text)
- Tambotseva,
L. V., Grinin, V. P., Rodgers B., & Koslova, O. V. 2001, AZh,
78, 514 (Astron. Rep., 45, 442)
(In the text)
- Tessier, E.,
Bouvier, J., Beuzit, J. L., & Brandner, W. 1994, ESO Mess., 78,
1 (In the text)
- Testi, L., Palla, F.,
& Natta, A. 1998, A&AS, 133, 81 [EDP Sciences] [NASA ADS] (In the text)
- Thé, P. S., &
TjinADjie, H. R. E. 1978, A&A, 62, 439 [NASA ADS] (In the text)
- Thé, P. S.,
TjinADjie, H. R. E., Bakker R., et al. 1981, A&AS, 44, 451 [NASA ADS] (In the text)
- Thé, P. S.,
Felenbok, P., Cuypers, H., & TjinADjie, H. R. E. 1985a,
A&A, 149, 429 [NASA ADS] (In the text)
- Thé, P. S.,
TjinADjie, H. R. E., Catala, C., Praderie, F., & Felenbok, P.
1985b, ESO Mess., 41, 8 [NASA ADS] (In the text)
- Thé, P. S.,
TjinADjie, H. R. E., Steenman, H., & Wesselius, P. R. 1986,
A&A, 155, 347 [NASA ADS] (In the text)
- Thé, P. S.,
deWinter, D., & Pérez, M. R. 1994, A&AS, 104, 315 [NASA ADS]
(TWP94)
- Thé, P. S.,
Pérez, M. R., Voshchinnikov, N. V., & vandenAncker, M. E.
1996, A&A, 314, 233 [NASA ADS] (In the text)
- Thiébaut, E.,
Bouvier, J., Blazit, A., Bonneau, D., Foy, F. C., & Foy, R.
1995, A&A, 303, 795 [NASA ADS] (In the text)
- TjinADjie, H. R. E.,
Remijn, L., & Thé, P. S. 1984, A&A, 134, 273 [NASA ADS] (In the text)
- TjinADjie, H. R. E.,
Thé, P. S., Andersen, J., et al. 1989, A&AS, 78, 1 [NASA ADS] (In the text)
- TjinADjie, H. R. E.,
Blondel, P. F. C., Brown, A., & Harper, G. M. 1998, ESA-SP,
413, 133 [NASA ADS], Proceedings Ultraviolet Astrophysics, Beyond the IUE
Final Archive, Sevilla, Spain, November 11-14, 1997
(In the text)
- TjinADjie, H. R. E.,
& Blondel, P. F. C., in preparation (Paper II)
- Ungerechts,
H., & Thaddeus, P. 1987, ApJS, 63, 645 [NASA ADS] [CrossRef] (In the text)
- Valenti, J. A.,
Johns-Krull, C. M., & Linsky, J. L. 2000, ApJS, 129, 399 [NASA ADS] [CrossRef] (In the text)
- Vidal-Madjar, A.,
Lagrange-Henri, A.-M., Feldman, P. D., et al. 1994, A&A, 290,
245 [NASA ADS]
-
Voshchinnikov, N. V. 1989, Afz, 30, 509 [NASA ADS] (Astroph., 30, 313)
-
Voshchinnikov, N. V., & Karjukin, V. V. 1994, A&A, 288,
883 [NASA ADS] (In the text)
- Walker, H. J.,
& Wolstencroft, R. D. 1988, PASP, 100, 1509 [NASA ADS] [CrossRef] (WW88)
-
Wallenquist, A. 1937, Uppsala Medd., 71
- Walter, F. M.,
Brown, A., Linsky, J. L., et al. 1987, ApJ, 314, 297 [NASA ADS] [CrossRef] (In the text)
- Wamsteker,
W., Driessen, C., Muñoz, J. R., et al. 1989, A&AS, 79,
1 [NASA ADS] (In the text)
- Warren, W. H.,
& Hesser, J. E. 1978, ApJS, 36, 497 [NASA ADS] [CrossRef] (In the text)
- Weaver, W. M. B.,
& Hobson, S. W. 1988, PASP, 100, 1443 [NASA ADS] [CrossRef]
- Whitney, B. A.,
Clayton, G. C., Schulte-Ladbeck, R. E., et al. 1993, ApJ, 417,
687 [NASA ADS] [CrossRef] (In the text)
- deWinter, D. 1998 (priv.
comm.)
(In the text)
- deWinter, D., &
Thé, P. S. 1990, Ap&SS, 166, 99 [NASA ADS]
- deWinter, D., &
vandenAncker, M. R. 1991 (priv. comm.)
(In the text)
- deWinter, D., vandenAncker,
M. E., Maira A., et al. 2001, A&A, 380, 609 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Yi, I. 1994, ApJ, 428,
760 [NASA ADS] [CrossRef] (In the text)
- Zajtseva, G. V.
1973, Per. Zv., 19, 63 (In the text)
- Zajtseva, G. V.
1986, Afz., 25, 471 [NASA ADS] (Astroph., 25, 626)
(In the text)
- Zajtseva, G.
V., & Kolotilov, E. A. 1973, Afz, 9, 185 [NASA ADS] (Astroph., 9,
104)
Online Material
![\begin{figure}
\par\includegraphics[angle=270,width=14.9cm,clip]{0269f004.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg233.gif) |
Figure 4:
Model calculations with 4 different spectral types, each with the
standard  -value (SK82). -value (SK82). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=270,width=14.9cm,clip]{0269f005.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg234.gif) |
Figure 5:
Model "solutions'' for NX Pup with 4 different  and d combinations
so that
and d combinations
so that
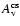 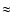 0
0
 708. 708. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=270,width=14.9cm,clip]{0269f006.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg235.gif) |
Figure 6:
Model calculations for NX Pup with 4 different BL types and sizes. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=270,width=14.9cm,clip]{0269f007.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg236.gif) |
Figure 7:
Model calculations for NX Pup with i=16 ,
45 ,
45 ,
70 ,
70 and 85
and 85 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=270,width=14.9cm,clip]{0269f009.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg238.gif) |
Figure 9:
As Fig. 4 but with changed  -values
to match the observed spectrum. -values
to match the observed spectrum. |
| Open with DEXTER |
Appendix A: Justification of the UV3C-model
In this section we give some arguments that justify our choice of the employed
model considering that several alternative interpretations of the UV
emission/excess (UVE) can be considered.
Although several of the discussed objects are known to be double stars, the UVEs
that appear when the observed spectrum is compared with a standard star of the
same -visual- spectral type have spectral shapes that correspond to a supergiant
spectrum.
The brightness, however, is far less than what would be expected from a
supergiant at the distance of the observed stellar system.
The same argument holds for the cases in which a giant spectrum was used.
A.2 Hot surface spots
Direct evidence of the presence of hot accretion spots at the stellar surface
has been found for the cTT DI Cep (Gómez de Castro & Fernández 1996).
This interpretation is based on the correlation between the variation in the UV
continuum and emission-line flux (in the SW-part of IUE) and on the simultaneous
variation in the brightness (
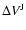 =0
=0
 2) with
2) with 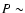 11
11
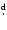 (Fernández & Eiroa 1995).
(Fernández & Eiroa 1995).
In our sample of PMS Ae/Fe stars, we have only one star, HD 163296 (A3 V), which
has been monitored in the SW-part of IUE with sufficient time-resolution to
test the possibility of a hot surface spot.
The stellar rotation period (
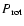 )
can be estimated from
)
can be estimated from
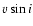 =
120+20-30
=
120+20-30
 (Fz85) and
(Fz85) and
 =1.76
=1.76
 (Table 2).
For i=57
(Table 2).
For i=57 ,
this results in
,
this results in
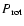 =13
=13
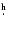 91
+4.63-2.00.
91
+4.63-2.00.
Two sequences of UV spectra have been obtained![[*]](/icons/foot_motif.gif) in 1986 and 1987 (Table F.5).
During these campaigns the FES camera operated well and could be used for
photometric monitoring with an accuracy of
in 1986 and 1987 (Table F.5).
During these campaigns the FES camera operated well and could be used for
photometric monitoring with an accuracy of 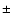 0
0
 05 in
05 in  .
.
In spite of many attempts to detect periodicities in the  -band fluxes and UV
emission-line fluxes with both Fourier-methods and information-entropy
minimalisation methods (Cincotta et al. 1995), no significant periodicity
could be found.
We were also not able no find any direct correlation between the flux
variations in the UV and visual.
The flux observed shortward of 1600 Å varies irregularly by at most 30%, but
never disappears completely.
Unless HD 163296 is seen "pole-on'' (which seems improbable in view of
-band fluxes and UV
emission-line fluxes with both Fourier-methods and information-entropy
minimalisation methods (Cincotta et al. 1995), no significant periodicity
could be found.
We were also not able no find any direct correlation between the flux
variations in the UV and visual.
The flux observed shortward of 1600 Å varies irregularly by at most 30%, but
never disappears completely.
Unless HD 163296 is seen "pole-on'' (which seems improbable in view of
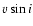
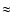 120
120
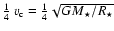 )
the hot UV emission
region has to be extended over an equatorial belt on the surface of the star
or over the boundary-layer of an accretion disc.
There are two possibilities for the existence of a hot belt at the stellar
surface: magnetic accretion from the accretion disc to the star and "neutral''
accretion that could occur for accretion through cool BLs.
The presence of a hot magnetic belt has also been assumed to interpret the
emission-line profiles of Ly
)
the hot UV emission
region has to be extended over an equatorial belt on the surface of the star
or over the boundary-layer of an accretion disc.
There are two possibilities for the existence of a hot belt at the stellar
surface: magnetic accretion from the accretion disc to the star and "neutral''
accretion that could occur for accretion through cool BLs.
The presence of a hot magnetic belt has also been assumed to interpret the
emission-line profiles of Ly ,
as seen in the high-resolution UV spectra of
HD 163296, HR 5999, and HD 104237 (Appendix D.4).
From these observations we derive that the emission belt could extend at least
to latitudes of 35
,
as seen in the high-resolution UV spectra of
HD 163296, HR 5999, and HD 104237 (Appendix D.4).
From these observations we derive that the emission belt could extend at least
to latitudes of 35 (Blondel et al. 1993).
The observations of HD 163296 show variability but no indication of periodicity
in the UV emission excess (
(Blondel et al. 1993).
The observations of HD 163296 show variability but no indication of periodicity
in the UV emission excess (
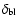 ), so that there is no evidence of spots that
persist longer than 14
), so that there is no evidence of spots that
persist longer than 14
 .
Similar variability was also found in the UVE of several other PMS Ae/Fe stars for which IUE observations were obtained at various dates, e.g. for
HD 104237, NX Pup and AK Sco (Table 2), but these observations
are too few and too widely separated in time to give any significant information
about possible periodicity in
.
Similar variability was also found in the UVE of several other PMS Ae/Fe stars for which IUE observations were obtained at various dates, e.g. for
HD 104237, NX Pup and AK Sco (Table 2), but these observations
are too few and too widely separated in time to give any significant information
about possible periodicity in
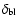 or the presence of hot spots.
or the presence of hot spots.
In contrast to the situation for T Tauri stars, there are indications that
large-scale magnetic fields do not play a dominant role in the accretion
process for Herbig emission-line stars.
This is suggested by the observation that the rotation velocities of PMS Be/Ae/Fe
stars are larger than those observed for T Tauri stars by a factor of
2.0-4.5 (Table 1).
The rotation velocities of T Tauri stars are in fact lower than expected from their
evolutionary contraction process and their accretion phases, which both tend to
spin these stars up during their PMS contraction.
The general explanation for the low rotation of the T Tauri stars is the braking
effect due to the coupling of the stellar magnetic field with the toroidal
component of the disc magnetic field outside the co-rotation radius (Cameron
et al. 1993, 1995; Yi 1994; Armitage & Clarke 1996).
Since the co-rotation radii of Herbig stars with masses around 2
 are close
to those of T Tauri stars (
are close
to those of T Tauri stars ( 1
1
 )
and both their contraction rates (PS93) and
mass accretion rates are of the same order as those of the T Tauri stars, the
difference in braking of the rotation can only be explained by the relative
weakness of the large-scale stellar magnetic field of the Herbig stars.
For stellar dynamo fields, this may perhaps be explained by the fact that, in
contrast to the fully convective Hayashi phases of T Tauri stars, convection
in more massive stars is limited to the surface layers during the first
contraction phases.
However, we cannot exclude the possibility that small-scale dynamo or fossile
stellar fields may be responsible for magnetic accretion in a non-uniform
activity belt at the stellar surface.
Such fields certainly play a role in supporting the (bipolar) outflow from the
BL, which is revealed by intense line emission (Paper II).
Instead of trying to model both accretion and outflow, we prefer to limit
ourselves here to the accretion proces, in particular, to the well-studied models
of "neutral'' (non-magnetic) accretion.
)
and both their contraction rates (PS93) and
mass accretion rates are of the same order as those of the T Tauri stars, the
difference in braking of the rotation can only be explained by the relative
weakness of the large-scale stellar magnetic field of the Herbig stars.
For stellar dynamo fields, this may perhaps be explained by the fact that, in
contrast to the fully convective Hayashi phases of T Tauri stars, convection
in more massive stars is limited to the surface layers during the first
contraction phases.
However, we cannot exclude the possibility that small-scale dynamo or fossile
stellar fields may be responsible for magnetic accretion in a non-uniform
activity belt at the stellar surface.
Such fields certainly play a role in supporting the (bipolar) outflow from the
BL, which is revealed by intense line emission (Paper II).
Instead of trying to model both accretion and outflow, we prefer to limit
ourselves here to the accretion proces, in particular, to the well-studied models
of "neutral'' (non-magnetic) accretion.
A.4 "Neutral'' accretion
Since there are no indications that magnetic fields play a dominant role in
the process of accretion on PMS Ae/Fe stars (except perhaps in controlling the
outflow perpendicular to the disc plane), we feel justified in comparing the
global BL parameters from our UV3C-model analysis with the predictions of
several self-consistent BL models for neutral accretion.
These models are based on the simultaneous solution of the equations of mass-,
radial momentum-, angular momentum-, and energy-conservation, together with the
boundary conditions for the inner and outer boundaries of the BL.
Some supplementory assumptions concerning the viscosity in the disc, the
equation of state, the opacity law, the rotation rate, and the mass outflow rate
have to be made as well.
Several 1-D stationary models with axial symmetry have been explored for 1
 stars.
These self-consistent models have in common that for
stars.
These self-consistent models have in common that for
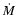
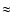 10-7
10-7
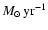 the structure of the BL can be separated into
two disinct regions: a narrow (
the structure of the BL can be separated into
two disinct regions: a narrow (
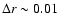
 )
dynamical region around
the star where the Kepler rotation of the disc is braked down to the stellar rotation
and, around this zone, a broader (
)
dynamical region around
the star where the Kepler rotation of the disc is braked down to the stellar rotation
and, around this zone, a broader (
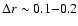
 )
and cooler thermal
region, where this viscous braking energy is dissipated by radiation.
)
and cooler thermal
region, where this viscous braking energy is dissipated by radiation.
The density- and temperature-structures of the BL strongly depend on the choice
of the inner boundary condition (Regev & Bertout 1995).
If the radiative flux at the inner boundary (or stellar surface) is negligible
and the viscosity parameter
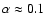 ,
the resulting BL will be hot
(8000-10 000 K) and narrow (
,
the resulting BL will be hot
(8000-10 000 K) and narrow (
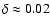
 ).
Such results were obtained by Popham et al. (1993) under the assumption of
optically-thick BL radiation.
However, if the inner boundary is required to have the surface temperature of
the star (Bertout & Regev 1992; Lioure & Le Contel 1994) a significant part
(10-30%) of the BL energy is radiated inward into the outer layers of the
star and creates a hot (
).
Such results were obtained by Popham et al. (1993) under the assumption of
optically-thick BL radiation.
However, if the inner boundary is required to have the surface temperature of
the star (Bertout & Regev 1992; Lioure & Le Contel 1994) a significant part
(10-30%) of the BL energy is radiated inward into the outer layers of the
star and creates a hot (
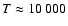 K) equatorial belt.
Godon (1996) repeated these model calculations with improved opacities in
order to account for the ionised and neutral regions in the BL and the disc.
For small values of
K) equatorial belt.
Godon (1996) repeated these model calculations with improved opacities in
order to account for the ionised and neutral regions in the BL and the disc.
For small values of  (
(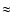 0.01) he finds cool (5000-6000 K)
and optically-thick (
0.01) he finds cool (5000-6000 K)
and optically-thick (
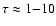 )
BL's, in agreement with earlier results,
but his thermal BL is broader (
)
BL's, in agreement with earlier results,
but his thermal BL is broader (
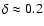
 ).
For higher values of
).
For higher values of  (0.1-1.0) the BL radiation becomes optically thin
(
(0.1-1.0) the BL radiation becomes optically thin
(
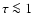 ), which corresponds to less efficient cooling, and its
temperature may rise to 8000-10 000 K.
These temperatures are similar to those obtained by Basri & Bertout (1989) for
the optically-thin approximation that they needed to fit the Balmer continuum
and line emission.
However, Godon (1996) finds larger thermal widths (up to 0.04
), which corresponds to less efficient cooling, and its
temperature may rise to 8000-10 000 K.
These temperatures are similar to those obtained by Basri & Bertout (1989) for
the optically-thin approximation that they needed to fit the Balmer continuum
and line emission.
However, Godon (1996) finds larger thermal widths (up to 0.04
 )
than these
authors.
)
than these
authors.
Later Kley & Lin (1996) also calculated the BL structure with a 2D
axial symmetric, non-stationary model for a 1
 star with a rotation rate of
0.1 of the brake-up rate.
For three representative mass accretion rates (10-7,
10-6,
10-4
star with a rotation rate of
0.1 of the brake-up rate.
For three representative mass accretion rates (10-7,
10-6,
10-4
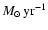 )
and
)
and  =0.01, the time evolution of the main physical
parameters (temperature, density, pressure, and angular momentum) was followed
in and perpendicular to the disc plane.
The final models are consistent with the results of the 1D stationary models.
For the case of the lowest
=0.01, the time evolution of the main physical
parameters (temperature, density, pressure, and angular momentum) was followed
in and perpendicular to the disc plane.
The final models are consistent with the results of the 1D stationary models.
For the case of the lowest 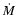 ,
there is some heating of the stellar
atmosphere over latitudes up to 5-10
,
there is some heating of the stellar
atmosphere over latitudes up to 5-10 ,
and for increasing accretion
rates, the width of the heated surface zone increases via 30
,
and for increasing accretion
rates, the width of the heated surface zone increases via 30 up to
the whole stellar surface. Although there is general agreement between the
2D and 1D models, the numerical values of the parameters in the equatorial
plane are somewhat different.
up to
the whole stellar surface. Although there is general agreement between the
2D and 1D models, the numerical values of the parameters in the equatorial
plane are somewhat different.
It should be noted here that the hot component that is present in the UV
spectra of the PMS Ae/Fe stars may be interpreted equally well by the radiation
from a hot equatorial belt on the stellar surface, as predicted by the models of
Regev & Bertout (1995) and Kley & Lin (1996).
An analysis in terms of such a model would be similar to the analysis employed
in this paper.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0269f0a1.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg323.gif) |
Figure A.1:
Comparison of several low-resolution UV spectra.
The arrows indicate the y-axis of the spectrum.
See Table A.1 for an identification of the marked lines. |
Table A.1:
Absorption features in the UV spectra (Fig. A.1) of some
PMS Ae/Fe stars, SX Cas, U Cep and 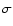 Cyg.
(n = narrow, b = broad, d = deep, s = shallow, e = emission instead
of absorption, : = uncertain value.)
Cyg.
(n = narrow, b = broad, d = deep, s = shallow, e = emission instead
of absorption, : = uncertain value.)
A.5 Interpretation of the UV-spectra
In most of our sample spectra (for spectral types later than A2), we observed a
residual spectral component shortward of 1800 Å, which is not present in the
photospheric spectra of the comparison stars of the same spectral type, given
in the IUE spectral atlases.
In this paper we have interpreted this component as the spectral contribution
of a hot BL formed in neutral disc accretion to the star.
This interpretation is based on the properties of the residual component, which
show up most clearly in late-type stars, such as NX Pup, V380 Ori, HK Ori, and
the early-type star
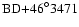 .
We observed two properties of this spectral component:
.
We observed two properties of this spectral component:
- (1)
- The (BL) continuum in the UV can be matched very well with that
of a late-B or early-A type supergiant (e.g.
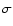 Cyg - B9 Iab),
corresponding to a Planck spectrum of
Cyg - B9 Iab),
corresponding to a Planck spectrum of
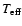
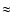 10 000 K.
The optical depth in the UV wavelength range (1200-3000 Å) is
10 000 K.
The optical depth in the UV wavelength range (1200-3000 Å) is  1,
and if we extrapolate the residual BL spectrum, we find
1,
and if we extrapolate the residual BL spectrum, we find
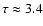 around
around
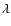 =3600 Å (where the flux of the supergiant reaches its maximum).
We therefore consider the UV spectrum of the BL in Herbig stars as optically-thick,
in agreement with expectations from theoretical models of BL, as
mentioned in Sect. A.4.
=3600 Å (where the flux of the supergiant reaches its maximum).
We therefore consider the UV spectrum of the BL in Herbig stars as optically-thick,
in agreement with expectations from theoretical models of BL, as
mentioned in Sect. A.4.
- (2)
- The SW-part of the spectra of the (BL) component
(Fig. A.1) are characterised by strong and broad absorption
features, similar to those observed in the spectra of B9 I-A2 I
type stars, as noted earlier in the SW-part of the spectrum of NX Pup by
TjinADjie et al. (1984).
A list of these absorption features with probable identifications is given in
Table A.1 for the five stars.
These features are sharpest in the spectra of
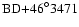 and V380 Ori and broader
(partly merged with neighbouring lines due to turbulence) in that of NX Pup.
They probably are blends of the strong resonance lines of Si II, Si III,
Al II, Al III, Fe II, and perhaps Si IV, as is expected above a hot
region of outflow.
The features observed in the Herbig stars are deeper than those observed in the
supergiants, which may indicate a higher column density.
The blended features in the spectrum of NX Pup are at least as broad as those
observed in the supergiants, which suggests a strong degree of turbulence in
the region of line formation.
This suggestion has to be checked by high-resolution spectroscopy.
The characterisation of the line-formation domain as a dense, hot, and probably
turbulent region suggests that this region is located immediately outside the
continuum source, which we interpret as the boundary-layer.
and V380 Ori and broader
(partly merged with neighbouring lines due to turbulence) in that of NX Pup.
They probably are blends of the strong resonance lines of Si II, Si III,
Al II, Al III, Fe II, and perhaps Si IV, as is expected above a hot
region of outflow.
The features observed in the Herbig stars are deeper than those observed in the
supergiants, which may indicate a higher column density.
The blended features in the spectrum of NX Pup are at least as broad as those
observed in the supergiants, which suggests a strong degree of turbulence in
the region of line formation.
This suggestion has to be checked by high-resolution spectroscopy.
The characterisation of the line-formation domain as a dense, hot, and probably
turbulent region suggests that this region is located immediately outside the
continuum source, which we interpret as the boundary-layer.
We should note here that similar features have been observed in the spectra,
taken outside eclipse, of SX Cas and U Cep (Plavec et al. 1982; Plavec 1983).
These
 stars are eclipsing binaries or cataclysmic variables
(CVs) consisting of a B7 star and a late-type giant in a phase of mass transfer.
The UV continua have been explained in terms of an accretion disc
boundary-layer around the receiving B-star.
The gross observational properties could be understood if the BL is a strongly
turbulent (Shore & King 1986) region.
During the eclipse of the B-star component in the CV, the UV continuum disappears
and is superseded by a rich emission-line spectrum of high-ionisation lines.
stars are eclipsing binaries or cataclysmic variables
(CVs) consisting of a B7 star and a late-type giant in a phase of mass transfer.
The UV continua have been explained in terms of an accretion disc
boundary-layer around the receiving B-star.
The gross observational properties could be understood if the BL is a strongly
turbulent (Shore & King 1986) region.
During the eclipse of the B-star component in the CV, the UV continuum disappears
and is superseded by a rich emission-line spectrum of high-ionisation lines.
![\begin{figure}
\par\includegraphics[angle=270,width=8.7cm,clip]{0269f0a2.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg326.gif) |
Figure A.2:
UV3C-model temperature distribution for BF Ori
compared with the radial temperature distribution of the 1D BL
model by Popham et al. (1993), both calculated for
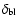 = 0.02.
(see Table 2 (7p) for the BF Ori parameters). = 0.02.
(see Table 2 (7p) for the BF Ori parameters). |
![\begin{figure}
\par\includegraphics[angle=270,width=8.7cm,clip]{0269f0a3.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg327.gif) |
Figure A.3:
As previous figure but for
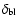 = 0.04. = 0.04. |
This is interpreted as the emission by the "chromosphere'' of the BL which
emerges when the BL itself is shielded by the eclipse.
A similar explanation can be given for the emission spectra of Herbig stars.
In most of the UV spectra of the PMS Ae/Fe stars of our sample we observed strong
emission-lines of O I, C II, C IV, Si II, Si III, Si IV, and
N V emerging from the low continuum shortward of 1800 Å.
We suggest that these lines are emitted outside of but close to the BL, which
itself (similar to the CV case) is shielded by the disc when the star is
observed "edge-on''.
A study of these emission regions will be presented in Paper II.
If the residual spectral component discussed above is indeed due to the BL, our
analysis with the UV3C model should yield
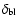 -values in the range of the values
predicted by theoretical models for the thermal region of optically-thick
boundary-layers.
We compared the radial temperature distribution, corresponding to the
-values in the range of the values
predicted by theoretical models for the thermal region of optically-thick
boundary-layers.
We compared the radial temperature distribution, corresponding to the
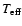 ,
,
 ,
,
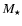 ,
,
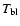 ,
and
,
and
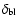 for the case of BF Ori, to the radial temperature
distributions for a 1
for the case of BF Ori, to the radial temperature
distributions for a 1
 star, as predicted by the 1D model for different
values of the viscosity parameter of Popham et al. (1993).
Although we have not seen their results for 2
star, as predicted by the 1D model for different
values of the viscosity parameter of Popham et al. (1993).
Although we have not seen their results for 2
 stars, we assume here that
the analytical formula may be extrapolated to somewhat higher mass.
For this we used the analytical expressions derived by Cantó et al. (1995),
which give good agreement with Popham's result for a wide range of parameters in
the 1
stars, we assume here that
the analytical formula may be extrapolated to somewhat higher mass.
For this we used the analytical expressions derived by Cantó et al. (1995),
which give good agreement with Popham's result for a wide range of parameters in
the 1
 case.
Figures A.2+A.3 show the temperature distribution
of our simple empirical BL compared with the distributions computed with the model
of Popham et al. (1993).
The difference between the temperature distributions for
case.
Figures A.2+A.3 show the temperature distribution
of our simple empirical BL compared with the distributions computed with the model
of Popham et al. (1993).
The difference between the temperature distributions for  =0.10 and
=0.10 and
 =0.01 in Figs. A.2+A.3 is consistent
with the results of Godon (1996) (Sect. A.4).
=0.01 in Figs. A.2+A.3 is consistent
with the results of Godon (1996) (Sect. A.4).
Appendix B: The input data
B.1 UV spectra from IUE
The input data for the analysis consisted of the reprocessed low dispersion
(ULDA and NEWSIPS taken from the archives at VILSPA, GSFC, and STSci) UV spectra
of 40 PMS Be/Ae/Fe stars and 3 cTTs and the visual magnitudes of the stars at the
moment of the exposures.
The SW and LW of each star spectrum were joined at 1950 Å, and in cases
where the large aperture (LAP) spectrum was overexposed, we used (parts of)
the small aperture (SAP) spectra instead, if available
(see Table F.6 for details).
For stars visible from the ESO at La Silla, Chile (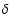 <+20
<+20 ), we
collected photometric data on the Walraven (WULBV) system.
If the
), we
collected photometric data on the Walraven (WULBV) system.
If the  -brightness derived from the Walraven photometry (Lub & Pel 1977)
agrees with
-brightness derived from the Walraven photometry (Lub & Pel 1977)
agrees with
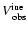 ,
we used the W-band flux (centered at 3236 Å, and
indicated by (w) in the figures) to check the observed flux at the far end of
the IUE LW-range.
In cases where the LW images were overexposed this W-band flux became
essential in the analysis of the spectra (e.g. Fig. 96).
,
we used the W-band flux (centered at 3236 Å, and
indicated by (w) in the figures) to check the observed flux at the far end of
the IUE LW-range.
In cases where the LW images were overexposed this W-band flux became
essential in the analysis of the spectra (e.g. Fig. 96).
The stars for which Walraven photometric observations have been obtained are
indicated in Table 1 Col. 9 by (+); see also deWinter et al.
2001.
It should be noted that for variable stars we do not have Walraven photometry
for all brightness phases (e.g. UX Ori, BF Ori).
Also in some cases (CQ Tau, V350 Ori) the Walraven fluxes are too high to be
indicated in the figure.
This may perhaps be caused by the difference in diaphragm of the Walraven
photometer and the IUE Field camera, which becomes important if the star has a
nebulae around it that radiates in the UV.
Immediately before an IUE spectral observation, the Fine Error Sensor (FES) in
the Field Camera Mode generally estimates a B-band flux of the object in
terms of FES-counts.
The derivation of  taken before 1991 was made with the FES calibration
given by Imhoff & Wasatonic (1986) and Barylak (1989), and for observations
between 1-1-1991 and 1994, we used the calibration by Pérez (1991).
We estimated the uncertainty of this procedure at
taken before 1991 was made with the FES calibration
given by Imhoff & Wasatonic (1986) and Barylak (1989), and for observations
between 1-1-1991 and 1994, we used the calibration by Pérez (1991).
We estimated the uncertainty of this procedure at
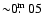 .
After 1994 the FES could not be used for accurate photometric measurements
because of the occurrence of stray light in the Field Camera.
For a number of observations we secured simultaneous ground-based
photometry on the Johnson-, Strömgren-, or Walraven-systems that support
the FES calibration method.
The FES magnitudes, converted to
.
After 1994 the FES could not be used for accurate photometric measurements
because of the occurrence of stray light in the Field Camera.
For a number of observations we secured simultaneous ground-based
photometry on the Johnson-, Strömgren-, or Walraven-systems that support
the FES calibration method.
The FES magnitudes, converted to  ,
are listed in Tables 2-6 as
,
are listed in Tables 2-6 as
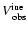 for each set of spectra.
for each set of spectra.
B.2 Distances
Most distances of stars associated with the nearby (d<300 )
star-formation
regions (RSF ) Taurus-Auriga, Ophiuchus, Lupus, Scorpius,
Corona Australis, and Chamaeleonis and those of the isolated Herbig stars
HD 163296, HD 104237, and HD 100546 have been evaluated by the Hipparcos project
(ESA 1997).
For each star the distance is given in Table 1 Col. 7 and
Appendix C.
The large uncertainties for some distances reflect the nebulous character of
these objects.
For some stars in our sample (HD 139614, HD 169142, and HD 142666) not observed
by Hipparcos, we took the estimates of Sylvester et al. (1996).
For the Herbig star candidates HD 95881 and HD 98922, we estimated a
spectroscopic parallax.
Distances
)
star-formation
regions (RSF ) Taurus-Auriga, Ophiuchus, Lupus, Scorpius,
Corona Australis, and Chamaeleonis and those of the isolated Herbig stars
HD 163296, HD 104237, and HD 100546 have been evaluated by the Hipparcos project
(ESA 1997).
For each star the distance is given in Table 1 Col. 7 and
Appendix C.
The large uncertainties for some distances reflect the nebulous character of
these objects.
For some stars in our sample (HD 139614, HD 169142, and HD 142666) not observed
by Hipparcos, we took the estimates of Sylvester et al. (1996).
For the Herbig star candidates HD 95881 and HD 98922, we estimated a
spectroscopic parallax.
Distances 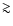 350
350 could not be determined with Hipparcos and were taken
from other works (e.g. Warren & Hesser were, for the Orion stars).
could not be determined with Hipparcos and were taken
from other works (e.g. Warren & Hesser were, for the Orion stars).
B.3 Spectral type of the stellar photosphere
Spectral classifications (Table 1) were obtained from
two sources: photometric classifications from the position of the object in
the (B-V) vs. (U-B) two-colour diagram (TCD hereafter) on the
Johnson or Walraven photometric systems and spectroscopic classifications from
high-resolution visual spectra.
In Table 1 we give the results of both methods, where most
of the spectroscopic classifications were taken from FJ84, HB88, and TWP94.
Since the
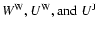 photometric passbands
are not in the wavelength range of the visual spectroscopy, we may expect
different results from the two classification methods.
photometric passbands
are not in the wavelength range of the visual spectroscopy, we may expect
different results from the two classification methods.
B.4 Foreground extinction
All the spectra (i.e. of both standard stars and PMS stars) were de-reddened
for foreground extinction before using them in the model-calculation.
This was done with the analytical UV-extinction law
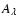 /
/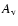 for
for
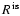 =3.1
from Cardelli et al. (1988, 1989).
The
=3.1
from Cardelli et al. (1988, 1989).
The
 -values of the PMS stars are listed in Table 1
Col. 4 and are usually based on the stars in their neighbourhood.
However, in the cases of R CrA, HD 97048, and Z CMa, it was found that
-values of the PMS stars are listed in Table 1
Col. 4 and are usually based on the stars in their neighbourhood.
However, in the cases of R CrA, HD 97048, and Z CMa, it was found that
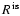 >3.1
due to the presence of intercluster clouds, so we used these anomalous values
for the interstellar de-reddening (Sects. C.42, C.30 for
details).
>3.1
due to the presence of intercluster clouds, so we used these anomalous values
for the interstellar de-reddening (Sects. C.42, C.30 for
details).
B.5 Disc inclination
An indication of the value of the inclination angle i of the disc, which is
defined as the angle between the line-of-sight and the rotation axis of the disc,
was obtained from several independent observational arguments.
In principle, the inclination could be determined from the IR part of the SED
where the contribution of the cool outer parts of the disc is largest.
However, in this part contributions from other sources, e.g. circumstellar dust
and dust in nearby reflection nebulosity may also be important.
Fortunately the shape of the UV spectrum in the wavelength range of the IUE is
not very sensitive to the value of i, so that only rough estimates of the
inclination are needed.
The various methods used to obtain estimates of the disc inclination
are discussed in Appendix D.
The results of these estimates are listed in Table 1
Col. 10 with index E for "edge-on'' (
 )
and P for "pole-on''
(
)
and P for "pole-on''
(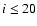
 ).
The observational arguments for E or P are given in the columns X, Y, Z.
).
The observational arguments for E or P are given in the columns X, Y, Z.
In column X the type of variability in the TCD is listed (r = along the
reddening line; o = other type of variability; n = no significant variability,
 denotes stars that had variability along the reddening line in the past,
i.e. changed from type r to n).
In column Y we give the EW (Å) of the 2400 Å absorption-feature in the
low-resolution UV spectra (
denotes stars that had variability along the reddening line in the past,
i.e. changed from type r to n).
In column Y we give the EW (Å) of the 2400 Å absorption-feature in the
low-resolution UV spectra (
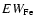 hereafter, Fig. D.1).
Column Z shows the shape classification (as introduced by Reipurth et al. 1996)
of the H
hereafter, Fig. D.1).
Column Z shows the shape classification (as introduced by Reipurth et al. 1996)
of the H -emission profile of each star.
-emission profile of each star.
Table B.1:
Published double-star parameters and spectral types, see also
Sect. 5.9 and Appendix C.
Appendix C: Stellar data used for the analyses
Our aim is to give here an updated review of the information that is
relevant for the choice of the stellar input parameters of the analyses,
such as distance, foreground extinction, and spectral type of the stars
in Tables 1 and B.1.
Section numbers correspond to the sequence numbers in the tables and
the labels in Fig. 41.
C.1 XY Per - HD 275877
This object is a visual double star (ADS 2788, Table B.1).
The ADS parameters have been confirmed by Hipparcos measurements and NIR
imaging by Testi et al. (1998).
The bright (western) component has a spectral type of early-A and the secondary
component has type mid-A (HB88).
The present photometric variability is not well known.
According to Boyd (1936), the object is most of the time at maximum brightness
with  =9
=9
 36 and
36 and
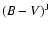 =0
=0
 52.
The uncertain FES calibration at the date of observation gives
52.
The uncertain FES calibration at the date of observation gives  =9
=9
 0.
If we assume that the observation was made at
0.
If we assume that the observation was made at  =9
=9
 36 with
36 with
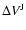 =0
=0
 6 at
that moment, we obtain
6 at
that moment, we obtain  =9
=9
 85 for the primary and
85 for the primary and  =10
=10
 45 for the
secondary component.
The distance of the object is uncertain.
Adams et al. (1935) give a spectroscopic parallax of 0
45 for the
secondary component.
The distance of the object is uncertain.
Adams et al. (1935) give a spectroscopic parallax of 0
 001, and the
Hipparcos Catalogue (ESA 1997) gives d=120
+88-36
001, and the
Hipparcos Catalogue (ESA 1997) gives d=120
+88-36 ;
but to
obtain this value 17% of the measurements had to be rejected, so that
this value is unreliable (AWT98).
However, it is highly probable that XY Per is located in DC L1449 of
RSF 1 Per B, which has
;
but to
obtain this value 17% of the measurements had to be rejected, so that
this value is unreliable (AWT98).
However, it is highly probable that XY Per is located in DC L1449 of
RSF 1 Per B, which has 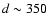
 (Ungerechts & Thaddeus 1987).
For HD 275874 (A4) in the immediate surroundings (at 8
(Ungerechts & Thaddeus 1987).
For HD 275874 (A4) in the immediate surroundings (at 8
 4, with a
comparable proper motion) we derive
4, with a
comparable proper motion) we derive

 0
0
 19.
19.
C.3 UX Ori - HD 293782
The spectral classification in the UV (TjinADjie et al. 1984; Grady et al. 1995)
agrees with that in the visual: A2-3 IIIe (HB88).
Its photometric and polarimetric variability is similar to other
UXORs (Zajtseva 1973; Zajtseva & Kolotilov 1973; Voshchinnikov
et al. 1988; Evans et al. 1989; Bibo & Thé 1990).
This peculiar variability has been interpreted by Grinin (1988) and by
Voschinnikov (1989) in terms of eclipses of an inclined, oblate spheroidal
dust envelope by optically-thick dust clouds passing the line-of-sight.
The Hipparcos measurements give a lower limit for the distance of 130 (AWT98).
The star is located in DC L1616 near the Orion OB1c association.
For UX Ori we adopted the parameters of this association:
d=400-430
(AWT98).
The star is located in DC L1616 near the Orion OB1c association.
For UX Ori we adopted the parameters of this association:
d=400-430 ,
,
 =0
=0
 06 (Warren & Hesser 1978).
Bertout et al. (1999) give indications that UX Ori is a double star
(Table B.1).
06 (Warren & Hesser 1978).
Bertout et al. (1999) give indications that UX Ori is a double star
(Table B.1).
C.4 HD 163296 - MWC275
The visual spectrum has been classified as A0 Ve by Thé et al. (1985a) and
as A7 Ve by Fz85.
Since the star is not associated with a star-formation region and does not show
significant photometric variability, it has not been considered as a typical
Herbig Ae star.
In spite of the lack of brightness variations, its spectrum shows strong
variability in the emission-lines of H ,
Ca II K, and Mg II h,k on a
time-scale of several hours (Thé et al. 1985b; Baade & Stahl 1989b; Catala et al. 1989).
The UV continuum shortward of 1600 Å varies on the same time-scale.
,
Ca II K, and Mg II h,k on a
time-scale of several hours (Thé et al. 1985b; Baade & Stahl 1989b; Catala et al. 1989).
The UV continuum shortward of 1600 Å varies on the same time-scale.
This variation is probably not caused by the presence of a double-star companion,
since radial velocity measurements by Baade & Stahl (1989b) show no evidence
of variation.
Catala et al. (1989) explain the variability in terms of the rotational modulation
of an outflow from active regions at the stellar surface.
The distance of the star has been determined from Hipparcos measurements:
122
+17-13 (ATT97).
Its foreground excess
(ATT97).
Its foreground excess
 is negligible.
The inclination was derived from a red-shifted Ly
is negligible.
The inclination was derived from a red-shifted Ly -component
(Appendix D.4, Blondel et al. 1993): 57
-component
(Appendix D.4, Blondel et al. 1993): 57 and from CO emission (Mannings & Sargent 1997): 58
and from CO emission (Mannings & Sargent 1997): 58 .
STIS imaging in the visual (Grady et al. 2000) confirmed the presence of the
disc, which extends to at least 450 AU from the star and has
.
STIS imaging in the visual (Grady et al. 2000) confirmed the presence of the
disc, which extends to at least 450 AU from the star and has 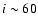
 .
STIS imaging near Ly
.
STIS imaging near Ly (Devine et al. 2000) confirmed the presence of in-
and outflow jets with
(Devine et al. 2000) confirmed the presence of in-
and outflow jets with
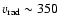
 .
.
C.5 HD 150193 - MWC863 - V2307 Oph
Its visual (FJ84) and UV spectra (this paper) are very similar to those of
HD 163296.
In the visual the star was classifed as A4e (Fz85).
There are no indications of photometric variability, but spectral variations
on short time-scales similar to HD 163296 have not been looked for.
In spite of its location, the connection of HD 150193 to the Ophiuchus
DC L1729 in Sco R1 at 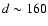
 was considered uncertain
(Elias 1978a), but this connection has now been confirmed by Hipparcos
measurements, 150
+50-30
was considered uncertain
(Elias 1978a), but this connection has now been confirmed by Hipparcos
measurements, 150
+50-30 (ATT97), which also reveal that the
star is a double system (Table B.1).
Because this distance is close to the minimum distance of the Ophiuchus
complex, we assume that the foreground excess is small e.g. 0
(ATT97), which also reveal that the
star is a double system (Table B.1).
Because this distance is close to the minimum distance of the Ophiuchus
complex, we assume that the foreground excess is small e.g. 0
 03.
Our high-resolution UV spectrum shows the presence of a red-shifted stellar
component to the Ly
03.
Our high-resolution UV spectrum shows the presence of a red-shifted stellar
component to the Ly -emission.
From the profile,
-emission.
From the profile, 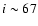
 was estimated (Appendix D.4).
was estimated (Appendix D.4).
C.7 BF Ori - BD-06  1259
1259
The visual spectrum of BF Ori is usually classified as A5e+sh (HB88,
Rostopchina 1999).
Photometric and polarimetric observations (e.g. Kilkenny et al. 1985; Herbst
et al. 1987; Hutchinson et al. 1994) show large and irregular variations,
similar to other UXORs.
The interpretation of these data can therefore be similar (Grinin et al. 1988)
to the observational results of WW Vul and UX Ori
(Sect. C.3).
The Hipparcos measurements give a lower limit to the distance of 210 (AWT98).
Its association with M42 in RSF 1 Ori A suggests
(AWT98).
Its association with M42 in RSF 1 Ori A suggests
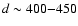
 and
and
 =0
=0
 06.
Bertout et al. (1999) indicate that this is a double star (Table B.1).
06.
Bertout et al. (1999) indicate that this is a double star (Table B.1).
C.8 HD 31648 - MWC480
From its visual spectrum Merrill et al. (1942) and Burbidge & Burbidge (1954)
concluded that HD 31648 is a peculiar shell star (type A3ep) with variable shell
components in the lines (Jaschek et al. 1988; Morrison 1997),
similar to HD 163296 (Sect. C.4) and HD 150193 (Sect. C.5).
Another similarity to these stars is that there are no indications of strong
photometric variability of HD 31648 (Pogodin 1987).
On the other hand, the three stars share several spectroscopic properties with
the Herbig Ae stars: P-Cygni profiles of the strong emission-lines of the Balmer
series and of Mg II h,k, a strong Ly -emission and a NIR excess.
Thus it seems jusified to consider these stars as PMS objects.
Its location in the neighbourhood of AB Aur suggests that HD 31648 may belong
to RSF 1 Tau.
The Hipparcos measurements (AWT98) give d=131
+24-18
-emission and a NIR excess.
Thus it seems jusified to consider these stars as PMS objects.
Its location in the neighbourhood of AB Aur suggests that HD 31648 may belong
to RSF 1 Tau.
The Hipparcos measurements (AWT98) give d=131
+24-18 for HD 31648
and 141
+23-17
for HD 31648
and 141
+23-17 for AB Aur, we assume for HD 31648 that
for AB Aur, we assume for HD 31648 that
 =0
=0
 02, equal to that of AB Aur.
From the CO interferometry of HD 31648, Dutrey (2000) derived i=38
02, equal to that of AB Aur.
From the CO interferometry of HD 31648, Dutrey (2000) derived i=38 .
.
C.9 HR 5999 - V856 Sco - HD 144668
The visual spectral classification of this star in the Lupus T3
association is A5-7 IIIe (Bessell & Eggen 1972; TjinADjie et al. 1989).
The object is strongly and irregularly variable in brightness (Bessell &
Eggen 1972; Thé & TjinADjie 1978; Thé et al. 1981; Baade & Stahl 1989a), as
well as in the line profiles and line strengths.
Although the photometric behaviour of HR 5999 is similar to that of the
UXORs, it is commonly not considered to be a member of this group, because
the star does not show the "blueing branch'' in the CMD of the UXORs.
An explanation for the absence of this branch in the CMD of HR 5999 may be the
depletion of small dust grains in its halo.
The distance of HR 5999 was derived by Bessell & Eggen (1972) and by Thé &
TjinADjie (1978) on the assumption that it is the same as that of the nearby
(45 )
common radial and proper motion companion HR 6000 (HD 144667).
Its photometric classification is B6 V, which implies that d=270
)
common radial and proper motion companion HR 6000 (HD 144667).
Its photometric classification is B6 V, which implies that d=270 and
and
 =0
=0
 06.
However, HR 6000 is a He-weak peculiar star, so the classification
from its spectrum should give a slightly cooler type (Garrison 1978;
Eggen 1998), about B7-8 V, which corresponds to d=234
06.
However, HR 6000 is a He-weak peculiar star, so the classification
from its spectrum should give a slightly cooler type (Garrison 1978;
Eggen 1998), about B7-8 V, which corresponds to d=234 and
and
 =0
=0
 03.
This value is an upper limit for
03.
This value is an upper limit for
 in the direction of HR 5999/6000.
Since there are no i.s. Na I D absorption lines in the spectrum of HR 6000,
its
in the direction of HR 5999/6000.
Since there are no i.s. Na I D absorption lines in the spectrum of HR 6000,
its
 is probably negligible.
We shall assume that both stars have the same foreground extinction.
The Hipparcos measurements have resulted in a value of 240
+61-39
is probably negligible.
We shall assume that both stars have the same foreground extinction.
The Hipparcos measurements have resulted in a value of 240
+61-39 for HR 6000 and 210
+50-30
for HR 6000 and 210
+50-30 for HR 5999 (ESA 1997, AWT98).
These values are still in the range of recent estimates of 140-250
for HR 5999 (ESA 1997, AWT98).
These values are still in the range of recent estimates of 140-250 for
the distance to the Lupus T3 cloud (Hughes et al. 1993), with which both
stars are thought to be associated.
The high-resolution Ly
for
the distance to the Lupus T3 cloud (Hughes et al. 1993), with which both
stars are thought to be associated.
The high-resolution Ly -profile of HR 5999 shows a red-shifted component, and
i=53
-profile of HR 5999 shows a red-shifted component, and
i=53 could be derived from its profile (Blondel et al. 1993;
Appendix D.4).
The star was detected to be a PMS
could be derived from its profile (Blondel et al. 1993;
Appendix D.4).
The star was detected to be a PMS 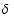 Scuti variable (Kurtz & Marang 1995) and
has a double-star companion (Table B.1).
Scuti variable (Kurtz & Marang 1995) and
has a double-star companion (Table B.1).
C.10 HD 39060 - 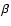 Pic
Pic
This star is generally considered as the prototype of a young A5-7 IV- V
star in the phase of its arrival on the ZAMS.
Its evolutionary status is discussed by Paresce (1991), Lanz et al. (1995), and
Brunini & Benvenuto (1996).
The Hipparcos measurements give d=19.3
+0.2-0.2 (Crifo et al. 1997).
Its
(Crifo et al. 1997).
Its
 is negligible (Sylvester et al. 1994).
The star has a thin circumstellar dust disc with
is negligible (Sylvester et al. 1994).
The star has a thin circumstellar dust disc with 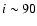
 (Smith &
Terrile 1984).
For our UV3C analysis we assume that the (hypothetical) accretion disc remnant
has the same inclination.
The star was recently discovered to be a ZAMS
(Smith &
Terrile 1984).
For our UV3C analysis we assume that the (hypothetical) accretion disc remnant
has the same inclination.
The star was recently discovered to be a ZAMS 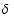 Scuti variable (Koen 2003).
Scuti variable (Koen 2003).
C.11 HD 104237 - DX Cha
This star in Cha III was classified by WW88 as A0e and has been
identified as a Herbig Ae star by Hu et al. (1989).
Along with  =6
=6
 6 it is the brightest Herbig Ae star so far.
From its low-resolution UV spectrum, Hu et al. (1991) classified HD 104237 as
A4 Ve.
Monitoring photometry and spectroscopy during 5 successive nights in 1991,
repeated in 1992, showed short-term variability in the emission-line fluxes but
no photometric variability: neither on short time-scales (hours or nights) nor
between the two years (deWinter et al. 2001).
High-resolution UV spectra, taken with IUE, show P-Cygni profiles
for the Mg II h,k emission-lines and strong indications of such profiles for
the emission-lines of C II, Si IV, and C IV.
Improved resolution and S/N for these profiles, obtained with the GHRS of HST,
suggests the presence of a bi-conical disc wind, originating in the inner
part of the accretion disc (Brown et al. 1997).
The distance of HD 104237 was estimated (Hu et al. 1991) from its close
(2
6 it is the brightest Herbig Ae star so far.
From its low-resolution UV spectrum, Hu et al. (1991) classified HD 104237 as
A4 Ve.
Monitoring photometry and spectroscopy during 5 successive nights in 1991,
repeated in 1992, showed short-term variability in the emission-line fluxes but
no photometric variability: neither on short time-scales (hours or nights) nor
between the two years (deWinter et al. 2001).
High-resolution UV spectra, taken with IUE, show P-Cygni profiles
for the Mg II h,k emission-lines and strong indications of such profiles for
the emission-lines of C II, Si IV, and C IV.
Improved resolution and S/N for these profiles, obtained with the GHRS of HST,
suggests the presence of a bi-conical disc wind, originating in the inner
part of the accretion disc (Brown et al. 1997).
The distance of HD 104237 was estimated (Hu et al. 1991) from its close
(2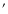 )
common-proper motion companion
)
common-proper motion companion
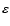 Cha (HR 4583, B9 V),
which has
Cha (HR 4583, B9 V),
which has 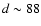
 .
However, by assuming that
.
However, by assuming that
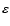 Cha is a ZAMS star and by accounting
for the double-star nature of
Cha is a ZAMS star and by accounting
for the double-star nature of
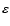 Cha itself, Eggen (1998) improved the
estimate to a value of
Cha itself, Eggen (1998) improved the
estimate to a value of  111
111 .
This is just within the range of the Hipparcos (ATT97) measurement:
116
+8-7
.
This is just within the range of the Hipparcos (ATT97) measurement:
116
+8-7 .
HD 104237 does not show much photometric variability:
.
HD 104237 does not show much photometric variability: 
 6
6
 60.
The UV spectrum indicates a type A7 IV, which gives
60.
The UV spectrum indicates a type A7 IV, which gives
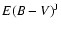 =0.02-0.04
=0.02-0.04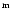 .
We assume that
.
We assume that
 corresponds to the lowest value; i.e.
corresponds to the lowest value; i.e.
 =0
=0
 02.
Knee & Prusti (1996) found evidence that these stars are located in a hole of
the molecular cloud in which they were formed, so that they have almost
no foreground extinction.
From the red-shifted component of Ly
02.
Knee & Prusti (1996) found evidence that these stars are located in a hole of
the molecular cloud in which they were formed, so that they have almost
no foreground extinction.
From the red-shifted component of Ly -emission, we derived i=53
-emission, we derived i=53 (Blondel et al. 1993, Appendix D.4).
The
(Blondel et al. 1993, Appendix D.4).
The 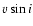 -value from Table 1 was estimated by us from
lines in the visual spectrum of HD 104237 (deWinter & vandenAncker 1991).
Also this star was found to be a PMS
-value from Table 1 was estimated by us from
lines in the visual spectrum of HD 104237 (deWinter & vandenAncker 1991).
Also this star was found to be a PMS 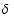 Scuti variable (Donati et al. 1997;
Kurtz & Müller 1999).
Scuti variable (Donati et al. 1997;
Kurtz & Müller 1999).
C.12 HD 169142 - MWC925
The star was identified as a nearby B9 V star by WW88.
Since it has H -emission and a strong NIR excess (Oud92) it was recognised as
a Herbig star (possibly a double star).
The photometric variability of HD 169142 is unknown.
From its visual spectrum Dunkin et al. (1997a,b) classified the star as
A5 Ve.
For this type Sylvester et al. (1996) derived d=145
-emission and a strong NIR excess (Oud92) it was recognised as
a Herbig star (possibly a double star).
The photometric variability of HD 169142 is unknown.
From its visual spectrum Dunkin et al. (1997a,b) classified the star as
A5 Ve.
For this type Sylvester et al. (1996) derived d=145 and
and
 <0
<0
 14.
For A7 Ve we find with Sylvester's
14.
For A7 Ve we find with Sylvester's
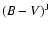 =0
=0
 29 that d=151
29 that d=151 and
and
 =0
=0
 0.
0.
C.13 HD 36112 - MWC758
Oud92 classified this star as A3e and MBW98 identified it as an Herbig Ae star.
Variations in the H -emission profiles on a time-scale of days were
observed by Beskrovnaya et al. (1996).
No photometric variations are known.
From the Hipparcos measurements d=200
+60-40
-emission profiles on a time-scale of days were
observed by Beskrovnaya et al. (1996).
No photometric variations are known.
From the Hipparcos measurements d=200
+60-40 was
derived (AWT98), and from the UV spectrum we conclude that the spectral type
must be A7 III.
With
was
derived (AWT98), and from the UV spectrum we conclude that the spectral type
must be A7 III.
With
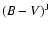 =0
=0
 29 (deWinter et al. 2001) we then find that
29 (deWinter et al. 2001) we then find that
 <0
<0
 07.
07.
C.14 HD 139614 - CD-42  10650
10650
WW88 classified this star close to RSF Sco/Oph as A7 Vz
and MWM98 recognised it as a Herbig Ae star.
Profiles of H (em), Na I D and He I (em) was observed by
Dunkin et al. (1997a) and MWM98.
The star may be a double star.
Its photometric variability is still unknown.
From Johnson photometry Sylvester et al. (1996) derived d=157
(em), Na I D and He I (em) was observed by
Dunkin et al. (1997a) and MWM98.
The star may be a double star.
Its photometric variability is still unknown.
From Johnson photometry Sylvester et al. (1996) derived d=157 and
and
 < 0
< 0
 03.
03.
C.15 HD 142666 - V1026 Sco
Also this object is situated near RSF Sco/Oph.
The object was classified as an A3 Vz star by WW88 and identified as a
Herbig Ae star by MWM98.
Profiles of H (em), He I, and Na I D were obtained by
Dunkin et al. (1997a) and MWM98.
HD 142666 is photometrically variable (MBW98), which was confirmed by the
observations with the Tycho instrument aboard the Hipparcos satellite
(Makarov et al. 1994).
From Johnson photometry of the star Sylvester et al. (1996) derived
a spectral type A8 Ve, d=114
(em), He I, and Na I D were obtained by
Dunkin et al. (1997a) and MWM98.
HD 142666 is photometrically variable (MBW98), which was confirmed by the
observations with the Tycho instrument aboard the Hipparcos satellite
(Makarov et al. 1994).
From Johnson photometry of the star Sylvester et al. (1996) derived
a spectral type A8 Ve, d=114 and
and
 <0
<0
 30.
From the EW's of the Na I D lines, observed by Dunkin et al. (1997a) we
derive with the Strömgren (1948) doublet method and the relation of
Hobbs (1974) that
30.
From the EW's of the Na I D lines, observed by Dunkin et al. (1997a) we
derive with the Strömgren (1948) doublet method and the relation of
Hobbs (1974) that
 <0
<0
 26.
MWM98 obtained
26.
MWM98 obtained
 =0
=0
 22 from Geneva photometry.
The star is a PMS
22 from Geneva photometry.
The star is a PMS  Scuti variable (Kurtz & Müller 2001).
Scuti variable (Kurtz & Müller 2001).
C.16 V346 Ori - HD 287841
The star is a rapid, strongly (
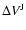 =1
=1
 9) irregular-variable, and from
the TCD we estimate a spectral type of A3-4.
Its CMD shows a "blueing branch'', which is typical for the UXORs.
The photometric time-variability was studied by Koval'chuk (1985),
who noted that deep (
9) irregular-variable, and from
the TCD we estimate a spectral type of A3-4.
Its CMD shows a "blueing branch'', which is typical for the UXORs.
The photometric time-variability was studied by Koval'chuk (1985),
who noted that deep (
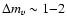
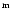 )
fadings in brightness
occur abruptly within 1 day and are followed by a return to the initial
brightness in 1-5 days.
The amplitude of the fading increases towards the UV.
High resolution spectra (deWinter 1991) show H
)
fadings in brightness
occur abruptly within 1 day and are followed by a return to the initial
brightness in 1-5 days.
The amplitude of the fading increases towards the UV.
High resolution spectra (deWinter 1991) show H -emission
filling-in the photospheric absorption profile.
Other low-resolution spectra show many metallic absorption lines, including
the Ca II (2) red-triplet, which indicate a late-A spectral type that is in
agreement with the classification A5 III of Zajtseva (1986).
The lower limit for the distance, obtained by Hipparcos (ATT98) is 130
-emission
filling-in the photospheric absorption profile.
Other low-resolution spectra show many metallic absorption lines, including
the Ca II (2) red-triplet, which indicate a late-A spectral type that is in
agreement with the classification A5 III of Zajtseva (1986).
The lower limit for the distance, obtained by Hipparcos (ATT98) is 130 so that it is not certain whether this star is a member of the Orion OB1a
complex.
V346 Ori was recently detected to be a PMS
so that it is not certain whether this star is a member of the Orion OB1a
complex.
V346 Ori was recently detected to be a PMS  Scuti variable
(Pinheiro et al. 2003).
Scuti variable
(Pinheiro et al. 2003).
C.18 V351 Ori - HD 38238
The photometric behaviour of this star, located in M78, a cluster in
DC Lyn 1630, is peculiar: before 1984/5 it behaved like a Herbig Ae star
with strong variations (
 =3
=3
 3) with a "blueing branch'' in the CMD,
while after 1985 the star is at maximum brightness and rarely varies.
In this respect its photometric behaviour is similar to that of BN Ori
(Sect. C.19) and FU Ori (Sect. C.23).
A flare was reported in 1982 by Koval'chuk (1984, 1986).
Spectroscopic information from the period before 1985 is scarce, but from a low
resolution blue spectrum Strom et al. (1975) estimated a spectral type of A0-2
from the strength of the Ba II and Ca II absorption lines.
In a low-resolution IDS spectrum taken in 1985 by H. Cuypers (unpubl.), the
H
3) with a "blueing branch'' in the CMD,
while after 1985 the star is at maximum brightness and rarely varies.
In this respect its photometric behaviour is similar to that of BN Ori
(Sect. C.19) and FU Ori (Sect. C.23).
A flare was reported in 1982 by Koval'chuk (1984, 1986).
Spectroscopic information from the period before 1985 is scarce, but from a low
resolution blue spectrum Strom et al. (1975) estimated a spectral type of A0-2
from the strength of the Ba II and Ca II absorption lines.
In a low-resolution IDS spectrum taken in 1985 by H. Cuypers (unpubl.), the
H line is partly filled-in.
The high-resolution spectra by vandenAncker et al. (1996) confirm this filling-in and
indicate a spectral type A5-7 IIIe.
This spectral type is in agreement with the photometric classifications of
Kilkenny et al. (1985) and Zajtseva (1986).
Hipparcos observations give a lower limit for the distance of 210
line is partly filled-in.
The high-resolution spectra by vandenAncker et al. (1996) confirm this filling-in and
indicate a spectral type A5-7 IIIe.
This spectral type is in agreement with the photometric classifications of
Kilkenny et al. (1985) and Zajtseva (1986).
Hipparcos observations give a lower limit for the distance of 210 (AWT98).
Because of its location in the association Ori OB1 b1 we assume
d=450
(AWT98).
Because of its location in the association Ori OB1 b1 we assume
d=450 and
and
 =0
=0
 06 for V351 Ori.
Marconi et al. (2000) observed that this star is a PMS
06 for V351 Ori.
Marconi et al. (2000) observed that this star is a PMS 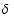 Scuti variable.
Scuti variable.
C.19 BN Ori - HD 245465
This star near 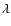 Ori has a remarkable photometric history:
between 1897 and 1947 the star was strongly and irregularly variable, with
amplitudes up to 4
Ori has a remarkable photometric history:
between 1897 and 1947 the star was strongly and irregularly variable, with
amplitudes up to 4
 (Dragomiretskaya 1965), similar to
BF Ori (Sect. C.7), T Ori, and UX Ori (Sect. C.3).
After 1947 the brightness increased by 0
(Dragomiretskaya 1965), similar to
BF Ori (Sect. C.7), T Ori, and UX Ori (Sect. C.3).
After 1947 the brightness increased by 0
 5 with small variations and finally
settled at
5 with small variations and finally
settled at  =9
=9
 65, where it stayed since 1965.
From the TCD a spectral type of A5-F2 can be estimated, while spectroscopic
classifications range from A7-F0 (Cannon 1931, Hb54) or A7-late-G (Shevchenko
1989).
The later spectral types may be interpreted by the presence of outer layers
in the envelope of the star, which contribute to a certain stratification in
this envelope, similar to that present in the envelope of FUORs in their
post-outburts phase.
The similarity of the lightcurve and spectroscopic features between BN Ori and
the "classical'' FUORs suggest that BN Ori is related to this class
(Shevchenko et al. 1997).
In this scenario the photospheric classification corresponds to A7-F0 III.
We will assume that the star belongs to the
65, where it stayed since 1965.
From the TCD a spectral type of A5-F2 can be estimated, while spectroscopic
classifications range from A7-F0 (Cannon 1931, Hb54) or A7-late-G (Shevchenko
1989).
The later spectral types may be interpreted by the presence of outer layers
in the envelope of the star, which contribute to a certain stratification in
this envelope, similar to that present in the envelope of FUORs in their
post-outburts phase.
The similarity of the lightcurve and spectroscopic features between BN Ori and
the "classical'' FUORs suggest that BN Ori is related to this class
(Shevchenko et al. 1997).
In this scenario the photospheric classification corresponds to A7-F0 III.
We will assume that the star belongs to the 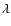 Orionis
association (Cr70) close to RSF 1 Ori B and therefore adopt
d=400
Orionis
association (Cr70) close to RSF 1 Ori B and therefore adopt
d=400 (from the mean parallax determined by Artiyukhina 1960) and
(from the mean parallax determined by Artiyukhina 1960) and
 =0
=0
 06 (from the Na I D lines determined by Shevchenko et al. 1997).
06 (from the Na I D lines determined by Shevchenko et al. 1997).
C.20 HD 35929 - BD-08  1128
1128
The spectral classification in the HD catalogue is A5.
From his photometry on the Strömgren system Olson (1979) derived
spectral type F5 and from their UBVRI-photometry Miroshnichenko et al.
(1997) classified the star as A8 Vz, which implies 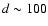
 .
However, the Hipparcos measurements led to
.
However, the Hipparcos measurements led to 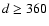
 (AWT98).
If we assume that the star belongs to the association Ori OB1c, with
(AWT98).
If we assume that the star belongs to the association Ori OB1c, with
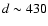
 and
and

 0
0
 06 (Warren & Hesser 1978) it should be a
giant.
From the flux rise in the IUE SW-spectral range we classify HD 35929 as
F0 IIIe (with
06 (Warren & Hesser 1978) it should be a
giant.
From the flux rise in the IUE SW-spectral range we classify HD 35929 as
F0 IIIe (with  = -0.3 and d = 400
= -0.3 and d = 400 ).
This star is a PMS
).
This star is a PMS 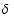 Scuti variable (Marconi et al. 2000).
Scuti variable (Marconi et al. 2000).
C.21 HD 144432 - CD-27  10778
10778
Visual spectra show a variable double H -emission profile, a weak and broad
He I 5876Å in emission, broad Na I D lines with emission-components, the
Ca II (2) red-triplet in emission, and an inverse P-Cygni profile for He I (1.08
-emission profile, a weak and broad
He I 5876Å in emission, broad Na I D lines with emission-components, the
Ca II (2) red-triplet in emission, and an inverse P-Cygni profile for He I (1.08 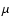 m) (Pérez et al. 2004; Grady et al. 1996; Dunkin et al. 1997a,b,
MWM98).
There is no record of photometrical variability.
This star in RSF Sco R1 was classified by WW88 as a ZAMS star of
spectral type A9-F0 at
m) (Pérez et al. 2004; Grady et al. 1996; Dunkin et al. 1997a,b,
MWM98).
There is no record of photometrical variability.
This star in RSF Sco R1 was classified by WW88 as a ZAMS star of
spectral type A9-F0 at 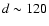
 .
Sylvester et al. (1996) arrives at the same conclusion from the Johnson
photometry.
If the star is a member of Sco OB2-2 (Pérez et al. 2004) then
d = 145
.
Sylvester et al. (1996) arrives at the same conclusion from the Johnson
photometry.
If the star is a member of Sco OB2-2 (Pérez et al. 2004) then
d = 145 .
However, the Hipparcos observation gives
.
However, the Hipparcos observation gives 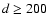
 (AWT98).
An
(AWT98).
An
 < 0
< 0
 03 was estimated by Sylvester et al. (1996).
MWM98 obtain
03 was estimated by Sylvester et al. (1996).
MWM98 obtain

 0
0
 15, but the application of the
Strömgren Doublet method to the Na I D EW's observed by Dunkin et al.
(1997a) gives us
15, but the application of the
Strömgren Doublet method to the Na I D EW's observed by Dunkin et al.
(1997a) gives us

 0
0
 02.
The low value of the foreground extinction is common to the other stars in the
neighbourhood of RSF Sco/ Oph: HD 139614 (Sect. C.14) and HR 5999
(Sect. C.9).
HD 144432 is a visual double star (Table B.1).
02.
The low value of the foreground extinction is common to the other stars in the
neighbourhood of RSF Sco/ Oph: HD 139614 (Sect. C.14) and HR 5999
(Sect. C.9).
HD 144432 is a visual double star (Table B.1).
C.22 BD+47  4206
4206
From objective prism spectra the star was classified as A9 III.
At present it is not known if H has an emission component.
There is no record of photometric variability.
The star is a member (n0.19) of the young BM And association with
d=440 (
has an emission component.
There is no record of photometric variability.
The star is a member (n0.19) of the young BM And association with
d=440 (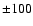 )
) and
and
 =0
=0
 05 (Aveni & Hunter 1969), which
is in the range of the Hipparcos result: 260
+166-74
05 (Aveni & Hunter 1969), which
is in the range of the Hipparcos result: 260
+166-74 (ESA 1997).
(ESA 1997).
C.23 FU Ori - BD+09  5427
5427
This peculiar star is the result of an outburst of a 16 magnitude
star in the last months of 1936.
Since the outburst the brightness has decreased slowly by a small amount until
it reached its present value of
magnitude
star in the last months of 1936.
Since the outburst the brightness has decreased slowly by a small amount until
it reached its present value of  =9
=9
 3.
Its visual spectrum after the outburst has been described by Hb66, who
classified the photospheric component as F2:p I - II from the Balmer
lines and the low-excitation lines of neutral and singly ionised metals.
The envelope is of type K-M deduced from the Ca II (2) red-triplet, which
points to a stratification of the atmosphere (see also BN Ori;
Sect. C.19).
Similar to Z CMa (Sect. C.30) the low-resolution UV spectrum of FU Ori
has been analysed by Kenyon et al. (1989), but in these analyses the IUE
SW-part (in which the BL dominates) has not been taken into account.
Since the precursor of FU Ori was a member of the Ori T4 association
(Kh59) it was presumably a T Tauri star, so that its mass cannot be much larger
than
3.
Its visual spectrum after the outburst has been described by Hb66, who
classified the photospheric component as F2:p I - II from the Balmer
lines and the low-excitation lines of neutral and singly ionised metals.
The envelope is of type K-M deduced from the Ca II (2) red-triplet, which
points to a stratification of the atmosphere (see also BN Ori;
Sect. C.19).
Similar to Z CMa (Sect. C.30) the low-resolution UV spectrum of FU Ori
has been analysed by Kenyon et al. (1989), but in these analyses the IUE
SW-part (in which the BL dominates) has not been taken into account.
Since the precursor of FU Ori was a member of the Ori T4 association
(Kh59) it was presumably a T Tauri star, so that its mass cannot be much larger
than  1
1
 .
Because of its location in the RSF Orion, we adopt d=450-500
.
Because of its location in the RSF Orion, we adopt d=450-500 and
and
 =0
=0
 06.
06.
C.25 CQ Tau - HD 36910
CQ Tau is situated in the T-association Tau T4 (Kh59).
This star is strongly and irregularly variable, similar to other UXORs.
From their collection of blue objective prism spectra obtained at various
brightness phases, Götz & Wenzel (1968) concluded that at bright phases
( <10
<10
 4) the star had spectral type A-F0, wheras during the fainter
phases it could be classified as A2-8.
In addition, for phases fainter than
4) the star had spectral type A-F0, wheras during the fainter
phases it could be classified as A2-8.
In addition, for phases fainter than  =11
=11
 1 the spectral type of CQ Tau
could vary between A2 and F7.
These classifications were mainly based on the strength of the Balmer and
Ca II K lines and of the strength of the G-band.
From model-fitting of the wings of the H
1 the spectral type of CQ Tau
could vary between A2 and F7.
These classifications were mainly based on the strength of the Balmer and
Ca II K lines and of the strength of the G-band.
From model-fitting of the wings of the H -line in a spectrum taken at
-line in a spectrum taken at
 =10
=10
 46, Berdyugin et al. (1990) concluded to a type F0 III.
The TCD photometric classification gave A8.
Artyukhina (1959) derives d=137
46, Berdyugin et al. (1990) concluded to a type F0 III.
The TCD photometric classification gave A8.
Artyukhina (1959) derives d=137 from the kinematic parallax.
Hipparcos gives d=100
+25-17
from the kinematic parallax.
Hipparcos gives d=100
+25-17 (AWT98).
Götz & Wenzel (1968) derived d=220
(AWT98).
Götz & Wenzel (1968) derived d=220 for the nearby (2
for the nearby (2
 )
G0 V reference star f with an
)
G0 V reference star f with an
 =0
=0
 10.
This G-star has not been observed by Hipparcos.
If we assume a uniform colour excess over the distance of 220
10.
This G-star has not been observed by Hipparcos.
If we assume a uniform colour excess over the distance of 220 we then
estimate that
we then
estimate that
 =0
=0
 068 for CQ Tau.
068 for CQ Tau.
C.26 NX Pup - CD-44  3318
3318
This variable star in the head of the cometary globule CG1 of the
Gum nebula, can be classified as F4-5 and sometimes F0-2 from its
position in the TCD (photometry by Brand et al. 1983; TjinADjie et al. 1984;
Ng 1986).
The short time-scale variability is correlated with a variable UVE for
different brightness stages of the star.
From its visual spectrum the star has been classified as F0-2 IIIe
(Irvine 1975; Brand et al. 1983; Reipurth 1983), in particular because of the
presence of the G-band.
On the other hand, several features in the visual spectrum resemble those of
the Herbig B9e star HD 250550 (Reipurth 1983) and the SW-part of the UV spectrum
is very similar to that of an A0 Ie type star (TjinADjie et al. 1984), which is
consistent with the flux distribution in the UV as observed by ANS (de Boer
1977).
In agreement with this the SED from UV to NIR could be matched by the flux
distribution of a strongly reddened A0 III star with an anomalous
circumstellar extinction law (TjinADjie et al. 1984).
The presence of the He I 5876 Å line could support this classification
(Böhm & Catala 1995).
However this line also occurs in late-type stars (e.g. RR Tau) and is highly
variable in strength and can even disappear (Grinin et al. 2001), so that
classification based on the occurance of the 5876 Å line is uncertain.
Recently, high angular resolution observations with the Fine Guidance Sensor
#3 aboard HST show that NX Pup is a double star with a separation of
0
 126 (
126 (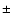 0
0
 007), a PA of 63
007), a PA of 63 ,
and a
,
and a
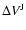 of 0
of 0
 64
(Bernacca et al. 1993, Table B.1).
These parameters were confirmed by Hipparcos measurements.
The companion was detected in the NIR by Brandner et al.
(1995, 1996), Tessier et al. (1994) and Schöller et al. (1996).
This secondary probably has a spectral type between F2 II and G5 IV.
From the association with the Gum nebula, we estimate d=450-500
64
(Bernacca et al. 1993, Table B.1).
These parameters were confirmed by Hipparcos measurements.
The companion was detected in the NIR by Brandner et al.
(1995, 1996), Tessier et al. (1994) and Schöller et al. (1996).
This secondary probably has a spectral type between F2 II and G5 IV.
From the association with the Gum nebula, we estimate d=450-500 (Brand et al. 1983).
According to Krautter (1980) the
(Brand et al. 1983).
According to Krautter (1980) the
 in the direction of NX Pup is
negligible.
in the direction of NX Pup is
negligible.
C.27 BD+46  3471 - V1578 Cyg
3471 - V1578 Cyg
This star was shown to be a double star (Pirzkal et al. 1997,
Table B.1).
The few available photometric observations (taken years apart) show differences,
but the course and the time-scale of the variability are not known so far.
The position of the star in the TCD corresponds with spectral type A5.
Classifications from the visual spectrum of
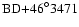 range from A2e (Str72) to
A4e (Fz85, Catala et al. 1986).
On the other hand, the spectrum of this star in the blue and UV is very
similar to that of NX Pup (Sect. C.26), which suggests that
range from A2e (Str72) to
A4e (Fz85, Catala et al. 1986).
On the other hand, the spectrum of this star in the blue and UV is very
similar to that of NX Pup (Sect. C.26), which suggests that
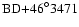 has a spectral type F0-2 III.
However, we have an additional argument to constrain the spectral type.
From the high-resolution Na I D observations of Catala et al. (1986) we
derive with the Strömgren doublet method (1948) a column density of
2.06
has a spectral type F0-2 III.
However, we have an additional argument to constrain the spectral type.
From the high-resolution Na I D observations of Catala et al. (1986) we
derive with the Strömgren doublet method (1948) a column density of
2.06  1013
1013
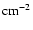 for Na I.
Since Na I can only be present in the foreground of the star, we obtain
an
for Na I.
Since Na I can only be present in the foreground of the star, we obtain
an
 =0
=0
 31 from the empirical relation between
31 from the empirical relation between
 and the i.s. H or
Na I D column density of Hobbs (1974).
Then the observed
and the i.s. H or
Na I D column density of Hobbs (1974).
Then the observed
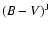 =0
=0
 41 and the values of
41 and the values of
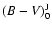 given by SK82 only
permit spectral types earlier than A5.
Our arguments do not constrain the distance.
The Hipparcos measurements give only a lower limit of d=280
given by SK82 only
permit spectral types earlier than A5.
Our arguments do not constrain the distance.
The Hipparcos measurements give only a lower limit of d=280 (AWT98).
The star is probably a member of the young open cluster IC 5146, for
which
(AWT98).
The star is probably a member of the young open cluster IC 5146, for
which  (
( 100)
100) (Elias 78c).
The value of
(Elias 78c).
The value of
 is in the same range as found for CMa R1
(Shevchenko et al. 1999), which has
is in the same range as found for CMa R1
(Shevchenko et al. 1999), which has  kpc.
The Na I D profiles in both cases indicate that part of the
kpc.
The Na I D profiles in both cases indicate that part of the
 -values may
be due to extinction in the association.
-values may
be due to extinction in the association.
C.28 HK Ori - MWC497
The star is a double star system (Leinert et al. 1997, Table B.1) in
which the secondary companion is much redder than the primary star and probably
contributes very little to the UV fluxes of the system.
The visual spectral classification of HK Ori is ambiguous and depends on the
features which are given most weight.
On the basis of the strength of the Balmer lines and the presence of faint
He I and Ca I lines Joy (1949) and Hb60a suggested a type A4 V, but
from the occurrence of He I and Fe II emission-lines Str72 concluded
to B7-8.
It is possible that the emission from the surrounding nebula contributes
to the spectrum.
Because of such ambiguities later catalogues are less explicit and only quote
A-Fe (Fz85) or Ae (HB88).
HK Ori is an irregular variable with a mean position in the TCD of the Johnson
and Walraven photometric systems which corresponds with F5.
If the star is a member of the Ori T1 association with d=400-460 (Kh59) and
(Kh59) and
 =0
=0
 06 and if we assume that its c.s. excess is small, its
visual magnitude
06 and if we assume that its c.s. excess is small, its
visual magnitude
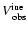 =11
=11
 5 constrains
5 constrains  to 3.3-2.8
to 3.3-2.8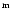 ,
which
corresponds to type F0-2 V or F8 IV to early-K IV (SK82).
,
which
corresponds to type F0-2 V or F8 IV to early-K IV (SK82).
C.29 AK Sco - HD 152404
AK Sco is situated in the border of the upper Sco subgroup of the
Sco-Cen association.
Considering its spectrum and in particular the presence of strong Li I
absorption, Hb60b classified AK Sco as a F5 IVe PMS star.
Later Andersen et al. (1989) showed that the star is a double-line
spectroscopic double star (Table B.1).
Accurate radial velocity measurements resulted to the orbital elements:
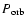 =13
=13
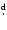 6, PA = 185
6, PA = 185 ,
e=0.47 and a mass-ratio of
,
e=0.47 and a mass-ratio of  1.
From the orbital elements, the spectral type, the intrinsic colour indices,
and the rotation velocities, Andersen et al. (1989) modeled the system by
comparing it with the MS double star RZ Cha.
The AK Sco-system probably consists of two 1.5
1.
From the orbital elements, the spectral type, the intrinsic colour indices,
and the rotation velocities, Andersen et al. (1989) modeled the system by
comparing it with the MS double star RZ Cha.
The AK Sco-system probably consists of two 1.5
 F5 IV stars with an
orbital inclination of 63
F5 IV stars with an
orbital inclination of 63 and semi-major axis of 35
and semi-major axis of 35
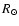 .
The distance and colour excess (at maximum brightness), derived by Andersen
et al. (1989) for spectral type F6 Ve are 200 (
.
The distance and colour excess (at maximum brightness), derived by Andersen
et al. (1989) for spectral type F6 Ve are 200 (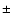 40)
40) and
0
and
0
 13 (
13 (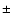 0.02).
The Hipparcos measurements give 150
+40-30
0.02).
The Hipparcos measurements give 150
+40-30 (AWT98).
At this distance the separation of the components is too small to resolve
them with the HST FES (Bernacca et al. 1995).
(AWT98).
At this distance the separation of the components is too small to resolve
them with the HST FES (Bernacca et al. 1995).
C.30 Z CMa - HD 53179
The star is a member of the CMa R1 association with 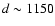
 (Claria 1974; Herbst et al. 1982).
The visual spectrum of Z CMa is complicated and shows simultaneous lines which
are characteristic for early (B5-8) and late (mid-F) spectral types (Str72,
FJ84, Covino et al. 1984; Hessman et al. 1991; Hamann & Persson 1992).
The spectral varability and the lightcurve suggest that the star is related to
the class of the FUORs.
Hartmann et al. (1989) showed that the line profiles in the red and NIR part of
the spectrum can be formed in a rotating accretion disc.
From these data and the SED of Z CMa they derive
(Claria 1974; Herbst et al. 1982).
The visual spectrum of Z CMa is complicated and shows simultaneous lines which
are characteristic for early (B5-8) and late (mid-F) spectral types (Str72,
FJ84, Covino et al. 1984; Hessman et al. 1991; Hamann & Persson 1992).
The spectral varability and the lightcurve suggest that the star is related to
the class of the FUORs.
Hartmann et al. (1989) showed that the line profiles in the red and NIR part of
the spectrum can be formed in a rotating accretion disc.
From these data and the SED of Z CMa they derive
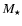
 1-3
1-3
 ,
an
inner disc radius of 9-16
,
an
inner disc radius of 9-16
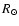 and
and 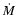
 10-3
10-3
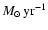 .
.
These values had to be revised after the speckle interferometric detection of a
companion star at 0
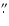 1 in the NIR (Koresko et al. 1991, Haas et al. 1993)
and in the visual (Barth et al. 1994, Thiébaut et al. 1995,
Table B.1).
This companion of 2100
1 in the NIR (Koresko et al. 1991, Haas et al. 1993)
and in the visual (Barth et al. 1994, Thiébaut et al. 1995,
Table B.1).
This companion of 2100
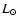 dominates the IR part of the SED, wheras the
FUOR-type star of only 640
dominates the IR part of the SED, wheras the
FUOR-type star of only 640
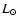 dominates in the visual.
Koresko et al. (1991) derived
dominates in the visual.
Koresko et al. (1991) derived
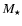 =2.3
=2.3
 ,
an inner disc radius of 20
,
an inner disc radius of 20
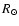 and
and 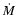 =6
=6  10-4
10-4
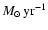 for the visual companion.
Occasionally (Feb. 1987 and Jan. 2000) the IR primary dominates the visual
spectrum with a spectral type B0 IIIe (vandenAncker et al. 1904)
Optical spectropolarimetry by Whitney et al. (1993) confirms this picture and
for the visual spectrum of the system the authors assume an effective spectral
type F5 I, which leads to
for the visual companion.
Occasionally (Feb. 1987 and Jan. 2000) the IR primary dominates the visual
spectrum with a spectral type B0 IIIe (vandenAncker et al. 1904)
Optical spectropolarimetry by Whitney et al. (1993) confirms this picture and
for the visual spectrum of the system the authors assume an effective spectral
type F5 I, which leads to
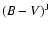 =0
=0
 7.
They separated this into
7.
They separated this into
 =0
=0
 2 and
2 and
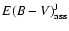 =0
=0
 5 with R=4.2 for the dust in
the CMa R1 association.
From a study of this association (Shevchenko et al. 1999) we conclude that
5 with R=4.2 for the dust in
the CMa R1 association.
From a study of this association (Shevchenko et al. 1999) we conclude that
 =0
=0
 16 and
16 and
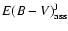 =0
=0
 20.
Similar to FU Ori (Sect. C.23) the UV spectrum of Z CMa has been
analysed by Kenyon et al. (1989), but also in this analysis the IUE SW-part
has been ignored.
For Z CMa we use d=1050 (
20.
Similar to FU Ori (Sect. C.23) the UV spectrum of Z CMa has been
analysed by Kenyon et al. (1989), but also in this analysis the IUE SW-part
has been ignored.
For Z CMa we use d=1050 ( 150)
150) ,
which was derived for the CMa R1
association (Shevchenko et al. 1999).
,
which was derived for the CMa R1
association (Shevchenko et al. 1999).
C.31 HD 199143 - BD-17  6127
6127
This star has an MK classification of F8 V, which was confirmed by
vandenAncker et al. (2000) from its SED.
These authors also reported many strong variable emission-lines in the spectra
taken with IUE and EUVE and a rapid rotation (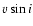
 125
125
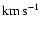 )
from lines
in the visual.
They suggested that the emission and the rapid rotation are due to an unseen
nearby T Tauri companion, which is spinning up the F8 V star by episodic mass
transfer.
Such a companion was recently detected by high-resolution NIR imaging by
Jayawardhana & Brandeker (1991) and by Neuhäuser et al. (2002) at a
distance of 1
)
from lines
in the visual.
They suggested that the emission and the rapid rotation are due to an unseen
nearby T Tauri companion, which is spinning up the F8 V star by episodic mass
transfer.
Such a companion was recently detected by high-resolution NIR imaging by
Jayawardhana & Brandeker (1991) and by Neuhäuser et al. (2002) at a
distance of 1
 from HD 199143.
They estimated the values given in Table C.1
from the Hipparcos distance measurement (47.7 (
from HD 199143.
They estimated the values given in Table C.1
from the Hipparcos distance measurement (47.7 (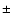 2.4)
2.4) )
and the theoretical evolutionary tracks (Palla & Stahler 1999).
Almost simultaneous observations by Chauvin et al. (2002) essentially confirm
these results, but their improved flux measurement in the J-band and the
corresponding choice of a slightly later spectral type (M2 V) for the
secondary star removes the excess in this band and therefore the need for
circumstellar dust around this star.
This does not give evidence of (recent) mass transfer from the secondary star.
For our UV spectral analysis we assume that
)
and the theoretical evolutionary tracks (Palla & Stahler 1999).
Almost simultaneous observations by Chauvin et al. (2002) essentially confirm
these results, but their improved flux measurement in the J-band and the
corresponding choice of a slightly later spectral type (M2 V) for the
secondary star removes the excess in this band and therefore the need for
circumstellar dust around this star.
This does not give evidence of (recent) mass transfer from the secondary star.
For our UV spectral analysis we assume that
 < 0
< 0
 01, since this value was
needed in order to fit the Kurucz model with
01, since this value was
needed in order to fit the Kurucz model with
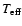 =6200 K and
=6200 K and
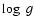 =4.3 (vandenAncker et al. 2000) to the observed SED of HD 199143A.
=4.3 (vandenAncker et al. 2000) to the observed SED of HD 199143A.
Table C.1:
Data for HD 199143 from Neuhäuser et al. (2002).
C.32 V380 Ori - BD-06  1253
1253
The star is a double-star system (Leinert et al. 1994), in which the secondary
companion is much redder than the primary star (the flux ratio is 0.31 at
2.2 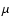 m) and probably contributes very little to the UV fluxes of the
system.
The doubler-star parameters are given in Table B.1.
The classification of its visual spectrum gives B8-A2e (Hb60a), which is
mainly based on the strength of the Balmer lines.
On the other hand Herbig also noted some similarities with the spectra of
the later type T Tauri stars and of Z CMa (Sect. C.30), in particular
the strong emission-components in many Fe II, Cr II, and Ti II lines.
Later it has been argued that these lines may be formed in an
envelope or in the surface wind around the star (Shevchenko 1994, 1998;
Rossi et al. 1999).
The Li I absorption line at 6707 Å (Corcoran & Ray 1995) may be due
to the secondary component, which therefore should have a spectral type of
F5 or later.
The position of the star in the TCD of the Johnson and Walraven photometric
systems varies irregularly in time between B4-B9 and F.
These variations are similar to what is observed for NX Pup (Sect. C.26),
and are clearly correlated with a variable UVE.
The minimum value of
m) and probably contributes very little to the UV fluxes of the
system.
The doubler-star parameters are given in Table B.1.
The classification of its visual spectrum gives B8-A2e (Hb60a), which is
mainly based on the strength of the Balmer lines.
On the other hand Herbig also noted some similarities with the spectra of
the later type T Tauri stars and of Z CMa (Sect. C.30), in particular
the strong emission-components in many Fe II, Cr II, and Ti II lines.
Later it has been argued that these lines may be formed in an
envelope or in the surface wind around the star (Shevchenko 1994, 1998;
Rossi et al. 1999).
The Li I absorption line at 6707 Å (Corcoran & Ray 1995) may be due
to the secondary component, which therefore should have a spectral type of
F5 or later.
The position of the star in the TCD of the Johnson and Walraven photometric
systems varies irregularly in time between B4-B9 and F.
These variations are similar to what is observed for NX Pup (Sect. C.26),
and are clearly correlated with a variable UVE.
The minimum value of
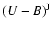 is zero, which corresponds with a type F.
Since V380 Ori is located in the Ori T2 association (NGC 1999)
of Ori OB1c, we assume that it has
is zero, which corresponds with a type F.
Since V380 Ori is located in the Ori T2 association (NGC 1999)
of Ori OB1c, we assume that it has 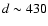
 and
and
 =0
=0
 06
(Warren & Hesser 1978).
In this case the average brightness
06
(Warren & Hesser 1978).
In this case the average brightness  =10
=10
 5 of the star leads to
5 of the star leads to
 =2
=2
 1, that corresponds to either a type A4-6 V or F-G IV.
1, that corresponds to either a type A4-6 V or F-G IV.
C.33 NV Ori - BD-05  1324
1324
Spectroscopic classifications of this star range from F0 IV (Strand 1958)
to F4-F8 III-V (Johnson 1964, HB88).
Low resolution spectra CCD spectra obtained by vandenAncker (1996)
in the visual and red show the presence of a weak G-band, a strong
O I 7774 Å absorption and the Ca II (2) red-triplet in
absorption, probably filled in by emission, as is present in the Balmer lines.
Johnson (1964) reports the presence of a weak Li I line.
The position of the star in the Johnson TCD is F0-F2.
The photometric variability is irregular, with a maximum amplitude of 0
 6.
The star is located in the Ori T2 association of Ori OB1c, so
that we also here assume that
6.
The star is located in the Ori T2 association of Ori OB1c, so
that we also here assume that 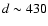
 and
and
 =0
=0
 06.
From
06.
From
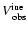 =10
=10
 0 we then find
0 we then find  =1
=1
 79, corresponding with a spectral
type F2-F4 III, that is in agreement with the spectroscopic and TCD
classifications.
79, corresponding with a spectral
type F2-F4 III, that is in agreement with the spectroscopic and TCD
classifications.
C.35 KK Oph - AS 220
The star is situated close to the edge of DC Barnard 59,
which is probably part of the 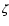 Oph nebula.
The visual spectrum of KK Oph was studied by FJ84 and by deWinter & Thé (1990).
It shows emission in H
Oph nebula.
The visual spectrum of KK Oph was studied by FJ84 and by deWinter & Thé (1990).
It shows emission in H ,
H
,
H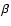 and [OI] at 6300 Å.
Because of the strength of H
and [OI] at 6300 Å.
Because of the strength of H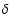 and H8 and the absence of He I the star
was classified (MK) as A5-7e.
The position of the star in the TCD of the Johnson and Walraven photometric
systems is A8 to F4.
In a new set of 478 photometric data between JD 2445881 and JD 2450672
(Herbst & Shevchenko 1999) the brightness of the star varies between 9
and H8 and the absence of He I the star
was classified (MK) as A5-7e.
The position of the star in the TCD of the Johnson and Walraven photometric
systems is A8 to F4.
In a new set of 478 photometric data between JD 2445881 and JD 2450672
(Herbst & Shevchenko 1999) the brightness of the star varies between 9
 40
and 12
40
and 12
 8 with
8 with
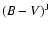 =0
=0
 47.
If we assume that at
47.
If we assume that at
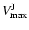 =9
=9
 4 the extinction was only due to interstellar
foreground, we find the data given in Table C.2.
For a type A5 IV we derive the same distance as determined by Wallenquist
(1937) for the front side of the dark nebulosity
4 the extinction was only due to interstellar
foreground, we find the data given in Table C.2.
For a type A5 IV we derive the same distance as determined by Wallenquist
(1937) for the front side of the dark nebulosity![[*]](/icons/foot_motif.gif) .
If KK Oph is in front of the dark nebula, then
.
If KK Oph is in front of the dark nebula, then 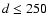
 ,
so that its
spectral classification has to be restricted to A5-F6 V-IV.
A NIRE in the SED of the star indicates the presence of circumstellar dust,
which supports the assumption that KK Oph is a PMS Ae/Fe star.
The star is a visual double star (Table B.1).
,
so that its
spectral classification has to be restricted to A5-F6 V-IV.
A NIRE in the SED of the star indicates the presence of circumstellar dust,
which supports the assumption that KK Oph is a PMS Ae/Fe star.
The star is a visual double star (Table B.1).
Table C.2:
Derived distances (pc) for KK Oph depending on the spectral
classification and the
 -value (in brackets).
-value (in brackets).
C.36 SU Aur - HD 282624
This star in the Aur T1 association was classified as G2 by CK79,
F7-G2 III by Kh85 and G2 III by HB88.
Since the star is a common proper-motion companion of AB Aur, we take the
distance as determined by Hipparcos measurements for AB Aur
(d=144
+20-20 ;
ATT97) and a foreground extinction
;
ATT97) and a foreground extinction
 =0
=0
 12 as determined for AB Aur by Felenbok et al. (1983).
Bertout et al. (1988) give
12 as determined for AB Aur by Felenbok et al. (1983).
Bertout et al. (1988) give 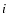 =
=
 .
Independently Akeson et al. (2002) give
.
Independently Akeson et al. (2002) give 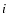 =
= 62
62 .
.
C.38 HD 283572 - V987 Tau
From the TCD we estimate a type G2-5, and from the high-resolution spectroscopy
in the visual and red, Walter et al. (1987) classify the star as G5 IV with
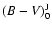 =0
=0
 77.
The distance obtained by Hipparcos is 128
+26-18
77.
The distance obtained by Hipparcos is 128
+26-18 (ESA 1997).
The photometric variation is very small.
At the largest brightness
(ESA 1997).
The photometric variation is very small.
At the largest brightness  =8
=8
 95,
95,
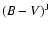 =0
=0
 80 so that
80 so that

 0
0
 03.
03.
C.39 BD+09  880 - HD 245185
880 - HD 245185
This star was classified as A5 in the HD catalogue and quoted as such by
HB88.
Its visual spectrum was studied by Penston et al. (1976) and FJ84.
The 1992-photometry of the star (deWinter et al. 2001), however, indicates a type
B9 in the TCD.
The mis-classification was the reason why the first attempt to obtain a
low-resolution UV spectrum of the star with IUE in 1984, was heavily
overexposed in the SW-part (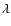 >1275 Å).
The brightness
>1275 Å).
The brightness  =9
=9
 93, and monitoring of the star by the LTPV-group
over several years has not revealed significant variability.
Since the star is a member of the
93, and monitoring of the star by the LTPV-group
over several years has not revealed significant variability.
Since the star is a member of the 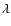 Orionis association
(Penston et al. 1976; Murdin & Penston 1977)
we have adopted
Orionis association
(Penston et al. 1976; Murdin & Penston 1977)
we have adopted 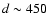
 and
and

 0
0
 06.
Because of its low
06.
Because of its low
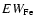 and its single H
and its single H -profile we assume that the star
is viewed "pole-on'' (see Appendix D.1 and D.3).
-profile we assume that the star
is viewed "pole-on'' (see Appendix D.1 and D.3).
C.40 HD 100546 - KR Mus
The star was identified as an Herbig B9 V emission-line star by Hu et
al. (1989) and has a brightness  =6
=6
 7.
From the SED they derived
7.
From the SED they derived 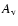 =0
=0
 20 which leads to d=188
20 which leads to d=188 .
However, from Hipparcos parallax measurements (ATT97) it follows that the
distance of HD 100546 is much smaller: 103
+6-6
.
However, from Hipparcos parallax measurements (ATT97) it follows that the
distance of HD 100546 is much smaller: 103
+6-6 .
Photometry of deWinter et al. (2001) shows no significant differences over 5
nights nor in comparison with the photometry by Hu et al. 1989.
The high-resolution UV spectra of this star show several indications of infall
of matter onto the star, e.g. stellar Ly
.
Photometry of deWinter et al. (2001) shows no significant differences over 5
nights nor in comparison with the photometry by Hu et al. 1989.
The high-resolution UV spectra of this star show several indications of infall
of matter onto the star, e.g. stellar Ly -emission (Talavera et al. 1994) and
variable red-shifted absorption components in the Mg II h,k resonance lines
and various Fe II lines (Grady et al. 1996).
From the profile of the red-shifted Ly
-emission (Talavera et al. 1994) and
variable red-shifted absorption components in the Mg II h,k resonance lines
and various Fe II lines (Grady et al. 1996).
From the profile of the red-shifted Ly emission-component we derived
emission-component we derived
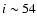
 (Appendix D.4).
Recent coronographic NICMOS images at 1.6
(Appendix D.4).
Recent coronographic NICMOS images at 1.6 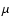 m reveal an elliptical
shape of the disc, extending to 380 AU from the star (Augereau et al. 2001).
From these observations they derived i=51
m reveal an elliptical
shape of the disc, extending to 380 AU from the star (Augereau et al. 2001).
From these observations they derived i=51 .
.
C.41 HD 98922 - CD-52  4340
4340
MBW98 classified this star as B9 V with a brightness  =6
=6
 77.
From photometry from 8 successive nights in 1992 by deWinter et al. (2001) we
know that the star is not variable on a short time-scale (days), and from the
TCD we estimate
77.
From photometry from 8 successive nights in 1992 by deWinter et al. (2001) we
know that the star is not variable on a short time-scale (days), and from the
TCD we estimate

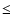 0
0
 05, so that with
05, so that with  =0
=0
 2 this gives
2 this gives
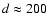
 .
However, Hipparcos measurements give a lower limit for the distance of 540
.
However, Hipparcos measurements give a lower limit for the distance of 540 (AWT98) which is very uncertain as the observational range of Hipparcos is
limited to
(AWT98) which is very uncertain as the observational range of Hipparcos is
limited to 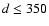
 .
The star is probably a spectroscopic double-star (Bond 1970; de Groot 1971,
Table B.1).
Similar to HD 100546 its high-resolution Ly
.
The star is probably a spectroscopic double-star (Bond 1970; de Groot 1971,
Table B.1).
Similar to HD 100546 its high-resolution Ly -profile shows indications for
the presence of a red-shifted component (Talavera et al. 1994).
From its shape we estimate
-profile shows indications for
the presence of a red-shifted component (Talavera et al. 1994).
From its shape we estimate 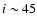
 (Appendix D.4).
(Appendix D.4).
C.42 HD 97048 - CU Cha
This B9.5 V star in the Cha T1 association was extensively studied
(Rydgren 1980; Thé et al. 1986).
There are no reports of significant variations in brightness of this star
( =8
=8
 40-8
40-8
 48) during the last 40 years (see e.g. deWinter et al. 2001).
The distance derived from the Hipparcos parallax measurements (ATT97) is
180
+30-20
48) during the last 40 years (see e.g. deWinter et al. 2001).
The distance derived from the Hipparcos parallax measurements (ATT97) is
180
+30-20 .
The
.
The
 can be estimated from that of HD 97240 (F5 V), which is close to the
position of HD 97048.
This star has no circumstellar excess (no NIR excess) and has
can be estimated from that of HD 97240 (F5 V), which is close to the
position of HD 97048.
This star has no circumstellar excess (no NIR excess) and has
 =0
=0
 05 with
05 with
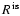 =5.0.
If we assume that the foreground excess in that direction is proportional
with distance, and that the distance and
=5.0.
If we assume that the foreground excess in that direction is proportional
with distance, and that the distance and
 of HD 97240 are 95
of HD 97240 are 95 and
0
and
0
 05, we conclude that
05, we conclude that

 0
0
 09 for HD 97048.
09 for HD 97048.
C.43 HD 95881 - CD-70  775
775
The MK classification of this star is A1-2 III-V and  =8
=8
 2.
Photometry of HD 95881 was given by MBW98, but photometric variability
of this star is unknown to us.
From the TCD MBW98 estimate
2.
Photometry of HD 95881 was given by MBW98, but photometric variability
of this star is unknown to us.
From the TCD MBW98 estimate
 =0
=0
 17, so with
17, so with  =0
=0
 2, this
gives
2, this
gives
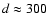
 .
On the basis of the
.
On the basis of the
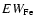 and the H
and the H -profile we assume that the system is
seen "edge-on'' (see Appendices D.1 and D.3).
-profile we assume that the system is
seen "edge-on'' (see Appendices D.1 and D.3).
Appendix D: Indications for the disc inclination
We use several observational sources in order to make an estimate of the
inclination of the accretion disc of a star in our sample.
None of these criteria are decisive in itself but together they may discriminate
between "edge-on'' and "pole-on'' view (Sect. B.5).
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{0269f0d1.ps} %
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg373.gif) |
Figure D.1:
Equivalent width of the Fe II absorption feature (
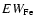 )
versus
spectral type of some program stars, indicated by ( )
versus
spectral type of some program stars, indicated by ( )
or (+)
when the star covers a spectral range (horizontal line).
The values of CQ Tau ( )
or (+)
when the star covers a spectral range (horizontal line).
The values of CQ Tau ( )
are lower limits, while for )
are lower limits, while for
 and HD 100546 we only have an upper limit (
and HD 100546 we only have an upper limit (
 ).
Open circles ( ).
Open circles ( )
denote comparison stars taken from the
IUE spectral atlases (Appendix G.6). )
denote comparison stars taken from the
IUE spectral atlases (Appendix G.6). |
D.1 Table 1-Col. Y
Gurzadyan & Rustambekova (1980) found that the strength of the Fe II
resonance absorption features in the UV spectrum of a shell star is increasing
with the thickness of the gas envelope with a rate, depending on the spectral
types of shell and star.
If we apply this to the non-spherical envelope of an accretion disc, the EW of
the 2400 Å Fe II absorption feature in the low-resolution UV spectrum
of an accreting PMS Ae/Fe star should be correlated with the inclination
in which we observe the disc.
If we plot the
 (in Å for a bandwidth of 40 Å) of standard stars
without shell (from the IUE spectral atlases) against their spectral types,
we obtain a band (SSB hereafter, which is the lineair least square of the points
plus 4 parallels on each side) that rises gradually for later spectral type
(Fig. D.1).
(in Å for a bandwidth of 40 Å) of standard stars
without shell (from the IUE spectral atlases) against their spectral types,
we obtain a band (SSB hereafter, which is the lineair least square of the points
plus 4 parallels on each side) that rises gradually for later spectral type
(Fig. D.1).
The corresponding EW's of the PMS Ae/Fe stars of our sample
(Table 1 Col. Y) are in general situated above the SSB,
an indication for the presence of thick gas envelopes.
The height of the points may be underestimated because of filling-in of the
2400 Å absorption feature by Fe II emission from the accretion disc.
However, for a few cases: NX Pup, V380 Ori, HK Ori, and
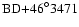 ,
the EW's
are even below the SSB, which requires filling-in and which suggests that the
corresponding envelopes are very thin in the direction of the observer.
Since there are no indications that these stars have intrinsically much
thinner gas envelopes than other Herbig stars of comparable spectral type
(comparable SEDs with large IRE) it seems more probable that we observe these
stars in a direction with low inclination, i.e. close to "pole-on''.
The number of such cases is small, in agreement with the expectation from the
statistics of inclination angles.
,
the EW's
are even below the SSB, which requires filling-in and which suggests that the
corresponding envelopes are very thin in the direction of the observer.
Since there are no indications that these stars have intrinsically much
thinner gas envelopes than other Herbig stars of comparable spectral type
(comparable SEDs with large IRE) it seems more probable that we observe these
stars in a direction with low inclination, i.e. close to "pole-on''.
The number of such cases is small, in agreement with the expectation from the
statistics of inclination angles.
D.2 Table 1-Col. X
The character of the photometric variability of the PMS Ae/Fe stars is another
indicator for the inclination of the disc.
Many of the stars in our sample were followed during photometric
monitoring campaigns.
A considerable amount of data has been secured by Kilkenny et al. (1985),
Herbst et al. (1994), Zajtseva (1986), the LTPV group of ESO observers
(1986-1996), the ROTOR-group (Taskent), the Hipparcos and Tycho projects (1997),
and several other groups.
The photometric data of the PMS Ae/Fe stars in our sample show several types of
variability in the TCD.
We distinguish the following types (Sect. B.5):
- 1.
-
a large group of stars (including the UXORs 2), which show strong
variations (up to 2 or 3 mag) along the reddening direction of the TCD.
Examples are: XY Per, WW Vul, UX Ori, BF Ori, HR 5999, HD 142666, V346 Ori,
V350 Ori, HD 35929, R CrA, CQ Tau, AK Sco, NV Ori, RR Tau, KK Oph, SU Aur,
RY Tau, and perhaps Z CMa.
This variability is characteristic for a variable circumstellar dust extinction,
which can result when we observe a rotating disc envelope with non-isotropic
dust column density more or less "edge-on''.
For these stars the variations in
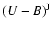 are approximately equal to those in
are approximately equal to those in
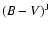 .
During deep brightness minima several of these stars (UX Ori, BF Ori, WW Vul,
CQ Tau, and RR Tau) show declines in
.
During deep brightness minima several of these stars (UX Ori, BF Ori, WW Vul,
CQ Tau, and RR Tau) show declines in
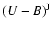 ("blueing'', Fig. D.2)
together with sudden, strong rises in linear polarisation.
These "blueing'' and polarisation excursions can be explained by the
contribution of a fine-dust halo, which becomes dominant during the obscuration
of the direct stellar light by very dense circumstellar clouds in the disc
(Grinin 1988).
The model for this type of variations works if the disc is observed more or
less "edge-on'' (i>60
("blueing'', Fig. D.2)
together with sudden, strong rises in linear polarisation.
These "blueing'' and polarisation excursions can be explained by the
contribution of a fine-dust halo, which becomes dominant during the obscuration
of the direct stellar light by very dense circumstellar clouds in the disc
(Grinin 1988).
The model for this type of variations works if the disc is observed more or
less "edge-on'' (i>60 ).
).
It may be noted that three stars, which are still far from the MS, lost their
c.s. dust in a sudden event some time ago: FU Ori (1936), BN Ori (1945), and
V351 Ori (1987) and are indicated with  in Table 1.
The latter two stars originally behaved photometrically as the stars of
type r, but should at present be classified as belonging to
type n.
FU Ori probably behaved similarly, but no data is available from before the
event.
in Table 1.
The latter two stars originally behaved photometrically as the stars of
type r, but should at present be classified as belonging to
type n.
FU Ori probably behaved similarly, but no data is available from before the
event.
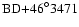 and HD 35929 are also far from the MS and show small brightness variations,
but recent episodes of c.s. dust dissipation have not been observed.
and HD 35929 are also far from the MS and show small brightness variations,
but recent episodes of c.s. dust dissipation have not been observed.
- 2.
- a small class of stars which shows strong "blueing'' variations for moderate
variations of
 (0
(0
 1-1
1-1
 0).
They rarely vary in the reddening direction.
In the TCD their variations in
0).
They rarely vary in the reddening direction.
In the TCD their variations in
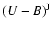 are 2-10 times larger than those in
are 2-10 times larger than those in
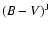 .
Examples are:
.
Examples are:
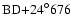 ,
NX Pup, HK Ori, Z CMa, V380 Ori, and HD 283572
(Fig. D.3).
We suggest that the strong U-band variations are correlated with a strong,
variable excess in the SW-part of the spectra, which is contributed by an
instable BL and hot inner disc of these stars (Sect. A.5).
These contributions are probably only detectable when the system is observed
approximately "pole-on'' (
,
NX Pup, HK Ori, Z CMa, V380 Ori, and HD 283572
(Fig. D.3).
We suggest that the strong U-band variations are correlated with a strong,
variable excess in the SW-part of the spectra, which is contributed by an
instable BL and hot inner disc of these stars (Sect. A.5).
These contributions are probably only detectable when the system is observed
approximately "pole-on'' (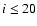
 ).
Rare variations in the reddening direction may be due to c.s. dust clouds
moving parallel to, but outside the disc plane.
).
Rare variations in the reddening direction may be due to c.s. dust clouds
moving parallel to, but outside the disc plane.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0269f0d2.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg374.gif) |
Figure D.2:
TCD & CMD of BF Ori ( type r)
based on data from sun.astro.wesleyan.edu/pub/ttauri, Herbst et al. 1994.
|
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0269f0d3.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg375.gif) |
Figure D.3:
TCD & CMD of NX Pup ( type o)
based on data from the LTPV group (ESO SR-8, SR-12, SR-14, & SR-16).
|
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0269f0d4.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg376.gif) |
Figure D.4:
TCD & CMD of HD 163296 ( type n)
based on data from sun.astro.wesleyan.edu/pub/ttauri, Herbst et al. 1994.
|
- 3.
- the remaining stars of our sample show only very small (<0
 1) variations in
brightness: HD 163296, HD 150193, HD 31648,
1) variations in
brightness: HD 163296, HD 150193, HD 31648, 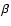 Pic, HD 104237, HD 169142, HD 36112,
HD 319614, HD 144432,
Pic, HD 104237, HD 169142, HD 36112,
HD 319614, HD 144432,
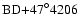 ,
,
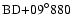 ,
HD 100546, and HD 97048
(Fig. D.4).
The amplitudes of the variations of this group are probably too small to
discriminate between high and low inclinations.
Most stars of this group have evolved to the neighbourhood of the ZAMS and
have not much circumstellar dust any more (Sect. 6.3),
so that photometric effects due to variations in c.s. dust column density
cannot be expected.
,
HD 100546, and HD 97048
(Fig. D.4).
The amplitudes of the variations of this group are probably too small to
discriminate between high and low inclinations.
Most stars of this group have evolved to the neighbourhood of the ZAMS and
have not much circumstellar dust any more (Sect. 6.3),
so that photometric effects due to variations in c.s. dust column density
cannot be expected.
The line in Figs. D.2-D.4 indicates the R=3.1reddening-line.
Stars for which no photometry is available are
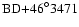 ,
HD 199143, HD 98922, and
HD 95881, so it is not possible to contain them in one of the previous groups
and are indicated with (-).
,
HD 199143, HD 98922, and
HD 95881, so it is not possible to contain them in one of the previous groups
and are indicated with (-).
Table D.1:
Review of inclination angles (in degrees) from Ly -emission-line profiles,
see Blondel et al. (1993) for details.
-emission-line profiles,
see Blondel et al. (1993) for details.
D.3 Table 1-Col. Z
Another diagnostic tool for the inclination of the disc is the shape of the
H -profile.
In a sample of 63 PMS Be/Ae/Fe stars Grinin & Rostopchina (1996) noted a correlation
between the type of H
-profile.
In a sample of 63 PMS Be/Ae/Fe stars Grinin & Rostopchina (1996) noted a correlation
between the type of H -profile and the amplitude of the photometric variability
of a Herbig star:
-profile and the amplitude of the photometric variability
of a Herbig star:
- (1)
- of stars with large amplitude (
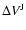 >1
>1
 )
the majority (73%) has a
2-component H
)
the majority (73%) has a
2-component H -profile, 13% has a P-Cygni-profile, while only 7% has a
single-profile.
-profile, 13% has a P-Cygni-profile, while only 7% has a
single-profile.
- (2)
- for the stars with smaller amplitude (
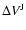 <0
<0
 6) 42% has a
2-component profile, 33% has a single-profile, and 20% has a
P-Cygni-profile.
6) 42% has a
2-component profile, 33% has a single-profile, and 20% has a
P-Cygni-profile.
In Table 1 we have used the profile classification
scheme of Reipurth et al. (1996):
- 1.
- single, symmetric profiles;
- 2.
- double profiles with <50% difference in peak intensity;
- 3.
- double profiles with >50% difference in peak intensity;
- 4.
- P-Cygni profiles.
The profile types are further specified by B or R, according to the position of
the stronger component (blue or red side).
From Table 1 we note that almost all stars with photometric
variability type r have class II or III H -profiles, whereas
the stars with variability type o: V380 Ori, HK Ori, and NX Pup have
profiles of type I or II.
The general correlation between H
-profiles, whereas
the stars with variability type o: V380 Ori, HK Ori, and NX Pup have
profiles of type I or II.
The general correlation between H -profile type and variability type suggests
that we can also use the H
-profile type and variability type suggests
that we can also use the H -profile type to indicate the inclination for those
stars in Table 1 that do not show significant photometric
variability (type n).
However, it should be kept in mind that the correlation, noted by Grinin and
Rostopchina, is only valid for 75% of the stars (NX Pup and V346 Ori belong
to the other 25%), so that this method for estimating the inclination has some
intrinsic uncertainty.
-profile type to indicate the inclination for those
stars in Table 1 that do not show significant photometric
variability (type n).
However, it should be kept in mind that the correlation, noted by Grinin and
Rostopchina, is only valid for 75% of the stars (NX Pup and V346 Ori belong
to the other 25%), so that this method for estimating the inclination has some
intrinsic uncertainty.
D.4 Stellar Lyman  -emission
-emission
In a few cases we have observed the Ly -line profiles in high-resolution with
IUE (Table D.1).
By fitting the shapes of the profiles of these lines we could determine the
inclination of these cases (Blondel et al. 1993; Talavera et al. 1994),
provided that the Ly
-line profiles in high-resolution with
IUE (Table D.1).
By fitting the shapes of the profiles of these lines we could determine the
inclination of these cases (Blondel et al. 1993; Talavera et al. 1994),
provided that the Ly -emission is produced by infalling ions.
The results for HD 163296, HR 5999, HD 104237, HD 150193, HD 98922, and HD 100546
agree with those derived with the
-emission is produced by infalling ions.
The results for HD 163296, HR 5999, HD 104237, HD 150193, HD 98922, and HD 100546
agree with those derived with the
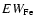 -method (Sect D.1).
These stars appear to have large inclinations (
-method (Sect D.1).
These stars appear to have large inclinations (
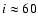
 ).
With IUE the Ly
).
With IUE the Ly -method is limited to those stars that were bright
enough to show detectable stellar Ly
-method is limited to those stars that were bright
enough to show detectable stellar Ly -emission in the SW-camera.
Stellar Ly
-emission in the SW-camera.
Stellar Ly -emission is confirmed by Hubble observations of HD 104237
(Brown et al. 1997) and HD 163296 (Devine et al. 2000).
-emission is confirmed by Hubble observations of HD 104237
(Brown et al. 1997) and HD 163296 (Devine et al. 2000).
Appendix E: ZAMS ages (Table 8)
Table E.1:
 values Bernasconi (1996), see also Fig. 43.
values Bernasconi (1996), see also Fig. 43.
Table E.2:
 values Siess B (1999).
values Siess B (1999).
Table E.3:
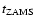 values Siess NG (2000).
values Siess NG (2000).
Appendix F: IUE images - PMS stars.
Table F.1:
Table F.2:
Table F.3:
Table F.4:
Table F.5:
The (sparse) LW-images marked with
** are used for a range of SW-images to complete the spectrum.
Table F.6:
Comments and notes to the Tables 1-5.
The first number of the image denotes IUE camera: 3 = SWP, 2 = LWR, 1 = LWP,
images not observed on the same run, but combined as they have acomparable
magnitude, are marked with (*).
The "notes'' refer to images used to complete the spectrum and applied flux
normalisation factors.
Appendix G: IUE images - Comparison stars.
Table G.1:
B stars, HD 202850 is 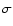 Cyg.
Cyg.
Table G.2:
A stars.
Table G.3:
F stars.
Table G.4:
G stars.
Table G.5:
K stars.
Table G.6:
References to Col. 2.
Copyright ESO 2006
![]() Pic) show indications of accretion, that affect the resulting spectral type of the stellar photosphere. Formerly this led to ambiguities in classificaton of PMS stars as the boundary-layer was not taken into consideration. We give evidence for an increase of the mass-accretion rate with stellar mass and for a decreases of this rate with stellar age.
Pic) show indications of accretion, that affect the resulting spectral type of the stellar photosphere. Formerly this led to ambiguities in classificaton of PMS stars as the boundary-layer was not taken into consideration. We give evidence for an increase of the mass-accretion rate with stellar mass and for a decreases of this rate with stellar age.
![]() Pic and
Pic and
![]() )
are well-known young
emission-line stars.
Our choice of stars is restricted by the availability of low-resolution UV
spectra (both IUE SW and LW).
A second restriction was made based on the quality of the observed spectra,
which eliminates the following 6 stars from Table 1:
WW Vul,
)
are well-known young
emission-line stars.
Our choice of stars is restricted by the availability of low-resolution UV
spectra (both IUE SW and LW).
A second restriction was made based on the quality of the observed spectra,
which eliminates the following 6 stars from Table 1:
WW Vul,
![]() ,
V350 Ori, R CrA, RR Tau, and RY Tau.
The main conclusion from our analysis is that the BL contribution to
the spectra in our sample can be simulated by spectra of type B5 I-A0 I,
most frequently B9 Iab.
In several cases the BL component in the UV spectrum is so strong that it
influences the photometric bands in the near-UV and, therefore, the spectral
classification based on photometry (e.g. NX Pup,
,
V350 Ori, R CrA, RR Tau, and RY Tau.
The main conclusion from our analysis is that the BL contribution to
the spectra in our sample can be simulated by spectra of type B5 I-A0 I,
most frequently B9 Iab.
In several cases the BL component in the UV spectrum is so strong that it
influences the photometric bands in the near-UV and, therefore, the spectral
classification based on photometry (e.g. NX Pup,
![]() ,
HK Ori, V380 Ori,
and KK Oph).
We also calculated the SEDs of the program stars in the visual and NIR.
Some of these stars - NX Pup, V380 Ori, HK Ori, and HD 139614 - are observed at low
inclinations (almost pole-on), which implies that their BL may also contribute
significantly to the UBV-fluxes.
The presence of this BL contribution may be an important reason why spectral
classifications of the stars based on different distinct features of the
spectrum have led to different spectral types.
,
HK Ori, V380 Ori,
and KK Oph).
We also calculated the SEDs of the program stars in the visual and NIR.
Some of these stars - NX Pup, V380 Ori, HK Ori, and HD 139614 - are observed at low
inclinations (almost pole-on), which implies that their BL may also contribute
significantly to the UBV-fluxes.
The presence of this BL contribution may be an important reason why spectral
classifications of the stars based on different distinct features of the
spectrum have led to different spectral types.
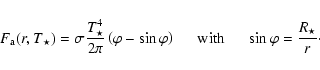
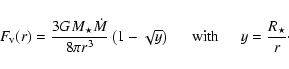
![]() ,
,
![]() ,
and
,
and
![]() was calculated from Eqs. (1)-(4), using the approximations
of BBB88.
The disc contribution is integrated outward up to 3.5
was calculated from Eqs. (1)-(4), using the approximations
of BBB88.
The disc contribution is integrated outward up to 3.5
![]() ,
which has proved
to be sufficient for the disc-contribution in the UV.
The disc inclination angle i enters into the contributions of the 3
components; in the photospheric component it is due to shadowing by the disc;
in the BL and disc components it results from screening by the star.
,
which has proved
to be sufficient for the disc-contribution in the UV.
The disc inclination angle i enters into the contributions of the 3
components; in the photospheric component it is due to shadowing by the disc;
in the BL and disc components it results from screening by the star.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{0269f001.ps} %
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg129.gif)
![]() )
(BBB88 Eqs. (5), (9), (11)) we indicate the intrinsic (Kurucz model)
)
(BBB88 Eqs. (5), (9), (11)) we indicate the intrinsic (Kurucz model)
![]() fluxes of the star, BL and disc by
fluxes of the star, BL and disc by
![]() respectively, we can normalise the sum of these fluxes to the "intrinsic
observed flux of the system'': the de-reddened observed flux
(
respectively, we can normalise the sum of these fluxes to the "intrinsic
observed flux of the system'': the de-reddened observed flux
(
![]() )
in
)
in ![]() (
(
![]() )
after additional
correction for the (yet unknown) circumstellar absorption
)
after additional
correction for the (yet unknown) circumstellar absorption
![]() in
in ![]() :
:
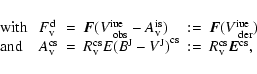
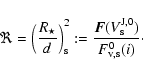
![]() /
/
![]() and
the normalisation factor in Eq. (9):
and
the normalisation factor in Eq. (9):
![\begin{figure}
\par\includegraphics[angle=270,width=8.2cm,clip]{0269f003.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg147.gif)
![]() correspond to variations in their UV spectra that can be approximated mainly by
variations in
correspond to variations in their UV spectra that can be approximated mainly by
variations in
![]() and
and
![]() (Tables 3-5).
Deviations in the spectra, which occur for high values of
(Tables 3-5).
Deviations in the spectra, which occur for high values of
![]() ,
could
be due to the changes in size or orientation of non-spherical circumstellar dust
grains (Sects. 5.2 and 5.6).
,
could
be due to the changes in size or orientation of non-spherical circumstellar dust
grains (Sects. 5.2 and 5.6).
![]() is labelled with (*) if
is labelled with (*) if
![]()
![]() 3.1
(Appendix B.4).
The h in Col. 7 denotes Hipparcos values (ESA 1997),
see Appendix C for supplementary information on each star.
Column 9 indicates if Walraven photometry was obtained for the star.
The inclination is indicated with E or P based on the methods (X, Y, Z)
described in Appendices B.5 and D.
3.1
(Appendix B.4).
The h in Col. 7 denotes Hipparcos values (ESA 1997),
see Appendix C for supplementary information on each star.
Column 9 indicates if Walraven photometry was obtained for the star.
The inclination is indicated with E or P based on the methods (X, Y, Z)
described in Appendices B.5 and D.
![]() see Table 3,
see Table 3, ![]() see Table 5.
see Table 5.![]() -band during the IUE spectral observation, we may vary 6
parameters:
(1) the ST and LC of the photosphere,
(2) the ST and LC of the BL,
(3) the stellar distance d,
(4) the width
-band during the IUE spectral observation, we may vary 6
parameters:
(1) the ST and LC of the photosphere,
(2) the ST and LC of the BL,
(3) the stellar distance d,
(4) the width ![]() of the BL,
(5) the disc inclination angle i, and
of the BL,
(5) the disc inclination angle i, and
![]() =
=
![]() /
/
![]() ,
which specifies the extinction law for the
circumstellar dust.
With such a number of parameters we cannot claim to determine these parameters
uniquely from the observed spectrum.
However, the various parameters fortunately have different effects on specific
wavelength regions in the calculated spectrum.
We show these effects here for the case of NX Pup:
,
which specifies the extinction law for the
circumstellar dust.
With such a number of parameters we cannot claim to determine these parameters
uniquely from the observed spectrum.
However, the various parameters fortunately have different effects on specific
wavelength regions in the calculated spectrum.
We show these effects here for the case of NX Pup:
![]() by a
change in
by a
change in
![]() .
Also for a change in distance (in cases where the distance is not well known),
a change in
.
Also for a change in distance (in cases where the distance is not well known),
a change in ![]() and
and
![]() sometimes produced equally good matches to the
observed spectrum.
Examples of such multiple solutions can be found in Table 2
and are discussed in the next section.
sometimes produced equally good matches to the
observed spectrum.
Examples of such multiple solutions can be found in Table 2
and are discussed in the next section.
![]() ),
filtered bright spot (
),
filtered bright spot (![]() ),
unfiltered bright spot (
),
unfiltered bright spot (![]() ),
resau mark (
),
resau mark (![]() ),
saturated (
),
saturated (![]() ),
outside PHOT region (
),
outside PHOT region (
![]() ),
other flag values i.e. MXLO-files (
),
other flag values i.e. MXLO-files (
![]() ).
).
![\begin{figure}
\par\includegraphics[angle=270,width=7.05cm,clip]{atlas/0269f010.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg171.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.05cm,clip]{atlas/0269f011.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg172.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.05cm,clip]{atlas/0269f012.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg173.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.05cm,clip]{atlas/0269f013.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg174.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.05cm,clip]{atlas/0269f014.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg175.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.05cm,clip]{atlas/0269f015.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg176.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.05cm,clip]{atlas/0269f016.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg177.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.05cm,clip]{atlas/0269f017.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg178.gif)
![]() 20% for the early A-types to
20% for the early A-types to ![]() 45% for
the F-type solutions.
The UV3C calculations suggest that in these cases the later type solutions
should be preferred, because they are capable of giving better agreement with the
observed spectrum in the long wavelength range of the UV spectrum.
More or less the same can be noted for KK Oph, although in this case the
increase in the BL contribution for the F-type solutions is not clear.
Another example is NX Pup, which was previously classified as B9, but from our
UV3C analysis should have an F2 III photosphere (Fig. 9).
Also for this star the increase in the contribution of the BL (
45% for
the F-type solutions.
The UV3C calculations suggest that in these cases the later type solutions
should be preferred, because they are capable of giving better agreement with the
observed spectrum in the long wavelength range of the UV spectrum.
More or less the same can be noted for KK Oph, although in this case the
increase in the BL contribution for the F-type solutions is not clear.
Another example is NX Pup, which was previously classified as B9, but from our
UV3C analysis should have an F2 III photosphere (Fig. 9).
Also for this star the increase in the contribution of the BL (![]() 25%) is
significant.
The relatively large BL contributions for NX Pup, HK Ori, and V380 Ori are
probably favoured by the small inclination angles of their discs.
This also explains the presence of many strong emission lines in the
LW-range (hires IUE) of NX Pup and V380 Ori.
25%) is
significant.
The relatively large BL contributions for NX Pup, HK Ori, and V380 Ori are
probably favoured by the small inclination angles of their discs.
This also explains the presence of many strong emission lines in the
LW-range (hires IUE) of NX Pup and V380 Ori.
![]()
![]() )
the emission-lines could be contributed
by a nearby nebula.
)
the emission-lines could be contributed
by a nearby nebula.
![\begin{figure}
\par\includegraphics[angle=270,width=16.2cm,clip]{0269f018.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg180.gif)
![]() Pic, the photospheric component clearly agrees better
with that of an A7 Vz star (Blondel & TjinADjie 1994) than
with that of an A5 Vz star (Kondo & Bruhweiler 1985),
see Fig. 18.
For an A8 Vz star (as proposed by Crifo et al. 1997),
with
Pic, the photospheric component clearly agrees better
with that of an A7 Vz star (Blondel & TjinADjie 1994) than
with that of an A5 Vz star (Kondo & Bruhweiler 1985),
see Fig. 18.
For an A8 Vz star (as proposed by Crifo et al. 1997),
with ![]() =2
=2
![]() 55 the agreement is very bad, even for d=18.2
55 the agreement is very bad, even for d=18.2![]() ,
which is the maximum possible (
,
which is the maximum possible (
![]() =0
=0
![]() 0).
Barrado y Navascués et al. (1999) derived
0).
Barrado y Navascués et al. (1999) derived
![]() =
=![]()
![]() for
for ![]() Pic.
Pic.
![]() Pic,
which is consistent with the image of the star, showing that the c.s. dust
disc is seen edge on (Smith & Terrile 1984).
However, variable red-shifted absorption components in several lines of ionised
metals were observed in the visual (Vidal-Majar et al. 1994), which points to
episodic infall of matter probably indicating that the accretion disc in
Pic,
which is consistent with the image of the star, showing that the c.s. dust
disc is seen edge on (Smith & Terrile 1984).
However, variable red-shifted absorption components in several lines of ionised
metals were observed in the visual (Vidal-Majar et al. 1994), which points to
episodic infall of matter probably indicating that the accretion disc in ![]() Pic
has already disappeared.
Pic
has already disappeared.
![]() Pic,
and therefore are also classified as A7 Vz stars.
Pic,
and therefore are also classified as A7 Vz stars.
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{0269f019.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg183.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{0269f020.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg184.gif)
![]() 5 times smaller than that of SU Aur.
5 times smaller than that of SU Aur.
![]()
![]() 7
7
![]() for FU Ori and
for FU Ori and
![]()
![]() 14
14
![]() for Z CMa (as estimated from the SEDs by Kenyon et al. 1988
and Hartmann et al. 1989).
In order to obtain such radii, we had to increase the
for Z CMa (as estimated from the SEDs by Kenyon et al. 1988
and Hartmann et al. 1989).
In order to obtain such radii, we had to increase the ![]() -values from -5.1
(SK82) up to -2.0.
Good agreement with the observed spectra could be obtained with a B7-9 I type BL of
-values from -5.1
(SK82) up to -2.0.
Good agreement with the observed spectra could be obtained with a B7-9 I type BL of ![]() 0.02
0.02
![]() .
Because the positions of the stars in the HRD are above the birthline
(Fig. 41), we cannot estimate their masses or ages.
Assuming
.
Because the positions of the stars in the HRD are above the birthline
(Fig. 41), we cannot estimate their masses or ages.
Assuming
![]()
![]() 0.5
0.5
![]() for FU Ori (a former T Tauri star) and 1.7
for FU Ori (a former T Tauri star) and 1.7
![]() for Z CMa (Hartmann et al. 1989), we then obtain accretion rates of
6
for Z CMa (Hartmann et al. 1989), we then obtain accretion rates of
6 ![]() 10-6
10-6
![]() for FU Ori and
for FU Ori and ![]() 3
3 ![]() 10-5
10-5
![]() for Z CMa.
However, taking the inclinations into account, the mass accretion rates
become 6
for Z CMa.
However, taking the inclinations into account, the mass accretion rates
become 6 ![]() 10-4 and 8
10-4 and 8 ![]() 10-4
10-4
![]() .
Z CMa is a double star, probably consisting of a
.
Z CMa is a double star, probably consisting of a ![]() 16
16
![]() B0 III primary
and a
B0 III primary
and a ![]() 3
3
![]() FUOR secondary (vandenAncker et al. 1904).
Since the UV spectrum is dominated by the FUOR component we neglected
the contribution of the embedded B0-component that only contributes in the
far IR.
FUOR secondary (vandenAncker et al. 1904).
Since the UV spectrum is dominated by the FUOR component we neglected
the contribution of the embedded B0-component that only contributes in the
far IR.
![]() -value marked with () is uncertain, as
the brightness is underestimated due to the degradation of the FES counter
after 1990 (Sect. B.1).
See Table 2 for the other input parameters.
The apparently good agreement of the 3 faint spectra (#10-12) at the long
wavelength is caused by the fact that we used the same (overexposed) image
LWR14027 in these cases.
-value marked with () is uncertain, as
the brightness is underestimated due to the degradation of the FES counter
after 1990 (Sect. B.1).
See Table 2 for the other input parameters.
The apparently good agreement of the 3 faint spectra (#10-12) at the long
wavelength is caused by the fact that we used the same (overexposed) image
LWR14027 in these cases.
![]() is the relative V-flux of the component.
is the relative V-flux of the component.![]() .
The values of
.
The values of
![]() and
and
![]() for fixed values (Table 2) of
the other parameters are listed in Table 5.
The rise in
for fixed values (Table 2) of
the other parameters are listed in Table 5.
The rise in
![]() can be interpreted roughly as an increase in the average size
of the obscuring c.s. dust grains.
This may be expected as a result of the passage of c.s. dust clouds with large
dust grains through the line of sight.
However, the UV spectra longward of 2500 Å for photometric phases with
can be interpreted roughly as an increase in the average size
of the obscuring c.s. dust grains.
This may be expected as a result of the passage of c.s. dust clouds with large
dust grains through the line of sight.
However, the UV spectra longward of 2500 Å for photometric phases with
![]() >6
>6
![]() 7 cannot completely be matched by an increase of
7 cannot completely be matched by an increase of
![]() only.
Apparently the shape of the extinction law also has to be changed.
only.
Apparently the shape of the extinction law also has to be changed.
![]()
![]()
![]() )
the extinction law is produced by
scattering from grains with sizes between 0.01
)
the extinction law is produced by
scattering from grains with sizes between 0.01 ![]() m and 0.25
m and 0.25 ![]() m with
m with
![]() =0.75, which is close to the standard composition of i.s.
grains.
For the fainter phases, however, the observed extinction law requires that
=0.75, which is close to the standard composition of i.s.
grains.
For the fainter phases, however, the observed extinction law requires that
![]() ,
and the sizes range from 0.1
,
and the sizes range from 0.1 ![]() m to 0.13
m to 0.13 ![]() m,
which means that the small grains are depleted, and that
m,
which means that the small grains are depleted, and that
![]()
![]() 2.5.
The depletion of small grains has been interpreted as the sweeping effect of
the stellar radiation (Thé et al. 1996).
At the same time, the EWs of the Fe II, Mn II, and Cr II resonance
absorption lines in the inner shell decrease when the star grows fainter
(Blondel et al. 1989).
2.5.
The depletion of small grains has been interpreted as the sweeping effect of
the stellar radiation (Thé et al. 1996).
At the same time, the EWs of the Fe II, Mn II, and Cr II resonance
absorption lines in the inner shell decrease when the star grows fainter
(Blondel et al. 1989).
![]() and 120
and 120![]() (Sect. C.1).
The first value was taken from RSF Per B to which the star seems to
belong, while the second is a very uncertain determination by the Hipparcos
program.
It appears that we can only find a double-star solution for d=350
(Sect. C.1).
The first value was taken from RSF Per B to which the star seems to
belong, while the second is a very uncertain determination by the Hipparcos
program.
It appears that we can only find a double-star solution for d=350![]() .
.
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{sed/0269fg21.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg191.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{sed/0269fg22.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg192.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{sed/0269fg23.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg193.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{sed/0269fg24.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg194.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{sed/0269fg25.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg195.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{sed/0269fg26.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg196.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{sed/0269fg27.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg197.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{sed/0269fg28.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg198.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{sed/0269fg29.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg199.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{sed/0269fg30.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg200.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{sed/0269fg31.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg201.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{sed/0269fg32.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg202.gif)
![]() 1988:
1988:
![]() =0
=0
![]() 42)
and at periastron (April 9
42)
and at periastron (April 9![]() 1988:
1988:
![]() =0
=0
![]() 09).
The magnitudes could be derived from the relative contributions of the two
high-resolution Mg II resonance line profiles of the components, taken on
the same dates.
We assumed that the primary has spectral type F5 V and then matched the
remaining spectrum of the secondary with the same spectral type F5 V (Sect. C.29).
09).
The magnitudes could be derived from the relative contributions of the two
high-resolution Mg II resonance line profiles of the components, taken on
the same dates.
We assumed that the primary has spectral type F5 V and then matched the
remaining spectrum of the secondary with the same spectral type F5 V (Sect. C.29).
![]() >1.6) are almost the
same.
But for AK Sco and
>1.6) are almost the
same.
But for AK Sco and
![]() (1.0 <
(1.0 <
![]() <1.5), we find smaller
<1.5), we find smaller
![]() ,
,
![]() ,
,
![]() ,
and
,
and ![]() -values than in Table 2, where these
stars were assumed to be single.
-values than in Table 2, where these
stars were assumed to be single.
![]() m) can be
found in NASA RP-1190 (1988).
m) can be
found in NASA RP-1190 (1988).
![\begin{figure}
\par\includegraphics[width=18cm,clip]{0269f041.eps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg210.gif)
![]() and
M-bands, with the strongest reduction near the J-band.
This is the main difference between the observed and the calculated SED
(Fig. 21) of HD 97048.
Similar improvements of predicted SEDs are shown in Hil92-Fig. 2 for UX Ori,
BF Ori, HD 150193, HR 5999, NX Pup, V380 Ori, HK Ori, KK Ori,
and
M-bands, with the strongest reduction near the J-band.
This is the main difference between the observed and the calculated SED
(Fig. 21) of HD 97048.
Similar improvements of predicted SEDs are shown in Hil92-Fig. 2 for UX Ori,
BF Ori, HD 150193, HR 5999, NX Pup, V380 Ori, HK Ori, KK Ori,
![]() ,
and
,
and
![]() in our program.
in our program.
![]() (Table 1), the estimated
inclinations and the derived stellar radii (Table 2) we expect
rotation periods of 14
(Table 1), the estimated
inclinations and the derived stellar radii (Table 2) we expect
rotation periods of 14
![]() ,
21
,
21
![]() ,
11
,
11
![]() ,
and 36
,
and 36
![]() ,
respectively.
In the five sequences the observations were spread over several phases
of the stellar rotations.
We noted variations in the emission-line fluxes, and variations in the
continuum may also be present.
The results of these analyses and alternative interpretations will be
discussed in Paper II.
,
respectively.
In the five sequences the observations were spread over several phases
of the stellar rotations.
We noted variations in the emission-line fluxes, and variations in the
continuum may also be present.
The results of these analyses and alternative interpretations will be
discussed in Paper II.
![]() =13
=13
![]() 6
(Andersen et al. 1989).
We took low and high-resolution UV spectra of successive apastron and
periastron phases in 1988
6
(Andersen et al. 1989).
We took low and high-resolution UV spectra of successive apastron and
periastron phases in 1988![]() .
Variations in emission-line fluxes and continuum fluxes were noted,
which is confirmed by visual spectroscopy (Alencar et al. 2003).
The variations in the visual spectra were interpreted in terms of inhomogeneities
in the common dust disc of the components.
However, UV-emission flux variability may point to stellar emission variability
and/or to uneven distribution of the emission regions on the surface of the binary
components.
(The estimated rotation period of the (equal) components is 17
.
Variations in emission-line fluxes and continuum fluxes were noted,
which is confirmed by visual spectroscopy (Alencar et al. 2003).
The variations in the visual spectra were interpreted in terms of inhomogeneities
in the common dust disc of the components.
However, UV-emission flux variability may point to stellar emission variability
and/or to uneven distribution of the emission regions on the surface of the binary
components.
(The estimated rotation period of the (equal) components is 17
![]() ,
which means
,
which means
![]() 11 rotations between apastron and periastron, e.g. between the observations
in April 1988: 7
11 rotations between apastron and periastron, e.g. between the observations
in April 1988: 7
![]() 778 (=0.56
778 (=0.56
![]() ).)
We will discuss these results in Paper II.
).)
We will discuss these results in Paper II.
![]() )
were derived from the energy balance
between the viscous energy produced in the disc and BL and the energy radiated
by the BL (Eq. (5)),
where the stellar influx on the inner layers of the disc (less than a few
percent) has been neglected.
Here we approximate the BL flux by that of the Planck spectrum
of the same
)
were derived from the energy balance
between the viscous energy produced in the disc and BL and the energy radiated
by the BL (Eq. (5)),
where the stellar influx on the inner layers of the disc (less than a few
percent) has been neglected.
Here we approximate the BL flux by that of the Planck spectrum
of the same
![]() as listed for the supergiant spectral type B8 I or
B9 I (SK82).
For the integrated spectral flux, this approximation is correct within a few
percent.
In the case of a co-rotating star, part of the viscous energy is used to
spin-up the star (see e.g. Kley & Lin 1996), so that the energy available
for BL radiation becomes less.
In order to observe the same radiation flux from the BL as in the non-rotating
situation (as calculated by the UV3C-model), we have to raise the viscous
dissipation, i.e. the accretion rate.
However, this correction could only be made by us for objects for which the
as listed for the supergiant spectral type B8 I or
B9 I (SK82).
For the integrated spectral flux, this approximation is correct within a few
percent.
In the case of a co-rotating star, part of the viscous energy is used to
spin-up the star (see e.g. Kley & Lin 1996), so that the energy available
for BL radiation becomes less.
In order to observe the same radiation flux from the BL as in the non-rotating
situation (as calculated by the UV3C-model), we have to raise the viscous
dissipation, i.e. the accretion rate.
However, this correction could only be made by us for objects for which the
![]() -value and the inclination angle i are known
(Table 1).
Then for a radially thin BL the integrated flux can be obtained from:
-value and the inclination angle i are known
(Table 1).
Then for a radially thin BL the integrated flux can be obtained from:
![]() moving supersonically with velocity v through a uniform cloud
medium of density
moving supersonically with velocity v through a uniform cloud
medium of density ![]() as an estimate of the accretion on the star-disc system:
as an estimate of the accretion on the star-disc system:
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{0269f042.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg223.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=14cm,clip]{0269f043.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg224.gif)
![]() ,
c, and v are gas density, sound speed, and relative velocity
of the gas averaged over some distance (e.g.
,
c, and v are gas density, sound speed, and relative velocity
of the gas averaged over some distance (e.g. ![]() 500 AU) in the large-scale
cloud.
Numerical simulations of star formation in self-gravitating turbulent clouds
have supplied values for the three quantities and enabled the authors to estimate
the coefficient K from Eq. (16).
For 104>
500 AU) in the large-scale
cloud.
Numerical simulations of star formation in self-gravitating turbulent clouds
have supplied values for the three quantities and enabled the authors to estimate
the coefficient K from Eq. (16).
For 104>![]() >103
>103
![]() ,
they find K=
,
they find K=
![]() (Fig. 42 dashed lines), while for
(Fig. 42 dashed lines), while for
![]() >104
>104
![]() the result is K=
the result is K=
![]() (Fig. 42 solid lines).
These K-values give a good account of the accretion rates that are found
in PMS objects of various masses.
Even accretion rates of 10-11
(Fig. 42 solid lines).
These K-values give a good account of the accretion rates that are found
in PMS objects of various masses.
Even accretion rates of 10-11
![]() are correctly predicted for brown dwarfs
of 0.03
are correctly predicted for brown dwarfs
of 0.03
![]() if K
if K ![]() 10-8.
Figure 42 may be compared with Muzerolle et al. (2005) Fig. 5.
The young PMS Be/Ae/Fe stars analysed in this paper have masses of 1.8-4.0
10-8.
Figure 42 may be compared with Muzerolle et al. (2005) Fig. 5.
The young PMS Be/Ae/Fe stars analysed in this paper have masses of 1.8-4.0
![]() .
A group of 14 stars is situated above the K=10-7.2 line and 11 below.
We note that 6 out of these 14 are associated with dark clouds
(Appendix C), while the second group of stars has only associations
with well-known regions of star formation.
Therefore, this second group follow the same trend as the T Tauri stars and seem
to be associated with clouds of similar densities, but higher than those of
brown dwarfs.
We conclude that the accretion rates that we measured for the PMS Be/Ae/Fe stars
are an extrapolation of the accretion rates obtained for T Tauri stars.
We note, however, that HD 163296 belongs to the "high rate group'' in spite of
the fact that it seems to be an "isolated'' star (e.g. no association with
clouds).
It is also not clear if the high rates for FU Ori and Z CMa are constant rates
in time (not related to the outbursts of these objects).
It could mean that they are associated with particularly dense parent cloud filaments.
The molecular parent cloud connection gives a good overall account of the mass
dependence of the derived accretion rates in terms of assumed differences in stellar
mass and gas densities of the associated filaments in the parent cloud.
However, the model is a static one and does not account for the further evolution
of the accretion in the star-disc systems of various mass.
It also ignores the role of the disc replenishment process played by the
nearby material, ejected in (bipolar) outflow by the star.
We shall now briefly discuss these points.
.
A group of 14 stars is situated above the K=10-7.2 line and 11 below.
We note that 6 out of these 14 are associated with dark clouds
(Appendix C), while the second group of stars has only associations
with well-known regions of star formation.
Therefore, this second group follow the same trend as the T Tauri stars and seem
to be associated with clouds of similar densities, but higher than those of
brown dwarfs.
We conclude that the accretion rates that we measured for the PMS Be/Ae/Fe stars
are an extrapolation of the accretion rates obtained for T Tauri stars.
We note, however, that HD 163296 belongs to the "high rate group'' in spite of
the fact that it seems to be an "isolated'' star (e.g. no association with
clouds).
It is also not clear if the high rates for FU Ori and Z CMa are constant rates
in time (not related to the outbursts of these objects).
It could mean that they are associated with particularly dense parent cloud filaments.
The molecular parent cloud connection gives a good overall account of the mass
dependence of the derived accretion rates in terms of assumed differences in stellar
mass and gas densities of the associated filaments in the parent cloud.
However, the model is a static one and does not account for the further evolution
of the accretion in the star-disc systems of various mass.
It also ignores the role of the disc replenishment process played by the
nearby material, ejected in (bipolar) outflow by the star.
We shall now briefly discuss these points.
![]() )
from the calculated models.
In contrast to the masses, the ages derived from the three models, are in
general very different.
This is mainly because small differences in mass from the various models lead
to large differences in age.
We expect higher ages from the models of Siess that include accretion, because
these models start with lower mass and therefore evolve more slowly than the
models with fixed mass.
Although this seems to be true if we compare the ages resulting from the
accretion-included models of Siess et al. (1999) and the fixed-mass models
of Bernasconi, it is less clear and often reversed if we compare the
accretion-included models of Siess et al. (1999) with the fixed-mass models
of Siess et al. (2000).
We find, however, that the differences in relative age (absolute age divided
by ZAMS age (Appendix E) for the same mass):
)
from the calculated models.
In contrast to the masses, the ages derived from the three models, are in
general very different.
This is mainly because small differences in mass from the various models lead
to large differences in age.
We expect higher ages from the models of Siess that include accretion, because
these models start with lower mass and therefore evolve more slowly than the
models with fixed mass.
Although this seems to be true if we compare the ages resulting from the
accretion-included models of Siess et al. (1999) and the fixed-mass models
of Bernasconi, it is less clear and often reversed if we compare the
accretion-included models of Siess et al. (1999) with the fixed-mass models
of Siess et al. (2000).
We find, however, that the differences in relative age (absolute age divided
by ZAMS age (Appendix E) for the same mass):
![]() =
=
![]() /
/
![]() are much smaller.
are much smaller.
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{0269f044.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg228.gif)
![]() )
and relative ages,
spectral type z indicates ZAMS.
)
and relative ages,
spectral type z indicates ZAMS.
![]() resulting from the
interpolation of the 3 sets of tracks.
In the latter case accretion during the evolution is taken into account.
The mass accretion rate was assumed to decrease exponentially after 4.5
resulting from the
interpolation of the 3 sets of tracks.
In the latter case accretion during the evolution is taken into account.
The mass accretion rate was assumed to decrease exponentially after 4.5![]() .
It should be noted that the relative ages obtained with the Case-B
grid are not systematically different from those obtained with the other 2
grids, although in Case-B the initial mass is lower and the initial evolution
slower than in the other models.
.
It should be noted that the relative ages obtained with the Case-B
grid are not systematically different from those obtained with the other 2
grids, although in Case-B the initial mass is lower and the initial evolution
slower than in the other models.
![]() <0.80
and that outside this range we only find lower rates.
Rates of <10-7
<0.80
and that outside this range we only find lower rates.
Rates of <10-7
![]() ,
which occur for 0.55<
,
which occur for 0.55<![]() <0.70,
appear to correspond to a group of non-variable stars, among which are the
formerly variable stars BN Ori and V351 Ori.
The stars in the trapezium shaped region labelled non-variable stars
mainly contains stars that are not photometrically variable
(details in Tables 2 and 8).
CQ Tau also appears in this region, presumably because its rate is derived from
spectra obtained at high brightness, in which the accretion activity is low
(Kozlova et al. 2000). Figure 43 suggests that:
<0.70,
appear to correspond to a group of non-variable stars, among which are the
formerly variable stars BN Ori and V351 Ori.
The stars in the trapezium shaped region labelled non-variable stars
mainly contains stars that are not photometrically variable
(details in Tables 2 and 8).
CQ Tau also appears in this region, presumably because its rate is derived from
spectra obtained at high brightness, in which the accretion activity is low
(Kozlova et al. 2000). Figure 43 suggests that:
![]() -band, by varying the spectral and
luminosity types of photosphere and BL, the width of the BL,
and the ratio of total to specific absorption for circumstellar dust
-band, by varying the spectral and
luminosity types of photosphere and BL, the width of the BL,
and the ratio of total to specific absorption for circumstellar dust
![]() .
From the UV3C-model parameters we obtained values for radius and luminosity
of the photosphere (which locates the star in the HRD), the circumstellar excess,
and values of the width and temperature of the BL, all of which allowed us
to estimate the accretion rate.
In the case of double stars the brightness ratio of the components gives an
additional constraint.
Two kinds of comparisons have been made:
.
From the UV3C-model parameters we obtained values for radius and luminosity
of the photosphere (which locates the star in the HRD), the circumstellar excess,
and values of the width and temperature of the BL, all of which allowed us
to estimate the accretion rate.
In the case of double stars the brightness ratio of the components gives an
additional constraint.
Two kinds of comparisons have been made:
![\begin{figure}
\par\includegraphics[angle=270,width=14.9cm,clip]{0269f004.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg233.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=14.9cm,clip]{0269f005.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg234.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=14.9cm,clip]{0269f006.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg235.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=14.9cm,clip]{0269f007.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg236.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=14.9cm,clip]{0269f008.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg237.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=14.9cm,clip]{0269f009.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg238.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{sed/0269fg33.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg239.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{sed/0269fg34.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg240.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{sed/0269fg35.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg241.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{sed/0269fg36.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg242.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{sed/0269fg37.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg243.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{sed/0269fg38.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg244.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{sed/0269fg39.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg245.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{sed/0269fg40.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg246.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f045.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg247.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f046.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg248.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f047.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg249.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f048.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg250.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f049.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg251.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f050.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg252.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f051.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg253.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f052.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg254.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f053.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg255.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f054.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg256.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f055.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg257.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f056.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg258.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f057.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg259.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f058.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg260.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f059.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg261.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f060.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg262.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f061.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg263.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f062.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg264.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f063.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg265.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f064.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg266.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f065.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg267.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f066.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg268.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f067.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg269.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f068.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg270.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f069.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg271.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f070.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg272.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f071.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg273.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f072.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg274.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f073.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg275.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f074.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg276.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f075.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg277.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f076.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg278.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f077.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg279.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f078.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg280.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f079.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg281.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f080.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg282.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f081.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg283.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f082.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg284.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f083.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg285.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f084.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg286.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f085.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg287.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f086.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg288.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f087.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg289.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f088.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg290.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f089.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg291.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f090.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg292.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f091.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg293.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f092.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg294.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f093.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg295.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f094.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg296.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f095.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg297.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f096.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg298.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f097.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg299.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f098.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg300.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f099.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg301.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f100.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg302.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f101.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg303.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f102.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg304.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f103.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg305.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f104.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg306.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f105.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg307.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f106.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg308.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f107.cps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg309.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f108.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg310.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f109.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg311.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.2cm,clip]{atlas/0269f110.cps} \end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg312.gif)
![]() )
can be estimated from
)
can be estimated from
![]() =
120+20-30
=
120+20-30
![]() (Fz85) and
(Fz85) and
![]() =1.76
=1.76
![]() (Table 2).
For i=57
(Table 2).
For i=57![]() ,
this results in
,
this results in
![]() =13
=13
![]() 91
+4.63-2.00.
91
+4.63-2.00.
![]() in 1986 and 1987 (Table F.5).
During these campaigns the FES camera operated well and could be used for
photometric monitoring with an accuracy of
in 1986 and 1987 (Table F.5).
During these campaigns the FES camera operated well and could be used for
photometric monitoring with an accuracy of ![]() 0
0
![]() 05 in
05 in ![]() .
.
![]() -band fluxes and UV
emission-line fluxes with both Fourier-methods and information-entropy
minimalisation methods (Cincotta et al. 1995), no significant periodicity
could be found.
We were also not able no find any direct correlation between the flux
variations in the UV and visual.
The flux observed shortward of 1600 Å varies irregularly by at most 30%, but
never disappears completely.
Unless HD 163296 is seen "pole-on'' (which seems improbable in view of
-band fluxes and UV
emission-line fluxes with both Fourier-methods and information-entropy
minimalisation methods (Cincotta et al. 1995), no significant periodicity
could be found.
We were also not able no find any direct correlation between the flux
variations in the UV and visual.
The flux observed shortward of 1600 Å varies irregularly by at most 30%, but
never disappears completely.
Unless HD 163296 is seen "pole-on'' (which seems improbable in view of
![]()
![]() 120
120
![]()
![]()
![]() )
the hot UV emission
region has to be extended over an equatorial belt on the surface of the star
or over the boundary-layer of an accretion disc.
There are two possibilities for the existence of a hot belt at the stellar
surface: magnetic accretion from the accretion disc to the star and "neutral''
accretion that could occur for accretion through cool BLs.
The presence of a hot magnetic belt has also been assumed to interpret the
emission-line profiles of Ly
)
the hot UV emission
region has to be extended over an equatorial belt on the surface of the star
or over the boundary-layer of an accretion disc.
There are two possibilities for the existence of a hot belt at the stellar
surface: magnetic accretion from the accretion disc to the star and "neutral''
accretion that could occur for accretion through cool BLs.
The presence of a hot magnetic belt has also been assumed to interpret the
emission-line profiles of Ly![]() ,
as seen in the high-resolution UV spectra of
HD 163296, HR 5999, and HD 104237 (Appendix D.4).
From these observations we derive that the emission belt could extend at least
to latitudes of 35
,
as seen in the high-resolution UV spectra of
HD 163296, HR 5999, and HD 104237 (Appendix D.4).
From these observations we derive that the emission belt could extend at least
to latitudes of 35![]() (Blondel et al. 1993).
The observations of HD 163296 show variability but no indication of periodicity
in the UV emission excess (
(Blondel et al. 1993).
The observations of HD 163296 show variability but no indication of periodicity
in the UV emission excess (
![]() ), so that there is no evidence of spots that
persist longer than 14
), so that there is no evidence of spots that
persist longer than 14
![]() .
Similar variability was also found in the UVE of several other PMS Ae/Fe stars for which IUE observations were obtained at various dates, e.g. for
HD 104237, NX Pup and AK Sco (Table 2), but these observations
are too few and too widely separated in time to give any significant information
about possible periodicity in
.
Similar variability was also found in the UVE of several other PMS Ae/Fe stars for which IUE observations were obtained at various dates, e.g. for
HD 104237, NX Pup and AK Sco (Table 2), but these observations
are too few and too widely separated in time to give any significant information
about possible periodicity in
![]() or the presence of hot spots.
or the presence of hot spots.
![]() stars.
These self-consistent models have in common that for
stars.
These self-consistent models have in common that for
![]()
![]() 10-7
10-7
![]() the structure of the BL can be separated into
two disinct regions: a narrow (
the structure of the BL can be separated into
two disinct regions: a narrow (
![]()
![]() )
dynamical region around
the star where the Kepler rotation of the disc is braked down to the stellar rotation
and, around this zone, a broader (
)
dynamical region around
the star where the Kepler rotation of the disc is braked down to the stellar rotation
and, around this zone, a broader (
![]()
![]() )
and cooler thermal
region, where this viscous braking energy is dissipated by radiation.
)
and cooler thermal
region, where this viscous braking energy is dissipated by radiation.
![]() ,
the resulting BL will be hot
(8000-10 000 K) and narrow (
,
the resulting BL will be hot
(8000-10 000 K) and narrow (
![]()
![]() ).
Such results were obtained by Popham et al. (1993) under the assumption of
optically-thick BL radiation.
However, if the inner boundary is required to have the surface temperature of
the star (Bertout & Regev 1992; Lioure & Le Contel 1994) a significant part
(10-30%) of the BL energy is radiated inward into the outer layers of the
star and creates a hot (
).
Such results were obtained by Popham et al. (1993) under the assumption of
optically-thick BL radiation.
However, if the inner boundary is required to have the surface temperature of
the star (Bertout & Regev 1992; Lioure & Le Contel 1994) a significant part
(10-30%) of the BL energy is radiated inward into the outer layers of the
star and creates a hot (
![]() K) equatorial belt.
Godon (1996) repeated these model calculations with improved opacities in
order to account for the ionised and neutral regions in the BL and the disc.
For small values of
K) equatorial belt.
Godon (1996) repeated these model calculations with improved opacities in
order to account for the ionised and neutral regions in the BL and the disc.
For small values of ![]() (
(![]() 0.01) he finds cool (5000-6000 K)
and optically-thick (
0.01) he finds cool (5000-6000 K)
and optically-thick (
![]() )
BL's, in agreement with earlier results,
but his thermal BL is broader (
)
BL's, in agreement with earlier results,
but his thermal BL is broader (
![]()
![]() ).
For higher values of
).
For higher values of ![]() (0.1-1.0) the BL radiation becomes optically thin
(
(0.1-1.0) the BL radiation becomes optically thin
(
![]() ), which corresponds to less efficient cooling, and its
temperature may rise to 8000-10 000 K.
These temperatures are similar to those obtained by Basri & Bertout (1989) for
the optically-thin approximation that they needed to fit the Balmer continuum
and line emission.
However, Godon (1996) finds larger thermal widths (up to 0.04
), which corresponds to less efficient cooling, and its
temperature may rise to 8000-10 000 K.
These temperatures are similar to those obtained by Basri & Bertout (1989) for
the optically-thin approximation that they needed to fit the Balmer continuum
and line emission.
However, Godon (1996) finds larger thermal widths (up to 0.04
![]() )
than these
authors.
)
than these
authors.
![]() star with a rotation rate of
0.1 of the brake-up rate.
For three representative mass accretion rates (10-7,
10-6,
10-4
star with a rotation rate of
0.1 of the brake-up rate.
For three representative mass accretion rates (10-7,
10-6,
10-4
![]() )
and
)
and ![]() =0.01, the time evolution of the main physical
parameters (temperature, density, pressure, and angular momentum) was followed
in and perpendicular to the disc plane.
The final models are consistent with the results of the 1D stationary models.
For the case of the lowest
=0.01, the time evolution of the main physical
parameters (temperature, density, pressure, and angular momentum) was followed
in and perpendicular to the disc plane.
The final models are consistent with the results of the 1D stationary models.
For the case of the lowest ![]() ,
there is some heating of the stellar
atmosphere over latitudes up to 5-10
,
there is some heating of the stellar
atmosphere over latitudes up to 5-10![]() ,
and for increasing accretion
rates, the width of the heated surface zone increases via 30
,
and for increasing accretion
rates, the width of the heated surface zone increases via 30![]() up to
the whole stellar surface. Although there is general agreement between the
2D and 1D models, the numerical values of the parameters in the equatorial
plane are somewhat different.
up to
the whole stellar surface. Although there is general agreement between the
2D and 1D models, the numerical values of the parameters in the equatorial
plane are somewhat different.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0269f0a1.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg323.gif)
![]() Cyg.
(n = narrow, b = broad, d = deep, s = shallow, e = emission instead
of absorption, : = uncertain value.)
Cyg.
(n = narrow, b = broad, d = deep, s = shallow, e = emission instead
of absorption, : = uncertain value.)
![\begin{figure}
\par\includegraphics[angle=270,width=8.7cm,clip]{0269f0a2.ps}
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg326.gif)
![]() <+20
<+20![]() ), we
collected photometric data on the Walraven (WULBV) system.
If the
), we
collected photometric data on the Walraven (WULBV) system.
If the ![]() -brightness derived from the Walraven photometry (Lub & Pel 1977)
agrees with
-brightness derived from the Walraven photometry (Lub & Pel 1977)
agrees with
![]() ,
we used the W-band flux (centered at 3236 Å, and
indicated by (w) in the figures) to check the observed flux at the far end of
the IUE LW-range.
In cases where the LW images were overexposed this W-band flux became
essential in the analysis of the spectra (e.g. Fig. 96).
,
we used the W-band flux (centered at 3236 Å, and
indicated by (w) in the figures) to check the observed flux at the far end of
the IUE LW-range.
In cases where the LW images were overexposed this W-band flux became
essential in the analysis of the spectra (e.g. Fig. 96).
![]() taken before 1991 was made with the FES calibration
given by Imhoff & Wasatonic (1986) and Barylak (1989), and for observations
between 1-1-1991 and 1994, we used the calibration by Pérez (1991).
We estimated the uncertainty of this procedure at
taken before 1991 was made with the FES calibration
given by Imhoff & Wasatonic (1986) and Barylak (1989), and for observations
between 1-1-1991 and 1994, we used the calibration by Pérez (1991).
We estimated the uncertainty of this procedure at
![]() .
After 1994 the FES could not be used for accurate photometric measurements
because of the occurrence of stray light in the Field Camera.
For a number of observations we secured simultaneous ground-based
photometry on the Johnson-, Strömgren-, or Walraven-systems that support
the FES calibration method.
The FES magnitudes, converted to
.
After 1994 the FES could not be used for accurate photometric measurements
because of the occurrence of stray light in the Field Camera.
For a number of observations we secured simultaneous ground-based
photometry on the Johnson-, Strömgren-, or Walraven-systems that support
the FES calibration method.
The FES magnitudes, converted to ![]() ,
are listed in Tables 2-6 as
,
are listed in Tables 2-6 as
![]() for each set of spectra.
for each set of spectra.
![]() denotes stars that had variability along the reddening line in the past,
i.e. changed from type r to n).
In column Y we give the EW (Å) of the 2400 Å absorption-feature in the
low-resolution UV spectra (
denotes stars that had variability along the reddening line in the past,
i.e. changed from type r to n).
In column Y we give the EW (Å) of the 2400 Å absorption-feature in the
low-resolution UV spectra (
![]() hereafter, Fig. D.1).
Column Z shows the shape classification (as introduced by Reipurth et al. 1996)
of the H
hereafter, Fig. D.1).
Column Z shows the shape classification (as introduced by Reipurth et al. 1996)
of the H![]() -emission profile of each star.
-emission profile of each star.
![]() (ATT97).
Its foreground excess
(ATT97).
Its foreground excess
![]() is negligible.
The inclination was derived from a red-shifted Ly
is negligible.
The inclination was derived from a red-shifted Ly![]() -component
(Appendix D.4, Blondel et al. 1993): 57
-component
(Appendix D.4, Blondel et al. 1993): 57![]() and from CO emission (Mannings & Sargent 1997): 58
and from CO emission (Mannings & Sargent 1997): 58![]() .
STIS imaging in the visual (Grady et al. 2000) confirmed the presence of the
disc, which extends to at least 450 AU from the star and has
.
STIS imaging in the visual (Grady et al. 2000) confirmed the presence of the
disc, which extends to at least 450 AU from the star and has ![]()
![]() .
STIS imaging near Ly
.
STIS imaging near Ly![]() (Devine et al. 2000) confirmed the presence of in-
and outflow jets with
(Devine et al. 2000) confirmed the presence of in-
and outflow jets with
![]()
![]() .
.
![]() 126 (
126 (![]() 0
0
![]() 007), a PA of 63
007), a PA of 63![]() ,
and a
,
and a
![]() of 0
of 0
![]() 64
(Bernacca et al. 1993, Table B.1).
These parameters were confirmed by Hipparcos measurements.
The companion was detected in the NIR by Brandner et al.
(1995, 1996), Tessier et al. (1994) and Schöller et al. (1996).
This secondary probably has a spectral type between F2 II and G5 IV.
From the association with the Gum nebula, we estimate d=450-500
64
(Bernacca et al. 1993, Table B.1).
These parameters were confirmed by Hipparcos measurements.
The companion was detected in the NIR by Brandner et al.
(1995, 1996), Tessier et al. (1994) and Schöller et al. (1996).
This secondary probably has a spectral type between F2 II and G5 IV.
From the association with the Gum nebula, we estimate d=450-500![]() (Brand et al. 1983).
According to Krautter (1980) the
(Brand et al. 1983).
According to Krautter (1980) the
![]() in the direction of NX Pup is
negligible.
in the direction of NX Pup is
negligible.
![]() 1 in the NIR (Koresko et al. 1991, Haas et al. 1993)
and in the visual (Barth et al. 1994, Thiébaut et al. 1995,
Table B.1).
This companion of 2100
1 in the NIR (Koresko et al. 1991, Haas et al. 1993)
and in the visual (Barth et al. 1994, Thiébaut et al. 1995,
Table B.1).
This companion of 2100
![]() dominates the IR part of the SED, wheras the
FUOR-type star of only 640
dominates the IR part of the SED, wheras the
FUOR-type star of only 640
![]() dominates in the visual.
Koresko et al. (1991) derived
dominates in the visual.
Koresko et al. (1991) derived
![]() =2.3
=2.3
![]() ,
an inner disc radius of 20
,
an inner disc radius of 20
![]() and
and ![]() =6
=6 ![]() 10-4
10-4
![]() for the visual companion.
Occasionally (Feb. 1987 and Jan. 2000) the IR primary dominates the visual
spectrum with a spectral type B0 IIIe (vandenAncker et al. 1904)
Optical spectropolarimetry by Whitney et al. (1993) confirms this picture and
for the visual spectrum of the system the authors assume an effective spectral
type F5 I, which leads to
for the visual companion.
Occasionally (Feb. 1987 and Jan. 2000) the IR primary dominates the visual
spectrum with a spectral type B0 IIIe (vandenAncker et al. 1904)
Optical spectropolarimetry by Whitney et al. (1993) confirms this picture and
for the visual spectrum of the system the authors assume an effective spectral
type F5 I, which leads to
![]() =0
=0
![]() 7.
They separated this into
7.
They separated this into
![]() =0
=0
![]() 2 and
2 and
![]() =0
=0
![]() 5 with R=4.2 for the dust in
the CMa R1 association.
From a study of this association (Shevchenko et al. 1999) we conclude that
5 with R=4.2 for the dust in
the CMa R1 association.
From a study of this association (Shevchenko et al. 1999) we conclude that
![]() =0
=0
![]() 16 and
16 and
![]() =0
=0
![]() 20.
Similar to FU Ori (Sect. C.23) the UV spectrum of Z CMa has been
analysed by Kenyon et al. (1989), but also in this analysis the IUE SW-part
has been ignored.
For Z CMa we use d=1050 (
20.
Similar to FU Ori (Sect. C.23) the UV spectrum of Z CMa has been
analysed by Kenyon et al. (1989), but also in this analysis the IUE SW-part
has been ignored.
For Z CMa we use d=1050 (![]() 150)
150)![]() ,
which was derived for the CMa R1
association (Shevchenko et al. 1999).
,
which was derived for the CMa R1
association (Shevchenko et al. 1999).
![]() -value (in brackets).
-value (in brackets).![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{0269f0d1.ps} %
\end{figure}](/articles/aa/full/2006/36/aa0269-04/Timg373.gif)
![]() ,
the EW's
are even below the SSB, which requires filling-in and which suggests that the
corresponding envelopes are very thin in the direction of the observer.
Since there are no indications that these stars have intrinsically much
thinner gas envelopes than other Herbig stars of comparable spectral type
(comparable SEDs with large IRE) it seems more probable that we observe these
stars in a direction with low inclination, i.e. close to "pole-on''.
The number of such cases is small, in agreement with the expectation from the
statistics of inclination angles.
,
the EW's
are even below the SSB, which requires filling-in and which suggests that the
corresponding envelopes are very thin in the direction of the observer.
Since there are no indications that these stars have intrinsically much
thinner gas envelopes than other Herbig stars of comparable spectral type
(comparable SEDs with large IRE) it seems more probable that we observe these
stars in a direction with low inclination, i.e. close to "pole-on''.
The number of such cases is small, in agreement with the expectation from the
statistics of inclination angles.
![]() in Table 1.
The latter two stars originally behaved photometrically as the stars of
type r, but should at present be classified as belonging to
type n.
FU Ori probably behaved similarly, but no data is available from before the
event.
in Table 1.
The latter two stars originally behaved photometrically as the stars of
type r, but should at present be classified as belonging to
type n.
FU Ori probably behaved similarly, but no data is available from before the
event.
![]() and HD 35929 are also far from the MS and show small brightness variations,
but recent episodes of c.s. dust dissipation have not been observed.
and HD 35929 are also far from the MS and show small brightness variations,
but recent episodes of c.s. dust dissipation have not been observed.
![]() -emission-line profiles,
see Blondel et al. (1993) for details.
-emission-line profiles,
see Blondel et al. (1993) for details.![]() values Bernasconi (1996), see also Fig. 43.
values Bernasconi (1996), see also Fig. 43.
![]() values Siess B (1999).
values Siess B (1999).![]() values Siess NG (2000).
values Siess NG (2000).![]() Cyg.
Cyg.