J. P. Hamaker
ASTRON, Netherlands Foundation for Research in Astronomy, Postbus 2, 7990 AA Dwingeloo, The Netherlands
Received 6 March 2006 / Accepted 7 June 2006
Abstract
Context. This is Paper V in a series on polarimetric aperture synthesis based on the algebra of ![]() matrices.
matrices.
Aims. It validates the matrix self-calibration theory of the preceding Paper IV and outlines the algorithmic methods that had to be developed for its application.
Methods. New avenues of polarimetric self-calibration opened up in Paper IV are explored by processing a simulated observation. To focus on the polarimetric issues, it is set up so as to sidestep some of the common complications of aperture synthesis, yet properly represent physical conditions. In addition to a representative collection of observing errors, the simulated instrument includes strongly varying Faraday rotation and antennas with unequal feeds. The selfcal procedure is described in detail, including aspects in which it differs from the scalar case, and its effects are demonstrated with a number of intermediate image results.
Results. The simulation's outcome is in full agreement with the theory. The nonlinear matrix equations for instrumental parameters are readily solved by iteration; a convergence problem is easily remedied with a new ancillary algorithm. Instrumental effects are cleanly separated from source properties without reference to changes in parallactic rotation during the observation. Polarimetric images of high purity and dynamic range result. As theory predicts, polarimetric errors that are common to all sources inevitably remain; prior knowledge of the statistics of linear and circular polarization in a typical observed field can be applied to eliminate most of them.
Conclusions. The paper conclusively demonstrates that matrix selfcal per se is a viable method that may foster substantial advancement in the art of radio polarimetry. For its application in real observations, a number of issues must be resolved that matrix selfcal has in common with its scalar sibling, such as the treatment of extended sources and the familiar sampling and aliasing problems. The close analogy between scalar interferometry and its matrix-based generalisation suggests that one may apply well-developed methods of scalar interferometry. Marrying these methods to those of this paper will require a significant investment in new software. Two such developments are known to be foreseen or underway.
Key words: instrumentation: interferometers - instrumentation: polarimeters - methods: data analysis - methods: observational - techniques: interferometric - techniques: polarimetric
This article is the fifth in a series in which a physics-based theory of polarimetric aperture synthesis is developed. Starting from a detailed description of a single interferometer in Paper I (Hamaker et al. 1996) and a qualitative investigation of a synthesis array as a whole in Paper II (Sault et al. 1996), the main line of our work progressed to the consideration of matrix-based self-calibration![]() .
Paper IV (Hamaker 2000) demonstrated that such calibration is indeed possible; the paper considers in mathematical terms the ambiguities that the solution is subject to and points out the close analogies with and important differences from scalar selfcal. The theory, however, gives no answer to the many questions one must ask about a practical implementation. This paper seeks to fill that void, by studying a computer simulation in which an observation with instrumental errors of a sky field containing unpolarized and polarized sources is self-calibrated with matrix-based algorithms.
.
Paper IV (Hamaker 2000) demonstrated that such calibration is indeed possible; the paper considers in mathematical terms the ambiguities that the solution is subject to and points out the close analogies with and important differences from scalar selfcal. The theory, however, gives no answer to the many questions one must ask about a practical implementation. This paper seeks to fill that void, by studying a computer simulation in which an observation with instrumental errors of a sky field containing unpolarized and polarized sources is self-calibrated with matrix-based algorithms.
Table 1: Poljargon.
It opens, in Sect. 2, with a brief summary of the results of Paper IV that form the basis of the present work. It highlights the distinction between the initial self-aligment, in which Sky and Instrument Models are developed, and the subsequent post-calibration in which the ambiguities left after self-alignment must be resolved. The simulated Sky field and Instrument are described in Sect. 3. Section 4 considers the matrix self-alignment cycle in detail; post-calibration is discussed in Sect. 5. Various complications along with expedients to deal with them are explained and illustrated with Sky images from the simulation. A few side remarks are collected in Sect. 6. Section 7 sums up the results and their possible consequences.
We assume that all antennas see the same "apparent'' Sky, i.e. they have identical primary antenna beams; this is a prerequisite for all forms of self-calibration![]() .
.
The notation for mathematical symbols is the same as in the preceding papers.
Bold-faced capitals represent ![]() matrices, bold-faced lower-case characters are column 2-vectors. For hermitian transposition or conjugation a dagger superscript is used. Roman font is reserved for constants, variables are italicized
matrices, bold-faced lower-case characters are column 2-vectors. For hermitian transposition or conjugation a dagger superscript is used. Roman font is reserved for constants, variables are italicized![]() .
Unless noted otherwise, primed variables indicate estimates obtained by model fitting.
.
Unless noted otherwise, primed variables indicate estimates obtained by model fitting.
The subscripts j,k denote the array's antennas, in combination they indicate
an interferometer. A third subscript t distinguishes the successive time intervals in
which observed coherencies are recorded. For consistency with the coherency
![]() ,
the notation
,
the notation
![]() for the Sky brightness in Paper IV has been replaced with
for the Sky brightness in Paper IV has been replaced with
![]() .
.
Paper IV rather ineptly uses the "variance'' function
![]() for what is known in linear algebra as the square of the Frobenius norm,
for what is known in linear algebra as the square of the Frobenius norm,
![]() .
I now use the latter notation.
.
I now use the latter notation.
The concepts and associated terminology developed in Paper IV play a crucial role in the present work. For the reader's convenience Table 1 summarises them here; a few new terms to be coined in this paper are also included.
This section summarises those parts of Paper IV that are relevant here; for full details, refer to that paper.
The electric field is represented by a column vector ![]() in cartesian or circular coordinates. Depending on whether the coherency is represented as a 4-vector (Paper I) or a
in cartesian or circular coordinates. Depending on whether the coherency is represented as a 4-vector (Paper I) or a ![]() matrix (Paper IV), the interferometer transfer equation can take two different forms. Here I use the coherency matrix
matrix (Paper IV), the interferometer transfer equation can take two different forms. Here I use the coherency matrix
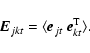 |
(1) |
Paper IV stresses the analogies between the algebras for scalars and matrices, which may be very helpful in developing an intuitive understanding of the latter. The most important correspondences are listed in Table 2.
Table 2: Scalar-matrix analogies.
By default, in this paper each Jones matrix represents a complete (dual) antenna path from the source down to the pair of voltage inputs to the correlator. It includes not only scalar gain and phase effects in parallel X and Y or L and R signal paths, but also interactions between the two, notably rotations and the cross-polarization in the feeds. (In the conventional quasi-scalar approach, such effects must be separately accounted for.) The set
Self-calibration operates entirely on the apparent Sky, i.e. the Sky multiplied with the primary antenna beam; in the matrix case, the latter is a Jones-matrix function of position ![]() .
Correction for this is best postponed until self-calibration is complete; it requires precise knowledge of the Jones-matrix primary beam - which is beyond the scope of this paper.
.
Correction for this is best postponed until self-calibration is complete; it requires precise knowledge of the Jones-matrix primary beam - which is beyond the scope of this paper.
We introduce the Stokes parameters I,Q,U and V by representing the coherency matrix in the form![]()
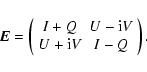 |
(3) |
Since the coherency ![]() and the Sky brightness
and the Sky brightness ![]() are related by a Fourier transformation (van Cittert-Zernike theorem) the above two equations also apply to
are related by a Fourier transformation (van Cittert-Zernike theorem) the above two equations also apply to ![]() .
I shall use the same notation for Stokes parameters, intensity and polvector in both domains; the distinction will be clear from the context.
.
I shall use the same notation for Stokes parameters, intensity and polvector in both domains; the distinction will be clear from the context.
The scalar/matrix analogy suggests that the hugely successful scalar method of self-calibration can be generalized to the matrix domain - which is indeed the case.
Given a set of observations
![]() ,
self-calibration seeks to invert the
M.E. to obtain values for
,
self-calibration seeks to invert the
M.E. to obtain values for
![]() and the corresponding Sky brightness
and the corresponding Sky brightness
![]() (where
(where ![]() are Sky coordinates). This is an ill-posed problem but, as in the scalar case, it can be regularized by the customary assumption that the Sky is "mostly empty''. Along with the Sky Model
are Sky coordinates). This is an ill-posed problem but, as in the scalar case, it can be regularized by the customary assumption that the Sky is "mostly empty''. Along with the Sky Model
![]() ,
the solution includes an Instrument Model
,
the solution includes an Instrument Model
![]() .
.
In the case of scalar selfcal the solution is unique except for an unknown positive multiplier![]() :
in addition to the correct Sky image
:
in addition to the correct Sky image
![]() and the corresponding visibilities
and the corresponding visibilities
![]() ,
all positive multiples of them also satisfy the M.E. provided one multiplies
,
all positive multiples of them also satisfy the M.E. provided one multiplies
![]() with a compensating factor.
with a compensating factor.
Paper IV derives the analogous property for the matrix case. The Sky-image solution that one obtains is - apart from the convolution with a scalar synthesised beam - related to the true Sky by a poldistortion transformation:
As argued in Paper IV, the solution ![]() is not really calibrated, since it includes the unknown factor
is not really calibrated, since it includes the unknown factor ![]() ;
we use the more percise term self-alignment instead. The solution
;
we use the more percise term self-alignment instead. The solution ![]() self-aligns the observations to satisfy our prior assumptions about the Instrument (no interferometer-based errors) and the Sky ("mostly empty''). Note that Eq. (6) is an in-place transformation that operates in the same way on every point in the image.
self-aligns the observations to satisfy our prior assumptions about the Instrument (no interferometer-based errors) and the Sky ("mostly empty''). Note that Eq. (6) is an in-place transformation that operates in the same way on every point in the image.
Like scalar selfcal, matrix self-alignment eliminates all the variable errors in the Instrument and replaces them with one error factor ![]() that is constant over all antennas j and times t. This mechanism applies not only to gains and phases, but also to polarimetric errors such as polarization leakage and rotations of linear polarization as well as intentional differences between antenna feeds (heterogeneous array).
that is constant over all antennas j and times t. This mechanism applies not only to gains and phases, but also to polarimetric errors such as polarization leakage and rotations of linear polarization as well as intentional differences between antenna feeds (heterogeneous array).
The transformation Eq. (6) can be factored as
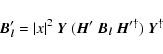 |
(8) |
Inverting the M.E. by self-alignment takes us only halfway; while being consistent with the observations, the Sky image ![]() that we obtain differs from the true one. Post-calibration is required to eliminate the spurious transformation
that we obtain differs from the true one. Post-calibration is required to eliminate the spurious transformation ![]() .
Here the M.E. is to no avail: all that we can extract from it is already in the self-aligned solution
.
Here the M.E. is to no avail: all that we can extract from it is already in the self-aligned solution ![]() .
Instead, a priori external information must be exploited to constrain
.
Instead, a priori external information must be exploited to constrain ![]() .
.
Self-alignment and post-calibration are, in principle, mutually independent. While inevitably and uncontrollably introducing unknown ![]() and
and ![]() transformations in its solutions, self-alignment is not affected by them. The latter is also true when we transform the data mid-stream - probably with the intention of making the process easier to control (cf. Sect. 5.1). In the theory, self-alignment precedes post-calibration, but in practice we may take an advance on the latter whenever we see fit to do so.
transformations in its solutions, self-alignment is not affected by them. The latter is also true when we transform the data mid-stream - probably with the intention of making the process easier to control (cf. Sect. 5.1). In the theory, self-alignment precedes post-calibration, but in practice we may take an advance on the latter whenever we see fit to do so.
Self-alignment cannot eliminate poldistortion because it cannot recognise it. More generally, a proper self-aligning algorithm should have little tendency to change the poldistortion with which it is initialised. Basically, one expects it to just transmit what it is offered.
Thus poldistortion, once introduced, will be transferred to the Instrument Model, hence to the Sky image and the Sky Model extracted from it, after which the next self-aligment cycle will transfer it to the next Instrument model, etc. To keep poldistortion low, it is important to prevent it from being inadvertently introduced. It is therefore important to apply a pre-calibration using the best initial nominal Instrument Model that one can get hold of.
The theory is clear on what we can and cannot expect self-alignment to achieve, but it does not tell us how a solution is obtained. In the scalar case the nonlinear selfcal equations can be solved iteratively, or linearised by taking logarithms; both methods have been used sucessfully and the solutions are usually robust. The non-commutativity of matrix multiplication precludes the use of logarithms, so solving the nonlinear equations directly is our only option. Stability and robustness of this process must be investigated.
Once we have a solution, we must consider post-calibration: How can we bring in prior astronomical and instrumental knowledge to suppress the unknown poldistortion?
![\begin{figure}
\par\includegraphics[width=10cm,clip]{5145geom.eps}
\end{figure}](/articles/aa/full/2006/34/aa5145-06/Timg44.gif) |
Figure 1: Synthesis-telecope geometry. Left: Antenna positions and feed orientations. Right: uv coverage. |
| Open with DEXTER | |
To answer these questions and develop practical algorithms, an observation with realistic errors of various sorts was simulated. The theory was used as a guideline in self-calibrating the observation.
A major advantage of a simulation is that it can be set up to focus on the polarimetric problem per se and sidestep the several distracting complications that beset aperture synthesis in the real world, such as interference, uv-convolution and aliasing, deficiencies of CLEAN, Sky curvature and projection effects. The following are the main features of the simulated observation:
Position-angle and ellipticity errors are drawn from Gaussian distributions centered on zero with an rms spread of some ![]() .
.
The matrix-based self-align procedure is shown in the top half of Table 3. It corresponds to conventional scalar self-calibration, extended with a number of matrix-specific algorithms. In relating scalar and matrix self-alignment, one may utilise the correspondences listed in Table 2.
The procedure simultaneously develops Models of the apparent Sky
![]() and the Instrument
and the Instrument
![]() that together satisfy Eq. (2) given the observed coherencies
that together satisfy Eq. (2) given the observed coherencies
![]() .
The following cycle is repeated iteratively:
.
The following cycle is repeated iteratively:
Table 3: Self-alignment and post-calibration in the simulation. Four iteration cycles are shown. Elements that deviate from, or are absent in, scalar selfcal are set in boldface. Operation classes: i = making Instrument Model; m = making Sky image; p = post-calibration operation; s = making Sky Model.
The elements in the self-alignment part of Table 3 that have no counterpart in scalar self-alignment are shown in boldface.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{5145raw.eps}
\end{figure}](/articles/aa/full/2006/34/aa5145-06/Timg52.gif) |
Figure 2:
Cycle-1 dirty images, made with nominal instrumental corrections; left V, right |
| Open with DEXTER | |
I used the relaxation algorithm (Appendix A.1 below) of Paper IV. Alternatively, a general-purpose non-linear equation solver routine may be used. In either case convergence turns out to be a problem - to be discussed in Sect. 4.3.
Because of its simplicity, the Paper IV algorithm is very suitable for experiments of the present type and cheap in execution. However, M. Brentjens (priv. comm.) finds that it may easily get stuck in a secondary minimum when many interferometers are missing (e.g. because of interference). He patched a general-purpose solver to deal with this problem. Whether the same can be done for the Paper IV algorithm we do not know.
An obvious first step is to CLEAN the intensity image in the standard way.
For an "empty'' Sky, it is a valid assumption that polarized flux can only exist where there is intensity![]() .
The Q,U,V images are actually three components of an image of the polvector
.
The Q,U,V images are actually three components of an image of the polvector ![]() .
The way to CLEAN them jointly is motivated by poldistortion theory: Apart from polconversion (to be discussed later), the principal error that remains in the final self-alignment cycles is a polrotation that leaves
.
The way to CLEAN them jointly is motivated by poldistortion theory: Apart from polconversion (to be discussed later), the principal error that remains in the final self-alignment cycles is a polrotation that leaves ![]() invariant. Thus, we may use a
invariant. Thus, we may use a ![]() image to indentify components, searching only the locations of I sources. Having identified a peak, we determine the individual Q,U,V fluxes and subtract components multiplied by the loop gain from the corresponding images.
image to indentify components, searching only the locations of I sources. Having identified a peak, we determine the individual Q,U,V fluxes and subtract components multiplied by the loop gain from the corresponding images.
This approach carries the obvious advantage that it is less sensitive to noise than searches in the separate ![]() and V images would be. It proved to be quite effective even in the early cycles, where errors other than polrotation might confuse the situation.
and V images would be. It proved to be quite effective even in the early cycles, where errors other than polrotation might confuse the situation.
For reasons to be discussed in Sect. 5.1, one may take an advance on post-calibration by interjecting Poldeconversion (removing polconversion) in the self-alignment procedure.
![\begin{figure}
\par\includegraphics[width=17.4cm,clip]{5145cyc2}
\end{figure}](/articles/aa/full/2006/34/aa5145-06/Timg54.gif) |
Figure 3:
Cycle-2 dirty images, corrected for instrumental errors fitted with the I-only Sky Model of cycle 1; left V, right |
| Open with DEXTER | |
In the Instrument fit, residuals rapidly decrease in the initial iterations. After that, the polrotation factor in the Instrument model continues to be adjusted in minute steps in an attempt to match the observed and Sky-Model polvectors; final convergence may require tens of thousands of steps. Apparently the polarized flux, totalling only about 1% of the intensity flux, is too weak to effectively drive the algorithm![]() .
A complementary algorithm (Appendix A.2) addresses this problem.
.
A complementary algorithm (Appendix A.2) addresses this problem.
I discussed above how errors once introduced may persist in the further processing. Such errors may also be introduced through the ![]() Sky Model when it is extracted from a poor image.
Sky Model when it is extracted from a poor image.
Figures 2 and 3 illustrate a case seen in practice. The pre-calibrated dirty image is of bad quality. The V image, that should be almost empty, is indicative of the error level in all three of the ![]() images. Yet a few sources were extracted from the
images. Yet a few sources were extracted from the ![]() image and included in the Sky Model. Several self-align cycles later, Stokes U was noted to have the wrong sign; the error was traced back to the very first
image and included in the Sky Model. Several self-align cycles later, Stokes U was noted to have the wrong sign; the error was traced back to the very first ![]() model.
model.
In a re-run, ![]() modeling was postponed. An I-only Sky from the first cycle served in cycle 2 to correct most of the complex-gain errors
modeling was postponed. An I-only Sky from the first cycle served in cycle 2 to correct most of the complex-gain errors![]() .
This improved the
.
This improved the ![]() images to the point where the major polarized sources could be reliably identified (Fig. 3).
images to the point where the major polarized sources could be reliably identified (Fig. 3).
![\begin{figure}
\par\includegraphics[width=17.4cm,clip]{5145polC.eps}
\end{figure}](/articles/aa/full/2006/34/aa5145-06/Timg56.gif) |
Figure 4: Poldeconversion. Shown are the differences of Q ( left) and I ( right) images after poldeconversion with those before. Circles mark the true source positions with areas proportional to intensity, bars indicate orientation and strength of true linear polarization. Note the flux scales. The Q image shows that poldeconversion has removed Q flux from every source. In the I image differences exist only where the source is truly polarized; positive and negative I differences reflect the bipolar nature of Q. |
| Open with DEXTER | |
Post-calibration is the process of eliminating the spurious poldistortion ![]() that appears in Eq. (6). Prior knowledge, both astrophysical and instrumental, may be harnessed for this purpose. The methods to be described rely on
that appears in Eq. (6). Prior knowledge, both astrophysical and instrumental, may be harnessed for this purpose. The methods to be described rely on ![]() being the same for the entire Sky field, as was discussed above.
being the same for the entire Sky field, as was discussed above.
While Stokes I is necessarily positive, ![]() approaches zero when summed over many (independent) sources; also, usually
approaches zero when summed over many (independent) sources; also, usually
![]() (although important exceptions exist, see Fender & Macquart 2003). Imposing these empirical findings as prior constraints on our Sky image, we can estimate the polarimetric errors and correct the image and our Sky and Instrument Models for them.
(although important exceptions exist, see Fender & Macquart 2003). Imposing these empirical findings as prior constraints on our Sky image, we can estimate the polarimetric errors and correct the image and our Sky and Instrument Models for them.
Table 4: The effect of polvector leveling. Shown is a list of the polarized sources in the final Sky Model. The true Vfluxes are compared with those obtained through self-alignment before and after the leveling. Leveling reduces all of them to near-zero except for one source which is indeed the one that is truly polarized.
Polconversion adds to all sources in a Sky image a polarization component with one and the same relative polarization ![]() .
This makes it quite conspicuous in a comparison of the I Sky Model and the CLEAN-residual
.
This makes it quite conspicuous in a comparison of the I Sky Model and the CLEAN-residual ![]() images.
images.
Poldeconversion is the operation of correcting for the polconversion matrix ![]() in Eq. (6). The simplest method is to keep polconverted
in Eq. (6). The simplest method is to keep polconverted ![]() flux out of the Sky Model, which one may do by stopping CLEAN before it starts picking it up significantly. In the immediately following Instrument fit, the polconversion-free Sky Model will then force the Instrument model to comply.
flux out of the Sky Model, which one may do by stopping CLEAN before it starts picking it up significantly. In the immediately following Instrument fit, the polconversion-free Sky Model will then force the Instrument model to comply.
Alternatively, one may use the Sky Model to subtract the sources identified as truly polarized from the newest dirty images. The ![]() flux in the remainder must then be polconverted I flux and the polconversion matrix
flux in the remainder must then be polconverted I flux and the polconversion matrix ![]() can be determined by a comparison (Appendix B.1). An example is shown in Fig. 4.
can be determined by a comparison (Appendix B.1). An example is shown in Fig. 4.
In any method of separating instrumental artifacts from true object features, some measure of human intervention may be necessary. In matrix selfcal, true source polarization must be distinguished from polconverted intensity. Since self-alignment produces very pure ![]() images, this was simple in my simulations; it may be less so with more complicated source morphologies - but probably much simpler than with quasi-scalar methods (e.g. Leppanen et al. 1995).
images, this was simple in my simulations; it may be less so with more complicated source morphologies - but probably much simpler than with quasi-scalar methods (e.g. Leppanen et al. 1995).
Poldeconversion should be applied as early as possible, lest CLEAN mistakenly consolidates some polconverted I flux in the Sky Model.
The linear polvectors for the true Sky reside in the QU plane (usually represented as "horizontal''). Polrotation may rotate them in this plane but also tilt the plane as a whole, giving rise to a V component for every
![]() source. We may "level'' all polvectors in the Sky Model by rotating the V axis to the vertical axis, minimising
source. We may "level'' all polvectors in the Sky Model by rotating the V axis to the vertical axis, minimising ![]() (Appendix B.2). If any significant V values remain, they are probably real. Table 4 demonstrates the effect.
(Appendix B.2). If any significant V values remain, they are probably real. Table 4 demonstrates the effect.
Out of an infinite set of possible rotations I choose the one that requires a minimal rotation angle: it achieves the required leveling with a minimal effect on
![]()
![]() .
.
As noted earler, the polconversion and polrotation operators may be represented in either order. Consequently, the order of the corrections can also be freely chosen. In Table 3 poldeconversion comes first; after that, there is no polconverted ![]() flux left that could be affected by polvector leveling. (If there were, it could be neutralised by another poldeconversion run.)
flux left that could be affected by polvector leveling. (If there were, it could be neutralised by another poldeconversion run.)
Self-alignment produces an Instrument model that includes the inverse of the poldistortion matrix ![]() .
One may estimate it by comparing the model with prior knowledge of the Instrument.
.
One may estimate it by comparing the model with prior knowledge of the Instrument.
A typical antenna channel can be described (Paper I) by a product of Jones matrices
where
For a comparison, we must extract corresponding values from our Instrument model
![]() .
The method for doing this is outlined in Appendix B.3. By correcting those differences that one finds, one may hope to further reduce the poldistortion left by the methods of Sect. 5.1.
.
The method for doing this is outlined in Appendix B.3. By correcting those differences that one finds, one may hope to further reduce the poldistortion left by the methods of Sect. 5.1.
Faraday polrotation remains as an error that can only be calibrated from external data. Note that antennas separated by large distances may experience different polrotations; these differences are absorbed by self-alignment, but one absolute polrotation must be determined otherwise in all cases.
Along with the main experiment discussed above, a number of side issues were explored to check the robustness of my approach.
The self-align algorithm was tested with various pre-calibrations of the Instrument, such as the nominal values, the model from the previous cycle or an arbitrary matrix constant such as one of the Pauli matrices (Paper IV). In all cases the residuals in the fit were the same and the speeds of convergence differed only marginally. Obviously, the poldistortion introduced did depend on the initial value set. As discussed above, one should preferably start with values that are close to those expected: Use the pre-calibrated Instrument Model in the first, and the freshly updated one in all following self-align cycles.
A heterogeneous array was chosen for simulation because it represents an innovative concept proposed by Paper IV. Notwithstanding its advantages, there are sound practical reasons why such an array has hitherto not been attractive. Firstly, for non-polarimetric observations a heterogeneous array needs four correlator channels per interferometer where two would suffice. Secondly, if the primary beams of the antennas have non-circular symmetry, the combination of such beams in different orientations adds to the complexity of synthesis imaging in a formidable way.
Yet the heterogeneous array is of more than academic interest. Indeed, in the context of this paper Faraday rotation is part of the Instrument, and since it is inherently variable with distance it will make any array heterogeneous that extends over "large'' distances. Under such conditions, every array must observe the full coherency even for unpolarized sources.
The differences between a heterogeneous and a homogeneous array are amply discussed in Paper IV: The weak connection between the sets of X and Y (or L and R) channels makes the homogeneous system vulnerable to a spurious phase difference between the two, resulting in a polrotation in the Sky Model (cf. Paper II). For the linearly polarized array this is a
![]() rotation that can be elimated by polvector leveling. For a circularly polarized array that will not work, because the RL phase difference engenders a
rotation that can be elimated by polvector leveling. For a circularly polarized array that will not work, because the RL phase difference engenders a
![]() rotation on which we have no a-priori handle.
rotation on which we have no a-priori handle.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5145pvCh.eps}
\end{figure}](/articles/aa/full/2006/34/aa5145-06/Timg73.gif) |
Figure 5:
Alignment of the linear polvectors observed at successive hour-angle
intervals by self-alignment. (a) Initially, the polvectors for successive hour angles are scattered in random directions by time-varying Faraday rotation. In the pre-calibrated image of cycle 1, their sum is much too small and badly misoriented. Most sources in the (b) In the self-alignment of cycle 2, that Sky Model serving as reference provides no clue for the alignment of the observed polvectors; they are scattered once more, in random directions. Their sum is changed but remains weak. Yet, since gain and phase errors have been much reduced, the strongest polarized sources are now clearly identifiable (Fig. 3). (c) The (d) Further cycles will reduce the remaining errors at a level that is not visible on the scale of this diagram. |
| Open with DEXTER | |
Faraday self-alignment is an important novelty. In quasi-scalar polarimetry, variable Faraday rotation can only be corrected by approximate estimates. The remaining variation mixes Q and U in such a way that effectively every polarized source is imaged with a different instrumental beam of poor quality. Matrix self-alignment suppresses this effect, makes the ![]() beams identical to the I beam and restores the images to their full dynamic range. Self-aligned Q and U images look even better than their I counterparts because there are fewer sources and hence less confusion of sidelobes; this can be seen in Fig. 3 (but the reproduction is probably not good enough to show it quite convincingly).
beams identical to the I beam and restores the images to their full dynamic range. Self-aligned Q and U images look even better than their I counterparts because there are fewer sources and hence less confusion of sidelobes; this can be seen in Fig. 3 (but the reproduction is probably not good enough to show it quite convincingly).
The mechanism of the Faraday alignment is sketched in Fig. 5.
I and ![]() fluxes in the final Sky Model agree (apart from a flux-scale factor) with the true Sky within .001 of the flux of the strongest source; having made my point, I did not try to improve this any further. I attach no great significance to this number. In the simulations, only the Instrument Model pretends to be realistic; other aspects of the observation were deliberately oversimplified in order to focus on the polarimetry issues.
fluxes in the final Sky Model agree (apart from a flux-scale factor) with the true Sky within .001 of the flux of the strongest source; having made my point, I did not try to improve this any further. I attach no great significance to this number. In the simulations, only the Instrument Model pretends to be realistic; other aspects of the observation were deliberately oversimplified in order to focus on the polarimetry issues.
The outcome of this study must be judged in relation to its purpose, which is validation of the theory of Paper IV and the development of supporting algorithms. On this count the results are entirely satisfactory. The poldistortion effects predicted have all been observed in (simulated) practice - sometimes as expected, sometimes as a surprise although they could have been expected. The latter cases in particular confirm the notion that poldistortion is an unavoidable artifact spawned by matrix self-alignment, in precisely the way that Paper IV foretells. On the practical side, a number of algorithms have been created that effectively deal with side problems which that paper hardly addresses.
Polarimetric errors in the self-aligned Sky image can be represented as a product of two poldistortion transformations. These are independent of each other and of spatial scattering by beam sidelobes, and both operate on all image points in the same way. The latter is a particularly valuable property, because it allows one to consider the statistics of the set of all (or a selected group of) Sky sources. By comparing them to the prior astrophysical knowledge that both linear and circular polarizations are zero on the average, one may estimate polconversion and polrotation and correct for them, without reference to external measurements such as a separate observation of a calibrator source. In this way, the great benefits of scalar intensity self-calibration get extended to polarimetry![]() .
As a complement, statistical comparison of the Instrument model to prior estimates of Instrument parameters gives us another handle on the poldistortion. The latter idea is, of course, not new but is given a broader scope here.
.
As a complement, statistical comparison of the Instrument model to prior estimates of Instrument parameters gives us another handle on the poldistortion. The latter idea is, of course, not new but is given a broader scope here.
The (pol)rotation of parallactic angle in azimuth/elevation-mounted antennas has often been suggested as a mechanism to separate intrumental effects from the observed Sky. Cotton (1993) and Roberts et al. (1994) have investigated this option at length. They show that it can be made to work to some extent, under suitable conditions, and with considerable manual labour. Matrix self-alignment and post-calibration replace such artisan methods by separating time-varying polrotation from the Sky in a clean, systematic and generally applicable way, using algorithms that require little more manual steering than simple scalar selfcal does.
The virtues of Faraday self-alignment have already been highlighted in Sect. 6.3. They are of particular importance for polarimetry toward lower frequencies since the rotation and its temporal variation increase with ![]() .
At long baselines, each antenna moreover experiences its own Faraday rotation, effectively making an array heterogeneous even if it had been built homogeneous. This possibility has not been explicitly considered here, but it is no more than a trivial departure from the static heterogeneity that has been simulated.
.
At long baselines, each antenna moreover experiences its own Faraday rotation, effectively making an array heterogeneous even if it had been built homogeneous. This possibility has not been explicitly considered here, but it is no more than a trivial departure from the static heterogeneity that has been simulated.
Notwithstanding the complications of practical aperture synthesis, scalar self-calibration has proven to be very effective with observing geometries and source morphologies much more complicated than those simulated here. With the ground rules for polarimetric selfcal now firmly established, and given the close analogies between the scalar and matrix domains, one may expect matrix selfcal likewise to be applicable in real-life situations.
Polarimetry is a nasty complication to the subject of Aperture Synthesis, which is already far from simple in itself. Although many observers are using them to obtain their astrophysical results, quasi-scalar methods have certainly not helped to endear the subject to them. To some, the Jones-matrix representation appears like a way of making things even more difficult. This notion is mistaken. Rather than complicating the matter, matrix methods simplify it, if only one is willing to accept matrix algebra as a tool. (A simple but characteristic measure of this simplification is the compactness of the formulas in the papers of this series as compared to that in the typical paper on quasi-scalar polarimetry.)
The matrix formulation provides a precise description of the physics of our receiver systems. Its awkward features reflect properties that are real but overlooked by the quasi-scalar method; for example, the non-commutativity of matrix multiplication reminds us that, in a dual-polarization signal path, the order of ionosphere, antenna, feed and receiver stages cannot be arbitarily changed in the way it can for a scalar chain. Such complexity is the inevitable consequence of very basic physics. The quasi-scalar method approaches it from the bottom up by splitting the problem into isolated morsels, treating them in mutual isolation, and ignoring the higher-order effects that do not fit. Matrix self-calibration proposes a top-down alternative that has no need for approximations: Each of the steps described above is motivated by the overall view that the Measurement Equation provides, and fits seamlessly into one coherent grand picture.
Further development in observing practice will depend on the creation of suitable software. Having endorsed the Measurement Equation as one of its foundations, AIPS++ would seem to be the foremost place to look for that, and it indeed already includes many of the matrix software mechanisms required. However, its present implementation of matrix selfcal was created too early to benefit from the concepts thatPapers IV and V have now firmly put in place. As a first step forward, the development group is engaged in a code cleanup that will pave the way for self-calibration upgrades in the future (G. Moellenbrock, priv. comm.). Another development is to be looked for in the Netherlands, where AIPS++ infrastructure is built into the new software for the LOFAR phased-array telescope. In order to deal with the unprecedented complexity of that instrument, full deployment of matrix-based data reduction methods is foreseen.
With this paper, the program of the series, Understanding radio polarimetry, has been successfully completed. Further development of polarimetric theory and practice will most likely take place in the context of applications.
Acknowledgements
I am much indebted to the management of ASTRON for the opportunity to conduct this long-term research project in an environment where the pressure from a host of shorter-term projects and immediate applications is continually felt. W.N. Brouw, R.J. Nijboer and J. Tinbergen kindly read the manuscript and provided useful suggestions. ASTRON is operated with financial support from the Netherlands Organisation for Scientific Research (NWO).
Most of the algorithms sketched below rely on the quaternion representation of matrices and the quaternion algebra that are introduced in Paper IV. In brief, Eq. (4) is generalised to all ![]() matrices:
matrices:
| (A.1) |
The algorithm of Paper IV, App. D.2, can be presented in a more transparent form. Given a set of observed coherencies
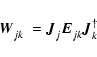 |
(A.2) |
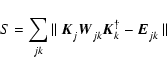 |
(A.3) |
Consider two arbitrary unit polvectors ![]() and
and ![]() which make an angle
which make an angle ![]() .
Rotating one into the other can be achieved through many different rotations (all of which have their axis in the bisecting plane of
.
Rotating one into the other can be achieved through many different rotations (all of which have their axis in the bisecting plane of ![]() and
and ![]() ). For the axis perpendicular to both vectors the rotation angle is equal to
). For the axis perpendicular to both vectors the rotation angle is equal to ![]() and minimal, which seems to be a desirable property. To find this minimal rotation, we take the quaternion product
and minimal, which seems to be a desirable property. To find this minimal rotation, we take the quaternion product
In the Instrument-fit procedure of Sect. 4.2, ![]() and
and ![]() above represent the polvectors of the Sky-Model and observed coherencies, respectively. We sum their product over all uv points to estimate the required rotation.
above represent the polvectors of the Sky-Model and observed coherencies, respectively. We sum their product over all uv points to estimate the required rotation.
If the observed field contains enough source flux that we may assume a priori to be unpolarized, we may use these sources as a reference against which polconversion can be estimated and then removed. Similarly, if there is enough linearly polarized flux we can use it to estimate how much of it has been polrotated into circular polarization and correct for that.
We may also compare the fitted Jones matrices
![]() to prior knowledge of
the instrument. To this end we must factor them to expose the parameters by
which an antenna channel is normally characterised: Rotations (Faraday,
parallactic, feed), feed configuration and errors, complex receiver gains.
to prior knowledge of
the instrument. To this end we must factor them to expose the parameters by
which an antenna channel is normally characterised: Rotations (Faraday,
parallactic, feed), feed configuration and errors, complex receiver gains.
Polconversion is characterised by the matrix ![]() in Eq. (7). For once I revert to the quasi-scalar approximation in which only one of its effects is considered, viz. the conversion of some I flux into a polvector flux for every source k
in Eq. (7). For once I revert to the quasi-scalar approximation in which only one of its effects is considered, viz. the conversion of some I flux into a polvector flux for every source k![]() :
:
| (B.1) |
![\begin{displaymath}\vec{p}_0' = \frac{ \displaystyle\sum[~ \vec{p}~ I ~] }{ \displaystyle\sum I^2 }
\end{displaymath}](/articles/aa/full/2006/34/aa5145-06/img93.gif) |
(B.2) |
An example from the simulation is shown in Fig. 4.
Consider the set of N real column vectors
![]() representing the polarized Sky Model, and a plane through the origin of QUV space whose normal is the column vector
representing the polarized Sky Model, and a plane through the origin of QUV space whose normal is the column vector ![]() .
The distance of a point
.
The distance of a point
![]() to the plane is
to the plane is
![]() .
We require the value of
.
We require the value of ![]() that minimises
that minimises
| (B.4) |
I show here the factoring procedure for a linearly polarized antenna where, in Eq. (9),
![]() .
For a circularly polarized one the analysis is only slightly more complicated. (The method shown here is simpler and more direct than the one suggested by Paper IV, and allows for the diagonal elements of
.
For a circularly polarized one the analysis is only slightly more complicated. (The method shown here is simpler and more direct than the one suggested by Paper IV, and allows for the diagonal elements of ![]() to differ.)
to differ.)
The equation to be satisfied for given ![]() is Eq. (9)
is Eq. (9)
To find the factors, perform the following steps:
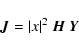 |
(B.6) |
| |
= | ||
| = | (B.8) |
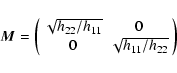 |
(B.10) |
| (B.11) |
| |
= | ||
| = | (B.12) | ||
| = |
Although the problem of representing an arbitrary three-dimensional rotation in terms of mutually perpendicular ones is well known, I had trouble finding direct references. The basic information is available in handbooks (e.g. Korn & Korn 1968) but some tedious algebra is needed to extract the necessary formulae.
The product Eq. (B.7) can be wtitten out in quaternion form as
| |
= | ||
| y0 | = | (B.13) | |
| y1 | = | ||
| y2 | = | ||
| y3 | = |
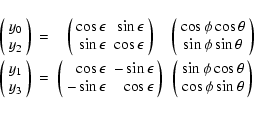 |
(B.14) |