A&A 455, 441-451 (2006)
DOI: 10.1051/0004-6361:20042606
Weak lensing measurements of dark matter halos of galaxies from
COMBO-17
M. Kleinheinrich1,2 - P. Schneider2 - H.-W. Rix1 - T. Erben2 - C. Wolf3 - M. Schirmer2 - K. Meisenheimer1 - A. Borch1 - S. Dye4 - Z. Kovacs1 - L. Wisotzki5
1 - Max-Planck-Institut für Astronomie, Königstuhl 17,
69117 Heidelberg, Germany
2 -
Institut für Astrophysik und Extraterrestrische Forschung,
Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
3 -
Department of Physics, Denys Wilkinson Bldg., University of
Oxford, Keble Road, Oxford, OX1 3RH, UK
4 -
School of Physics and Astronomy, Cardiff University, 5 The
Parade, Cardiff, CF24 3YB, UK
5 -
Astrophysikalisches Institut Potsdam, An der Sternwarte 16,
14482 Potsdam, Germany
Received 23 December 2004 / Accepted 19 April 2006
Abstract
We present mass estimates for dark
matter halos around galaxies from the COMBO-17 survey using weak
gravitational lensing. COMBO-17, with photometry in 17 optical
filters, provides precise photometric redshifts and
spectral classification for objects with R<24. This permits
to select and sort lens and source galaxies by their redshifts and lens
luminosity or color, which bypasses
many uncertainties in other weak lensing analyses arising from broadly
estimated source and lens redshifts. We study the shear created
by dark matter halos around 12 000 galaxy lenses at redshifts
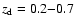 by fitting the mass normalization of either
singular isothermal spheres (SIS) or Navarro-Frenk-White (NFW)
profiles to background source orientations around the whole lens sample.
We also consider halos around
blue and red subsamples separately and constrain the scaling
of halo mass with light. For the NFW model, we find virial masses
by fitting the mass normalization of either
singular isothermal spheres (SIS) or Navarro-Frenk-White (NFW)
profiles to background source orientations around the whole lens sample.
We also consider halos around
blue and red subsamples separately and constrain the scaling
of halo mass with light. For the NFW model, we find virial masses
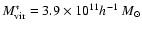 for blue and
for blue and
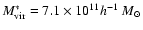 for red
galaxies of
for red
galaxies of
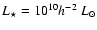 ,
respectively. The 1-
,
respectively. The 1-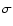 uncertainty on
uncertainty on
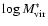 for the whole lens
sample is about 0.2.
We compare our results to those obtained from the Red-Sequence
Cluster Survey (RCS) and the Sloan Digital Sky Survey
(SDSS). Taking differences in the actual modelling into account, we
find very good agreement with these surveys.
for the whole lens
sample is about 0.2.
We compare our results to those obtained from the Red-Sequence
Cluster Survey (RCS) and the Sloan Digital Sky Survey
(SDSS). Taking differences in the actual modelling into account, we
find very good agreement with these surveys.
Key words: gravitational lensing - galaxies:
fundamental parameters - galaxies: statistics - cosmology: dark
matter
1 Introduction
Dark matter is the dominant mass component in the universe and
also the major constituent of cosmological structures like galaxy
clusters or galaxies. Therefore, dark matter plays a fundamental
role in the formation and evolution of these structures. Our
understanding of structure formation is thus limited by our
ability to map the dark matter distribution in these objects. In
this paper, we will investigate the dark matter distribution
around galaxies.
Several methods have been applied to measure masses of galaxies:
rotation curves of spiral galaxies provided the first evidence for
dark matter in galaxies (e.g. Sofue & Rubin 2001). In elliptical
galaxies, the dynamics of e.g. the stellar population itself,
globular clusters or planetary nebulae can be used
(e.g. Danziger 1997). However, these methods can only be
applied over radii where luminous tracers are available (a few
tens of kpc) and suffer from typical problems of dynamical
studies, e.g. the unknown degree of anisotropy (Rix et al. 1997).
In a few cases it is possible to measure masses from X-rays or,
within the Einstein radius, from strong lensing
(e.g. Kochanek et al. 2004).
Only two methods are currently in use to probe dark matter halos
of galaxies at scales of about
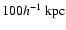 or
larger: weak gravitational lensing and the dynamics of satellite
galaxies. At these scales, the baryonic contribution to the mass
is negligible, so that basically just the dark matter around
galaxies is probed. In the beginning, satellite dynamics was only
applied to isolated spiral galaxies
(Zaritsky & White 1994; Zaritsky et al. 1997,1993). Later, early-type
galaxies were investigated
(Prada et al. 2003; McKay et al. 2002; Brainerd & Specian 2003; Conroy et al. 2005), and now
galaxies in denser environments and at much fainter magnitudes are
also studied (van den Bosch et al. 2004). Weak gravitational lensing
has become a standard tool in recent years. Its main advantage
over satellite dynamics it that no assumptions on the dynamical
state of the galaxies under consideration have to be made.
or
larger: weak gravitational lensing and the dynamics of satellite
galaxies. At these scales, the baryonic contribution to the mass
is negligible, so that basically just the dark matter around
galaxies is probed. In the beginning, satellite dynamics was only
applied to isolated spiral galaxies
(Zaritsky & White 1994; Zaritsky et al. 1997,1993). Later, early-type
galaxies were investigated
(Prada et al. 2003; McKay et al. 2002; Brainerd & Specian 2003; Conroy et al. 2005), and now
galaxies in denser environments and at much fainter magnitudes are
also studied (van den Bosch et al. 2004). Weak gravitational lensing
has become a standard tool in recent years. Its main advantage
over satellite dynamics it that no assumptions on the dynamical
state of the galaxies under consideration have to be made.
Galaxy-galaxy lensing is the technique which uses the image
distortions of background galaxies to study the mass distribution
in foreground galaxies. Galaxy-galaxy lensing and satellite
dynamics are independent methods and it is very desirable to have
both methods available for comparison of results. Weak
gravitational lensing is similar to the use of satellite dynamics
in the sense that only statistical investigations are possible due
to the weakness of the gravitational shear and the small number of
satellites per primary galaxy. The most recent results from both
techniques are summarized in Brainerd (2004).
Galaxy-galaxy lensing was measured for the first time by
Brainerd et al. (1996). In early work, people concentrated on
isothermal models for describing the lenses
(Hoekstra et al. 2003; Brainerd et al. 1996; Griffiths et al. 1996; Wilson et al. 2001; Hudson et al. 1998; dell'Antonio & Tyson 1996; Fischer et al. 2000; Smith et al. 2001).
The best-constrained parameter was the effective halo velocity
dispersion for 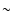
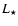 galaxies, assuming a scaling
relation between the velocity dispersion and the luminosity
according to the Tully-Fisher and Faber-Jackson relations. The
Tully-Fisher index
galaxies, assuming a scaling
relation between the velocity dispersion and the luminosity
according to the Tully-Fisher and Faber-Jackson relations. The
Tully-Fisher index 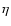 in this relation (see Sect. 4) was typically assumed according to measurements
from the central parts of the galaxies. Only Hudson et al. (1998)
were able to put at least a lower limit on
in this relation (see Sect. 4) was typically assumed according to measurements
from the central parts of the galaxies. Only Hudson et al. (1998)
were able to put at least a lower limit on 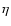 .
More generally,
the galaxy-mass correlation function was later investigated
(Sheldon et al. 2004; McKay et al. 2001) and the Navarro-Frenk-White (NFW)
profile was considered (Hoekstra et al. 2004; Seljak 2002; Guzik & Seljak 2002).
The Sloan Digital Sky Survey (SDSS) has turned out to be extremely
powerful for galaxy-galaxy lensing studies
(Seljak 2002; Sheldon et al. 2004; Seljak et al. 2005; McKay et al. 2001; Fischer et al. 2000; Guzik & Seljak 2002).
Most of its success is due to the fact that the SDSS provides a
large sample of lens galaxies with measured spectra. The spectra
provide very accurate redshifts and classification of the lens
galaxies. Therefore, it is possible to measure dark matter halos
as function of luminosity, spectral type or environment of the
galaxies. However, the SDSS is a very shallow survey and is thus
only able to measure lens galaxies around
.
More generally,
the galaxy-mass correlation function was later investigated
(Sheldon et al. 2004; McKay et al. 2001) and the Navarro-Frenk-White (NFW)
profile was considered (Hoekstra et al. 2004; Seljak 2002; Guzik & Seljak 2002).
The Sloan Digital Sky Survey (SDSS) has turned out to be extremely
powerful for galaxy-galaxy lensing studies
(Seljak 2002; Sheldon et al. 2004; Seljak et al. 2005; McKay et al. 2001; Fischer et al. 2000; Guzik & Seljak 2002).
Most of its success is due to the fact that the SDSS provides a
large sample of lens galaxies with measured spectra. The spectra
provide very accurate redshifts and classification of the lens
galaxies. Therefore, it is possible to measure dark matter halos
as function of luminosity, spectral type or environment of the
galaxies. However, the SDSS is a very shallow survey and is thus
only able to measure lens galaxies around
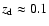 .
The question of halo properties at higher redshift and of
evolution cannot be addressed. Therefore, substantial effort goes
into measurements of galaxy-galaxy lensing at higher redshift with
at least rough redshift estimates for the lenses from e.g. photometric redshifts. Currently available are the Hubble Deep
Fields which are far too small to provide statistically clean
samples free from cosmic variance. Wilson et al. (2001) addressed
the question of evolution, but only for early-type galaxies.
Hoekstra et al. (2003) had redshifts available for part of their
lenses, but not yet enough to split the lenses into subsamples and
to study their properties separately. Hoekstra et al. (2004) use the
larger Red-Sequence Cluster Survey (RCS) with deep observations.
No redshift or color information is available, yet, so that again
only properties averaged over all classes of galaxies can be
investigated.
.
The question of halo properties at higher redshift and of
evolution cannot be addressed. Therefore, substantial effort goes
into measurements of galaxy-galaxy lensing at higher redshift with
at least rough redshift estimates for the lenses from e.g. photometric redshifts. Currently available are the Hubble Deep
Fields which are far too small to provide statistically clean
samples free from cosmic variance. Wilson et al. (2001) addressed
the question of evolution, but only for early-type galaxies.
Hoekstra et al. (2003) had redshifts available for part of their
lenses, but not yet enough to split the lenses into subsamples and
to study their properties separately. Hoekstra et al. (2004) use the
larger Red-Sequence Cluster Survey (RCS) with deep observations.
No redshift or color information is available, yet, so that again
only properties averaged over all classes of galaxies can be
investigated.
Here, we will use the COMBO-17 survey which is a deep survey, that
provides accurate photometric redshifts and spectral
classification from observations in a total of 17 filters
(Wolf et al. 2003,2004,2001). This data set allows us to
probe lens galaxies at higher redshift (
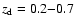 ),
to derive the relation between luminosity and velocity dispersion
(or mass) instead of assuming it and to measure dark matter halos
for blue and red galaxies separately. In addition to the singular
isothermal sphere (SIS) we will also apply the NFW profile
(Navarro et al. 1995,1996,1997).
),
to derive the relation between luminosity and velocity dispersion
(or mass) instead of assuming it and to measure dark matter halos
for blue and red galaxies separately. In addition to the singular
isothermal sphere (SIS) we will also apply the NFW profile
(Navarro et al. 1995,1996,1997).
This paper is organized as follows: in Sect. 2 we
briefly describe the data set and in Sect. 3 our
method of measuring galaxy-galaxy lensing. Section 4
gives our results from the SIS model and Sect. 5
those from the NFW profile. In Sect. 6 we
investigate how our measurements are affected by the presence of
large foreground clusters in one of the survey fields. In Sect. 7 we will compare our results to those from the
RCS and the SDSS. We close with a summary in Sect. 8. Throughout the paper we assume
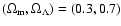 and
and
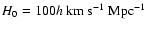 .
.
2 Data
Our analysis is based on the COMBO-17 survey.
COMBO-17, "Classifying Objects by Medium-Band Observations in 17 filters'',
comprises observations in five broad-band filters
(UBVRI) and 12 medium-band filters that are used to derive
reliable classification and redshift estimates for objects down to
R=24. Extensive comparison with spectroscopic redshifts from
YVDS (Le Fèvre et al. 2005) has shown that the median precision of
the COMBO-17 redshift estimates is
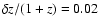 (Wolf et al. 2004).
(Wolf et al. 2004).
COMBO-17 covers three disjoint fields of
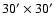 each. Only one
of the survey fields is a "random field''; a second is centered on
the Chandra Deep Field South, and the third was chosen to study
the supercluster system Abell 901a/b, Abell 902 and represents
thus an overdense line-of-sight. In Sect. 6 we
will investigate the influence of the supercluster system on the
galaxy-galaxy lensing measurement. The average of these three
fields should not be too far from cosmic average.
each. Only one
of the survey fields is a "random field''; a second is centered on
the Chandra Deep Field South, and the third was chosen to study
the supercluster system Abell 901a/b, Abell 902 and represents
thus an overdense line-of-sight. In Sect. 6 we
will investigate the influence of the supercluster system on the
galaxy-galaxy lensing measurement. The average of these three
fields should not be too far from cosmic average.
The data set used here is exactly the same as in the
method-focused companion paper Kleinheinrich et al. (2005).
We refer the reader to this paper for details on
the COMBO-17 survey and the shape measurements and
just summarize the most relevant points. The
COMBO-17 (Wolf et al. 2003, 2004) project provided deep
R-band imaging (
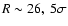 )
at a seeing of
(
)
at a seeing of
(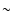
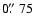 )
over three disjoint fields of about 0.26 square
degrees each, along with redshift estimates
from 17 band photometry, which are accurate to
)
over three disjoint fields of about 0.26 square
degrees each, along with redshift estimates
from 17 band photometry, which are accurate to
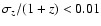 (at R<21) and to
(at R<21) and to
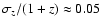 at the redshift sample limit of
at the redshift sample limit of
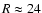 .
The R-band images, which are the basis of the
image shape measurements for the lensing analysis, were augmented
with public archival ESO data, and reduced with a pipeline that
was optimized for weak lensing (Schirmer et al. 2003).
Shapes, expressed by the complex ellipticity
.
The R-band images, which are the basis of the
image shape measurements for the lensing analysis, were augmented
with public archival ESO data, and reduced with a pipeline that
was optimized for weak lensing (Schirmer et al. 2003).
Shapes, expressed by the complex ellipticity 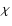 ,
were measured with a variant of the KSB algorithm (Luppino & Kaiser 1997; Kaiser et al. 1995; Hoekstra et al. 2000), as implemented by Erben et al. (2001).
,
were measured with a variant of the KSB algorithm (Luppino & Kaiser 1997; Kaiser et al. 1995; Hoekstra et al. 2000), as implemented by Erben et al. (2001).
![\begin{figure}
\par\includegraphics[width=6cm,clip]{2606fi1a.ps}\hspace*{3mm}
\includegraphics[width=6cm,clip]{2606fi1b.ps} \end{figure}](/articles/aa/full/2006/32/aa2606-04/Timg43.gif) |
Figure 1:
Left panel: averaged tangential shear
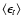 as a
function of projected separation between lens and source; right panel: same as left panel
but sources being rotated by 45 degrees.
as a
function of projected separation between lens and source; right panel: same as left panel
but sources being rotated by 45 degrees. |
| Open with DEXTER |
2.1 Tangential shear measurement
Before presenting our more rigorous analysis of the COMBO-17 data,
exploiting the full reshift and lens luminosity information in the data,
we show in Fig. 1 a measurement of the mean tangential shear.
This estimator has long been used to present a weak lensing signal
(e.g. Brainerd et al. 1996).
The shear estimates in the left panel of Fig. 1 were obtained
as follows: we selected as lenses
all galaxies in the magnitude range R=18-22 (Vega) with redshift
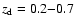 ,
as sources all galaxies with R=18-24 and
,
as sources all galaxies with R=18-24 and
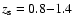 and considered only lens-source pairs
with separations
and considered only lens-source pairs
with separations
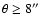 (see Sect. 3.1).
The tangential shear of a given source, at position
(see Sect. 3.1).
The tangential shear of a given source, at position
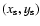 and with psf-corrected ellipticity
and with psf-corrected ellipticity
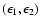 ,
relative to a given lens at
position
,
relative to a given lens at
position
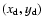 is defined as
is defined as
![$\epsilon_t=-[\epsilon_1 \cos~(2\alpha) +\epsilon_2 \sin~(2\alpha)]$](/articles/aa/full/2006/32/aa2606-04/img49.gif) ,
where
,
where
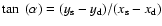 .
.
We bin the lens-source pairs by their projected separation r at the redshift of the
lens and calculate a weighted mean tangential shear
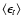 for
all pairs per bin. The weighting takes into account only the noise in the
psf-corrected ellipticities
for
all pairs per bin. The weighting takes into account only the noise in the
psf-corrected ellipticities 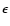 of the sources. The weight of each source
is taken as the inverse of the variance
of the sources. The weight of each source
is taken as the inverse of the variance
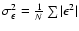 of the N=20 objects being closest to the source in
of the N=20 objects being closest to the source in 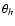 - S/N space. Here,
- S/N space. Here,
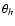 is the half-light radius and S/N is the signal-to-noise of the source - see
Erben et al. (2001) and Kleinheinrich et al. (2005) for details on this weighting scheme.
In particular, no weighting according to the luminosity of the lens is applied. The error
bars are obtained from repeating this measurement a hundred times with randomized
source orientations.
is the half-light radius and S/N is the signal-to-noise of the source - see
Erben et al. (2001) and Kleinheinrich et al. (2005) for details on this weighting scheme.
In particular, no weighting according to the luminosity of the lens is applied. The error
bars are obtained from repeating this measurement a hundred times with randomized
source orientations.
The right panel of Fig. 1 was obtained in the same way as the left panel, but after
rotating the sources by 45 degrees. The signal is consistent with zero indicating that the
measured tangential shear is indeed due to gravitational lensing.
Note that we do not use the measurement of the mean tangential shear in our actual
analysis of the data, as this approach does not exploit e.g. the redshift
and luminosity information we have for lenses.
However, the plots shown in Fig. 1 might be helpful
for comparison with results from other data sets.
3 Method
To quantify statistically the shear induced
into background images by foreground galaxy halos (the
"galaxy-galaxy lensing'') we use the maximum-likelihood method
proposed by Schneider & Rix (1997). Assuming a specific halo lens
model one can compute the shear
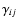 on each source jfrom each lens i. In practise, we use only those lenses whose
projected separation r at the redshift of the lens does not exceed
a given
on each source jfrom each lens i. In practise, we use only those lenses whose
projected separation r at the redshift of the lens does not exceed
a given
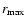 .
Sources too close to the field
boundaries, which might be lensed by galaxies outside the area of
the data set, are excluded.
.
Sources too close to the field
boundaries, which might be lensed by galaxies outside the area of
the data set, are excluded.
Because the shear from individual galaxies is weak and because
several halos may contribute comparably to the shear of a given
source position we sum the shear contribution from different
lenses to derive the total shear acting on source j:
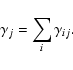 |
(1) |
From the shear and the observed, psf-corrected ellipticity
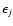 one can estimate the intrinsic ellipticity
one can estimate the intrinsic ellipticity
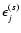 ,
,
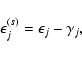 |
(2) |
observed in the absence of lensing. Note that the ellipticity in
this notation is a vector in the complex plane that also encodes
the position angle of an elongated image. The probability for
observing this intrinsic ellipticity is given by
![\begin{displaymath}
P\left(\epsilon_{j}^{(s)}\right)=\frac{1}{\pi\sigma_{\epsilo...
...ert\epsilon_{j}^{(s)}\vert^{2}}{\sigma_{\epsilon}^{2}}\right]}
\end{displaymath}](/articles/aa/full/2006/32/aa2606-04/img59.gif) |
(3) |
where
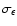 is the width of the intrinsic ellipticity
distribution and the dependence on the absolute value only encodes
an isotropic orientation of projected orientation. Multiplying the
probabilities from all sources gives the likelihood for a given
set of parameters of the lens model. The value of
is the width of the intrinsic ellipticity
distribution and the dependence on the absolute value only encodes
an isotropic orientation of projected orientation. Multiplying the
probabilities from all sources gives the likelihood for a given
set of parameters of the lens model. The value of
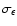 must be estimated for each source individually,
because it depends on its signal-to-noise and half-light radius,
see Sect. 2.1 and Kleinheinrich et al. (2005) for details; typical values are
must be estimated for each source individually,
because it depends on its signal-to-noise and half-light radius,
see Sect. 2.1 and Kleinheinrich et al. (2005) for details; typical values are
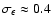 .
.
In this approach the most likely model is one that produces
shear-corrected source orientations that are isotropically
oriented.
Note that in this modelling approach the common statistic of
shear strength vs. projected radius (shown in Fig. 1)
is never used,
as we use a S/N-optimized individual shear estimate for each image,
which depends on the global lens model.
3.1 Lens and source selection
With the COMBO-17 data set we can select lenses and sources based
on their redshifts. We only use objects classified as galaxies or
likely galaxies by COMBO-17. Both lenses and sources lie in the
magnitude range R=18-24 (Vega). The bright limit was set to avoid
saturation, while the faint limit is given by the magnitude limit
down to which the classification and redshift estimation in COMBO-17
works reliably. Note that with such redshifts we are able to include
faint lenses and bright sources.
Our lens sample consists of all galaxies with redshift
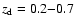 .
Lenses with higher redshifts would not add
much to the constraints because only a small number of sources
would lie behind them. Lenses at smaller redshifts are excluded
because for them a given
.
Lenses with higher redshifts would not add
much to the constraints because only a small number of sources
would lie behind them. Lenses at smaller redshifts are excluded
because for them a given
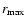 corresponds to a
large angular separation
corresponds to a
large angular separation 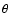 .
Because we exclude all sources
for which lenses might lie outside the field boundaries we would
therefore have to exclude too many sources.
.
Because we exclude all sources
for which lenses might lie outside the field boundaries we would
therefore have to exclude too many sources.
![\begin{figure}
\par\includegraphics[angle=-90,width=6cm,clip]{2606fi2a.ps}\hspace*{3mm}
\includegraphics[angle=-90,width=6cm,clip]{2606fi2b.ps} \end{figure}](/articles/aa/full/2006/32/aa2606-04/Timg64.gif) |
Figure 2:
Constraints on the velocity dispersion
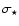 and the
Tully-Fisher index
and the
Tully-Fisher index 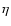 for the SIS model with
for the SIS model with
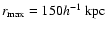 using all lenses ( left panel)
and subsamples of blue and red lenses ( right panel). Contours are 1-, 2-
and 3-
using all lenses ( left panel)
and subsamples of blue and red lenses ( right panel). Contours are 1-, 2-
and 3-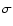 . . |
| Open with DEXTER |
We chose sources with individual redshift estimates in the redshift
range
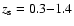 ,
although in principle we could also
include sources for which only statistical
redshifts are available. However, in Kleinheinrich et al. (2005) we
found that the inclusion of these sources does not improve the
constraints, probably because sources that are too faint to get
individual redshift estimates also have too noisy shape
measurements. A potential lens-source pair is only evaluated if
,
although in principle we could also
include sources for which only statistical
redshifts are available. However, in Kleinheinrich et al. (2005) we
found that the inclusion of these sources does not improve the
constraints, probably because sources that are too faint to get
individual redshift estimates also have too noisy shape
measurements. A potential lens-source pair is only evaluated if
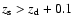 .
The minimum redshift difference
of dz=0.1 is chosen to remove pairs where, due to redshift
errors, the source is actually in front of the lens or physically
close to it. Thus, we minimize the contamination from intrinsic
alignments (King & Schneider 2002; Heymans & Heavens 2003).
.
The minimum redshift difference
of dz=0.1 is chosen to remove pairs where, due to redshift
errors, the source is actually in front of the lens or physically
close to it. Thus, we minimize the contamination from intrinsic
alignments (King & Schneider 2002; Heymans & Heavens 2003).
In the absence of survey image edges and systematic shape measurement
errors, there is no a priori need to set a value for
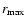 ;
the large number of images with tiny shear contributions from a given
lens galaxy should still add signal to the estimate. However, in
practice a choice of
;
the large number of images with tiny shear contributions from a given
lens galaxy should still add signal to the estimate. However, in
practice a choice of
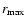 is sensible for a variety of
reasons. First, a SIS model has a diverging cumulative mass profile
that is unphysical. Second, a very large value of
is sensible for a variety of
reasons. First, a SIS model has a diverging cumulative mass profile
that is unphysical. Second, a very large value of
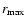 excludes too many source images from the analysis due to edge effects.
Third, at separations of
excludes too many source images from the analysis due to edge effects.
Third, at separations of 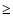
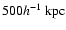 our underlying
halo model assumption, that halos are spherical, isolated and
spatially uncorrelated, breaks down. Therefore, we probe lens galaxy
halos out to some projected, physical distance
our underlying
halo model assumption, that halos are spherical, isolated and
spatially uncorrelated, breaks down. Therefore, we probe lens galaxy
halos out to some projected, physical distance
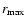 from
their center. With individual lens redshifts, this can be converted to
an angular separation
from
their center. With individual lens redshifts, this can be converted to
an angular separation
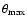 that can vary among
different lens-source pairs. When working with the SIS model
(Sect. 4) we use
that can vary among
different lens-source pairs. When working with the SIS model
(Sect. 4) we use
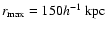 ,
,
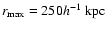 and
and
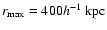 .
Note that for radii larger
than
.
Note that for radii larger
than
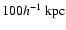 ,
there is evidence (e.g. Prada et al. 2003)
from satellite dynamics, that a SIS is a poor approximation to the dark
matter profile. When modelling the lenses by NFW profiles we use a maximum
separation of
,
there is evidence (e.g. Prada et al. 2003)
from satellite dynamics, that a SIS is a poor approximation to the dark
matter profile. When modelling the lenses by NFW profiles we use a maximum
separation of
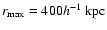 to ensure that
the region around the virial radius is probed even for the most massive
galaxies.
to ensure that
the region around the virial radius is probed even for the most massive
galaxies.
Shapes can only be measured reliably if objects do not have nearby
images. Therefore, we only use lens-source pairs with a
minimum angular separation
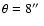 .
At
.
At
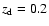 this translates into a physical separation
this translates into a physical separation
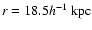 ,
at
,
at
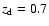 into
into
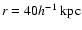 .
.
In addition to fitting halo properties by averaging over all lenses, we
will also consider blue and red subsamples based on rest-frame
colors. The definitions of "red'' and "blue'' are based on the "red
sequence'' of galaxies in the color-luminosity plane, found to be
present to 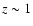 in COMBO-17 (Bell et al. 2004). Galaxies with
in COMBO-17 (Bell et al. 2004). Galaxies with
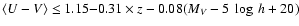 define the blue sample
while all other galaxies are in the red sample (Bell et al. 2004).
In total, our data set contains 11 230 blue and 2580 red lens
candidates. The average redshift and SDSS r-band rest-frame
luminosities are
define the blue sample
while all other galaxies are in the red sample (Bell et al. 2004).
In total, our data set contains 11 230 blue and 2580 red lens
candidates. The average redshift and SDSS r-band rest-frame
luminosities are
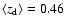 and
and
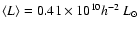 for the blue
sample and
for the blue
sample and
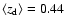 and
and
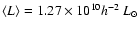 for the red sample,
respectively.
for the red sample,
respectively.
4 Results from the SIS model
The density distribution of the SIS is given by
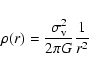 |
(4) |
where
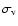 is the velocity dispersion of a galaxy. Because in our
galaxy-galaxy lensing analysis we have to average over lenses
with a range of luminosities, we use Faber-Jackson and
Tully-Fisher-like relations between the SIS velocity dispersion and
luminosity:
is the velocity dispersion of a galaxy. Because in our
galaxy-galaxy lensing analysis we have to average over lenses
with a range of luminosities, we use Faber-Jackson and
Tully-Fisher-like relations between the SIS velocity dispersion and
luminosity:
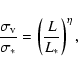 |
(5) |
where 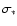 is the velocity dispersion of an L* galaxy. We
use
is the velocity dispersion of an L* galaxy. We
use
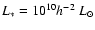 measured in the SDSS r-band. For the
Faber-Jackson and Tully-Fisher relations, which refer to the inner
measured in the SDSS r-band. For the
Faber-Jackson and Tully-Fisher relations, which refer to the inner
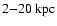 ,
a scaling index of
,
a scaling index of
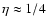 or
or
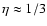 is found.
is found.
The (aperture) mass-to-light ratio of the galaxies is determined
by 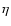 :
:
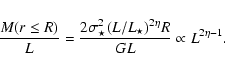 |
(6) |
So for 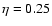 one has
one has
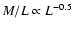 inside a fixed
aperture while
inside a fixed
aperture while
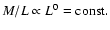 requires
requires
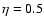 .
.
For each lens-source pair the shear amplitude is given by
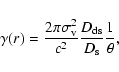 |
(7) |
resulting in an image stretch perpendicular to the projected lens-source
direction.
The left panel of Fig. 2 shows likelihood contours (the
product of all terms as in Eq. (3))
when all lenses are used and
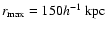 is
adopted. The best-fit parameters (with their 68%
confidence regions) are
is
adopted. The best-fit parameters (with their 68%
confidence regions) are
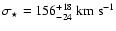 and
and
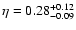 .
These estimates for the halo properties agree very well with values
for the stellar body from the Tully-Fisher or Faber-Jackson relation,
although the radial scale
probed here is an order of magnitude larger. The (aperture)
mass-to-light ratio scales with luminosity as
.
These estimates for the halo properties agree very well with values
for the stellar body from the Tully-Fisher or Faber-Jackson relation,
although the radial scale
probed here is an order of magnitude larger. The (aperture)
mass-to-light ratio scales with luminosity as
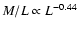 .
The mass-to-light ratio at fixed radius therefore
decreases with increasing luminosity.
.
The mass-to-light ratio at fixed radius therefore
decreases with increasing luminosity.
Table 1:
Results for the SIS model for different lens samples and
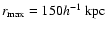 .
.
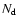 ,
,
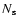 and
and 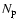 are the numbers of lenses, sources and
pairs in each measurement. Note that the number of sources can vary for
different lens selections because not all source candidates are always lying
within
are the numbers of lenses, sources and
pairs in each measurement. Note that the number of sources can vary for
different lens selections because not all source candidates are always lying
within
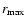 of a lens. The best fit values of
of a lens. The best fit values of 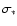 and
and
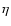 are given with 1-
are given with 1-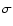 error bars. The last two columns give the
aperture mass within
error bars. The last two columns give the
aperture mass within
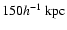 and the corresponding
mass-to-light ratio.
and the corresponding
mass-to-light ratio.
We also explored values of
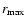 larger than
larger than
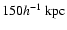 .
For
.
For
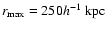 we find
we find
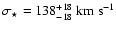 and
and
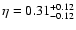 while for
while for
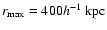 we find
we find
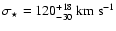 and
and
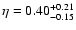 .
There is a clear decrease in
.
There is a clear decrease in
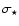 when larger scales of the galaxy halos are probed.
Further, we see a systematic increase of
when larger scales of the galaxy halos are probed.
Further, we see a systematic increase of 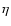 with scale. These
trends of
with scale. These
trends of
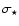 and
and 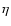 with scale show that the model
adopted here to describe the lenses is too simple. Several causes
are possible: the density profiles of dark matter halos might
decline more steeply than r-2 as also implied by satellite
dynamics (Prada et al. 2003). Alternatively, the environment of the lens
galaxies might contribute differently on different scales or the
contribution of different subclasses of lenses might change with
scale. This all clearly shows that when comparing results from
different galaxy-galaxy lensing studies it is important to compare
measurements obtained at similar scales.
with scale show that the model
adopted here to describe the lenses is too simple. Several causes
are possible: the density profiles of dark matter halos might
decline more steeply than r-2 as also implied by satellite
dynamics (Prada et al. 2003). Alternatively, the environment of the lens
galaxies might contribute differently on different scales or the
contribution of different subclasses of lenses might change with
scale. This all clearly shows that when comparing results from
different galaxy-galaxy lensing studies it is important to compare
measurements obtained at similar scales.
For
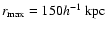 ,
the results of splitting the lens
sample into blue and red subsamples, according to the definition from
Bell et al. (2004), are shown in the right panel of Fig. 2 and in
Table 1. For the color-separated sample (right panel of Fig. 1)
we have ignored the (basically uncorrelated) shear contributions from the
lenses of the respectively other color-bin; however, we have verified that
a simultaneous fit of both sub-samples yields indistinguishable results.
The red sample contains only 20% of all lenses by
number but yields even tighter constraints than the fourfold larger blue
sample. This clearly demonstrates that the galaxy-galaxy lensing
signal is dominated by red galaxies. Furthermore, at a given luminosity
red galaxies have a larger velocity dispersion than blue
galaxies. The best-fit velocity dispersion at
,
the results of splitting the lens
sample into blue and red subsamples, according to the definition from
Bell et al. (2004), are shown in the right panel of Fig. 2 and in
Table 1. For the color-separated sample (right panel of Fig. 1)
we have ignored the (basically uncorrelated) shear contributions from the
lenses of the respectively other color-bin; however, we have verified that
a simultaneous fit of both sub-samples yields indistinguishable results.
The red sample contains only 20% of all lenses by
number but yields even tighter constraints than the fourfold larger blue
sample. This clearly demonstrates that the galaxy-galaxy lensing
signal is dominated by red galaxies. Furthermore, at a given luminosity
red galaxies have a larger velocity dispersion than blue
galaxies. The best-fit velocity dispersion at 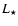 is about 40% larger
for red galaxies implying that their (aperture) mass is about
twice that of blue galaxies. The scaling
is about 40% larger
for red galaxies implying that their (aperture) mass is about
twice that of blue galaxies. The scaling 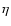 does not differ
between the two subsamples.
does not differ
between the two subsamples.
5 Results from the NFW profile
5.1 Model
The density distribution of the NFW profile
(Navarro et al. 1995,1996,1997) is given by
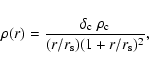 |
(8) |
where
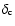 is a characteristic density,
is a characteristic density,
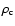 is the
critical cosmological density and
is the
critical cosmological density and 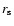 is a scale
radius. At
is a scale
radius. At
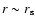 the density profile turns from
the density profile turns from
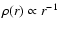 to
to
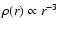 .
The virial radius
.
The virial radius
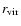 is defined as the radius inside
which the mean density is 200 times the mean density of the
universe. (NB: this is not the same definition of the virial radius
as the one based on 200 times the critical density of theuniverse.)
The mass inside the virial radius defines the virial mass
is defined as the radius inside
which the mean density is 200 times the mean density of the
universe. (NB: this is not the same definition of the virial radius
as the one based on 200 times the critical density of theuniverse.)
The mass inside the virial radius defines the virial mass
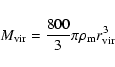 |
(9) |
with
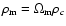 .
The ratio between virial radius und
scale radius is the concentration
.
The ratio between virial radius und
scale radius is the concentration
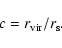 |
(10) |
From Eqs. (8)-(10) follows the
relation between the characteristic density and the concentration
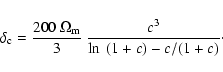 |
(11) |
In analogy to the Tully-Fisher and Faber-Jackson relations, which
imply a relation between luminosity and mass, we impose a similar
relation between the virial radius (a proxy for the virial mass)
and luminosity here,
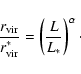 |
(12) |
The virial mass-to-light ratio is thus given by
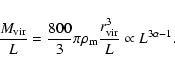 |
(13) |
A constant mass-to-light ratio
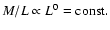 requires
requires
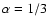 .
.
The shear from the NFW model is calculated in
Bartelmann (1996) and Wright & Brainerd (2000).
Formally, NFW profiles are a two-parameter family, e.g. with
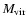 and c as possible choices. Yet, for a given cosmological
model (e.g.
and c as possible choices. Yet, for a given cosmological
model (e.g. 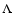 CDM), redshift (e.g.
CDM), redshift (e.g.
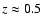 )
and halo mass
scale, N-body simulations show that c has only little scatter.
)
and halo mass
scale, N-body simulations show that c has only little scatter.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{2606fig3.ps} \end{figure}](/articles/aa/full/2006/32/aa2606-04/Timg137.gif) |
Figure 3:
Constraints on the virial radius
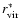 and the
concentration c for the NFW profile obtained from the full lens
sample with
and the
concentration c for the NFW profile obtained from the full lens
sample with
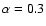 fixed and
fixed and
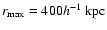 .
The viral radius .
The viral radius
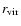 and
the concentration c are defined as detailed in Sect. 5.1.
and
the concentration c are defined as detailed in Sect. 5.1. |
| Open with DEXTER |
First, we try to constrain the virial radius
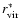 and the concentration c for a fixed
and the concentration c for a fixed 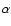 .
Figure
3 shows results for the whole lens sample with
.
Figure
3 shows results for the whole lens sample with
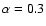 and
and
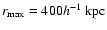 .
Using
.
Using 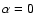 instead does not change the shape
of the contours but just shifts them toward lower values of
instead does not change the shape
of the contours but just shifts them toward lower values of
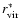 .
As Fig. 3 shows, weak lensing provides
only poor constraints on c: only a lower bound can be obtained.
The 1-
.
As Fig. 3 shows, weak lensing provides
only poor constraints on c: only a lower bound can be obtained.
The 1-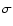 lower limit for c alone is c>29, the 2-
lower limit for c alone is c>29, the 2-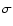 lower limit is c>11. In the following, we will use a fixed
lower limit is c>11. In the following, we will use a fixed
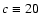 .
This choice is somewhat arbitrary. However, smaller values of c are
disfavoured by our data. We checked that assuming a smaller c does not
change the best-fit results of our fits but would increase the error bars
.
This choice is somewhat arbitrary. However, smaller values of c are
disfavoured by our data. We checked that assuming a smaller c does not
change the best-fit results of our fits but would increase the error bars![[*]](/icons/foot_motif.gif) .
.
Using all lenses,
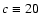 and
and
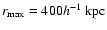 we obtain the likelihood contours shown in the left panel of
Fig. 4. The best-fit parameters with 1-
we obtain the likelihood contours shown in the left panel of
Fig. 4. The best-fit parameters with 1-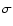 error bars are
error bars are
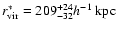 and
and
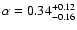 .
The corresponding virial mass is
.
The corresponding virial mass is
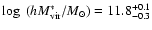 .
This mass estimate is considerably smaller than the mass estimate
from the SIS model (
.
This mass estimate is considerably smaller than the mass estimate
from the SIS model (
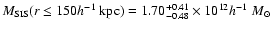 ,
see Table 1), although the
virial mass even encloses a larger radius than the aperture used
for the SIS model. Wright & Brainerd (2000) already pointed out that for
galaxy-sized halos the SIS model yields much larger mass estimates
than the NFW model. Decreasing
,
see Table 1), although the
virial mass even encloses a larger radius than the aperture used
for the SIS model. Wright & Brainerd (2000) already pointed out that for
galaxy-sized halos the SIS model yields much larger mass estimates
than the NFW model. Decreasing
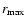 from
from
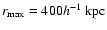 to
to
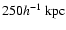 or
or
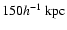 yields larger
yields larger
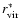 and smaller
and smaller 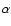 ,
,
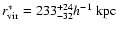 and
and
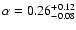 for
for
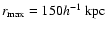 .
Unlike the SIS model, the
differences here are within the 1-
.
Unlike the SIS model, the
differences here are within the 1-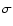 uncertainties.
Therefore, it seems that the NFW profile provides a better fit to
the data than the SIS model. However, the tendency to larger
virial radii for decreasing
uncertainties.
Therefore, it seems that the NFW profile provides a better fit to
the data than the SIS model. However, the tendency to larger
virial radii for decreasing
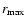 might indicate that
our modelling of NFW profiles also needs refinements.
might indicate that
our modelling of NFW profiles also needs refinements.
For the NFW model with
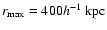 we
obtain a scaling of the virial mass-to-light ratio with luminosity
as
we
obtain a scaling of the virial mass-to-light ratio with luminosity
as
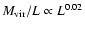 implying almost the same mass-to-light
ratio for all luminosities. In contrast, we find a decreasing
mass-to-light ratio at fixed radius with increasing luminosity for
the SIS model. However, the scaling relation found from the SIS
model is only marginally excluded at the 1-
implying almost the same mass-to-light
ratio for all luminosities. In contrast, we find a decreasing
mass-to-light ratio at fixed radius with increasing luminosity for
the SIS model. However, the scaling relation found from the SIS
model is only marginally excluded at the 1-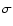 level by the
measurement from the NFW model.
level by the
measurement from the NFW model.
Analogously to the SIS case, we split the lens sample into a blue and
a red subsample; the results, using
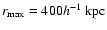 ,
are shown in the right panel of
Fig. 4 and in Table 2. We find that red galaxies
have a larger virial radius at a given luminosity
,
are shown in the right panel of
Fig. 4 and in Table 2. We find that red galaxies
have a larger virial radius at a given luminosity 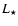 and a
larger
and a
larger 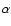 than blue galaxies. However, the significance of these
differences is only about 1
than blue galaxies. However, the significance of these
differences is only about 1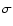 .
The larger virial radius for the red
galaxies implies a virial mass that is almost a factor of 2 larger
than that of equally luminous blue galaxies. Even within the virial
radius of the blue
.
The larger virial radius for the red
galaxies implies a virial mass that is almost a factor of 2 larger
than that of equally luminous blue galaxies. Even within the virial
radius of the blue 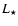 galaxies, the mass of red
galaxies, the mass of red 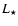 galaxies
is much larger,
galaxies
is much larger,
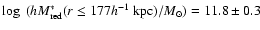 .
Formally, the best-fit mass-to-light ratios scale with luminosity
as
.
Formally, the best-fit mass-to-light ratios scale with luminosity
as
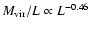 for blue galaxies and as
for blue galaxies and as
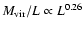 for red ones, but for both subsamples a
mass-to-light ratio independent of luminosity is consistent with the data.
for red ones, but for both subsamples a
mass-to-light ratio independent of luminosity is consistent with the data.
![\begin{figure}
\par\includegraphics[angle=-90,width=6.2cm,clip]{2606fi4a.ps}\hspace*{3mm}
\includegraphics[angle=-90,width=6.2cm,clip]{2606fi4b.ps} \end{figure}](/articles/aa/full/2006/32/aa2606-04/Timg153.gif) |
Figure 4:
Constraints on the virial radius
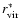 and its scaling
with luminosity (
and its scaling
with luminosity (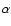 )
inside )
inside
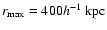 for the NFW profile using all lenses ( left
panel) and subsamples of blue and red lenses ( right panel). Contours are
1-, 2- and 3-
for the NFW profile using all lenses ( left
panel) and subsamples of blue and red lenses ( right panel). Contours are
1-, 2- and 3-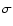 . . |
| Open with DEXTER |
Table 2:
Constraints on dark matter halos of galaxies modelled by
NFW profiles for different lens samples and
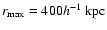 .
.
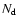 ,
,
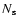 and
and
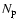 are the numbers of lenses, sources and pairs in each
measurement. These numbers differ from those given in Table 1
because of the larger
are the numbers of lenses, sources and pairs in each
measurement. These numbers differ from those given in Table 1
because of the larger
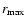 used here. The virial radius
used here. The virial radius
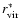 and
and 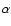 are fitted quantities (see Fig. 4), the virial mass
are fitted quantities (see Fig. 4), the virial mass
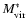 and the virial
mass-to-light ratio
and the virial
mass-to-light ratio
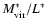 are calculated from
are calculated from
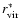 .
.
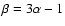 gives the scaling of
gives the scaling of
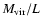 with luminosity,
with luminosity,
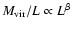 .
All errors are 1-
.
All errors are 1-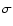 .
.
6 Influence of clusters
One of the COMBO-17 fields - the A 901 field - has been chosen
specifically to study the supercluster composed of the components
Abell 901a, 901b and 902 at a redshift of z=0.16(Gray et al. 2002,2004). Later, another cluster (named CBI in
Taylor et al. 2004) was detected behind Abell 902 using the 3D
distribution of galaxies. The masses of these four clusters were
measured jointly using weak lensing (Taylor et al. 2004). Table 3
shows central positions, redshifts and
velocity dispersions for the different clusters modelled as SISs.
We address in this section the influence of these clusters on our
galaxy-galaxy lensing measurements. Two measurements are compared:
one ignoring the presence of the clusters and one including the
shear from the clusters
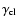 .
In the second case,
Eq. (2) becomes
.
In the second case,
Eq. (2) becomes
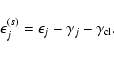 |
(14) |
The shear of the clusters is computed assuming isothermals spheres
(see Eq. (7)) with the parameters from Table 3.
The lens galaxies are also modelled as
isothermal spheres, see Sect. 4. Instead of using
the shear 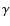 of the clusters we also tried using the reduced
shear
of the clusters we also tried using the reduced
shear
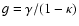 and including the magnification
and including the magnification
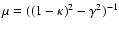 to correct the luminosities of
the lenses, the convergence
to correct the luminosities of
the lenses, the convergence 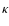 here, being calculated from
the SIS fits of the clusters. We found that the difference to just
using
here, being calculated from
the SIS fits of the clusters. We found that the difference to just
using 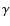 in both cases is negligible.
in both cases is negligible.
The S 11 field contains the cluster Abell 1364 at a redshift
z=0.11 for which we fit a velocity dispersion
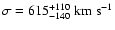 .
As for the foreground
clusters in the A 901 field, we compare measurements for the S 11
field, first including and then ignoring the cluster shear. We
find that the cluster shear is negligible for the S 11 field.
.
As for the foreground
clusters in the A 901 field, we compare measurements for the S 11
field, first including and then ignoring the cluster shear. We
find that the cluster shear is negligible for the S 11 field.
Table 3:
Central positions, redshifts and velocity dispersions of
the known
clusters in the A 901 field (Taylor et al. 2004).
Because only lens galaxies with
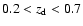 have been
considered, the lens sample should
contain no galaxies that lie in the foreground clusters
(Abell 901a/b, Abell 902). The expectation is that the foreground
clusters will not influence the galaxy-galaxy lensing measurements
because the shear from the foreground clusters will be in random
directions with respect to the orientations of the lens-source
pairs used for galaxy-galaxy lensing.
have been
considered, the lens sample should
contain no galaxies that lie in the foreground clusters
(Abell 901a/b, Abell 902). The expectation is that the foreground
clusters will not influence the galaxy-galaxy lensing measurements
because the shear from the foreground clusters will be in random
directions with respect to the orientations of the lens-source
pairs used for galaxy-galaxy lensing.
The left panel of Fig. 5 shows likelihood
contours obtained from the A 901 field both ignoring and including
the shear from the foreground clusters Abell 901a/b and Abell 902.
The shear from CBI is ignored. Hardly any difference is seen
between both cases, from which we measure
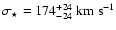 and
and
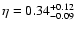 (1-
(1-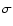 errors).
errors).
![\begin{figure}
\par\includegraphics[angle=-90,width=6.2cm,clip]{2606fi5a.ps}\hspace*{3mm}
\includegraphics[angle=-90,width=6.2cm,clip]{2606fi5b.ps} \end{figure}](/articles/aa/full/2006/32/aa2606-04/Timg178.gif) |
Figure 5:
Influence of the clusters shear on the galaxy-galaxy lensing
measurement. Solid lines refer to measurements ignoring the cluster
shear, dashed lines to measurements including the cluster shear. In the
left panel, only the foreground clusters Abell 901a/b and Abell 902 are
taken into account. In the right panel also the background cluster CBI is
used. A maximum projected separation between lenses and sources of
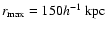 is used.
is used. |
| Open with DEXTER |
As a second test we ignore the cluster shear but exclude all
sources from the galaxy-galaxy lensing measurement for which the
convergence 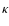 (and thus the shear
(and thus the shear 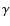 )
from the
foreground clusters exceeds some threshold. Figure
6 shows that from the foreground clusters
alone
)
from the
foreground clusters exceeds some threshold. Figure
6 shows that from the foreground clusters
alone
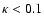 for almost all sources. The maximum is
for almost all sources. The maximum is
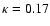 .
Therefore the weak shear limit is still valid in
Eq. (14). When excluding all sources with
.
Therefore the weak shear limit is still valid in
Eq. (14). When excluding all sources with
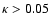 (224 out of 6481 sources), the difference to the
measurement using all sources is negligible. When excluding
further sources, the contours start to widen significantly but
maintain the same minimum. This widening can be explained by the
decreasing number statistics. In particular, we do not see any
hint of a bias from the clusters. When excluding the 22% of
sources with
(224 out of 6481 sources), the difference to the
measurement using all sources is negligible. When excluding
further sources, the contours start to widen significantly but
maintain the same minimum. This widening can be explained by the
decreasing number statistics. In particular, we do not see any
hint of a bias from the clusters. When excluding the 22% of
sources with
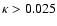 ,
the 3-
,
the 3-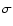 contour remains
closed. The best-fit parameters with 1-
contour remains
closed. The best-fit parameters with 1-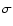 errors are then
errors are then
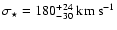 and
and
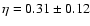 .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2606fig6.ps} \end{figure}](/articles/aa/full/2006/32/aa2606-04/Timg185.gif) |
Figure 6:
Histogram over  due to the foreground clusters only
(solid) and due to the foreground clusters and CBI together (dashed).
due to the foreground clusters only
(solid) and due to the foreground clusters and CBI together (dashed). |
| Open with DEXTER |
The cluster CBI has a redshift z=0.48 and therefore some of the
lens galaxies will reside in the cluster halo. This implies that
additional mass is present around these galaxies. Ignoring the
cluster CBI, this additional mass will be assigned to the galaxies
and thus the derived masses (or velocity dispersions) will be too
high. Guzik & Seljak (2002) modelled this case for the SDSS data. They
find from theoretical models that clusters increase the shear
measurements of galaxies. The strength of this effect depends on
the distance from the lens center, it increases from zero toward a
maximum around
 and then decreases
again. The peak contribution and the shape of the decrease depend
on the details of the model.
and then decreases
again. The peak contribution and the shape of the decrease depend
on the details of the model.
The right panel of Fig. 5 shows the same as the
left panel but this time includes the shear from CBI in the
cluster measurement. Although the change in the contours is
clearly visible, the shear from the background cluster CBI does
not seem to have a big influence; the contours only widen
marginally. The best-fit parameters with their 1- errors
become
errors
become
 and
and
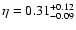 .
Note, however, that the resolution
of our grid in parameter space is only
.
Note, however, that the resolution
of our grid in parameter space is only
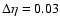 .
.
As a second test we again ignore the cluster shear and exclude
objects with large 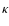 from both the foreground clusters and
CBI. Figure 6 shows a histogram of
from both the foreground clusters and
CBI. Figure 6 shows a histogram of
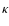 ,
the maximum of which is
,
the maximum of which is
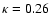 .
When excluding
all sources with
.
When excluding
all sources with
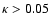 we obtain likelihood contours
similar to the case when including the cluster shear. 345 out of
6481 sources are then excluded. Excluding further sources results
in wider contours. The 3-
we obtain likelihood contours
similar to the case when including the cluster shear. 345 out of
6481 sources are then excluded. Excluding further sources results
in wider contours. The 3-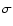 contour stays closed when we
exclude sources with
contour stays closed when we
exclude sources with
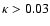 .
These are 22% of all sources
and the contours do not shift compared to the case where the
cluster shear is ignored.
.
These are 22% of all sources
and the contours do not shift compared to the case where the
cluster shear is ignored.
A third test is to exclude all lenses that are close to the center
of the background cluster CBI. We exclude every lens lying within
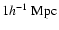 projected separation from the cluster center
(corresponding to
projected separation from the cluster center
(corresponding to
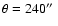 angular separation) and with
a redshift difference less than 0.2. These are 221 out of 4444 lenses.
The likelihood contours hardly change when these lenses
are excluded.
angular separation) and with
a redshift difference less than 0.2. These are 221 out of 4444 lenses.
The likelihood contours hardly change when these lenses
are excluded.
From all these tests we conclude that our results are not biased
from the presence of several clusters in the A 901 field. This
conclusion also holds when the SIS model is fitted within
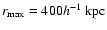 instead of
instead of
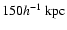 .
The little influence even the background
cluster CBI has might be surprising but it is understandable given
the small number of lenses that actually reside within this
cluster. In particular we note that the comparably large value of
.
The little influence even the background
cluster CBI has might be surprising but it is understandable given
the small number of lenses that actually reside within this
cluster. In particular we note that the comparably large value of
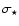 obtained from the A 901 field which is about
1-
obtained from the A 901 field which is about
1-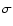 higher than from all three fields together is not
caused directly by the clusters. Instead, it seems that cosmic
variance is still an issue even on the scales of our survey
fields.
higher than from all three fields together is not
caused directly by the clusters. Instead, it seems that cosmic
variance is still an issue even on the scales of our survey
fields.
7 Comparison to other surveys
In this section, we compare our results to
those from previous galaxy-galaxy lensing studies. Any such comparison
is limited by the very different data sets and
techniques used in the different investigations. For our
comparison, we concentrate on results from the RCS
(Hoekstra et al. 2004) and the SDSS (Seljak et al. 2005; Guzik & Seljak 2002)
data.
7.1 Comparison to the RCS
The galaxy-galaxy lensing analysis
from the RCS (Hoekstra et al. 2004) is in many regards similar to
the one presented here and thus very suitable for a comparison of
results. Both surveys reach a comparable depth so that one can
expect that comparable sets of lens galaxies are probed. Further,
Hoekstra et al. (2004) use the maximum-likelihood technique by
Schneider & Rix (1997), model lenses as SISs and by NFW profiles
and fit to a fiducial lens galaxy with a characteristic luminosity
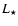 ,
just as we do. Note, in particular, that Hoekstra et al. (2004)
use the same definition of the virial radius of the NFW profile as we do
(see Sect. 5.1).
,
just as we do. Note, in particular, that Hoekstra et al. (2004)
use the same definition of the virial radius of the NFW profile as we do
(see Sect. 5.1).
However, crucial differences exist. The
area of the RCS used for the galaxy-galaxy lensing analysis is
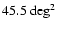 ,
so about 60 times larger than that used
here. On the other hand, Hoekstra et al. (2004) only have
observations in a single filter available. Therefore, they have to
select lenses and sources based on magnitude cuts and they have to
use redshift probability distributions for estimating luminosities
and for shear calibration. Furthermore, Hoekstra et al. (2004) can
only investigate lens galaxy halos on an angular scale while we are
able to probe the same physical scale of all lenses. Third, there is
no easy way to implement halo scalings with luminosity, nor to
separate lenses by their rest-frame color.
Hoekstra et al. (2004) fit their models within 2' which they
estimate corresponds to about
,
so about 60 times larger than that used
here. On the other hand, Hoekstra et al. (2004) only have
observations in a single filter available. Therefore, they have to
select lenses and sources based on magnitude cuts and they have to
use redshift probability distributions for estimating luminosities
and for shear calibration. Furthermore, Hoekstra et al. (2004) can
only investigate lens galaxy halos on an angular scale while we are
able to probe the same physical scale of all lenses. Third, there is
no easy way to implement halo scalings with luminosity, nor to
separate lenses by their rest-frame color.
Hoekstra et al. (2004) fit their models within 2' which they
estimate corresponds to about
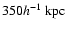 at the
mean redshift of the lenses. This is considerably larger than the
region we probe for the SIS model (
at the
mean redshift of the lenses. This is considerably larger than the
region we probe for the SIS model (
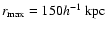 )
and comparable to the region probed for the
NFW profile (
)
and comparable to the region probed for the
NFW profile (
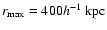 ). Another
difference lies in the definition of the fiducial luminosity. We
use
). Another
difference lies in the definition of the fiducial luminosity. We
use
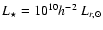 measured in the SDSS
r-band while Hoekstra et al. (2004) use
measured in the SDSS
r-band while Hoekstra et al. (2004) use
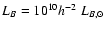 as reference. From our data set we
calculate that lenses with
as reference. From our data set we
calculate that lenses with
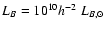 have
SDSS-r-band luminosities of about
have
SDSS-r-band luminosities of about
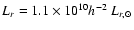 .
In Kleinheinrich et al. (2005) it is
shown for the SIS that it is not possible to constrain the scaling
relation between velocity dispersion and luminosity without
multi-color data. Therefore, Hoekstra et al. (2004) have to assume
this scaling relation unlike being able to fit it as we do.
.
In Kleinheinrich et al. (2005) it is
shown for the SIS that it is not possible to constrain the scaling
relation between velocity dispersion and luminosity without
multi-color data. Therefore, Hoekstra et al. (2004) have to assume
this scaling relation unlike being able to fit it as we do.
For better comparability with the RCS results we redo our fit to
the SIS model with
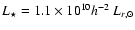 and
and
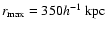 .
We obtain
.
We obtain
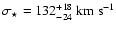 and
and
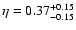 from the whole lens sample.
from the whole lens sample.
Hoekstra et al. (2004) do not specifically fit the SIS model using
the maximum-likelihood technique of Schneider & Rix (1997).
Instead, they fit the SIS model to the measured galaxy-mass
cross-correlation, and they constrain the truncated SIS model
using the maximum-likelihood technique. The velocity dispersion
obtained from the truncated SIS model becomes that of the SIS in
the limit of infinite truncation parameter s. In both cases,
Hoekstra et al. (2004) assume a scaling relation as in Eq. (5) with 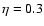 and a characteristic luminosity
and a characteristic luminosity
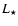 as detailed in Sect. 7.1. From
the galaxy-mass cross-correlation function they obtain
as detailed in Sect. 7.1. From
the galaxy-mass cross-correlation function they obtain
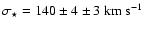 .
The truncated SIS yields
.
The truncated SIS yields
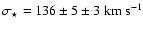 .
Both results are in good
agreement with our results. Conversely, we are able to confirm the
value of
.
Both results are in good
agreement with our results. Conversely, we are able to confirm the
value of 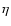 adopted by Hoekstra et al. (2004).
adopted by Hoekstra et al. (2004).
The error bars of Hoekstra et al. (2004) are about 5 times smaller
than ours. From the difference in area between the RCS and
COMBO-17 one would even expect a factor of about
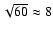 difference. That their error bars are not that much smaller can
be attributed to the detailed classification and redshifts
available in COMBO-17. In Kleinheinrich et al. (2005) it is shown
that the error bar on
difference. That their error bars are not that much smaller can
be attributed to the detailed classification and redshifts
available in COMBO-17. In Kleinheinrich et al. (2005) it is shown
that the error bar on
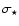 increases by about 30% when
redshifts are omitted. The influence of accurate redshift
estimates on the determination of
increases by about 30% when
redshifts are omitted. The influence of accurate redshift
estimates on the determination of 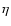 is found to be much more
severe - from just a single passband no meaningful constraints on
is found to be much more
severe - from just a single passband no meaningful constraints on
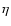 can be derived. This explains why we are able to fit
can be derived. This explains why we are able to fit 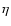 while Hoekstra et al. (2004) had to assume a fixed value.
while Hoekstra et al. (2004) had to assume a fixed value.
For better comparability with the RCS we also redo our fit to the
NFW profile with
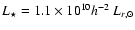 and
and
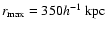 .
We obtain
.
We obtain
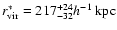 and
and
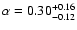 from the whole lens sample. This
corresponds to a virial mass
from the whole lens sample. This
corresponds to a virial mass
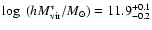 .
.
The exact modelling of Hoekstra et al. (2004) is somewhat different
from ours. While we fit the virial radius and its scaling with
luminosity, Hoekstra et al. (2004) assume scaling relations between
the maximum rotation velocity and virial mass, respectively, with
luminosity and fit the virial velocity
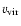 and the
scale radius rs. The virial velocity is directly related to the
virial mass and virial radius by
and the
scale radius rs. The virial velocity is directly related to the
virial mass and virial radius by
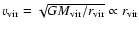 .
All three quantities are independent of the scale
radius rs. Therefore, we can readily compare our results on the
virial mass to those from Hoekstra et al. (2004). They find
.
All three quantities are independent of the scale
radius rs. Therefore, we can readily compare our results on the
virial mass to those from Hoekstra et al. (2004). They find
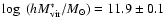 in good agreement with our result. Furthermore, their constraint
on the scale radius
in good agreement with our result. Furthermore, their constraint
on the scale radius
 is
roughly consistent with the scale radius implied by the virial
radius we find and the concentration we assume.
is
roughly consistent with the scale radius implied by the virial
radius we find and the concentration we assume.
7.2 Comparison to the SDSS
While COMBO-17 and the RCS are both
deep surveys from which lens galaxies at redshifts
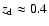 can be probed, the SDSS is a much
shallower survey with a correspondingly small average lens
redshift. To date, several observational weak lensing analyses
have been published investigating different aspects of dark matter
halos of galaxies and using consecutively larger parts of the
survey
(Seljak 2002; Sheldon et al. 2004; Seljak et al. 2005; McKay et al. 2001; Fischer et al. 2000; Guzik & Seljak 2002).
For the comparison to our results we will concentrate on the
results by Guzik & Seljak (2002).
can be probed, the SDSS is a much
shallower survey with a correspondingly small average lens
redshift. To date, several observational weak lensing analyses
have been published investigating different aspects of dark matter
halos of galaxies and using consecutively larger parts of the
survey
(Seljak 2002; Sheldon et al. 2004; Seljak et al. 2005; McKay et al. 2001; Fischer et al. 2000; Guzik & Seljak 2002).
For the comparison to our results we will concentrate on the
results by Guzik & Seljak (2002).
Guzik & Seljak (2002) use the halo model for their galaxy-galaxy
lensing analysis. This model takes not only the contribution from
galaxies themselves into account but also from the surrounding
group and cluster halos. This of course complicates the
comparison. On the other hand, Guzik & Seljak (2002) find that on
average only about 20% of the galaxies are non-central galaxies,
for which the group/cluster contribution is important. Therefore,
the group/cluster contribution to our mass estimates is probably
well within our error bars. Guzik & Seljak (2002) only fit NFW
profiles to their data. They define the virial radius as radius
inside which the mean density is 200 times the critical density of
the universe. Therefore, we have to multiply our virial masses by
a factor 0.79 to compare them to theirs. Similar to our approach,
Guzik & Seljak (2002) assume a relation between mass and luminosity
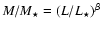 .
.
 and
and 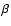 are derived
from different passbands. Here, we just compare to the results
from the r'-band in which the reference luminosity is
are derived
from different passbands. Here, we just compare to the results
from the r'-band in which the reference luminosity is
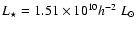 .
.
Assuming that group/cluster halos only contribute to the faintest
lens galaxies, Guzik & Seljak (2002) find a virial mass
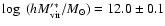 .
and
.
and
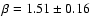 .
Our measurement of
.
Our measurement of
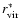 implies
for a galaxy with
implies
for a galaxy with
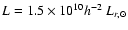 a virial
radius of
a virial
radius of
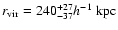 .
Here, we have used the measured
.
Here, we have used the measured
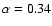 and ignored its
errors and still use our definition of the virial radius. Changing
to the definition adopted by Guzik & Seljak (2002) this corresponds to
a virial mass of
and ignored its
errors and still use our definition of the virial radius. Changing
to the definition adopted by Guzik & Seljak (2002) this corresponds to
a virial mass of
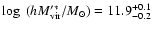 in very good agreement with the result from the SDSS. Our measurement
of
in very good agreement with the result from the SDSS. Our measurement
of
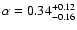 corresponds to
corresponds to
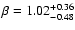 .
This is smaller than the value found
by Guzik & Seljak (2002) but the difference is not very significant.
When Guzik & Seljak (2002) assume the same group/cluster contribution
for all luminosity bins, their best-fit
.
This is smaller than the value found
by Guzik & Seljak (2002) but the difference is not very significant.
When Guzik & Seljak (2002) assume the same group/cluster contribution
for all luminosity bins, their best-fit 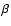 drops to
drops to
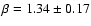 .
Therefore it might well be that the
differences between COMBO-17 and the SDSS concerning the scaling
between mass and light is due to the differences in the modelling.
.
Therefore it might well be that the
differences between COMBO-17 and the SDSS concerning the scaling
between mass and light is due to the differences in the modelling.
Guzik & Seljak (2002) also split the lens sample into early- and
late-type subsamples. Both samples contain about equal numbers.
This already indicates that these subsamples cannot be too similar
to our subsamples of red and blue galaxies in which only about
20% of all galaxies belong to the red subsample. However, we
should at least be able to see similar trends from late-type to
early-type galaxies as from blue to red ones. Guzik & Seljak (2002)
fix the scaling of the mass with luminosity to the value derived
for the whole lens sample (
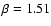 )
and also adopt the same
)
and also adopt the same
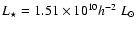 for both subsamples.
For late-type galaxies they find a virial mass of
for both subsamples.
For late-type galaxies they find a virial mass of 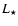 -galaxies of
-galaxies of
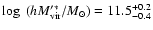 ,
for early-type galaxies they find
,
for early-type galaxies they find
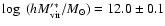 ,
We scale the virial radii of blue and red galaxies measured at
,
We scale the virial radii of blue and red galaxies measured at
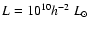 to the higher
to the higher 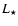 used by
Guzik & Seljak (2002) using the measured
used by
Guzik & Seljak (2002) using the measured 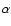 for the two samples
and calculate from that the virial masses assuming the same
definition as Guzik & Seljak (2002). We obtain
for the two samples
and calculate from that the virial masses assuming the same
definition as Guzik & Seljak (2002). We obtain
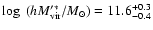 for the blue sample and
for the blue sample and
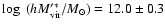 for the red sample. The agreement with the SDSS results is
surprisingly good given the different definitions of the
subsamples and the different lens redshifts. Most importantly,
from both surveys we see the same trend that early-type or red
galaxies have 2-3 times more massive halos than late-type or blue
galaxies at the same luminosity.
for the red sample. The agreement with the SDSS results is
surprisingly good given the different definitions of the
subsamples and the different lens redshifts. Most importantly,
from both surveys we see the same trend that early-type or red
galaxies have 2-3 times more massive halos than late-type or blue
galaxies at the same luminosity.
8 Summary
We have presented a galaxy-galaxy lensing
analysis of three fields from the COMBO-17 survey. Despite the
limited area, the data set is unique at intermediate redshift in
its extensive redshift information that allows us to separate the
12 000 lens
galaxies according to their physical properties such as luminosity
and rest-frame colors. Although one of these fields is centered
on a foreground supercluster, we have shown that our measurements
are not biased from the presence of the supercluster. In addition,
a cluster at z=0.48 behind the supercluster was also found to
have remarkably little influence.
Using a model to link lens galaxies to their dark matter halos, either
SIS or NFW, we constrained the halo parameters through galaxy-galaxy
lensing. For both halo models, we find that, at the same luminosity
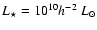 ,
red galaxies have dark matter halos
about twice as massive as blue ones. For SIS models within
,
red galaxies have dark matter halos
about twice as massive as blue ones. For SIS models within
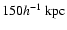 we obtain
we obtain
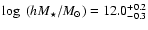 for blue galaxies and
for blue galaxies and
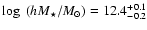 for red galaxies. Adopting NFW profiles we find virial masses
for red galaxies. Adopting NFW profiles we find virial masses
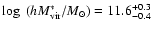 for blue galaxies and
for blue galaxies and
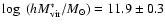 for red galaxies. Note that the virial masses are defined as
masses inside a sphere with mean density equal to 200 times the
mean density of the universe. For
for red galaxies. Note that the virial masses are defined as
masses inside a sphere with mean density equal to 200 times the
mean density of the universe. For
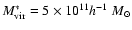 this
is about
this
is about
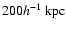 .
Changing this definition to the mass
inside a sphere with mean density equal to 200 times the critical
density of the universe would lower the virial masses by about
20%. The mass estimates from the SIS model are considerably
larger than from the NFW profile although the virial radii exceed
the aperture adopted for the mass estimate of the SISs. However,
it has been shown by Wright & Brainerd (2000) that such behaviour is
expected.
.
Changing this definition to the mass
inside a sphere with mean density equal to 200 times the critical
density of the universe would lower the virial masses by about
20%. The mass estimates from the SIS model are considerably
larger than from the NFW profile although the virial radii exceed
the aperture adopted for the mass estimate of the SISs. However,
it has been shown by Wright & Brainerd (2000) that such behaviour is
expected.
For both models, we also fit the scaling between mass and
luminosity. In the SIS model we find approximately the same
scaling for blue and red galaxies, about
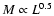 inside
inside
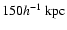 .
For the NFW model we find a
similar scaling relation for blue galaxies, but
.
For the NFW model we find a
similar scaling relation for blue galaxies, but
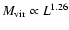 for red galaxies. The
differences between the two models and between the two subsamples
for the NFW model may arise from the different scales over which
the fitted mass-luminosity relation applies. For the SIS model it
is always fitted over a fixed aperture of
for red galaxies. The
differences between the two models and between the two subsamples
for the NFW model may arise from the different scales over which
the fitted mass-luminosity relation applies. For the SIS model it
is always fitted over a fixed aperture of
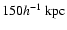 while for the NFW profile it only applies to the mass within the
virial radius that differs between blue and red galaxies.
while for the NFW profile it only applies to the mass within the
virial radius that differs between blue and red galaxies.
Finally, we compared our results to those obtained from the RCS
and the SDSS. We pointed out that for such a comparison it is
indispensable to compare results from similar modellings. As far
as possible we translated our measurements to the modelling approaches
of Hoekstra et al. (2004) for the RCS and Guzik & Seljak (2002) for the
SDSS and found consistent results. We deem this
remarkable, at least because the modelling of Guzik & Seljak (2002)
is very different from ours. A more exact comparison between
COMBO-17 and the SDSS adopting the same techniques is beyond the
scope of this paper, although such an investigation would be very
valuable. The fact that both surveys probe galaxies in different
redshift ranges would in principle allow a measurement of the
evolution of dark matter halos.
Acknowledgements
We thank the anonymous referee for helpful suggestions. C.W. was supported by a
PPARC Advanced Fellowship. M.K. acknowledges
support by the BMBF/DLR (project 50 OR 0106)), by the DFG under
the project SCHN 342/3-1, and by the DFG-SFB 439.
-
Bartelmann, M. 1996, A&A, 313, 697 [NASA ADS] (In the text)
- Bell, E. F.,
Wolf, C., Meisenheimer, K., et al. 2004, ApJ, 608, 752 [NASA ADS] [CrossRef] (In the text)
- Brainerd,
T. G. 2004, in The New Cosmology: Conference on Strings and
Cosmology, ed. R. E. Allen, D. V. Nanopoulos, &
C. N. Pope, AIP Conf. Proc., 743, 129
(In the text)
- Brainerd,
T. G., & Specian, M. A. 2003, ApJ, 593, L7 [NASA ADS] [CrossRef]
- Brainerd,
T. G., Blandford, R. D., & Smail, I. 1996, ApJ, 466,
623 [NASA ADS] [CrossRef] (In the text)
- Bullock,
J. S., Kolatt, T. S., Sigad, Y., et al. 2001, MNRAS,
321, 559 [NASA ADS] [CrossRef]
- Conroy, C.,
Newman, J. A., Davis, M., et al. 2005, ApJ, 635, 982 [NASA ADS] [CrossRef]
- Danziger,
I. J. 1997, in Dark and Visible Matter in Galaxies and
Cosmological Implications, ASP Conf. Ser., 117, 28
(In the text)
-
dell'Antonio, I. P., & Tyson, J. A. 1996, ApJ, 473,
L17 [NASA ADS] [CrossRef]
- Erben, T., Van
Waerbeke, L., Bertin, E., Mellier, Y., & Schneider, P. 2001,
A&A, 366, 717 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Fischer, P.,
McKay, T. A., Sheldon, E., et al. 2000, AJ, 120,
1198 [NASA ADS] [CrossRef]
- Gray, M. E.,
Taylor, A. N., Meisenheimer, K., et al. 2002, ApJ, 568,
141 [NASA ADS] [CrossRef]
- Gray, M. E.,
Wolf, C., Meisenheimer, K., et al. 2004, MNRAS, 347, L73 [NASA ADS] [CrossRef]
-
Griffiths, R. E., Casertano, S., Im, M., & Ratnatunga,
K. U. 1996, MNRAS, 282, 1159 [NASA ADS]
- Guzik, J., &
Seljak, U. 2002, MNRAS, 335, 311 [NASA ADS] [CrossRef]
- Heymans, C.,
& Heavens, A. 2003, MNRAS, 339, 711 [NASA ADS] [CrossRef]
- Hoekstra,
H., Franx, M., & Kuijken, K. 2000, ApJ, 532, 88 [NASA ADS] [CrossRef]
- Hoekstra,
H., Franx, M., Kuijken, K., Carlberg, R. G., & Yee,
H. K. C. 2003, MNRAS, 340, 609 [NASA ADS] [CrossRef]
- Hoekstra,
H., Yee, H. K. C., & Gladders, M. D. 2004, ApJ,
606, 67 [NASA ADS] [CrossRef]
- Hudson,
M. J., Gwyn, S. D. J., Dahle, H., & Kaiser, N.
1998, ApJ, 503, 531 [NASA ADS] [CrossRef]
- Kaiser, N.,
Squires, G., & Broadhurst, T. 1995, ApJ, 449, 460 [NASA ADS] [CrossRef]
- King, L., &
Schneider, P. 2002, A&A, 396, 411 [EDP Sciences] [NASA ADS] [CrossRef]
-
Kleinheinrich, M., Rix, H.-W., Erben, T., et al. 2005,
A&A, 439, 513 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Kochanek,
C. S., Schneider, P., & Wambsganss, J. 2004, Gravitational
Lensing: Strong, Weak & Micro, Proceedings of the 33rd Saas-Fee
Advanced Course, ed. G. Meylan, P. Jetzer & P. North (Berlin:
Springer-Verlag)
(In the text)
- Le
Fèvre, O., Vettolani, G., Garilli, B., et al. 2005,
A&A, 439, 845 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Luppino,
G. A., & Kaiser, N. 1997, ApJ, 475, 20 [NASA ADS] [CrossRef]
- McKay,
T. A., Sheldon, E. S., Racusin, J., et al. 2001,
[arXiv:astro-ph/0108013]
- McKay,
T. A., Sheldon, E. S., Johnston, D., et al. 2002,
ApJ, 571, L85 [NASA ADS] [CrossRef]
- Navarro,
J. F., Frenk, C. S., & White, S. D. M.
1995, MNRAS, 275, 720 [NASA ADS]
- Navarro,
J. F., Frenk, C. S., & White, S. D. M.
1996, ApJ, 462, 563 [NASA ADS] [CrossRef]
- Navarro,
J. F., Frenk, C. S., & White, S. D. M.
1997, ApJ, 490, 493 [NASA ADS] [CrossRef]
- Prada, F.,
Vitvitska, M., Klypin, A., et al. 2003, ApJ, 598, 260 [NASA ADS] [CrossRef]
- Rix, H., de Zeeuw,
P. T., Cretton, N., van der Marel, R. P., & Carollo,
C. M. 1997, ApJ, 488, 702 [NASA ADS] [CrossRef] (In the text)
- Schirmer,
M., Erben, T., Schneider, P., et al. 2003, A&A, 407,
869 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Schneider, P., & Rix, H. 1997, ApJ, 474, 25 [NASA ADS] [CrossRef] (In the text)
- Seljak, U.
2002, MNRAS, 334, 797 [NASA ADS] [CrossRef]
- Seljak, U.,
Makarov, A., Mandelbaum, R., et al. 2005,
Phys. Rev. D, 71, 043511 [NASA ADS] [CrossRef]
- Sheldon,
E. S., Johnston, D. E., Frieman, J. A., et al.
2004, AJ, 127, 2544 [NASA ADS] [CrossRef]
- Smith,
D. R., Bernstein, G. M., Fischer, P., & Jarvis, M.
2001, ApJ, 551, 643 [NASA ADS] [CrossRef]
- Sofue, Y., &
Rubin, V. 2001, ARA&A, 39, 137 [NASA ADS] (In the text)
- Taylor,
A. N., Bacon, D. J., Gray, M. E., et al. 2004,
MNRAS, 353, 1176 [NASA ADS] [CrossRef] (In the text)
- van
den Bosch, F. C., Norberg, P., Mo, H. J., & Yang, X.
2004, MNRAS, 352, 1302 [NASA ADS] [CrossRef] (In the text)
- Wilson, G.,
Kaiser, N., Luppino, G. A., & Cowie, L. L. 2001, ApJ,
555, 572 [NASA ADS] [CrossRef]
- Wolf, C., Dye, S.,
Kleinheinrich, M., et al. 2001, A&A, 377, 442 [EDP Sciences] [NASA ADS] [CrossRef]
- Wolf, C.,
Meisenheimer, K., Rix, H.-W., et al. 2003, A&A, 401,
73 [EDP Sciences] [NASA ADS]
- Wolf, C.,
Meisenheimer, K., Kleinheinrich, M., et al. 2004, A&A,
421, 913 [EDP Sciences] [NASA ADS] [CrossRef]
- Wright,
C. O., & Brainerd, T. G. 2000, ApJ, 534, 34 [NASA ADS] [CrossRef] (In the text)
- Zaritsky,
D., & White, S. D. M. 1994, ApJ, 435, 599 [NASA ADS] [CrossRef]
- Zaritsky,
D., Smith, R., Frenk, C., & White, S. D. M. 1993,
ApJ, 405, 464 [NASA ADS] [CrossRef]
- Zaritsky,
D., Smith, R., Frenk, C., & White, S. D. M. 1997,
ApJ, 478, 39 [NASA ADS] [CrossRef]
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[width=6cm,clip]{2606fi1a.ps}\hspace*{3mm}
\includegraphics[width=6cm,clip]{2606fi1b.ps} \end{figure}](/articles/aa/full/2006/32/aa2606-04/Timg43.gif)
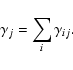
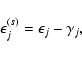
![\begin{displaymath}
P\left(\epsilon_{j}^{(s)}\right)=\frac{1}{\pi\sigma_{\epsilo...
...ert\epsilon_{j}^{(s)}\vert^{2}}{\sigma_{\epsilon}^{2}}\right]}
\end{displaymath}](/articles/aa/full/2006/32/aa2606-04/img59.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=6cm,clip]{2606fi2a.ps}\hspace*{3mm}
\includegraphics[angle=-90,width=6cm,clip]{2606fi2b.ps} \end{figure}](/articles/aa/full/2006/32/aa2606-04/Timg64.gif)
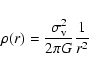
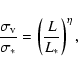
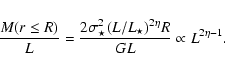
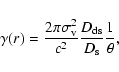
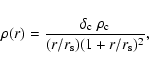
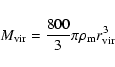
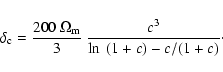
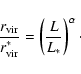
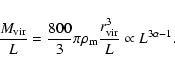
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{2606fig3.ps} \end{figure}](/articles/aa/full/2006/32/aa2606-04/Timg137.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=6.2cm,clip]{2606fi4a.ps}\hspace*{3mm}
\includegraphics[angle=-90,width=6.2cm,clip]{2606fi4b.ps} \end{figure}](/articles/aa/full/2006/32/aa2606-04/Timg153.gif)
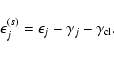
![\begin{figure}
\par\includegraphics[angle=-90,width=6.2cm,clip]{2606fi5a.ps}\hspace*{3mm}
\includegraphics[angle=-90,width=6.2cm,clip]{2606fi5b.ps} \end{figure}](/articles/aa/full/2006/32/aa2606-04/Timg178.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2606fig6.ps} \end{figure}](/articles/aa/full/2006/32/aa2606-04/Timg185.gif)