Note that the value of c is dependent on our definition of the virial radius. Unfortunately, there is no unique definition of the virial radius in the literature. Sometimes it is referred to as the radius inside which the mean density is some over-density times the mean density of the universe, and sometimes as the radius inside which the mean density is some over-density times the critical density of the universe. Changing the definition of the virial radius would change relation (11) and therefore c. The shape of the density profile remains unaffected so that the values of the scale radius 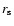$r_{\rm s}$ and the characteristic density 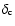$\delta_{\rm c}$ do not change. Defining the virial radius as the radius inside which the mean density is 200 times the critical density instead of our definition from Sect. 5.1 would lower the concentration from c=20 to approximately c'=12.4. 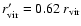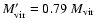The virial radius would therefore become about $r_{\rm vir}'=0.62~r_{\rm vir}$ and the virial mass $M_{\rm vir}'=0.79~M_{\rm vir}$ . 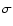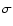The lower limits on c that we obtained from our data would roughly become c'>18 (1- $\sigma$ ) and c'>7 (2- $\sigma$ ). Our choice of 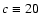$c\equiv 20$ (c'=12.4) appears somewhat large for galaxy-sized halos (see e.g. Bullock et al. 2001), however, we stress that smaller values of c are disfavoured by our data.

We emphasize the differences in the definition of the virial radius here only for clarity and easier comparability to other works. All figures and results presented in this paper use the definition of the virial radius given in Sect. 5.1.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.