A&A 455, 61-72 (2006)
DOI: 10.1051/0004-6361:20064882
E. Westra1 - D. Heath Jones1,2 - C. E. Lidman3 - K. Meisenheimer4 - R. M. Athreya5 - C. Wolf6 - T. Szeifert3 - E. Pompei3 - L. Vanzi3
1 - Research School of Astronomy & Astrophysics, The
Australian National University, Cotter Road, Weston Creek ACT 2611,
Australia
2 -
Anglo-Australian Observatory, PO Box 296, Epping NSW 1710, Australia
3 -
European Southern Observatory, Casilla 19001, Santiago 19,
Chile
4 - Max Planck Institut für Astronomie, Königstuhl 17,
69117 Heidelberg, Germany
5 - National Centre for Radio Astrophysics, Tata Institute of
Fundamental Research Pune University Campus, Post Bag 3,
Ganeshkhind Pune 411007, India
6 - Department of Astrophysics, Denys Wilkinson Building,
University of Oxford, Keble Road, Oxford, OX1 3RH, UK
Received 20 Jaunary 2006 / Accepted 28 April 2006
Abstract
Context. Wide-field narrowband surveys are an efficient way of searching large volumes of high-redshift space for distant galaxies.
Aims. We describe the Wide Field Imager Lyman-Alpha Search (WFILAS) over 0.74 sq. degree for bright emission-line galaxies at
![]() .
.
Methods. WFILAS uses deep images taken with the Wide Field Imager (WFI) on the ESO/MPI 2.2 m telescope in three narrowband (70 Å), one encompassing intermediate band (220 Å) and two broadband filters, B and R. We use the novel technique of an encompassing intermediate band filter to exclude false detections. Images taken with broadband B and R filters are used to remove low redshift galaxies from our sample.
Results. We present a sample of seven Ly![]() emitting galaxy candidates, two of which are spectroscopically confirmed. Compared to other surveys all our candidates are bright, the results of this survey complements other narrowband surveys at this redshift. Most of our candidates are in the regime of bright luminosities, beyond the reach of less voluminous surveys. Adding our candidates to those of another survey increases the derived luminosity density by
emitting galaxy candidates, two of which are spectroscopically confirmed. Compared to other surveys all our candidates are bright, the results of this survey complements other narrowband surveys at this redshift. Most of our candidates are in the regime of bright luminosities, beyond the reach of less voluminous surveys. Adding our candidates to those of another survey increases the derived luminosity density by ![]() 30%. We also find potential clustering in the Chandra Deep Field South, supporting overdensities discovered by other surveys. Based on a FORS2/VLT spectrum we additionally present the analysis of the second confirmed Ly
30%. We also find potential clustering in the Chandra Deep Field South, supporting overdensities discovered by other surveys. Based on a FORS2/VLT spectrum we additionally present the analysis of the second confirmed Ly![]() emitting galaxy in our sample. We find that it is the brightest Ly
emitting galaxy in our sample. We find that it is the brightest Ly![]() emitting galaxy (1
emitting galaxy (1
![]() erg s-1 cm-2) at this redshift to date and the second confirmed candidate of our survey. Both objects exhibit the presence of a possible second Ly
erg s-1 cm-2) at this redshift to date and the second confirmed candidate of our survey. Both objects exhibit the presence of a possible second Ly![]() component redward of the line.
component redward of the line.
Key words: galaxies: high-redshift - galaxies: evolution - galaxies: starburst
Detections of both galaxies and QSOs at ![]() (Djorgovski et al. 2001; Fan et al. 2002; Becker et al. 2001) indicate that the Universe was
largely reionised at that epoch. The recent three-year WMAP
results combined with other cosmological surveys suggest an epoch of
reionisation around
(Djorgovski et al. 2001; Fan et al. 2002; Becker et al. 2001) indicate that the Universe was
largely reionised at that epoch. The recent three-year WMAP
results combined with other cosmological surveys suggest an epoch of
reionisation around ![]() (Spergel et al. 2006), consistent with
both QSO results (Fan et al. 2002) and the epoch predicted by structure
formation models (Gnedin & Ostriker 1997; Haiman & Loeb 1998). While the UV contributions
of QSOs and AGN are almost certainly not responsible for reionisation
(Barger et al. 2003), faint star forming galaxies need to exist in
extraordinary numbers if they are to be the cause (Yan & Windhorst 2004).
However, analyses of the Hubble Ultra Deep Field failed to find
sufficient numbers of faint galaxies to support this idea
(Bouwens et al. 2005; Bunker et al. 2004). Therefore, it is crucial to investigate
what the contribution to the ionising UV flux is from young stellar
populations of star forming galaxies.
(Spergel et al. 2006), consistent with
both QSO results (Fan et al. 2002) and the epoch predicted by structure
formation models (Gnedin & Ostriker 1997; Haiman & Loeb 1998). While the UV contributions
of QSOs and AGN are almost certainly not responsible for reionisation
(Barger et al. 2003), faint star forming galaxies need to exist in
extraordinary numbers if they are to be the cause (Yan & Windhorst 2004).
However, analyses of the Hubble Ultra Deep Field failed to find
sufficient numbers of faint galaxies to support this idea
(Bouwens et al. 2005; Bunker et al. 2004). Therefore, it is crucial to investigate
what the contribution to the ionising UV flux is from young stellar
populations of star forming galaxies.
Broadly speaking, two classes of star-forming galaxy dominate high
redshift surveys: Lyman Break Galaxies (LBGs) and Lyman-![]() Emitters (LAEs). LBG surveys, which now number in the thousands of
objects at z = 3 to 5, find clumpy source distributions and a
two-point angular correlation function indicative of strong clustering
(Ouchi et al. 2004; Giavalisco & Dickinson 2001; Hildebrandt et al. 2005; Foucaud et al. 2003; Adelberger et al. 2003; Allen et al. 2005).
LAEs also show evidence for clustering although many of the LAE
surveys target fields surrounding known sources such as
proto-clusters, radio galaxies and QSOs
(e.g. Steidel et al. 2000; Stiavelli et al. 2001; Ouchi et al. 2005; Møller & Fynbo 2001; Venemans et al. 2002). On
average, LAEs number 1.5
Emitters (LAEs). LBG surveys, which now number in the thousands of
objects at z = 3 to 5, find clumpy source distributions and a
two-point angular correlation function indicative of strong clustering
(Ouchi et al. 2004; Giavalisco & Dickinson 2001; Hildebrandt et al. 2005; Foucaud et al. 2003; Adelberger et al. 2003; Allen et al. 2005).
LAEs also show evidence for clustering although many of the LAE
surveys target fields surrounding known sources such as
proto-clusters, radio galaxies and QSOs
(e.g. Steidel et al. 2000; Stiavelli et al. 2001; Ouchi et al. 2005; Møller & Fynbo 2001; Venemans et al. 2002). On
average, LAEs number 1.5 ![]() 104 deg-2 per unit
redshift down to 1.5
104 deg-2 per unit
redshift down to 1.5 ![]() 10-17 erg s-1 cm-2 at
z = 3.4 and 4.5 (Hu et al. 1998). Also, their consistently small size
(
10-17 erg s-1 cm-2 at
z = 3.4 and 4.5 (Hu et al. 1998). Also, their consistently small size
(![]() 0.6 h-1 kpc) suggests they are subgalactic clumps
residing in the wind-driven outflows of larger unseen hosts
(e.g. Bland-Hawthorn & Nulsen 2004). Such mechanisms provide a
straightforward means of UV photon escape from the host galaxy,
efficiently reionising the surrounding IGM in a way than ordinary LBGs
can not.
0.6 h-1 kpc) suggests they are subgalactic clumps
residing in the wind-driven outflows of larger unseen hosts
(e.g. Bland-Hawthorn & Nulsen 2004). Such mechanisms provide a
straightforward means of UV photon escape from the host galaxy,
efficiently reionising the surrounding IGM in a way than ordinary LBGs
can not.
The most efficient way to find LAEs is through imaging surveys using a combination of broad- and narrowband filters. The advent of wide field cameras has allowed systematic imaging searches that have been carried out to build up samples of candidate LAEs at high redshifts (e.g. Ajiki et al. 2003; Hu et al. 2004; Rhoads et al. 2003; Wang et al. 2005). The availability of high throughput spectrographs on 8 to 10 m-class telescopes has enabled the spectroscopic confirmation of these galaxies. Such direct imaging searches typically cover 102-103 times the volume of blind long-slit spectroscopic searches (e.g. Table 4 in Santos et al. 2004). Furthermore, candidates from narrowband surveys always have an identifiable emission feature that is well separated from sky lines courtesy of the filter design. This is in contrast to other methods, including the widely-used "dropout'' technique (e.g. Steidel et al. 1999).
Table 1:
Narrowband surveys for Ly![]() at z = 5.7.
at z = 5.7.
The narrowband filter design leads to a higher candidate LAE selection
efficiency than other techniques. The only way to secure the
identification of the emission line is spectroscopic follow-up. The
most common low redshift interlopers are the emission line doublets of
[O II]
![]() 3726, 3728 and [O III]
3726, 3728 and [O III]
![]() 4959, 5007. These can be identified by obtaining spectra with a
resolution
4959, 5007. These can be identified by obtaining spectra with a
resolution
![]() to separate the line pair. Other emission
lines, such as H
to separate the line pair. Other emission
lines, such as H![]() and H
and H![]() ,
can be identified by neighbouring lines.
The narrowband technique has been successfully applied by many authors
in order to discover galaxies at redshift 5-6
(e.g. Hu et al. 2004; Ajiki et al. 2003; Dawson et al. 2004; Rhoads et al. 2003; Maier et al. 2003) and to locate
galaxies at redshift 6-7 (Stanway et al. 2004; Cuby et al. 2003; Kodaira et al. 2003).
Likewise, we employ the narrowband technique in the Wide Field Imager
Lyman-Alpha Search (WFILAS) to find galaxies at
,
can be identified by neighbouring lines.
The narrowband technique has been successfully applied by many authors
in order to discover galaxies at redshift 5-6
(e.g. Hu et al. 2004; Ajiki et al. 2003; Dawson et al. 2004; Rhoads et al. 2003; Maier et al. 2003) and to locate
galaxies at redshift 6-7 (Stanway et al. 2004; Cuby et al. 2003; Kodaira et al. 2003).
Likewise, we employ the narrowband technique in the Wide Field Imager
Lyman-Alpha Search (WFILAS) to find galaxies at ![]() .
In Paper I
in this series (Westra et al. 2005), we described a compact LAE at
z=5.721 discovered by our survey.
.
In Paper I
in this series (Westra et al. 2005), we described a compact LAE at
z=5.721 discovered by our survey.
In this Paper, we describe the survey design and sample analysis of
WFILAS. In Sect. 2 we describe the scope of the
survey and the observing strategy. The data reduction is described in
Sect. 3. Section 4 outlines the
candidate selection and Sect. 5 outlines sample
properties and comparison to other surveys. We discuss the
spectroscopic follow-up of two candidates in
Sect. 6. Throughout this paper we assume a flat
Universe with
![]() and a
Hubble constant H0 = 70 km s-1 Mpc-1. All quoted magnitudes are in the
AB system (Oke & Gunn 1983)
and a
Hubble constant H0 = 70 km s-1 Mpc-1. All quoted magnitudes are in the
AB system (Oke & Gunn 1983)![]() .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{4882fg1.eps}
\end{figure}](/articles/aa/full/2006/31/aa4882-06/Timg26.gif) |
Figure 1:
Filter set used for the WFILAS Survey. a) The broadband
BR and intermediate M815 (815/22 nm) passbands. b) The
M815 intermediate passband ( solid line) and three
purpose-built narrowbands New A (810/7), N817 (817/7) and N824 (824/7), shown over the wavelength region targeted for Ly |
| Open with DEXTER | |
The sky area surveyed by the WFILAS is ![]() 0.74 sq. degree. We
observed three fields in broadbands B, R and in an intermediate
width filter centred at 815 nm encompassing three narrowband filters
(Fig. 1). The adoption of an additional intermediate
width filter encompassing the multiple narrowband width filters is a
novel approach compared to previous narrowband surveys. The
application of the intermediate band filter enables us to drastically
reduce the number of spurious detections in the narrowband filters.
The narrow width of the narrowband filters (FWHM = 7 nm) gives a
prominent appearance to emission line objects. Furthermore, the three
chosen fields are spread across the sky to enable us to average out
variations in cosmic variance. Our search has covered one of the
largest co-moving volumes compared to other surveys.
Table 1 compares WFILAS with other published
surveys.
0.74 sq. degree. We
observed three fields in broadbands B, R and in an intermediate
width filter centred at 815 nm encompassing three narrowband filters
(Fig. 1). The adoption of an additional intermediate
width filter encompassing the multiple narrowband width filters is a
novel approach compared to previous narrowband surveys. The
application of the intermediate band filter enables us to drastically
reduce the number of spurious detections in the narrowband filters.
The narrow width of the narrowband filters (FWHM = 7 nm) gives a
prominent appearance to emission line objects. Furthermore, the three
chosen fields are spread across the sky to enable us to average out
variations in cosmic variance. Our search has covered one of the
largest co-moving volumes compared to other surveys.
Table 1 compares WFILAS with other published
surveys.
The observations were taken with the Wide Field Imager
(WFI; Baade et al. 1999) on the ESO/MPI 2.2 m telescope at the Cerro
La Silla Observatory, Chile. The data were taken over 65 separate
nights from 2001 January 19 to 2003 December 1. The WFI is a mosaic of
eight (
![]() )
2k
)
2k ![]() 4k CCDs arranged to give a field of
view of 34'
4k CCDs arranged to give a field of
view of 34' ![]() 33'. The pixels are 0
33'. The pixels are 0
![]() 238 on a side.
238 on a side.
As WFILAS was planned as joint project of ESO Santiago and the
COMBO-17 team at MPIA Heidelberg, three fields were selected to
overlap with the COMBO-17 survey, i.e. their extended Chandra Deep
Field South (CDFS), SGP (South Galactic Pole) and S11 fields. The
coordinates of the field centres and the exposure times in each of the
filters for each field are given in Table 2. All three
fields are at high Galactic latitude (
![]() )
and have
extinctions less than E(B-V) = 0.022 mag (Schlegel et al. 1998).
)
and have
extinctions less than E(B-V) = 0.022 mag (Schlegel et al. 1998).
Table 2:
WFILAS fields, filter set exposure times and detection
limits. The entries under each field heading list: (a) the
total exposure time (ks), (b) the flux for a 2![]() detection on 6 pixel diameter aperture (
detection on 6 pixel diameter aperture (![]() Jy) and (c) the final
seeing (''), in each filter.
Jy) and (c) the final
seeing (''), in each filter.
We employ standard broadband B and R filters. The intermediate
band (FWHM = 22 nm) observatory filter is centred at 815 nm. The
three custom made narrowband (FWHM = 7 nm) filters are centred at
810 nm, 817 nm and 824 nm. The transmission profiles of the filters
are shown in Fig. 1. The intermediate and narrowband
filters are designed to fit in the atmospheric 815 nm OH-airglow
window, where the brightness of the sky background is low and hence
favourable to detect Ly![]() emission at redshift
emission at redshift ![]() 5.7. The data
taken with the intermediate band filter confirm detections of the
Ly
5.7. The data
taken with the intermediate band filter confirm detections of the
Ly![]() line in one of the narrowband filters. The broadband B and Rdata, which were taken from the COMBO-17 survey (Wolf et al. 2004), are
used to confirm the absence of continuum blueward of the Ly
line in one of the narrowband filters. The broadband B and Rdata, which were taken from the COMBO-17 survey (Wolf et al. 2004), are
used to confirm the absence of continuum blueward of the Ly![]() line
and to avoid sample contamination by lower redshift emission line
galaxies (e.g. H
line
and to avoid sample contamination by lower redshift emission line
galaxies (e.g. H![]() at
at
![]() ,
or [O II] at
,
or [O II] at
![]() ).
).
To establish the photometric zero-point of the intermediate and narrowband filters two spectrophotometric standard stars (LTT3218 and LTT7987; Bessell 1999) were observed.
Between 10-50 exposures were taken for each intermediate and narrowband filter for each field. The exposure times varied between 1000 and 1800 s per frame, with a typical exposure time of around 1600 s. All frames are background-limited despite the low night sky emission in this spectral region. The median, first and last decile of both seeing and background are given in Table 3.
Table 3:
The median, first and last decile of background and seeing for the
WFILAS narrowband imaging for all three fields combined. One
pixel corresponds to 0
![]() 238.
238.
The data were processed with standard IRAF![]() routines (MSCRED TASK) and our own specially
designed scripts. The initial steps in the reduction process consist
of removing the zero level offset with bias frames, normalising
pixel-to-pixel sensitivity differences with twilight flatfield frames
and removal of fringes with fringe frames. During these steps, the 8
CCDs that make up a single WFI image are treated independently. These
processes are described in detail below.
routines (MSCRED TASK) and our own specially
designed scripts. The initial steps in the reduction process consist
of removing the zero level offset with bias frames, normalising
pixel-to-pixel sensitivity differences with twilight flatfield frames
and removal of fringes with fringe frames. During these steps, the 8
CCDs that make up a single WFI image are treated independently. These
processes are described in detail below.
Normally, the overscan region of the science frames can be used to remove the zero level offset. However, it was noticed that the bias frames contained significant intermediate scale structure (10-30 pixels). To remove this, bias frames were taken on every day of our observations and averaged into a bias frame for that day. In order to minimise the noise added to the data by subtracting the bias, the bias frames were smoothed by 5 pixels and 30 pixels in horizontal and vertical direction of the CCDs, respectively, and subsequently medianed. The structures are stable over periods of several months. Therefore, it was possible to use bias frames from different nights without degrading the quality of the data.
Typically, five twilight flatfield frames were taken in one night for one or more filters. The frames were medianed and the science data was divided by the median. Hence pixel-to-pixel sensitivity differences were removed. The structure in the individual flatfield frames was stable over a period of several weeks. Frames taken on different nights could thus be reused. Any differences between flatfield frames were due to the appearance or disappearance of dust features, or large scale illumination differences. The differences rarely amounted to more than a few percent.
The raw data in the intermediate and narrowband filters show fringe patterns with amplitudes of up to 10% which was only partially removed after the data had been flatfielded. To entirely remove the fringe pattern, we subtracted a fringe frame created from 10-30 science frames. The fringing is very stable over time, so we were able to use data spanning several months. Certain science frames still show fringe patterns because they are contaminated by either moonlight or twilight. Residual differences in the level of the background between the different CCDs were removed by subtracting the median background level from each CCD.
To produce the final deep images we only used images with a seeing of
less than 5 pixels (=1
![]() 2) and without significant residual
fringing. To make the combining of the images possible, we had to
apply an astrometric correction based on stars from the USNO CCD
Astrograph Catalogue 2 (UCAC2; Zacharias et al. 2004) in the three
observed fields. The frames have a set pixel scale of 0
2) and without significant residual
fringing. To make the combining of the images possible, we had to
apply an astrometric correction based on stars from the USNO CCD
Astrograph Catalogue 2 (UCAC2; Zacharias et al. 2004) in the three
observed fields. The frames have a set pixel scale of 0
![]() 238
pixel-1 with North up and East left. The images were weighted
according to their exposure time and combined using the IRAF
"mscstack'' routine rejecting deviant pixels. Table 2
summarises the depth, image quality and total exposure time, for each
coadded frame.
238
pixel-1 with North up and East left. The images were weighted
according to their exposure time and combined using the IRAF
"mscstack'' routine rejecting deviant pixels. Table 2
summarises the depth, image quality and total exposure time, for each
coadded frame.
Initial source catalogues were created for each of the 8 narrowband
images. Each catalogue contains the photometry for the sources in all
6 filters. We used the SExtractor source detection software (version
2.3.2, double image mode; Bertin & Arnouts 1996). Sources were selected when at
least 5 pixels were 0.8![]() above the noise level in the
narrowband image used for detection. The photometry was measured in
two apertures, 6 and 10 pixels in diameter (=1
above the noise level in the
narrowband image used for detection. The photometry was measured in
two apertures, 6 and 10 pixels in diameter (=1
![]() 4 and 2
4 and 2
![]() 4,
respectively). The 6 pixel aperture was used to maximise the
signal-to-noise of the flux of the objects, while the larger 10 pixel
aperture was used for the more accurate determination of the total
flux and hence the star formation rate.
4,
respectively). The 6 pixel aperture was used to maximise the
signal-to-noise of the flux of the objects, while the larger 10 pixel
aperture was used for the more accurate determination of the total
flux and hence the star formation rate.
Some authors have found that SExtractor underestimates flux uncertainties (Feldmeier et al. 2002; Labbé et al. 2003). SExtractor estimates the uncertainties using various assumptions that are often not valid (e.g. perfect flatfielding, perfect sky subtraction). The pixel-to-pixel noise in our data is slightly correlated because the scatter in the counts summed in 6 pixel apertures is about 10% higher than what one would derive from the measured pixel-to-pixel RMS.
We devised a method to correct the uncertainties given by SExtractor to
their true values as follows. First, sources with flux in all filters
and their M815 magnitude between 16 and 23 were selected. Sources
brighter than M815 = 16 are typically saturated, while those fainter
than M815 = 23 are incomplete (see Sect. 4.3
for a further discussion of incompleteness). The
![]() colour (where
N is any of narrowband filters New A, N817, or N824) is the same for any
flat continuum source. Therefore, the spread in the
colour (where
N is any of narrowband filters New A, N817, or N824) is the same for any
flat continuum source. Therefore, the spread in the
![]() colour
will be the same as the true flux uncertainty from the two
contributing filters. Next, the sources were binned into 200-source
bins based on their M815 magnitude. In Fig. 2 we plot
the
colour
will be the same as the true flux uncertainty from the two
contributing filters. Next, the sources were binned into 200-source
bins based on their M815 magnitude. In Fig. 2 we plot
the
![]() colour versus the M815 magnitude of one of our S11
catalogues. Mean values for the
colour versus the M815 magnitude of one of our S11
catalogues. Mean values for the
![]() colour, M815, N magnitude
and the mean of the SExtractor uncertainty were calculated for each bin.
The uncertainty in the colour for each object was determined by adding
the uncertainty of M815 and N in quadrature (
colour, M815, N magnitude
and the mean of the SExtractor uncertainty were calculated for each bin.
The uncertainty in the colour for each object was determined by adding
the uncertainty of M815 and N in quadrature (
![]() ). The interval in which 68.3% of the
objects were closest to this mean colour was used to infer the actual
1
). The interval in which 68.3% of the
objects were closest to this mean colour was used to infer the actual
1![]() colour uncertainty. We assumed that the ratio between the
old uncertainties
colour uncertainty. We assumed that the ratio between the
old uncertainties ![]() and
and ![]() was the same for the new
uncertainties
was the same for the new
uncertainties ![]() and
and ![]() .
We related between the new
and old uncertainty in the intermediate and narrowband flux using the
function
.
We related between the new
and old uncertainty in the intermediate and narrowband flux using the
function
![]() ,
where a is the zero-offset for the uncertainty in
the flux of bright sources and b is the ratio between the new and
old uncertainty for the flux of the faintest sources. The parameters
a and b correspond to imperfections in the photometry and wrongly
assumed background by SExtractor, respectively.
,
where a is the zero-offset for the uncertainty in
the flux of bright sources and b is the ratio between the new and
old uncertainty for the flux of the faintest sources. The parameters
a and b correspond to imperfections in the photometry and wrongly
assumed background by SExtractor, respectively.
Typically, the correction factors are moderate (between
![]() 30-50%) for the faint sources in the catalogues. Even
though the correction factors are moderate, we assume that the
corrections for the uncertainties in the broadband B and R are
irrelevant, since they are used in a different way than the
intermediate and narrowband images (see Sect. 4.2).
30-50%) for the faint sources in the catalogues. Even
though the correction factors are moderate, we assume that the
corrections for the uncertainties in the broadband B and R are
irrelevant, since they are used in a different way than the
intermediate and narrowband images (see Sect. 4.2).
![\begin{figure}
\par\includegraphics[width=8.8cm, clip]{4882fg2.eps}
\end{figure}](/articles/aa/full/2006/31/aa4882-06/Timg45.gif) |
Figure 2:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm]{4882fg3a.eps} \includegraphics[w...
...\huge$B$ }
\makebox[0pt][l]{\hspace{0.838\textwidth} \huge$R$ }
\end{figure}](/articles/aa/full/2006/31/aa4882-06/Timg46.gif) |
Figure 3:
Thumbnails of each region in which the candidate LAEs
appears. The thumbnails cover a 19'' |
| Open with DEXTER | |
The following four criteria were applied to select our candidate LAEs from the eight initial source catalogues:
We note here the importance of the usage of the intermediate band filter. If we were to reapply all the criteria except for criterion 3, i.e. we do not use the intermediate band images, we would obtain 284 candidates instead of the 33 for visual inspection.
The AB-magnitudes, derived line fluxes and luminosities for the
candidates are shown in Table 6. To convert between
AB-magnitudes and line flux in erg s-1 cm-2 we use the following
relation:
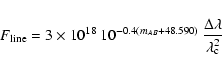 |
(1) |
From the Hubble Deep Field (HDF) galaxy number-count data for the F814W filter (Williams et al. 1996) we computed completeness corrections for our eight source catalogues. The HDF counts are determined over the magnitude range I814 = 22-29, and agree well with our galaxy counts over all narrowband filters in the range N = 22-24. Figure 4 shows the counts for the F814W filter in the HDF and for the N817 filter in the S11 field. Figure 4 also shows the linear fit used as the basis for the calculation of the detection completeness. The fit is done to the combined number count data over two intervals: N817 = [20, 22.5], where the WFILAS counts are complete, and I814 = [22.5, 25], where the HDF counts are linear.
![\begin{figure}
\includegraphics[width=8.5cm, clip]{4882fg4.eps}
\end{figure}](/articles/aa/full/2006/31/aa4882-06/Timg50.gif) |
Figure 4: Galaxy counts as a function of AB-magnitude for the N817 filter in the S11 field. Plotted are the N817 source counts of the S11 field ( crosses) together with the I814 galaxy counts of the Hubble Deep Field ( squares). The solid line indicates the fitted linear relation between the magnitude and galaxy count. |
| Open with DEXTER | |
Detection completeness is defined as the ratio of WFILAS sources to the number expected from the number-count relation. Figure 5 shows the derived detection completeness for each filter-field combination used for WFILAS. The differences are mainly due to unequal exposure times, although filter throughput and image quality also play a role. These could explain the overall lower sensitivity of the N824 filter, as can be inferred from Fig. 5. Additionally, we correct for detection completeness arising due to the intermediate band selection criterion. We constructed a noise image by stacking the intermediate band images without registering. The completeness is defined as the rate of recovery of artificially inserted objects.
![\begin{figure}
\includegraphics[width=8.5cm, clip]{4882fg5a.eps}\par\medskip
\...
...s}\par\medskip
\includegraphics[width=8.5cm, clip]{4882fg5c.eps}
\end{figure}](/articles/aa/full/2006/31/aa4882-06/Timg51.gif) |
Figure 5: Detection of completeness as function of magnitude derived from the galaxy density-magnitude relation as described in Sect. 4. From top to bottom the CDFS, S11 and SGP fields are shown. No N817 data are available for the SGP field. |
| Open with DEXTER | |
Given the different sensitivities of each filter-field combination, we
define a homogeneous subsample of our initial candidate sample, using
the candidates from our four most sensitive field-filter combinations.
We call this our "complete'' sample (4 of the 7 LAEs; marked in
Table 6), because once defined, we use the curves in
Fig. 5 to correct the detected candidate numbers
for incompleteness, in contrast to our initial "incomplete'' sample
(all 7 LAEs). The purpose of the subsample is that it lies within a
uniform flux limit. Figure 5 shows that our four
best filter-field combinations consist of the New A and N817 filters in
both the CDFS and S11 fields. These four field-filter combinations
reach at least 50% completeness at
![]() = 23.38, or
= 23.38, or
![]() erg s-1 cm-2. We take this as the flux limit of
our complete sample. As such, the number density derived from the
complete sample is a more accurate measure of the density of sources
down to the nominated flux limit than the number density of the
incomplete sample. Figure 6 shows the luminosity
distribution of the complete sample alongside our initial candidate
list, which we call the "incomplete'' sample. It shows that in using
completeness corrections our detected source density is up by 50%.
erg s-1 cm-2. We take this as the flux limit of
our complete sample. As such, the number density derived from the
complete sample is a more accurate measure of the density of sources
down to the nominated flux limit than the number density of the
incomplete sample. Figure 6 shows the luminosity
distribution of the complete sample alongside our initial candidate
list, which we call the "incomplete'' sample. It shows that in using
completeness corrections our detected source density is up by 50%.
In the previous section we introduced two sets of candidate LAEs: the
full (but incomplete) sample of seven candidate LAEs and a subsample
thereof, complete to
![]() erg s-1 cm-2 (the complete sample). The flux limit of the incomplete sample is
almost twice the limit of the complete sample
(
erg s-1 cm-2 (the complete sample). The flux limit of the incomplete sample is
almost twice the limit of the complete sample
(
![]() erg s-1 cm-2).
erg s-1 cm-2).
![\begin{figure}
\includegraphics[width=8.5cm, clip]{4882fg6.eps} \end{figure}](/articles/aa/full/2006/31/aa4882-06/Timg56.gif) |
Figure 6: Line luminosity distribution of the candidate LAEs. Two samples are indicated: all the candidates, but not corrected for completeness ( solid) and the candidates in the complete sample, i.e. candidates of the four deepest narrowband images with a magnitude cut-off at 50% completeness of the worst of these four images ( dashed). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm, clip]{4882fg7a.eps}\par\medskip...
...ludegraphics[width=6.375cm, clip]{4882fg7b.eps}\hspace*{1cm}}
\par\end{figure}](/articles/aa/full/2006/31/aa4882-06/Timg57.gif) |
Figure 7:
a) Line luminosity distribution of the complete
sample of candidate LAEs ( solid histograms) together with
the candidates from Ajiki et al. (2003) ( dashed histograms).
Both samples are corrected for completeness. The errorbars are
derived using Poisson statistics. Furthermore, two Schechter
function fits are indicated: one to the combined WFILAS and Ajiki
sample ( dotted) and one to Ajiki sample only ( long
dashed). b) The 68.3%, 95.4% and 99.7% confidence
limits for the fitting parameters L* and |
| Open with DEXTER | |
| Log (L (erg s-1)) | Log ( |
| 42.7 |
|
| 42.8 |
|
| 42.9 |
|
| 43.0 |
|
| 43.1 |
|
| 43.2 |
|
| 43.3 |
|
| 43.4 |
|
To examine the luminosity distribution of our sample we use the
Schechter function (Schechter 1976), as it is a good representation
of the data at bright luminosities. From this, the luminosity density
![]() of a distribution with a limiting luminosity
of a distribution with a limiting luminosity
![]() is given by
is given by
We examine the influence of non-detections of bright (
![]() )
LAEs for the total Ly
)
LAEs for the total Ly![]() luminosity density by employing the same
method as Ajiki et al. (2003), another narrowband imaging survey aimed at
finding LAEs at
luminosity density by employing the same
method as Ajiki et al. (2003), another narrowband imaging survey aimed at
finding LAEs at
![]() .
In the interest of comparison, we
follow Ajiki et al. exactly and adopt the Fujita et al. (2003)
values for
.
In the interest of comparison, we
follow Ajiki et al. exactly and adopt the Fujita et al. (2003)
values for ![]() (-1.53) and
(-1.53) and ![]() (10-2.62 Mpc-3). Their approach was to solve
Eq. (2) for L*, instead of fitting a Schechter
function. Fixing
(10-2.62 Mpc-3). Their approach was to solve
Eq. (2) for L*, instead of fitting a Schechter
function. Fixing ![]() and allowing L* and
and allowing L* and ![]() to vary
imposes a strong prior on the final fit, it allows us to compare
directly to the results of Ajiki et al. by preserving their
method. The luminosity density
to vary
imposes a strong prior on the final fit, it allows us to compare
directly to the results of Ajiki et al. by preserving their
method. The luminosity density
![]() was calculated by summing
the luminosity of all candidates (corrected for completeness) and
divided by the corresponding survey volume. With the given survey
limits the equation can be solved for L*. Equation (2)
yields the total luminosity density when
was calculated by summing
the luminosity of all candidates (corrected for completeness) and
divided by the corresponding survey volume. With the given survey
limits the equation can be solved for L*. Equation (2)
yields the total luminosity density when
![]() .
We have done
this for three cases: for the candidates of Ajiki et al. (case
A), the complete sample of our candidates (case B) and a combined
sample of these two surveys (case C). For our complete sample we
derive a higher L* (+0.12 dex; case B) than Ajiki et al. (2003, case A) which implies an increase of the luminosity density
.
We have done
this for three cases: for the candidates of Ajiki et al. (case
A), the complete sample of our candidates (case B) and a combined
sample of these two surveys (case C). For our complete sample we
derive a higher L* (+0.12 dex; case B) than Ajiki et al. (2003, case A) which implies an increase of the luminosity density
![]() of
of ![]() 30%. If we scale the luminosity contribution
of the candidates from Ajiki et al. to our volume and combine
the two samples, L* is higher (
30%. If we scale the luminosity contribution
of the candidates from Ajiki et al. to our volume and combine
the two samples, L* is higher (
![]() ;
case C).
Table 7 summarises the results. Detecting LAEs of
such bright luminosity at this redshift demonstrates the necessity of
wide field surveys, such as WFILAS, to provide a sample of LAEs at the
bright end.
;
case C).
Table 7 summarises the results. Detecting LAEs of
such bright luminosity at this redshift demonstrates the necessity of
wide field surveys, such as WFILAS, to provide a sample of LAEs at the
bright end.
As a second approach, we tried fitting a Schechter function to the
combined WFILAS and Ajiki et al. (2003) dataset, using a minimised
![]() fit (Fig. 7). We did not use the two
lowest luminosity bins of Ajiki et al. (2003) to constrain the fit because
these force the function to decline at the faint end. Instead, we set
the faint end slope to
fit (Fig. 7). We did not use the two
lowest luminosity bins of Ajiki et al. (2003) to constrain the fit because
these force the function to decline at the faint end. Instead, we set
the faint end slope to ![]() = -1.53, similar to the H
= -1.53, similar to the H![]() luminosity function at
luminosity function at ![]() from Fujita et al. (2003), on which
Ajiki et al. based their work. Figure 7b
shows a strong correlation between L* and
from Fujita et al. (2003), on which
Ajiki et al. based their work. Figure 7b
shows a strong correlation between L* and ![]() due to the slow
turn-over at the bright end.
due to the slow
turn-over at the bright end.
From the fitting there are three results to conclude. Firstly, incorporating the four completeness-corrected WFILAS galaxies into the Ajiki et al. (2003) galaxies better constrains the bright end of the luminosity function. Furthermore, it seems that the current generation of surveys is only just reaching the volume coverage necessary to discover LAEs with L>L*. The histogram in Fig. 7 shows a decreasing number of sources at the faint end. At face value, this could suggest that the ionising flux of the less luminous sources may be insufficient to escape the slowly expanding envelope of neutral hydrogen that surrounds the H II region in the LAE. Consequently, the sources are undetected and the faint end of the luminosity distribution decreases. However, it is difficult to detect faint LAEs and so the possibility of detection incompleteness cannot be ruled out.
![\begin{figure}
\par\includegraphics[width=7cm, clip]{4882fg8a.eps}\par\medskip
...
....eps}\par\medskip
\includegraphics[width=7cm, clip]{4882fg8c.eps}
\end{figure}](/articles/aa/full/2006/31/aa4882-06/Timg75.gif) |
Figure 8:
Sky distribution of candidate line emitters per field with
North up and East to the left for the a) CDFS, b) S11
and c) SGP fields. The "1'', "2'' and "3'' labels correspond to
the New A, N817 and N824 filters, respectively. The gridlines are
separated by 7
|
| Open with DEXTER | |
Figure 8 shows the sky distribution of our candidates
in each field. All candidates but one are in the CDFS and S11 fields.
The only candidate in the SGP field is brighter than the candidates in
the other fields (line flux ![]() 10-16 erg s-1 cm-2). The reason
for this is that the M815 filter for the SGP field has a shorter
exposure time and lower signal-to-noise than the other fields.
10-16 erg s-1 cm-2). The reason
for this is that the M815 filter for the SGP field has a shorter
exposure time and lower signal-to-noise than the other fields.
In the CDFS field we note that our three candidates appear to be
spatially clustered. Additionally, we note that the confirmed z=5.78i-drop galaxy of Bunker et al. (2003) is at the same redshift as the
WFILAS candidates in this field, just like four candidate LAEs from a
narrowband survey by Ajiki et al. (2006). We did not detect these four
candidates since they are fainter than the detection limits of WFILAS
in this field. Wang et al. (2005) have also done a narrowband survey of
the CDFS field. They also find evidence for an overdensity of
![]() sources in this field. Similarly, Malhotra et al. (2005) find
an overdensity at redshift 5.9
sources in this field. Similarly, Malhotra et al. (2005) find
an overdensity at redshift 5.9 ![]() 0.2 in the HUDF.
0.2 in the HUDF.
![\begin{figure}
\par\includegraphics[width=8.5cm, clip]{4882fg9.ps}
\end{figure}](/articles/aa/full/2006/31/aa4882-06/Timg77.gif) |
Figure 9:
A 38'' |
| Open with DEXTER | |
A pre-image with an intermediate band filter (FWHM = 13 nm) centred
at 815 nm was taken with VLT/FORS2 on 2005 August 9. The
0
![]() 252 pix-1 plate scale undersamples the
252 pix-1 plate scale undersamples the ![]() 0.5''stellar point spread function of the frames which were taken during
excellent seeing. SGP_8884 is unresolved, implying that the
FWHM of the emitting region is
0.5''stellar point spread function of the frames which were taken during
excellent seeing. SGP_8884 is unresolved, implying that the
FWHM of the emitting region is ![]() 2.2 kpc. A
38''
2.2 kpc. A
38'' ![]() 38'' region around the object is shown in
Fig. 9.
38'' region around the object is shown in
Fig. 9.
The spectroscopy consists of four exposures of 900 s, taken on 2005 October 3 with FORS2 using the 1028z grism and a 1'' slit. The frames were overscan subtracted and flatfielded. They were combined by summing individual frames, thereby removing cosmic rays in the process.
![\begin{figure}
\par\includegraphics[width=8.5cm, clip]{4882fg10.eps}
\end{figure}](/articles/aa/full/2006/31/aa4882-06/Timg79.gif) |
Figure 10:
( Top) Flux calibrated spectrum of the confirmed
candidate LAE SGP_8884, the brightest candidate in our sample.
The histogram shows the observed spectrum. Indicated in grey is the
best-fitting single component model after convolution with the
instrumental profile. The heavy bold lines indicate three regions
for which we have calculated a mean continuum. ( Bottom)
Residuals from the observed data minus model fit. The histograms
indicate the 1 |
| Open with DEXTER | |
The spectrum was flux calibrated using a standard star (HD 49798)
taken with a 5'' slit and corrected for slit-loss. This was
calculated assuming a Gaussian source profile with a FWHM of 0
![]() 72
as measured from the spatial direction of the spectrum. The flux lost
due to the 1'' slit was calculated and added to the spectrum of the
object.
72
as measured from the spatial direction of the spectrum. The flux lost
due to the 1'' slit was calculated and added to the spectrum of the
object.
Figure 10 shows the reduced spectrum of SGP_8884
alongside its best model fit. The spectrum has an asymmetric line
profile, similar to our previously confirmed candidate LAE
(Westra et al. 2005). It unlikely originates from a redshifted [O II] line
at ![]() because the resolution of our spectrum is high enough to
resolve the [O II]
because the resolution of our spectrum is high enough to
resolve the [O II]
![]() 3726, 3728. Figure 11 shows the spectrum of one such
[O II] emitter at z=1.18 which was included in the same observations
as SGP_8884. Furthermore, we do not find any other spectral features
in our spectrum, such as H
3726, 3728. Figure 11 shows the spectrum of one such
[O II] emitter at z=1.18 which was included in the same observations
as SGP_8884. Furthermore, we do not find any other spectral features
in our spectrum, such as H![]() or [ N II], which could classify the
emission coming from a lower redshift galaxy. Hence, we identify the
line as Ly
or [ N II], which could classify the
emission coming from a lower redshift galaxy. Hence, we identify the
line as Ly![]() at z=5.652. With a total spectral line flux of
(1.0
at z=5.652. With a total spectral line flux of
(1.0 ![]() 0.1)
0.1) ![]() 10-16 erg s-1 cm-2 (slit-loss
corrected), SGP_8884 is the brightest LAE at redshift
10-16 erg s-1 cm-2 (slit-loss
corrected), SGP_8884 is the brightest LAE at redshift ![]() 5.7 to
date. The line flux derived from the spectrum is consistent with the
flux derived from narrowband photometry
(9.5
5.7 to
date. The line flux derived from the spectrum is consistent with the
flux derived from narrowband photometry
(9.5 ![]() 1.4)
1.4) ![]() 10-17 erg s-1 cm-2, which is given
in Table 6. The spectral line flux corresponds to a line
luminosity of
10-17 erg s-1 cm-2, which is given
in Table 6. The spectral line flux corresponds to a line
luminosity of
![]() = 3.5
= 3.5 ![]() 1043 erg s-1 and
a star formation rate of 32
1043 erg s-1 and
a star formation rate of 32 ![]() yr-1, using the star
formation conversion rate of Ajiki et al. (2003). If we adopt
yr-1, using the star
formation conversion rate of Ajiki et al. (2003). If we adopt
![]() 16 pixels (=32 kpc2) as an upper limit to the size of
the emitting region, we derive a star formation rate surface density
of
16 pixels (=32 kpc2) as an upper limit to the size of
the emitting region, we derive a star formation rate surface density
of ![]()
![]() 1
1 ![]() yr-1 kpc-2.
yr-1 kpc-2.
Following earlier works (e.g. Hu et al. 2004; Westra et al. 2005; Dawson et al. 2002) we
fitted a single component model to the Ly![]() line SGP_8884. The model
consists of a truncated Gaussian with complete absorption blueward of
the Ly
line SGP_8884. The model
consists of a truncated Gaussian with complete absorption blueward of
the Ly![]() line centre. We find an excess of flux in the observed data
compared to the model around 8110 Å. This suggests the presence of
a second line component redward of the main peak. To test this, we
measured the mean continuum levels, both red- and blueward of the
line, as well as across the red-flanking region of the line. The
continuum is calculated as the weighted mean of the flux density over
this region. This yields for continuum in the red-flanking region a
flux density of (3.2
line centre. We find an excess of flux in the observed data
compared to the model around 8110 Å. This suggests the presence of
a second line component redward of the main peak. To test this, we
measured the mean continuum levels, both red- and blueward of the
line, as well as across the red-flanking region of the line. The
continuum is calculated as the weighted mean of the flux density over
this region. This yields for continuum in the red-flanking region a
flux density of (3.2 ![]() 0.8)
0.8) ![]() 10-19 erg s-1 cm-2 Å-1.
Red- and blueward of the Ly
10-19 erg s-1 cm-2 Å-1.
Red- and blueward of the Ly![]() line the continuum is
(-1.0
line the continuum is
(-1.0 ![]() 0.8)
0.8) ![]() 10-19 erg s-1 cm-2 Å-1 and
(0.9
10-19 erg s-1 cm-2 Å-1 and
(0.9 ![]() 0.6)
0.6) ![]() 10-19 erg s-1 cm-2 Å-1, respectively.
These continuum levels are indicated by the heavy bold lines in
Fig. 10. The lower limit for the rest frame equivalent
width derived from the continuum of the red flank is 46 Å. The rest
frame equivalent width derived from the 2
10-19 erg s-1 cm-2 Å-1, respectively.
These continuum levels are indicated by the heavy bold lines in
Fig. 10. The lower limit for the rest frame equivalent
width derived from the continuum of the red flank is 46 Å. The rest
frame equivalent width derived from the 2![]() upper limit of the
continuum redward of the line is 125 Å.
upper limit of the
continuum redward of the line is 125 Å.
| |
Figure 11:
( Left) Two dimensional spectrum of an [O II] emitting
galaxy at z=1.18 in the SGP field. ( Right) The extracted
one dimensional spectrum. We are able to easily resolve the [O II]
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm, clip]{4882fg12.eps}
\end{figure}](/articles/aa/full/2006/31/aa4882-06/Timg85.gif) |
Figure 12:
Comparison of the Ly |
| Open with DEXTER | |
Table 5: Parameters for the single component model to SGP_8884 before convolution with the instrumental profile. We also include the parameters for the single component and the two double component models of the previously confirmed LAE S11_5236 (Westra et al. 2005). These parameters differ slightly from Westra et al., since we have subsequently corrected the spectrum of S11_5236 for slit-losses.
To see if the excess of flux in the red flank of the Ly![]() line can be
explained by an outflow, we fit a second Gaussian component to the
spectrum of SGP_8884, as we did to the spectrum of S11_5236 in
Westra et al. (2005). This yields an extremely faint and broad second
component (
line can be
explained by an outflow, we fit a second Gaussian component to the
spectrum of SGP_8884, as we did to the spectrum of S11_5236 in
Westra et al. (2005). This yields an extremely faint and broad second
component (
![]() erg s-1 cm-2 Å-1 and
erg s-1 cm-2 Å-1 and
![]() km s-1). The precise parameters for the red
component are difficult to constrain given its faint and broad
profile. The parameters from the single component model for SGP_8884
and the single and double component models for S11_5236 are given in
Table 5.
km s-1). The precise parameters for the red
component are difficult to constrain given its faint and broad
profile. The parameters from the single component model for SGP_8884
and the single and double component models for S11_5236 are given in
Table 5.
The Ly![]() emission we see is due to intense star formation rates
synonymous with local starburst galaxies. Star formation rates per
unit area in excess of 0.1
emission we see is due to intense star formation rates
synonymous with local starburst galaxies. Star formation rates per
unit area in excess of 0.1 ![]() yr-1 kpc2 are prone to
produce large scale outflows of neutral hydrogen from a galaxy,
powered by the supernovae and stellar winds of massive stars
(Heckman 2002). The most efficient way for Ly
yr-1 kpc2 are prone to
produce large scale outflows of neutral hydrogen from a galaxy,
powered by the supernovae and stellar winds of massive stars
(Heckman 2002). The most efficient way for Ly![]() to escape from the
compact star forming regions is due to scattering of the photons by
the entrained neutral hydrogen (Chen & Neufeld 1994). The kinematics and
orientation of the outflowing neutral hydrogen can alter the Ly
to escape from the
compact star forming regions is due to scattering of the photons by
the entrained neutral hydrogen (Chen & Neufeld 1994). The kinematics and
orientation of the outflowing neutral hydrogen can alter the Ly![]() profile by absorbing photons bluer if along the line of sight, or
backscattering redder than Ly
profile by absorbing photons bluer if along the line of sight, or
backscattering redder than Ly![]() if behind and receding
(e.g. Dawson et al. 2002). Ly
if behind and receding
(e.g. Dawson et al. 2002). Ly![]() emission can also arise when large
scale shocks from starburst winds impinge on clumps (
emission can also arise when large
scale shocks from starburst winds impinge on clumps (![]() 100 pc)
of condensed gas accreting onto the halo (Bland-Hawthorn & Nulsen 2004).
100 pc)
of condensed gas accreting onto the halo (Bland-Hawthorn & Nulsen 2004).
Table 6:
The candidate list of the WFILAS survey after the selection
as described in Sect. 4. From left to right are
the object name, the B, R, M815, New A, N817 and N824 AB-magnitudes, line flux calculated from the narrowband
magnitude in which the object was detected and line luminosity. For
all measurements less than ![]() the
the ![]() upper limit has
been given.
upper limit has
been given.
Table 7:
Calculation of the Schechter function parameter L* and
luminosity density
![]() according to Ajiki et al. (2003) for
their sample, our complete sample and the combination of the two.
For each sample the luminosity density has been derived from the sum
of the candidate luminosities divided by the corresponding survey
volume. Then Eq. (2) was solved for L*, with given
according to Ajiki et al. (2003) for
their sample, our complete sample and the combination of the two.
For each sample the luminosity density has been derived from the sum
of the candidate luminosities divided by the corresponding survey
volume. Then Eq. (2) was solved for L*, with given
![]() and
and ![]() from Ajiki et al. (2003). Finally, the entire
luminosity function was integrated to give the final luminosity
density.
from Ajiki et al. (2003). Finally, the entire
luminosity function was integrated to give the final luminosity
density.
Most examples of asymmetric Ly![]() emission at
emission at ![]() show an
extended tail implying backscattering over a fairly wide range of
velocities beyond the central Ly
show an
extended tail implying backscattering over a fairly wide range of
velocities beyond the central Ly![]() emission (e.g. Fig. 9
of Hu et al. 2004). The limiting physical size of SGP_8884
(FWHM < 2.2 kpc) is consistent with the scale of emitting regions
in the local starburst galaxy M 82 which span 0.5 to 1 kpc
(Courvoisier et al. 1990; Blecha et al. 1990). This, and the scale of its outflow,
make it fairly typical of both the starbursting sources seen at
emission (e.g. Fig. 9
of Hu et al. 2004). The limiting physical size of SGP_8884
(FWHM < 2.2 kpc) is consistent with the scale of emitting regions
in the local starburst galaxy M 82 which span 0.5 to 1 kpc
(Courvoisier et al. 1990; Blecha et al. 1990). This, and the scale of its outflow,
make it fairly typical of both the starbursting sources seen at
![]() and their local counterparts.
and their local counterparts.
The tentative discovery of a second component in S11_5236
(Westra et al. 2005) could be explained by either an expanding shell of
neutral hydrogen (Ahn et al. 2003; Dawson et al. 2002), or by infall of the IGM onto
the LAE (Dijkstra et al. 2005). The flux of the intrinsic Ly![]() line
depends heavily on the model. It is suggested that the total intrinsic
Ly
line
depends heavily on the model. It is suggested that the total intrinsic
Ly![]() flux emerging from these sources is underestimated by an order
of magnitude (e.g. Dijkstra et al.). Therefore, the star
formation rates derived from the observed Ly
flux emerging from these sources is underestimated by an order
of magnitude (e.g. Dijkstra et al.). Therefore, the star
formation rates derived from the observed Ly![]() lines could be heavily
underestimated.
lines could be heavily
underestimated.
Figure 12 shows a comparison between the line
profiles of the two LAEs discovered with WFILAS. S11_5236 differs
from SGP_8884 in that a clear peak, ![]() 20-90 km s-1 wide,
is seen
20-90 km s-1 wide,
is seen ![]() 400 km s-1 redward of Ly
400 km s-1 redward of Ly![]() (Westra et al. 2005). The red
component is narrower (
(Westra et al. 2005). The red
component is narrower (![]() 15%) and relatively stronger than
SGP_8884. The difference in the width of the red component is even
more pronounced (
15%) and relatively stronger than
SGP_8884. The difference in the width of the red component is even
more pronounced (![]() 30%) when we compare the main peak of the
two-component fits to the spectrum of S11_5236 to the single peak of
the one-component fits to the spectrum of SGP_8884. This can clearly
be seen in panels a and e of Fig. 12.
30%) when we compare the main peak of the
two-component fits to the spectrum of S11_5236 to the single peak of
the one-component fits to the spectrum of SGP_8884. This can clearly
be seen in panels a and e of Fig. 12.
Ultimately, such outflows are thought to be responsible for the
chemical enrichment of the IGM by ![]() (Aguirre et al. 2001). Outflows
are a process facilitating the escape of UV photons, which are the
origin for the UV background (Madau et al. 1999).
(Aguirre et al. 2001). Outflows
are a process facilitating the escape of UV photons, which are the
origin for the UV background (Madau et al. 1999).
Most of our candidates are in the regimes of bright luminosities,
beyond the reach of less voluminous surveys. Adding our candidates to
those of earlier such surveys results in an integrated luminosity
density
![]() % higher than found by such surveys
alone. We also find potential clustering in our CDFS field, supporting
overdensities discovered by other surveys. Spectroscopic follow-up for
confirmation in this area will be crucial.
% higher than found by such surveys
alone. We also find potential clustering in our CDFS field, supporting
overdensities discovered by other surveys. Spectroscopic follow-up for
confirmation in this area will be crucial.
Two candidates have been confirmed to be LAEs at ![]() by means
of spectroscopy. One of these galaxies is the brightest LAEs at this
redshift. The broad, asymmetric profiles of the Ly
by means
of spectroscopy. One of these galaxies is the brightest LAEs at this
redshift. The broad, asymmetric profiles of the Ly![]() line of both
objects are consistent with neutral hydrogen backscattering of a
central starbursting source.
line of both
objects are consistent with neutral hydrogen backscattering of a
central starbursting source.
Acknowledgements
The authors wish to thank the Max-Planck-Institut für Astronomie and the DDT grant of the European Southern Observatory for providing the narrow band filters which are crucial to the WFILAS survey. The broadband and part of the intermediate band data were kindly provided by the COMBO-17 team (Wolf et al. 2004). We also like to thank the anonymous referee for his/her useful suggestions and comments. E.W. wishes to thank A. Frebel for her useful comments and discussions regarding this paper and the Astronomical Society of Australia Travel Grant. D.H.J. is supported as a Research Associate by the Australian Research Council Discovery-Projects Grant (DP-0208876), administered by the Australian National University. C.W. is supported by a PPARC Advanced Fellowship.