Table 7:
Calculation of the Schechter function parameter L* and
luminosity density
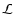 according to Ajiki et al. (2003) for
their sample, our complete sample and the combination of the two.
For each sample the luminosity density has been derived from the sum
of the candidate luminosities divided by the corresponding survey
volume. Then Eq. (2) was solved for L*, with given
according to Ajiki et al. (2003) for
their sample, our complete sample and the combination of the two.
For each sample the luminosity density has been derived from the sum
of the candidate luminosities divided by the corresponding survey
volume. Then Eq. (2) was solved for L*, with given
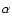 and
and 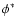 from Ajiki et al. (2003). Finally, the entire
luminosity function was integrated to give the final luminosity
density.
from Ajiki et al. (2003). Finally, the entire
luminosity function was integrated to give the final luminosity
density.
| |
 |
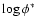 |
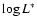 |
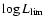 |
log V |
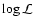 |
Comment |
| |
|
Mpc-3 |
erg s-1 |
erg s-1 |
Mpc3 |
erg s-1 Mpc-3 |
|
| Case A |
- |
- |
- |
42.85 |
5.26 |
39.04 |
Sum of the candidates from Ajiki et al. (2003) |
| |
-1.53 |
-2.62 |
42.61 |
42.85 |
5.26 |
39.04 |
Integrated luminosity function down to Ajiki et al. (2003) survey limit (
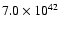 erg s-1) erg s-1) |
| |
-1.53 |
-2.62 |
42.61 |
- |
- |
40.27 |
Integration of the entire luminosity function |
| Case B |
- |
- |
- |
43.26 |
5.71 |
38.36 |
Sum of the candidates from completeness corrected WFILAS sample |
| |
-1.53 |
-2.62 |
42.74 |
43.26 |
5.71 |
38.36 |
Integrated luminosity function down to the limit of the completeness corrected sample (
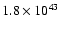 erg s-1) erg s-1) |
| |
-1.53 |
-2.62 |
42.74 |
- |
- |
40.39 |
Integration of the entire luminosity function |
| Case C |
- |
- |
- |
42.85 |
5.84 |
39.19 |
Sum of the combined WFILAS and Ajiki et al. (2003) samples low luminosity corrections |
| |
-1.53 |
-2.62 |
42.66 |
42.85 |
5.84 |
39.19 |
Integrated luminosity function down to Ajiki et al. (2003) survey limit (
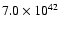 erg s-1) erg s-1) |
| |
-1.53 |
-2.62 |
42.66 |
- |
- |
40.32 |
Integration of the entire luminosity function |