A&A 455, 325-338 (2006)
DOI: 10.1051/0004-6361:20054598
Ch. Helling1 - P. Woitke2
1 - Astrophysics Missions Division, Research and Scientific Support Department ESTEC, ESA, PO Box 299, 2200 AG Noordwijk, The Netherlands
2 -
Sterrewacht Leiden, PO Box 9513, 2300 RA Leiden, The Netherlands
Received 28 November 2005 / Accepted 28 April 2006
Abstract
In this paper, we propose a kinetic description for the
growth and evaporation of oxygen-rich, dirty dust particles, which
consist of numerous small islands of different solid materials like
Mg2SiO4, SiO2, Al2O3, Fe and TiO2. We assume
that the total surface of such a grain collects
condensible molecules from the gas phase and that these molecules
are rapidly transported by diffusive hopping on the surface to the
respective solid islands, where finally the constructive surface
chemical reactions take place which increase the size of the
grain. Applied to a typical dust forming region in a brown dwarf
atmosphere, turbulent temperature fluctuations enable the creation
of first seed particles (nucleation) at high supersaturation
ratios. These seeds are then quickly covered by different solid
materials in a simultaneous way, which results in dirty grains. Our
treatment by moment equations allows for the calculation of the
time-dependent material composition of the dust grains and the
elemental composition of the gas phase. We argue that the depletion
of condensible elements from the gas phase by dust formation
may be incomplete and occurs in a patchy, non-uniform way which
possibly makes metallicity measurements highly uncertain.
Key words: stars: atmospheres - stars: low-mass, brown dwarfs - methods: numerical - astrochemistry
Dust is an essential part of brown dwarf atmospheres. It controls the opacity of the dust/gas mixture and influences the chemical, thermal and dynamical state of the atmosphere. Dust consumes condensible elements from the gas phase which weakens molecular absorption lines (Kirkpatrick et al. 1999; Burgasser et al. 2002; Geballe et al. 2002). Dust formation is a time-dependent process which may be the reason for non-periodic short-term variability (Bailer-Jones & Mund 1999, 2001a,b; Martín et al. 2001; Gelino et al. 2002; Maiti et al. 2005), recently also seen in polarisation measurements (Mènard et al. 2002; Maiti et al. 2005; Zapatero Osorio et al. 2005). Rockenfeller et al. (2006) point out evidence that more L dwarfs are non-periodically variable compared to M dwarfs. Spectro-polarimetry provides furthermore a possibility to measure the vertical distribution of the dust particles and their mean size in the atmosphere (Stam et al. 1999; Sengupta & Krishan 2001; Sengupta 2003; Sengputa & Kwok 2005; Stam & Hovenier 2005), if the refractory index of the dust grain material is known.
However, the actual material composition of the dust grains is difficult to constrain by observations, because it is an ill-posed problem with ambiguities concerning grain composition, lattice structure, size and shape distribution, and eventually dirty inclusions.
In this paper, we will argue for the formation of dirty dust grains in brown dwarf atmospheres from theoretical arguments. We consider the dust formation to take place in atmospheric upwinds powered by convective motions (see Helling 2003). The gas in these upwinds originates from the deep interior of the brown dwarf and is hence seed particle free - different from the condensation of water on aerosols in the Earth atmosphere. Therefore, the first process to occur in the dust formation circle must be the nucleation (seed particle formation) which requires much lower temperatures (higher supersaturation) as compared to the temperature where large solid particles are thermally stable. Once these seeds have formed, a large variety of condensible materials is already thermally stable, and different grain materials may grow on the surface on these seeds simultaneously. Thus, the formation of inhomogeneous dust particles with inclusions of different kinds of solid materials suggests itself.
Other theoretical works on dust formation in substellar
atmospheres have not considered this basic problem. For example, dust
formation is parameterised by a sedimentation efficiency
![]() in Ackerman & Marley (2001), by a critical temperature
in Ackerman & Marley (2001), by a critical temperature
![]() in Tsuji (2002), or by a maximum supersaturation ratio
in Tsuji (2002), or by a maximum supersaturation ratio
![]() in Cooper et al. (2003). The chemical homogeneity of the dust
particles is always taken for granted, leading to well separated
distributions of pure dust particles consisting of different
materials, strictly following the dust stability sequence (see e.g.
Lodders & Fegley 2005).
in Cooper et al. (2003). The chemical homogeneity of the dust
particles is always taken for granted, leading to well separated
distributions of pure dust particles consisting of different
materials, strictly following the dust stability sequence (see e.g.
Lodders & Fegley 2005).
Based on such assumptions, static brown dwarf model atmospheres
were developed which provided the first understanding of brown dwarf
spectra (e.g. Allard et al. 2001; Tsuji
2002, and above cited works). Due to the parameterised treatment of dust formation, certain
limiting cases needed to be considered, namely entirely dust
enshrouded brown dwarfs (seemingly appropriate for spectral types
![]() L2
L2![]() L4) and entirely dust cleared (settled) brown
dwarf atmospheres (
L4) and entirely dust cleared (settled) brown
dwarf atmospheres (![]() T1
T1![]() T9). The above mentioned
parameterisation by Tsuji allows for first ideas to understand the
L-T transition region (Tsuji 2005).
T9). The above mentioned
parameterisation by Tsuji allows for first ideas to understand the
L-T transition region (Tsuji 2005).
The present paper is the continuation of the work presented in Helling et al. (2001, 2004, Papers I and IV) and Woitke & Helling (2003, 2004, Papers II and III). Papers I and IV have investigated the key role of turbulence in the process of dust formation in substellar atmospheres on small spatial scales with a simple model for core-mantle grains. In Papers II and III, we have developed a large-scale quasi-static model for cloud layers in brown dwarf atmospheres including the evaporation and gravitational settling of size-dependent dust particles composed of one solid material. Helling et al. (2006) show a first study of the spectral appearance of such a chemically heterogeneous dust cloud layer.
In the present paper, we develop a kinetic description for the growth and evaporation of dirty dust particles (Sect. 2), which allows for a calculation of the time-dependent material composition of the dust grains and the consumption/enrichment of condensible elements in the gas phase. Section 3 describes an application of this theory to a small, actively condensing region in a brown dwarf atmosphere. In Sect. 4, we present our results and evaluate the influence of the sticking coefficient on our results. We discuss the need for seed particle formation and the possible consequences of dust formation for metallicity-determinations in Sect. 5, and draw our conclusive summary in Sect. 6.
The dense, oxygen-rich gas of a substellar (e.g. brown dwarf) atmosphere consists of a variety of molecules (see Fig. 5) which can contribute simultaneously to the growth of different stable solid phases. We therefore expect the forming grains to consist of more than one solid material and to become patchy ("dirty''). If the surrounding temperature increases, for example because such a grain sinks downward in the atmosphere due to gravity, some of the solids start to become thermally unstable sooner than others, causing their evaporation.
Works in solid state physics show that the growth of one solid phase on another, already existing, alien solid surface results in aggregates of small islands (e.g. Chan et al. 2004). Chen et al. (2000) show, for instance, that copper islands form on TiO2 surfaces, the size of which stays almost constant. The number of islands increases, if more copper settles on the surface. Furthermore, McCarty (2003) argues that solid islands shrink at a nearly constant rate during evaporation. Buyevich & Tre'yakov (1994) describe the formation of islands with a stochastic model showing that the supersaturation and the surface coverage by the new phase are functions of time.
| |
Figure 1:
Sketch of the surface chemical processes involved in the
growth and evaporation of an island of solid material s at the
surface of a dirty dust grain. The total surface area
|
| Open with DEXTER | |
In order to model the dust in brown dwarf atmospheres, we must describe both the growth and the evaporation processes quantitatively. The following assumptions are made (see Fig. 1):
In the following we will follow the basic idea of a dust moment method
developed by Gail & Sedlmayr (1988)![]() . We express the
evaporation rates of the different solid phases in a dirty grain by
applying detailed balance considerations (Milne relations) to the
growth rates with respect of a carefully defined reference state.
We formulate the general problem in size space and define the dust
moments in Sect. 2.1. The growth rates are quantified in
Sect. 2.1.1 and the reference state is introduced
in Sect. 2.1.2. Section 2.2 summarises the
results for the modified growth velocity for dirty grains.
. We express the
evaporation rates of the different solid phases in a dirty grain by
applying detailed balance considerations (Milne relations) to the
growth rates with respect of a carefully defined reference state.
We formulate the general problem in size space and define the dust
moments in Sect. 2.1. The growth rates are quantified in
Sect. 2.1.1 and the reference state is introduced
in Sect. 2.1.2. Section 2.2 summarises the
results for the modified growth velocity for dirty grains.
We consider a size distribution of dirty dust grains denoted by
![]() .
As argued in Dominik et al. (1993) it is favourable to work with the grain
volume V instead of the grain radius or the monomer number as
size coordinate in case of dirty grains. The master equation for the
grains in size interval
.
As argued in Dominik et al. (1993) it is favourable to work with the grain
volume V instead of the grain radius or the monomer number as
size coordinate in case of dirty grains. The master equation for the
grains in size interval ![]() as affected by the various surface
chemical reactions R, is given by
as affected by the various surface
chemical reactions R, is given by
The Knudsen numbers are assumed to be appropriately large to
consider a sub-sonic flow of freely impinging molecules to the grain
surface (see Paper II for details). Furthermore, we will only
consider type I surface reactions![]() in the main text of the paper. Type II and type III
reactions are treated in detail in Appendix B. According to
our assumptions outlined in Sect. 2, the growth (
in the main text of the paper. Type II and type III
reactions are treated in detail in Appendix B. According to
our assumptions outlined in Sect. 2, the growth (![]() )
and evaporation (
)
and evaporation (
![]() )
rates, which cause a
(de-)population of the considered volume interval
)
rates, which cause a
(de-)population of the considered volume interval
![]() (see also Fig. 5 in Paper II), can be expressed by
(see also Fig. 5 in Paper II), can be expressed by
In the following, we eliminate the evaporation rate coefficient
![]() by a detailed balance consideration. In complete
thermodynamic equilibrium, each process is exactly balanced by its
reverse process. This reference state, which will be denoted by
by a detailed balance consideration. In complete
thermodynamic equilibrium, each process is exactly balanced by its
reverse process. This reference state, which will be denoted by
![]() ,
is characterised by phase equilibrium with the
considered solid (S=1), which is in a pure state (
,
is characterised by phase equilibrium with the
considered solid (S=1), which is in a pure state (
![]() )
and has an infinite flat surface. Furthermore, thermal
equilibrium between gas and solid (
)
and has an infinite flat surface. Furthermore, thermal
equilibrium between gas and solid (
![]() ), and
chemical equilibrium in the gas phase (
), and
chemical equilibrium in the gas phase (
![]() )
are
valid. In this reference state, the growth and evaporation rates
according Eqs. (4)-(7) are given by
)
are
valid. In this reference state, the growth and evaporation rates
according Eqs. (4)-(7) are given by
Table 1:
Chemical surface reactions r assumed to form one new unit
of the solid material s in the grain mantel. The efficiency of the
reaction is limited by the key species, which has the lowest
abundance among the reactants. The notation
![]() in the
r.h.s. column means that only every second collision (and sticking)
event initiates one reaction of kind r to form the dust
species s (see
in the
r.h.s. column means that only every second collision (and sticking)
event initiates one reaction of kind r to form the dust
species s (see
![]() in Eqs. (24),
(29)).
in Eqs. (24),
(29)).
Inserting this Milne relation and the Eqs. (12)
and (13) into
Eqs. (4)-(7) leads to the following
equations
| (14) | |||
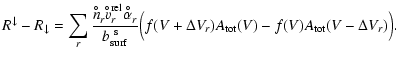 |
(15) |
For type II and type III reactions, the functional shape of the
ratio between growth and evaporation rates (Eq. (17)) remains the same, but S must be replaced by a
suitably defined reaction supersaturation ratio Sr and the explicit
formulae for
![]() and
and
![]() are different (see
Patzer et al. 1998 for type II reactions). The exact definition of
Sr is given in Appendix B. In most cases, Sr is
approximately given by a certain power of S, i.e.
are different (see
Patzer et al. 1998 for type II reactions). The exact definition of
Sr is given in Appendix B. In most cases, Sr is
approximately given by a certain power of S, i.e.
![]() (Eq. (B.8)). For the remainder of this paper, we will
assume thermal and chemical equilibrium
(Eq. (B.8)). For the remainder of this paper, we will
assume thermal and chemical equilibrium![]() and hence
and hence
![]() for all surface reaction types.
for all surface reaction types.
The remainder of the derivation of the dust moment equations is
analog to Gail & Sedlmayr (1988). The result is
According to our assumptions about the micro-physics of the growth and evaporation processes (see Sect. 2), the different solid islands can grow and evaporate simultaneously. Therefore, the net effect of single surface reactions (- growth or evaporation?) must be disentangled from the net effect for the entire dirty grain
| Reaction r | Entire grain | |
| growth |
|
|
| evaporation |
|
|
whereas in case of pure grains (
![]() ), the
supersaturation ratio S alone determines the sign of all individual
reactions (in thermal and chemical equilibrium), i.e. also the net effect
for the growth or evaporation of dust grains.
), the
supersaturation ratio S alone determines the sign of all individual
reactions (in thermal and chemical equilibrium), i.e. also the net effect
for the growth or evaporation of dust grains.
For the following numerical simulations of the growth and
evaporation of dirty grains we need to determine
![]() for all participating solid materials. As the most simple choice,
we assume that all islands of all considered solid materials are
well-mixed inside the dust grains
for all participating solid materials. As the most simple choice,
we assume that all islands of all considered solid materials are
well-mixed inside the dust grains
Disregarding drift motions and diffusive mixing, the elemental
composition of the dust component reflects the integral consumption of
elements from the local gas
![]() since the
onset of the dust formation process at t=0. Assuming furthermore
that there is a unique relation between the missing elements in the gas phase
and the material composition of the grains we can write
since the
onset of the dust formation process at t=0. Assuming furthermore
that there is a unique relation between the missing elements in the gas phase
and the material composition of the grains we can write
The gas element conservation equations as affected by nucleation, growth
and evaporation are given by
Before we proceed to more complex applications of our theoretical approach in a forthcoming paper we will first discuss a simple as possible hydrodynamic set-up in order to illustrate the principle mechanisms and chemical feedbacks involved. We feel that this is necessary because of the complex interaction between chemical gas phase composition and dust formation process and their feedback on temperature and velocity field. For this purpose we also refrain from the complex turbulence model used in Paper IV but utilise the simple model of colliding expansion waves as used in Paper I. Our model represents an initially dust-free and hot ascending gas element in a brown dwarf atmosphere which is influenced by sound waves generated in the turbulent environment. At a first glance, this scenario seems very special. But in fact, astrophysical dust formation can be assumed to proceed always in a slowly cooling flow (e.g. Sedlmayr 1999), where turbulent variations will facilitate to overcome the nucleation barrier in most cases.
Section 3.1 summarises the complete set of model equations for a compressible, dust-forming gas. Section 3.2 describes the numerical features of the simulation code, initial and boundary conditions.
Complex A: hydrodynamics. The hydrodynamical equations for an inviscid, compressible fluid with radiative cooling are
Complex B1: chemical equilibrium. In contrast to the hydrodynamic simulations presented in Papers I and IV, we calculate now the actual molecular abundances of our dust forming species in chemical equilibrium. We have implemented a chemical equilibrium routine involving 10 elements (H, C, N, O, S, Ti, Si, Mg, Fe, Al) which where chosen to cover the most important gas phase species for dust formation. We calculate the abundances of 36 molecules (H2, N2, NH3, CH4, HCN, CO, CO2, H2O, H2S, SiS, SO, HS, SiO, SiH, SiH4, SiO2, SiN, SO2, TiC, TiC2, TiO, TiO2, TiS, AlOH, AlO2H, Al2O, AlH, AlS, MgS, MgO, MgOH, MgH, Mg(OH)2, FeO, FeS, Fe(OH)2). We have checked that this reduced chemical equilibrium code yields approximately the same concentrations as the full chemical equilibrium code used in Paper II + III (14 elements and 155 molecules) with an error of less than about 10%. The molecular input data are the same and the element abundances applied are given in Appendix C.
Complex B2: dust formation. The dust formation including nucleation, growth and evaporation is modelled as described in Sect. 2. The system of equations is given in Sect. 2.2 and was solved in its dimensionless form.
We do only consider the formation of solid dust grains and our material quantities are not explicitely set to treat liquid phases.
The nucleation rate J* is calculated for homogeneous
(TiO2)N-clusters via
We consider the simultaneous growth of the solids TiO2[s], SiO2[s], Fe[s], Mg2SiO4[s] and Al2O3[s] onto the TiO2seed particles. The chemical surface reactions causing the growth and evaporation of these solids are listed in Table 1. We have selected these reactions to include all abundant reactants for a wide range of thermodynamic conditions (see Sect. 4.4.1). According to the number of solids formed, we have 5 blocks of chemical reactions. Many of the reactions involve also H2O (as oxygen source) and H2 (see Sect. 4.4).
It remains to specify the growth rate coefficients ![]() ,
also called sticking coefficient. Andersen et al. (2003) have demonstrated the effect of this parameter on the mass loss efficiency of AGB stars. The
mass loss rate increases with increasing sticking coefficient since dust forms faster. This conclusion is straightforward, it is
not as straightforward to know the proper value for
,
also called sticking coefficient. Andersen et al. (2003) have demonstrated the effect of this parameter on the mass loss efficiency of AGB stars. The
mass loss rate increases with increasing sticking coefficient since dust forms faster. This conclusion is straightforward, it is
not as straightforward to know the proper value for ![]() for each of the chemical reactions r involved into the formation of
the respective solid s (see Table 1). We follow the assumptions and citations in Paper I and use
for each of the chemical reactions r involved into the formation of
the respective solid s (see Table 1). We follow the assumptions and citations in Paper I and use
![]() but discuss its implications in more detail in Sect. 4.6.
but discuss its implications in more detail in Sect. 4.6.
Complex B3: Element conservation. The element conservation is calculated according to Eq. (29) for the six affected elements O, Si, Mg, Fe, Al and Ti (+ sulphur S and hydrogen H) in their dimensionless form.
Fully time-dependent solutions of the model equations have been obtained by applying a multi-dimensional hydro code (Smiljanovski et al. 1997) which has been extended in order to treat the complex of dust formation and element conservation (Helling et al. 2001). We solve 17 differential equation of which the energy equation, the dust moment equations, and the 8 element conservation equation (including S and H) can become very stiff due to the dust formation and its feedbacks.
Spatial dimension and grid resolution: for the purpose of this paper to demonstrate the temporal behaviour of an oxygen-rich gas forming dirty grains in a brown dwarf atmosphere, one-dimensional models are sufficient. The spatial resolution is 500 grid points and the size of the domain is
Model setup: the chosen parameters and initial conditions describe an initially hot and dust-free gas element in a slightly cooler, turbulent environment. The initial value for the gas temperature is chosen as
![\begin{figure}
\includegraphics[width=8.2cm]{4598fig2.eps}
\end{figure}](/articles/aa/full/2006/31/aa4598-05/Timg190.gif) |
Figure 2:
Local hydro- and thermodynamical processes in a dust-forming gas
as affected by expansion waves (dashed : 0.01 s, solid: 0.15 s, dotted: 5 s).
1st row: l.h.s. density |
| Open with DEXTER | |
Boundary conditions: the boundaries are transparanet and the same as in Paper I.
Initial conditions: the gas is assumed to contain initially neither seed nor dust particles Lj(t=0)=0. The element abundances are initially solar
Material data: we use equilibrium constants fitted to the thermodynamical molecular data from the electronic version of the JANAF tables (Chase et al. 1985). The details on the material data for the dust complex are given in Appendix C. The gas and dust opacities are not treated in detail in this paper. We assume
![\begin{figure}
\par\mbox{\includegraphics[width=5.02cm,clip]{4598fig3a.eps}\qqua...
...3b.eps}\qquad
\includegraphics[width=5.4cm,clip]{4598fig3c.eps} }\end{figure}](/articles/aa/full/2006/31/aa4598-05/Timg199.gif) |
Figure 3:
Local details of the dust formation process and the
evolution of the chemical abundances in the gas phase. The
colours/line-styles indicate the dust species (and assigned elements) as
follows. Dark blue/full: TiO2[s] (Ti); brown/short
dash-dot: SiO2[s] (Si); green/long dash-dot: Fe[s] (Fe);
orange/long dashed: Mg2SiO4[s] (Mg), light blue/dotted:
Al2O3[s] (Al); red/dashed: [no assigned dust species] (O).
1st row: supersaturation ratios S (*), 2nd row: inverse surface
area non-equilibrium factors
|
| Open with DEXTER | |
Figure 2 depicts the results for the simulation of an initially hot dust-hostile region of a substellar atmosphere (e.g. an ascending convective element) which is affected by expansion waves representing single turbulence events (eddies).
At the first depicted instant of time (dashed: 0.01 s, i.e. prior to the superposition of the two expansion waves) no or only very little nucleation takes place.
The second instant of time (solid: 0.15 s) shows the time of
constructive superposition of the two expansion waves. The
temperature falls below the nucleation threshold for TiO2-seed
formation, and
the nucleation rate has a maximum. A considerable amount of small dust
particles form (
![]() cm-3) which enforce
radiative cooling toward
cm-3) which enforce
radiative cooling toward
![]() due to increased opacity.
due to increased opacity.
Long after this superposition event (dotted: 5 s)
the central dust formation site has reached a steady state
characterised by pressure equilibrium, radiative equilibrium
(
![]() ), and a phase equilibrium (see
next paragraph).
), and a phase equilibrium (see
next paragraph).
Figure 3 shows the results of the dust complex
and the depletion of the gas phase for the same instants of time as depicted
in Fig. 2, but only for the dust formation site,
i.e. between
![]() .
Note that Fig. 3 dipicts S for all compounds but for Al2O2[s] and Mg2SiO4
.
Note that Fig. 3 dipicts S for all compounds but for Al2O2[s] and Mg2SiO4
![]() (
(
![]() ,
see Table 1 and Appendix B) is plotted.
,
see Table 1 and Appendix B) is plotted.
The first instant of time (t=0.01 s, left column) shows the situation prior to the event of efficient
nucleation. The most stable solid materials (![]() at x=0.25) are Al2O3[s], Fe[s], and TiO2[s] but the
non-existence of seed particles hinders its condensation. The supersaturation of TiO2[s] is not yet sufficiently high to
initiate nucleation. Mg2SiO4[s] is thermally unstable (
at x=0.25) are Al2O3[s], Fe[s], and TiO2[s] but the
non-existence of seed particles hinders its condensation. The supersaturation of TiO2[s] is not yet sufficiently high to
initiate nucleation. Mg2SiO4[s] is thermally unstable (![]() )
in the region(s) not affected by the
expansion waves. SiO2[s] is everywhere thermally unstable.
The gas abundances are throughout solar.
)
in the region(s) not affected by the
expansion waves. SiO2[s] is everywhere thermally unstable.
The gas abundances are throughout solar.
The second time step (t=0.15 s, 2nd column) depicts
the situation at the time of constructive superposition of the two expansion
waves (compare caption Fig. 2). The corresponding temperature minimum results in a considerable
increase of the supersaturation ratios, causing in this example
the thermal stability of all considered solid materials. The reciprocal surface non-equilibrium factors
![]() indicate the volume
fractions of the dirty grains. The growth rates of the different solid
materials is mostly given by kinetic constraints (mainly the
abundance of the key reactant). Mg2SiO4[s] growths the fastest
followed by SiO2[s], Fe[s], Al2O3[s] and TiO2[s] is the
slowest. The dust particles are still small (
indicate the volume
fractions of the dirty grains. The growth rates of the different solid
materials is mostly given by kinetic constraints (mainly the
abundance of the key reactant). Mg2SiO4[s] growths the fastest
followed by SiO2[s], Fe[s], Al2O3[s] and TiO2[s] is the
slowest. The dust particles are still small (
![]() m) and the growth is not exhaustive yet.
The gas abundances are still approximately solar.
m) and the growth is not exhaustive yet.
The gas abundances are still approximately solar.
The third time step (t=5 s, right column)
demonstrates the relaxation of the dust-forming system towards
phase equilibrium. In the very centre of the superposition region,
growth and evaporation already balance each other, hence
![]() and
and
![]() for all reactions. Outside of
the central region, further relaxation is still going on, where the
growth of the solids becomes slower due to the decreasing abundances
of the gaseous reactants via consumption.
In the central region, the grains have reached their
final size (
for all reactions. Outside of
the central region, further relaxation is still going on, where the
growth of the solids becomes slower due to the decreasing abundances
of the gaseous reactants via consumption.
In the central region, the grains have reached their
final size (
![]() m) with a material
composition that is mainly given by element abundance
constraints. Most of the dust volume is filled by Mg2SiO4[s],
followed by SiO2[s], Fe[s], Al2O3[s] and TiO2[s]. The
reduced element abundances reflect these amounts of condensates.
m) with a material
composition that is mainly given by element abundance
constraints. Most of the dust volume is filled by Mg2SiO4[s],
followed by SiO2[s], Fe[s], Al2O3[s] and TiO2[s]. The
reduced element abundances reflect these amounts of condensates.
![\begin{figure}
\par\mbox{\includegraphics[width=4.4cm,clip]{4598fig4a.eps}\includegraphics[width=4.31cm,clip]{4598fig4b.eps} }\end{figure}](/articles/aa/full/2006/31/aa4598-05/Timg213.gif) |
Figure 4:
Dust volume fractions, expressed by
|
| Open with DEXTER | |
Figure 4 depicts the dust volume fractions
![]() (Eq. (25))
as function of time for the five solid species taken into account
Mg2SiO4[s], SiO2[s], Fe[s], Al2O3[s], and TiO2[s] (bottom
panels). For a better overview, we also plot the cumulative volume fractions
(upper panels).
(Eq. (25))
as function of time for the five solid species taken into account
Mg2SiO4[s], SiO2[s], Fe[s], Al2O3[s], and TiO2[s] (bottom
panels). For a better overview, we also plot the cumulative volume fractions
(upper panels).
Quickly after the onset of nucleation, the initial TiO2 seed
particles are covered by forsterite Mg2SiO4[s] (
![]() ),
silica SiO2[s] (
),
silica SiO2[s] (
![]() ),
with further inclusions of
solid iron (
),
with further inclusions of
solid iron (
![]() )
and corundum Al2O3[s] (
)
and corundum Al2O3[s] (
![]() ). The rutile TiO2[s]
fraction is constantly decreasing with increasing grain size and finally negligible
(<0.1%). Provided that the different solid materials are all
sufficiently stable (
). The rutile TiO2[s]
fraction is constantly decreasing with increasing grain size and finally negligible
(<0.1%). Provided that the different solid materials are all
sufficiently stable (![]() ), the rates of volume increase at
early phases are not related to stability considerations. They are
rather constrained by the following kinetic quantities: (i) the
abundance of the key reactant for the growth reactions in the gas phase,
(ii) its thermal velocity and (iii) the monomer volume of the
respective solid.
), the rates of volume increase at
early phases are not related to stability considerations. They are
rather constrained by the following kinetic quantities: (i) the
abundance of the key reactant for the growth reactions in the gas phase,
(ii) its thermal velocity and (iii) the monomer volume of the
respective solid.
The small wiggles in the SiO2[s] and Mg2SiO4[s] volume
fractions are related to the evolution of the temperature T (compare
Fig. 6). The minimum temperature due to
constructive superposition of expansion waves is achieved at
![]() s. The radiative equilibrium temperatur is slightly higher and
the forsterite Mg2SiO4[s]
becomes temporarily thermally unstable and partly re-evaporate. The
final composition in the relaxed phase equilibrium state
(
s. The radiative equilibrium temperatur is slightly higher and
the forsterite Mg2SiO4[s]
becomes temporarily thermally unstable and partly re-evaporate. The
final composition in the relaxed phase equilibrium state
(
![]() )
favours Mg2SiO4[s]
(
)
favours Mg2SiO4[s]
(
![]() )
over SiO2[s] (
)
over SiO2[s] (
![]() ). The still
relatively small contribution of solid iron (
). The still
relatively small contribution of solid iron (
![]() )
is
partly caused by its exceptionally small monomer volume (see
Table B.1).
)
is
partly caused by its exceptionally small monomer volume (see
Table B.1).
![\begin{figure}
\par\includegraphics[width=14.2cm,clip]{4598fig5.eps}
\end{figure}](/articles/aa/full/2006/31/aa4598-05/Timg224.gif) |
Figure 5:
Gas phase chemistry: particle densities |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.3cm,clip]{4598fig6a.eps}\quad
\includegraphics[width=8.3cm,clip]{4598fig6b.eps} }\par\end{figure}](/articles/aa/full/2006/31/aa4598-05/Timg228.gif) |
Figure 6:
Evolution of temperature, dust, and chemistry at the centre
of wave interaction (x=0.25, l.h.s.: short-term - r.h.s.: long-term).
Left panels on l.h.s.:
1st row: temperature T [1900 K],
2nd row: nucleation rate per hydrogen nuclei
|
| Open with DEXTER | |
The composition of the gas phase is not only an important pre-condition for the process of dust formation, it is also a result of dust formation. Figure 6 shows the time evolution of the temperature, the chemical composition of the gas phase, and some dust quantities at the site of constructive wave superposition x=0.25 (l.h.s.: short term - r.h.s.: long term).
In order to clarify the temperature dependence of the molecular
concentrations, we have additionally plotted those concentrations as
function of T in Fig. 5 for two sets of
element abundances![]() . The l.h.s. of Fig. 5 shows the results
for the initial (solar) element abundances, and the r.h.s. of
Fig. 5 for those element abundances which are achieved
at late stages in the dust formation model, when the dust-forming gas
has reached phase equilibrium.
. The l.h.s. of Fig. 5 shows the results
for the initial (solar) element abundances, and the r.h.s. of
Fig. 5 for those element abundances which are achieved
at late stages in the dust formation model, when the dust-forming gas
has reached phase equilibrium.
Consequently, not only supersaturation and surface coverage by the different solids are functions of time, as it was also shown by Buyevich & Tre'yakov (1994) who adopt a stochastic approach, also the remaining gas phase abundance vary with time.
The basis for the chemical composition of the gas phase is its element
composition. Concerning the dust forming elements, oxygen (O) is
initially most abundant, followed by iron (Fe), magnesium (Mg),
silicon (Si), aluminum (Al), and titan (Ti). The carbon-to-oxygen
ratio is
![]() for the solar abundances given in
Table C.1 according to Asplund et al. (2005). The resulting concentrations are shown
on the l.h.s. of Fig. 5.
for the solar abundances given in
Table C.1 according to Asplund et al. (2005). The resulting concentrations are shown
on the l.h.s. of Fig. 5.
O complex: most of the oxygen is chemically bound into H2O. The next most abundant oxygen carrier is CO down to about 1200 K (not depicted).
Fe complex: atomic iron is the most abundant iron species down to about 1150 K, where Fe(OH)2 takes over. FeS, FeO and FeH (not depicted) are less important.
Mg complex: magnesium is most abundant in its atomic form down to about 1300 K, where MgOH and then Mg(OH)2 become more abundant. MgH is also abundant at high temperatures. MgS, MgO and MgN are less important.
Si complex: SiO is clearly dominant, followed by SiS, down to about 800 K, where SiH4 becomes the most abundant Si-species (not depicted). Silicon atoms and other silicon molecules (SiH, SiO2, Si2) are less important.
Al complex: the aluminium chemistry is complex. At higher temperatures, Al is mainly present in its atomic form, but already at about 2100 K, AlOH is more abundant than Al. Furthermore, AlO2H and Al2O are abundant molecules in the entire depicted T-interval. AlS and AlO are also abundant at high temperatures, and Al2O2 at very low temperatures. Other aluminum molecules like AlN and AlO2are less important.
Ti complex: at high temperatures, TiO is the most abundant Ti molecule, but already at 1600 K, TiO2 becomes more abundant. Ti atoms and the TiS molecule are less important.
We conclude that in the temperature window 1800-1000 K, suitable for dust formation, atomic Fe (followed by Fe(OH)2), atomic Mg (followed by Mg(OH)2), SiO (followed by SiS), AlOH (followed by Al2O) and TiO2 (followed by TiO) can be identified as the most important gaseous species for dust formation. The bulk solid phase is expected to form from these gaseous species.
These findings hold even for the metal-deficient case (r.h.s. of Fig. 5) where dust formation has reduced the metal abundances in the gas phase by many orders of magnitude. Polyatomic molecules with larger stoichiometric coefficients (e.g. Al2O, TiO2) are more affected by metal depletion. These conclusions have led us to the selection of the surface reactions listed in Table 1.
During the early stages of dust formation (see l.h.s. of
Fig. 6), the gas element abundances stay almost
constant because the degrees of condensation
![]() remain small. The evolution of the gas
composition during these stages is mainly a consequence of the changing
temperature, favouring more complex molecules as the temperature
decreases. The growth time-scale of the different solid materials is
rather similar.
remain small. The evolution of the gas
composition during these stages is mainly a consequence of the changing
temperature, favouring more complex molecules as the temperature
decreases. The growth time-scale of the different solid materials is
rather similar.
After the formation of dust is completed (after about 0.5 s) the
long-term behaviour of the element abundances and molecular
concentrations are still affected by ongoing element depletion (r.h.s. of
Fig. 6). An exponential decrease of the gas
element abundances
![]() by about one (Si) to six (Ti)
orders of magnitude is evident, until constant values are achieved at
later stages. This behaviour results from a relaxation toward phase
equilibrium characterised by
by about one (Si) to six (Ti)
orders of magnitude is evident, until constant values are achieved at
later stages. This behaviour results from a relaxation toward phase
equilibrium characterised by
![]() ,
where
the growth and evaporation reactions finally balance each other (see
Sect. 2.1.2).
,
where
the growth and evaporation reactions finally balance each other (see
Sect. 2.1.2).
The time-scale for this relaxation can be derived from
Eq. (29). Assuming that the growth process occurs
at high supersaturation ratios (![]() )
and is dominated by
a single growth reaction
)
and is dominated by
a single growth reaction ![]() with a key reactant of maximum
concentration
with a key reactant of maximum
concentration
![]() (disregarding stoichiometry here),
Eq. (29) can then be written as
(disregarding stoichiometry here),
Eq. (29) can then be written as
![\begin{displaymath}\frac{{\rm d}\epsilon_{\rm x}}{{\rm d}t} = -~\sqrt[3]{36\pi}~...
...\epsilon_{\rm x}
v^{\rm rel}_{\tilde{r}} \alpha_{\tilde{r}} .
\end{displaymath}](/articles/aa/full/2006/31/aa4598-05/img234.gif) |
(35) |
![\begin{figure}
\par\mbox{\includegraphics[width=10.2cm,clip]{4598fig7a.eps}\qqua...
...ncludegraphics[width=5cm,clip,bb=39 150 291 685 ]{4598fig7b.eps} }\end{figure}](/articles/aa/full/2006/31/aa4598-05/Timg240.gif) |
Figure 7:
Same as l.h.s of Figs. 6 and 4, but for
|
| Open with DEXTER | |
The final values for the degrees of condensation depend strongly
on the final temperature in the medium (the final atmospheric height
of the ascending convective element) as known from phase equilibrium
calculations (see e.g. Sharp & Hübner 1990). For the
chosen value for
![]() K,
SiO2[s] is not very stable, resulting in final
degrees of condensation of only about 80% for Si, and Mg reaches only 95%.
In contrast, Al2O3[s], Fe[s] and TiO2[s] are
more stable, resulting in almost 100% condensation of Al, Fe and
Ti. The degree of condensation of oxygen remains small (about 20%),
however increasing the C/O ratio from initially 0.537 to finally 0.719.
K,
SiO2[s] is not very stable, resulting in final
degrees of condensation of only about 80% for Si, and Mg reaches only 95%.
In contrast, Al2O3[s], Fe[s] and TiO2[s] are
more stable, resulting in almost 100% condensation of Al, Fe and
Ti. The degree of condensation of oxygen remains small (about 20%),
however increasing the C/O ratio from initially 0.537 to finally 0.719.
It is noteworthy that although the dust formation process is
quickly completed (
![]() after 0.14 s,
after 0.14 s,
![]() after 0.4 s,
after 0.4 s,
![]() after 1 s) the depletion of the element abundances
takes more time (up to 2.2 s for Ti), if the initial and final
values for the respective gas element abundance differ by many orders of
magnitude, which takes many
after 1 s) the depletion of the element abundances
takes more time (up to 2.2 s for Ti), if the initial and final
values for the respective gas element abundance differ by many orders of
magnitude, which takes many
![]() .
.
An ascending convective gas element in a brown dwarf atmosphere
always moves along the direction of decreasing temperature,
until it cools and dissolves in the surrounding gas, finally
achieving the thermodynamical conditions of the ambient gas.
Estimates for typical convective turn-over
time-scales result in
![]() min (
min (
![]() cm,
cm,
![]() cm/s).
cm/s).
In the course of the dust formation process in such a plum or bubble,
radiative cooling occurs with increasing efficiency as the amount of
dust increases. For the situation considered (caption Fig. 2) the
radiative cooling time-scale ranges from
![]() s without dust formation and
s without dust formation and
![]() s
with dust formation, if the plum is considered to radiate like a black
body (Eq. (25) in Paper I and
s
with dust formation, if the plum is considered to radiate like a black
body (Eq. (25) in Paper I and
![]() cm-1,
cm-1,
![]() cm-1)
cm-1)![]() ,
,![]() .
Hence, the gas / dust mixture will reach fast the radiative
equilibrium temperature
.
Hence, the gas / dust mixture will reach fast the radiative
equilibrium temperature
![]() also if it is considerably
smaller than the temperature from which such a convective element
originates, i.e. in our case
also if it is considerably
smaller than the temperature from which such a convective element
originates, i.e. in our case
![]() .
.
So far we have studied the results for convective plums or
bubbles that do not ascend very high in the atmosphere (
![]() K). Now we demonstrate the
results for
K). Now we demonstrate the
results for
![]() K,
simulating dust-forming bubbles that reach much higher layers
(Fig. 7).
K,
simulating dust-forming bubbles that reach much higher layers
(Fig. 7).
The principle evolution of dust and gas is similar compared to
the previous case. However, the nucleation rate reaches
higher values, which causes
the creation of about 103 times more dust particles in comparison
to the previous case, which therefore remain much smaller
![]() m. The intermediate minimum of
m. The intermediate minimum of
![]() at
at
![]() s is a consequence of this fast
production of seed particles. Such a distribution of small
grains results in a much larger total surface area of the dust
component
s is a consequence of this fast
production of seed particles. Such a distribution of small
grains results in a much larger total surface area of the dust
component
![]() which eventually accelerates all growth and
evaporation processes.
which eventually accelerates all growth and
evaporation processes.
Consequently, the dust formation is completed very rapidly
(
![]() s) after the maximum of nucleation has
occurred at
s) after the maximum of nucleation has
occurred at
![]() s. Also the subsequent depletion of
the gas phase proceeds faster. The gas phase is virtually free
of Si, Al, Fe, and Ti after about 0.18 s. Now, Mg2SiO3[s] is the last stable which result in a final degree of
condensation of only
s. Also the subsequent depletion of
the gas phase proceeds faster. The gas phase is virtually free
of Si, Al, Fe, and Ti after about 0.18 s. Now, Mg2SiO3[s] is the last stable which result in a final degree of
condensation of only
![]() for Mg.
The rapid temperature drop
to
for Mg.
The rapid temperature drop
to
![]() K causes also a considerable change of the chemical
composition of the gas phase. Complex molecules like Fe(OH)2 and
AlO2H become very abundant. This temperature effect is partly
masked by the influence of the decreasing gas phase element
abundances.
K causes also a considerable change of the chemical
composition of the gas phase. Complex molecules like Fe(OH)2 and
AlO2H become very abundant. This temperature effect is partly
masked by the influence of the decreasing gas phase element
abundances.
The r.h.s. of Fig. 7 shows the resulting
material composition of the dust particles, close to phase
equilibrium.
The majority of Si disappears
in Mg2SiO4[s] which is in competition with the
SiO2[s]
formation. The consequence is the incomplete
condensation of Mg.
The final dust volume composition according to the present model is
about 56% Mg2SiO4[s],
![]() SiO2[s],
8% Fe[s], 1% Al2O3[s] and <0.1% TiO2[s].
The fraction of Mg2SiO4[s] did decrease somewhat in favour of SiO2[s] compared to the hotter case in
Sect. 4.3. This is a tendency relevant for the spectral appearance of dust cloud layers where the upper-most, cool
layers will mostly influence the IR spectrum.
SiO2[s],
8% Fe[s], 1% Al2O3[s] and <0.1% TiO2[s].
The fraction of Mg2SiO4[s] did decrease somewhat in favour of SiO2[s] compared to the hotter case in
Sect. 4.3. This is a tendency relevant for the spectral appearance of dust cloud layers where the upper-most, cool
layers will mostly influence the IR spectrum.
We have presented results from our theoretical model of oxygen-rich heterogeneous dust formation. Major input properties for every
model are material quantities. The sticking coefficient ![]() is such an input value to our dust formation model and it
describes the efficiency of a chemical surface reactions r to contribute to the growth of the grain mantle
(Sect. 2.1.1). One source to obtain these values are experiments and only a few seem to exist for non-icy
particles. Hashimoto (1990) considers the destruction of Mg2SiO4[s] and summarized
is such an input value to our dust formation model and it
describes the efficiency of a chemical surface reactions r to contribute to the growth of the grain mantle
(Sect. 2.1.1). One source to obtain these values are experiments and only a few seem to exist for non-icy
particles. Hashimoto (1990) considers the destruction of Mg2SiO4[s] and summarized
![]() for
SiO2[s
for
SiO2[s
![]() ,
,
![]() for SiO2[s]
for SiO2[s]
![]() SiO2 (r=4, 5 in
Table 1),
SiO2 (r=4, 5 in
Table 1),
![]() ,
and
,
and
![]() .
Hence, the formation of
Mg2SiO4[s] and SiO2[s] has to overcome a reaction barrier while metals do not. The experiments by Nagahara & Ozawa
(1996) suggest
.
Hence, the formation of
Mg2SiO4[s] and SiO2[s] has to overcome a reaction barrier while metals do not. The experiments by Nagahara & Ozawa
(1996) suggest
![]() .
Obeying the facts that experimental data differ and that the sticking process
would also depend on details like the structure of the already existing surface and its temperature, we performed test calculation
to illustrate the principle influence of the sticking coefficients on the results presented in Sect. 4. Case
#0 is the standard setting of this paper, case #1 considers SiO2[s] and Mg2SiO4[s] with similar
.
Obeying the facts that experimental data differ and that the sticking process
would also depend on details like the structure of the already existing surface and its temperature, we performed test calculation
to illustrate the principle influence of the sticking coefficients on the results presented in Sect. 4. Case
#0 is the standard setting of this paper, case #1 considers SiO2[s] and Mg2SiO4[s] with similar
![]() ,
case
#2 has a decreased
,
case
#2 has a decreased ![]() for one of the SiO2[s] reactions, and case #4 resembles the most extreme values given in
Hashimito (1990).
for one of the SiO2[s] reactions, and case #4 resembles the most extreme values given in
Hashimito (1990).
![\begin{figure}
\par\mbox{\includegraphics[width=4.02cm,clip]{4598fig8a.eps}\quad
\includegraphics[width=4.5cm,clip]{4598fig8b.eps} }\end{figure}](/articles/aa/full/2006/31/aa4598-05/Timg269.gif) |
Figure 8:
Influence of reaction kinetics on the cumulative volume fraction
|
| Open with DEXTER | |
Table 2: Influence of the sticking coefficients. For reaction index r see Table 1.
In principle, a decreasing sticking coefficient causes a decreasing growth speed. We demonstrate this for the cumulative
volume fraction
![]() and the degree of condensation
and the degree of condensation ![]() in Fig. 8, because
in Fig. 8, because
![]() is linked to the spectral appearance of a dust cloud layer,
is linked to the spectral appearance of a dust cloud layer, ![]() demonstrates the influence on the gas
phase chemistry.
demonstrates the influence on the gas
phase chemistry.
We observe a difference in the short-term (l.h.s.) and in the long-term (r.h.s.) behavior of our dust forming system. The
short-term behavior is influenced by the dust kinetics, therefore large differences occur between the case #0 (![]() )
and
the other cases where
)
and
the other cases where
![]() .
The results for case #1 and case #2 are very similar because
.
The results for case #1 and case #2 are very similar because ![]() differs for only one
reaction (r=5). The relaxation towards phase equilibrium takes longer the smaller the sticking coefficients are (case #0
differs for only one
reaction (r=5). The relaxation towards phase equilibrium takes longer the smaller the sticking coefficients are (case #0
![]() case #1 and #2
case #1 and #2
![]() case #3). Case #3 considers the smallest
case #3). Case #3 considers the smallest ![]() for the two major dust
compounds SiO2[s] and Mg2SiO4[s], and hence, has the longest relaxation time. The slowest relaxation occurs for the
Mg-complex in case #3 because all Mg2SiO4-reactions proceed with the same, low
for the two major dust
compounds SiO2[s] and Mg2SiO4[s], and hence, has the longest relaxation time. The slowest relaxation occurs for the
Mg-complex in case #3 because all Mg2SiO4-reactions proceed with the same, low ![]() ,
in contrast to SiO2[s] where
only one reaction has a comparably small
,
in contrast to SiO2[s] where
only one reaction has a comparably small ![]() .
It becomes, however, clear that one slow compound influences the relaxation
towards phase equilibrium of the whole dust chemistry. Figure 8 illustrates that the actual relaxation
time depends very much on the values of the sticking coefficient which is not known for part of the reactions, or which has large
uncertainties as stated by Hashimoto (1990) for
.
It becomes, however, clear that one slow compound influences the relaxation
towards phase equilibrium of the whole dust chemistry. Figure 8 illustrates that the actual relaxation
time depends very much on the values of the sticking coefficient which is not known for part of the reactions, or which has large
uncertainties as stated by Hashimoto (1990) for
![]() ,
or for which different experiments result in different
values (
,
or for which different experiments result in different
values (
![]() :
Hashimoto 1990; Nagahara & Ozawa 1996).
:
Hashimoto 1990; Nagahara & Ozawa 1996).
Eventually the system reaches phase equilibrium and the results are the same in all four cases (r.h.s. Fig. 8) including gas phase depletion.
The thermo- and hydrodynamic conditions in brown dwarf atmospheres may at first appear similar to the Earth's atmosphere, which raises an important and repeatedly asked question. Namely, if seed formation is really an important issue for the formation of dust in brown dwarfs and gas giant planets.
The formation of water droplets in the Earth atmosphere is triggered by the presence of so-called aerosols. Aerosols are very
small liquid or solid particles, which remain suspended over a long period of time since they are thermally stable and their drift
velocities are very small. Aerosols are for instance volcanic dust particles injected into the atmosphere by the most violent
eruptions (e.g. El Chichon, Mexico 1982, temporal albedo increase of 10%). Another way of aerosol production is fire in the
tropics, smoke-tracks, and tire particles. The main Earth aerosols, however, are H2SO4-water droplets (
![]() m)
from sulphur release by volcanoes, coal burning, and decomposition of organic matter (Traub 2005, priv. com.). All these aerosols
serve as seed particles - maybe coated with patches of sulfur (Korhonen et al. 2003) - for formation of water
droplets and can be washed out from the terrestrial atmosphere by rain. If there are many of such seeding aerosols, the number of
liquid droplets increases, and the size of the rain droplets decreases (compare J*,
m)
from sulphur release by volcanoes, coal burning, and decomposition of organic matter (Traub 2005, priv. com.). All these aerosols
serve as seed particles - maybe coated with patches of sulfur (Korhonen et al. 2003) - for formation of water
droplets and can be washed out from the terrestrial atmosphere by rain. If there are many of such seeding aerosols, the number of
liquid droplets increases, and the size of the rain droplets decreases (compare J*, ![]() ,
,
![]() between
Figs. 6 and 7), which enables these particles to sustain longer in the atmosphere
since their gravitational drift velocities are smaller.
between
Figs. 6 and 7), which enables these particles to sustain longer in the atmosphere
since their gravitational drift velocities are smaller.
Brown dwarfs and giant gas planets do not provide any of the aforementioned mechanisms for seed particle formation. Instead, both constantly mix up hot gas from the deep interior, where the thermal stability of solids and liquids is not provided, into the atmosphere. This changes the picture of rain formation known from the Earth atmosphere considerably. In brown dwarf atmosphere, the dust formation happens in upwinds just at those temperatures where the very first seed particles can be formed, making the nucleation and the influence of turbulence on the nucleation to key issues for the discussion of dust formation in brown dwarf atmospheres.
The situation in giant gas planets, which can be much cooler, will be again different. Here, the same dust formation processes may occur in very deep layers, but the observable surface layers are so cool that the formation of more volatile species like ice particles becomes important. The formation of such secondary particles must be discussed on top of the refractory grain formation in deeper layers. The refractory dust particles, as considered in this paper, will probably serve as seeds for the more volatile species in the upper atmosphere.
Burgasser (2004) and Burgasser et al. (2004) have presented evidence (i.e. high proper motions) for the discovery of halo brown dwarfs. Halo brown dwarfs are old objects, which suggests that they are primordially metal poor and that they have probably all cooled into the T dwarf regime, as for example the 2MASS brown dwarf 0034+0523 (Burgasser et al. 2004). Hence, they should exhibit an even stronger metal deficiency than other halo stars or stars in the galactic plane of similar age because of the additional metal depletion by dust formation and settling in brown dwarfs.
According to the results of this paper, this additional metal depletion by dust formation, which could mimic primordial metal abundances, is very difficult to determine by models. The depletion time-scale is the longest among all chemical and dust formation time-scales, which suggests that phase equilibrium is not valid in the outer layers (see Helling et al. 2005; and conclusions of Paper III). Due to the ongoing mixing, the depletion is expected to be incomplete which means that a lot more metal carrying molecules like FeH, CaH and TiO can be present in comparison to phase equilibrium.
Dust formation will proceed via every available chemical channel and therefore influence the element abundance of almost every species. Exceptions being the noble gases, hydrogen and maybe some peculiar elements which do not possess a stable solid phase. A possible way out of this masking effect might be that in case of primordial stars, all metal abundances should be approximately reduced by some constant factor. Dust formation, in contrast, discriminates strongly between different metals. The results of this paper, for example, suggests that Al and Fe should be much more depleted than Si and Mg. Lodders & Fegley (2005) have suggested that if GeH4 can be detected instead of SiH4, and H2S can be detected instead of Fe binding molecules, the metal deficiency in very cool objects should be caused by dust consumption.
Cowan et al. (2005) suggested a metal abundance of
![]() Fe/H
Fe/H
![]() for galactic halo giant stars,
and [Fe/H]>-1 for galactic disk stars (Cowan et al. 2002). Extreme
sub-dwarfs are known to have [Fe/H
for galactic halo giant stars,
and [Fe/H]>-1 for galactic disk stars (Cowan et al. 2002). Extreme
sub-dwarfs are known to have [Fe/H
![]() (Gizis et al. 1997). For comparison, the differences of metal element
abundances
(Gizis et al. 1997). For comparison, the differences of metal element
abundances
![]() due to our dust formation model (see
Fig. 6) are [Ti/H]=-6, [Fe/H]=-3, [Al/H]=-4,
[Mg/H]=-1, [Si/H]=-0.5 in the final state, which is
per definition the logarithmic difference to the solar, i.e. our
initial, values. Obviously, these deficiencies are not of similar orders
of magnitude and not correlated with iron. It follows that a
brown dwarf atmosphere with a chemical composition as calculated from
our model could in fact mimic primordial low metal abundances.
due to our dust formation model (see
Fig. 6) are [Ti/H]=-6, [Fe/H]=-3, [Al/H]=-4,
[Mg/H]=-1, [Si/H]=-0.5 in the final state, which is
per definition the logarithmic difference to the solar, i.e. our
initial, values. Obviously, these deficiencies are not of similar orders
of magnitude and not correlated with iron. It follows that a
brown dwarf atmosphere with a chemical composition as calculated from
our model could in fact mimic primordial low metal abundances.
We have proposed a model for the formation of dirty dust particles in brown dwarf atmospheres, which consist of numerous small islands of different solid materials like Mg2SiO4[s], SiO2[s], Al2O3[s], Fe[s] and TiO2[s]. This idea is supported by experimental findings (Sect. 2) and observations of coated terrestrial dust particles (see Korhonen et al. 2003). Assuming that the impinging molecules are rapidly transported by hopping on the surface to the respective solid islands, we have derived a general moment method for the treatment of nucleation, growth and evaporation for such dirty grains with an oxygen-rich element composition. Our approach allows to determine the time-dependent size distribution and solid material composition of the dirty grains, and the time-dependent chemical composition of the gas phase.
Our model is motivated by laboratory results and by the necessity of the key process of nucleation (seed particle formation) to occur first. In order to stabilise small clusters in the gas phase and so to initiate the nucleation process, low temperatures must be achieved (causing the required supersaturation). At such temperatures, a variety of solid materials is already thermally stable which suggests that if seed particles are once formed, they will be immediately covered by different solid materials in a simultaneous way, which results in dirty grains.
In order to overcome this nucleation barrier, turbulence is an important issue which may temporarily provide the required low temperatures, e.g. by the superposition of expansion waves. Locally higher nucleation rates result in smaller grains which sustain longer in the atmosphere since their gravitational drift velocities (gravitational settling) are smaller. Thus, the proposed turbulent scenario for dust formation leads to a patchy, non-uniform distribution of dust with e.g. a spatially varying size and material distribution.
In application to convective gas elements that ascend in the brown dwarf atmosphere, radiative cooling is also important for the dust formation. Such ascending bubbles are hotter than in radiative equilibrium. Consequently, if once dust forms and the opacity of the gas/dust mixture increases, radiative cooling causes a rapid decrease of the temperature which influences the resulting dust quantities.
Considering typical densities of 10-3.5 g cm-3 in brown dwarf atmospheres, the dust formation process results to be fast (between 0.1 s and 0.5 s), but the consumption of metal atoms from the gas phase takes longer, which suggests that the gas phase depletion by dust formation can be incomplete, i.e. less than predicted by phase equilibrium models. Together with the patchy, non-uniform appearance of the dust due to turbulence, the incomplete depletion makes metallicity measurements highly uncertain.
The initial dust growth phase after nucleation onset proceeds far away from phase equilibrium and the resulting solid material composition of the dirty dust particles are at first given by kinetic constraints. However, at later stages, when the gas phase is strongly depleted, the material composition of the grains is actually not frozen in, but less stable materials like SiO2[s] and Mg2SiO4[s] slowly evaporate and the newly liberated metals can form other, more stable condensates at low temperatures at radiative equilibrium level. In this way, the material composition of the dust particles approaches final values as known from phase equilibrium considerations.
The final solid material composition of the dirty dust grains
depends hence strongly on the temperature in the respective
atmospheric layer. Considering a temperature interval from
![]() K, we find changing volume fractions of
the considered solid materials. The fractions of silica SiO2[s] and solid iron Fe[s] increased on the cost of Mg2SiO4[s].
K, we find changing volume fractions of
the considered solid materials. The fractions of silica SiO2[s] and solid iron Fe[s] increased on the cost of Mg2SiO4[s].
The dust formation leads to different degrees of gas phase depletion for different elements. This selective nature of the dust formation may help to disentangle primordial from dust-affected metallicities.
Acknowledgements
We thank the referees, Dr. Joseph Nuth III and Dr. Erwin Sedlmayr for interesting suggestions to the manuscript. We thank Stephan Schlemmer and Wing-Fai Thi for enlightning discussion on the mansucrip's subject. W. A. Taub is thanked for sharing his knowledge on aerosols with us. Ch.H. acknowledges the Berliner Programm zur Förderung der Chancengleichheit von Frauen in Wissenschaft und Lehre and the ESA Research Fellowship program at ESTEC in Noordwijk. P.W. has been supported in the frame of the ASTROHYDRO3D initiative by the NWO Computational Physics programme, grant 614.031.017. Ch.H. is particular gratefully to Vincent Icke and Tim de Zeeuw for the host support during the period of work at the Sterrewacht Leiden. The computer support at the Sterrewacht Leiden and at ESTEC is highly acknowledged. Most of the literature search was done with ADS.
We consider molecules of kind MN (the "clusters'') which are
composed of exactly N units. M1 is the "monomer''. In chemical
equilibrium (CE) we can apply the law of mass action to the
following hypothetic reaction of type I
| (A.1) |
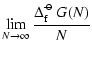 |
= | (A.3) | |
| = | 1 | (A.4) |
With the thermal equation of state for an N-cluster in chemical equilibrium,
![]() ,
it follows for sufficiently large clusters which obey
,
it follows for sufficiently large clusters which obey
![]()
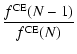 |
= | 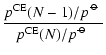 |
(A.6) |
| = | 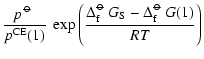 |
(A.7) | |
| = | 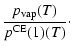 |
(A.8) |
Equation (A.12) states the supersaturation ratio S of
the monomer in the gas phase over the respective solid
material. Strictly speaking, S equals the ratio between the growth
rate and the spontaneous evaporation rate of type I surface reactions
in thermal and chemical equilibrium (see Eq. (17)) and in
consideration of only one pure solid (
![]() ).
).
However, typical surface reactions for oxygen-rich dust particles are much
more complicated, for example
The proper definition of Sr goes as follows. First, we quantify the
forward and backward reaction rates per surface area by assuming that
these reactions are triggered by the thermally impinging collision rates
of two key species
(in our example Mg and H2) with particle densities nf,r and
nb,r, respectively:
| = | (B.2) | ||
| = | (B.3) |
Next, we introduce a reference state, designated by ![]() ,
where
the gas is in phase equilibrium with the solid s affected by
reaction r. This state is characterised by detailed balance
where each reaction must be balanced exactly by its
reverse. Hence, we can write
,
where
the gas is in phase equilibrium with the solid s affected by
reaction r. This state is characterised by detailed balance
where each reaction must be balanced exactly by its
reverse. Hence, we can write
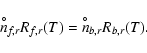 |
(B.4) |
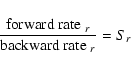 |
(B.5) |
The question remains, however, how the reference state is defined
precisely. For this purpose, we carry out the following thought
experiment as sketched in Fig. B.1. We consider a gas of
arbitrary element composition
![]() (
(
![]() )
)![]() and
bring it in contact with the considered solid s. Now we close the
system and wait, giving the system enough time to build up more solid
material s from the gas phase or to partially evaporate material s,
until an equilibrium is achieved, where all growth reactions are
balanced by their reverse, including the (possibly only hypothetical)
monomer addition reaction which occurs at S=1. Now we can measure
the changed element abundances
and
bring it in contact with the considered solid s. Now we close the
system and wait, giving the system enough time to build up more solid
material s from the gas phase or to partially evaporate material s,
until an equilibrium is achieved, where all growth reactions are
balanced by their reverse, including the (possibly only hypothetical)
monomer addition reaction which occurs at S=1. Now we can measure
the changed element abundances
![]() and the correspondingly
changed partial pressures
and the correspondingly
changed partial pressures
![]() .
Due to stoichiometric constraints,
the element abundances in the reference state will satisfy
.
Due to stoichiometric constraints,
the element abundances in the reference state will satisfy
Equations (B.6) and (B.7), with X being the root
of S=1, offer a unique way to define the reaction supersaturation
ratios Sr for all surface reactions (types I, II or III). The technical disadvantage of this general method, however,
is that it requires several calls of the gas phase chemical
equilibrium routine as function of X, which itself is a complicated
iterative procedure. Therefore, in hydrodynamical applications, the
presented method is unacceptably slow and we seek for a further
simplification. In any case, we have
![]() according to the outlined procedure, consistent with the
statements at the end of Appendix A.
according to the outlined procedure, consistent with the
statements at the end of Appendix A.
The results of the presented general method as function of temperature
are shown in Fig. B.2 for the surface reactions listed in
Table 1. For type I surface reactions, the backward
rate is spontaneous and a key species for the backward reaction does
not exist (nb,r=1). Consequently, we find
![]() and
and
![]() for type I.
for type I.
Table B.1:
Monomer volumes
![]() of solid materials from
(Lüttke 2002) and fit coefficients ci for the calculation of
the saturation vapour pressures and difference Gibbs free
energies. (*): Paper III - (**): Sharp & Huebner
(1990).
of solid materials from
(Lüttke 2002) and fit coefficients ci for the calculation of
the saturation vapour pressures and difference Gibbs free
energies. (*): Paper III - (**): Sharp & Huebner
(1990).
None of the reactions in Table 1 is actually of
type II. The main difference to type III reactions is that the
identification of the key species is trivial since there is simply
only one choice for the forward and backward reactions. Considering,
for example, the important reaction for the growth of carbonaceous
grains
![]() ,
we have
,
we have
![]() .
Since only carbon is
affected by the outlined procedure to reach the reference state,
we have
.
Since only carbon is
affected by the outlined procedure to reach the reference state,
we have
![]() ,
and since
,
and since
![]() ,
we find
Sr=(S)2. This is exactly the result of Patzer et al. (1998) for this
type II reaction in case of thermal and chemical equilibrium.
,
we find
Sr=(S)2. This is exactly the result of Patzer et al. (1998) for this
type II reaction in case of thermal and chemical equilibrium.
Concerning the most relevant type III reactions, we find that the
following approximation is quite accurate in most cases (compare
Fig. B.2):
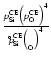 .
Using
.
Using
We observe, however, significant deviations from this rule at low S(high T) concerning the solids SiO2[s] and Mg2SiO4[s]
(TiO2[s], Fe[s] and Al2O3[s] are OK). For undersaturation, we
need to increase the element abundances to achieve S=1. This leads
finally to a significant and steady increase of
![]() with increasing T, for higher T even for
with increasing T, for higher T even for
![]() and
and
![]() .
However, these deviations only occur at
.
However, these deviations only occur at ![]() ,
which is an extreme value of undersaturation which never occurs in
realistic time-dependent models. We want to note, finally, that our
theoretical approach favours the evaporation of SiO2[s] via
spontaneous decomposition into monomers (inverse reaction 4) athigh T, since
,
which is an extreme value of undersaturation which never occurs in
realistic time-dependent models. We want to note, finally, that our
theoretical approach favours the evaporation of SiO2[s] via
spontaneous decomposition into monomers (inverse reaction 4) athigh T, since
![]() for high T, which is consistent
with the experimental results of Hashimoto (1990).
for high T, which is consistent
with the experimental results of Hashimoto (1990).
The monomer supersaturation ratios are calculated according to
Eq. (A.12) where the nominator in the exponential term in
Eq. (A.12) is fitted by
![]() .
The fit coefficients are mostly taken from Sharp &
Huebner (1990). Only TiO2 was treated separately by fitting JANAF
table data (electronic version of Chase et al. 1986) with
.
The fit coefficients are mostly taken from Sharp &
Huebner (1990). Only TiO2 was treated separately by fitting JANAF
table data (electronic version of Chase et al. 1986) with
![]() (see Paper III). The coefficients ci are
summarised in Table B.1.
(see Paper III). The coefficients ci are
summarised in Table B.1.
Table C.1: Initial (solar) element abundances from Asplund et al. (2005). All abundances decreased partly considerably compared to Anders & Grevesse (1989).