... grains[*]
Appendices are only available in electronic form at http://www.edpsciences.org 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... molecules[*]
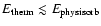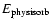Hopping requires $E_{\rm therm}\lesssim E_{\rm physisorb}$, where $E_{\rm physisorb}$ is the binding energy of an alien ad-molecule on a solid surface. The efficiency of the hopping process depends hence on the temperature. If $E_{\rm therm}$ is too small, the arriving molecules can not move at the grains surface. If $E_{\rm therm}$ is too large, the just arrived molecule recoils from the surface (Gail & Sedlmayr 1984). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...1988)[*]
Venables (1993) review such rate equation models discussing several experimental studies to show how these concepts can be applied. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... reactions[*]
For molecules M and grains S we define:
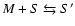type I reaction: $M + S\leftrightarrows S^{\prime}$
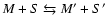type II reaction: $M + S\leftrightarrows M^{\prime} + S^{\prime}$
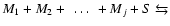type III reaction: $M_1 + M_2 +~\ldots~ + M_j + S \leftrightarrows$
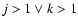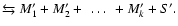( $j>1 \vee k>1$) $\leftrightarrows M_1^{\prime} + M_2^{\prime} +~\ldots~ + M_k^{\prime} + S^{\prime}.$ 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... equilibrium[*]
Due to the high densities in substellar atmospheres, deviations from thermal and chemical equilibrium are unlikely to occur, unless the atmosphere is illuminated from the outside. A fast collisional energy exchange between dust and gas is assured and hence 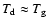$T_{\rm d} \approx T_{\rm g}$ (see Fig. 4 in Paper II). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...2003)[*]
Note that e.g. Al2O3[s] can only be formed in the presence of a pre-existing surface, but is not considered as nucleation species due to the lack of a stable monomer Al2O3 in the gas phase (see Patzer 2004). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... abundances[*]
Figure 5 has been calculated with the full chemical equilibrium code (14 elements and 155 molecules) which enables us to cross-check the reduced version of the chemical equilibrium code used during the hydrodynamic simulations. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...)[*]
Note the error in the 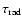$\tau_{\rm rad}$ estimation in Eq. (25) in Paper I. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...[*][*]
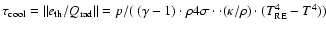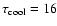The exact value depends on the definition of the cooling time-scale considered. If $\tau_{\rm cool}= \Vert e_{\rm th}/Q_{\rm rad}\Vert= p/(~(\gamma-1)\cdot\rho 4\sigma\cdot \cdot(\kappa/\rho)\cdot (T_{\rm RE}^4-T^4))$, it follows $\tau_{\rm cool}=16$ s and 0.53 s without and with dust, respectively. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...$k=\rm H,He,C,N,O,...$)[*]
This is different from Dominik et al. (1993), who assumed that the element composition of the gas resembles that of the solid, which we think is incorrect. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Copyright ESO 2006