A&A 453, 699-715 (2006)
DOI: 10.1051/0004-6361:20054353

The diagnosis of the mean quadratic magnetic field of Ap stars

G. Mathys - S. Hubrig

European Southern Observatory, Casilla 19001, Santiago 19, Chile

Received 13 October 2005 / Accepted 12 January 2006

Abstract
Aims. We assess the validity of the method of determination of the mean quadratic field modulus and we explore its limits.
Methods. We analyse high spectral resolution, high signal-to-noise spectra of a few Ap stars, and of a superficially normal main-sequence A star, recorded over a broad wavelength range with EMMI at the NTT.
Results. We introduce a revised form of the regression equation describing the dependence of the second-order moment of the line profiles about their centre, in natural light, on various parameters of the corresponding transitions. We show that interpretation of the observed dependences allows one to determine the mean quadratic magnetic field modulus of the studied stars, and their . We explain why the contributions to the quadratic field of the mean square magnetic field modulus and of the mean square longitudinal field cannot in general be disentangled. For those stars of the sample that have resolved magnetically split lines, we show that the derived values of the quadratic field are mostly consistent with the values of the mean longitudinal magnetic field and of the mean magnetic field modulus at the observed phase. However there are some hints that they may occasionally slightly underestimate the actual field. This suggests that the method is unlikely to yield spurious field detections. In addition, we illustrate the importance for this type of analyses of using, as far as possible, samples of lines of a single ion, and to specify in the presentation of the results which ion was used.
Conclusions. The results presented in this paper lend strong support to the validity of the quadratic field diagnostic method to obtain a realistic quantitative characterisation of the magnetic fields Ap and related stars.

Key words: stars: chemically peculiar - stars: magnetic fields - methods: data analysis - line: profiles

   
1 Introduction

Early studies of stellar magnetic fields were based on spectra recorded on photographic plates. Because only limited signal-to-noise ratio was achievable, magnetic field diagnosis was to a large extent restricted to consideration of those quantities that could be derived from measurements of wavelengths of entire lines (or line components), such as the mean longitudinal magnetic field (which is determined from measurement of the wavelength shift of spectral lines between spectra recorded in opposite circular polarisations - see e.g. Mathys 1991) and the mean magnetic field modulus (which is derived from the wavelength separation of the split Zeeman components of magnetically resolved spectral lines in spectra recorded in natural light - see e.g. Mathys et al. 1997). Yet a lot of additional information is contained in the line profiles. Exploitation of this information has become feasible with the advent of CCDs as astronomical detectors. This has led to the development of new diagnostic techniques. One of them, which has already proved quite successful in a number of studies of Ap and Bp stars (e.g., Mathys 1993, 1995a,b; Mathys & Hubrig 1997) is the moment technique, originally developed by Mathys (1988). In this method, the shapes of the spectral line profiles are characterised by their moments of various order about the line centre. The dependences of these moments on atomic parameters characterising the transitions responsible for the observed lines are interpreted in terms of various moments of the stellar magnetic field. This interpretation is performed within the framework of a treatment of the line formation that can be more or less simple or elaborate. In practice, in all the applications of the moment technique until now, we have closely followed the original suggestion of Mathys (1988), using a semi-empirical approach based on the a priori rather rough weak-line approximation for the interpretation of the behaviour of the moments of the spectral lines.

Under this form, the moment technique has a number of advantages. Its application is much more straightforward than that of numerical synthesis or inversion of line profiles, which require large amounts of complex, time-consuming numerical computation. While the amount of work involved in the latter numerical methods scales roughly like the number of spectral lines under consideration, the diagnostic potential of the moment technique increases with the number of lines studied, at essentially no cost. The simultaneous consideration of several diagnostic lines allows one to identify otherwise unrecognised blends, since the affected line(s) usually yield discrepancies compared to those lines that actually are unblended. Furthermore, it is in principle possible to take advantage from the fact that different lines have different Zeeman patterns to enhance the diagnostic return (within certain limits - in the specific case considered in this paper, see the more detailed discussion of Sect. 3.2).

Through the moment technique, one derives a number of moments of the stellar magnetic field, which characterise the latter in a global manner, over the stellar hemisphere visible at the time of the observation. The quantities obtained in that way are to a large extent independent from specific assumptions regarding the structure of the field. The latter can be modelled from the consideration of the variations of the above-mentioned field moments with rotation phase. The difference between this approach and the one generally followed in numerical line profile synthesis or inversion is that, in the moment technique, the steps of extraction of the information from the observational data (which deals mostly with the physics of the line formation) and of modelling of the magnetic field structure (which is essentially a geometrical problem) are separated. In particular, one may for instance rather easily try to apply various modelling strategies to one single set of field moments, in order to assess the impact of the assumptions underlying the model on the derived field structure.

It can also be noted that the moment technique can be applied to study line profiles recorded in any of the four Stokes parameters. Simultaneous consideration of several Stokes parameters at the modelling stage of course enhances the diagnostic possibilities (all four Stokes parameters being necessary for full constraint of the magnetic field geometry).

But the advantage of the moment technique that has probably proved most important in the studies realised so far through its application is that, thanks to the fact that it uses global parameters integrated over whole spectral lines to characterise the profile shapes, it is especially well suited to the analysis of spectra that do not have a very high resolution or a very high signal-to-noise. This asset of methods of diagnosis of stellar physical properties from the consideration of moments of spectral lines has also been noted in applications to other contexts (e.g., Castor et al. 1981).

The applications of the moment technique to the determination of stellar magnetic fields that we have published so far were mostly based on such data obtained at moderate resolution ( $\lambda/\Delta\lambda\sim1.6\times10^4$- $3.9\times10^4$ and signal-to-noise ratio (S/N 70-200), over a fairly limited wavelength range (with spectral coverages ranging from approximately 700 to 1200 Å, and a central wavelength close to 6100 Å). The drawback is that observational material suffering from this kind of limitations is not well suited to verify really well the degree of reliability and of accuracy achieved in the field diagnosis. Of course, the approach that we have followed so far has received some theoretical justification and is supported by the consistency of the results derived with independent measurements of other moments of the magnetic fields of the studied stars. But it appears important to investigate more completely the adequacy of the method by applying it to better data, and to explore in that way the limits of accuracy achievable in the diagnosis of the magnetic field moments. This is the purpose of the present work, for the specific case of the determination of the mean quadratic magnetic field from the study of the second-order moments of the line profiles recorded in unpolarised light (that is, in the Stokes parameter I). Compared to the data used in previous applications of the moment technique, the spectra analysed in this study typically have a spectral resolution twice as large (or more), their signal-to-noise ratio is also twice as high in most cases, and they cover a spectral range from 2.5 to 4 times broader. Accordingly the number of diagnostic lines that can be used in the analysis is frequently 10 times greater than in previous studies. While more recent observational data available e.g. in observatory archives may in some specific aspects be even better than the spectra considered in this paper, the additional gain that could come from their consideration is small compared to this major step, and it should not be expected to lead to qualitatively different conclusions. In other words, the results of the present analysis are representative of the state of the art in the application of the moment technique for diagnosis of the mean quadratic magnetic field of Ap stars.

In the next section, we describe the observational material used for this study. The analysis procedure is presented in detail in Sect. 3, and the results obtained are discussed in Sect. 4.

   
2 Observations and reduction

The spectra analysed in this paper have been recorded in 1996 on February 2, June 8 and June 9 (UT) at ESO with the New Technology Telescope (NTT) and the ESO Multi Mode Instrument (EMMI). The red arm of EMMI was used, in the cross-dispersed echelle mode. The main dispersing element was the EMMI grating #14 (all part numbers given here are internal ESO numbers), a 31.6 lines/mm echelle grating mounted in an R4 configuration. As cross-disperser, the EMMI grism #5 (600 lines/mm) was employed. The detector was CCD #36, a Tektronix with $2048\times2048$ pixels of $24\times24$ $\mu$m². Setting the entrance slit of the spectrograph to a width of 0 $.\!\!^{\prime\prime}$9, a resolving power $\lambda/\Delta\lambda\approx7\times10^4$ was achieved over the whole wavelength range covered (4060-6740 Å).

Flat field spectra were recorded with the same instrumental configuration from the observation of the illumination of a white screen inside the NTT dome by white lamps mounted on the top ring of the telescope and installed on the dome floor. For each observing night, several such exposures were recorded and averaged so that the achieved signal-to-noise ratio was high enough with respect to the expected quality of the scientific exposures.

For the purpose of wavelength calibration, we obtained spectra of a thorium-argon arc lamp, whose light was fed into EMMI through an integrating sphere mounted on the adaptor between the telescope and the instrument. Even though it is known that EMMI suffers from some flexures as a result of its movement to compensate for sky rotation at the Nasmyth focus, we preferred not to repeat the wavelength calibration exposure for each position of the instrument, for the sake of saving observing time. Accordingly, a single arc spectrum was taken for each night. This is believed not to be a major drawback: the EMMI flexures mostly introduce global shifts of the spectrum, that is, change the zero point of the dispersion relation, but they only negligibly affect the higher-order coefficients of this relation. Since we are primarily interested in achieving a good internal wavelength accuracy (to study line broadening) but we have no need for precise absolute wavelengths (e.g., we do not aim at determining radial velocities), the flexure error in the wavelength calibration is acceptable.

Data reduction was performed using the ESO image processing package MIDAS. Echelle orders were automatically detected by the method of the Hough transform, and a two-dimensional polynomial fit was computed to define their location on the CCD. For both the scientific and the flat field frames, the background scattered light was modelled by fitting its level in the interorders by a 2-dimensional cubic spline. The result was subtracted from the corresponding exposure, prior to the division of the scientific frame by the flat field. The echelle orders were then extracted from the resulting frames. They were normalised to the continuum one by one, dividing them by polynomials fitted to high points of the spectra that were identified by cursor entry on a display.

The wavelength calibration was performed in two steps. First, an automatic search for suitable arc lines was executed on the wavelength calibration exposures, and their positions were determined by fitting Gaussian to them. Two such lines in the overlapping part of two echelle orders were identified interactively. Using these identifications as a starting point, an automatic iterative procedure was run to identify as many lines as possible. These identifications were used to define a dispersion relation for each echelle order, $\lambda=P_m(x)$, where $\lambda$ is the line nominal wavelength, x is the position of the centre of the Gaussian fitted to it in the dispersion direction, and m is the echelle order where the line occurs. The functions P_m (one per echelle order) are taken to be polynomial.

Although the above-described procedure gives reasonable results in most cases, on some occasions (typically, for a few of the about 60 orders of an EMMI echelle spectrum such as those discussed here), it may yield significantly erroneous results. This appears to result essentially from the fact that dispersion relations are derived independently for each echelle order, and errors mostly occur for orders where the number of suitable calibration lines is small or where their distribution across the order is very uneven. But even for orders with apparently enough, well distributed calibration lines, misidentification may sometimes occur and lead to the derivation of a spurious calibration relation. Therefore, it appeared desirable to use the above-mentioned procedure only as a first guess and to complement it by a second step. This second step is inspired by the procedure originally introduced by Hensberge & Verschueren (1989), already applied in a somewhat different manner by Mathys (1991) for the reduction of echelle spectra recorded with another instrument. A global fit of the wavelength as a function of the position of the line on the CCD in the dispersion direction and of the order number is performed. Differences between the fitted and actual wavelengths are calculated for each line. Lines for which this difference exceeds three times the rms deviation for the whole sample are removed from it, and a new fit is computed. The procedure is iterated until all the ThAr lines left have fitted wavelengths differing from their actual wavelengths by at most three times the rms deviation for the whole sample. This is very quickly achieved in general, typically in about 5 iterations. Only a very small number of lines (usually less than 10 in a sample of several hundred) have to be discarded to improve very significantly the overall accuracy of the wavelength calibration. The 2-dimensional dispersion law proves to be adequately represented by a function of the form:

 

$$\lambda(m,x) \big[a_0+b_0~m+\left(a_1+b_1~m+b_2~m^2\right)~x$$ =

$$+~\left(a_2+b_3~m+b_4~m^2\right)~x^2$$

$$+~\left(a_3+b_5~m+b_6~m^2\right)~x^3$$

$$+~\left(a_4+b_7~m+b_8~m^2\right)~x^4\big]$$

$$\times~ \left(1+c_1~m+c_2~m^2+c_3~m^3+c_4~m^4\right)^{-1} .$$ (1)

This form of the dispersion function was derived empirically, starting from the one used by Hensberge & Verschueren (1989) and adding terms as required until the fit residuals no longer showed any systematic dependence on x or on m.

The rms deviation of the wavelengths of the Th and Ar lines about the best fit eventually derived is of the order of 2 mÅ. This value gives a good estimate of the internal accuracy achieved in the wavelength calibration. This calibration is applied to the normalised scientific spectrum by assigning to each pixel of the latter the corresponding fitted wavelength. Contrary to the MIDAS usage, the spectra are not rebinned to a constant wavelength step, since this was found to introduce some degradation of the line profiles. The latter is small but nevertheless would have a non-negligible impact on the quadratic magnetic field diagnosis, in which it would appear like an additional source of noise.

With this wavelength calibration procedure, recombining (averaging) the contributions of adjacent echelle orders in the regions where they overlap would require resampling them: we preferred not to do so, so as to keep the line profile information exactly as originally recorded. Therefore, when merging the echelle orders into one single piece encompassing the whole wavelength range covered, in the regions where two orders would have overlapped, we kept only the contribution of one of them and simply discarded the other. The dividing point for keeping the contribution of one or the other order involved was taken as the middle of the overlap interval. Such a rough procedure obviously entails some loss of information, but not much, because in the adopted instrumental configuration, order overlaps are quite small. Furthermore, this loss in signal-to-noise ratio of the affected spectral intervals was judged to be less detrimental to the projected type of analysis than the effect of the wavelength resampling that would have been required to avoid it.

Table 1: Journal of observations and parameters of the studied stars.

The journal of the observations is given in Table 1, together with some relevant physical parameters of the observed stars. The first three columns give the HD number, an alternative identification, and the spectral type. Spectral types are from Renson et al. (1991), except for HD 91375 (Gray & Garrison 1987). The heliocentric Julian Date of mid-observation appears in Col. 4, and the signal-to-noise (S/N) ratio per pixel of the reduced spectrum in Col. 5. In Cols. 6 and 9, one finds values of the effective temperature and of as derived in the references mentioned in Cols. 7 and 10, respectively. For HD 133792, was estimated from Strömgren photometry by application of the method of Moon & Dworetsky (1985). Only determinations based on spectra obtained at a resolution comparable to the ones used in the present observations have been considered. The values of estimated from the spectra analysed in this work are also given in Col. 8. The last two columns give the rotation period and the corresponding reference.

As is well known, evaluation of the S/N ratio achieved in spectra of Ap stars is hampered by the difficulty to identify a spectral region sufficiently free of lines, so that it can be considered representative of the true continuum. In all stars of the present sample but HD 137949, the S/N ratio was estimated from measurement of the rms deviation of the reduced spectrum about the fitted continuum in a "clean'' spectral interval redwards of H$\alpha$; for HD 137949, which is particularly line-rich, a "line-free'' stretch bluewards of H$\alpha$ was preferred. In all cases, the derived value, as given in Table 1, must be regarded as a lower limit of the actually achieved S/N ratio at the wavelength at which it was determined. However, the S/N ratio across the whole recorded spectral range varies due to the wavelength dependence of the transmission of the cross-disperser grism and to the blaze effect of the echelle grating. Taking these efficiency variations into account, we estimate that the S/N ratio per pixel at any point of a given spectrum is comprised within a factor 1.5 of the value quoted for this spectrum in Table 1.

The values of appearing in Col. 8 of Table 1 were estimated by spectral synthesis of the magnetically insensitive line Fe I  $\lambda~5434.5$. This line is visible in all the studied stars but HD 96446 (which is too hot); however it is quite weak in HD 94660 and in HD 116458. In most stars, it has broad wings, for which a good fit cannot be achieved with a simple model, and which are probably indicative of the existence of abundance stratification in the atmosphere of these stars. Study of such effects is beyond the scope of the present work, so that the current estimates were derived by optimising the fit of the central part of the line. The related uncertainties should be kept in mind.

Most of the stars that have been observed within the framework of this project are Ap stars with resolved magnetically split lines. These stars appear well suited to the purpose of this study because the mean magnetic field modulus that is derived from the measurement of the wavelength separation of the split components of their spectral lines (Mathys et al. 1997) bears some relation to the mean quadratic magnetic field. One can take advantage of this to check the consistency of the diagnosis of the latter as well as to gain additional insight into the structure of the magnetic field. This will be discussed in more detail in Sect. 4.2.

We have also recorded a spectrum of HD 96446, a peculiar B2 star, which is one of the hottest non-degenerate magnetic stars known. The main motivation for including this star in the sample was that it has a very "clean'' spectrum, with a considerable number of well defined weak spectral lines that can be used for magnetic field diagnosis. As mentioned in Sect. 1, all the applications of the moment technique so far have resorted to the weak-line approximation: HD 96446 is definitely one of the cases where this approximation is best justified. In particular, it is noteworthy that the field diagnostic lines are in average at least ten times weaker for HD 96446 than for the other Ap stars studied in this paper. The latter can be regarded as representative of most Ap stars.

For comparison purposes, as well as to probe the limits of the present approach for magnetic field detection, we have also included in the studied sample two stars that are unlikely to have a strong magnetic field, HD 91375 and HD 133792. The former is a superficially normal A2IV star (Gray & Garrison 1987), while the latter is an A0p SrCr star (Renson et al. 1991) with a quite pronounced peculiar character. Both stars, have very sharp spectral lines. They were studied by Mathys (1990a), who found no indication of the presence of a magnetic field.

   
3 Analysis

The second-order moment $\ensuremath {R_{I}^{(2)}(\lambda _I)}$ of a spectral line profile recorded in unpolarised light about its centre of gravity $\lambda_I$ is defined as:

$$\ensuremath{R_{I}^{(2)}(\lambda_I)} ={1\over\ensuremath{W_\la... ...(\lambda)~\ensuremath{(\lambda-\lambda_I)} ^2~{\rm d}\lambda .$$ (2)

The integration runs over the whole width of the observed line (see Mathys 1988 for details). $\ensuremath{W_\lambda}$ is the line equivalent width; $\ensuremath{r_{\ensuremath{{\cal F}_I}}}$ is the line profile:

$$\ensuremath{r_{\ensuremath{{\cal F}_I}}} =1-(\ensuremath{{\cal F}_I} /\ensuremath{{\cal F}_{I_{\rm c}}} ) .$$ (3)

$\ensuremath{{\cal F}_I}$ (resp. $\ensuremath{{\cal F}_{I_{\rm c}}}$) is the integral over the visible stellar disk of the emergent intensity in the line (resp. in the neighbouring continuum).

For each spectrum, we have measured $\ensuremath {R_{I}^{(2)}(\lambda _I)}$ for samples of apparently unblended lines that will be specified below. The equivalent width $\ensuremath{W_\lambda}$, the centre of gravity $\lambda_I$, and the second-order moment $\ensuremath {R_{I}^{(2)}(\lambda _I)}$ have been computed by simple integration of the observed line profiles. This has been described in more detail in Sect. 2 of Mathys (1994). The measurement uncertainties have also been evaluated as explained in that reference.

These measurements were analysed through a semi-empirical approach inspired from the one originally introduced by Stenflo & Lindegren (1977) to study the magnetic field of the sun. Namely, for a statistical sample of spectral lines, dependences of the second-order moments of the profiles on other parameters characterising the line were sought and quantified through a multiple linear regression analysis. As a guideline for this search and as a tool for the interpretation of its outcome, we used the results established by Mathys (1988) in his original study of the line profile moments in the presence of a magnetic field.

According to that reference, the second-order moment $\ensuremath {R_{I}^{(2)}(\lambda _I)}$ can be expressed as:

 

$$\ensuremath{R_{I}^{(2)}(\lambda_I)} =\ensuremath{\Phi^{(2)}(\lamb... ...~\ensuremath{\langle H^2\rangle} +D_2~\ensuremath{\langle H_z^2\rangle}\right).$$ (4)

The second term of the right hand side of this equation accounts for the Doppler broadening of the considered line resulting from the star's rotation, and the third one for the effect of the magnetic field. The first term includes all the other contributions to the line width. Each of these terms will be described in greater detail in the following subsections.

   
3.1 Rotational Doppler broadening

The wavelength dependence of the rotational Doppler broadening term in the expression of $\ensuremath {R_{I}^{(2)}(\lambda _I)}$ is contained in the factor $\ensuremath{\Delta\lambda_{\rm R}} ^2$. Namely,

$$\ensuremath{\Delta\lambda_{\rm R}} =\lambda_0~(v/c)~\sin i ,$$ (5)

where $\lambda_0$ is the nominal (laboratory) wavelength of the transition, v the stellar equatorial velocity, and i the angle between the stellar rotation axis and the line of sight.

$\ensuremath{\langle{x^2}\rangle}$ is the line-intensity weighted average over the stellar disk of the square of the distance x to the plane defined by the stellar rotation axis and the line of sight (this distance is expressed as a fraction of the stellar radius). A typical value of this average is 1/5. Its derivation and the assumptions underlying it have been described by Mathys (1995b). Depending on how closely the assumptions made represent the actual physical conditions in the stars of interest, the actual value of $\ensuremath{\langle{x^2}\rangle}$ may not be exactly 1/5, but the latter should be an acceptable approximation for all practical purposes of the present study.

   
3.2 Magnetic broadening

S₂ and D₂ are atomic parameters characterising the Zeeman pattern of the transition in a manner appropriate to the study of the second order moment of the Stokes I profile of the line originating from that transition. They are defined in terms of the coefficients $\ensuremath{C^{(1)}_{2}}$ and $\ensuremath{C^{(0)}_{2}}$ introduced by Mathys & Stenflo (1987):

  

$$S_2=\ensuremath{C^{(1)}_{2}} +\ensuremath{C^{(0)}_{2}} ,$$ (6)

$$D_2=\ensuremath{C^{(1)}_{2}} -\ensuremath{C^{(0)}_{2}} .$$ (7)

They can also be expressed as linear combinations of the squared effective Landé factor of the transition and of the second-order moments of its $\sigma_+$ and $\pi$ components about their respective centre of gravity. S₂ characterises the total width of the transition, or more precisely, the spread of all the components, weighted by their strengths. The difference S₂-D₂ characterises the spread of the $\pi$ components, weighted by their strengths: it is a measure of the degree of anomaly of the Zeeman pattern. In particular, it is zero if the pattern is a triplet. (For more about the interpretation of the physical meaning of those coefficients, see Mathys 1993.)

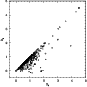	Figure 1: Comparison of the atomic parameters S2 and D2 for all the transitions considered in the present analysis. Different symbols are used to distinguish lines of different ions: open circles for Fe I, filled circles for Fe II, asterisks for Cr II, open triangles for O II, and filled triangles for N II.
Open with DEXTER

The numerical values of $\ensuremath{C^{(1)}_{2}}$ and $\ensuremath{C^{(0)}_{2}}$ (hence of S₂ and D₂) are computed through application of Eqs. (37) and (38) of Mathys & Stenflo (1987) from the total angular momentum quantum numbers J₁and J₂ and the Landé factors g₁ and g₂ of the levels between which the transition takes place. In the present work, the Landé factors are retrieved from Kurucz's CD-ROM No. 23 (see http://kurucz.harvard.edu/cdroms.html). Those values are the experimental ones, when they are available, or they have been derived from fairly sophisticated computations of the atomic eigenvectors. Those computed values have been shown to be, in general, considerably better than those computed by simple formulae for pure atomic coupling schemes such as LS- or J₁l-coupling (Mathys 1990b).

The factor $\ensuremath{\Delta\lambda_{\rm Z}} ^2$ in the magnetic term in the expression of the second-order moment of the line profile accounts for the wavelength dependence of this line broadening effect:

$$\ensuremath{\Delta\lambda_{\rm Z}} =k~\lambda_0^2,$$ (8)

with $k=4.67\times10^{-13}$ Å^-1 G^-1.

The moments of the magnetic field that contribute to the second-order moment of the line intensity profile are the mean square magnetic field modulus $\ensuremath{\langle H^2\rangle}$ and the mean square longitudinal magnetic field $\ensuremath{\langle H_z^2\rangle}$. They are the line-intensity weighted averages over the visible stellar hemisphere resp. of the square of the modulus of the magnetic vector, and of the square of its component along the line of sight. Their formal expression has been given elsewhere (e.g., Mathys 1989, 1995b).

In practice, one often encounters difficulties to separate the contributions of $\ensuremath{\langle H^2\rangle}$ and $\ensuremath{\langle H_z^2\rangle}$. Their origin is apparent in Fig. 1, where D₂ is plotted against S₂ for all the lines analysed in all the stars studied in this work. One can see that the vast majority of the points are strongly concentrated towards the diagonal S₂=D₂, or in other words, that there are only few lines for which D₂ is much smaller than S₂. Physically, this reflects the fact that most of the considered lines have Zeeman patterns that do not depart very strongly from triplets.

This problem had already been demonstrated by Mathys (1995b). It cannot be overcome in the present analysis, even though it relies on the study of many more lines measured with significantly better precision. Accordingly, we use the same workaround as Mathys (1995b). Namely, we introduce a parameter $\alpha=\ensuremath{\langle H_z^2\rangle} /\ensuremath{\langle H^2\rangle}$and we rewrite the combination of the mean square field modulus and of the mean square longitudinal field appearing in Eq. (4) under the form:

$$S_2~\ensuremath{\langle H^2\rangle} +D_2~\ensuremath{\langle ... ..._2\over 1+\alpha}~(1+\alpha)~\ensuremath{\langle H^2\rangle} .$$ (9)

Mathys (1995b) had shown that, within the limits of the achievable accuracy, the quantity $(1+\alpha)~\ensuremath{\langle H^2\rangle} =\ensuremath{\langle H^2\rangle} +\ensuremath{\langle H_z^2\rangle}$ does not significantly depend on the value of $\alpha$. Thus this quantity (to which we refer to as the mean square magnetic field) appears to characterize well the stellar magnetic field. It can be derived by fixing $\alpha$ to any arbitrary value (between 0 and 1). In what follows, we adopt $\alpha=1/3$, which should be close to the actual value of the ratio of $\ensuremath{\langle H_z^2\rangle} /\ensuremath{\langle H^2\rangle}$ in most real situations (Mathys 1995b).

   
3.3 Other line broadening agents

The term $\ensuremath{\Phi^{(2)}(\lambda_I)}$ in the expression of the second-order moment of the unpolarized line profile appearing in Eq. (4) accounts for all the broadening agents that have not been considered in the previous two subsections. It is the second-order moment about the line centre of the hypothetical line profile that would be observed in the absence of magnetic broadening and of rotational Doppler broadening.

One definite contribution to this second-order moment is the instrumental profile. Assuming that this profile is symmetrical (an excellent approximation for the observational material upon which the present work is based), its effect can be accounted for by writing $\ensuremath{\Phi^{(2)}(\lambda_I)}$ under the form (Mathys 1988):

$$\ensuremath{\Phi^{(2)}(\lambda_I)} =\ensuremath{\Psi^{(2)}(\lambda_I)} +\ensuremath{{\cal F}^{(2)}(\lambda_I)} ,$$ (10)

where $\ensuremath{{\cal F}^{(2)}(\lambda_I)}$ is the second-order moment of the instrumental profile at the wavelength of the line under consideration. With the instrumental configuration used for this study, the resolving power is essentially constant over the whole wavelength range covered. That is, the width of the instrumental profile varies linearly with wavelength, similarly to the Doppler width. By analogy with the latter (see Sect. 3.1 and below), the second-order moment of the instrumental profile can be written, emphasizing its wavelength dependence:

$$\ensuremath{{\cal F}^{(2)}(\lambda_I)} =F~\lambda_I^2,$$ (11)

where F is a constant.

$\ensuremath{\Psi^{(2)}(\lambda_I)}$ represents the part of $\ensuremath{\Phi^{(2)}(\lambda_I)}$ that is contributed by the star. It can be regarded as the second-order moment about its centre of the hypothetical line profile that would be observed with a spectrograph of infinite resolving power in the absence of magnetic broadening and of rotational Doppler broadening. It always includes a Doppler contribution, due to the thermal motion of the ions from which the line is formed. This contribution can be isolated by writing the moment $\ensuremath{\Psi^{(2)}(\lambda_I)}$ under the form (Mathys 1988):

$$\ensuremath{\Psi^{(2)}(\lambda_I)} =\ensuremath{\Psi_0^{(2)}(\lambda_I)} +\ensuremath{\Delta\lambda_{\rm D}} ^2/2,$$ (12)

with $\ensuremath{\Delta\lambda_{\rm D}} =(\zeta_0/c)~\lambda_0$. $\zeta_0$ is the most probable line-of-sight velocity of the ion responsible for the studied line in a reference frame corotating with the star. In addition to the thermal motion, it may contain a contribution from the microturbulence.

$\ensuremath{\Psi_0^{(2)}(\lambda_I)}$ accounts for all the remaining contributions to the total line width. In what follows we shall refer to it as the intrinsic line profile. For weak lines, $\ensuremath{\Psi_0^{(2)}(\lambda_I)}$ should be equal to the second-order moment of the line absorption profile about its centre. Transfer effects will complicate the picture. Rather than attempting to derive a theoretical expression for $\ensuremath{\Psi_0^{(2)}(\lambda_I)}$, we shall, along with Mathys (1988), assume that it is possible to derive an empirical relation between it and a number M of parameters Q_m ( $m=1,\ldots,M$) characterizing the observed line and the transition from which it originates (such as the equivalent width, the excitation potential of the lower level, etc.), and that this relation can be put under the form:

$$\ensuremath{\Psi_0^{(2)}(\lambda_I)} =a_0+\sum_{m=1}^M\sum_{n=1}^{N(m)}a_{mn}~Q_m^n.$$ (13)

Figure 2: Contribution of the intrinsic ( left), Doppler ( centre), and magnetic ( right) parts of the profiles of the lines of Fe I observed in HD 116114 to their second-order moment about their centre ( see text). The dashed line is the term of the least-squares fit of the observations corresponding to that contribution. The relative weights of the different lines in the regression analysis yielding this best fit line are illustrated by the sizes of the dots representing them.

Open with DEXTER

From the above considerations, one can infer that the way in which $\ensuremath{\Phi^{(2)}(\lambda_I)}$ depends on other parameters should generally be different for different ions. For instance, the contribution of the thermal motion to $\zeta_0$ depends on the mass of the ion. Also, a possible dependence of $\ensuremath{\Psi_0^{(2)}(\lambda_I)}$ on the excitation potential of the lower level of the transition would obviously not be the same for all ions. Accordingly, to achieve the best accuracy, the analysis will be based on samples of spectral lines of a single ion. One can, of course, for a given star, study separately line samples for different ions. The comparison of the results obtained from the consideration of those samples may also prove useful. This will be discussed in more detail in Sect. 4.2.5.

   
3.4 Application

As explained above, we have applied a semi-empirical approach to diagnose the magnetic fields of the studied stars from consideration of the second-order moments of their spectral lines about their centre. Namely, we have determined these moments for a selected sample of lines and we have made attempts to identify and to characterise their dependences on other line parameters. Taking the considerations of the previous sections as guidelines, we have tried to find relations of the form:

 

$$\ensuremath{R_{I}^{(2)}(\lambda_I)} =a_0+a_1~{1\over 5}{\lambda_0... ...er4}~\ensuremath{\Delta\lambda_{\rm Z}} ^2 +\sum_m\sum_{n=1}^{N(m)}a_{mn}Q_m^n.$$ (14)

We have tried to fit such relations to our measurements. As in our previous analyses based on the moment technique, we have weighted these fits by the inverse of the mean-square errors of the $\ensuremath {R_{I}^{(2)}(\lambda _I)}$measurements for the individual lines (see Mathys 1994 for details). We have tried to use various parameters or combinations of parameters for Q_m: $W_\lambda$ (the line equivalent width), $W_\lambda~\lambda_0/c$, $W_\lambda~\lambda_0^2/c^2$, $W_\lambda~\lambda_0^4/c^4$, $\chi_{\rm e}$ (the excitation potential of the lower level of the transition), $\chi_{\rm e}~\lambda_0/c$, $\chi_{\rm e}~\lambda_0^2/c^2$, $\chi_{\rm e}~\lambda_0^4/c^4$, $\chi_{\rm e}~W_\lambda$, and $\chi_{\rm e}~W_\lambda~\lambda_0^2/c^2$. The one whose inclusion allowed us to obtain the best representation of the behaviour of $\ensuremath {R_{I}^{(2)}(\lambda _I)}$ is $\ensuremath{W_\lambda~\lambda_0^2/c^2}$. Once we have taken it into account, we have checked that we could not find any remaining significant dependence on any of the other parameters listed above, and that the only power of $\ensuremath{W_\lambda~\lambda_0^2/c^2}$ significantly contributing is the second (n=2 in Eq. (14)), to the exclusion of the first or of higher powers of this quantity. We have checked in particular that the inclusion of those additional, useless parameters would not have any significant effect on the value of the fit parameter a₂, from which the stellar magnetic field is diagnosed. We have performed those checks for all the studied stars, for all the samples of lines sufficiently populated to allow the necessary multi-parameter fits to be performed meaningfully.

Therefore, we conclude that the dependences of the second-order moment of the Stokes I line profiles about their centre on the other parameters characterizing those lines are satisfactorily represented by a relation of the following form:

 

$$\ensuremath{R_{I}^{(2)}(\lambda_I)} =a_0+a_1~{1\over 5}{\lambda_0... ...nsuremath{\Delta\lambda_{\rm Z}} ^2 +a_3~W_\lambda^2{\lambda_0^4\over c^4}\cdot$$ (15)

Finally, we have found that, when we use Eq. (15) to fit the measurements of $\ensuremath {R_{I}^{(2)}(\lambda _I)}$, the value of the parameter a₀ (constant term) that we derive does not in general differ significantly from zero. Namely, the ratio of the derived value of a₀ to its standard error $\sigma(a_0)$ is smaller than 2 (in absolute value) for 17 of the 20 line samples whose analysis is reported in Sect. 3.4. The 3 exceptions turn out to be the 3 cases in which the derived values of $\sigma(a_0)$ are smallest: the lines of Fe I and Fe II in HD 91375, and the lines of Cr II in HD 133792. These are also the cases where the standard deviation of the measured values $\ensuremath {R_{I}^{(2)}(\lambda _I)}$ with respect to the best fit by expression (16) is smallest. This indicates that, at the accuracy achievable in most cases, the constant term in Eq. (15) can be safely neglected, and the dependence of $\ensuremath {R_{I}^{(2)}(\lambda _I)}$ on the other line parameters can be adequately represented by the relation:

$$\ensuremath{R_{I}^{(2)}(\lambda_I)} =a_1~{1\over 5}{\lambda_0... ...lambda_{\rm Z}} ^2 +a_3~W_\lambda^2{\lambda_0^4\over c^4}\cdot$$ (16)

That this is acceptable for the purpose of this study is further confirmed by the fact that there is no significant difference between the values of a₂ and of its uncertainty $\sigma(a_2)$ that are derived through application of Eqs. (15) or (16).

	Figure 3: Same as Fig. 2 for the lines of Fe I observed in HD 133792. Note that the ordinate range is nearly one order of magnitude smaller than in Fig. 2.
Open with DEXTER

The dependences appearing in Eq. (16) are illustrated in Fig. 2 in the case of the Fe I lines of the cool Ap star HD 116114. We have identified in this star 89 lines of Fe I that appear reasonably blend-free: this sample is about 10 times more populous than the line samples that could be used by Mathys (1995b) for most stars (see Mathys 1991). We have measured the second-order moments of the profiles of those lines about their centre, and we have computed a weighted fit of those measurements by a relation of the form given by Eq. (16). We have then isolated the contribution of one of the terms appearing in the right-hand side of Eq. (16) by subtracting from the measured values of $\ensuremath {R_{I}^{(2)}(\lambda _I)}$ the fitted contribution of the other two terms, and we have plotted the residual against the relevant parameter. More explicitly, we have plotted:

• $[\ensuremath{R_{I}^{(2)}(\lambda_I)} -a_1~\lambda_0^2/(5c^2)-a_2(3S_2+D_2)~\ensuremath{\Delta\lambda_{\rm Z}} ^2/4]$against $(\ensuremath{W_\lambda} ^2\lambda_0^4/c^4)$ in the left panel of Fig. 2;
• $[\ensuremath{R_{I}^{(2)}(\lambda_I)} -a_2~(3S_2+D_2)~\ensuremath{\Delta\lambda_{\rm Z}} ^2/4-a_3~\ensuremath{W_\lambda} ^2~\lambda_0^4/c^4]$against $[\lambda_0^2/(5c^2)]$ in the centre panel of Fig. 2;
• $[\ensuremath{R_{I}^{(2)}(\lambda_I)} -a_1~\lambda_0^2/(5c^2)-a_3~\ensuremath{W_\lambda} ^2~\lambda_0^4/c^4]$against $[(3S_2+D_2)~\ensuremath{\Delta\lambda_{\rm Z}} ^2/4]$ in the right panel of Fig. 2.

These can be regarded as the contribution to the second-order moments of, resp., the intrinsic, Doppler (and instrumental), and magnetic parts of the line profile. For easy comparison of the relative importance of the three effects, the same ordinate scale has been used in all three panels of Fig. 2. In the considered case, the main line broadening agent appears to be the magnetic field. This is not surprising, since HD 116114 has magnetically resolved lines (first reported by Mathys et al. 1993), which implies that the Zeeman splitting is large compared to the width of the individual line components.

	Figure 4: The values for the Cr II lines analysed in HD 94660 of the three independent variables appearing in the right-hand sides of Eqs. (15) and (16) are plotted against each other, pair by pair, as a check of possible mutual correlations between these variables.
Open with DEXTER

The opposite situation is found in HD 133792, a star that is, at most, weakly magnetic. The second-order moments of 144 Fe I lines have been measured in this star. The same dependences of those moments as for HD 116114 are illustrated in Fig. 3. Again, the ordinate scale is the same in the three panels of this figure, for easy intercomparison, but note the difference of scale with respect to Fig. 2: the lines of HD 133792 are much narrower than those of HD 116114. The main contribution to $\ensuremath {R_{I}^{(2)}(\lambda _I)}$ in HD 133792 comes from the Doppler/instrumental term. The latter appears to be of the same order as in HD 116114: the difference between the two stars comes from the fact that the contributions of the other two terms of the right-hand side of Eq. (16) are smaller in HD 133792. The slope of the dependence of $\ensuremath {R_{I}^{(2)}(\lambda _I)}$ on $\ensuremath{W_\lambda} ^2/\lambda_0^4 c^4$ is similar in both stars, but the Fe I lines are stronger (by a factor of the order of 2) in HD 116114: this accounts for the larger contribution of the intrinsic line profile to the second-order moments of the observed profiles. Finally, the term with the smallest contribution to $\ensuremath {R_{I}^{(2)}(\lambda _I)}$ is the magnetic one: this reflects the fact that HD 133792 has quite sharp spectral lines showing no evidence for magnetic splitting or broadening. From this observation, Mathys et al. (1997) have estimated that the mean magnetic field modulus of HD 133792 is probably not exceeding 1 kG: this is fully consistent with the value of $(1160\pm233)$ G that we derive for the quadratic field of this star (see Sect. 4.2).

In multi-parameter fits such as considered here, ambiguities may arise if correlations exist between the independent variables. In order to test this eventuality, we plotted the independent variables against each other, two by two. This illustrated in Fig. 4 for the Cr II lines of HD 94660. There is absolutely no correlation between $(\ensuremath{W_\lambda} ^2\lambda_0^4/c^4)$ and the other two independent variables. But there is a loose correlation between the latter, which results primarily from the power of the nominal line wavelength entering their expression: $\lambda_0^2$ for one, $\lambda_0^4$ for the other. Therefore when they are plotted against each other, the points cluster around a parabolic curve, with a scatter corresponding to the range of values of the magnetic parameters S₂ and D₂. This scatter, and the fact that different powers of the wavelength appear in the expressions of $[(3S_2+D_2)~\ensuremath{\Delta\lambda_{\rm Z}} ^2/4]$and of $[\lambda_0^2/(5c^2)]$, minimise the correlation between these two parameters in the linear regression. However, due to noise in the data, the presence of some residual crosstalk between the fit parameters a₁ and a₂ cannot be totally ruled out. By contrast, there should be no ambiguity at all between a₃, on the one hand, and either of a₁ or a₂, on the other hand.

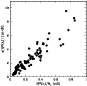	Figure 5: Plot of the estimated error of the second-order moment of the profiles of the lines of Fe II observed in HD 94660 against the ratio of the second-order moment of these lines to their equivalent width.
Open with DEXTER

Figure 5 illustrates the meaning of the weighting applied in the regression analysis. In this case, the example shown corresponds to the Fe II lines of HD 94660. The weighting factor that is applied is the inverse of the square of the parameter appearing in ordinate in this figure, $\sigma[\ensuremath{R_{I}^{(2)}(\lambda_I)} ]$. In other words, the higher the representative point of a spectral line appears in the figure, the lower the weight given to this line in the regression analysis. Figure 5 clearly shows a linear relation between $\sigma[\ensuremath{R_{I}^{(2)}(\lambda_I)} ]$ and $[\ensuremath{R_{I}^{(2)}(\lambda_I)} /\ensuremath{W_\lambda} ]$. In practice, this means that, at given equivalent width, the broader a line, the lower its weight in the regression analysis. Intuitively, this weighting makes sense, because the measurement of broader, shallower lines is more difficult, their limits are less well defined and integration over them is more sensitive to noise in the spectra. Nevertheless, the broadest lines are also those that are most sensitive to the magnetic field, so that the adopted weighting might be suspected to some extent to have an adverse effect in the determination of the latter. Conversely, for a given line width, stronger lines are given a higher weight than weaker lines. Again, this is consistent with the intuitive perception that the parameters of the profile of a strong line can be determined more accurately. However, the adequacy of such a weighting in a technique in which the interpretation of the results is based on the weak line approximation may admittedly appear questionable.

Table 2: Dependences of $\ensuremath {R_{I}^{(2)}(\lambda _I)}$: least-square fit parameters (without constant term).

Table 3: Dependences of $\ensuremath {R_{I}^{(2)}(\lambda _I)}$: least-square fit parameters (with a constant term).

In spite of its abovedescribed apparent shortcomings, weighting the regression analysis by $1/\sigma^2[\ensuremath{R_{I}^{(2)}(\lambda_I)} ]$ appears justified for the following reasons:

• as already shown in a somewhat different context (Mathys 1994), the uncertainties of the fit parameters derived from the weighted regressions are consistently smaller than for unweighted regressions;
• consistently with the above, the scatter of the low weight points about the best fit curves in the various figures illustrating this paper is generally larger than that of the high weight points, but there does not appear to be any significant systematic difference of behaviour between the high and low weight points (i.e., for instance, the low weight points are not concentrated above - or below - the best-fit line);
• while the weak line approximation underlies the interpretation of the a₂ fit parameter in terms of the magnetic field (see Sects. 3.2 and 4.2), transfer effects for lines that are not weak are to a significant extent dealt with by the introduction of the heuristic term in a₃ in the regression equations.

   
4 Results

We shall now present the results of the systematic application to the observational material described in Sect. 2 of the analysis strategy introduced and illustrated in the previous section.

The coefficients derived through least-square fits of measurements of $\ensuremath {R_{I}^{(2)}(\lambda _I)}$ for samples of lines of various ions in the studied stars by the function introduced in Eq. (16) are given in Table 2. The columns are, in order, the HD number of the star, the ion under consideration, the number n of lines of this ion included in the fit, the fit coefficients and their standard errors, and the rms deviation of the measurements with respect to the best fit, multiplied by 10³. The numerical values of the fit parameters correspond to the use of the following units for the quantities appearing in Eq. (15): Ų for $\ensuremath {R_{I}^{(2)}(\lambda _I)}$, Å for $\lambda_0$ and $\ensuremath{\Delta\lambda_{\rm Z}}$, mÅ for $\ensuremath{W_\lambda}$, and km s^-1 for c.

As mentioned in Sect. 3.4, for the Fe I and Fe II lines in HD 91375, and for the Cr II lines of HD 133792, the fit forced through the origin of Eq. (16) is not quite satisfactory, since a significant, non-zero value is found for the free constant term a₀ if a fit function of the form given by Eq. (15) is used. The fit parameters for this latter case are given in Table 3. The format is the same as for Table 2, except for the addition of columns for the constant term a₀ and its standard deviation. That the overall quality of the fit is slightly improved by inclusion of the free constant term is reflected by the fact that the rms deviations of interest are somewhat smaller in Table 3 than in Table 2. Allowing a non-zero value for a₀ also has some impact on the other fit parameters. For a₁, very different values are obtained through the use of fit functions 15 or 16, while a₃ is almost independent of which of these two forms is adopted. The behaviour of the coefficient of the magnetic term, a₂, is intermediate: it does change if Eq. (15) is used instead of Eq. (16), but this change remains within the respective uncertainty ranges. This result is, obviously, of great importance since our primary purpose is magnetic field diagnosis: the latter appears not to depend critically on the choice of the form of the fit function between the two possibilities considered in this paper.

On the other hand, for HD 96446, a significant value cannot be derived for the coefficient a₃. This can be attributed to the fact that the range spanned by the values of $(\ensuremath{W_\lambda} ^2~\lambda_0^4/c^4)$ for the measured lines of N II and O II in this star is at least three times narrower than the range of values of this independent variable for the measured lines of Fe I, Fe II, or Cr II in the other studied stars. Accordingly, the possible dependence of on $(\ensuremath{W_\lambda} ^2~\lambda_0^4/c^4)$ is undefined. This does not imply that the relation between the second-order moment of the Stokes I line profiles and the line equivalent width is different for the lines analysed in HD 96446 from what it is of for sets of lines of other ions in the other stars of the considered sample, but only reflects the fact that this relation is not constrained by the available observational data in the present case.

Accordingly, for HD 96446, the following simplified form of Eq. (16) has been fitted to the observed values of :

$$\ensuremath{R_{I}^{(2)}(\lambda_I)} =a_1~{1\over 5}{\lambda_0... ... +a_2~{3S_2+D_2\over4}~\ensuremath{\Delta\lambda_{\rm Z}} ^2 ,$$ (17)

yielding the fit parameters reported in Table 2. The values of the fit parameters a₁ and a₂ that are obtained using the form (17) of the regression function are not significantly different from those derived by application of Eq. (16). We have also checked that the constant term a₀ remains negligible when the a₃ term is omitted.

In the following subsections, we shall discuss the interpretation of the regression coefficients a₁ and a₂ in terms of physical parameters characterizing the atmosphere of the studied stars. The physical meaning of a₃ will not be considered, since this coefficient pertains to a term that has been introduced to account empirically for radiative transfer effects whose detailed treatment would require the use of sophisticated numerical tools. The development and application of such tools is outside the scope of the present work: actually, one of the main purposes of the use of the moment technique for magnetic field diagnosis is to allow one to derive meaningful constraints without needing to resort to heavy, time-consuming numerical calculations.

   
4.1 Stellar rotation

From the considerations developed in Sect. 3, the regression coefficient a₁ can be expanded as a sum of several terms:

$$a_1=v^2~\sin^2 i+5F~c^2+10~k~\ensuremath{T_{\rm {eff}}} /m_{\rm {ion}}+a_1^\prime ,$$ (18)

where k is Boltzmann's constant, $\ensuremath{T_{\rm {eff}}}$ the star's effective temperature, and $m_{{\rm ion}}$ the mass of the ion responsible for the studied lines. The first three terms on the right-hand side of Eq. (18) account, resp., for rotational Doppler broadening, instrumental broadening, and thermal Doppler broadening. The last term, $a^\prime_1$, includes all the other contributions to the line width with a Doppler-like wavelength dependence. That is, in the first place, Doppler broadening due to non-rotational and non-thermal velocities (microturbulence, or if they exist, any kind of macroscopic motions of material in the line forming region - such as macroturbulence or even pulsation). Possibly, $a^\prime_1$ might also include some contribution of the intrinsic line profile with a wavelength dependence similar to that of a Doppler effect. As a matter of fact, we do not aim at unravelling here the exact nature of $a^\prime_1$, and we can restrict ourselves to noting that this parameter must always be greater than or equal to zero. Accordingly, an upper limit of the projected equatorial velocity of the star can be derived from a₁ provided that the contributions of instrumental and thermal broadenings can be estimated.

For the observational material of interest, the instrumental profile is well approximated by a Gaussian with a full width at half maximum of $\lambda/7\times 10^4$. This corresponds to $F=3.673\times 10^{-11}$.

Accordingly, one has:

$$\ensuremath{v~\sin i}\leq[a_1-16.53-8.255\times10^{-2}~\ensuremath{T_{\rm {eff}}} /A]^{1/2}$$ (19)

( $\ensuremath{v~\sin i}$ in km s^-1, a₁ in km² s^-2, and $\ensuremath{T_{\rm {eff}}}$ in K). A is the atomic mass of the element whose lines are analysed.

Table 4: Mean quadratic magnetic field and upper limit of .

The results obtained through application of this formula are presented in Table 4. Missing entries in the last column of this table (where the derived upper limits are given) correspond to cases where the term between square brackets in the right-hand side of Eq. (19) is negative, so that its square root cannot be calculated. Such mathematically meaningless situation arises, of course, from the measurement uncertainties. This kind of numerical problem is particularly prone to occur for the stars of the present sample, which have been selected primarily because of their slow rotation. The uncertainties of the upper limits that are given in Table 4 are derived from the standard deviations $\sigma(a_1)$ appearing in Tables 2 and 3, hence correspond to line-to-line scatter about the best fit regression (15) or (16). As can be seen from Eq. (19), the uncertainty affecting the effective temperature should also, in principle, be taken into account. But in practice, it is always much smaller than $\sigma(a_1)$, hence it can be safely neglected.

The slow rotation of the studied stars also restricts the significance of the constraints that can be derived. The relative uncertainties affecting the upper limits obtained by application of Eq. (19) are generally not small. Furthermore, any additional unrecognised line broadening agent with a rotation-like wavelength dependence (such as micro- or macroturbulence) may contribute to increase the derived upper limit by a considerable fraction of the actual value. Accordingly, the constraint that can be derived through the method described here would, relatively, be more meaningful for stars rotating faster than those of the present sample. Thus only limited conclusions can be drawn for the latter.

In particular, the current sample is poorly suited to assessing the exactitude and accuracy that can be achieved in determinations with the present method. Consideration of faster rotating stars should be much more telltale in that respect. Such stars will be studied in future works.

In general, the upper limits that are derived for the stars of the present sample seem rather conservative. This is best illustrated by an example. The star HD 116458 has a rotation period of $P=148\hbox{$.\!\!^{\rm d}$ }39$(Mathys et al. 2003). Its radius has been estimated by Hubrig et al. (2000) to be $R=(3.54\pm0.39)$ $R_{\odot}$. From this, one can derive the value of its equatorial velocity: $v=50.6R/P=1.21\pm0.13$ km s^-1. This is considerably lower than the upper limits of derived from analysis of the lines of Fe II (5.8 km s^-1) or of Cr II (5.1 km s^-1). These two upper limits are mutually consistent within their uncertainties. But both are considerably larger than any plausible value of v. Thus not only they do not bring any new constraint (in particular, they do not set an upper limit on the angle i), but also they suggest that the "Doppler'' term in the expression of the second order moments includes, besides the rotational Doppler effect, quite significant contributions of line broadening agents that have a similar wavelength dependence, which are represented by the $a^\prime_1$ term in Eq. (18). These extra line broadening agents may or not be other Doppler contributions, due to various types of local motion in the stellar atmosphere (e.g., microturbulence).

Some additional insight can be gained from comparison of the upper limits of Table 4 with the estimates of Cols. 8 and 9 of Table 1. Let us recall that the values in Col. 8 correspond to the fit of a magnetically insensitive line of Fe I. For 4 of the 9 stars of the sample (HD 81009, HD 91375, HD 116114, and HD 137949), the most populated of the line samples used in the present analysis also corresponds to Fe I. For these 4 stars, the agreement between the spectrum synthesis value of from Table 1 and the upper limit of Table 4 is remarkably good. The Fe I sample also contains the largest number of lines for HD 133792; for this star, the upper limit of Table 4 is only marginally greater than the value of Col. 8 of Table 1: they are in any event mutually consistent. For Fe I in HD 116458, there is formal agreement between the estimate of Col. 8 of Table 1 and the upper limit of Table 4, but the significance of this result is questionable due to the small size of the Fe I line sample. The more populated samples of Fe II and Cr II lines yield significantly larger upper limits of , which are marginally consistent with the value derived by Nielsen & Wahlgren (2000) from fitting of a line of Fe II, but which, as mentioned above, are definite overestimates of the actual value of this quantity. The same can be said for the upper limit derived from the Fe II line sample for HD 94660, which however is fully consistent with the value that we estimated from synthesis of the line Fe I  $\lambda~5434.5$; both are definite gross overestimates of the actual value of . No conclusive comparison can be achieved for the remaining two stars, HD 47103 and HD 96446, although one may note that the upper limit given in Table 4 for the latter is not inconsistent with the value published by Matthews & Bohlender (1991). To summarise this comparison, there is no indication that the values (or upper limits) of derived in this analysis suffer from any systematic effects compared with the results obtained by spectrum synthesis, although there is some suspicion that, for some stars, both approaches may tend to overestimate , for reasons at present unclear, whose detailed discussion is outside the scope of the present work.

   
4.2 Mean quadratic magnetic field

As pointed out in Sect. 3.2, the mean square magnetic field characterises well the stellar magnetic field. For practical purposes, it is often more convenient to consider its square root, $\ensuremath{\langle H_{\rm q}\rangle}\equiv\ensuremath{(\langle H^2\rangle+\langle H_z^2\rangle)^{1/2}}$, which has the dimension of a magnetic field: this quantity, which was first introduced by Mathys (1995b), is called the mean quadratic magnetic field. Its derivation through the regression analysis presented in Sect. 3.4 is straightforward, since one has:

$$\ensuremath{\langle H_{\rm q}\rangle} =\sqrt{a_2}.$$ (20)

The derived values of are presented in Col. 4 of Table 4. Their uncertainties are computed from the standard deviations $\sigma(a_2)$ appearing in Tables 2 and 3, hence are "formal'' uncertainties corresponding to line-to-line scatter about the best fit regression (15) or (16). Other sources of possible errors have not been considered. The number of lines included in the analysis is given in Col. 3, and the ion to which these lines pertain is identified in Col. 2.

For a given star, the uncertainty affecting the quadratic field value is strongly dependent on the number of lines from which this field moment was derived: the larger the sample of lines that could be analysed, the smaller the uncertainty of the obtained value of . This is a strong indication that the derived uncertainties primarily reflect random errors in the measurements of the line profiles, rather than some physical effects not properly accounted for in the analysis. Accordingly, under the assumption that the lines of different ions sample the stellar photosphere in the same manner, hence that the same value of the mean quadratic magnetic field should be obtained regardless of the ion whose lines are analysed, the determination of this field moment achieved from consideration of the largest line set should be the most reliable and accurate one. Accordingly, for the following discussion, we shall take as reference for each star the value of determined from analysis of the ion for which the greatest number of lines could be measured. (The possible existence of ion-to-ion differences in the quadratic field determinations will in turn be discussed in Sect. 4.2.5.)

   
4.2.1 Mean quadratic magnetic field vs. mean magnetic field modulus and mean longitudinal magnetic field

It is useful to compare, for a given star, the value of the mean quadratic field with those of two other field moments:

• the mean magnetic field modulus , that is, the line-intensity weighted average over the stellar disk of the modulus of the magnetic vector;
• the mean longitudinal magnetic field , that is, the line-intensity weighted average over the stellar disk of the component of the magnetic vector along the line of side.

The formal expressions of these two moments have been given elsewhere (e.g., Mathys 1989). The following relations are valid, quite generally:

  

$$\ensuremath{\langle H\rangle} ^2\leq\ensuremath{\langle H^2\rangle} ,$$ (21)

$$\ensuremath{\langle H_z\rangle} ^2\leq\ensuremath{\langle H_z^2\rangle} .$$ (22)

The differences between the left- and right-hand sides of these relations reflect the dispersion of the values of the modulus of the magnetic vector (resp., of its line-of-sight component) across the stellar disk. For the modulus, this dispersion cannot be very large (otherwise, one would not observe resolved magnetically split line components: they would be smeared out by the spread in the distribution of the field values). It can be considerably larger for the longitudinal component, as the field can reverse its polarity over the visible stellar hemisphere. Combining Eqs. (21) and (22), one gets:

$$(\ensuremath{\langle H\rangle} ^2+\ensuremath{\langle H_z\rangle} ^2)^{1/2}\leq\ensuremath{\langle H_{\rm q}\rangle} ,$$ (23)

which can be regarded as a condition of consistency of the mean quadratic magnetic field with the mean field modulus and the mean longitudinal field. Checking that this condition is fulfilled represents a meaningful test of the validity of the approach followed to determine the mean quadratic field.

Of course, comparison of the two sides of Eq. (23) requires consideration of the various field moments that are involved at the same rotation phase. For those stars of the sample whose period is known, the values of and at the phase corresponding to the observation time given in Table 1 were computed from the best fits to the variation curves of these field moments computed by Mathys et al. (in preparation) for HD 81009, HD 94660, HD 116114 and HD 116458, and by Mathys (1994) for HD 96446 (the lines of HD 96446 are not resolved, hence there are no determinations of the mean field modulus). The rotation period of HD 137949 may be of the order of 75 y or longer (Mathys et al. 1997), and a full rotation cycle has not been observed yet. The mean field modulus has not significantly varied between the discovery of resolved magnetically split lines in this star in March 1991 (Mathys & Lanz 1992) and the last observation of Mathys et al. (in preparation), obtained in September 1998. Accordingly, we adopted the average of all the measurements performed during that time interval (Mathys et al. 1997; and in preparation) as the value of the field modulus at the time of the analysed EMMI observation. The same applies for measurements of the mean longitudinal field of HD 137949 performed between April 1995 and June 1997 (Mathys et al., in preparation). The rotation period of HD 47103 is unknown, but no definite variation has been detected by Mathys et al. (in preparation) for either (between January 1996 and January 1998) or (between December 1995 and September 1998), so that averages of all the measurements of these authors are considered as adequate for the present purpose. The adopted values of and appear in Cols. 2 and 3 of Table 5. The corresponding values of $(\ensuremath{\langle H\rangle} ^2+\ensuremath{\langle H_z\rangle} ^2)^{1/2}$ are given in Col. 4, for comparison with the quadratic field determinations shown in Col. 5. As indicated above, the latter correspond to the ion for which the largest number of spectral lines could be included in the analysis. For the sake of simplicity, the uncertainty of quoted in Table 5 is the average of the two (positive and negative) errors appearing in Table 4. This simplification has no impact on the present discussion. For the longitudinal field and the field modulus, the uncertainties given in Table 5 are, according to the way in which the adopted field moments were obtained, the standard deviation of all the averaged measurements, or the uncertainty derived by application of error propagation to the uncertainties of the parameters of the curves fitted to the variations of the considered field moments.

Table 5: Mean magnetic field modulus, mean longitudinal magnetic field and mean quadratic magnetic field.

Comparison of Cols. 4 and 5 of Table 5 shows that the consistency condition expressed by Eq. (23) is fulfilled, within the uncertainties. This lends support to the validity of the approach followed to derive the mean quadratic magnetic field. That this fulfilment is somewhat marginal for HD 94660 and, to a lesser extent, HD 137949, may

• either reflect the fact that the dispersion across the visible stellar hemisphere of the local values of the modulus and of the line-of-sight component of the magnetic field vector is small. This interpretation receives some support from the fact that the full amplitudes of variation of (326 G) and, especially, of (160 G) for HD 94660 are among the smallest observed in any Ap star with resolved magnetically split lines. For HD 137949, these amplitudes are not known: no variation of has been detected yet, while, taking into account the most recent observations of Mathys et al. (in preparation), it is not implausible that the difference of $\sim$700 G between Mathys & Hubrig's (1997) values of and Babcock's (1958) early determination is close to the full amplitude of the variation of this field moment.
• or indicate that the derived value of somewhat underestimates the actual mean quadratic magnetic field. This possibility is borne, to some extent, by the fact that the upper limits derived for seem somewhat high (see Sect. 4.1): one may suspect that, due e.g. to the measurement errors, there may be some crosstalk between the a₁ and a₂ terms of Eqs. (15) and (16) in the regression analysis carried out to determine these parameters. The possibility that such crosstalk may occur is borne by the fact that the independent variables $[(3S_2+D_2)~\ensuremath{\Delta\lambda_{\rm Z}} ^2/4]$ and $[\lambda_0^2/(5c^2)]$ are not entirely uncorrelated, as discussed in Sect. 3.4.

In any event, the small difference between the values appearing in Cols. 4 and 5 of Table 5 for HD 94660 and HD 137949 provides a convincing indication that the field moment value derived by the method described in this paper does not overestimate the actual stellar field. This in particular gives some confidence that the method is not likely to produce spurious magnetic field detections.

   
4.2.2 Magnetic field detection

In the best cases, when a sufficient number of spectral lines can be included in the analysis, and these lines lend themselves well to accurate line profile measurements (e.g., the line density in the spectrum is low enough so that most lines are almost totally free from blends), the formal uncertainty of the derived mean quadratic magnetic field can be as low as $\sim$200 G. Considering a determination at the $3\sigma$ level as significant, this corresponds to a detection threshold of the order of 600 G. This implies that the method described in this paper should allow one to detect magnetic fields considerably weaker than those that can be found by observation of resolved magnetically split lines, for which Mathys et al. (1997) estimate a lower limit of observability of approximately 1.7 kG. Of course, mean longitudinal magnetic field measurements are sensitive to much weaker fields, down to a few tens of Gauss (e.g., Shorlin et al. 2002). But such fields are detectable only provided that they have enough large-scale organisation so that contributions of various parts of the stellar surface do not cancel out in spectropolarimetric observations, and that the geometry of the observation (i.e., the relative orientations of the magnetic field and of the line of sight) is favourable. Mean quadratic field determinations are not affected by such a restriction.

For two of the stars of the present sample in which no magnetic field had been detected before, a determination of the quadratic field at a level slightly exceeding $4\sigma$ is reported in Table 4: HD 91375 and HD 133792. In both cases, this result just above the threshold of significance is obtained from analysis of the lines of Fe I, which is the ion for which the largest number of spectral lines could be measured. No magnetic field was detected from consideration of the considerably less numerous lines of a second ion (Fe II in HD 91375, Cr II in HD 133792), for which the derived value of regression coefficient a₂ does not significantly differ from 0, whether the regression is forced through the origin or not (see Tables 2 and 3).

   
4.2.3 HD 133792

That a magnetic field can be detected in HD 133792 is not particularly surprising, since this is a typical Ap star. But the result is significant in relation with the apparent existence of a discontinuity in the distribution of the mean magnetic field moduli of Ap stars reported by Mathys et al. (1997). Indeed these authors could not find any Ap star with resolved magnetically split lines having a mean field modulus, averaged over the rotation period ( ), smaller than 2.8 kG. This result appears to reflect an intrinsic stellar property because:

• the instrumentation and analysis technique used in the considered work should allow to be measured down to $\sim$1.7 kG; values as low as 2.2 kG have, as a matter of fact, been determined at some phases for at least one star (HD 59435; see Wade et al. 1996, 1999);
• in about half of the known Ap stars with magnetically resolved lines, the average over the rotation period of the mean field modulus, $\ensuremath{{\langle H\rangle}_{\rm {av}}}$, is comprised between 2.8 and 5.0 kG: the distribution of the field moduli is highly peaked towards low values, and its abrupt low limit at 2.8 kG starkly contrasts with its long tail towards the high values, spreading out to 34 kG.

However, it remained unclear if the sharp edge observed around 2.8 kG in the distribution of the field modulus is a cutoff (i.e., Ap stars either have magnetic fields whose mean modulus, averaged over the rotation period, is greater than or equal to 2.8 kG, or they do not have any observable magnetic field at all), or if it is a discontinuity in the distribution of . The latter possibility would imply that the distribution of the field modulus is bimodal. That is, no magnetic Ap star has a mean field modulus, averaged over the rotation period, comprised between 1.7 and 2.8 kG, but besides the peak around 5 kG identified in Mathys et al.'s (1997) study of the Ap stars with magnetically resolved split lines, a number of Ap stars have weaker observable fields, comprising a second peak in the distribution, below 1.7 kG. This interpretation seems somewhat easier to reconcile with the mean longitudinal field distribution, which extends continuously down to the detection limit (Landstreet 1992; Bychkov et al. 2003), or at least down to a threshold value of the order of a few 10 G (Aurière et al. 2004). This is not conclusive, though, since the already mentioned strong dependence of on both the stellar field structure and the geometry of the observation makes it a rather poorly suited quantity to characterise the actual field strength.

Even if one leaves aside, for a while, the fact that the value of the quadratic field that is derived here for HD 133792 is only just above the significance threshold, this single detection is not, by itself, sufficient to establish definitely the existence of a population of magnetic Ap stars with a mean magnetic field modulus, averaged over the stellar rotation cycle, on the weak field side of the 1.7-2.8 kG gap of the distribution. Instead, the result obtained here shows only that:

• HD 133792 does have a magnetic field;
• as a consequence of Eq. (21), $\ensuremath{\langle H\rangle}\leq1.16$ kG at the time of observation.

However, one cannot rule out the possibility that the mean field modulus of HD 133792 may be considerably larger at other phases, so that its average value over a whole rotation period is not smaller than 2.8 kG. This is not implausible, since there are several known cases of Ap stars whose mean field modulus varies with a relatively large amplitude so that it is, during part of their period, smaller than the 2.8 kG lower limit of the distribution. The example of HD 59435 has already been pointed out above, while HD 9996 and HD 18078 show resolved magnetically split lines during part of their cycle only (Mathys et al. 1997). Nevertheless, comparison of the the June 1996 EMMI spectrum analysed here with two ESO CES spectra recorded, resp., in April 1989 and in February 2000, fails to reveal any significant variation of the profile of the line Fe II  $\lambda~6149$ or of any neighbouring line. This may indicate either that HD 133792 does not vary spectroscopically (e.g. because its rotation axis lies along the line of sight), or that its rotation period is much longer than 11 years, or more unlikely, that, if the period is short, the three spectra of this star currently at our disposal have fortuitously been recorded close to the same rotation phase!

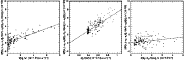	Figure 6: Same as Fig. 2 for the lines of Fe I observed in HD 91375.
Open with DEXTER

Furthermore, the value of 1160 G that we derive for the mean quadratic magnetic field of HD 133792 is quite consistent with the value of the mean modulus of the field, 1150 G, inferred by Ryabchikova et al. (2004) from modelling of a VLT/UVES spectrum recorded in March 2003 by spectrum synthesis.

On the other hand, other field modulus values below 1.7 kG have been reported in HD 176232 by Kochukhov et al. (2002) (1500 G) and by Leone et al. (2003) (1.4 kG), and in HD 204411 by Ryabchikova et al. (2005) (750 G).

While each of the above results taken in isolation does not represent conclusive evidence of the existence of magnetic fields with mean moduli (averaged over a stellar rotation period) lower than 1.7 kG, their conjunction strongly supports the existence of such fields, and it lends further credibility to the existence of a gap in the distribution of $\ensuremath{{\langle H\rangle}_{\rm {av}}}$ between approximately 1.7 and 2.3 kG. The present example of the analysis of HD 133792 also suggests that the mean quadratic field determination method discussed in this paper is well suited for further investigation of this question.

   
4.2.4 HD 91375

The derivation of a nonzero mean quadratic magnetic field in HD 91375 is more unexpected. Indeed it is generally accepted that superficially normal A stars do not have detectable magnetic fields. The most recent and constraining observational evidence supporting this conclusion has been provided by Shorlin et al. (2002), who failed to measure any mean longitudinal magnetic field significantly differing from zero in MuSiCoS spectropolarimetric observations of a sample of 22 normal stars of spectral types F, A, and B, in spite of achieving some the most precise determinations of ever obtained (with in several cases $\sigma(\ensuremath{\langle H_z\rangle} )<10$ G). Unfortunately, HD 91375 was not part of the sample studied by these authors. As a matter of fact, one of the motivations for including HD 91375 in the present programme was to use it as a magnetically null check star, for verification that the analysis method employed here does not yield spurious magnetic field detections. Accordingly, a straightforward possible interpretation of the non-null result that is obtained here is that it is indeed spurious. Even if it is correct, this interpretation should not be regarded as seriously questioning the overall validity of the method of magnetic field diagnosis developed in this work, since the derived value of is only slightly above the significance threshold. Instead, the detection achieved in HD 91375 should only be seen as a warning that the formal uncertainties that are obtained may slightly underestimate the actual errors, hence that one should exert care not to overinterpret marginally significant quadratic field determinations and detections. But it does not question the reliability of values of that stand well above the uncertainty level (say, at $10~\sigma$ or more, as is the case for all other stars of the present sample bar HD 133792), which is strongly supported by the arguments presented in Sec. 4.2.1.

As a matter of fact, those arguments also rather suggest that the analysis method applied here is more likely to underestimate the quadratic field than to generate a spurious non-null value, so that one cannot a priori discount the quadratic field measured in HD 91375 as spurious. The visual impression of the dependences of $\ensuremath {R_{I}^{(2)}(\lambda _I)}$ illustrated in Fig. 6 actually tends to lend support to the reality of the detection.

More generally, the fact that quite stringent upper limits are now obtained for longitudinal fields of normal A stars does not rule out that such stars may have sizeable magnetic fields with more complex structures, even though as pointed out by Shorlin et al. (2002), it sets increasingly strict constraints on the complexity of the structure that these fields must have so that they have no net detectable effect in disk-integrated circularly polarised line profiles. On the other hand, one may note that main-sequence early A stars with very low tend to show some degree of chemical peculiarity (Ramella et al. 1989). Abt (2000) even recently argued that slow rotation is a sufficient condition for A stars to become chemically peculiar (but this claim raises some reservations: see Mathys 2004 and Royer et al. 2004).

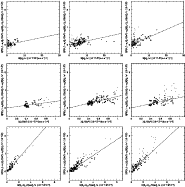Figure 7: Contribution of the intrinsic ( top row), Doppler ( centre row), and magnetic ( bottom row) parts of the profiles of the lines of Fe I ( left column), Fe II ( centre column) and Cr II ( right column), observed in HD 116458 to their second-order moment about their centre ( see text). The dashed line is the term of the least-squares fit of the observations of each ion corresponding to that contribution. The relative weights of the different lines in the regression analysis yielding this best fit line are illustrated by the sizes of the symbols representing them.

Open with DEXTER

   
4.2.5 Mean quadratic magnetic field determinations using diagnostic lines of different ions

In Sect. 4.2, we have assumed that analysis of sets of lines of different ions should yield the same value of the mean quadratic magnetic field. However this cannot a priori be taken for granted. Let us now consider this point in more detail.

In practice, one can see from Table 4 that significant differences between the values of derived from the analysis of lines of different ions are found for only two stars: HD 81009 (Fe I and Cr II) and HD 116458 (Fe I, Fe II, and Cr II). For the rest of the sample, all studied line sets yield values of the quadratic field that are consistent within their estimated uncertainties.

The small number of Cr II lines that could be measured in HD 81009 sets severe limitations on the amount of information that can be extracted from their consideration towards understanding the discrepancy between the value of obtained from their analysis and from that of the more populated Fe I line sample. In particular, it does not lend itself well to the separation of the contributions of the various terms of the right-hand side of Eq. (15), and actually increases the probability that unrecognised cross-talk may occur between these terms due to an unfortunate combination of random errors in measured values of the second-order moments of the Stokes I line profiles. In other words, the analysed Cr II line sample may not be sufficiently populated to guarantee that the standard deviations provided by the regression are meaningful enough from a statistical standpoint so that they can be safely used as estimates of the uncertainties affecting the derived quantities. It may well be that these uncertainties are somewhat underestimated, so that the discrepancy between the values of the quadratic field determined from the two studied ions is only apparent.

The case of HD 116458 is more telltale, in particular as far as the discrepancy between the values of derived from consideration of the Fe II and Cr II line sets are concerned. Indeed these two sets are among the most populated of all line samples considered in this work. The dependences between line parameters that are found from their analysis are well defined, and the inconsistency between the quadratic field values that they reveal is quite significant. The size of the analysed line sets allows one to gain more insight into the origin of this inconsistency. Furthermore, HD 116458 is one of only two stars of the present sample for which the quadratic field could be determined from analysis of lines of three different ions. (The other is HD 47103, in which only few lines can be analysed for each ion - the largest line set for HD 47103 is smaller than the smallest one for HD 116458.)

In particular, the large line sets suitable for analysis of HD 116458 allow one to visualise the dependence differences in scatter plots such as those that have been produced for individual ions in Figs. 2, 3, and 6. Figure 7 illustrates the contributions to the second-order moments of the observed line profiles of, resp., their intrinsic, Doppler and magnetic parts.

Figure 8: Same as Fig. 2, for the lines of Fe II observed in HD 116458, after exclusion from the sample of those for which $\ensuremath{W_\lambda} ^2~\lambda_0^4/c^4>10^{-8}$ Å6 km-4 s4. The dashed line is the term of the least-squares fit of the observations of all ions corresponding to that contribution. The relative weights of the different lines in the regression analysis yielding this best fit line are illustrated by the sizes of the symbols representing them.

Open with DEXTER

We see that the correlations between these contributions and the atomic parameters appearing in abscissa are very well defined, for all three ions. The only possible exception is the intrinsic part of the Fe I line profiles, mostly because the analysed line sample is small, and it spans a much smaller range of $\ensuremath{W_\lambda} ^2~\lambda_0^4/c^2$ values than for Fe II and Cr II. A priori, we would not expect this to increase the errors in the analysis, since the fact that lines have in average smaller equivalent widths should guarantee that the weak line approximation is better fulfilled. However, could it be that because of this, in the numerical analysis, the contribution of the intrinsic part of the line profiles to their second-order moments are underestimated? Since the range of values of $\ensuremath{W_\lambda} ^2~\lambda_0^4/c^2$is small, would it not be better to use a constant to account for the intrinsic part of the observed profile? In order to test this, we repeated the analysis of the Fe I lines of HD 116458, fitting their observed second-order moments with the following simplified form of Eq. (15):

 

$$\ensuremath{R_{I}^{(2)}(\lambda_I)} =a_0+a_1~{1\over 5}{\lambda_0^2\over c^2} +a_2~{3S_2+D_2\over4}~\ensuremath{\Delta\lambda_{\rm Z}} ^2.$$ (24)

The derived value of a₀ does not significantly differ from zero, while a₂ hardly changes at all with respect to the value found with a fit of the form given by Eq. (16). Hence all the contribution of the intrinsic part of the line profile is absorbed in the Doppler term, a₁, for which indeed a value considerably larger than the one appearing in Table 2 is obtained. This is not physically meaningful: as we have seen in Sect. 4.1, for this star must be less than 1.2 km s^-1, which is consistent with the value of a₁resulting from application of Eq. (16). Thus use of this latter form of the fitting function appears fully justified. In particular, the concern that the limited range of equivalent widths in the Fe I sample may lead to derivation of spuriously large quadratic magnetic field values can be safely discarded.

Conversely, the Fe II line sample contains a small number of lines that are stronger than any line of the other two samples. Thus, it is a priori the one for which improperly dealt with radiative transfer effects may potentially have the largest impact. Also, as far as the numerical analysis is concerned, the spread of the $\ensuremath{W_\lambda} ^2~\lambda_0^4/c^2$ values is the main difference between the Fe I and Fe II samples, which are also those for which, from the point of view of the physics of the star, the differences between the derived fit parameters are most surprising. Because the number of strong lines in the Fe II sample is fairly small, constraints on a possible higher-order dependence of the line profile moments on line intensity (e.g., a term in $(\ensuremath{W_\lambda} ^2~\lambda_0^4/c^2)^2$ are not strong, and such a dependence could plausibly be overlooked. In order to check this, we have repeated the analysis of the Fe II line profiles, restricting it to those lines for which $\ensuremath{W_\lambda} ^2~\lambda_0^4/c^2\leq10^{-8}$ Å⁶ km^-4 s⁴; this sample contains 75 lines. The results are shown in Fig. 8. Although the regression slopes are visibly somewhat different, the differences between the fit coefficients derived for this restricted line samples and the whole Fe II line sample of Table 2 remain within the limits of their uncertainties. The somewhat larger value of the mean quadratic field that is obtained from consideration of the restricted sample, $\ensuremath{\langle H_{\rm q}\rangle} =5118\pm216$ G becomes marginally consistent with the value derived from the Cr II lines, but it remains irreconcilable with the value of this field moment resulting from the analysis of the Fe I lines.

In Sect. 4.2.1, we have found hints of the existence of some amount of crosstalk between the Doppler and magnetic contributions to the second-order moments of the line profiles. While this effect may affect to some extent the outcome of the analysis of HD 116458, it cannot account for the differences between the quadratic field values derived from consideration of the lines of the different ions. For the reddest lines, the difference between the values of the a₂coefficient for Fe I and Fe II correspond to a difference of Doppler contribution to the second-order moments of the line profiles of the order of $3\times10^{-3}$ Å², while the difference of the Zeeman contributions for the most magnetically sensitive lines can reach up to $8\times10^{-3}$ Å². On the other hand, between Fe II and Cr II, the values of the a₁coefficient are not significantly different, but those of the a₂coefficient are. Crosstalk with the intrinsic term, besides being unexpected (see Sect. 3.4), also does not appear to account for most of the differences between the magnetic field values found from the analysis of different ions, since the values of both a₂ and a₃ are greater for Cr II than for Fe II.

In summary, we cannot identify any major flaw of the regression analysis that could account for spurious differences between the quadratic field values derived from the analysis of different ions. Therefore, we are led to conclude that the observed quadratic field differences represent an actual stellar property. In principle, one should be able to confirm this conclusion by comparing the mean field modulus values determined from resolved lines of the three considered ions. In practice, though, the field is not strong enough for this to be feasible at the resolution of the data analysed in this paper.

If indeed the ion-to-ion quadratic field differences are real, they indicate that the spectral lines of the considered ions sample the stellar atmosphere in different manners. In this respect, differences between values derived from the analysis of Fe and of Cr may not be particularly surprising, since they may just reflect different inhomogeneous (horizontal) distribution of the two elements on the stellar surface. Even though our data do not lend themselves to checking that this interpretation is correct in the specific case of HD 116458, such inhomogeneity differences are common in Ap stars. But they are not known to occur between different ions of the same element, so that they are unlikely to explain a difference of the quadratic field values diagnosed from lines of the first and second ion of Fe. With the increasing emergence of evidence that Ap star atmospheres are strongly stratified (e.g. Ryabchikova 2004, and references therein), it might be tempting to assign the latter tentatively to different depths of formation of the Fe I and Fe II lines. But even if the existence of such stratification could be confirmed in the present case, this interpretation would require a vertical gradient of the magnetic field of more than 1 kG over the height of the photosphere, which would be quite extreme and is not supported by any other observational result. In conclusion, more detailed studies are required to establish beyond any doubt the reality of the different field values derived from analysis of lines of different ions, as well as to understand their origin.

The fact that differences may (do) exist between the results of the analysis of sets of lines of different ions does not question the validity of the method of determination of the mean quadratic magnetic field discussed in this paper. But it calls for caution: as far as possible, determinations of the quadratic field (and of other field moments) should be based on samples of lines of a single ion, and in the publication of the derived field value, the ion from which it was obtained should always be specified.

   
5 Conclusion

In this work, we have analysed high spectral resolution, high signal-to-noise spectra of a few Ap stars, and of a superficially normal main-sequence A star, recorded over a broad wavelength range, to assess the validity of the method of determination of the mean quadratic field modulus and to explore its limits. We have introduced a revised form of the regression equation describing the dependence of the second-order moment of the line profiles about their centre, in natural light, on various parameters of the corresponding transitions. We have shown that interpretation of the observed dependences allows one to determine the mean quadratic magnetic field modulus of the studied stars, and their . We have explained why the contributions to the quadratic field of the mean square magnetic field modulus and of the mean square longitudinal field cannot in general be disentangled. For those stars of the sample that have magnetically resolved split lines, we have shown that the derived values of the quadratic field are mostly consistent with the values of the mean longitudinal magnetic field and of the mean magnetic field modulus at the observed phase. However there are some hints that they may occasionally slightly underestimate the actual field. This suggests that the method is unlikely to yield spurious field detections, lending support to the reality of the mild fields found for the first time in the Ap star HD 133792 and, more intriguingly, in the superficially normal A star HD 91375. Nevertheless, because these detections are only slightly above the significance threshold, confirmation is called for. The tendency to underestimate the quadratic field may plausibly be due to limited crosstalk between the Doppler and Zeeman terms of the regression equation. In addition, we have illustrated the importance for this type of analyses of using, as far as possible, samples of lines of a single ion, and to specify in the presentation of the results which ion was used, since in some stars, analysis of samples of lines of different ions yield different values of the quadratic field. The data presently available are insufficient to allow us to fully understand the origin of these ion-to-ion differences; additional observations are needed for their investigation. The results presented in this paper lend strong support to the validity of the quadratic field determination method to obtain a realistic quantitative characterisation of the magnetic fields of, at least, slowly rotating stars. While there is no observational indication that the approach could fail at higher , and no theoretical argument suggesting it, this cannot be directly ascertained from analysis of actual data, since in the presence of faster rotation, magnetic splitting of spectral lines is smeared out, so that the mean magnetic field modulus cannot be determined and its value can no longer be used as a consistency check of the quadratic field measurement. The effect of increased rotation, as well as the risk of spurious detections in weakly magnetic stars, are best assessed using synthetic spectra: this will be the object of a future paper, currently in preparation, which will complement this study to further establish the applicability of the quadratic field diagnostic method.

Acknowledgements

The authors are grateful to Dr. Pierre Martin for performing part of the observations used in this work, and to Dr. Igor Savanov for his help in evaluating the of the studied stars through spectrum synthesis. A large fraction of this study has been carried out during stays of GM in the Department Physics and Astronomy of the University of Western Ontario (London, Ontario, Canada). GM thanks Prof. John D. Landstreet for giving him the opportunity of these visits. Financial support received from the ESO Director General's Discretionary Fund also contributed to make these stays possible.

References

• Abt, H. A. 2000, ApJ, 544, 933 [NASA ADS] [CrossRef] (In the text)
• Aurière, M., Silvester, J., Wade, G. A., et al. 2004, in The A-Star Puzzle, ed. J. Zverko, J. Ziznovský, S. J. Adelman, & W. W. Weiss (Cambridge Univ. Press), IAU Symp., 224, 633 (In the text)
• Babcock, H. W. 1958, ApJS, 3, 141 [NASA ADS] [CrossRef] (In the text)
• Babel, J., North, P., & Queloz, D. 1995, A&A, 303, L5 [NASA ADS]
• Bychkov, V. D., Bychkova, L. V., & Madej, J. 2003, A&A, 407, 631 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Castor, J. I., Lutz, J. H., & Seaton, M. J. 1981, MNRAS, 194, 547 [NASA ADS] (In the text)
• Cowley, C. R., & Mathys, G. 1998, A&A, 339, 165 [NASA ADS]
• Gray, R. O., & Garrison, R. F. 1987, ApJS, 65, 581 [NASA ADS] [CrossRef] (In the text)
• Hensberge, H., & Verschueren, W. 1989, The Messenger, 58, 51 (In the text)
• Hubrig, S., North, P., & Mathys, G. 2000, ApJ, 539, 352 [NASA ADS] [CrossRef]
• Kochukhov, O., Landstreet, J. D., Ryabchikova, T., Weiss, W. W., & Kupka, F. 2002, MNRAS, 337, L1 [NASA ADS] [CrossRef] (In the text)
• Kurtz, D. W., Elkin, V. G., & Mathys, G. 2005, MNRAS, 358, L6 [NASA ADS]
• Landstreet, J. D. 1992, ARA&A, 4, 35 (In the text)
• Lemke, M. 1989, A&A, 225, 125 [NASA ADS]
• Leone, F., Vacca, W. D., & Stift, M. J. 2003, A&A, 409, 1055 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Mathys, G. 1988, A&A, 189, 179 [NASA ADS] (In the text)
• Mathys, G. 1989, Fundam. Cosmic Phys., 13, 143 [NASA ADS] (In the text)
• Mathys, G. 1990a, A&A, 232, 151 [NASA ADS] (In the text)
• Mathys, G. 1990b, A&A, 236, 527 [NASA ADS] (In the text)
• Mathys, G., 1991, A&AS, 89, 121 [NASA ADS] (In the text)
• Mathys, G. 1993, in Peculiar versus Normal Phenomena in A-Type and Related Stars, ed. M. M. Dworetsky, F. Castelli, & R. Faraggiana, ASP Conf. Ser., 44, 232 (In the text)
• Mathys, G. 1994, A&AS, 108, 547 [NASA ADS] (In the text)
• Mathys, G. 1995a, A&A, 293, 733 [NASA ADS] (In the text)
• Mathys, G. 1995b, A&A, 293, 746 [NASA ADS] (In the text)
• Mathys, G. 2004, in Stellar Rotation, ed. A. Maeder, & P. Eenens (ASP), IAU Symp., 215, 270 (In the text)
• Mathys, G., & Stenflo, J. O. 1987, A&A, 171, 368 [NASA ADS] (In the text)
• Mathys, G., & Lanz, T. 1992, A&A, 256, 169 [NASA ADS] (In the text)
• Mathys, G., & Hubrig, S. 1997, A&AS, 124, 475 [EDP Sciences] [NASA ADS] (In the text)
• Mathys, G., Landstreet, J. D., & Lanz, T. 1993, in Peculiar versus normal phenomena in A-type and related stars, ed. M. M. Dworetsky, F. Castelli, & R. Faraggiana, ASP Conf. Ser., 44, 300 (In the text)
• Mathys, G., Hubrig, S., Landstreet, J. D., Lanz, T., & Manfroid, J. 1997, A&AS, 123, 353 [EDP Sciences] [NASA ADS] (In the text)
• Matthews, J. M., & Bohlender, D. A. 1991, A&A, 243, 148 [NASA ADS] (In the text)
• Moon, T. T., & Dworetsky, M. M. 1985, MNRAS, 217, 305 [NASA ADS] (In the text)
• Nielsen, K., & Wahlgren, G. M. 2000, A&A, 356, 146 [NASA ADS] (In the text)
• Ramella, M., Gerbaldi, M., Faraggiana, R., & Böhm, C. 1989, A&A, 209, 233 [NASA ADS] (In the text)
• Renson, P., Gerbaldi, M., & Catalano, F. A. 1991, A&AS, 89, 429 [NASA ADS] (In the text)
• Royer, F., Zorec, J., & Gómez, A. E. 2004, in The A-Star Puzzle, ed. J. Zverko, J. Ziznovský, S. J. Adelman, & W. W. Weiss (Cambridge Univ. Press), IAU Symp., 224, 55 (In the text)
• Ryabchikova, T. 2004, in The A-Star Puzzle, ed. J. Zverko, J. Ziznovský, S. J. Adelman, & W. W. Weiss (Cambridge Univ. Press), IAU Symp., 224, 283 (In the text)
• Ryabchikova, T., Piskunov, N., Savanov, I., Kupka, F., & Malanushenko, V. 1999, A&A, 343, 229 [NASA ADS]
• Ryabchikova, T., Leone, F., Kochukhov, O., & Bagnulo, S. 2004, in The A-Star Puzzle, ed. J. Zverko, J. Ziznovský, S. J. Adelman, & W. W. Weiss (Cambridge Univ. Press), IAU Symp., 224, 580 (In the text)
• Ryabchikova, T., Leone, F., & Kochukhov, O. 2005, A&A, 438, 973 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Shorlin, S. L. S., Wade, G. A., Donati, J.-F., et al. 2002, A&A, 392, 637 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Stenflo, J. O., & Lindegren, L. 1977, A&A, 59, 367 [NASA ADS] (In the text)
• Wade, G. A., North, P., Mathys, H., & Hubrig, S. 1996, A&A, 314, 491 [NASA ADS] (In the text)
• Wade, G. A., Mathys, G., & North, P. 1999, A&A, 347, 164 [NASA ADS] (In the text)
• Wade, G. A., Debernardi, Y., Mathys, G., et al. 2000, A&A, 361, 991 [NASA ADS]
• Zboril, M., & North, P. 1999, A&A, 345, 244 [NASA ADS]