A&A 453, 353-361 (2006)
DOI: 10.1051/0004-6361:20054689
The size of the stability regions of Jupiter Trojans
F. Freistetter
Astrophysikalisches Institut, Universität Jena, Schillergässchen 2-3, 07745 Jena, Germany
Received 14 December 2005 / Accepted 15 February 2006
Abstract
Context. We have known about the Trojan group of asteroids since 1906. With a suspected number comparable to that of the main-belt, they move around the Lagrangian points L4 and L5 of the Sun-Jupiter system.
Aims. During the past century the Trojan asteroids were the topic of many studies of their orbital dynamics and stability. In recent years it has been possible to perform extensive numerical simulations of the motion of these asteroids and thus also to investigate the size and structure of the stability region around the Lagrangian points. The aim of this work is to find new numerical estimates of the size and shape of the stability region. Additionally, the problem of the asymmetry between the two Trojan groups (there seem to be more asteroids in L4 than in L5) is investigated.
Methods. We investigate the extension of this regions in the (
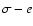 )
and (
)
and (
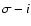 )
plane (where
)
plane (where
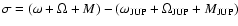 )
and show how the initial inclination and initial eccentricity change the size and shape of this region. The problem of Trojan asymmetry is investigated by directly analyzing the evolution of orbital parameters.
)
and show how the initial inclination and initial eccentricity change the size and shape of this region. The problem of Trojan asymmetry is investigated by directly analyzing the evolution of orbital parameters.
Results. We find both that there is a "critical'' eccentricity of
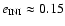 that plays an important role in the dynamics of Trojan asteroids and influences the structure of the stability regions and that the region of the small amplitudes of
that plays an important role in the dynamics of Trojan asteroids and influences the structure of the stability regions and that the region of the small amplitudes of
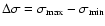 is larger for L4 due to the influence of Saturn and thus the L4 group of Trojans seems to be more stable than the L5 group.
is larger for L4 due to the influence of Saturn and thus the L4 group of Trojans seems to be more stable than the L5 group.
Key words: celestial mechanics - minor planets, asteroids - methods: N-body simulations
Since the first discovery of a Trojan asteroid by Max Wolf in Heidelberg in 1906, the problem of the motion around the Lagrangian point evolved from what was a purely theoretical case study into an important part of Solar System dynamics. One of the first studies of the stability regions around the Lagrangian points was made by Rabe (1967,1968). Érdi then investigated the motion of Trojans analytically in many papers (e.g. Érdi 1981,1984,1988,1996,1997).
Other analytical studies were done by Bien (1980) for Trojans with high inclinations, by Bien & Schubart (1984) for the influence of secular resonances, by Schubart & Bien (1987) for the relation between the orbital elements, and by Namouni (1999), Namouni et al. (1999), and Namouni & Murray (2000), who investigated the effect of eccentricity and inclination on the motion of Trojans. Numerical integrations to investigate their motion of were performed e.g. by Mikkola & Innanen (1992,1995) and Marzari et al. (2003). Morais (1999) derived a secular theory for the Trojan type motion, Giorgilli & Skokos (1997) used the Nekhoroshev theorem to investigate the stability regions, and several authors used semi-analytical or mapping methods to study the dynamics of Trojans (e.g. Celletti & Giorgilli 1991; Skokos & Dokoumetzidis 2001; Beaugé & Roig 2001; Sándor et al. 2002; Sándor & Érdi 2003; Efthymiopoulos 2005). Milani (1993,1994) used numerical methods to calculate the proper elements of the Trojans and showed that the orbits of some real ones are chaotic (the chaoticity of some Trojan orbits have also been mentioned earlier by Shoemaker et al. 1989). These chaotic orbits and the connected escape of Trojan asteroids were also studied numerically by many authors (e.g. Pilat-Lohinger et al. 1999; Dvorak & Tsiganis 2000; Tsiganis et al. 2000; Marzari & Scholl 2002).
Due to the increasing number of discovered Trojans and the increase in computer power, it is now possible to numerically investigate the stability regions around the Lagrangian points in great detail and extend the early analytical borders obtained by Rabe (1967). Such studies were performed e.g. by Levison et al. (1997), Schwarz & Gyergyovits (2003), Brasser et al. (2004), Schwarz et al. (2004), Dvorak & Schwarz (2005), Tsiganis et al. (2005), and Robutel et al. (2005). An additional problem that is closely connected to these studies is the different number of Trojans observed near L4 and L5. There seem to be significantly more near L4 than L5![[*]](/icons/foot_motif.gif) , the reason for this behavior is still unknown (see Sect. 5 for details).
, the reason for this behavior is still unknown (see Sect. 5 for details).
The present work has two main goals. First, we want to extend the existing studies of the stability regions around the Lagrangian points and, second, we want to search for real numerical evidence of a dynamical difference between L4 and L5 Trojans that can be seen directly in the evolution of the orbital elements. Thus, Sect. 2 will give an overview on the methods and models used in this work; Sect. 3 will investigate the motion in the direct vicinity of the Lagrangian points; Sect. 4 will investigate the structure of the stability regions, and Sect. 5 will review the problem of the different number of L4 and L5 Trojans and use the results obtained during this work to get some new insights.
Table 1:
Models and initial conditions.
2 Methods
The dynamical evolution of many Trojan asteroids shows chaotic features; see e.g. Milani (1993), Milani et al. (1997) for an investigation of asteroids in stable chaotic motion (ASCs) or Karlsson (1984). Thus it is necessary to use different integration techniques and models to find out whether some dynamical effects are real or an artificial bias due to the influence of chaos. For this study, we used three different numerical integration methods:
- Lie integration method (LIE):
this method is based on Lie Series and is very accurate. It has an adaptive stepsize and can handle close encounters and high values of eccentricity. For details see Lichtenegger (1984), Hanslmeier & Dvorak (1984), or Asghari et al. (2004).
- Hybrid symplectic/Bulirsh-Stoer integrator (HYB): this is the hybrid routine from the Mercury 6 package by Chambers (1999). It is very fast but only moderately accurate and can also handle close encounters.
- Bulirsh-Stoer method (B-S): this is the general Bulirsh-Stoer routine from the Mercury 6 package by Chambers (1999). It is very accurate but slow. The results from this method were used as a "reference'' to compare the validity of the other methods.
To analyze the data, the following two parameters were used:
The dynamical models used for this work are listed in Table 1. Only the elements e, i, and 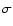 (and thus the mean anomaly M) were changed, while the remaining initial orbital elements were set equal to that of Jupiter. We did not vary a for two reasons: first, this has already been done by others (see Sect. 4), and second, it can be seen that the variation in e and i is much larger than the variation in a by looking on the distribution of Trojan orbital elements. We neglected the inner planets in the integrations (but their mass was added to that of the Sun) and used only the outer ones (with their actual orbital elements obtained from the JPL Horizons database).
We are aware that these initial conditions are not totally natural. Nevertheless, we decided to use these initial conditions because they were also used in the parameter studies by other authors (e.g. Dvorak & Schwarz 2005; Pál & Süli 2004) so that our findings can be compared to these works and can be used as useful extensions of their results. Also (see Sect. 5.6), the results are sound and in good agreement with existing data. Future work (see Sect. 6) will also include calculations with "natural'' initial conditions (e.g. by using the proper elements).
(and thus the mean anomaly M) were changed, while the remaining initial orbital elements were set equal to that of Jupiter. We did not vary a for two reasons: first, this has already been done by others (see Sect. 4), and second, it can be seen that the variation in e and i is much larger than the variation in a by looking on the distribution of Trojan orbital elements. We neglected the inner planets in the integrations (but their mass was added to that of the Sun) and used only the outer ones (with their actual orbital elements obtained from the JPL Horizons database).
We are aware that these initial conditions are not totally natural. Nevertheless, we decided to use these initial conditions because they were also used in the parameter studies by other authors (e.g. Dvorak & Schwarz 2005; Pál & Süli 2004) so that our findings can be compared to these works and can be used as useful extensions of their results. Also (see Sect. 5.6), the results are sound and in good agreement with existing data. Future work (see Sect. 6) will also include calculations with "natural'' initial conditions (e.g. by using the proper elements).
According to the models, different dynamical configurations were used:
- OSS: the outer solar system (including Sun, Jupiter, Saturn, Uranus, and Neptune);
- SJS: including Sun, Jupiter, and Saturn;
- SJA: including only Sun and Jupiter (in fact, this model is equivalent to the elliptic, restricted three-body problem).
Two of the models were integrated for 50 Myrs - a time scale that is long enough to investigate the consequences of most of the dynamical effects (see e.g. Dvorak & Schwarz 2005 or Tsiganis et al. 2000). The remaining two models were integrated for 10 Myrs to see how the size and shape of the stability regions already change on relatively short timescales.
3 Stable librations around L4 and L5
![\begin{figure}
\par\includegraphics[angle=270,width=8.3cm,clip]{4689f1a.ps}\par\vspace*{2mm}
\includegraphics[angle=270,width=8.3cm,clip]{4689f1b.ps}\end{figure}](/articles/aa/full/2006/25/aa4689-05/Timg37.gif) |
Figure 1:
Distribution of the real L4 (bars) and L5 (lines) Trojans (for 01.01.2005 00 UT) with respect to their eccentricities ( top) and inclinations ( bottom). |
| Open with DEXTER |
At first we want to investigate the motion in the direct vicinity of the Lagrangian points. Thus, in model 1 (see Table 1), we varied only the initial eccentricity (between 0 and 0.2) and the initial inclination (between 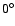 and
and 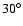 ). Figure 1 shows that this choice of initial conditions covers the variation in the elements of the real Trojans. The initial semimajor axis was set equal to that of Jupiter and the initial mean anomaly equal to the values of L4 and L5 such that the asteroids are always placed initially in the vicinity of the Lagrangian points. The integration time was 107 years and all planets of the outer solar system (OSS) were used as perturbers. To test the validity of the three integration methods, all of them were used for this model.
). Figure 1 shows that this choice of initial conditions covers the variation in the elements of the real Trojans. The initial semimajor axis was set equal to that of Jupiter and the initial mean anomaly equal to the values of L4 and L5 such that the asteroids are always placed initially in the vicinity of the Lagrangian points. The integration time was 107 years and all planets of the outer solar system (OSS) were used as perturbers. To test the validity of the three integration methods, all of them were used for this model.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4689f2.ps}\end{figure}](/articles/aa/full/2006/25/aa4689-05/Timg40.gif) |
Figure 2:
Values of
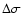 in the (e-i) plane for L4 ( left) and L5 ( right) calculated with a Bulirsh-Stoer integrator ( top), a hybrid integrator ( middle), and using the Lie-Integration method ( bottom).
in the (e-i) plane for L4 ( left) and L5 ( right) calculated with a Bulirsh-Stoer integrator ( top), a hybrid integrator ( middle), and using the Lie-Integration method ( bottom). |
| Open with DEXTER |
Figure 2 shows the results. Here we plotted the value of
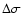 for the different initial values of e and i.
The first thing to notice is that there is no influence of the integration method - all three of them delivered the same output
for the different initial values of e and i.
The first thing to notice is that there is no influence of the integration method - all three of them delivered the same output![[*]](/icons/foot_motif.gif) . It can also be seen that L4 and L5 behave similarly, although there is a small region of larger libration (
. It can also be seen that L4 and L5 behave similarly, although there is a small region of larger libration (
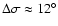 )
near
)
near 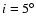 and e=0.15 that seems to be larger for L5 than for L4, which indicates that the dynamical properties of L5 induce larger librations if the eccentricity is increased. It can also be seen that the region enclosed by the innermost contour-line - indicating libration-widths smaller than
and e=0.15 that seems to be larger for L5 than for L4, which indicates that the dynamical properties of L5 induce larger librations if the eccentricity is increased. It can also be seen that the region enclosed by the innermost contour-line - indicating libration-widths smaller than 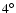 - is smaller for L5 than for L4 (see details in Sect. 5).
- is smaller for L5 than for L4 (see details in Sect. 5).
![\begin{figure}
\par\includegraphics[angle=270,width=8.2cm,clip]{4689f3a.ps}\par\vspace*{2mm}
\includegraphics[angle=270,width=8.2cm,clip]{4689f3b.ps}\end{figure}](/articles/aa/full/2006/25/aa4689-05/Timg43.gif) |
Figure 3:
Dependence of
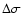 on the eccentricity for L4 ( top) and L5 ( bottom) for Model 1 (HYB).
on the eccentricity for L4 ( top) and L5 ( bottom) for Model 1 (HYB). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=270,width=8.2cm,clip]{4689f4a.ps}\par\vspace*{2mm}
\includegraphics[angle=270,width=8.2cm,clip]{4689f4b.ps}\end{figure}](/articles/aa/full/2006/25/aa4689-05/Timg44.gif) |
Figure 4:
Dependence of
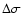 on the inclination for L4 ( top) and L5 ( bottom) and different initial values of the eccentricity for Model 1 (HYB).
on the inclination for L4 ( top) and L5 ( bottom) and different initial values of the eccentricity for Model 1 (HYB). |
| Open with DEXTER |
Figures 3 and 4 show the interaction between initial eccentricity, initial inclination, and libration around the Lagrangian points in more detail: in Fig. 3 it is shown that in general an increase of eccentricity also causes higher values of
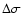 ,
independent of i. An interesting feature can be seen near values of the initial eccentricity of
,
independent of i. An interesting feature can be seen near values of the initial eccentricity of
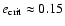 :
here the lines for the different initial values of i cross. That means that for initial eccentricities lower than
:
here the lines for the different initial values of i cross. That means that for initial eccentricities lower than
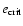 ,
low inclinations cause smaller librations around L4 or L5 and high inclinations cause larger librations, whereas for initial eccentricities that are higher than
,
low inclinations cause smaller librations around L4 or L5 and high inclinations cause larger librations, whereas for initial eccentricities that are higher than
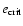 lower initial inclinations cause larger librations (and vice versa). Thus, if a Trojan asteroid has an eccentricity higher than
lower initial inclinations cause larger librations (and vice versa). Thus, if a Trojan asteroid has an eccentricity higher than
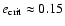 ,
its inclination also has to be high to be protected from close encounters and thus ejection of the system. Figure 4 shows the same behavior: the width of libration increases with increasing values of the initial inclination when the initial eccentricity is lower than
,
its inclination also has to be high to be protected from close encounters and thus ejection of the system. Figure 4 shows the same behavior: the width of libration increases with increasing values of the initial inclination when the initial eccentricity is lower than
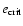 and decreasing otherwise.
and decreasing otherwise.
4 Size of the stability region
The size and structure of the stability region has been investigated by many authors in the past. Rabe in 1967 was one of the first to give an analytical boundary of stability based on the proper eccentricity and the libration amplitude (
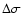 ). He showed that all known Trojans (in 1966) lie inside this region of stability
). He showed that all known Trojans (in 1966) lie inside this region of stability![[*]](/icons/foot_motif.gif) . In 1997, Levison et al. performed extensive numerical integrations and showed that the region of effective stability - on a timescale of 4.5 Gyr - is smaller than that derived by Rabe. Robutel et al. (2005) use frequency analysis to investigate the stability of Trojans around L4 in the (a-e) plane (for the SJS model) and identify the main resonances that "form the dynamical skeleton and dictate the long-term dynamics of the Trojan asteroids''. Tsiganis et al. (2005) also researched the effective stability regions of the Trojan asteroids and found a power-law statistical correlation between the Lyapunov time and the escape time of Trojans on chaotic orbits. They also show that the regions of effective stability contain bodies that become chaotic. Dvorak & Schwarz (2005) investigated the size of the stability regions around the Lagrangian points in the (
. In 1997, Levison et al. performed extensive numerical integrations and showed that the region of effective stability - on a timescale of 4.5 Gyr - is smaller than that derived by Rabe. Robutel et al. (2005) use frequency analysis to investigate the stability of Trojans around L4 in the (a-e) plane (for the SJS model) and identify the main resonances that "form the dynamical skeleton and dictate the long-term dynamics of the Trojan asteroids''. Tsiganis et al. (2005) also researched the effective stability regions of the Trojan asteroids and found a power-law statistical correlation between the Lyapunov time and the escape time of Trojans on chaotic orbits. They also show that the regions of effective stability contain bodies that become chaotic. Dvorak & Schwarz (2005) investigated the size of the stability regions around the Lagrangian points in the (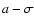 )
plane and mapped the stability region by using the Lyapunov characteristic exponents (LCEs).
Since two of the aforementioned works (Dvorak & Schwarz 2005; Robutel et al. 2005) already deal with the dependence of the size of the stability region on the variation in the semimajor axis, we restricted this work to an investigation of the dependence on eccentricity and inclination.
)
plane and mapped the stability region by using the Lyapunov characteristic exponents (LCEs).
Since two of the aforementioned works (Dvorak & Schwarz 2005; Robutel et al. 2005) already deal with the dependence of the size of the stability region on the variation in the semimajor axis, we restricted this work to an investigation of the dependence on eccentricity and inclination.
![\begin{figure}
\par\includegraphics[angle=270,width=8.2cm,clip]{4689f5a.ps}\par\...
...space*{4mm}
\includegraphics[angle=270,width=8.2cm,clip]{4689f5c.ps}\end{figure}](/articles/aa/full/2006/25/aa4689-05/Timg51.gif) |
Figure 5:
Extension of the stability regions in the (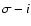 )
plane around L4 ( left) and L5 ( right) for an initial eccentricity of )
plane around L4 ( left) and L5 ( right) for an initial eccentricity of
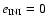 ( top),
( top),
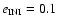 ( second row),
( second row),
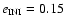 ( third row),
( third row),
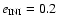 ( fourth row), and
( fourth row), and
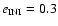 ( bottom): dark colors show unstable motion; light colors denote stable motion. The vertical lines indicate the position of the Lagrangian points; the integration was performed in the OSS model.
( bottom): dark colors show unstable motion; light colors denote stable motion. The vertical lines indicate the position of the Lagrangian points; the integration was performed in the OSS model. |
| Open with DEXTER |
Figure 5 shows the results from the integration of model 2. In this model also 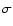 was varied and thus the test particles are now spread out along the orbit of Jupiter in the neighborhood of the Lagrangian points unlike in model 1. Additionally, the integration time was increased to
was varied and thus the test particles are now spread out along the orbit of Jupiter in the neighborhood of the Lagrangian points unlike in model 1. Additionally, the integration time was increased to
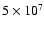 years. The contour plots give the value of the escape time in its dependence on the initial inclination and
years. The contour plots give the value of the escape time in its dependence on the initial inclination and 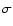 values. The first thing to notice is the asymmetry in the
values. The first thing to notice is the asymmetry in the 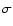 values: the stable zone extends unevenly wide around the position of the Lagrangian points. For values lower than
values: the stable zone extends unevenly wide around the position of the Lagrangian points. For values lower than 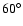 (L4) (or higher than
(L4) (or higher than 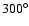 (L5)) the orbits are less stable than in the other direction (note that Jupiter has
(L5)) the orbits are less stable than in the other direction (note that Jupiter has
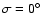 ). For low eccentricities (
). For low eccentricities (
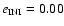 ,
Fig. 5 top), there are almost no unstable orbits; also the plots for
,
Fig. 5 top), there are almost no unstable orbits; also the plots for
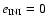 and
and
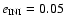 are almost identical; we have omitted the figure for
are almost identical; we have omitted the figure for
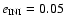 .
The size of the stable region around the Lagrangian points decreases for higher values of e (Fig. 5 second and third row,
.
The size of the stable region around the Lagrangian points decreases for higher values of e (Fig. 5 second and third row,
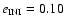 and
and
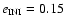 ). Here the difference between the two "directions'' can be seen very clearly: in the direction towards Jupiter, the border of the stable region shows almost no changes with the initial inclination, whereas towards the opposite direction to Jupiter the border of stability decreases when the initial inclination increases (Fig. 5, second row) or becomes very diffuse (Fig. 5, third row). In Fig. 5 (third row) a "bulge''-like structure is visible for inclinations around
). Here the difference between the two "directions'' can be seen very clearly: in the direction towards Jupiter, the border of the stable region shows almost no changes with the initial inclination, whereas towards the opposite direction to Jupiter the border of stability decreases when the initial inclination increases (Fig. 5, second row) or becomes very diffuse (Fig. 5, third row). In Fig. 5 (third row) a "bulge''-like structure is visible for inclinations around
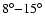 and
and
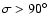 (or smaller than
(or smaller than 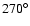 )
where the stability region has its largest extension, corresponding to the distribution of actual inclinations in Fig. 1, where the maximum also lies in this region.
Figure 5 (fourth row) (
)
where the stability region has its largest extension, corresponding to the distribution of actual inclinations in Fig. 1, where the maximum also lies in this region.
Figure 5 (fourth row) (
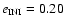 )
)![[*]](/icons/foot_motif.gif) shows the further decrease in the size of the stable region, and it can again be observed that the largest extension of the stability region lies at medium values of inclination
For an initial eccentricity of
shows the further decrease in the size of the stable region, and it can again be observed that the largest extension of the stability region lies at medium values of inclination
For an initial eccentricity of
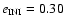 (Fig. 5, bottom), almost no stable orbits are left
(Fig. 5, bottom), almost no stable orbits are left![[*]](/icons/foot_motif.gif) . In the direction towards the position of Jupiter, the region of stability has more or less disappeared; the only place left for stable motion is towards the region opposite to Jupiter and for higher values of inclination.
. In the direction towards the position of Jupiter, the region of stability has more or less disappeared; the only place left for stable motion is towards the region opposite to Jupiter and for higher values of inclination.
![\begin{figure}
\par\includegraphics[angle=270,width=7.8cm,clip]{4689f6a.ps}\par\...
...space*{4mm}
\includegraphics[angle=270,width=7.8cm,clip]{4689f6c.ps}\end{figure}](/articles/aa/full/2006/25/aa4689-05/Timg65.gif) |
Figure 6:
Stability region in the (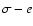 )
plane for an initial inclination of )
plane for an initial inclination of
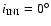 ( top),
( top),
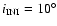 ( second row),
( second row),
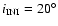 ( third row),
( third row),
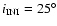 ( fourth row), and
( fourth row), and
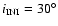 ( bottom): dark colors show unstable motion; light colors denote stable motion. The vertical lines indicate the position of the Lagrangian points at
( bottom): dark colors show unstable motion; light colors denote stable motion. The vertical lines indicate the position of the Lagrangian points at
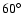 (L4) and
(L4) and
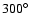 (L5); the integration was performed in the OSS model.
(L5); the integration was performed in the OSS model. |
| Open with DEXTER |
Figure 6 shows the results from the integration of model 3. The contour-plots show the value of the escape time depending on the initial values of the eccentricity and 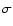 which are different from model 2, where only the extended neighborhood of the Lagrangian points was investigated. Here the whole range
which are different from model 2, where only the extended neighborhood of the Lagrangian points was investigated. Here the whole range
![$\sigma=[0^\circ,360^\circ]$](/articles/aa/full/2006/25/aa4689-05/img66.gif) was integrated. It can be seen in Fig. 6 that the shape of the stable region is now different from the stable region of model 2: now the borders on both sides (towards the direction of Jupiter and towards the opposite direction) are inclined. But the dependence of the limiting value of
was integrated. It can be seen in Fig. 6 that the shape of the stable region is now different from the stable region of model 2: now the borders on both sides (towards the direction of Jupiter and towards the opposite direction) are inclined. But the dependence of the limiting value of 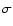 on the initial eccentricity is less steep for the direction towards Jupiter. Another remarkable feature can be seen by comparing the region above values of
on the initial eccentricity is less steep for the direction towards Jupiter. Another remarkable feature can be seen by comparing the region above values of
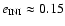 with the one below: the borders of the upper region show very little dependence on the initial eccentricity and are almost constant, whereas the borders of the lower region vary in the way described above.
with the one below: the borders of the upper region show very little dependence on the initial eccentricity and are almost constant, whereas the borders of the lower region vary in the way described above.
This upper region remains almost constant in shape and size until
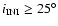 where it starts shrinking (see Table 2 for details). In this model the "critical'' eccentricity
where it starts shrinking (see Table 2 for details). In this model the "critical'' eccentricity
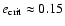 plays a different role than in model 1 (see Sect. 3). There, all test particles were placed in the vicinity of the Lagrangian points (no variation of
plays a different role than in model 1 (see Sect. 3). There, all test particles were placed in the vicinity of the Lagrangian points (no variation of 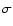 )
and a high inclination caused smaller perturbations than a low inclination when
)
and a high inclination caused smaller perturbations than a low inclination when
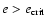 (and vice versa). In model 3 (where we varied
(and vice versa). In model 3 (where we varied 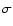 from
from 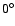 to
to 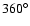 ), a high initial inclination is now no longer a protection against perturbations, and it causes more unstable orbits than a low initial inclination. Nevertheless the stability region above
), a high initial inclination is now no longer a protection against perturbations, and it causes more unstable orbits than a low initial inclination. Nevertheless the stability region above
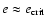 shows the abovementioned different behavior under the influence of inclination.
shows the abovementioned different behavior under the influence of inclination.
The behavior of the lower region is more complex. No dramatic change is visible until
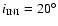 .
At this value the stable region starts to "intrude'' the region opposite to Jupiter near the line
.
At this value the stable region starts to "intrude'' the region opposite to Jupiter near the line
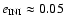 .
This process continues as
.
This process continues as
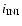 becomes larger, although the total percentages of stable orbits in the region
becomes larger, although the total percentages of stable orbits in the region
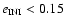 remains more or less constant. Figure 1 shows that the maximum of the eccentricity distribution of real Trojans also lies around
remains more or less constant. Figure 1 shows that the maximum of the eccentricity distribution of real Trojans also lies around
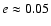 .
.
Table 2:
Percentage of stable orbits for model 3.
To see how the outer planets influence the size of the stability region, all three different sets of perturbing bodies were used for integration (OSS, SJS, and SJA) in model 4.
For all three cases, the stability region in the (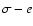 )
plane was integrated for two different values of initial inclination (
)
plane was integrated for two different values of initial inclination (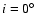 and
and
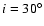 ). Figure 7 shows the contour plots for L4
). Figure 7 shows the contour plots for L4![[*]](/icons/foot_motif.gif) . It is clear that, in the absence of the perturbation of all other outer planets, the SJA model will show a large amount of stable orbits; the two regions of instability are placed at higher eccentricities and far away from the position of the Lagrangian point. Figure 7 (bottom left) again shows the asymmetry concerning the different directions (towards Jupiter or towards the opposite direction) caused by the configuration of the system. Whereas Trojans placed in the region near Jupiter (
. It is clear that, in the absence of the perturbation of all other outer planets, the SJA model will show a large amount of stable orbits; the two regions of instability are placed at higher eccentricities and far away from the position of the Lagrangian point. Figure 7 (bottom left) again shows the asymmetry concerning the different directions (towards Jupiter or towards the opposite direction) caused by the configuration of the system. Whereas Trojans placed in the region near Jupiter (
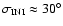 )
are stable only for low initial eccentricities (
)
are stable only for low initial eccentricities (
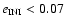 ), the Trojans placed in the opposite region (
), the Trojans placed in the opposite region (
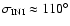 )
are stable up to initial eccentricities of
)
are stable up to initial eccentricities of
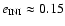 .
.
In Fig. 7 (bottom right) the initial inclination was increased to 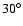 and now there is not much difference between the two regions. On both "sides'' stable orbits have to have an initial eccentricity lower than
and now there is not much difference between the two regions. On both "sides'' stable orbits have to have an initial eccentricity lower than
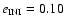 although the instability region for high eccentricities is smaller in the region near Jupiter. Figure 7 (top and middle) shows no serious difference, so Uranus and Neptune not seem to have any strong influence on the dynamics of Trojans (at least over the timescale of this integration!). Therefore it is also reasonable to conclude that any dynamical difference between the Lagrangian groups L4 and L5 is due to the perturbations of Saturn. This topic will be investigated in the next section.
although the instability region for high eccentricities is smaller in the region near Jupiter. Figure 7 (top and middle) shows no serious difference, so Uranus and Neptune not seem to have any strong influence on the dynamics of Trojans (at least over the timescale of this integration!). Therefore it is also reasonable to conclude that any dynamical difference between the Lagrangian groups L4 and L5 is due to the perturbations of Saturn. This topic will be investigated in the next section.
5 The difference between the two Trojan populations
![\begin{figure}
\par\includegraphics[angle=270,width=8.3cm,clip]{4689f7.ps}\end{figure}](/articles/aa/full/2006/25/aa4689-05/Timg83.gif) |
Figure 7:
Stability region in the (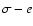 )
plane around L4 for the OSS model ( top), the SJS model ( middle), and the SJA model ( bottom). The left column shows the stability region for an initial inclination of )
plane around L4 for the OSS model ( top), the SJS model ( middle), and the SJA model ( bottom). The left column shows the stability region for an initial inclination of
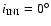 ;
the right column for ;
the right column for
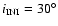 .
The vertical lines indicate the position of the Lagrangian point. .
The vertical lines indicate the position of the Lagrangian point. |
| Open with DEXTER |
One important fact that has not yet been explained completely is the difference between the populations of L4 and L5 Trojans (see Fig. 8 that shows how the number of known Trojans increases during the past years). There are several possible explanations for this phenomenon:
- 1.
- Observational reasons: the asteroids in L5 could be smaller, darker, or have higher inclinations than in L4 and thus are more difficult to observe.
- 2.
- Different formation processes: if the formation processes in the vicinity of L4 had better conditions, there would be more asteroids than in L5. It could also be possible that asteroids are more likely captured near L4 than L5.
- 3.
- Catastrophic event: a catastrophic event during the formation of the Solar System could be responsible for the smaller number of L5 asteroids.
- 4.
- Chaotic capture: recent works have shown that the Trojan asteroids may have been captured by Jupiter and that this process shows chaotic features that could be responsible for the asymmetry.
- 5.
- Dynamical reasons: due to the gravitational influence of the other large planets, the region around L4 could be more stable than the one around L5. The difference could also be due to non-gravitational forces that act differently on the two Lagrangian points.
Points 1), 3), and 4) are not the subject of this work; also, to investigate point 2) one needs different dynamical models than the ones used here. Thus this work will only deal with point 5). Nevertheless, since we were not able to find a review article on this topic, we want to try to summarize the existing results before presenting the results of this work. Because of the many effects that can be responsible for the difference in the Trojan population, one has to be very careful when interpreting the results. Thus, to ensure that our interpretation of the existing works is not biased in any sense, instead of summarizing the results in our own words, we want to cite the major points of the existing works as direct quotations.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{4689f8.eps}\end{figure}](/articles/aa/full/2006/25/aa4689-05/Timg85.gif) |
Figure 8:
Number of Trojan asteroids discovered near L4 and L5 in the years 1999-2005. During the past years, the fraction of the two groups was always near
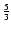 . . |
| Open with DEXTER |
Shoemaker et al. (1989) present an observational reason for the difference.
They wrote: "It appears to be an accident of history that the L4 region has been more thoroughly explored''. Because in that time the L5 region was located on the sky near the Milky Way, observational conditions were not equal to that of L4; thus, this was thought to be the reason for the asymmetry.
This argument was also cited in later years in (2000) by Fleming & Hamilton and by Kuchner et al. (2000) as a reason for the difference between the number of observed asteroids. But Fig. 8 shows that the difference between the two populations is still present although many new discoveries have been made in recent years. The number of observed Trojans around the L4 equilibrium point is still significantly larger than around L5, with the fraction between these two groups close to
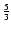 .
The reason could also be a higher inclination of the L5 Trojans that make them more difficult to discover. In fact Fig. 1 shows that the percentage of known L5 Trojans with high inclinations is higher than the one for L4. Additionally, there could be a difference in the size distribution of the two groups that causes a different probability of observation. But the size distribution of Trojans is still not fully understood (see e.g. Marzari et al. 1996, 1997 or Tsiganis et al. 2005). Also, the present size distribution is closely connected to the formation process of Trojans.
.
The reason could also be a higher inclination of the L5 Trojans that make them more difficult to discover. In fact Fig. 1 shows that the percentage of known L5 Trojans with high inclinations is higher than the one for L4. Additionally, there could be a difference in the size distribution of the two groups that causes a different probability of observation. But the size distribution of Trojans is still not fully understood (see e.g. Marzari et al. 1996, 1997 or Tsiganis et al. 2005). Also, the present size distribution is closely connected to the formation process of Trojans.
Peale (1993) searched for the reason for the difference by investigating the formation of Trojans. He simulated the evolution of Trojan precursors in the primordial solar nebula and found an asymmetric distribution of Trojan asteroids due to the eccentricity of Jupiter. But his results showed that the stability of bodies around L5 is increased, while the stability of bodies around L4 is decreased, which is opposite to the situation we observe today. He argues that the collisional evolution of the Trojans from the time of the formation until today "may have skewed the mass distribution in such a way as to mask what was there initially''. This result was confirmed by Marzari & Scholl (1998), who write that
"According to this asymmetry, we expect that more small planetesimals are captured in L5 than in L4 in the earlier stages of Trojan evolution''. Thus, the subsequent collisional evolution would show more impacts in L5, and this higher impact rate could be the reason for the asymmetry.
There seem to be indications that the subsequent collisional evolution of Trojan asteroids indeed favors the L4 group. In 2001, Beaugé & Roig used semi-analytical models and identified several asteroidal families and clusters around L4 and L5. They write that "The clusters detected in L5 are much less significant than those in L4, even allowing for the difference in the base population''.
Up to now we know of no work that has investigated the special case of a catastrophic event that may have depleted the L5 population sometime during the evolution of the Solar System. Nevertheless, this could be a possible reason. It is known that collisions between protoplanets have happened during the formation of the Solar System and also that several larger protoplanets (comparable to the Earth) were ejected from the outer Solar System (see e.g. Goldreich et al. 2004). Such an escaping protoplanet could have come close to the L5 group and subsequently induced an ejection of small bodies.
A recent work by Morbidelli et al. (2005) investigates the possible capture of Trojan asteroids by Jupiter. It is suggested that the asteroids formed in more distant regions and then, during the time when the giant planets migrated inwards, were captured by Jupiter in the Trojan-type motion. This capture was only possible during a short time span, just after Jupiter and Saturn crossed their mutual 1:2 resonance. During this time, the dynamics of the Trojan region were completly chaotic. Their simulations reproduce the orbital distribution of the Trojans, and the chaotic process of capture may also account for the difference between the L4 and L5 populations.
One of the first who tried to find a dynamical solution was Barber (1986). He investigated the influence of Saturn and found "little difference'' between the two groups. Only in one special case - for inclinations near 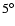 ,
an eccentricity near e=0.05, and libration amplitudes between
,
an eccentricity near e=0.05, and libration amplitudes between 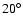 and
and 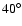 - did he find that L5 Trojans are less stable than L4 Trojans when one includes Saturn in the model. However, the integration time of his model was only one million years. Additionally only a relatively large time-step could be used and thus "[...] the truncation error became important''. He concludes " [...] any conclusion that Saturn is responsible for the L4/L5 differentiation must be tentative indeed''. If we check model 2 of our work (see Fig. 5) for
- did he find that L5 Trojans are less stable than L4 Trojans when one includes Saturn in the model. However, the integration time of his model was only one million years. Additionally only a relatively large time-step could be used and thus "[...] the truncation error became important''. He concludes " [...] any conclusion that Saturn is responsible for the L4/L5 differentiation must be tentative indeed''. If we check model 2 of our work (see Fig. 5) for
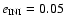 ,
we find that at
,
we find that at
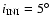 all orbits are stable for L4 (41 out of 41) and 38 out of 41 are stable for L5. Thus in this special case, L5 is more unstable than L4, but for any decisive conclusion a larger sample has to be checked.
all orbits are stable for L4 (41 out of 41) and 38 out of 41 are stable for L5. Thus in this special case, L5 is more unstable than L4, but for any decisive conclusion a larger sample has to be checked.
Recently, several new dynamical studies were performed to identify a possible difference due to the perturbation of Saturn. Pál & Süli (2004) investigated the stability regions around the Lagrangian points in the (a-e) plane and for the non-singular elements (h-k). As an indicator of stability they did not directly use the orbital elements but rather several chaos indicators, namely the Fourier spectra numbers (FSN) and Lyapunov characteristic exponent (LCE).
Their plots "[...] show clearly that the size of the stable region around the two Lagrangian points is smaller around the trailing point''. But there were differences between their calculated mean values of the longitude of the perihelion and the observed one, which indicates some problems with the fitting procedure and the determination of the stable regions.
Schwarz et al. (2004) and Dvorak & Schwarz (2005) also present some numerical indications (based on the evaluation of Lyapunov exponents) that the difference between the numbers of L4 and L5 Trojans is indeed due to a dynamical effect and not an observational bias.
But they also conclude that the results - found with the aid of the LCE - could be biased by the choice of initial conditions.
5.6 Results
In this subsection we now want to summarize the results of our calculations concerning the difference between the two Trojan groups. We want to emphasize again that we rely only on the evolution of the actual orbital elements, not on any chaos indicator. Chaos indicators are a very important and valuable tool; but since it is still not clear if the reason for the difference between L4 and L5 is dynamical, we are reluctant to use it here because the application of e.g. Lyapunov characteristic numbers could cause a bias in the results (see Pál & Süli 2004).
![\begin{figure}
\par\includegraphics[angle=270,width=7.4cm,clip]{4689f9a.ps}\par\vspace*{2mm}
\includegraphics[angle=270,width=7.4cm,clip]{4689f9b.ps}\end{figure}](/articles/aa/full/2006/25/aa4689-05/Timg90.gif) |
Figure 9:
Top: borders of the region where the libration width
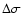 of the Trojans is smaller than
of the Trojans is smaller than 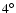 (Model 1 - HYB). The region for L5 is clearly smaller. Bottom: same in the SJA model. No significant difference can be seen.
(Model 1 - HYB). The region for L5 is clearly smaller. Bottom: same in the SJA model. No significant difference can be seen. |
| Open with DEXTER |
Table 3:
Percentage of stable orbits for model 2.
Figure 9 (left) shows some results of the model 1 (HYB, OSS) integration. We show the borders of the region where the libration width
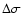 is smaller than
is smaller than 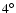 .
This value was chosen because we want to investigate the stability in the direct vicinity of Lagrangian points. A small libration width ensures that the asteroid always stays near the Lagrangian point. The value of
.
This value was chosen because we want to investigate the stability in the direct vicinity of Lagrangian points. A small libration width ensures that the asteroid always stays near the Lagrangian point. The value of 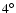 is somewhat arbitrary, but turned out to be good choice
is somewhat arbitrary, but turned out to be good choice![[*]](/icons/foot_motif.gif) . It is clearly visible that the abovementioned region is smaller around the Lagrangian point L5 than around L4. Before we draw some conclusions from this fact, we want to summarize again some properties of the integration that was performed in this case (model 1):
. It is clearly visible that the abovementioned region is smaller around the Lagrangian point L5 than around L4. Before we draw some conclusions from this fact, we want to summarize again some properties of the integration that was performed in this case (model 1):
- 1.
- The test asteroids of this model were placed in the vicinity of L4 (L5); i.e. the initial value of the mean anomaly M was always
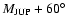 (
(
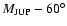 ). Only the initial eccentricity and initial inclination were varied according to the distribution of the real asteroids.
). Only the initial eccentricity and initial inclination were varied according to the distribution of the real asteroids.
- 2.
- Compared to the other models, the integration time was relatively short (10 Myrs).
Thus, because of 1), the results of this model can be used to describe the direct vicinity of the Lagrangian points, in contrast to the other models, where large areas surrounding Jupiters orbit were investigated. The libration width describes the amplitude an asteroid has when it is moving around the Lagrangian points. In this case, it indicates the maximum separation a body had from the Lagrangian point during the integration. Figure 9 (top) now shows that there are almost twice as many asteroids with very small amplitudes (
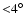 )
around L4 than L5 - already on the relatively short timescale of 10 Myrs! Since the two Lagrangian points are dynamically equivalent in the restricted three-body problem and since the results described in the former section showed that the influence of Uranus and Neptune is negligible, this is a strong indication that any dynamical difference between the two Lagrangian points is due to the influence of Saturn. To check this assumption, we repeated the integration for the SJA model, now only including the Sun and Jupiter. Figure 9 (bottom) shows that now the two regions are almost identical. Thus we can confirm that any dynamical difference must indeed be due to the influence of Saturn!
)
around L4 than L5 - already on the relatively short timescale of 10 Myrs! Since the two Lagrangian points are dynamically equivalent in the restricted three-body problem and since the results described in the former section showed that the influence of Uranus and Neptune is negligible, this is a strong indication that any dynamical difference between the two Lagrangian points is due to the influence of Saturn. To check this assumption, we repeated the integration for the SJA model, now only including the Sun and Jupiter. Figure 9 (bottom) shows that now the two regions are almost identical. Thus we can confirm that any dynamical difference must indeed be due to the influence of Saturn!
The situation becomes more complicated when we take longer time scales and different initial conditions into account. Tables 3 and 4 show the numbers of stable asteroids in models 2 and 3. We see that for model 2 the percentage of stable bodies around L4 and L5 is comparable, although the numbers are higher for L4 (except for very high initial eccentricities) by 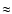 1%. This difference is too small to make any conclusions on a probable dynamical difference between the two Lagrangian points. We find a similar behavior for model 3
1%. This difference is too small to make any conclusions on a probable dynamical difference between the two Lagrangian points. We find a similar behavior for model 3![[*]](/icons/foot_motif.gif) : the difference between the two values is even less.
: the difference between the two values is even less.
We should also note that the fact that there seem to be slightly more stable asteroids around L5 than L4 for higher initial inclinations could support the thesis that the difference is due to observational reasons. If there were more L5 Trojans with highly inclined orbits, they would be more difficult to observe than in L4.
Table 4:
Percentage of stable orbits for model 3.
In the case of model 2, the integration time (50 Myrs) was five times longer than for model 3 (10 Myrs). But in both cases, we see no real difference between the stability of the two Lagrangian points. Thus, the fact that there is a difference for model 1 and none for models 2 and 3 is due not to the integration time but to the choice of initial conditions (although we suspect that a difference would appear if one would increase the integration time considerably).
6 Conclusions
The main goal of this work was to investigate the shape and size of the stability regions around the Lagrangian points L4 and L5 of the Sun-Jupiter system. This was done by investigating the results of several different numerical integrations. We investigated the libration around the Lagrangian points (model 1), show the dependence of the size and shape of the stability region on the initial eccentricity in the (
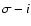 )
plane (model 2) and of the initial inclination in the (
)
plane (model 2) and of the initial inclination in the (
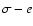 )
plane (model 3), and investigated the influence of the perturbing planets Neptune, Uranus, Saturn, and Jupiter (model 4).
)
plane (model 3), and investigated the influence of the perturbing planets Neptune, Uranus, Saturn, and Jupiter (model 4).
-
We find that a "critical initial eccentricity''
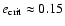 exists that determines the behavior of the stability region. In model 1 it gives the "border'' where the influence of the initial inclinations changes from destabilizing to stabilizing behavior. In the (
exists that determines the behavior of the stability region. In model 1 it gives the "border'' where the influence of the initial inclinations changes from destabilizing to stabilizing behavior. In the (
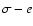 )
plane this initial eccentricity separates two regions: for
)
plane this initial eccentricity separates two regions: for
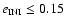 the percentage of stable orbits stays almost constant with increasing initial inclination, whereas for
the percentage of stable orbits stays almost constant with increasing initial inclination, whereas for
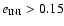 the percentage of stable orbits decreases with increasing initial inclination. In the (
the percentage of stable orbits decreases with increasing initial inclination. In the (
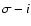 )
plane we observe a "bulge-like'' structure for values around
)
plane we observe a "bulge-like'' structure for values around
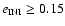 .
.
-
The results from the models were also used to check if a dynamical reason exists for the difference between the number of asteroids observed in the L4 and L5 groups. We found a different dynamical behavior due to Saturn for model 1 but not for models 2, 3, or 4. This is explained as follows. The initial conditions for models 2 and 3 were chosen such that the stability region around the Lagrangian points and its borders could be mapped in full detail; therefore we placed test particles at many different values of the initial mean anomaly M. In model 1 all test particles were initially located close to the Lagrangian points (
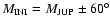 ). The initial conditions for eccentricity and inclination were chosen in such a way as to resemble the distribution of real Trojans. Thus model 1 best describes the dynamical situation in the vicinity of the Lagrangian points where the real Trojan asteroids also move, whereas the initial conditions of models 2 and 3 also cover large areas where no real Trojans are observed. The difference in model 1 was found by direct analysis of the time evolution of orbital elements (not using any chaos indicators that could have biased the results); it is large and distinctive - thus we can conclude that this effect is indeed due to the influence of Saturn and not a numerical artefact.
). The initial conditions for eccentricity and inclination were chosen in such a way as to resemble the distribution of real Trojans. Thus model 1 best describes the dynamical situation in the vicinity of the Lagrangian points where the real Trojan asteroids also move, whereas the initial conditions of models 2 and 3 also cover large areas where no real Trojans are observed. The difference in model 1 was found by direct analysis of the time evolution of orbital elements (not using any chaos indicators that could have biased the results); it is large and distinctive - thus we can conclude that this effect is indeed due to the influence of Saturn and not a numerical artefact.
The results of this work give rise to some interesting topics and questions that will be investigated in a future work:
- What is the underlying reason for the observed "bulge-like'' structures in models 2 and 3? An analysis of the secular and mean-motion resonances will be needed to clarify these patterns.
- How does the motion of Trojans depend in detail on the value of
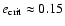 ? New numerical integrations near this initial value of eccentricity are necessary.
? New numerical integrations near this initial value of eccentricity are necessary.
- Is the reason for the difference in the numbers of observed Trojans near L4 and L5 indeed a dynamical one, due to the influence of Saturn? The results of this work support these theses but are not conclusive enough. New integrations for very long timescales and for carefully chosen sets of initial conditions will be performed.
Acknowledgements
Part of the numerical integrations were accomplished on the NIIDP (National Information Infrastructure Development Program) supercomputer in Hungary. We want to thank Dr. Rudolf Dvorak and Dr. Richard Schwarz for valuable comments and Dr. Áron Süli for assistance with the NIIDP supercomputer.
- Asghari, N.,
Broeg, C., Carone, L., et al. 2004, A&A, 426, 353 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Barber, G. 1986, in
Asteroids, comets, meteors II, ed. C. I. Lagerkvist, B. A.
Lindblad, H. Lundstedt, & H. Rickman, 161
(In the text)
- Beaugé, C.,
& Roig, F. 2001, Icarus, 153, 391 [NASA ADS] [CrossRef] (In the text)
- Bien, R. 1980, The Moon
and the Planets, 22, 163 [NASA ADS] [CrossRef] (In the text)
- Bien, R., &
Schubart, J. 1984, CMDA, 34, 425 (In the text)
- Brasser, R.,
Heggie, D. C., & Mikkola, S. 2004, CMDA, 88, 123 [NASA ADS] (In the text)
- Celletti, A.,
& Giorgilli, A. 1991, CMDA, 50, 31 [NASA ADS] (In the text)
- Chambers, J.
1999, MNRAS, 304, 793 [NASA ADS] [CrossRef] (In the text)
- Dvorak, R., &
Tsiganis, K. 2000, CMDA, 78, 125 [NASA ADS] (In the text)
- Dvorak, R., &
Schwarz, R. 2005, CMDA, 92, 19 [NASA ADS] (In the text)
- Efthymiopoulos, Ch.
2004, CMDA, 92, 29 [NASA ADS] (In the text)
- Érdi, B. 1981,
CMDA, 24, 377 [NASA ADS] (In the text)
- Érdi, B. 1984,
CMDA, 34, 425 (In the text)
- Érdi, B. 1988,
CMDA, 43, 303 (In the text)
- Érdi, B. 1996,
CMDA, 34, 425 (In the text)
- Érdi, B. 1997,
CMDA, 65, 149 [NASA ADS]
- Flemming, H.,
& Hamilton, D. 2000, Icarus, 148, 479 [NASA ADS] [CrossRef] (In the text)
- Giorgilli,
A., & Skokos, C. 1997, A&A, 317, 254 [NASA ADS] (In the text)
- Goldreich,
P., Lithwick, Y., & Sari, R. 2004, ApJ, 614, 497 [NASA ADS] [CrossRef] (In the text)
- Hanslmeier,
A., & Dvorak, R. 1984, A&A, 132, 203 [NASA ADS] (In the text)
- Karlsson, O.
2004, A&A, 413, 1153 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Kuchner, M. J.,
Reach, W. T., & Brown, M. E. 2000, Icarus, 145, 44 [NASA ADS] [CrossRef] (In the text)
- Levison, H.,
Shoemaker, E., & Shoemaker, C. 1997, Nature, 385, 42 [NASA ADS] [CrossRef] (In the text)
-
Lichtenegger, H. 1984, CMDA, 34, 357 (In the text)
- Marzari, F.,
Scholl, H., & Farinella, P. 1996, Icarus, 119, 192 [NASA ADS] [CrossRef] (In the text)
- Marzari, F.,
Farinella, P., Davis, D. R., Scholl, H., & Campo Bagatin, A.
1997, Icarus, 125, 39 [NASA ADS] [CrossRef] (In the text)
- Marzari, F.,
& Scholl, H. 1998, Icarus, 131, 41 [NASA ADS] [CrossRef] (In the text)
- Marzari, F.,
& Scholl, H. 2002, Icarus, 159, 328 [NASA ADS] [CrossRef] (In the text)
- Marzari, F.,
Tricarico, P., & Scholl, H. 2003, MNRAS, 345, 1091 [NASA ADS] [CrossRef] (In the text)
- Mikkola, S.,
& Innanen, K. 1992, AJ, 104, 1641 [NASA ADS] [CrossRef] (In the text)
- Mikkola, S.,
& Innanen, K. 1995, Earth, Moon and Planets, 71, 195
- Milani, A. 1993,
CMDA, 57, 59 [NASA ADS] (In the text)
- Milani, A. 1994, in
Asteroids, Comets, Meteors, ed. A. Milani, M. Di Martino, & A.
Cellino (Kluwer), 159
- Milani, A., Nobili,
A., & Knezevic, Z. 1997, Icarus, 125, 13 [NASA ADS] [CrossRef] (In the text)
- Morais, M. H. M.
1999, A&A, 350, 318 [NASA ADS] (In the text)
- Morbidelli,
A., Levison, H. F., Tsiganis, K., & Gomes, R. 2005, Nature,
435, 462 [NASA ADS] [CrossRef] (In the text)
- Namouni, F.
1999, Icarus, 137, 293 [NASA ADS] [CrossRef] (In the text)
- Namouni, F.,
& Murray, C. D. 2000, CMDA, 76, 131 [NASA ADS] (In the text)
- Namouni, F.,
Christou, A. A., & Murray, C. D. 1999, Physical Review Letters,
83, 13 (In the text)
- Pál, A., &
Süli, Á. 2004, in Proceedings of the British-Hungarian
N+N Workshop for Young Researchers On Computer processing and use
of satellite data in astronomy and astrophysics and 3rd Workshop of
Young Researchers in Astronomy & Astrophysics, ed. E.
Forgács-Dajka, K. Petrovay, & R. Erdélyi, 285
(In the text)
- Peale, S. J. 1999,
Icarus, 106, 308 [NASA ADS] [CrossRef] (In the text)
- Pilat-Lohinger, E.,
Dvorak, R., & Tsiganis, K. 1999, CMDA, 73, 117 [NASA ADS] (In the text)
- Rabe, E. 1967, AJ, 72,
10 [NASA ADS] [CrossRef] (In the text)
- Rabe, E. 1968, AJ, 73,
732 [NASA ADS] [CrossRef]
- Robutel, P.,
Gabern, F., & Jorba, A. 2005, CMDA, 92, 53 [NASA ADS] (In the text)
- Sándor, Zs.,
& Érdi, B. 2003, CMDA, 86, 301 [NASA ADS] (In the text)
- Sándor, Zs.,
Érdi, B., & Murray, C. D. 2003, CMDA, 84, 355 [NASA ADS] (In the text)
- Schwarz, R.,
& Gyergyovits, M. 2003, in Proceedings of the 3rd
Austrian-Hungarian workshop on Trojans and related topics, ed. F.
Freistetter, R. Dvorak, & B. Érdi (Eötvös
University Press), 71
(In the text)
- Schwarz, R.,
Gyergyovits, M., & Dvorak, R. 2004, CMDA, 90, 139 [NASA ADS] (In the text)
- Schubart, J.,
& Bien, R. 1987, A&A, 175, 299 [NASA ADS] (In the text)
- Shoemaker,
E., Shoemaker, C., & Wolfe, R. 1989, in Asteroids II, ed. R.
Binzel, T. Gehrels, & M. Matthews (University of Arizona
Press), 487
(In the text)
- Skokos, C., &
Dokoumetzidis, A. 2001, A&A, 367, 729 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Tsiganis, K.,
Dvorak, R., & Pilat-Lohinger, E. 2000, A&A, 354, 1091 [NASA ADS] (In the text)
- Tsiganis, K.,
Varvoglis, H., & Dvorak, R. 2005, CMDA, 92, 71 [NASA ADS] (In the text)
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[angle=270,width=8.3cm,clip]{4689f1a.ps}\par\vspace*{2mm}
\includegraphics[angle=270,width=8.3cm,clip]{4689f1b.ps}\end{figure}](/articles/aa/full/2006/25/aa4689-05/Timg37.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4689f2.ps}\end{figure}](/articles/aa/full/2006/25/aa4689-05/Timg40.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.2cm,clip]{4689f3a.ps}\par\vspace*{2mm}
\includegraphics[angle=270,width=8.2cm,clip]{4689f3b.ps}\end{figure}](/articles/aa/full/2006/25/aa4689-05/Timg43.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.2cm,clip]{4689f4a.ps}\par\vspace*{2mm}
\includegraphics[angle=270,width=8.2cm,clip]{4689f4b.ps}\end{figure}](/articles/aa/full/2006/25/aa4689-05/Timg44.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.2cm,clip]{4689f5a.ps}\par\...
...space*{4mm}
\includegraphics[angle=270,width=8.2cm,clip]{4689f5c.ps}\end{figure}](/articles/aa/full/2006/25/aa4689-05/Timg51.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.8cm,clip]{4689f6a.ps}\par\...
...space*{4mm}
\includegraphics[angle=270,width=7.8cm,clip]{4689f6c.ps}\end{figure}](/articles/aa/full/2006/25/aa4689-05/Timg65.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.3cm,clip]{4689f7.ps}\end{figure}](/articles/aa/full/2006/25/aa4689-05/Timg83.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.4cm,clip]{4689f9a.ps}\par\vspace*{2mm}
\includegraphics[angle=270,width=7.4cm,clip]{4689f9b.ps}\end{figure}](/articles/aa/full/2006/25/aa4689-05/Timg90.gif)