- ...L
![[*]](/icons/foot_motif.gif)
- As of March 6, there are 1121 L4 Trojans and 885 L5 Trojans.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... output
![[*]](/icons/foot_motif.gif)
- In the following we will only present the pictures obtained with the hybrid integration method (HYB). Additional calculations have shown that all three methods give the same output; thus for all future integrations we have neglected the LIE and B-S methods.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... stability
![[*]](/icons/foot_motif.gif)
- For an initial value of
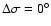 ,
the stability region encloses all values of proper eccentricity that are lower than
,
the stability region encloses all values of proper eccentricity that are lower than 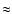 0.21; this value decreases to
0.21; this value decreases to 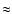 0.1 for an initial
0.1 for an initial
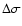 of
of 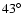 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
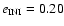 )
)![[*]](/icons/foot_motif.gif)
- We have omitted the figure for
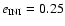 because it shows no new information.
because it shows no new information.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... left
![[*]](/icons/foot_motif.gif)
- Note that for high eccentricities the position of Lagrangian points differs from
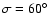 and
and
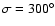 .
Strictly speaking, these values are only valid for the restricted (circular) three-body problem.
.
Strictly speaking, these values are only valid for the restricted (circular) three-body problem.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...L
![[*]](/icons/foot_motif.gif)
- The behavior of L5 was not different from L4 - thus we omit the corresponding figure.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... choice
![[*]](/icons/foot_motif.gif)
- Note that we have obtained similar results for
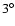 or
or 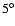 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... model 3
![[*]](/icons/foot_motif.gif)
- The percentage gives the number of stable orbits in between
![$\sigma=[0^\circ,120^\circ]$](/articles/aa/full/2006/25/aa4689-05/img96.gif) for L4 and
for L4 and
![$\sigma=[240^\circ,360^\circ]$](/articles/aa/full/2006/25/aa4689-05/img97.gif) for L5.
for L5.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.