A&A 453, 155-162 (2006)
DOI: 10.1051/0004-6361:20054466
A. Mérand1,3 - P. Kervella1 - V. Coudé du Foresto1 - G. Perrin1 - S. T. Ridgway2,3 - J. P. Aufdenberg2 - T. A. ten Brummelaar3 - H. A. McAlister3 - L. Sturmann3 - J. Sturmann3 - N. H. Turner3 - D. H. Berger3
1 - LESIA, UMR 8109, Observatoire de Paris, 5 place Jules
Janssen, 92195 Meudon, France
2 - National Optical Astronomy Observatories 950 North Cherry
Avenue, Tucson, AZ 85719, USA
3 - Center for High Angular
Resolution Astronomy, Georgia State University, PO Box 3965,
Atlanta, Georgia 30302-3965, USA
Received 3 November 2005 / Accepted 11 March 2006
Abstract
We present the results of long-baseline interferometric
observations of the classical Cepheids Polaris and ![]() Cep in the
near infrared K' band (1.9-2.3
Cep in the
near infrared K' band (1.9-2.3 ![]() m), using the FLUOR instrument of
the CHARA Array. Following our previous detection of a circumstellar
envelope (CSE) around
m), using the FLUOR instrument of
the CHARA Array. Following our previous detection of a circumstellar
envelope (CSE) around ![]() Car (Kervella et al. 2006), we report
similar detections around Polaris and
Car (Kervella et al. 2006), we report
similar detections around Polaris and ![]() Cep. Owing to the large
data set acquired on Polaris, in both the first and second lobes of
visibility function, we have detected the presence of a circum-stellar
envelope (CSE), located at
Cep. Owing to the large
data set acquired on Polaris, in both the first and second lobes of
visibility function, we have detected the presence of a circum-stellar
envelope (CSE), located at ![]() stellar radii, accounting for
stellar radii, accounting for
![]() % of the stellar flux in the K band. A similar model is
applied to the
% of the stellar flux in the K band. A similar model is
applied to the ![]() Cep data, which shows improved agreement
compared to a model without CSE. Finally, we find that the bias in
estimating the angular diameter of
Cep data, which shows improved agreement
compared to a model without CSE. Finally, we find that the bias in
estimating the angular diameter of ![]() Cep in the framework of
the Baade-Wesselink method (Mérand et al. 2005b) is of the order of
Cep in the framework of
the Baade-Wesselink method (Mérand et al. 2005b) is of the order of ![]() or less in the K band. A complete study of the influence of
the CSE is proposed in this context, showing that at the optimum
baseline for angular diameter variation detection, the bias is of the
order of the formal precision in the determination of the
or less in the K band. A complete study of the influence of
the CSE is proposed in this context, showing that at the optimum
baseline for angular diameter variation detection, the bias is of the
order of the formal precision in the determination of the ![]() Cep
pulsation amplitude (
Cep
pulsation amplitude (![]() ).
).
Key words: stars: variables: Cepheids - stars: circumstellar matter -
stars: individual: Polaris (![]() Ursae Minoris) - stars:
individual:
Ursae Minoris) - stars:
individual: ![]() Cephei - techniques: interferometric - techniques: high angular resolution
Cephei - techniques: interferometric - techniques: high angular resolution
Using low resolution interferometry (e.g. small baselines at which the
star is under resolved) in the near infrared and mid-infrared, we
recently reported the discovery of a circumstellar envelope (CSE)
around the 35 day period Cepheid ![]() Car (Kervella et al. 2006). The
presence of this feature may disturb the application of the classical
Baade-Wesselink (BW) method, which aims at determining distances by
measuring simultaneously the variations of angular and linear
diameters.
Car (Kervella et al. 2006). The
presence of this feature may disturb the application of the classical
Baade-Wesselink (BW) method, which aims at determining distances by
measuring simultaneously the variations of angular and linear
diameters.
Stellar interferometry has demonstrated a capability to measure precise Cepheid distances and the calibration zero point of the their Period-Luminosity relation (Kervella et al. 2004a). With the recent calibration of the BW method, thanks to the direct p-factor measurement by interferometry (Mérand et al. 2005b), it is now mandatory to study the Cepheid center-to-limb darkening (CLD) and the possible presence of CSEs in order to constrain two of the last sources of possible bias in the interferometric BW method. A morphological model is required in order to derive the angular diameter from a single baseline visibility measurement. If the assumed CLD differs from the actual one, or if the circumstellar emission is present, the derived angular diameters can be biased, possibly leading to a biased distance estimation in the BW method.
Following our recent study of ![]() Car, we present in this work near
infrared observations of Polaris (
Car, we present in this work near
infrared observations of Polaris (![]() UMi,
HR 424, HD 8890) and complementary observations of
UMi,
HR 424, HD 8890) and complementary observations of
![]() Cep (HR 8571, HD 213306) using the
FLUOR (Fiber Link Unit for Optical Recombination) beam combiner
installed at the CHARA (Center for High Angular Resolution Astronomy)
Array. Polaris is the brightest Cepheid in the northern skies and
offers the best opportunity to measure the CLD and detect the presence
of a CSE. A great amount of data was collected, 65 calibrated data
points using 4 different baselines (projected length from 19 to 246 m), to disentangle the CLD and CSE characterization from the
possible close companion and radial pulsation detection. We show that
these two latter effects have not been detected in our dataset,
whereas the presence of a CSE is mandatory to explain a visibility
deficit observed at
Cep (HR 8571, HD 213306) using the
FLUOR (Fiber Link Unit for Optical Recombination) beam combiner
installed at the CHARA (Center for High Angular Resolution Astronomy)
Array. Polaris is the brightest Cepheid in the northern skies and
offers the best opportunity to measure the CLD and detect the presence
of a CSE. A great amount of data was collected, 65 calibrated data
points using 4 different baselines (projected length from 19 to 246 m), to disentangle the CLD and CSE characterization from the
possible close companion and radial pulsation detection. We show that
these two latter effects have not been detected in our dataset,
whereas the presence of a CSE is mandatory to explain a visibility
deficit observed at
![]() ,
as in
,
as in ![]() Car.
Car.
We also present complementary observations of the Cepheid ![]() Cep
with medium baselines (
Cep
with medium baselines (
![]() ), following our
determination of its p-factor using very long baselines
(Mérand et al. 2005b). The final characteristics of the CSEs detected
around Polaris and
), following our
determination of its p-factor using very long baselines
(Mérand et al. 2005b). The final characteristics of the CSEs detected
around Polaris and ![]() Cep are qualitatively in agreement with
what has been found for
Cep are qualitatively in agreement with
what has been found for ![]() Car.
Car.
Finally, we present a formal analysis of the bias introduced to the BW method in presence of the CSE.
Observations were undertaken in the near infrared (K' band,
![]() )
at the CHARA Array
(ten Brummelaar et al. 2005) using FLUOR, the Fiber Linked Unit for
Optical Recombination (Coudé du Foresto et al. 2003). The FLUOR Data reduction
software (DRS) (Kervella et al. 2004b; Coudé du Foresto et al. 1997), was used to
extract the squared modulus of the coherence factor between the two
independent apertures from the fringe pattern.
)
at the CHARA Array
(ten Brummelaar et al. 2005) using FLUOR, the Fiber Linked Unit for
Optical Recombination (Coudé du Foresto et al. 2003). The FLUOR Data reduction
software (DRS) (Kervella et al. 2004b; Coudé du Foresto et al. 1997), was used to
extract the squared modulus of the coherence factor between the two
independent apertures from the fringe pattern.
The baselines were chosen according to the Polaris and ![]() Cep
angular sizes (approximately 3 and 1.5 mas, respectively), wavelength
of observation and desired spatial resolution. Polaris must be
observed at i) low spatial resolution (
Cep
angular sizes (approximately 3 and 1.5 mas, respectively), wavelength
of observation and desired spatial resolution. Polaris must be
observed at i) low spatial resolution (
![]() )
in order
to detect the CSE and the possible faint companion, ii) high
resolution (in the first lobe of the visibility profile, near the
first null) in order to detect the pulsation with optimum sensitivity
and iii) at the top of the second lobe in order to measure the
CLD. This led to the choice of CHARA baselines i) S1-S2
(b=33 m), E1-E2 (b=66 m), ii) W2-E2 (b=156 m) and iii) W1-E2 (b=251 m). Concerning
)
in order
to detect the CSE and the possible faint companion, ii) high
resolution (in the first lobe of the visibility profile, near the
first null) in order to detect the pulsation with optimum sensitivity
and iii) at the top of the second lobe in order to measure the
CLD. This led to the choice of CHARA baselines i) S1-S2
(b=33 m), E1-E2 (b=66 m), ii) W2-E2 (b=156 m) and iii) W1-E2 (b=251 m). Concerning ![]() Cep, the only
requirement for the complementary data was to reach
Cep, the only
requirement for the complementary data was to reach
![]() ,
where the CSE is believed to be easily detectable. This criteria led
to projected baselines of roughly 150 m, corresponding to W2-E2 and
S2-W2 at the CHARA Array. These latter baselines were chosen with
similar length but different orientation, in order to investigate
possible asymmetry in the CSE, if present.
,
where the CSE is believed to be easily detectable. This criteria led
to projected baselines of roughly 150 m, corresponding to W2-E2 and
S2-W2 at the CHARA Array. These latter baselines were chosen with
similar length but different orientation, in order to investigate
possible asymmetry in the CSE, if present.
Calibrator stars were chosen in two different catalogs: B02 (Bordé et al. 2002) for stars larger than 2.0 mas in diameter and M05 (Mérand et al. 2005a) for stars smaller than 2.0 mas using criteria defined in this latter work (see Table 1). We used calibrators from B02 for baselines smaller than 100 m, while for larger baselines we used calibrators from M05. The two catalogs are very similar by their characteristics: M05 is an extension of B02 using the very same procedure to estimate angular diameters. Therefore no trend is expected when using data calibrated with stars coming from these two catalogs.
Table 1: Calibrators used for the observations. "SP'' stands for spectral type. Uniform Disk diameters, given in mas, are only intended for computing the expected squared visibility in the K band.
Polaris has the largest angular size of all northern population I Cepheids. This star is therefore the best candidate for CLD measurements using an interferometer.
Because Polaris lies near the North celestial pole, the projected baseline remains almost constant in length while varying in position angle during the night (see Fig. 1).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{4466fig1.eps}
\end{figure}](/articles/aa/full/2006/25/aa4466-05/Timg36.gif) |
Figure 1: u-v map, in meters. Up is north and right is east. Each data point lies on a circle corresponding to the baseline because of the near-polar position in the sky of Polaris. |
| Open with DEXTER | |
Claret (2000) tabulated limb darkening coefficients from
hydrostatic ATLAS models. If we use the following parameters
![]() ,
,
![]() and solar metallicity, we get
in the database the following LD coefficients for the K band:
and solar metallicity, we get
in the database the following LD coefficients for the K band:
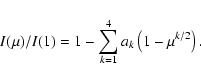 |
(1) |
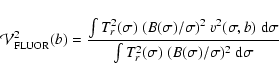 |
(2) |
The only parameter adjusted in the fit is the angular diameter of the
star, which is found to be
![]() mas. The
corresponding reduced
mas. The
corresponding reduced ![]() is 4.5 (Table 2). Note that
we take into account the correlations between error bars of different
data points. These correlations come from the multiple use of a single
calibrator in the dataset. They are properly treated according to the
formalism developed by Perrin (2003).
is 4.5 (Table 2). Note that
we take into account the correlations between error bars of different
data points. These correlations come from the multiple use of a single
calibrator in the dataset. They are properly treated according to the
formalism developed by Perrin (2003).
In Fig. 2, we display the data points and the models. The
solid line corresponds to the hydrostatic CLD model for Polaris from
Claret (2000). It appears that the model fails to reproduce the
data in the second lobe (see W1-E1 baseline) and marginally
intermediate baselines (E1-E2), where
![]() .
.
Table 2:
Best fit model parameters for Polaris and its
CSE.
![]() is the stellar angular diameter (mas),
is the stellar angular diameter (mas),
![]() the CLD coefficient,
the CLD coefficient,
![]() the shell angular
diameter (mas), w the shell width (mas) and
the shell angular
diameter (mas), w the shell width (mas) and
![]() the
relative brightness (Fig. 3). Last column
tabulates the reduced
the
relative brightness (Fig. 3). Last column
tabulates the reduced ![]() .
Only parameters with error bars
(lower scripts) have been fitted. The first line is the
hydrostatic model; the second line is the adjusted CLD; the
model of the last line includes a shell.
.
Only parameters with error bars
(lower scripts) have been fitted. The first line is the
hydrostatic model; the second line is the adjusted CLD; the
model of the last line includes a shell.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{4466fig2.eps}
\end{figure}](/articles/aa/full/2006/25/aa4466-05/Timg52.gif) |
Figure 2: Results of fit for different models. Squared visibility with respect to baseline. Solid line is the hydrostatic CLD from Claret (2000), dotted line is a fitted power law CLD while the dashed line is the hydrostatic model surrounded by the shell (see Table 2 for the models parameters). Note that solid and dotted line overlap in the main panel, the S1-S2 and E1-E2 small panels. |
| Open with DEXTER | |
Because the second lobe is not well reproduced by the hydrostatic
model, a simple way to improve the model is to adjust the strength of
the CLD. Indeed, the CLD profile changes the scale of the first lobe
(not its shape) and the height of the second lobe. For this purpose we
chose a single parameter CLD law, the power law:
![]() (Michelson & Pease 1921; Hestroffer 1997). The
hydrostatic model computed from Claret coefficients for
Polaris corresponds to
(Michelson & Pease 1921; Hestroffer 1997). The
hydrostatic model computed from Claret coefficients for
Polaris corresponds to
![]() .
Even using a single parameter
CLD model compared to the 4-parameters Claret's law, corresponding V2 only differ at most by 10-3 (relative) in the first two lobes. We therefore prefer to use a single parameter CLD law (the
power law), for the sake of simplicity.
.
Even using a single parameter
CLD model compared to the 4-parameters Claret's law, corresponding V2 only differ at most by 10-3 (relative) in the first two lobes. We therefore prefer to use a single parameter CLD law (the
power law), for the sake of simplicity.
The best fit, adjusting ![]() as a free parameter, leads to
as a free parameter, leads to
![]() mas and
mas and
![]() ;
the
reduced
;
the
reduced ![]() is then 2.5 (Table 2, second line). Based
on the
is then 2.5 (Table 2, second line). Based
on the ![]() ,
the fit is significantly better: the hydrostatic CLD led to
,
the fit is significantly better: the hydrostatic CLD led to ![]() of 4.5. The CLD is stronger than predicted by
hydrostatic models and the corresponding angular diameter is thus
larger, as expected. However, before trying to interpret this result
in terms of photospheric characteristics, one should notice that this
model still fails to fit the mid-first lobe (see E1-E2 panel in
Fig. 2, dotted line, which actually overlaps with the solid
line). The measured V2 data are lower than computed for a limb
darkened disk. A change in CLD affects primarily the second lobe
(higher spatial frequencies), and only the scale of the first lobe.
In order to change the shape of the first lobe, one has to invoke
something larger that Polaris itself to disturb the lower spatial
frequencies. Thus, we think that this strong CLD is not realistic.
of 4.5. The CLD is stronger than predicted by
hydrostatic models and the corresponding angular diameter is thus
larger, as expected. However, before trying to interpret this result
in terms of photospheric characteristics, one should notice that this
model still fails to fit the mid-first lobe (see E1-E2 panel in
Fig. 2, dotted line, which actually overlaps with the solid
line). The measured V2 data are lower than computed for a limb
darkened disk. A change in CLD affects primarily the second lobe
(higher spatial frequencies), and only the scale of the first lobe.
In order to change the shape of the first lobe, one has to invoke
something larger that Polaris itself to disturb the lower spatial
frequencies. Thus, we think that this strong CLD is not realistic.
When seeking possible explanations for the departure around
![]() ,
two obvious possibilities must be considered before
invoking a CSE: Polaris is a pulsating star and a
spectroscopic-astrometric binary as well (Wielen et al. 2000). We shall
now show that neither of these two hypotheses can explain the
discrepancy in the first lobe.
,
two obvious possibilities must be considered before
invoking a CSE: Polaris is a pulsating star and a
spectroscopic-astrometric binary as well (Wielen et al. 2000). We shall
now show that neither of these two hypotheses can explain the
discrepancy in the first lobe.
If the departure detected at V2 is believed to be due to the
companion, it should vary with the position angle angle of the
projected baseline. Our sampled range in projection angle is
quite large and densely populated for E1-E2
(Fig. 1). However the departure does not change
significantly with respect to projection angle of the baselines. As
seen in Fig. 2: the V2 recorded using E1-E2 are consistent
within their errors. Because our typical V2 precision is of the
order of 3%, the companion must be as faint as 1.5% of the main star
flux, or less (in the K band), in order to remain undetected by
CHARA/FLUOR. Moreover, based on non detection in UV and X-ray,
Evans et al. (2002) estimate that the companion mass is between 1.7 and 1.4 solar masses. Thus, this star is most likely a main sequence star
of similar spectral type (but lower luminosity) to
Polaris. Wielen et al. (2000), in their study of the astrometric orbit,
conclude that the difference in magnitude between the two components
is
![]() from which we deduce, because of the similarity in
spectral type,
from which we deduce, because of the similarity in
spectral type,
![]() .
This corresponds to a flux
ratio of
.
This corresponds to a flux
ratio of
![]() which translates into an interferometric V2 modulation twice as large,
which translates into an interferometric V2 modulation twice as large,
![]() or half a
percent.
or half a
percent.
According to the latest radial velocity surveys, the radial pulsation
of Polaris is of the order of 0.4% in diameter
(Moskalik & Gorynya 2005). In the case of FLUOR, for which the relative
error in squared visibility (
![]() )
is almost constant,
the most effective baseline to search for diameter variations
maximizes the following criterion: for a given baseline b and
angular diameter
)
is almost constant,
the most effective baseline to search for diameter variations
maximizes the following criterion: for a given baseline b and
angular diameter ![]() ,
a diameter increase of
,
a diameter increase of
![]() should lead to the maximum relative increase in squared visibility
should lead to the maximum relative increase in squared visibility
![]() .
Thus, the optimum baseline maximizes (in absolute
value) the dimensionless quantity
.
Thus, the optimum baseline maximizes (in absolute
value) the dimensionless quantity ![]() ,
which we call the
amplification factor:
,
which we call the
amplification factor:
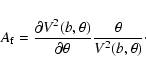 |
(3) |
We demonstrated that neither the companion nor the pulsation can be
detected in our dataset. These phenomena cannot explain the visibility
departure we observed at
![]() and can be therfore
neglected.
and can be therfore
neglected.
Following the study on ![]() Car, we shall now explore the possible
presence of a CSE around Polaris. We will adopt a ring-like model for
the CSE. The image of the object, as seen by the interferometer, is
supposed to be a limb-darkened star, surrounded by a ring. Note that
the ring does not represent a flat disk, it is the two dimensional
projection of the surrounding shell. This model contains five
parameters (see Fig. 3): the star angular diameter (
Car, we shall now explore the possible
presence of a CSE around Polaris. We will adopt a ring-like model for
the CSE. The image of the object, as seen by the interferometer, is
supposed to be a limb-darkened star, surrounded by a ring. Note that
the ring does not represent a flat disk, it is the two dimensional
projection of the surrounding shell. This model contains five
parameters (see Fig. 3): the star angular diameter (
![]() ), its limb darkening coefficient (
), its limb darkening coefficient (![]() ), the ring
mean diameter (
), the ring
mean diameter (
![]() ), its width (w) and the flux ratio between
the two components
), its width (w) and the flux ratio between
the two components
![]() .
Apart from a star surrounded by a
ring, this model can reproduce a single star (
.
Apart from a star surrounded by a
ring, this model can reproduce a single star (
![]() )
or a
star with an uniformly bright environment (
)
or a
star with an uniformly bright environment (
![]() ).
).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{4466fig3.eps}
\end{figure}](/articles/aa/full/2006/25/aa4466-05/Timg71.gif) |
Figure 3:
Our simple CSE model: a star and a ring, as seen by the
interferometer. The star (in the center) is characterized by its
angular diameter
|
| Open with DEXTER | |
The number of parameters (5) is too large compared to our
dataset. Not that we do not have enough data points, but because these
data points are bundled in four sets, one for each baseline. This is
due to the particular position of Polaris in the sky (near the pole)
and because our model is centro-symmetric. We choose to fix the center
to limb darkening coefficient to the value predicted by hydrostatic
models (
![]() ). Moreover, we also realized that the ring
width does not play a significant role in the minimization: we fixed this parameter to different values, from 0.01 mas (very sharp ring) to 1 mas (diluted ring) and always obtained results for the other
parameters within one sigma error bar. This is probably due to our
lack of spatial resolution, which prevented us to actually resolve the
ring width. Finally, only three parameters were adjusted: the stellar
angular diameter, the shell angular diameter and its flux ratio. The
best model is a CSE accounting for
). Moreover, we also realized that the ring
width does not play a significant role in the minimization: we fixed this parameter to different values, from 0.01 mas (very sharp ring) to 1 mas (diluted ring) and always obtained results for the other
parameters within one sigma error bar. This is probably due to our
lack of spatial resolution, which prevented us to actually resolve the
ring width. Finally, only three parameters were adjusted: the stellar
angular diameter, the shell angular diameter and its flux ratio. The
best model is a CSE accounting for ![]() % of the stellar flux
and
% of the stellar flux
and ![]() mas in angular diameter, whereas the stellar angular
diameter is
mas in angular diameter, whereas the stellar angular
diameter is
![]() mas. The reduced
mas. The reduced ![]() is 1.4
(Table 2).
is 1.4
(Table 2).
Interestingly, though the CLD has the same as before (
![]() ,
solid line in the same figure), the second lobe is lower than in the
model without an envelope: the shell lowers the second lobe. This can
be explained easily: since the shell is completely resolved at these
baselines (its own visibility is extremely low), it only contributes
as an uncorrelated flux and reduces the visibility by a factor
,
solid line in the same figure), the second lobe is lower than in the
model without an envelope: the shell lowers the second lobe. This can
be explained easily: since the shell is completely resolved at these
baselines (its own visibility is extremely low), it only contributes
as an uncorrelated flux and reduces the visibility by a factor
![]() where
where ![]() and
and ![]() are the total fluxes
of the two components (star and shell respectively).
are the total fluxes
of the two components (star and shell respectively).
The CLD cannot be constrained from our data, not because they are not
sensitive to it (we do have data in the second lobe), but rather owing
to the limited number of free parameters the u-v coverage
authorizes. In terms of least square minimization, the reduced ![]() is already close to its reasonable minimum. Adding a free
parameter does not improve the fit - worse, it complicates the
minimization algorithm and the error bar estimations. The only thing
allowed, is to explore changes in the fixed value for the CLD parameter.
is already close to its reasonable minimum. Adding a free
parameter does not improve the fit - worse, it complicates the
minimization algorithm and the error bar estimations. The only thing
allowed, is to explore changes in the fixed value for the CLD parameter.
The ![]() does not change much but it is still interesting to watch
the behavior of the free parameters. The main effect of changing the
CLD is to change the stellar diameter accordingly. Indeed, this is
just a well known effect of the limb darkening, as the equivalent
uniform disk diameter remains the same. The second lobe changes
slightly, as expected: increasing the strength of the CLD lowers the
second lobe. More interestingly, the flux ratio between the
CSE and the star changes significantly. We previously noted that the
shell would lower the second lobe. If the CLD lowers it too, the shell
does not have to be as bright to compensate the effects of a
shallow CLD. Yet it is not possible to let the shell disappear
completely: the V2 deficit still has to be fitted. Furthermore,
the size of the shell does not change, since it is not constrained by
the second lobe but by the position (in term of baseline) of the
deficit at low spatial frequencies.
does not change much but it is still interesting to watch
the behavior of the free parameters. The main effect of changing the
CLD is to change the stellar diameter accordingly. Indeed, this is
just a well known effect of the limb darkening, as the equivalent
uniform disk diameter remains the same. The second lobe changes
slightly, as expected: increasing the strength of the CLD lowers the
second lobe. More interestingly, the flux ratio between the
CSE and the star changes significantly. We previously noted that the
shell would lower the second lobe. If the CLD lowers it too, the shell
does not have to be as bright to compensate the effects of a
shallow CLD. Yet it is not possible to let the shell disappear
completely: the V2 deficit still has to be fitted. Furthermore,
the size of the shell does not change, since it is not constrained by
the second lobe but by the position (in term of baseline) of the
deficit at low spatial frequencies.
Therefore it is not possible to draw conclusions regarding Polaris'
intrinsic CLD. We chose not to constrain this parameter and fixed it
to a plausible value. Firstly, the quality of the fit is good enough
(as judged by ![]() )
to conclude that this value is compatible with
our data set. Secondly, our model is not realistic enough that we can
hope measuring the CLD with good accuracy. However, we suggest that
the CLD of Polaris is probably consistent with the value expected from
hydrostatic simulations.
)
to conclude that this value is compatible with
our data set. Secondly, our model is not realistic enough that we can
hope measuring the CLD with good accuracy. However, we suggest that
the CLD of Polaris is probably consistent with the value expected from
hydrostatic simulations.
We tested our best fit geometry with a physical model, such
as the one used by Perrin et al. (2004) for Mira stars: this model is a
simple radiative transfer calculation for a single layer shell
surrounding a star. The shell is a self emitting black body, like the
star itself. This type of model and our ring model lead to similar
geometries for the object, as seen by the interferometer. In the model
described by Perrin et al. (2004), the shell temperature can be computed
using a simple radiative equilibrium model, such as presented in
Ireland et al. (2005). Using silicate opacities (Suh 1999) and a
black body spectrum for the Cepheid (
![]() K),
we found an equilibrium temperature of the order of 2500 K at 3 stellar radii, which does not allow silicate dust grains to
survive. Based on this test, the observed circumstellar
emission is unlikely to be due to thermal emission from a silicate
dust shell. This conclusion does not apply to Mira stars
(
K),
we found an equilibrium temperature of the order of 2500 K at 3 stellar radii, which does not allow silicate dust grains to
survive. Based on this test, the observed circumstellar
emission is unlikely to be due to thermal emission from a silicate
dust shell. This conclusion does not apply to Mira stars
(
![]() K), for which the equilibrium
temperature is much lower for a shell at the same distance.
K), for which the equilibrium
temperature is much lower for a shell at the same distance.
A model consisting in a limb darkened star surrounded by a shell is an
important improvement compared over the simple darkened disk model.
The first lobe visibility deficit, for E1-E2 baseline, is understood
to be due to the presence of a CSE consisting of a dim ring
![]() times larger than the star itself. The width of the ring
is not known, and can be either thin or extended. However, the flux
ratio between the CSE and the star is accurately known and does not
depends on the width of the adopted ring:
times larger than the star itself. The width of the ring
is not known, and can be either thin or extended. However, the flux
ratio between the CSE and the star is accurately known and does not
depends on the width of the adopted ring: ![]() %. It is not
possible to well constrain the intrinsic CLD of the star. However,
our choice of a CLD computed from hydrostatic model
(Claret 2000), combined with a CSE lead to a model
consistent with the interferometric data.
%. It is not
possible to well constrain the intrinsic CLD of the star. However,
our choice of a CLD computed from hydrostatic model
(Claret 2000), combined with a CSE lead to a model
consistent with the interferometric data.
In a recent study, we observed ![]() Cep (Mérand et al. 2005b) and
applied the Baade-Wesselink (BW) method to the interferometric V2 measurements. These measurements were obtained at very long baselines,
between 235 and 315 m where
Cep (Mérand et al. 2005b) and
applied the Baade-Wesselink (BW) method to the interferometric V2 measurements. These measurements were obtained at very long baselines,
between 235 and 315 m where
![]() .
This range
was chosen from among the whole dataset because it maximized the
amplification factor criterion. The remaining data, acquired at
medium baselines, did not contribute significantly to the angular
diameter determination; moreover, their phase coverage was poor.
.
This range
was chosen from among the whole dataset because it maximized the
amplification factor criterion. The remaining data, acquired at
medium baselines, did not contribute significantly to the angular
diameter determination; moreover, their phase coverage was poor.
It was not possible to even suspect the presence of a shell based only
on the longest baseline observations. Considering the experience with
Polaris (above) and previously with ![]() Car, it appears the the CSE is only detectable using a combination of several different spatial
frequencies. Thus, we here combine the sparse medium baseline data
acquired on
Car, it appears the the CSE is only detectable using a combination of several different spatial
frequencies. Thus, we here combine the sparse medium baseline data
acquired on ![]() Cep in 2004 with more recent observations,
obtained in 2005, at baselines where the CSE should show up clearly,
if it exists:
Cep in 2004 with more recent observations,
obtained in 2005, at baselines where the CSE should show up clearly,
if it exists:
![]() %. We shall also use the data set
presented in Mérand et al. (2005b) in order to have consistent spatial
frequency coverage between
%. We shall also use the data set
presented in Mérand et al. (2005b) in order to have consistent spatial
frequency coverage between
![]() and the first visibility
minimum. The purpose of these observations was to detect the presence
of a CSE and study the impact on the angular diameter estimation.
and the first visibility
minimum. The purpose of these observations was to detect the presence
of a CSE and study the impact on the angular diameter estimation.
In order to disentangle the presence of the CSE from the visibility
time-modulation caused by the angular radial pulsation
![]() ,
we define the pseudo baseline
,
we define the pseudo baseline
![]() as:
as:
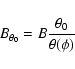 |
(4) |
Table 3:
Best fit model parameters for ![]() Cep and
its CSE.
Cep and
its CSE.
![]() is the stellar angular diameter (mas),
is the stellar angular diameter (mas),
![]() the CLD coefficient,
the CLD coefficient,
![]() the shell angular
diameter (mas), w the shell width (mas) and
the shell angular
diameter (mas), w the shell width (mas) and
![]() the
relative brightness (Fig. 3). Last column
tabulates the reduced
the
relative brightness (Fig. 3). Last column
tabulates the reduced ![]() .
Only parameters with error bars
(lower scripts) have been fitted. Note that in the second line,
.
Only parameters with error bars
(lower scripts) have been fitted. Note that in the second line,
![]() ,
,
![]() ,
w and
,
w and
![]() ,
are
set to the values found for Polaris (see Table 2).
,
are
set to the values found for Polaris (see Table 2).
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{4466fig4.eps}
\end{figure}](/articles/aa/full/2006/25/aa4466-05/Timg91.gif) |
Figure 4:
All |
| Open with DEXTER | |
Owing of the incompleteness of the ![]() Cep data set, compared to
Polaris, we must use a simpler model, especially concerning the size
of the CSE. As a first approximation, we choose to adopt the Polaris
model, scaled to the appropriate angular diameter. Compared to
parameter values given in Table 2, only
Cep data set, compared to
Polaris, we must use a simpler model, especially concerning the size
of the CSE. As a first approximation, we choose to adopt the Polaris
model, scaled to the appropriate angular diameter. Compared to
parameter values given in Table 2, only
![]() is
adjusted, while
is
adjusted, while
![]() is fixed to the value found
for Polaris. In parallel, we will fit the angular diameter using a the
CLD model adopted in Mérand et al. (2005b). The important result will lie
in the difference between the two stellar angular diameter estimates.
is fixed to the value found
for Polaris. In parallel, we will fit the angular diameter using a the
CLD model adopted in Mérand et al. (2005b). The important result will lie
in the difference between the two stellar angular diameter estimates.
The results of the fit (Table 3), as well as the
visibility data points with respect to the pseudo baseline, are
presented in Fig. 4. The revised diameter, using the CSE
model, is
![]() (
(
![]() )
to be compared to
)
to be compared to
![]() (
(
![]() )
with no CSE. The quantity of interest
is the diameter bias
)
with no CSE. The quantity of interest
is the diameter bias ![]() :
:
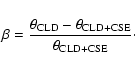 |
(5) |
It is interesting to note that the Polaris model fits exactly the
![]() Cep data without any modifications, except for the angular
scale.
Cep data without any modifications, except for the angular
scale.
Two different aspects of the ![]() Cep CSE can now to be studied:
its possible asymmetry and possible relative brightness
change during the pulsation phase. The first aspect requires a study
at different baseline projection angles of the visibility deficit at
Cep CSE can now to be studied:
its possible asymmetry and possible relative brightness
change during the pulsation phase. The first aspect requires a study
at different baseline projection angles of the visibility deficit at
![]() ,
whereas the second requires a good phase
coverage. Our data set contains data at
,
whereas the second requires a good phase
coverage. Our data set contains data at
![]() with a
baseline projection angle range of ninety degrees and with
excellent phase coverage (considering our data were acquired at five
different epochs).
with a
baseline projection angle range of ninety degrees and with
excellent phase coverage (considering our data were acquired at five
different epochs).
In order to estimate the possible asymmetry or variability, we should
consider the deficit between the measured visibility and that expected
from the limb darkened model:
![]() at
at
![]() (lower left sub-plot in
Fig. 4). This deficit is plotted with respect to the
baseline projection angle and pulsation phase in
Fig. 5. At our level of precision, the CSE seems to be
symmetric and stable through the pulsation. A more elaborate model is
thus not justified.
(lower left sub-plot in
Fig. 4). This deficit is plotted with respect to the
baseline projection angle and pulsation phase in
Fig. 5. At our level of precision, the CSE seems to be
symmetric and stable through the pulsation. A more elaborate model is
thus not justified.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{4466fig5.eps}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{4466fig6.eps}
\end{figure}](/articles/aa/full/2006/25/aa4466-05/Timg100.gif) |
Figure 5:
|
| Open with DEXTER | |
A similar examination of the Polaris measurements leads to the same conclusion - the Polaris CSE appears symmetric and constant in time.
Interferometric angular diameter measurements are always model dependent. In the case of stars without shells, it is necessary to correct for the CLD. In the case of single baseline observations of Cepheids, if a shell has to be taken into account the correction is no longer straightforward and depends on what baseline is used.
To understand this, we should evaluate the multiplicative bias
introduced when measuring an angular diameter using a single baseline
and not allowing for the presence of the CSE. This approach
differs from the previous section, where we considered the whole
![]() Cep data set. Most Cepheid studies have not benefited from a
similarly extensive coverage of spatial frequencies:
e.g. Kervella et al. (2004a) or Mérand et al. (2005b). In these latter
cases, in order to optimize the use of observing time, interferometric
observations were recorded over a very restricted range of baselines.
Cep data set. Most Cepheid studies have not benefited from a
similarly extensive coverage of spatial frequencies:
e.g. Kervella et al. (2004a) or Mérand et al. (2005b). In these latter
cases, in order to optimize the use of observing time, interferometric
observations were recorded over a very restricted range of baselines.
Let us call
![]() the squared visibility of the star without
the shell when observed at the baseline b, and
the squared visibility of the star without
the shell when observed at the baseline b, and
![]() for the star with the CSE, at the same baseline. Then, the bias
for the star with the CSE, at the same baseline. Then, the bias ![]() in diameter is, at the first approximation:
in diameter is, at the first approximation:
| |
= | (6) | |
| = | 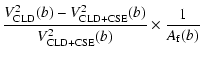 |
(7) |
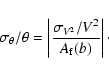 |
(8) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4466fig7.eps}
\end{figure}](/articles/aa/full/2006/25/aa4466-05/Timg115.gif) |
Figure 6:
Bias introduced when determining a Cepheid angular
diameter using a single V2 measurement at a given baseline and
not taking into account the presence of the CSE, as a function of
projected baseline (solid line). The dashed line is the
formal error when deriving the angular diameter from a single
V2 measurement, assuming a 3% error on that measurement. The
angular size chosen for this example is the average
angular size of |
| Open with DEXTER | |
Figure 6 shows ![]() for the
for the ![]() Cep CSE parameters
reported in Table 3. Our Baade-Wesselink
observations used angular diameters determined at baselines ranging
from 235 to 313 m (Mérand et al. 2005b). At such baselines, it appears
that the bias is at most of the order of -1%, whereas the diameter
formal error is slightly larger. One should notice this is not the
case at the shortest baselines, where the bias exceeds the formal
error.
Cep CSE parameters
reported in Table 3. Our Baade-Wesselink
observations used angular diameters determined at baselines ranging
from 235 to 313 m (Mérand et al. 2005b). At such baselines, it appears
that the bias is at most of the order of -1%, whereas the diameter
formal error is slightly larger. One should notice this is not the
case at the shortest baselines, where the bias exceeds the formal
error.
It is important to take into account this bias when applying the BW
pulsation parallax method. Indeed, any multiplicative bias in angular
diameter will lead to a multiplicative bias in distance, by the same
amount. The pulsation parallax equation is (Mérand et al. 2005b):
In the case of ![]() Cep, the angular diameter was at most
overestimated by a factor 1.01. Since the star appears larger than it
actually is, our formal distance would have been under-estimated. In
the case of our previous study, d has been fixed to the estimation
of Benedict et al. (2002),
Cep, the angular diameter was at most
overestimated by a factor 1.01. Since the star appears larger than it
actually is, our formal distance would have been under-estimated. In
the case of our previous study, d has been fixed to the estimation
of Benedict et al. (2002),
![]() .
We evaluated p,
the projection factor, instead (Eq. (9)). Our value
.
We evaluated p,
the projection factor, instead (Eq. (9)). Our value
![]() ,
should at most be revised to the lower value
of
,
should at most be revised to the lower value
of
![]() .
.
In future high precision interferometric BW observations, it will be necessary to determine and allow for the CSE bias. The best choice, in terms of spatial resolution, will be to observe in the first visibility lobe near the first minimum, in order to maximize the amplification factor. These observations will lead to the best formal angular diameter precision and the lowest bias due to the shell.
This conclusion relies on what we think the CSE looks like in the near-infrared K band. However, it seems likely that the CSE effects on the interferometric angular diameter estimation are less important at shorter wavelengths.
After ![]() Car, we report the interferometric detection in the near
infrared of circumstellar emission around two additional Cepheids:
Polaris and
Car, we report the interferometric detection in the near
infrared of circumstellar emission around two additional Cepheids:
Polaris and ![]() Cep. Polaris was studied in detail and we were
able to apply a simple CSE model consisting in a star limb
darkened according to hydrostatic models, surrounded by a dim
(
Cep. Polaris was studied in detail and we were
able to apply a simple CSE model consisting in a star limb
darkened according to hydrostatic models, surrounded by a dim
(![]() % of the stellar flux),
% of the stellar flux), ![]() stellar diameters CSE. This model also explains the deficit in the visibility profile
detected for
stellar diameters CSE. This model also explains the deficit in the visibility profile
detected for ![]() Cep. The three Cepheids have quite different
characteristics: Polaris has a small amplitude and a short period;
Cep. The three Cepheids have quite different
characteristics: Polaris has a small amplitude and a short period;
![]() Cep has a large amplitude, short period whereas
Cep has a large amplitude, short period whereas ![]() Car
has a large amplitude and long period. The (limited) measurements are
consistent with similar circumstellar emission geometries in the three
cases studied.
Car
has a large amplitude and long period. The (limited) measurements are
consistent with similar circumstellar emission geometries in the three
cases studied.
We computed the bias due to the presence of the CSE in the
Baade-Wesselink method framework. The bias, in terms of distance, is
smallest when the largest first-lobe baselines are used
(
![]() ), and is at most 1%, under the current
error contribution of interferometric measurements
(Mérand et al. 2005b).
), and is at most 1%, under the current
error contribution of interferometric measurements
(Mérand et al. 2005b).
The presence of CSEs, with similar characteristics, around all
Cepheids for which sufficient interferometric data are available,
raises the possibility that this is a widespread phenomenon. Possible
mass loss from Cepheids has been reviewed by Szabados (2003):
slight infrared excesses have been detected for almost all Cepheids
observed by IRAS, independently of the pulsating period. These
observational constraints lead to a mass loss rate of the order of 10-10 to 10-8 ![]() yr-1.
yr-1.
Mass loss is expected for Cepheids. This is a consequence of the
theoretical Cepheid mass deficit. The deficit is the ratio between two
different mass estimates: the evolutionary mass and the pulsational
mass. The first, ![]() ,
is derived from the Mass-Luminosity (M-L)
relation computed from evolutionary numerical codes; the second,
,
is derived from the Mass-Luminosity (M-L)
relation computed from evolutionary numerical codes; the second,
![]() ,
is derived using the Period-Mass-Radius relation (P-M-R),
computed from non-linear pulsation numerical codes. The ratio
,
is derived using the Period-Mass-Radius relation (P-M-R),
computed from non-linear pulsation numerical codes. The ratio
![]() is known to be smaller than unity. Even if the problem has
been known for a long time and partially solved by refinements in
numerical codes (Cox 1980), recent numerical investigations led
to
is known to be smaller than unity. Even if the problem has
been known for a long time and partially solved by refinements in
numerical codes (Cox 1980), recent numerical investigations led
to
![]() for galactic Cepheids
(Bono et al. 2001). According to these authors, this discrepancy between
for galactic Cepheids
(Bono et al. 2001). According to these authors, this discrepancy between ![]() and
and ![]() might be explained by the fact that evolutionary codes
do not take into account mass loss in the He-burning phase (post main
sequence). The phase lasts 25 My For a 5
might be explained by the fact that evolutionary codes
do not take into account mass loss in the He-burning phase (post main
sequence). The phase lasts 25 My For a 5 ![]() Cepheid and
2.5 My for a 11
Cepheid and
2.5 My for a 11 ![]() ,
assuming a 10% mass loss, a rough
calculation leads to mass loss rates of the order of what is deduced
from IRAS measurements.
,
assuming a 10% mass loss, a rough
calculation leads to mass loss rates of the order of what is deduced
from IRAS measurements.
The direct detection of CSEs around Cepheids at distances of only a
few stellar radii is a confirmation that these stars are experiencing
substantial mass loss. The three Cepheids are significantly different
one from another: we have three different periods (![]() 4,
4, ![]() 5.4and
5.4and ![]() 35 days), thus different masses; different pulsation
amplitude (<
35 days), thus different masses; different pulsation
amplitude (<![]() for Polaris and
for Polaris and ![]()
![]() for
for ![]() Car and
Car and ![]() Cep). This phenomenon cannot be neglected in future Cepheid
studies, presumably having implications for evolutionary and
pulsational codes, or while determining distances using the BW method.
Cep). This phenomenon cannot be neglected in future Cepheid
studies, presumably having implications for evolutionary and
pulsational codes, or while determining distances using the BW method.
Acknowledgements
The authors would like to thank all the CHARA Array and Mount Wilson Observatory day-time and night-time staff for their support during the installation of the FLUOR beam combiner and during the observations presented in this work. The CHARA Array was constructed with funding from Georgia State University, the National Science Foundation, the W. M. Keck Foundation, and the David and Lucile Packard Foundation. The CHARA Array is operated by Georgia State University with support from the College of Arts and Sciences, from the Research Program Enhancement Fund administered by the Vice President for Research, and from the National Science Foundation under NSF Grant AST 0307562.