A&A 451, 821-833 (2006)
DOI: 10.1051/0004-6361:20054085
M. Nardini1,2 - G. Ghisellini1 - G. Ghirlanda1 - F. Tavecchio1 - C. Firmani1,3 - D. Lazzati4
1 - Osservatorio Astronomico di Brera, via Bianchi 46, 23807 Merate, Italy
2 -
Univ. di Milano-Bicocca, P.za della Scienza 3, 20126 Milano, Italy
3 -
Instituto de Astronomía, UNAM, AP 70-264, 04510 México, DF, México
4 -
JILA, University of Colorado, Boulder, CO 80309-0440, USA
Received 22 August 2005 / Accepted 16 January 2006
Abstract
We studied the optical afterglows of the 24 pre-SWIFT gamma-ray bursts (GRBs) with both known spectroscopic redshift and published estimates of the optical extinction in the source frame.
We found an unexpected clustering of the optical-afterglow luminosities
measured 12 h (source frame time) after the trigger.
For 21 out of 24 bursts, the distribution of the optical luminosities is narrower than
the distribution of the X-ray luminosities, and even narrower than
the distribution of the ratio between the monochromatic optical luminosities
and the total isotropic, emitted prompt energy.
Three bursts stand out from the distribution of the other
sources, being underluminous by a factor ![]() 15.
We compare this result with another somewhat analogous result concerning
the luminosity of the X-ray afterglows studied earlier.
We constructed the optical to X-ray spectral energy
distribution for all our GRBs.
For all but a minority of them, the optical and the X-ray emissions
are consistent with being produced by the same radiation process.
We discuss our results in the framework of the "standard''
external-shock synchrotron model. Finally, we consider the behavior of the first GRBs of known
redshifts detected by SWIFT.
We find that these SWIFT GRBs entirely confirm our findings.
15.
We compare this result with another somewhat analogous result concerning
the luminosity of the X-ray afterglows studied earlier.
We constructed the optical to X-ray spectral energy
distribution for all our GRBs.
For all but a minority of them, the optical and the X-ray emissions
are consistent with being produced by the same radiation process.
We discuss our results in the framework of the "standard''
external-shock synchrotron model. Finally, we consider the behavior of the first GRBs of known
redshifts detected by SWIFT.
We find that these SWIFT GRBs entirely confirm our findings.
Key words: gamma rays: bursts - radiation mechanisms: non-thermal - X-rays: general
The commonest approach to comparing directly the afterglow emission
of different bursts is to compute the light curves in the observer's
reference frame, in terms of their fluxes vs. the
observed time
![]() .
However, when the redshift is known, a more fruitful approach
is to compare the light curves of the luminosities
of different bursts, using the rest-frame time
.
However, when the redshift is known, a more fruitful approach
is to compare the light curves of the luminosities
of different bursts, using the rest-frame time
![]() .
Although such attempts have already been done
(see, e.g. Gendre & Boër 2005, hereafter GB05; Kumar & Piran 2000),
they mainly concerned the X-ray luminosities of relatively small
samples of GRBs, and not the optical luminosities (but see Berger et al. 2005, for a study of the first SWIFT bursts). From these earlier studies (see also Piran et al. 2000) it appeared
that the X-ray afterglow luminosities (calculated at the same
time in the rest frame) were characterized by a smaller dispersion
than the dispersion of the total energies radiated during the
prompt emission (but see Berger et al. 2003, for a different conclusion).
In addition, Boër & Gendre (2000) and GB05 found that the
X-ray afterglow luminosities showed a tendency to cluster
in two groups (different by a factor
.
Although such attempts have already been done
(see, e.g. Gendre & Boër 2005, hereafter GB05; Kumar & Piran 2000),
they mainly concerned the X-ray luminosities of relatively small
samples of GRBs, and not the optical luminosities (but see Berger et al. 2005, for a study of the first SWIFT bursts). From these earlier studies (see also Piran et al. 2000) it appeared
that the X-ray afterglow luminosities (calculated at the same
time in the rest frame) were characterized by a smaller dispersion
than the dispersion of the total energies radiated during the
prompt emission (but see Berger et al. 2003, for a different conclusion).
In addition, Boër & Gendre (2000) and GB05 found that the
X-ray afterglow luminosities showed a tendency to cluster
in two groups (different by a factor ![]() 30 in luminosity)
with a small dispersion within each group.
These authors also tried to draw conclusions from the
optical luminosity, but were not successful because the absorption
was largely unknown at that time, and because of too small a sample.
30 in luminosity)
with a small dispersion within each group.
These authors also tried to draw conclusions from the
optical luminosity, but were not successful because the absorption
was largely unknown at that time, and because of too small a sample.
These earlier results prompted us to study the behavior
of the optical afterglow luminosities. One of the main initial motivations of our study was the possibility that what seems to be a "dichotomy'' in the X-ray afterglow luminosity
could also be present in the optical, therefore helping to understand
the problem of the so-called "dark'' bursts, those with a detected
X-ray afterglow but no optical detection. De Pasquale et al. (2003), when comparing
GRBs (all with detected X-ray afterglow) with and without optical
detection, found that "dark'' GRBs tend to be fainter in the X-ray,
by a factor ![]() 5 in flux at the same observed time.
We, however, expect a greater dispersion of the optical luminosity
(at a given rest-frame time) than the corresponding
dispersion of the X-ray luminosities. This is because electrons emitting X-rays by the synchrotron process probably cool on a dynamical timescale (also several hours after trigger),
and this implies (in the standard synchrotron fireball model)
that the emitted X-ray emission is insensitive to the density of the
external medium producing the external shocks.
On the contrary, it is likely that electrons emitting in the optical
do not cool in a dynamical timescale (about a day after the prompt phase),
so the optical emission does depend on the density of
the circumburst material. If the dispersion introduced by this effect is not too large,
some sort of "dichotomy'' could survive and then flag
the existence of two families of GBRs with two different
average afterglow luminosities. Dark GRBs could then be thought to belong to the underluminous family, therefore be more difficult to detect.
This is all the more so in the optical,
if some extinction in the host galaxy is present.
5 in flux at the same observed time.
We, however, expect a greater dispersion of the optical luminosity
(at a given rest-frame time) than the corresponding
dispersion of the X-ray luminosities. This is because electrons emitting X-rays by the synchrotron process probably cool on a dynamical timescale (also several hours after trigger),
and this implies (in the standard synchrotron fireball model)
that the emitted X-ray emission is insensitive to the density of the
external medium producing the external shocks.
On the contrary, it is likely that electrons emitting in the optical
do not cool in a dynamical timescale (about a day after the prompt phase),
so the optical emission does depend on the density of
the circumburst material. If the dispersion introduced by this effect is not too large,
some sort of "dichotomy'' could survive and then flag
the existence of two families of GBRs with two different
average afterglow luminosities. Dark GRBs could then be thought to belong to the underluminous family, therefore be more difficult to detect.
This is all the more so in the optical,
if some extinction in the host galaxy is present.
The results presented in the following are instead quite puzzling, since - contrary to the simple expectations mentioned above - the optical afterglow luminosities show a degree of clustering that is tighter than the one shown by the X-ray afterglow luminosities. We indeed find an indication (albeit still weak, due to small statistics) of a dichotomy in the optical luminosity distributions. But, more intriguingly, we find an unexpected optical luminosity clustering of the large majority of the bursts analyzed by us (21 out of 24). In order to understand it, we have constructed, for all GRBs of our sample, the optical to X-rays spectral energy distribution (SED) at a given time, assembling information contained in the optical multiband photometry and in the X-ray continuum flux and spectrum. This allows to see if both the optical and the X-ray fluxes are consistent with being produced by a single electron population by the synchrotron process, or if there is some indication of X-ray fluxes being produced by an additional component (i.e. a possibly emergent inverse Compton flux in the X-ray band), and therefore responsible for the larger dispersion of X-ray luminosities with respect to the optical ones. As we will show, this is not the case for most of the sources.
We also consider in Sect. 5 the bursts detected by SWIFT and for which the redshift is known. All of them but GRB 050401, GRB 050525, and GRB 050730 lack information about the optical absorption in their hosts. With this caveat, we calculate their optical luminosities and find that they are consistent with the clustering properties of the other bursts. Instead, we find that, on average, they are more powerful in X-rays with respect to the pre-SWIFT bursts so they broaden the X-ray luminosity distribution. We finally discuss these results in the framework of the standard fireball external shocks synchrotron scenario, and the possible implications for dark bursts.
Throughout this paper, we adopt a cosmology with
![]() and
and
![]() .
.
Table 1:
Optical properties of GRBs in our sample. References are given for
![]() ,
,
![]() ,
,
![]() and
and
![]() .
.
To compare the rest frame optical luminosities of different GRBs, we applied all the relevant cosmological and extinction corrections to the GRB light curves.
In particular, one of our selection criteria is that the
absorption
![]() in the host galaxy is already known from the literature.
in the host galaxy is already known from the literature.
We collected from the literature all GRBs of known spectroscopic
redshift z, detected optical afterglow, known optical spectral
index, and known optical
extinction in the host rest frame
![]() .
The total number of GRBs with measured redshifts is more than 50
(as of July 31st, 2005) and 24 of those fulfilling our selection criteria.
They are listed in Table 1.
This list includes 13 out of the 17 GRBs present in the list of GB05.
The 4 missing GRBs are: GRB 970228 (for which there is no
estimate of
.
The total number of GRBs with measured redshifts is more than 50
(as of July 31st, 2005) and 24 of those fulfilling our selection criteria.
They are listed in Table 1.
This list includes 13 out of the 17 GRBs present in the list of GB05.
The 4 missing GRBs are: GRB 970228 (for which there is no
estimate of
![]() ), GRB 000210 and GRB 000214 (with no
detected optical afterglow), and GRB 980425 (an anomalous GRB associated
with the 1998bw supernova).
), GRB 000210 and GRB 000214 (with no
detected optical afterglow), and GRB 980425 (an anomalous GRB associated
with the 1998bw supernova).
In Table 1 we report, for every GRB in our sample, the
redshift, the optical spectral index
![]() ,
the Galactic absorption
,
the Galactic absorption
![]() (taken from Schlegel 1998 maps except for GRB 011121 for which we also report
the values quoted in the corresponding references),
the host rest frame absorption
(taken from Schlegel 1998 maps except for GRB 011121 for which we also report
the values quoted in the corresponding references),
the host rest frame absorption
![]() ,
the absorption
,
the absorption
![]() at the rest-frame frequency
at the rest-frame frequency
![]() ,
the extinction and k-corrected monochromatic luminosity
,
the extinction and k-corrected monochromatic luminosity ![]() (at the source frame frequency corresponding to the R band) and the references of the optical spectral
index and extinction value.
(at the source frame frequency corresponding to the R band) and the references of the optical spectral
index and extinction value.
Figure 1 shows the behavior of the observed
R-band fluxes as a function of the observed time
![]() for
all bursts listed in Table 1.
In this figure the fluxes are corrected for the Galactic extinction only.
In Fig. 2 we show the distribution of the observed fluxes
at the same observed time (12 h after trigger).
Fitting the distribution of the observed optical fluxes
with a Gaussian gives a (logarithmic) dispersion of
for
all bursts listed in Table 1.
In this figure the fluxes are corrected for the Galactic extinction only.
In Fig. 2 we show the distribution of the observed fluxes
at the same observed time (12 h after trigger).
Fitting the distribution of the observed optical fluxes
with a Gaussian gives a (logarithmic) dispersion of
![]() (see Table 2).
Note that the Gaussian fit is poor, and the real distribution could have
an even larger dispersion.
(see Table 2).
Note that the Gaussian fit is poor, and the real distribution could have
an even larger dispersion.
The monochromatic optical luminosities can be calculated from
the observed monochromatic flux ![]() by applying the
cosmological spectral and time corrections, as
by applying the
cosmological spectral and time corrections, as
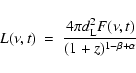 |
(1) |
All luminosities are given at the same rest-frame time after trigger,
which we chose to be 12 h. This choice satisfies the following requirements:
i) the data sampling is maximized;
ii) for the large majority of bursts, the jet break has not yet occurred;
iii) it allows an easy comparison with the X-ray luminosities
calculated by GB05, calculated at the same time.
For densely sampled optical light curves, we have directly taken the flux measured at
![]() h. When this flux was not available, we
interpolated between data before and after this time.
There are 2 cases (GRB 020813 and GRB 030329) in which a break in the light curve
(very likely a jet break) occurs before 12 h. In these cases we
have extrapolated the flux from data before the break time.
h. When this flux was not available, we
interpolated between data before and after this time.
There are 2 cases (GRB 020813 and GRB 030329) in which a break in the light curve
(very likely a jet break) occurs before 12 h. In these cases we
have extrapolated the flux from data before the break time.
The observed flux
![]() was corrected for both galactic
and rest-frame extinction. We calculated the
was corrected for both galactic
and rest-frame extinction. We calculated the ![]() values
for the extinction in the burst's host galaxies by assuming the
extinction curve of the Milky Way (Pei 1992), evaluated at the
wavelength
values
for the extinction in the burst's host galaxies by assuming the
extinction curve of the Milky Way (Pei 1992), evaluated at the
wavelength
![]() Å (unless specifically stated
otherwise in the original reference).
There are cases in which different authors find slightly different
values for
Å (unless specifically stated
otherwise in the original reference).
There are cases in which different authors find slightly different
values for
![]() and for
and for
![]() ,
i.e. the dereddened
value of the optical spectral index.
There is some degeneracy between these two quantities
when the available data are poorly sampled and affected by relatively
large uncertainties. In the large majority of cases, the method used to find the
intrinsic extinction is to assume that the spectrum is a power law,
and the fit returns the best values of the spectral index and
,
i.e. the dereddened
value of the optical spectral index.
There is some degeneracy between these two quantities
when the available data are poorly sampled and affected by relatively
large uncertainties. In the large majority of cases, the method used to find the
intrinsic extinction is to assume that the spectrum is a power law,
and the fit returns the best values of the spectral index and
![]() .
The two quantities are, however, somewhat correlated, since increasing
.
The two quantities are, however, somewhat correlated, since increasing
![]() gives a flatter
gives a flatter ![]() .
In addition, different results can be obtained by using different
extinction curves. Therefore, for completeness, we list the different
values of
.
In addition, different results can be obtained by using different
extinction curves. Therefore, for completeness, we list the different
values of
![]() and
and
![]() found by different authors
in Table 1, and the corresponding value of the optical luminosity.
The first line of every multiple entry in Table 1
corresponds to what we used for the histograms for Fig. 4
and for the following analysis.
However, one can see that the different values of the extinction and
spectral indices do not change the derived luminosities by a large amount.
Indeed, the width of the optical luminosity distribution is not affected by
these uncertainties.
found by different authors
in Table 1, and the corresponding value of the optical luminosity.
The first line of every multiple entry in Table 1
corresponds to what we used for the histograms for Fig. 4
and for the following analysis.
However, one can see that the different values of the extinction and
spectral indices do not change the derived luminosities by a large amount.
Indeed, the width of the optical luminosity distribution is not affected by
these uncertainties.
Figure 3 shows the distribution of the extinction values
![]() in the host.
Despite nearly half of the bursts have zero or
almost-zero host absorption, the extinction correction is crucial to obtain
the strong clustering of the optical luminosities shown in
Fig. 5. Without this correction, the optical luminosity distribution has a width
of
in the host.
Despite nearly half of the bursts have zero or
almost-zero host absorption, the extinction correction is crucial to obtain
the strong clustering of the optical luminosities shown in
Fig. 5. Without this correction, the optical luminosity distribution has a width
of
![]() (see Table 2).
This is partly due to those GRBs at high redshift for which even a moderate
value of
(see Table 2).
This is partly due to those GRBs at high redshift for which even a moderate
value of
![]() implies a relatively large absorption at the
rest-frame frequency
implies a relatively large absorption at the
rest-frame frequency
![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4085fig1.ps}\end{figure}](/articles/aa/full/2006/21/aa4085-05/Timg50.gif) |
Figure 1: Light curves in terms of observed fluxes versus observed time since the burst trigger for the 24 GRBs reported in Table 1. Fluxes have been corrected only for the galactic extinction. The references for all the plotted data are given in the appendix. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{4085fig2.ps}\end{figure}](/articles/aa/full/2006/21/aa4085-05/Timg51.gif) |
Figure 2:
Histogram of the observed fluxes (in mJy) in the R-band (Cousin system)
12 h after the trigger (observer frame - from Fig. 1). All
fluxes have been corrected for the foreground galactic extinction
only. Superimposed to the histogram is a Gaussian fit to the data
with mean value |
| Open with DEXTER | |
In Fig. 4 we show the light curves in terms of the optical
luminosities in the R-band as a function of the rest-frame time.
As can be seen, there is a clear clustering of the light curves
when corrected for the cosmological and extinction effects with respect
to the light curves shown in Fig. 1.
Most of the luminosities at 12 h (since trigger) clusters
around
![]() 30.65 (see Fig. 5).
This is the main result of our paper.
There are three exceptions, i.e. GRB 980613, GRB 011121, and GRB 021211,
which stand out from the bulk of the other bursts by being underluminous by
a factor
30.65 (see Fig. 5).
This is the main result of our paper.
There are three exceptions, i.e. GRB 980613, GRB 011121, and GRB 021211,
which stand out from the bulk of the other bursts by being underluminous by
a factor ![]() 15 with respect to the other GRBs.
15 with respect to the other GRBs.
Table 2: Distribution width of different quantities, according to a Gaussian fit.
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{4085fig3.ps}\end{figure}](/articles/aa/full/2006/21/aa4085-05/Timg61.gif) |
Figure 3:
Histogram of the host absorption values
|
| Open with DEXTER | |
Some of the light curves shown in Fig. 4 appear peculiar, in particular:
Boër & Gendre (2000) have analyzed the behavior of the optical afterglow of the bursts studied in their paper (8 in total), without applying the dereddening of the extinction of the host (at that time largely unavailable). They did not find any clustering, nor a dichotomy, although (even without correcting for the absorption of the host), they noted that the distribution of the intrinsic optical luminosities was narrower than the distribution of the observed fluxes. The choice of 12 h rest frame is not critical for our results, as can be seen in Fig. 4, as long as the chosen time is less than the jet break time for most bursts.
![\begin{figure}
\par\includegraphics[width=16.35cm,clip]{4085fig4.ps}\end{figure}](/articles/aa/full/2006/21/aa4085-05/Timg65.gif) |
Figure 4:
Light curves of the optical luminosities as a function of the
rest-frame time. The three underluminous GRBs are labelled.
All data have been corrected for extinction (both Galactic and host).
The references for the observed magnitudes can be found in the
appendix. The references for the values of the spectral index |
| Open with DEXTER | |
Our result is surprising in many respects, as mentioned in the
introduction. We can compare this narrow clustering of the optical luminosity with
the distribution of the prompt-emission isotropic energy
![]() for the same bursts (see Table 4). The
for the same bursts (see Table 4). The
![]() distribution (if fitted with a Gaussian)
has a much larger dispersion of
distribution (if fitted with a Gaussian)
has a much larger dispersion of
![]() (see Table 2).
Another unexpected result concerns the distribution of the ratio
of
(see Table 2).
Another unexpected result concerns the distribution of the ratio
of
![]() .
Since we expect that the afterglow luminosity depends upon the isotropic kinetic energy of the fireball,
which should be measured by
.
Since we expect that the afterglow luminosity depends upon the isotropic kinetic energy of the fireball,
which should be measured by
![]() ,
we naively expect this distribution to have a smaller dispersion than either the
,
we naively expect this distribution to have a smaller dispersion than either the
![]() or the
or the
![]() distribution. Instead, the
distribution. Instead, the
![]() distribution has a dispersion
distribution has a dispersion
![]() ,
even larger than the
dispersion of
,
even larger than the
dispersion of
![]() .
.
The three underluminous bursts, (i.e. GRB 980613, 011121, 021211)
that seem to form a separate "family'' are more than 4![]() dimmer than the majority of bursts.
For GRB 011121 and GRB 021211 the two parameters
dimmer than the majority of bursts.
For GRB 011121 and GRB 021211 the two parameters
![]() and
and
![]() have possible different estimates (see Table 1). Here we adopted the values reported in the first line of Table 1. However, if we consider the other possible choices, the implied
have possible different estimates (see Table 1). Here we adopted the values reported in the first line of Table 1. However, if we consider the other possible choices, the implied
![]() would be even smaller, making these two bursts even more
inconsistent (more than 4.5
would be even smaller, making these two bursts even more
inconsistent (more than 4.5![]() )
with the distribution of the bulk of the other GRBs.
Instead, concerning the GRBs with different estimates of
)
with the distribution of the bulk of the other GRBs.
Instead, concerning the GRBs with different estimates of
![]() and
and
![]() that fall in the more populated group, using the other choices
would shift their luminosities by less than one
that fall in the more populated group, using the other choices
would shift their luminosities by less than one ![]() (except for GRB 980703, for which the shift would be 1.7
(except for GRB 980703, for which the shift would be 1.7![]() ).
).
The three underluminous bursts do not seem to have any distinguishing property other than their smaller optical luminosities: all three have "normal'' optical decays, spectral indices and extinction values. However, 2 of these GRBs lie on the faint portion of the X-ray luminosity distribution, see Fig. 6 (for the third there is no X-ray detected afterglow). On the other hand, the faint end of the X-ray luminosity distribution also contains bursts that belong to the "bright'' optical family (i.e. GRB 011211 and GRB 030326). GRB 000210 and GRB 000214, lying at the faint extreme of the X-ray luminosity distribution, are dark bursts.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{4085fig5.ps}\end{figure}](/articles/aa/full/2006/21/aa4085-05/Timg70.gif) |
Figure 5:
Histogram of the monochromatic optical luminosities 12 h
(rest frame) after the trigger for the 24 GRBs reported in
Table 1 and shown in Fig. 4.
Data have been dereddened both for Galactic and host extinction.
The solid red line represents the Gaussian fit to the data
with mean value |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{4085fig6.ps}\end{figure}](/articles/aa/full/2006/21/aa4085-05/Timg71.gif) |
Figure 6: Histogram of the X-ray luminosities 12 h (rest frame) after the trigger, calculated in the rest frame band [4-20 keV]. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4085fig7.ps}\end{figure}](/articles/aa/full/2006/21/aa4085-05/Timg72.gif) |
Figure 7:
X-ray monochromatic [2 keV, rest frame] luminosity
as a function of the optical monochromatic
[R band, rest frame] luminosity at 12 h after trigger.
The dashed lines correspond to different broad-band spectral
indices
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{4085fig8.ps}\end{figure}](/articles/aa/full/2006/21/aa4085-05/Timg74.gif) |
Figure 8:
Optical monochromatic luminosity ( top panel)
and X-ray [4-20 keV] luminosities ( mid panel)
at 12 h after trigger (rest frame time)
as a function of the isotropic emitted energy during the
prompt phase (integrated between 1 keV and 10 MeV, see Ghirlanda et al. 2004).
Circles correspond to bursts having both optical and X-ray data.
Triangles are GRBs with optical but no X-ray data.
Stars are the two GRBs (as labelled) with X-rays but no
optical data. We also show GRB 970228, for which there is no information on
the amount of extinction in the host (square).
The dashed line is the linear regression fit
(
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4085fig9.ps}\end{figure}](/articles/aa/full/2006/21/aa4085-05/Timg75.gif) |
Figure 9:
For those bursts of measured
|
| Open with DEXTER | |
Table 3:
X-ray properties of the GRBs with known redshift and
data collected from the literature. ![]() and
and
![]() are the temporal and spectral
power law indices, respectively [i.e.
are the temporal and spectral
power law indices, respectively [i.e.
![]() ].
].
![]() is the observed X-ray flux integrated in the reported energy band and
is the observed X-ray flux integrated in the reported energy band and
![]() is the monochromatic X-ray luminosity at 12 h (rest frame) calculated at 10 keV.
is the monochromatic X-ray luminosity at 12 h (rest frame) calculated at 10 keV.
When studying the X-ray afterglow light curves, GB05 found that the
distribution of the rest frame [4-20] keV![]() X-ray luminosities is bimodal, clustering around two values.
We expanded the original list of GB05 by including
of three more GRBs: GRB 020405, GRB 020813, GRB 021004.
We also slightly modified some of the data presented in
their original table, as new information is now available for some of
the bursts. For this reason we have collected the
information about the X-ray data in Table 3, with the
appropriate references. We find a more continuous distribution than do GB05,
as can be seen in Fig. 6, without
clear clustering or a clear separation in two GRB "families''.
X-ray luminosities is bimodal, clustering around two values.
We expanded the original list of GB05 by including
of three more GRBs: GRB 020405, GRB 020813, GRB 021004.
We also slightly modified some of the data presented in
their original table, as new information is now available for some of
the bursts. For this reason we have collected the
information about the X-ray data in Table 3, with the
appropriate references. We find a more continuous distribution than do GB05,
as can be seen in Fig. 6, without
clear clustering or a clear separation in two GRB "families''.
Figure 6 shows that the distribution of X-ray luminosities
is wider than the distribution of the optical luminosities.
A Gaussian fit (although poor) gives a dispersion
![]() (see Table 2).
Figure 7 shows the monochromatic [2 keV, rest frame]
X-ray luminosity as a function of the optical monochromatic
luminosity [R-band] 12 h after trigger, in the rest frame.
Dashed diagonal lines correspond to lines of constant broad band
spectral indices
(see Table 2).
Figure 7 shows the monochromatic [2 keV, rest frame]
X-ray luminosity as a function of the optical monochromatic
luminosity [R-band] 12 h after trigger, in the rest frame.
Dashed diagonal lines correspond to lines of constant broad band
spectral indices
![]() between the optical (R-band) and the
X-ray (2 keV), defined as
between the optical (R-band) and the
X-ray (2 keV), defined as
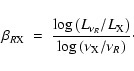 |
(2) |
Figure 8 shows both the optical and X-ray luminosities
as a function of
![]() ,
the isotropic energy emitted
during the prompt phase. There is no correlation in the case of the
optical luminosities (top panel), while there is some correlation in
the case of X-ray luminosities, albeit not very strong (chance
probability
,
the isotropic energy emitted
during the prompt phase. There is no correlation in the case of the
optical luminosities (top panel), while there is some correlation in
the case of X-ray luminosities, albeit not very strong (chance
probability ![]()
![]() 10-3). Both quantities (
10-3). Both quantities (![]() and
and
![]() ), being isotropic, depend on the aperture angle of the jet
), being isotropic, depend on the aperture angle of the jet
![]() .
For those GRBs for which we know
.
For those GRBs for which we know
![]() (13 objects), we can construct the collimation
corrected quantities by multiplying by
(13 objects), we can construct the collimation
corrected quantities by multiplying by
![]() .
After doing that, the correlation between the X-ray luminosity and
the
.
After doing that, the correlation between the X-ray luminosity and
the ![]() -ray energy disappears (bottom panel of Fig. 9).
-ray energy disappears (bottom panel of Fig. 9).
We would have expected the same effect in the case of
the optical luminosities; i.e. there should be an apparent correlation
when considering isotropic quantities, but there is not (upper panel
of Fig. 8).
Furthermore, the distribution of the collimation-corrected optical
luminosities becomes not narrower, but slightly broader than
the distribution of the isotropic luminosities,
as can be seen from the upper panel of Fig. 9, which
also shows that there is no correlation between the
collimation-corrected optical luminosities and prompt emitted
energies. We have also verified that
there is no correlation between the optical or the X-ray luminosity
and the spectral peak energy
![]() of the prompt emission.
of the prompt emission.
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{4085fig10.ps}\end{figure}](/articles/aa/full/2006/21/aa4085-05/Timg88.gif) |
Figure 10: Optical to X-ray spectral energy distribution for all GRBs in our sample. Data are simultaneous, at the rest-frame time labelled in each panel. Sources of data: GRB 970228: optical: Reichart (1999); X-rays: Costa et al. (1997). GRB 970508: Galama et al. (1998); Piro et al. (1998). GRB 971214: Wijers et al. (1999); Stratta et al. (2004). GRB 980613: Hjorth et al. (2002); Costa (1999). GRB 980703: Vreeswijk et al. (1999); De Pasquale et al. (2003). GRB 990123: Galama et al. (1999); Heise et al. (1999). GRB 990510: optical: Harrison et al. (1999); X-rays: Gendre & Boër (2005). GRB 991216: Halpern et al. (2000), Garnavich et al. (2000); Piro et al. (2000). GRB 000210: Piro et al. (2002). GRB 000214: Antonelli et al. (2000). GRB 000301c: Jensen et al. (2001). GRB 000418: Klose et al. (2000). GRB 000911: Masetti et al. (2005). GRB 000926: optical: Fynbo et al. (2001). X-rays: Gendre & Boër (2005). GRB 010222: optical: Masetti et al. (2001). X-rays: Gendre & Boër (2005). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{4085fig11.ps}\end{figure}](/articles/aa/full/2006/21/aa4085-05/Timg89.gif) |
Figure 11: Optical to X-ray spectral energy distribution for all GRBs in our sample. Data are simultaneous, at the rest-frame time labelled in each panel. Sources of data: GRB 010921: Price et al. (2002). GRB 011121: optical: Garnavich et al. (2003); X-rays: Gendre & Boër (2005). GRB 020124: Hjorth et al. (2003). GRB 020405: Masetti et al. (2003); Mirabal et al. (2003). GRB 020813: optical: Covino et al. (2003); X-rays: Butler et al. (2003). GRB 021004: optical: Pandey et al. (2003); X-rays: Butler et al. (2003). GRB 021211: Nysewander et al. (2005). GRB 030323: Vreeswijk et al. (2004). GRB 030226: optical: Pandey et al. (2004); X-rays: Gendre & Boër (2005). GRB 030329: optical: Bloom et al. (2004); Matheson et al. (2003); X-rays: Gendre & Boër (2005). GRB 030429: Jakobsson et al. (2004). |
| Open with DEXTER | |
Figures 10 and 11 show the optical to X-ray spectral energy distribution (SED) for all bursts in our sample. Data are plotted in the rest frame of the source, after being corrected for extinction. In constructing the SED we considered the optical multiband photometry at as consistent a time as possible with the X-ray observations, requiring the least possible extrapolation from data taken at other times. In some cases (i.e. GRB 030226 and GRB 030329), we plotted two SED for each burst corresponding to two different observing times or, in the case of GRB 010222, corresponding to two different choices of host-galaxy optical extinction. The captions of these figures report the original sources of data.
This figure shows that in a large fraction of cases the optical to X-ray data seem to be consistent with being produced by the same emission process. In a minority of cases (GRB 000926, possibly GRB 020405, and the earlier SED of GRB 030226), the optical spectrum is steeper than the X-ray spectrum, suggesting that they are produced by a different component. One obvious possibility is the inverse Compton process dominating the X-ray flux at the observing times. There is finally one case (GRB 020813) where the optical and the X-ray emission smoothly join, but the peak of the overall SED lies above the X-ray band. To summarize:
At the time of writing (November 2005), there are 18 long GRBs detected by SWIFT for which the redshift has been spectroscopically determined. We list them in Table 5, together with their redshifts, galactic extinction, and, when possible, the calculated optical luminosities (at 12 h rest frame). We also list the X-ray luminosities calculated in the (rest frame) 4-20 keV band, 12 h after trigger.
We alert the reader that for all these GRBs but GRB 050401, GRB 050525,
and GRB 050730 there is no information yet about
the optical extinction in the rest frame of the source.
Therefore the listed value of
![]() is not
corrected for extinction in the rest frame and it is k-corrected assuming
is not
corrected for extinction in the rest frame and it is k-corrected assuming
![]() ,
except for GRB 050401, for which we used
,
except for GRB 050401, for which we used
![]() and
and ![]() (Watson et al. 2005) GRB 050525,
for which we used the values given in Blustin et al. (2005).
For GRB 050730 Starling et al. (2005) give a measured value of
(Watson et al. 2005) GRB 050525,
for which we used the values given in Blustin et al. (2005).
For GRB 050730 Starling et al. (2005) give a measured value of ![]() .
The optical light curves of the 14 SWIFT bursts with redshift
are shown in Fig. 12,
superposed to the light curves (green or light grey symbols) of the other bursts.
For the remaining 4 SWIFT bursts with known redshift, we could not find
enough information in the literature to plot their light curve.
In Fig. 13 we show the histogram of the optical
luminosities after the addition of the 14 SWIFT bursts for which
we could calculate this quantity.
As can be seen, although the behavior of the light curve of
some of the SWIFT bursts is peculiar, their
.
The optical light curves of the 14 SWIFT bursts with redshift
are shown in Fig. 12,
superposed to the light curves (green or light grey symbols) of the other bursts.
For the remaining 4 SWIFT bursts with known redshift, we could not find
enough information in the literature to plot their light curve.
In Fig. 13 we show the histogram of the optical
luminosities after the addition of the 14 SWIFT bursts for which
we could calculate this quantity.
As can be seen, although the behavior of the light curve of
some of the SWIFT bursts is peculiar, their
![]() at 12 h is entirely consistent with the distribution
found previously.
at 12 h is entirely consistent with the distribution
found previously.
The X-ray luminosity distribution with the addition of these SWIFT bursts is shown in Fig. 14. The SWIFT bursts appear, on average, more luminous in X-rays
than the pre-SWIFT bursts. This is probably due to the fact that the average redshift of SWIFT bursts is somewhat higher than the average redshift of the other bursts.
(
![]()
![]() 1.3 for the bursts listed in Table 5
vs.
1.3 for the bursts listed in Table 5
vs.
![]()
![]() 0.9 for the bursts listed in Table 4.)
0.9 for the bursts listed in Table 4.)
We conclude that the indications coming from the first SWIFT bursts with known redshift strongly confirm the picture presented in this paper. Despite the difference in average redshift, and despite the broadening of the X-ray luminosity distribution, the clustering of the large majority of the optical luminosities is confirmed. In addition, the SWIFT bursts also confirm the existence of a dichotomy of the optical luminosity distribution, with the presence of an underluminous family.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4085fig12.eps}\end{figure}](/articles/aa/full/2006/21/aa4085-05/Timg97.gif) |
Figure 12:
Superposed light curves of the optical
luminosities in the rest frame of the 14 GRBs detected by SWIFT with
enough photometric data to the light curves already shown in Fig. 4 (grey dots).
The luminosities of all SWIFT GRBs are corrected only for the
galactic absorption, except for GRB 050401, for which
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4085fig13.eps}\end{figure}](/articles/aa/full/2006/21/aa4085-05/Timg98.gif) |
Figure 13:
Like Fig. 5 with added, the monochromatic optical
luminosities 12 h (rest frame) after the trigger of the 14 GRBs
discovered by SWIFT whose intrinsic luminosities could be calculated
from the photometric data.
We caution the reader that the optical luminosities
of all SWI bursts (except GRB 050401, GRB 050525 and GRB 050730)
are uncorrected
for the host galaxy absorption and are k-corrected assuming a the same optical spectral index ( |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{4085fig14.ps}\end{figure}](/articles/aa/full/2006/21/aa4085-05/Timg99.gif) |
Figure 14: Like Fig. 6, the X-ray [4-20 keV] luminosities 12 h (rest frame) after the trigger of the 11 GRBs discovered by SWIFT whose intrinsic luminosities could be calculated from the data found in Nousek et al. (2005; for GRB 050730, see Perri et al. 2005; for GRB 050820, see Page et al. 2005). |
| Open with DEXTER | |
Table 4:
Values of redshift,
![]() and the
semiaperture jet angle
and the
semiaperture jet angle
![]() used in Fig. 8,
taken from Ghirlanda et al. (2004).
When present, the values in parenthesis are the errors.
used in Fig. 8,
taken from Ghirlanda et al. (2004).
When present, the values in parenthesis are the errors.
Table 5: SWIFT long bursts with spectroscopically measured redshift.
The main result of our study is the clustering of the optical luminosities of the afterglows of GRBs. That is, bursts with widely different isotropic gamma-ray emitted energies are nevertheless similar in their optical output.
This result is unexpected for several reasons:
i) the optical luminosities, for the time of interest,
do not dominate the bolometric radiated output;
ii) in contrast to the X-ray frequencies, likely to be
above the cooling frequency
![]() ,
the optical frequencies
are likely to be smaller than
,
the optical frequencies
are likely to be smaller than
![]() .
This is confirmed by the simultaneous SED shown in Figs. 10 and 11.
This implies that the optical emission does indeed depend on the
density of the interstellar medium, n.
A range in the values of n should then contribute to increase
the dispersion of the optical luminosities;
iii) similar to the X-ray luminosities,
.
This is confirmed by the simultaneous SED shown in Figs. 10 and 11.
This implies that the optical emission does indeed depend on the
density of the interstellar medium, n.
A range in the values of n should then contribute to increase
the dispersion of the optical luminosities;
iii) similar to the X-ray luminosities,
![]() also
depends from the product of
also
depends from the product of
![]() and a function
on the equipartition parameters
and a function
on the equipartition parameters
![]() and
and
![]() .
The observed clustering implies a corresponding "clustering''
of the values of the isotropic kinetic energy and of the
equipartition parameters.
.
The observed clustering implies a corresponding "clustering''
of the values of the isotropic kinetic energy and of the
equipartition parameters.
In order to understand what has been observed, we should
investigate the implications of these two facts:
i) for the majority of bursts,
![]() is between the optical
and the X-ray band after a few hours (to a day) from trigger;
ii) the distribution of the optical luminosities is narrower
than the distribution of X-ray luminosities.
Here we very briefly discuss these facts in the framework
of the standard external shock synchrotron model.
is between the optical
and the X-ray band after a few hours (to a day) from trigger;
ii) the distribution of the optical luminosities is narrower
than the distribution of X-ray luminosities.
Here we very briefly discuss these facts in the framework
of the standard external shock synchrotron model.
As previously noted by Panaitescu & Kumar (2000, 2001, 2002)
having
![]() between the optical and X-ray bands
a day after the trigger implies a relatively low value
of
between the optical and X-ray bands
a day after the trigger implies a relatively low value
of
![]() (and n). For convenience, we report here Eq. (27) (for homogeneous ISM density)
and Eq. (28) (for a r-2 wind profile) of Panaitescu & Kumar (2000) for
(and n). For convenience, we report here Eq. (27) (for homogeneous ISM density)
and Eq. (28) (for a r-2 wind profile) of Panaitescu & Kumar (2000) for
![]() :
:
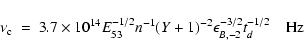 |
(3) |
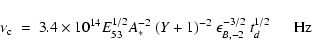 |
(4) |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4085fig15.ps}\end{figure}](/articles/aa/full/2006/21/aa4085-05/Timg112.gif) |
Figure 15:
Examples of spectra calculated using the prescriptions of
Panaitescu & Kumar (2000), at 12 h after trigger.
Dashed lines correspond to a homogeneous ISM case
(with density n=1 cm-3); solid lines to a wind profile
of the density (with |
| Open with DEXTER | |
In order to find the simplest possible reason for
the clustering of the optical luminosities, we
again used the analytical prescriptions of Panaitescu & Kumar (2000)
to construct light curves and spectra at a given time.
Figure 15 shows some examples of spectra
calculated at 12 h after trigger, assuming for all cases
the same kinetic energy (E=1053 erg), the same
![]() value, the same
value, the same
![]() ,
and external density (n=1 cm-3 for the homogeneous ISM case
and
,
and external density (n=1 cm-3 for the homogeneous ISM case
and ![]()
![]()
![]() yr-1 and v=103 km s-1for the wind case). What changes is only the slope of the electron distribution p.
As can be seen, we indeed find in this case that the optical luminosities
are distributed in a much narrower range than the X-ray luminosities.
This is due to the fact that the cooling frequency changes
with changing p as a result of Compton losses being important,
and decreasing for smaller p.
Note also that this is true both for the homogeneous and the wind case.
yr-1 and v=103 km s-1for the wind case). What changes is only the slope of the electron distribution p.
As can be seen, we indeed find in this case that the optical luminosities
are distributed in a much narrower range than the X-ray luminosities.
This is due to the fact that the cooling frequency changes
with changing p as a result of Compton losses being important,
and decreasing for smaller p.
Note also that this is true both for the homogeneous and the wind case.
We stress that this example is only illustrative, and does not
pretend to give an exhaustive explanation of our results, since there
can be other solutions in which more than one parameter is changing.
Keeping this in mind, the observed clustering of the optical luminosities
would then require that the kinetic (isotropically equivalent)
energy is distributed in a narrow range, as are the equipartition
parameters.
Furthermore,
![]() (and/or the density n) should be
small, and the Compton Y parameter relatively large.
(and/or the density n) should be
small, and the Compton Y parameter relatively large.
Our results can help in understanding why a significant fraction of bursts with detected X-ray afterglows are not detected in the optical, even now in the SWIFT era, which allows very early optical observations both onboard through UVOT and on the ground through several robotic telescopes. Although our samples are still limited, it appears that there is a family of optically underluminous objects (dimmer by an order of magnitude than the average for the main family). These bursts are the obvious candidates for being missed in the optical, especially in the presence of absorption in the host galaxy (Nardini et al. in prep.).
We can wonder if these GRBs appear underluminous because of
an underestimation of the intrinsic absorption.
In this respect, we note that for GRB 011121 three different authors
all estimate a null value of
![]() ,
while they differ
somewhat on the value of the Galactic extinction.
To be conservative, we have taken the highest value of those.
For GRB 021211, there are two estimates of
,
while they differ
somewhat on the value of the Galactic extinction.
To be conservative, we have taken the highest value of those.
For GRB 021211, there are two estimates of
![]() ,
so
we used the conservative choice, taking the higher value.
For GRB 980613 there is only one estimate of
,
so
we used the conservative choice, taking the higher value.
For GRB 980613 there is only one estimate of
![]() ,
but a constraint on the maximum possible value of
,
but a constraint on the maximum possible value of
![]() comes from its SED.
From Fig. 10 it can be seen that the optical luminosity
of this burst cannot be larger than a factor of ten from what
is plotted, if we require a smooth joining of the extrapolated
optical/X-ray spectra.
This would barely bring this burst to the faint end of the luminous family.
However, in this case the SED would appear anomalous, because the
peak of the spectrum would be in the optical-near-UV (in contrast
to the majority of the other bursts), and the optical spectral index
resulting from such a large correction would be
flatter than
comes from its SED.
From Fig. 10 it can be seen that the optical luminosity
of this burst cannot be larger than a factor of ten from what
is plotted, if we require a smooth joining of the extrapolated
optical/X-ray spectra.
This would barely bring this burst to the faint end of the luminous family.
However, in this case the SED would appear anomalous, because the
peak of the spectrum would be in the optical-near-UV (in contrast
to the majority of the other bursts), and the optical spectral index
resulting from such a large correction would be
flatter than
![]() ,
again in contrast to the other bursts.
,
again in contrast to the other bursts.
We do not know yet if these few underluminous bursts are the tip of the iceberg of much more numerous populations, and we do not know the corresponding spread in luminosities. We believe that SWIFT will clarify this point.
The main results of our study are:
Acknowledgements
We thank the Italian MIUR for funding (Cofin grant 2003020775_002).