A&A 450, 407-413 (2006)
DOI: 10.1051/0004-6361:20054474
M. Lundqvist1 - H. Nilsson1 - G. M. Wahlgren1 - H. Lundberg2 - H. L. Xu2,3,4 - Z.-K. Jang3 - D. S. Leckrone5
1 - Atomic Astrophysics, Lund Observatory, Lund University, Box 43, 221 00 Lund, Sweden
2 - Atomic Physics, Department of Physics, Lund Institute of Technology, Box 118, 221 00 Lund, Sweden
3 - Department of Physics, Jilin University, ChangChun, 130023, PR China
4 - Department of Physics, Engineering and Optics, Laval University, Quebec City, G1K 7P4, Canada
5 - Laboratory for Astronomy and Solar Physics, NASA Goddard Space Flight Center, Code 681, Greenbelt, MD, 20771, USA
Received 4 November 2005 / Accepted 29 December 2005
Abstract
Aims. We present new and improved radiative lifetimes for eight levels in Hf I and 18 levels in Hf II, along with oscillator strengths and wavelengths for 195 transitions in Hf II. With these data we determine the abundance of hafnium in two chemically peculiar stars: the hot-Am star HR 3383 and the HgMn star ![]() Lupi, and discuss the implications of the new data to the hafnium abundance for the Sun and the metal-poor galactic halo stars CS 22892-052 and CS 31082-001.
Lupi, and discuss the implications of the new data to the hafnium abundance for the Sun and the metal-poor galactic halo stars CS 22892-052 and CS 31082-001.
Methods. The oscillator strengths are derived by combining radiative lifetimes measured with the laser induced fluorescence technique and branching fractions determined from intensity calibrated Fourier transform spectra. The hafnium abundance in the two sharp-lined peculair stars is determined by comparison of spectra obtained from instruments onboard the Hubble Space Telescope with synthetic spectra, while the abundance of hafnium in the solar photosphere and the metal-poor halo stars is discussed in terms of rescaling previous investigations using the new gf values.
Results. The abundance enhancement of hafnium has been determined in HR 3383 to be +1.7 dex and that for ![]() Lupi A is +1.3 dex. In the course of the analysis we have also determined an abundance enhancement for molybdenum in HR 3383 to be +1.2 dex, which is similar to that known for
Lupi A is +1.3 dex. In the course of the analysis we have also determined an abundance enhancement for molybdenum in HR 3383 to be +1.2 dex, which is similar to that known for ![]() Lupi A. The abundances in the metal-poor halo stars CS 31082-001 and CS 22892-052 were rescaled to log
Lupi A. The abundances in the metal-poor halo stars CS 31082-001 and CS 22892-052 were rescaled to log
![]() and -0.82 respectively, with smaller 1
and -0.82 respectively, with smaller 1![]() uncertainty. This has the effect of improving the theoretical fits of r-process nucleosynthesis to abundance data for heavy elements. The change of gf values also implies that the hafnium abundance in the solar photosphere should be reduced by up to 0.2 dex, thereby inducing a discrepancy with the meteoritic hafnium abundance.
uncertainty. This has the effect of improving the theoretical fits of r-process nucleosynthesis to abundance data for heavy elements. The change of gf values also implies that the hafnium abundance in the solar photosphere should be reduced by up to 0.2 dex, thereby inducing a discrepancy with the meteoritic hafnium abundance.
Key words: atomic data - line: identification - stars: abundances
Hafnium is a heavy trace element (Z = 72) that has been investigated in relatively few stars. However, it can be an element of interest to diverse fields, such as elemental diffusion in the atmospheres of chemically peculiar (CP) stars and chemical evolution from old galactic halo stars, by virtue of its numerous stable isotopes.
The solar photospheric abundance of hafnium, log
![]() ,
on a scale where
,
on a scale where
![]() ,
is currently attributed to the work of Andersen et al. (1976), who determined this abundance from synthetic spectrum fitting of six lines in the solar spectrum. At this abundance level, hafnium is among the least abundant elements in nature. Other examples of hafnium abundance determination include the solar-like abundance for the bright F0 Ib star Canopus (Reynolds et al. 1988), the work of Yushchenko et al. (2005b) for
,
is currently attributed to the work of Andersen et al. (1976), who determined this abundance from synthetic spectrum fitting of six lines in the solar spectrum. At this abundance level, hafnium is among the least abundant elements in nature. Other examples of hafnium abundance determination include the solar-like abundance for the bright F0 Ib star Canopus (Reynolds et al. 1988), the work of Yushchenko et al. (2005b) for ![]() Scuti in determining an abundance pattern similar to that for Am-Fm stars, and the enigmatic roAp star HD 101065 (Cowley et al. 2000).
Scuti in determining an abundance pattern similar to that for Am-Fm stars, and the enigmatic roAp star HD 101065 (Cowley et al. 2000).
Sneden et al. (1996) claimed a first detection of Hf II in a metal-poor halo star. They detected two Hf II lines (
![]() 3719.28, 3793.38 Å) in the spectrum of CS 22892-052, with a mean abundance of log
3719.28, 3793.38 Å) in the spectrum of CS 22892-052, with a mean abundance of log
![]() (1
(1![]() uncertainty 0.14). They compared their results for a number of heavy elements to calculations of the contribution of r- and s-processes in the solar abundances, scaling the solar pattern to best match the abundances of the elements
uncertainty 0.14). They compared their results for a number of heavy elements to calculations of the contribution of r- and s-processes in the solar abundances, scaling the solar pattern to best match the abundances of the elements
![]() .
This gave clear indications of a pure r-process contribution to the heavy element abundances of CS 22982-052. Later, Sneden et al. (2003) reanalyzed the elemental abundances in CS 22892-052 resulting in a mean hafnium abundance of
.
This gave clear indications of a pure r-process contribution to the heavy element abundances of CS 22982-052. Later, Sneden et al. (2003) reanalyzed the elemental abundances in CS 22892-052 resulting in a mean hafnium abundance of
![]() .
.
Hill et al. (2002) derived abundances for a large number of elements in the metal-poor halo star CS 31082-001. The use of two Hf II lines (
![]() 3399.793, 3719.276) lead to an abundance of log
3399.793, 3719.276) lead to an abundance of log
![]() .
Abundances were compared with a calculated scaled solar r-process pattern, resulting in a good fit to the abundances of the elements between barium and thulium. However, the fit for several elements, including hafnium, osmium and lead, fell outside the assignment of the uncertainties. In the case of osmium the discrepancy would later be ascribed to the atomic data, and with new gf values (Ivarsson et al. 2003) the osmium abundance also fit the solar r-process pattern.
.
Abundances were compared with a calculated scaled solar r-process pattern, resulting in a good fit to the abundances of the elements between barium and thulium. However, the fit for several elements, including hafnium, osmium and lead, fell outside the assignment of the uncertainties. In the case of osmium the discrepancy would later be ascribed to the atomic data, and with new gf values (Ivarsson et al. 2003) the osmium abundance also fit the solar r-process pattern.
Yushchenko et al. (2005a) investigated the Hf II ![]() 4093.155 line in the halo star HD 221170, deriving a hafnium enhancement relative to iron that places it above the scaled r-process abundance distribution for heavy elements. Based on their work with a number of heavy elements they conclude that the r-process is not universal.
4093.155 line in the halo star HD 221170, deriving a hafnium enhancement relative to iron that places it above the scaled r-process abundance distribution for heavy elements. Based on their work with a number of heavy elements they conclude that the r-process is not universal.
The Hf II line data used to interpret stellar spectra dates back more than forty years to the era of photographic plates. Corliss & Bozman (1962) (hereafter CB) measured log gf values for Hf I and Hf II in arc spectra for a large number of lines over the wavelength interval 2000-9000 Å. Andersen et al. (1976) (hereafter APH) measured lifetimes for nine levels in Hf II using the beam-foil technique and rescaled the results of CB. The results of the two groups agree to within an uncertainty of typically 10% for the levels above 30 000 cm-1 but for lower levels they deviate considerably. However, the work of APH is limited to relatively few transitions at optical and near-IR wavelengths.
Our need for accurate oscillator strengths at UV wavelengths, to analyse spectra of warm stars, motivates the experimental work presented here.In this work we report radiative lifetimes of eight Hf I levels and 18 Hf II levels, measured with the laser induced fluorescence (LIF) technique. Branching fractions (BFs) for transitions from the Hf II levels have been measured from Fourier transform (FT) spectra. Combining the new lifetimes with the BFs, 195 absolute oscillator strengths have been derived. In addition to the BFs we have measured accurate wavelengths for the 195 Hf II lines. These data are applied to the determination of the hafnium abundance in the chemically peculiar stars ![]() Lupi (HgMn) and HR 3383 (hot-Am), and they are discussed in terms of possible revisions of the hafnium abundance for the Sun and the galactic halo stars CS 22892-052 and CS 31082-001.
Lupi (HgMn) and HR 3383 (hot-Am), and they are discussed in terms of possible revisions of the hafnium abundance for the Sun and the galactic halo stars CS 22892-052 and CS 31082-001.
For the lifetime experiments we apply the LIF technique, as performed in previous experiments at the Lund Laser Centre. Free neutral and singly-ionised hafnium atoms were produced by laser ablation utilizing pulses from a Nd:YAG laser, characterised by a 532 nm wavelength, 10 Hz repetition rate, 10 ns duration and variable pulse energy (2-10 mJ). The laser pulses were focused onto the surface of a hafnium foil, which was rotating in a vacuum chamber with a pressure of about 10-6 mbar. In order to obtain the required excitation wavelengths during the LIF measurements a second injection-seeded and Q-switched Nd:YAG laser was used to pump a dye laser operated with the dye DCM. Before the pulses from the Nd:YAG laser were sent to the dye laser, they were shortened to about 1 ns in a watercell compressor based on stimulated Brillouin scattering. Depending on excitation wavelength for the investigated levels different non-linear processes were adopted to obtain UV radiation in the range 208 to 380 nm. The second harmonic of the dye laser was obtained in a KDP crystal. The third-order harmonic of the dye laser could be produced by mixing the second harmonic with the fundamental frequency of the dye laser in a BBO crystal. To extend the tuneable wavelength range further, the laser beam could be frequency shifted in a hydrogen cell using stimulated Raman scattering. The excitation beam was directed into the vacuum chamber and interacted with the ablated atoms and ions about 1 cm above the foil. The two Nd:YAG lasers were externally trigged by a delay generator, which enabled a free variation of the delay time between the ablation and excitation laser pulses. The fluorescence, released at the decay of the excited levels, was focused onto the entrance slit of a 1/8 m monochromator equipped with a micro-channel-plate photomultiplier tube (200 ps rise time). A transient digitizer was used to record and average the signals from the photomultiplier. Finally, the average time-resolved signals were transferred to a computer for the lifetime evaluations. For the shorter lifetimes the excitation pulse was also recorded and the lifetime was obtained in a deconvolution procedure, thus avoiding effects of the limited time response of the detection system. A more detailed discription of the setup can be found in Li et al. (2000).
The results of the lifetime measurements are presented in Table 3 for Hf I and Table 4 for Hf II.
Hafnium spectra covering the wavenumber region 12 500 to 55 000 cm-1 (![]() 1800-8000 Å) were recorded with the Chelsea instrument FT500 UV FT spectrometer at Lund Observatory using a resolution of 0.035 cm-1. A water-cooled hollow cathode discharge with a cathode made out of a 5 cm long, 5 mm thick hafnium tube with a inner bore diameter of 2.5 mm was used as the light source. Spectra were recorded with discharge currents between 0.1 and 0.5 A, at an argon carrier gas pressure of 1.6 mbar. To derive relative intensities, the spectra were corrected for the instrumental response by using a tungsten ribbon lamp between 12 500 and 22 300 cm-1, known Ar II brancing ratios from Whaling et al. (1993) between 20 000 to 30 000 cm-1, and a deuterium lamp for wavenumbers above 27 800 cm-1.
1800-8000 Å) were recorded with the Chelsea instrument FT500 UV FT spectrometer at Lund Observatory using a resolution of 0.035 cm-1. A water-cooled hollow cathode discharge with a cathode made out of a 5 cm long, 5 mm thick hafnium tube with a inner bore diameter of 2.5 mm was used as the light source. Spectra were recorded with discharge currents between 0.1 and 0.5 A, at an argon carrier gas pressure of 1.6 mbar. To derive relative intensities, the spectra were corrected for the instrumental response by using a tungsten ribbon lamp between 12 500 and 22 300 cm-1, known Ar II brancing ratios from Whaling et al. (1993) between 20 000 to 30 000 cm-1, and a deuterium lamp for wavenumbers above 27 800 cm-1.
Hafnium has six naturally occurring stable isotopes (A = 174, 176, 177, 178, 179, 180), of which two are odd and might be expected to show hyperfine structure. None of these effects were resolved in the FT spectra, but many lines show asymmetric and broadened profiles as seen in Fig. 1. The broad foot on this particular line is one of the largest deviations from a Voigt profile seen in our data.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{4474fig1.EPS}
\end{figure}](/articles/aa/full/2006/16/aa4474-05/Timg17.gif) |
Figure 1:
The profile of the resonance line 5d6s2 a2D3/2-5d6s (a3D)6p z4F5/2 Hf II |
| Open with DEXTER | |
The BF of a line is derived by dividing the intensity of the line by the sum of the intensities of all lines coming from the same upper level,
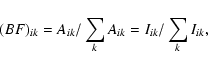 |
(1) |
Wavelengths for the Hf II lines were measured from the FT spectra using a center-of-gravity technique, since the line profiles are far from Voigt profiles no curve fitting was attempted. The spectra were wavelength calibrated by Ar II lines reported by Whaling et al. (1995). The line density of the hafnium spectra is high and some cases of line blending were seen. The 11 lines affected by line blending are marked in Table 5. The importance of the blends is reflected in the uncertainties attached to the gf value. The lines still having a small uncertainty are only blended with weak lines in either wing where the effect of the blend is small. A few lines are more severely blended and, therefore, have larger uncertainties.
The transition probability (A-value) of a line can be derived from the relation:
In Table 5 the BFs and log gf values are presented and compared with the values of APH and CB. In Figs. 2 and 3 the new log gf values are plotted against the difference between the new log gf values and the values determined by CB and APH, respectively. The comparison with the values of CB shows a large scatter with an offset of approximately -0.4. The comparison with APH in Fig. 3 shows a smaller scatter and the offset is only about -0.1. Andersen et al. rescaled the log gf values of CB using new lifetimes, but the uncertainty in the BF part is still present.
| |
Figure 2:
Comparison of the oscillator strengths from Corliss & Bozman (1962) with the values derived in this work. |
| Open with DEXTER | |
| |
Figure 3:
Comparison of the oscillator strengths from Andersen et al. (1976) with the values derived in this work. |
| Open with DEXTER | |
The total uncertainty presented in Table 5 is derived with contributions from the intensity measurements, the intensity calibration, the combination of different spectral regions, the self-absorption correction, the corrections for residuals and the lifetime measurements. The uncertainties are estimated as described in Sikström et al. (2002).
We have investigated the hafnium abundance in two sharp-lined chemically peculiar (CP) stars, ![]() Lupi (=HD 141556, B9.5IVp HgMn + A2 Vm) and HR 3383 (=HD 72660, A1Vm), by fitting synthetic spectra to high-resolution ultraviolet spectra taken with the Hubble Space Telescope (HST). Both the HgMn and Am CP star classes are known to exhibit elemental abundances that are enhanced above the solar system values. The determination of elemental abundances for
Lupi (=HD 141556, B9.5IVp HgMn + A2 Vm) and HR 3383 (=HD 72660, A1Vm), by fitting synthetic spectra to high-resolution ultraviolet spectra taken with the Hubble Space Telescope (HST). Both the HgMn and Am CP star classes are known to exhibit elemental abundances that are enhanced above the solar system values. The determination of elemental abundances for ![]() Lupi A has been a focus of the
Lupi A has been a focus of the ![]() Lupi Pathfinder project (Leckrone et al. 1999). For the heaviest stable elements the recent additions of osmium and iridium to the analysis of
Lupi Pathfinder project (Leckrone et al. 1999). For the heaviest stable elements the recent additions of osmium and iridium to the analysis of ![]() Lupi A has defined an enhancement peak that is comprised of the elements platinum, gold, mercury, and thallium (Ivarsson et al. 2004). Now, with the consideration of hafnium this project has realized defining the abundance distribution with the use of accurate atomic data for all stable elements heavier than the lanthanides (
Lupi A has defined an enhancement peak that is comprised of the elements platinum, gold, mercury, and thallium (Ivarsson et al. 2004). Now, with the consideration of hafnium this project has realized defining the abundance distribution with the use of accurate atomic data for all stable elements heavier than the lanthanides (
![]() ).
).
Spectral data for ![]() Lupi were obtained using the HST Goddard High Resolution Spectrograph (GHRS) and have been described by Brandt et al. (1999) and Leckrone et al. (1999). With only a limited spectral coverage we were fortunate to work with the line Hf II
Lupi were obtained using the HST Goddard High Resolution Spectrograph (GHRS) and have been described by Brandt et al. (1999) and Leckrone et al. (1999). With only a limited spectral coverage we were fortunate to work with the line Hf II ![]() 2683, which has the largest gf value in our laboratory sample. The FTS profile for this line is well fitted by a Voigt profile, and shows no effects of hyperfine or isotope structure, such as is observed for Hf II
2683, which has the largest gf value in our laboratory sample. The FTS profile for this line is well fitted by a Voigt profile, and shows no effects of hyperfine or isotope structure, such as is observed for Hf II ![]() 3399.790 (Fig. 1). Other lines of near comparable strength are either blended or do not exist in our GHRS dataset. Although three GHRS observations of
3399.790 (Fig. 1). Other lines of near comparable strength are either blended or do not exist in our GHRS dataset. Although three GHRS observations of ![]() Lupi were made at this wavelength setting, only one (Z28H010L) is useful for our purpose. The uncertainties in the companion star spectral synthesis preclude the use of the other two observations for analyzing this line.
Lupi were made at this wavelength setting, only one (Z28H010L) is useful for our purpose. The uncertainties in the companion star spectral synthesis preclude the use of the other two observations for analyzing this line.
The GHRS spectrum was analysed in a manner similar to previously published results. Model atmospheres created with the ATLAS9 code (Kurucz 1993a) with model parameters (
![]() K,
log g = 3.8,
K,
log g = 3.8,
![]() km s-1,
km s-1,
![]() km s-1 for the primary star and
km s-1 for the primary star and
![]() K, log g = 4.2,
K, log g = 4.2,
![]() km s-1,
km s-1,
![]() km s-1 for the secondary) were used in the SYNTHE (Kurucz 1993b) synthetic spectrum code. Atomic line data were taken from the compilation of Kurucz (1993b) with the exception of data discussed in this work. Elemental abundances for elements other than hafnium were taken from Leckrone et al. (1999). The computed spectra were coadded, taking into account the wavelength dependent luminosity ratio (
km s-1 for the secondary) were used in the SYNTHE (Kurucz 1993b) synthetic spectrum code. Atomic line data were taken from the compilation of Kurucz (1993b) with the exception of data discussed in this work. Elemental abundances for elements other than hafnium were taken from Leckrone et al. (1999). The computed spectra were coadded, taking into account the wavelength dependent luminosity ratio (
![]() )
and the wavelength shift between the components
(
)
and the wavelength shift between the components
(
![]() Å) at the time of the observation, based upon the ephemeris of Dworetsky (1972). The resulting spectrum was convolved with the instrument broadening function, modeled as a Gaussian of resolving power
R = 86 560 for the relevant echelle order, and placed on the laboratory wavelength scale by shifting the observed spectrum to match spectral features of iron-group elements. Figure 4 presents the comparison of the observation with synthetic spectra computed for hafnium enhancements of
[Hf/H] =
Å) at the time of the observation, based upon the ephemeris of Dworetsky (1972). The resulting spectrum was convolved with the instrument broadening function, modeled as a Gaussian of resolving power
R = 86 560 for the relevant echelle order, and placed on the laboratory wavelength scale by shifting the observed spectrum to match spectral features of iron-group elements. Figure 4 presents the comparison of the observation with synthetic spectra computed for hafnium enhancements of
[Hf/H] =
![]() ,
1.0, 1.3, and 1.5 dex. We adopt [Hf/H] = 1.3, though the value should be considered an upper limit due to data noise (maximum S/N = 140), small uncertainties in the luminosity ratio, and unknowns regarding certain elemental abundances for the secondary star. The feature at this wavelength does not appear to be an instrument artifact.
,
1.0, 1.3, and 1.5 dex. We adopt [Hf/H] = 1.3, though the value should be considered an upper limit due to data noise (maximum S/N = 140), small uncertainties in the luminosity ratio, and unknowns regarding certain elemental abundances for the secondary star. The feature at this wavelength does not appear to be an instrument artifact.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{4474fig4.ps}
\end{figure}](/articles/aa/full/2006/16/aa4474-05/Timg36.gif) |
Figure 4:
Spectrum fitting for Hf II |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{4474fig5.ps}
\end{figure}](/articles/aa/full/2006/16/aa4474-05/Timg37.gif) |
Figure 5: Synthetic spectrum fitting for HR 3383. The observation (solid) is compared with synthetic spectra (dotted) computed for abundance enhancements of hafnium [Hf/H] = 0.0, 1.7 dex and molybdenum [Mo/H] = 0.0, 1.2 dex. The strong central feature not present in the synthetic spectrum is unidentified. |
| Open with DEXTER | |
High-resolution ultraviolet spectra of the hot-Am star HR 3383 were taken with the HST Space Telescope Imaging Spectrograph (STIS) (HST Prop GO9455, PI R. Peterson). The data, extracted from the HST data archive MAST and reduced by the STIS team at Goddard Space Flight Center (private communication), have a nominal resolving power of
![]() /
/
![]() ,
and display a typical S/N of near 100. Three spectral images were utilized in this analysis (ID numbers O6LM51030, O6LM51010, O6LM51020) that span the wavelength region 2128-2888 Å.
,
and display a typical S/N of near 100. Three spectral images were utilized in this analysis (ID numbers O6LM51030, O6LM51010, O6LM51020) that span the wavelength region 2128-2888 Å.
Synthetic spectra for HR 3383 were computed with the SYNTHE code, using an ATLAS9 model atmosphere for the atmospheric parameters
![]() ,
,
![]() ,
,
![]() km s-1. A rotational velocity (
km s-1. A rotational velocity (![]() )
of
5.5 km s-1 was determined from the data, which is lower than the
6.5 km s-1 value of Adelman et al. (2004). This difference is attributed to the higher resolving power of the STIS long wavelength spectra relative to the data used at shorter wavelengths, which allowed us to determine a lower rotational velocity.
)
of
5.5 km s-1 was determined from the data, which is lower than the
6.5 km s-1 value of Adelman et al. (2004). This difference is attributed to the higher resolving power of the STIS long wavelength spectra relative to the data used at shorter wavelengths, which allowed us to determine a lower rotational velocity.
Table 1: Hf II lines in HR 3383.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{4474fig6.ps}
\end{figure}](/articles/aa/full/2006/16/aa4474-05/Timg45.gif) |
Figure 6:
Hf II |
| Open with DEXTER | |
From our experimental line sample (Table 5) only two Hf II lines, ![]() 2683.39 and the weaker
2683.39 and the weaker ![]() 2820.225, were detected in the stellar spectrum. For the former, Fig. 5 presents a comparison of the HR 3383 observation with synthetic spectra computed for the solar abundance and an enhancement over the solar value of [Hf/H] = 1.7 dex. This enhancement yields a best fit to the spectrum to within an uncertainty of
2820.225, were detected in the stellar spectrum. For the former, Fig. 5 presents a comparison of the HR 3383 observation with synthetic spectra computed for the solar abundance and an enhancement over the solar value of [Hf/H] = 1.7 dex. This enhancement yields a best fit to the spectrum to within an uncertainty of ![]() 0.2 dex for the combination of R and
0.2 dex for the combination of R and ![]() specified above, and our placement of the continuum.
specified above, and our placement of the continuum.
To achieve the best fit the observed spectrum was shifted by -0.840 Å to place it on the laboratory rest frame. As a result of noise an uncertainty of ![]() 0.004 Å is tolerated to fit many of the spectral features. The absolute wavelength scale was set by the Cr II
0.004 Å is tolerated to fit many of the spectral features. The absolute wavelength scale was set by the Cr II ![]() 2683.443 line, as its wavelength has been measured by FT spectroscopy to an uncertainty of approximately 1 mÅ. The continuum level was set by matching the high points in the spectrum found within several angstroms of the Hf II line. The uncertainty in the continuum placement is between 1-2%. The Hf II
2683.443 line, as its wavelength has been measured by FT spectroscopy to an uncertainty of approximately 1 mÅ. The continuum level was set by matching the high points in the spectrum found within several angstroms of the Hf II line. The uncertainty in the continuum placement is between 1-2%. The Hf II ![]() 2683 line serves as the main indicator of the hafnium abundance in this star due to the nature of the atomic data.
2683 line serves as the main indicator of the hafnium abundance in this star due to the nature of the atomic data.
Four Hf II lines from the list of CB have also been incorporated into this analysis of the Hf II spectrum. All lines are located longward of 2600 Å, and thus avoid the most severe regions of line blending. Table 1 presents the oscillator strengths and derived abundances for the six lines used in the analysis of HR 3383. Abundances quoted are for the new gf values when a line has an entry from CB. Figure 6 presents the comparison between observed and synthetic spectra for one of these lines, Hf II ![]() 2641.410, which is the most prominent of the Hf II lines we have studied. Two of these lines yield an abundance for hafnium that is similar to that determined from the new line data, and two result in a noticeably lower abundance. There is a high likelihood that the oscillator strengths from CB are systematically higher than would be determined by modern techniques, such as the LIF method employed here. If corrected, this would lead to a somewhat higher abundance. This possibility is borne out by our comparison of gf values between CB and this study, as presented in Fig. 2.
2641.410, which is the most prominent of the Hf II lines we have studied. Two of these lines yield an abundance for hafnium that is similar to that determined from the new line data, and two result in a noticeably lower abundance. There is a high likelihood that the oscillator strengths from CB are systematically higher than would be determined by modern techniques, such as the LIF method employed here. If corrected, this would lead to a somewhat higher abundance. This possibility is borne out by our comparison of gf values between CB and this study, as presented in Fig. 2.
In the course of our work on Hf II we became aware of two obvious lines of Mo II in the spectrum of HR 3383. These lines are noted in Fig. 5. A search for other Mo II lines of comparable strength showed them to be blended. The abundance of molybdenum was determined for HR 3383 using the wavelength and oscillator strength data of Sikström et al. (2001). A best fit was obtained for an abundance of
![]() dex, which is an enhancement of +1.2 dex over the solar abundance. The abundance of molybdenum in
dex, which is an enhancement of +1.2 dex over the solar abundance. The abundance of molybdenum in ![]() Lupi A has been reported by Leckrone et al. (1999) to be log
Lupi A has been reported by Leckrone et al. (1999) to be log
![]() .
.
Table 2: Rescaled abundances in CS 22892-052 and CS 31082-001.
In applying the same approach to the results of Hill et al. (2002) on CS 31082-001 a descrepancy appears. The previously derived abundance from the Hf II ![]() 3399.273 line is
3399.273 line is
![]() and would increase to -0.38 after the new gf value is substituted for the old one, while the abundance for the line
and would increase to -0.38 after the new gf value is substituted for the old one, while the abundance for the line ![]() 3719.273 stays almost the same (
3719.273 stays almost the same (
![]() changes to -0.72), resulting in an increase in the uncertainty. Figure 6 in Hill et al. (2002) shows synthetic spectrum fits to the
changes to -0.72), resulting in an increase in the uncertainty. Figure 6 in Hill et al. (2002) shows synthetic spectrum fits to the ![]() 3399.273 line for three different abundances. It is suspected that the final abundance has been misquoted in their text, since, in their figure it is clear that the synthetic spectrum with an abundance of
3399.273 line for three different abundances. It is suspected that the final abundance has been misquoted in their text, since, in their figure it is clear that the synthetic spectrum with an abundance of
![]() ,
and not the spectrum with
,
and not the spectrum with
![]() ,
has the best fit. This would explain the discrepancy with the 1
,
has the best fit. This would explain the discrepancy with the 1![]() uncertainty becoming larger and would instead decrease it to 0.04. In Table 2 the abundance read from the figure is used to show what their abundance would be if it were scaled using the new log gf values. The hafnium abundance in CS 31082-001 then becomes log
uncertainty becoming larger and would instead decrease it to 0.04. In Table 2 the abundance read from the figure is used to show what their abundance would be if it were scaled using the new log gf values. The hafnium abundance in CS 31082-001 then becomes log ![]() = -0.75. Applying the re-evaluated hafnium abundance to the comparison Hill et al. (2002) makes between the abundances in CS 31082-001 and scaled solar r-process abundances, shifts the hafnium point towards the solar r-process pattern strengthening the fit to it. It should be noted that using the abundance derived from Fig. 6 in Hill et al. (2002) gives a value slightly closer to the solar r-process pattern, with the log gf values of Andersen et al. (1976), than with the new values from this work, although the uncertainty decreases with the new values.
= -0.75. Applying the re-evaluated hafnium abundance to the comparison Hill et al. (2002) makes between the abundances in CS 31082-001 and scaled solar r-process abundances, shifts the hafnium point towards the solar r-process pattern strengthening the fit to it. It should be noted that using the abundance derived from Fig. 6 in Hill et al. (2002) gives a value slightly closer to the solar r-process pattern, with the log gf values of Andersen et al. (1976), than with the new values from this work, although the uncertainty decreases with the new values.
With these new data the abundance of hafnium for two CP stars has been determined, which both extends our knowledge of heavy element abundances and highlights an interesting difference. For ![]() Lupi A the hafnium abundance derived here is consistent with previous results for the heavy elements tantalum, tungsten, rhenium, osmium, iridium, lead, and bismuth in that we have determined an abundance enhancement, or upper limit, at the enhancement level of approximately 1 dex. By contrast, the elements platinum, gold, mercury, and thallium stand out as enhanced by more than four orders of magnitude.
Lupi A the hafnium abundance derived here is consistent with previous results for the heavy elements tantalum, tungsten, rhenium, osmium, iridium, lead, and bismuth in that we have determined an abundance enhancement, or upper limit, at the enhancement level of approximately 1 dex. By contrast, the elements platinum, gold, mercury, and thallium stand out as enhanced by more than four orders of magnitude.
The somewhat cooler Am star HR 3383 has been documented as having an enhancement of gold of +1.9 dex (Adelman et al. 2004), which is similar to the hafnium enhancement presented here (+1.7 dex). Spectral lines of other platinum-group elements have also been detected by us in the UV spectrum of HR 3383 (work in progress) and point to similar enhancements. Therefore, over a short span of spectral type (B9.5 to A1) there exists a remarkably different behaviour for the heaviest elements, with certain of them having a tendancy for extreme enhancements. One caveat to these results is that we assume that the hafnium isotope composition for these two stars is also solar-like. We are unable to derive any isotope composition information from the data. Evidence for isotope anomalies in HgMn stars is common, and suspected for hot-Am stars. Therefore, if the isotope composition differs from that of the Sun, then the abundances must be adjusted.
Rescaling the hafnium abundances in the metal-poor halo stars CS 22892-052 (Sneden et al. 1996) and CS 31082-001 (Hill et al. 2002) with the new log gf values decreases the 1![]() uncertainty of the result in both stars considerably. In CS 22892-052 the rescaled abundance becomes log
uncertainty of the result in both stars considerably. In CS 22892-052 the rescaled abundance becomes log
![]() ,
or
,
or
![]() if assuming the abundance of Sneden et al. (2003), with 1
if assuming the abundance of Sneden et al. (2003), with 1![]() uncertainty of 0.007. The lack of infromation on individual lines of Hf II used by Sneden et al. (2003) precludes us from choosing between those two values. In
CS 31082-001 the rescaled abundance becomes
uncertainty of 0.007. The lack of infromation on individual lines of Hf II used by Sneden et al. (2003) precludes us from choosing between those two values. In
CS 31082-001 the rescaled abundance becomes
![]() ,
using the abundance of Fig. 6 in Hill et al. (2002), 1
,
using the abundance of Fig. 6 in Hill et al. (2002), 1![]() uncertainty of 0.04. The re-evaluated abundance of CS 31082-001 now better fits the scaled solar r-process pattern, which together with the recently updated abundance for osmium (Ivarsson et al. 2003) strengthening the theory of an universal r-process in the early galaxy.
uncertainty of 0.04. The re-evaluated abundance of CS 31082-001 now better fits the scaled solar r-process pattern, which together with the recently updated abundance for osmium (Ivarsson et al. 2003) strengthening the theory of an universal r-process in the early galaxy.
Comparison of the gf values for Hf II presented here with those of APH suggests that the solar hafnium abundance may be underestimated by between 0.1 and 0.2 dex. Two of the six lines (Hf II
![]() 3253.70, 3535.54) used by APH are found by us to have log gf values more negative, by amounts of 0.25 and 0.15 dex, respectively. For a similar abundance analysis procedure, where we would substitute our gf values for those of APH, this would imply that the solar abundance is approximately 0.2 dex larger than their derived value. Three other lines considered by APH are also in our dataset, with two of them (
3253.70, 3535.54) used by APH are found by us to have log gf values more negative, by amounts of 0.25 and 0.15 dex, respectively. For a similar abundance analysis procedure, where we would substitute our gf values for those of APH, this would imply that the solar abundance is approximately 0.2 dex larger than their derived value. Three other lines considered by APH are also in our dataset, with two of them (
![]() 3399.790, 3569.034) now having lower log gf values by 0.12 dex. The third line (
3399.790, 3569.034) now having lower log gf values by 0.12 dex. The third line (![]() 3719.273) has a similar gf value in both studies. However, these three lines were not used by APH in their final abundance determination as a result of severe line blending. For these five lines in common to both studies, the average difference between the new and APH log gf values is -0.12 dex. From Fig. 3 we show that other lines in our comparison samples are, on average, systematically of lower log gf value than those of APH. Therefore, we conclude that the canonical solar photospheric hafnium abundance should be re-scaled upwards, to a value near
3719.273) has a similar gf value in both studies. However, these three lines were not used by APH in their final abundance determination as a result of severe line blending. For these five lines in common to both studies, the average difference between the new and APH log gf values is -0.12 dex. From Fig. 3 we show that other lines in our comparison samples are, on average, systematically of lower log gf value than those of APH. Therefore, we conclude that the canonical solar photospheric hafnium abundance should be re-scaled upwards, to a value near
![]() .
We hesitate to assign stringent uncertainties to this number, since considerable uncertainty can arise from the continuum placement in the analysis of the solar spectrum, as pointed out by APH. The uncertainties of the gf values for our data are at the 10 - 20% level for the lifetime measurements, which are marginally lower uncertainties than those quoted by APH. An interesting result of increasing the solar photospheric hafnium abundance is to increase the discrepancy between the solar system hafnium abundance as determined from chondritic meteorites
(
.
We hesitate to assign stringent uncertainties to this number, since considerable uncertainty can arise from the continuum placement in the analysis of the solar spectrum, as pointed out by APH. The uncertainties of the gf values for our data are at the 10 - 20% level for the lifetime measurements, which are marginally lower uncertainties than those quoted by APH. An interesting result of increasing the solar photospheric hafnium abundance is to increase the discrepancy between the solar system hafnium abundance as determined from chondritic meteorites
(
![]() (Lodders 2003) and our suggestion of a rescaling of the photosphere value (
(Lodders 2003) and our suggestion of a rescaling of the photosphere value (
![]() ).
).
Acknowledgements
We would like to thank the Lund Laser Center for providing time to conduct this experiment. Some of the data presented in this paper were obtained from the Multimission Archive at the Space Telescope Science Institute (MAST). STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. Support for MAST for non-HST data is provided by the NASA Office of Space Science via grant NAG5-7584 and by other grants and contracts.
Table 3: Experimental radiative lifetimes of Hf I.
Table 4: Experimental radiative lifetimes of Hf II.
Table 5: Hf II branching fractions (BFs) and log gf-values sorted by upper level.
Table 6: Finding list for Hf II transitions sorted by wavelength.