... spectrum[*]
Appendices A-G are only available in electronic form at http://www.edpsciences.org 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... SDSS[*]
http://www.sdss.org/ 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... of 2dF[*]
http://www.mso.anu.edu.au/2dFGRS/ 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... KAOS[*]
http://www.noao.edu/kaos/ 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... Surveyor[*]
http://astro.estec.esa.nl/Planck 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... SPT[*]
http://astro.uchicago.edu/spt 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...[*]
Here instead of the usual multipole number 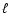$\ell$ we have plotted the CMB angular power spectrum against the wavenumber k. For the "concordance'' cosmological model $\ell = 9990~k[h~{\rm Mpc}^{-1}]$. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... criteria[*]
For the exact details of the selection criteria see Eisenstein et al. (2001). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... WMAP[*]
http://lambda.gsfc.nasa.gov/product/map/ 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... itself[*]
In principle one can build the angular masks using the raw tiling information, but as we show later our approximate treatment is probably acceptable, since the results are stable against small uncertainties in the mask. The issues of survey boundaries and completeness fluctuations (expected to be small due to the very effective tiling algorithm by Blanton et al. 2003) could certainly be addressed in more detail. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... SDSS[*]
The transformations between various coordinate systems used by the SDSS are given e.g. in Stoughton et al. (2002). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... [*]
Including all the modes down to the scales of 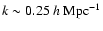$k \sim 0.25~h~{\rm Mpc}^{-1}$ the effective value for 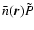$\bar{n}(\vec{r})\tilde{P}$ drops to 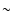$\sim $1.5. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... catalog[*]
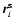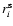We assume that the survey selection does not have any angular dependence other than the applied angular mask i.e. we can replace $\vec{r}^{\rm s}_i$ by the modulus $r^{\rm s}_i$. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...(Jing, 2005)[*]
For the NGP filter this sum equals 1, and so one recovers the original shot noise term in Eq. (1). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... simulations[*]
http://www.mpa-garching.mpg.de/Virgo/ 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... matrix[*]
Since now we are also able to handle quasi-nonlinear mode-mode couplings. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... us[*]
In calculating this contribution to the covariance matrix we have taken the best fit model parameters as obtained in Sect. 6. The smallness of this term is caused by the high value of the parameter M0 i.e. the majority of the "occupied'' halos contain only one LRG. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...[*]
This matrix along with the power spectrum results in Fig. 5 is also given in a tabular form in Appendix G. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... kernels[*]
We prefer to use "coupling kernels'' instead of the more common "window functions'' since the word "window'' has already been used to mean the modulus square of the Fourier transform of the weighted survey volume. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
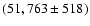
...$(51,763 \pm 518)$[*]
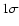The $1\sigma $ Poisson error in this case would be 228. The large-scale structure amplifies the variability in the number of objects and a factor of a few increase above the Poissonian case seems to be reasonable. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... "smoothed''[*]
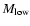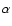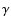The best fit $M_{{\rm low}}$, $\alpha$, M0 and $\gamma$ for the "smoothed'' models differ slightly from the values quoted above for the "wiggly'' spectra. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... counterparts[*]
Dropping the first power spectrum bin the obtained 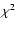$\chi^2$ values are 5.0 and 16.5. 5.0 is an anomalously low value of 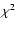$\chi^2$ for 12 degrees of freedom. (One would expect 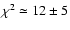$\chi^2 \simeq 12 \pm 5$.) If we would have used the simple FKP covariance matrix instead of the one obtained from the mock catalogs, the resulting 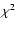$\chi^2$ values would be even lower: 2.9 and 8.5, respectively. This might hint that the 2nd order Lagrangian approach, although very successful, might still have problems in capturing some extra mode-mode couplings. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...c[*]
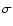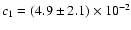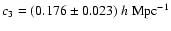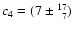Here and in the following the errors refer to the 1-$\sigma$ level. Values for the other parameters are as follows: $c_1 = (4.9 \pm 2.1)\times 10^{-2}$, $c_3 = (0.176 \pm 0.023)~h~{\rm Mpc}^{-1}$, $c_4 = (7 \pm {}^{17}_{\phantom{1}7})$. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... spectrum[*]
To be precise, in redshift space the two-point correlation function and power spectrum are no longer exact Fourier transforms of each other. Nevertheless, we think that this simplified exercise is still useful. Also, as the correlation function estimator in Eq. (30) is an edge-corrected estimator, we use an unconvolved model spectra here. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... here[*]
For a clear discussion of this see Daniel Eisenstein's home page http://cmb.as.arizona.edu/~eisenste/acousticpeak/ 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... software[*]
Further tests can be found in Hütsi (2005) 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... simulations[*]
http://www.mpa-garching.mpg.de/Virgo/ 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... cells[*]
Due to the large cell size the truncation of the initial spectrum has a rather mild effect. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... sampler[*]
We use a simple model where the intensity of the inhomogeneous Poisson process is linearly related to the underlying density field. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...[*]
Here as in the previous figure the SDSS LRG selection functions are not yet applied. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... trispectrum[*]
Here only the contribution due to the 1-halo term is given. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...)[*]
To avoid confusion we do not call them window functions since the word "window'' has been already used to mean the Fourier transform of the survey volume. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... elements[*]
The metric in the new frame is an identity matrix. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Copyright ESO 2006