A&A 449, 891-902 (2006)
DOI: 10.1051/0004-6361:20053939
G. Hütsi1,2
1 - Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1,
86740 Garching bei München, Germany
2 - Tartu Observatory, Tõravere 61602, Estonia
Received 29 July 2005 / Accepted 1 December 2005
Abstract
We calculate the redshift-space power spectrum of the Sloan Digital Sky Survey (SDSS) Data Release 4 (DR4) Luminous Red Galaxy (LRG) sample, finding evidence for a full series of acoustic features down to the scales of ![]()
![]() .
This corresponds to the 7th peak in the CMB angular power spectrum. The acoustic scale derived,
.
This corresponds to the 7th peak in the CMB angular power spectrum. The acoustic scale derived,
![]() ,
agrees very well with the "concordance'' model prediction and also with the one determined via the analysis of the spatial two-point correlation function by Eisenstein et al. (2005, ApJ, 633, 560). The models with baryonic features are favored by
,
agrees very well with the "concordance'' model prediction and also with the one determined via the analysis of the spatial two-point correlation function by Eisenstein et al. (2005, ApJ, 633, 560). The models with baryonic features are favored by
![]() over their "smoothed'' counterparts without any oscillatory behavior. This is not only an independent confirmation of results by Eisenstein et al. (2005), made with different methods and software but also, to our knowledge, is the first determination of the power spectrum of the SDSS LRG sample.
over their "smoothed'' counterparts without any oscillatory behavior. This is not only an independent confirmation of results by Eisenstein et al. (2005), made with different methods and software but also, to our knowledge, is the first determination of the power spectrum of the SDSS LRG sample.
Key words: large-scale structure of Universe
At the beginning of the 1970's it was already realized that acoustic waves in the tightly coupled baryon-photon fluid prior to the epoch of recombination will lead to characteristic maxima and minima in the post-recombination matter power spectrum. The same mechanism is also responsible for the prominent peak structure in the CMB angular power spectrum (Peebles & Yu 1970; Doroshkevich et al. 1978; Sunyaev & Zeldovich 1970). The scale of these features reflects the size of the sound horizon, which itself is fully determined given the physical densities
![]() and
and
![]() .
The acoustic horizon can be calibrated using the CMB data, thus turning it into a standard ruler which can be used to carry out classical cosmological tests. For example, if we are able to measure the redshift and angular intervals corresponding to the physically known acoustic scale in the matter power spectrum at a range of redshifts, we can immediately find the angular diameter distance
.
The acoustic horizon can be calibrated using the CMB data, thus turning it into a standard ruler which can be used to carry out classical cosmological tests. For example, if we are able to measure the redshift and angular intervals corresponding to the physically known acoustic scale in the matter power spectrum at a range of redshifts, we can immediately find the angular diameter distance ![]() and Hubble parameter H as a function of redshift. Having good knowledge of these dependencies allows us to place constraints on the properties of the dark energy. To carry out this project one needs a tracer population of objects whose clustering properties with respect to the underlying matter distribution are reasonably well understood. There have been several works discussing the use of galaxies (Hu & Haiman 2003; Blake & Glazebrook 2003; Linder 2003; Seo & Eisenstein 2003) and clusters of galaxies (Hu & Haiman 2003; Hütsi 2005; Majumdar & Mohr 2004) for this purpose. What is most important is that already currently existing galaxy redshift surveys have lead to the detection of acoustic features in the spatial distribution of galaxies, thus providing clear support for the standard gravitational instability picture of cosmic structure formation. In Eisenstein et al. (2005) the detection of the acoustic "bump'' in the two-point redshift-space correlation function of the SDSS
and Hubble parameter H as a function of redshift. Having good knowledge of these dependencies allows us to place constraints on the properties of the dark energy. To carry out this project one needs a tracer population of objects whose clustering properties with respect to the underlying matter distribution are reasonably well understood. There have been several works discussing the use of galaxies (Hu & Haiman 2003; Blake & Glazebrook 2003; Linder 2003; Seo & Eisenstein 2003) and clusters of galaxies (Hu & Haiman 2003; Hütsi 2005; Majumdar & Mohr 2004) for this purpose. What is most important is that already currently existing galaxy redshift surveys have lead to the detection of acoustic features in the spatial distribution of galaxies, thus providing clear support for the standard gravitational instability picture of cosmic structure formation. In Eisenstein et al. (2005) the detection of the acoustic "bump'' in the two-point redshift-space correlation function of the SDSS![]() LRG sample was announced. The discovery of similar features in the power spectrum of 2dF
LRG sample was announced. The discovery of similar features in the power spectrum of 2dF![]() galaxies is presented in Cole et al. (2005). These results clearly demonstrate the promise of future dedicated galaxy redshift surveys like KAOS
galaxies is presented in Cole et al. (2005). These results clearly demonstrate the promise of future dedicated galaxy redshift surveys like KAOS![]() Similarly, useful measurements of the acoustic scale may be obtained by the planned SZ cluster surveys like those of the PLANCK Surveyor
Similarly, useful measurements of the acoustic scale may be obtained by the planned SZ cluster surveys like those of the PLANCK Surveyor![]() spacecraft and SPT
spacecraft and SPT![]() (Hütsi 2005) and also with future large photometric redshift surveys (Blake & Bridle 2005). For the SZ surveys one needs an additional optical follow-up to obtain estimates for the cluster redshifts. In this paper we calculate the redshift-space power spectrum of the SDSS LRG sample finding evidence for acoustic oscillations down to the scales of
(Hütsi 2005) and also with future large photometric redshift surveys (Blake & Bridle 2005). For the SZ surveys one needs an additional optical follow-up to obtain estimates for the cluster redshifts. In this paper we calculate the redshift-space power spectrum of the SDSS LRG sample finding evidence for acoustic oscillations down to the scales of ![]()
![]() ,
which effectively correspond to the 7th peak in the CMB angular power spectrum. These scales in the CMB are very strongly damped due to the finite width of the last-scattering surface and also due to the Silk damping (Silk 1968). This can be seen in Fig. 1
,
which effectively correspond to the 7th peak in the CMB angular power spectrum. These scales in the CMB are very strongly damped due to the finite width of the last-scattering surface and also due to the Silk damping (Silk 1968). This can be seen in Fig. 1![]() where the CMB data is plotted in a somewhat unusual way to enhance the acoustic features at the high wavenumber damping tail. Also, at those scales the secondary CMB anisotropies (mostly the thermal Sunyaev-Zeldovich effect; Sunyaev & Zeldovich 1980,1972) start to dominate over the primary signal. On the other hand, features in the matter power spectrum, although small (
where the CMB data is plotted in a somewhat unusual way to enhance the acoustic features at the high wavenumber damping tail. Also, at those scales the secondary CMB anisotropies (mostly the thermal Sunyaev-Zeldovich effect; Sunyaev & Zeldovich 1980,1972) start to dominate over the primary signal. On the other hand, features in the matter power spectrum, although small (![]()
![]() fluctuations), are preserved by the linear evolution and so allow probe of acoustic phenomena at scales smaller than the ones accessible by CMB studies.
fluctuations), are preserved by the linear evolution and so allow probe of acoustic phenomena at scales smaller than the ones accessible by CMB studies.
The paper is structured as follows. In Sect. 2 we describe the dataset to be analyzed. Section 3 presents the method of the power spectrum calculation. In Sect. 4 we determine power spectrum errors and the covariance matrix. Section 5 discusses the convolution effect of the survey window. Analytical model spectra are presented in Sect. 6. The results of the measurement of the acoustic scale are given in Sect. 7. A correlation function analysis is carried out in Sect. 8. In Sect. 9 we compare the measured power spectrum with the published results for the 2dF and SDSS main sample, and conclude in Sect. 10.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{3939_f01.eps}
\end{figure}](/articles/aa/full/2006/15/aa3939-05/Timg24.gif) |
Figure 1:
Acoustic oscillations in the CMB ( upper panel) and linear matter power spectrum ( lower panel) for the "concordance'' cosmological model. Here, as we have plotted the spectra against spatial wavenumber k, we have changed the standard notation of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3939_f02.eps}
\end{figure}](/articles/aa/full/2006/15/aa3939-05/Timg25.gif) |
Figure 2: Comoving number density of galaxies as a function of comoving distance. Smooth solid line shows a cubic spline fit to the number density estimated for 50 discrete radial bins. |
| Open with DEXTER | |
Since the selection criteria are very complicated, involving both cuts in magnitude and in color, and also due to the steepness of the luminosity function, the usual method of using only the luminosity function to determine radial selection function does not work here (Zehavi et al. 2005). Rather we build the radial selection function as a smooth spline fit to the number density profiles shown in Fig. 2. To calculate distances we use the cosmological parameters as given by the WMAP![]() "concordance'' model (Spergel et al. 2003). Unfortunately the coverage masks of the SDSS DR4 spectroscopic sample are not available in a readily accessible format and so we chose to build the angular survey masks using the galaxy data itself
"concordance'' model (Spergel et al. 2003). Unfortunately the coverage masks of the SDSS DR4 spectroscopic sample are not available in a readily accessible format and so we chose to build the angular survey masks using the galaxy data itself![]() . As the number density of galaxies in the sample is rather high, one can determine relatively accurately the beginning, end and also possible gaps in the scan stripes. We have built angular masks using both the whole DR4 galaxy sample and LRGs only. The measured power spectra are practically identical with only some minor differences at smaller scales (see Fig. 6). This can be seen as an indication that our power spectrum measurements are stable against small uncertainties in the survey geometry. The angular distribution of the galaxies and also the boundaries of the survey mask built in the above-mentioned way (using all the galaxies) is shown in Fig. 3. Here the angular positions are plotted using the survey coordinate system of the SDSS
. As the number density of galaxies in the sample is rather high, one can determine relatively accurately the beginning, end and also possible gaps in the scan stripes. We have built angular masks using both the whole DR4 galaxy sample and LRGs only. The measured power spectra are practically identical with only some minor differences at smaller scales (see Fig. 6). This can be seen as an indication that our power spectrum measurements are stable against small uncertainties in the survey geometry. The angular distribution of the galaxies and also the boundaries of the survey mask built in the above-mentioned way (using all the galaxies) is shown in Fig. 3. Here the angular positions are plotted using the survey coordinate system of the SDSS![]() .
.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3939_f03.eps}
\end{figure}](/articles/aa/full/2006/15/aa3939-05/Timg28.gif) |
Figure 3:
Angular distribution of galaxies given in the SDSS survey coordinates
|
| Open with DEXTER | |
We have selected all the objects that have a spectrum classified as galaxy (i.e. SpecClass=2) and are additionally flagged as GALAXY_RED or GALAXY_RED_II (i.e. PrimTarget bit mask set as 0x20 or 0x4000000, respectively). Only galaxies for which the redshift confidence parameter, zConf, is greater than 0.95 were used.
We apply lower and upper redshift cutoffs of 0.16 and 0.47 as also done in Eisenstein et al. (2005). The lower cutoff is needed since the color cuts that define the LRG sample break down for redshifts below ![]() 0.2 (Eisenstein et al. 2001). For the analysis presented in this paper we have excluded the three southern stripes since these just increase the sidelobes of the survey window without adding much extra volume. We have also removed some minor parts of the sample to obtain a more continuous and smoother chunk of volume. In total the analyzed galaxy sample covers
0.2 (Eisenstein et al. 2001). For the analysis presented in this paper we have excluded the three southern stripes since these just increase the sidelobes of the survey window without adding much extra volume. We have also removed some minor parts of the sample to obtain a more continuous and smoother chunk of volume. In total the analyzed galaxy sample covers ![]()
![]() over
over ![]() 3850 square degrees on the sky and contains 51 763 galaxies.
3850 square degrees on the sky and contains 51 763 galaxies.
The FKP estimate for a 3D pseudospectrum is:
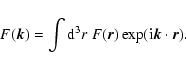 |
(2) |
| (4) | |||
| (5) |
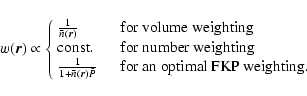 |
(6) |
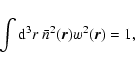 |
(7) |
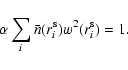 |
(8) |
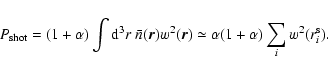 |
(9) |
![\begin{displaymath}\mathcal{W}(\vec{k}) = \left[\frac{\prod \limits_{i=1}^3 \sin...
...{{\rm Ny}}}\right)}\right]^3, \quad \vec{k} = (k_1,k_2,k_3) .
\end{displaymath}](/articles/aa/full/2006/15/aa3939-05/img60.gif) |
(11) |
![$\displaystyle \sum \limits_{\vec{n} \in \mathbb{Z}} \vert\mathcal{W}(\vec{k}+2k...
...ght)
+ \frac{2}{15}\sin^4\left(\frac{\pi k_i}{2k_{{\rm Ny}}}\right)\right]\cdot$](/articles/aa/full/2006/15/aa3939-05/img63.gif) |
(12) |
Thus, our power spectrum calculation consists of the following steps:
We determine power spectrum errors by three different methods:
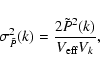 |
(16) |
![\begin{displaymath}V_{\rm eff} = \frac{\left[\int {\rm d}^3r ~\bar{n}^2(\vec{r})...
...\left[1+ \frac{1}{\bar{n}(\vec{r})\tilde{P}(k)}\right]^2}\cdot
\end{displaymath}](/articles/aa/full/2006/15/aa3939-05/img86.gif) |
(17) |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3939_f04.eps}
\end{figure}](/articles/aa/full/2006/15/aa3939-05/Timg89.gif) |
Figure 4:
Power spectrum of the SDSS LRG sample with the bin width
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3939_f05.eps}
\end{figure}](/articles/aa/full/2006/15/aa3939-05/Timg90.gif) |
Figure 5:
Power spectrum of the SDSS LRG sample with the bin width
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3939_f06.eps}\end{figure}](/articles/aa/full/2006/15/aa3939-05/Timg91.gif) |
Figure 6: The comparison of the different power spectrum error estimates. For clarity slight relative shifts of the data points have been applied. The errorbars resulting from the 1st method are the rightmost ones and the ones from the 3rd method are displayed in the middle. The lines show cubic spline fits to the data points. The solid line corresponds to the case when all the available galaxy data is used to find the angular mask of the survey, while the dashed line represents the case when LRGs only are used for this purpose. |
| Open with DEXTER | |
The comparison of the power spectrum errorbars calculated in the different ways is provided in Fig. 6. We see that the various error estimates are in very good agreement. In the following we will use only the errorbars given by the 3rd method.
So far we have only found the diagonal terms of the covariance matrix. In order to answer the question of how strongly different power spectrum bins are correlated, we must estimate the full covariance matrix.
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{3939_f07.eps}
\end{figure}](/articles/aa/full/2006/15/aa3939-05/Timg92.gif) |
Figure 7: Covariance ( left column) and correlation matrices ( right column). Top row represents the results from the FKP prescription (see Eq. (18)) and the middle row the ones from 1000 mock catalogs. The last row displays the nonlinear contribution due to the 1-halo term. |
| Open with DEXTER | |
The FKP result for the full covariance matrix, Cij, is a simple generalization of the Eq. (13):
The results for the covariance matrix calculation are given in Fig. 7. Here the left hand column shows the covariance and the right hand column the respective correlation matrices:
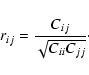 |
(19) |
In the following calculations we mostly use the covariance matrix given in the middle row of Fig. 7![]() .
.
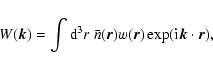 |
(21) |
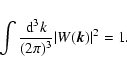 |
(22) |
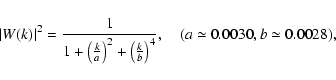 |
(23) |
Since the survey geometry of the analyzed SDSS LRG sample is far from spherically symmetric, an isotropized window in Fig. 8 gives only a poor representation of the true 3D window, which is displayed as an isosurface corresponding to the isovalue of 0.01 in Fig. 9.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3939_f08.eps}
\end{figure}](/articles/aa/full/2006/15/aa3939-05/Timg101.gif) |
Figure 8:
Isotropized survey window. Here the normalization is taken such that |W(0)|=1. The light gray stripe marks the region where the window is above |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=7.5cm,clip]{3939_f09.ps}\end{figure}](/articles/aa/full/2006/15/aa3939-05/Timg104.gif) |
Figure 9:
3D survey window embedded in a box with a side length of
|
| Open with DEXTER | |
In order to compare theoretical models to the measured power spectrum we have to take into account the smearing effects caused by the survey window. Using Eq. (20) we can express an isotropized power spectrum as:
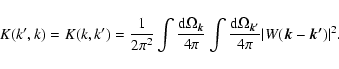 |
(25) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3939_f10.eps}
\end{figure}](/articles/aa/full/2006/15/aa3939-05/Timg107.gif) |
Figure 10:
Coupling kernels
|
| Open with DEXTER | |
 |
(26) |
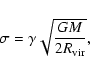 |
(27) |
For the model fitting we have used the Levenberg-Marquardt method as described in Press et al. (1992) with modifications (described in Appendix E) that allow us to incorporate correlations between the data points. As the input data we take the power spectrum estimates given in Fig. 5. The covariance matrix used is the one shown in the middle row of Fig. 7. We also perform fits where we use one additional power spectrum bin on a larger scale (not shown in Fig. 5). All of this data are given in a tabular form in Appendix G. The transfer functions needed for the linear spectra are taken from Eisenstein & Hu (1998). There the authors also provide transfer function fits where the baryonic acoustic oscillations have been removed. We use these "smoothed out'' transfer functions to assess the significance of the oscillatory features we see in the data. Throughout this paper we have kept the cosmology fixed to the best-fit WMAP "concordance'' model (Spergel et al. 2003). The implications for the cosmology, and especially for the dark energy equation of state parameter, are planned to be worked out in a future paper.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{3939_f11.eps}
\end{figure}](/articles/aa/full/2006/15/aa3939-05/Timg114.gif) |
Figure 11:
|
| Open with DEXTER | |
As the cosmology is kept fixed, we have only four free parameters. In order to eliminate some of the degeneracies between the parameters we have imposed one additional constraint. We have demanded that the resulting number of galaxies should agree with the one that is observed with a relative error of ![]() i.e.
i.e.
![]()
![]() . The resulting
. The resulting ![]() error "ellipses'' for the free parameters are shown in Fig. 11. The "ellipses'' appear deformed since instead of
error "ellipses'' for the free parameters are shown in Fig. 11. The "ellipses'' appear deformed since instead of
![]() and M0 we have fitted
and M0 we have fitted
![]() and
and ![]() .
We have marked with crosses the best fit values:
.
We have marked with crosses the best fit values:
![]() ,
,
![]() ,
,
![]() and
and
![]() .
The model spectra corresponding to these best fit parameters are shown in Figs. 4 and 5. In both figures we have also given the simple linear spectra multiplied by the square of the bias parameter b=1.95. In Fig. 4 we have additionally demonstrated the effect of the window convolution. There the dashed lines correspond to the unconvolved case. In Fig. 5, along with the "wiggly'' spectra we have shown their "smoothed'' counterparts. Using all the 16 power spectrum bins (the 1st not shown in Fig. 5) plus an additional constraint on the total number of galaxies, resulting in 17-4 = 13 independent degrees of freedom, we obtain
.
The model spectra corresponding to these best fit parameters are shown in Figs. 4 and 5. In both figures we have also given the simple linear spectra multiplied by the square of the bias parameter b=1.95. In Fig. 4 we have additionally demonstrated the effect of the window convolution. There the dashed lines correspond to the unconvolved case. In Fig. 5, along with the "wiggly'' spectra we have shown their "smoothed'' counterparts. Using all the 16 power spectrum bins (the 1st not shown in Fig. 5) plus an additional constraint on the total number of galaxies, resulting in 17-4 = 13 independent degrees of freedom, we obtain ![]() values of 8.8 and 19.9 for the "wiggly'' and "smoothed''
values of 8.8 and 19.9 for the "wiggly'' and "smoothed''![]() models, respectively. So the models with oscillations are favored by
models, respectively. So the models with oscillations are favored by
![]() over their "smoothed'' counterparts
over their "smoothed'' counterparts![]() . Since both models have the same number of free parameters, and if additionally the assumption of Gaussianity is valid, the Bayesian approach should give similar results. Actually, Bayesian results should favor "wiggly'' models even more, since prior weight for these should probably be taken higher (assuming knowledge of the other experimental results).
. Since both models have the same number of free parameters, and if additionally the assumption of Gaussianity is valid, the Bayesian approach should give similar results. Actually, Bayesian results should favor "wiggly'' models even more, since prior weight for these should probably be taken higher (assuming knowledge of the other experimental results).
To measure the scale of the acoustic oscillations we divide the spectrum shown in Fig. 5 by the best fitting "smoothed'' spectrum. The result of this procedure is given in the upper panel of Fig. 12. There the solid line shows a cubic spline fit to the data points and the long-dashed line corresponds to the best fitting model spectrum also shown in Fig. 5. The above data is fitted with a parametric form:
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3939_f12.eps}
\end{figure}](/articles/aa/full/2006/15/aa3939-05/Timg130.gif) |
Figure 12: Upper panel: power spectrum from Fig. 5 divided by the best fitting "smoothed'' spectrum. Solid line shows a cubic spline fit to the data points and long-dashed line corresponds to the best "wiggly'' model. The short-dashed line represents the most favorable fit from the parametric family of Eq. (28). Lower panel: various input power spectra used to calculate the two-point correlation function. The dashed line is the cubic spline fit from the upper panel. The solid lines represent a transition sequence from the best fitting "wiggly'' model to the best "smoothed'' model. In each step we have erased more oscillatory features. For clarity slight vertical shifts have been introduced. |
| Open with DEXTER | |
The sinusoidal modulation in the power spectrum is a consequence of the adiabatic initial conditions. By relaxing this assumption
and fitting with a more general functional form:
![\begin{displaymath}f(x)=1+c_1\cdot\sin(c_2\cdot x + c_3)\exp\left[\left(-\frac{x}{c_4}\right)^{c_5}\right]
\end{displaymath}](/articles/aa/full/2006/15/aa3939-05/img131.gif) |
(29) |
Eisenstein et al. (2005) determined various distance scales (like Dv, which is a specific combination of the comoving distances along and perpendicular to the line of sight (see their Eq. (2))) and their ratios, using SDSS LRGs and the constraints from other cosmological sources. The typical relative accuracy of these measurements is ![]()
![]() ,
which seems worse than the accuracy of the acoustic scale measurement,
,
which seems worse than the accuracy of the acoustic scale measurement,
![]() i.e.
i.e. ![]()
![]() ,
presented in this paper. This apparent inconsistency can be attributed to the fact that in our analysis, as stated above, we have kept the cosmology fixed to the WMAP "concordance'' model, whereas the Eisenstein et al. (2005) estimates include the extra uncertainties due to the imperfect knowledge of the various cosmological parameters. Of course, the given length of the acoustic scale,
,
presented in this paper. This apparent inconsistency can be attributed to the fact that in our analysis, as stated above, we have kept the cosmology fixed to the WMAP "concordance'' model, whereas the Eisenstein et al. (2005) estimates include the extra uncertainties due to the imperfect knowledge of the various cosmological parameters. Of course, the given length of the acoustic scale,
![]() ,
can be easily transformed in order to accommodate other preferences for the background cosmology. We also note that the use of the parametric form in Eq. (28) might be too restrictive, since the acoustic modulation in the case of adiabatic models can be only approximately described as a damped sinusoidal wave (Eisenstein & Hu 1998). For this reason the given sound horizon constraint should not be used in cosmological parameter studies. Instead one should directly use the measured power spectrum in combination with the parametrized models that are physically well motivated.
,
can be easily transformed in order to accommodate other preferences for the background cosmology. We also note that the use of the parametric form in Eq. (28) might be too restrictive, since the acoustic modulation in the case of adiabatic models can be only approximately described as a damped sinusoidal wave (Eisenstein & Hu 1998). For this reason the given sound horizon constraint should not be used in cosmological parameter studies. Instead one should directly use the measured power spectrum in combination with the parametrized models that are physically well motivated.
We determine the two-point correlation function of the SDSS LRGs using the edge-corrected estimator given by Landy & Szalay (1993):
![$\displaystyle \sigma^2_{\xi}(r_i) = \frac{N-1}{N}\sum \limits_{j=1}^N \left[\xi_j(r_i) -\bar{\xi}(r_i)\right]^2 ,$](/articles/aa/full/2006/15/aa3939-05/img140.gif) |
(31) | ||
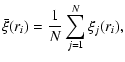 |
(32) |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3939_f13.eps}
\end{figure}](/articles/aa/full/2006/15/aa3939-05/Timg142.gif) |
Figure 13: Left panel: two-point correlation functions as determined in this paper (circles with solid lines) and by Eisenstein et al. (2005). Right panel: correlation functions corresponding to the models shown in the lower panel of Fig. 12 in comparison to the one obtained directly from the data. Here all the data points have been lowered by 0.0035. |
| Open with DEXTER | |
It would be interesting to study how the oscillations in the observed power spectrum transform into the peak in the two-point correlation function seen at the scale of ![]()
![]() .
For this purpose we use the cubic spline fit shown in Fig. 12 and extend it outside of the observed range by smoothly joining it to the power spectrum of the best fitting "smoothed'' model. The correlation function is now simply calculated as the Fourier transform of the power spectrum
.
For this purpose we use the cubic spline fit shown in Fig. 12 and extend it outside of the observed range by smoothly joining it to the power spectrum of the best fitting "smoothed'' model. The correlation function is now simply calculated as the Fourier transform of the power spectrum![]() . The resulting correlation function is plotted with a dashed line in the right panel of Fig. 13. To study the significance of the oscillatory features in the power spectrum in relation to the observed peak in the correlation function, we have calculated correlation functions for several models that have oscillations "switched off'' at various scales. The spectra of these models are shown with solid lines in the lower panel of Fig. 12, where for clarity we have introduced slight vertical shifts between the curves, so that the scales where the transition to the featureless spectrum takes place are easily visible. The corresponding correlation functions are given with solid lines in the right hand panel of Fig. 13. As expected, we see the peak in the correlation function becomes broader and also decreases in amplitude as we successively erase features in the power spectrum. This clearly demonstrates the importance of many of the fluctuations in the power spectrum to produce a relatively sharp feature in the two-point correlation function.
. The resulting correlation function is plotted with a dashed line in the right panel of Fig. 13. To study the significance of the oscillatory features in the power spectrum in relation to the observed peak in the correlation function, we have calculated correlation functions for several models that have oscillations "switched off'' at various scales. The spectra of these models are shown with solid lines in the lower panel of Fig. 12, where for clarity we have introduced slight vertical shifts between the curves, so that the scales where the transition to the featureless spectrum takes place are easily visible. The corresponding correlation functions are given with solid lines in the right hand panel of Fig. 13. As expected, we see the peak in the correlation function becomes broader and also decreases in amplitude as we successively erase features in the power spectrum. This clearly demonstrates the importance of many of the fluctuations in the power spectrum to produce a relatively sharp feature in the two-point correlation function.
In order to achieve good agreement we have lowered all the data points by 0.0035 in the right hand panel of Fig. 13. Similar shifts were also suggested in Eisenstein et al. (2005) in order to get a better match to the theoretical models. A 0.0035 shift in ![]() translates to the
translates to the ![]() shift in the mean density. Thus, if one wishes to determine the amplitude of the correlation function correctly at those large scales, one has to determine the survey selection function with a very high precision, which in practice is very difficult to achieve. By using model spectra that have more large scale power than the "concordance'' cosmology predicts (as might be suggested by Fig. 4), we are able to match the amplitude of the correlation function without any additional vertical shifts. Here we try to avoid making any definite conclusions. The behavior of the power spectrum on the largest scales is a whole interesting topic on its own and there exist much better methods than the direct Fourier approach to investigate these issues (see e.g. Tegmark et al. 1998).
shift in the mean density. Thus, if one wishes to determine the amplitude of the correlation function correctly at those large scales, one has to determine the survey selection function with a very high precision, which in practice is very difficult to achieve. By using model spectra that have more large scale power than the "concordance'' cosmology predicts (as might be suggested by Fig. 4), we are able to match the amplitude of the correlation function without any additional vertical shifts. Here we try to avoid making any definite conclusions. The behavior of the power spectrum on the largest scales is a whole interesting topic on its own and there exist much better methods than the direct Fourier approach to investigate these issues (see e.g. Tegmark et al. 1998).
In this section we compare our power spectrum measurements with the ones obtained by Percival et al. (2001) and Cole et al. (2005) for the 2dF redshift survey and by Tegmark et al. (2004) for the SDSS main galaxy sample. The results of this comparison are provided in Figs. 14 and 15. For clarity we have given a variant of Fig. 14 where we have omitted the errorbars. The amplitudes of the SDSS main and 2dF spectra have been freely adjusted to match the clustering strength of the SDSS LRGs. The corresponding bias parameters with respect to the SDSS LRGs are 0.53, 0.61 and 0.50 for the 2dF sample analyzed by Percival et al. (2001), for the one analyzed by Cole et al. (2005), and for the SDSS main sample, respectively. Percival et al. (2001) also provide power spectrum measurements for
![]() but without errorbars. These small-scale measurements along with our SDSS LRG results are shown with solid lines in Fig. 14.
but without errorbars. These small-scale measurements along with our SDSS LRG results are shown with solid lines in Fig. 14.
In general the shapes of the spectra agree remarkably well. With the only exception of the Tegmark et al. (2004) results, the power spectrum bins are significantly correlated. Also the Tegmark et al. (2004) measurements are corrected for the redshift space distortions.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3939_f14.eps}
\end{figure}](/articles/aa/full/2006/15/aa3939-05/Timg149.gif) |
Figure 14: The comparison of spectra from different surveys. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3939_f15.eps}
\end{figure}](/articles/aa/full/2006/15/aa3939-05/Timg150.gif) |
Figure 15: The same as Fig. 14 with the errorbars omitted. |
| Open with DEXTER | |
The existence of baryonic features in the galaxy power spectrum is very important, allowing one (in principle) to obtain the Hubble parameter H and angular diameter distance dA as a function of redshift, this way opening up a possibility to constrain properties of the dark energy (Hu & Haiman 2003). The currently existing largest redshift surveys, which are still quite shallow, do not yet provide enough information to do this properly. On the other hand, it is extremely encouraging that even with the current generation of redshift surveys we are already able to see traces of acoustic oscillations in the galaxy power spectrum, showing the promise for dedicated future surveys like KAOS. We have seen that acoustic features seem to survive at mildly nonlinear scales (
![]() ), which is in agreement with the results of the recent N-body simulations (Springel et al. 2005; Seo & Eisenstein 2005). In order to fully exploit the available information one needs a complete understanding of how nonlinear effects influence these features. Nonlinear bias and redshift space distortions also add complications. In general, redshift-space distortions, biasing and nonlinear evolution do not create any oscillatory modulation in the power spectrum and so acoustic features should be readily observable.
So far there have been only a few works studying these important issues (e.g. Springel et al. 2005; White 2005; Seo & Eisenstein 2005) and currently we do not have a full theoretical description of them. In our paper we have modeled the above-mentioned effects using the results from the 2nd order Lagrangian perturbation theory in combination with the Halo Model. Although these models are very successful in capturing many important aspects of structure formation, they are still approximations.
), which is in agreement with the results of the recent N-body simulations (Springel et al. 2005; Seo & Eisenstein 2005). In order to fully exploit the available information one needs a complete understanding of how nonlinear effects influence these features. Nonlinear bias and redshift space distortions also add complications. In general, redshift-space distortions, biasing and nonlinear evolution do not create any oscillatory modulation in the power spectrum and so acoustic features should be readily observable.
So far there have been only a few works studying these important issues (e.g. Springel et al. 2005; White 2005; Seo & Eisenstein 2005) and currently we do not have a full theoretical description of them. In our paper we have modeled the above-mentioned effects using the results from the 2nd order Lagrangian perturbation theory in combination with the Halo Model. Although these models are very successful in capturing many important aspects of structure formation, they are still approximations.
The existence of baryonic oscillations in the galaxy power spectrum gives us important information about the underlying cosmological model and the mechanism of structure formation. First, it confirms the generic picture of the gravitational instability theory where the structure in the Universe is believed to have been formed by the gravitational amplification of the small perturbations layed down in the early Universe. Under linear gravitational evolution all the density fluctuation modes evolve independently i.e. all the features in the power spectrum will be preserved. We are now indeed able to identify features in the low redshift galaxy power spectrum that correspond to the fluctuations seen in the CMB angular power spectrum (which probes redshifts
![]() ), providing strong support for this standard picture of structure formation. We can even probe scales that are inaccessible to CMB studies due to the strong damping effects and steeply rising influence of the secondary anisotropies, effectively reaching wavenumbers that correspond to the 6th-7th peak in the CMB angular power spectrum. Second, the ability to observe baryonic features in the low redshift galaxy power spectrum demands rather high baryonic to total matter density ratio. In Blanchard et al. (2003) it has been shown that it is possible to fit a large body of observational data with an Einstein-de Sitter type model if one adopts a low value for the Hubble parameter and relaxes the usual assumptions about the single power law initial spectrum. In the light of our results these models are disfavored due to the fact that the high dark matter density completely damps the baryonic features. Finally, purely baryonic models are also ruled out since for them the expected acoustic scale would be roughly two times larger than observed here
), providing strong support for this standard picture of structure formation. We can even probe scales that are inaccessible to CMB studies due to the strong damping effects and steeply rising influence of the secondary anisotropies, effectively reaching wavenumbers that correspond to the 6th-7th peak in the CMB angular power spectrum. Second, the ability to observe baryonic features in the low redshift galaxy power spectrum demands rather high baryonic to total matter density ratio. In Blanchard et al. (2003) it has been shown that it is possible to fit a large body of observational data with an Einstein-de Sitter type model if one adopts a low value for the Hubble parameter and relaxes the usual assumptions about the single power law initial spectrum. In the light of our results these models are disfavored due to the fact that the high dark matter density completely damps the baryonic features. Finally, purely baryonic models are also ruled out since for them the expected acoustic scale would be roughly two times larger than observed here![]() . Thus the data seems to demand a weakly interacting nonrelativistic matter component and all the models that try to replace this dark matter component with "something else'' e.g. modifying the laws of gravity, might have severe difficulties in fitting these new observational constraints.
. Thus the data seems to demand a weakly interacting nonrelativistic matter component and all the models that try to replace this dark matter component with "something else'' e.g. modifying the laws of gravity, might have severe difficulties in fitting these new observational constraints.
Acknowledgements
I thank Rashid Sunyaev and the referee for helpful comments and suggestions. I acknowledge the International Max-Planck Research School on Astrophysics for a graduate fellowship and the support provided through Estonian Ministry of Education and Recearch project TO 0062465S03 and and ESF grant 5347.Funding for the creation and distribution of the SDSS Archive has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Aeronautics and Space Administration, the National Science Foundation, the US Department of Energy, the Japanese Monbukagakusho, and the Max Planck Society. The SDSS Web site is http://www.sdss.org/
The SDSS is managed by the Astrophysical Research Consortium (ARC) for the Participating Institutions. The Participating Institutions are The University of Chicago, Fermilab, the Institute for Advanced Study, the Japan Participation Group, The Johns Hopkins University, the Korean Scientist Group, Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington.
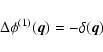 |
(B.3) |
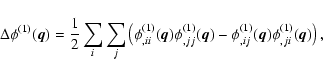 |
(B.4) |
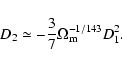 |
(B.5) |
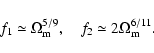 |
(B.7) |
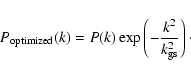 |
(B.8) |
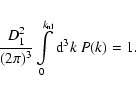 |
(B.9) |
In our calculations we assume the WMAP "concordance'' cosmology (Spergel et al. 2003). The linear power spectrum is taken from Eisenstein & Hu (1998). We build a 2LPT density field on a 2563-grid with
![]() cell size using the same number of particles as the number of grid cells
cell size using the same number of particles as the number of grid cells![]() . Four copies of this box are combined to form a large
. Four copies of this box are combined to form a large
![]() volume. Out of that big box a sample of "galaxies'' is selected with a radial number density as given in Fig. 2 and with an angular mask presented in Fig. 3. The parameters of the Poisson sampler
volume. Out of that big box a sample of "galaxies'' is selected with a radial number density as given in Fig. 2 and with an angular mask presented in Fig. 3. The parameters of the Poisson sampler![]() are tuned to give a sample with a bias parameter
are tuned to give a sample with a bias parameter
![]() in agreement with the observed value for the SDSS LRG sample. The redshift-space catalog is built by altering the radial distances of the "galaxies'' by
in agreement with the observed value for the SDSS LRG sample. The redshift-space catalog is built by altering the radial distances of the "galaxies'' by
![]() ,
where
,
where ![]() is the radial component of the peculiar velocity field (see Eq. (B.6)) and
is the radial component of the peculiar velocity field (see Eq. (B.6)) and
![]() .
.
In Fig. B.1 we show a
![]() thick slice through a box with
thick slice through a box with
![]() side length. The underlying density field is presented as a gray scale image with white dots marking the positions of the "galaxies''. The power spectrum of the sample of
side length. The underlying density field is presented as a gray scale image with white dots marking the positions of the "galaxies''. The power spectrum of the sample of ![]() 350 000 "galaxies'' is shown in Fig. B.2
350 000 "galaxies'' is shown in Fig. B.2![]() . We see that the shape of the spectrum is in good agreement with the linearly evolved power spectrum up to the scales of
. We see that the shape of the spectrum is in good agreement with the linearly evolved power spectrum up to the scales of
![]() .
.
This approach gives us a "galaxy'' sample that has realistic large-scale clustering properties. In terms of the Halo Model (see Appendix C) the halo-halo clustering term is properly accounted for. 2LPT also gives reasonably accurate higher order correlations on quasi-nonlinear scales (e.g. Scoccimarro & Sheth 2002; Bouchet et al. 1995).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3939_f18.eps}\end{figure}](/articles/aa/full/2006/15/aa3939-05/Timg187.gif) |
Figure B.2:
The power spectrum of |
The halo model description of the spatial clustering of galaxies is a development of the original idea by Neyman & Scott (1952), where one describes the correlations of the total point set as arising from two separate terms: (i) the 1-halo term, that describes the correlations of galaxies populating the same halo, (ii) the 2-halo term, which takes into account correlations of the galaxies occupying different halos. For a thorough review see Cooray & Sheth (2002). Here we briefly give the results relevant to the current paper (see Cooray 2004; Seljak 2001).
The power spectrum of galaxies in redshift space can be given as:
| P(k) = P1h(k) + P2h(k) , | (C.1) |
| (C.2) | |||
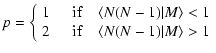 |
(C.3) |
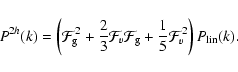 |
(C.4) |
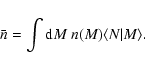 |
(C.8) |
After specifying the background cosmology the above described model has four free parameters: M0, ![]() (Eq. (C.9)),
(Eq. (C.9)), ![]() (Eq. (C.12)) and
(Eq. (C.12)) and
![]() .
The last parameter
.
The last parameter
![]() represents the lower boundary of the mass integration i.e. halos with masses below
represents the lower boundary of the mass integration i.e. halos with masses below
![]() are assumed to be "dark''.
are assumed to be "dark''.
One can also use the halo model to estimate nonlinear contributions to the power spectrum covariance matrix. The additional term to the covariance matrix
CijNL (i,j denote power spectrum bins) arising from the parallelogram configurations of the trispectrum![]() is given by (Cooray 2004):
is given by (Cooray 2004):
| (C.14) |
In this appendix we provide analytical fitting formulae for the coupling kernels K(k,k') in Eq. (24)![]() . The analytic form is motivated by the fact that the angle averaged survey window |W(k)|2 (see Fig. 8) can be reasonably well approximated by the analytical form:
. The analytic form is motivated by the fact that the angle averaged survey window |W(k)|2 (see Fig. 8) can be reasonably well approximated by the analytical form:
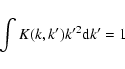 |
(D.3) |
Depending on the values of a and b there are two different solutions.
![\begin{displaymath}K(k,k') = \frac{C}{kk'}\ln \left[ \frac{g(k-k')}{g(k+k')} \right] ,
\end{displaymath}](/articles/aa/full/2006/15/aa3939-05/img212.gif) |
(D.4) |
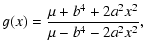 |
(D.5) | ||
| (D.6) |
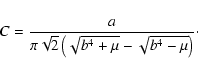 |
(D.7) |
![\begin{displaymath}K(k,k') = \frac{C}{kk'} \left[ g(k+k') - g(k-k') \right] ,
\end{displaymath}](/articles/aa/full/2006/15/aa3939-05/img216.gif) |
(D.8) |
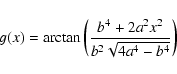 |
(D.9) |
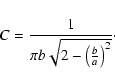 |
(D.10) |
Using their notation, ![]() is now calculated as:
is now calculated as:
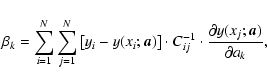 |
(E.2) |
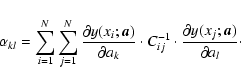 |
(E.3) |
Under the assumption that statistical fluctuations
![]()
![]() in Eq. (E.1) are Gaussian distributed, with covariance matrix Cij, one can easily derive probability density function (pdf) for the quantity
in Eq. (E.1) are Gaussian distributed, with covariance matrix Cij, one can easily derive probability density function (pdf) for the quantity ![]() ,
and thus open up a way to estimate the goodness of fit. The
,
and thus open up a way to estimate the goodness of fit. The ![]() goodness-of-fit estimator is usually exploited in the case of independent Gaussian variables. Here we show that calculating
goodness-of-fit estimator is usually exploited in the case of independent Gaussian variables. Here we show that calculating ![]() for the correlated Gaussian data as given in Eq. (E.1), one obtains the same result that is well known for the independently distributed case.
for the correlated Gaussian data as given in Eq. (E.1), one obtains the same result that is well known for the independently distributed case.
According to our assumption
![]() is Gaussian distributed:
is Gaussian distributed:
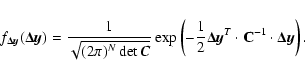 |
(F.1) |
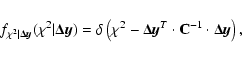 |
(F.2) |
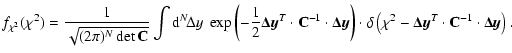 |
(F.3) |
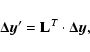 |
(F.4) |
| (F.5) |
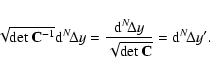 |
(F.6) |
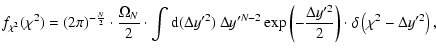 |
(F.7) |
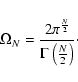 |
(F.8) |
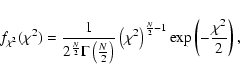 |
(F.9) |
Now it is straightforward to calculate p-values describing the goodness of fit.
Table G.1: Measured SDSS LRG power spectrum and covariance matrix from 1000 mock catalogs.