A&A 449, 827-836 (2006)
DOI: 10.1051/0004-6361:20054180

Chromaticity in all-reflective telescopes for astrometry

D. Busonero1,2 - M. Gai1 - D. Gardiol1 - M. G. Lattanzi1 - D. Loreggia1


1 - National Institute of Astrophysics (INAF), Astronomical Observatory of Turin, via Osservatorio 20, 10025 Pino Torinese, Turin, Italy
2 - University of Siena, Department of Physics, via Roma 56, 53100 Siena, Italy

Received 9 September 2005 / Accepted 20 October 2005

Abstract
Aims. Chromatic effects are usually associated with refractive optics, so reflective telescopes are assumed to be free from them. We show that all-reflective optics still bears significant levels of such perturbations, which are especially critical to modern micro-arcsecond astrometric experiments.
Methods. We analyze the image formation and measurement process to derive a precise definition of the chromatic variation of the image position, and we evaluate the key aspects of optical design with respect to chromaticity.
Results. The fundamental requirement related to chromaticity is the symmetry of the optical design and of the wavefront errors. Finally, we address some optical engineering issues, such as manufacturing and alignment, providing recommendations to minimize the degradation that chromaticity introduces into astrometry.

Key words: astrometry - methods: data analysis - space vehicles: instruments - techniques: high angular resolution - telescopes

1 Introduction

Chromatism is usually defined for refractive optics as an aberration due to the light dispersion of the glass with the refractive index; this induces a perturbation on the image profile, depending upon the source color. In astrometry, it provides a variation in the apparent star position, i.e. an astrometric error.

This effect can be reduced by using more complex refractive systems (doublets, triplets, etc.), taking advantage of the different dispersion of glasses to achieve a certain degree of compensation. For most purposes, the only way to avoid chromatism is considered to be adoption of a completely reflecting design. Here, we show that, at the demanding level of modern astrometry, reflective optics is still affected by significant chromatic effects, which we will refer to as "chromaticity''. We investigate the source of the chromaticity and provide recommendations for its minimization in optical design, manufacturing, and alignment.

Currently, space astrometry experiments are being designed and implemented with the goal of micro-arcsecond (hereafter, $\rm {\mu as}$) measurements. We will refer to the framework of the Gaia mission, approved within the space science program of ESA for launch before 2012. Built upon the implementation of the Hipparcos (ESA 1997) concept, with the benefit of modern technology and more advanced astrophysical understanding, Gaia aims to measure absolute position, parallax and annual proper motion of $\sim$109 objects with a typical accuracy of $\sim$15  $\rm {\mu as}$ for V=15 stars, with survey completeness to V=18 and limiting magnitude V=20 (Perryman et al. 2001). Hipparcos's payload was already affected by chromaticity at the mas-level, and during Gaia's design phase it soon became apparent that its all-reflective optics would also be affected by chromaticity at a similar level (Lattanzi et al. 1998). Therefore chromaticity in Gaia must be suppressed by more than two orders of magnitude.

  \begin{figure} \par\includegraphics[angle=-90,width=8.2cm,clip]{4180fig1a.ps}\includegraphics[angle=-90,width=8.2cm,clip]{4180fig1b.eps} \end{figure} Figure 1: A Gaia-like astrometric payload layout. Left: the set of two telescopes combined at mirror M4 (planar drawing). Right: individual telescope layout. LOS A and LOS B are the two lines of sight implemented in this two-telescope configuration.
Open with DEXTER

We describe how the aberrations of a realistic all-reflective optical system can lead to chromaticity as a consequence of light diffraction, even when propagation occurs in a practically non-dispersive medium as would be the case for payloads sent outside the Earth's atmosphere. Although our discussion focuses on Gaia, the concepts and considerations developed here about sources of chromatic errors and how to deal with them can apply to all experiments wishing to reach astrometric accuracy down to the mas-level and beyond.

The aspects evidenced by our study of chromaticity are of critical importance for compiling detailed error budgets and deciding on actions for controlling systematic errors. Also, the degree of detail in instrument and measurement models required to keep chromaticity at the $\rm {\mu as}$-level can help prevent (during design), monitor (throughout operations), and correct (in data reduction) other possible sources of systematic errors associated with an image profile and its temporal and spatial variations. A possible method for chromaticity correction is described in Gai & Cancelliere (2005).

In Sect. 2, we recall the relevant basic principles of a global astrometric mission like Gaia[*]. In Sect. 3, we introduce chromaticity for an all-reflecting optical system through a simplified analytical model, which is also utilized to prove the linear dependence of chromaticity on wavelength. Section 4 presents the chromaticity analysis for a realistic representation of the Gaia optical system. Section 5 provides prescriptions for minimizing chromaticity in optical designs. In Sect. 6, we present the field-of-view (FOV) distribution of chromaticity and methods for its reduction. Finally, conclusions are drawn in Sect. 7.

   
2 Telescopes for global astrometry

Global astrometry is the direct measurement of angular position, parallax, and proper motion, i.e. of those fundamental parameters that define, along with the line-of-sight (LOS) velocity, the location and status of motion of every object in space. The success of the Hipparcos mission established that the only meaningful way to achieve global astrometry is from a space-born platform. Suitable observing strategies and a sufficiently long operational life-time would allow the whole sky to be covered repeatedly thus providing the means to derive positions and their variations with time. As the result of renewed interest in global astrometry by the astronomical community worldwide, several missions are being considered by the major space astronomy communities. In Japan studies are underway on the near-infrared astrometry mission JASMINE (Gouda et al. 2005) for a possible launch in 2014. In the United States, the NASA funded concept study for the possible development of the Origins Billion Star Survey (OBSS) is close to completion (Johnston et al. 2005), while teams at Jet Propulsion Laboratory (JPL) are well into the development of SIM (Space Interferometry Mission), due for launch in 2011 (Marr 2003).

In Europe, following formal approval in 2000, the European Space Agency (ESA) is developing its new astrometric mission Gaia, which is based on the same two-FOV's scanning satellite concept implemented on Hipparcos, and is meant to increase the measurement capabilities of its predecessor by about two orders of magnitude.

Two different optical systems were considered during the study phase, so that we will not know the optical configuration that will fly on Gaia before final selection of the industrial contractor (expected by early 2006). However, this is not a problem for the scope of this work as both designs are based on all-reflective optics, and we can still refer to one of them without loss of generality. We chose to refer to the configuration known in Gaia jargon as the "Baseline Configuration'' (Perryman et al. 2001). It consists of the combination of two off-axis, three-mirror monolithic telescopes mounted on a common optical bench, as shown in Fig. 1 (left). The individual telescope has an effective focal length (EFL) of 46.7 m and a rectangular collecting area of $1.4 \times 0.5\ \rm {m^{2}}$, resulting in a central lobe size (analogous to the Airy diameter for circular pupils) of $\sim$ $ 250 \times 700$ mas at the effective wavelength $\lambda_{\rm {eff}} = 700$ nm. We constructed a computer model of the Baseline Configuration by utilizing the CODE V optical modelling package (ORA 1995), and optimized the system over a FOV of $0\hbox{$.\!\!^\circ$ }66 \times 0\hbox{$.\!\!^\circ$ }66$ by closely following the procedure described in Loreggia et al. (2004). With reference to Fig. 1 (right), the optical train of each telescope consists of seven elements: three mirrors (M1, M2, M3) with optical power, three flat mirrors (M4, M5, M6) for beam-folding, and the focal plane (FP). The FOV covers the angular ranges $[-0\hbox{$.\!\!^\circ$ }33, 0\hbox{$.\!\!^\circ$ }33]$ in the along-scan direction and $[0\hbox{$.\!\!^\circ$ }20, 0\hbox{$.\!\!^\circ$ }86]$ in the across-scan direction; the off-axis design is required to avoid vignetting. One of the possible implementations investigated for the Gaia FP assembly calls for an array of 17 (along-scan) $\times$ 10 (across-scan) CCDs working in time delay integration (TDI) mode (Saint-Pe et al. 2000). Each along-scan strip of devices hosts: two chips for the functions of target detection and confirmation, eleven CCDs for the repeated astrometric measurement, four units for broadband photometry. The rationale for photometry is both astrophysical (stellar classification) and technical (chromaticity correction discussed below).

During each transit, the image of a target on any of the eleven astrometric CCDs is binned across scan, and centered along scan, providing independent one-dimensional location estimates of comparable precision (Gai et al. 2001 and references therein). The composition of repeated along-scan measurements, taken for every location on the sky with different orientations, allows the determination of the bi-dimensional angular coordinates in a common reference system ("global sphere reconstruction''). The evolution of the apparent source position during the mission lifetime ($\sim$5 years) yields absolute parallax and proper motion.

Note that the relative orientation of the two telescopes, i.e. the base angle (BA), is a key factor of the measurement process: the on-sky separation between two stars entering the two different FOV's is obtained from the measured difference in FP coordinates plus the BA; therefore, configuration perturbations of a few nm, negligible as to the optical response, are critical to astrometry as they can induce errors up to several tens  $\rm {\mu as}$. Laser-based metrology lines are expected to monitor and (if necessary) to control the BA stability that also sets stringent constraints on payload thermal stability (Gardiol et al. 2004).

3 Chromaticity

   
3.1 A basic analytical model

Chromaticity in all-reflective optical systems can be defined as the shift in the FP location of the images of two sources of different spectral types sharing the same direction in object space. Also, chromaticity is an intrinsic characteristic of diffraction that cannot be neglected when the targeted accuracy level is at the mas level and higher, as was the case for Hipparcos and will be for Gaia.

We verified the presence of chromaticity is mainly related to wavelength; sampling of the telescope point spread function (PSF) and dimensions of the read-out region of the FP play a secondary role in the actual amount of chromaticity displayed by the realization of any all-reflective optical design.

Also, we will see that for a symmetric PSF there is no chromaticity apart from possible residual effects due to sampling and other noise sources (e.g. photon noise). On the other hand, for an asymmetric[*] PSF, most of the chromatic effect, ${\Delta}$, can be modelled for every location estimators tested as a linear function of the change in effective wavelength $\delta\lambda_{\rm {eff}}$, characterizing the spectral difference of the sources, through a coefficient g(x,y) that depends on the local shape of the PSF, f(x,y), i.e. on the contributions of the aberrations over the FOV:

 \begin{displaymath}{\Delta}= g(x,y)\cdot \delta\lambda_{\rm {eff}}, \end{displaymath} (1)

where (x,y) are linear coordinates on the FP.

We illustrate relation (1) with the help of ad hoc analytical model. We choose an asymmetric, one-dimensional bell-shaped curve, in the form of a deformed Gaussian profile, i.e. of different width on the opposite sides of its peak value (at y=0)[*]:

 \begin{displaymath}f(y)= \frac{1}{\lambda\sigma_{0}\sqrt{2{\rm\pi}}} \cdot \exp ... ...pace{0.1in}\sigma = \sigma_{0}+\epsilon\frac{y}{\vert y\vert}, \end{displaymath} (2)

$\epsilon$ being the "asymmetry'' factor ( $\epsilon \ll \sigma_0$). For continuity of the PSF, we must set

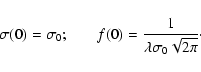\begin{displaymath}\sigma(0)=\sigma_{0} ;\hspace{0.25in} f(0)= \frac{1}{\lambda\sigma_{0}\sqrt{2{\rm\pi}}} \cdot \end{displaymath} (3)

Note that the position of the maximum is the origin, independent of $\lambda$.

For two different wavelengths $\lambda_{1}<\lambda_{2}$, the normalization condition requires that the maximum value decreases as the curve width increases. This agrees with the physical condition that in the diffraction limit, the PSF of an optical system increases in linear size with the wavelength. In particular, the PSF is a function of the wavelength $\lambda$, the position on the FP y, and of the characteristic linear dimension D of the optical system, in a well-defined form required for dimensional reasons:

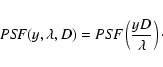\begin{displaymath}{\it PSF}(y,\lambda,D) = {\it PSF}\left(\frac{yD}{\lambda}\right)\cdot \end{displaymath} (4)

This is the typical form of the argument of the diffraction pattern for the analytical reference cases solved in the literature. Therefore, a change in wavelength corresponds, for the PSF, to a scaling of the FP coordinates; any parameter weighted with this distribution will be affected by such variation.

Let us evaluate the behavior of, e.g. the center of gravity (COG) estimator, for the model in Eq.  (2) over the region of interest [-a,a]:

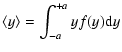                                             $\displaystyle \langle y \rangle = \int_{-a}^{+a} yf(y) {\rm d}y$  
    $\displaystyle \quad=\displaystyle{\frac{\lambda}{\sqrt{2{\rm\pi}}}}\left[4\epsi... ...dot\exp{-\frac{1}{2}\left[\frac{a}{\lambda(\sigma_0-\epsilon)}\right]^2}\right.$  
    $\displaystyle \left.\quad\quad-\displaystyle{\frac{(\sigma_0+\epsilon)^2}{\sigm... ...\right]^2}\right]\sim \displaystyle{\frac{\lambda4\epsilon}{\sqrt{2{\rm\pi}}}},$ (5)

where the approximation is valid for $a > \sigma_0 \lambda$. The COG represents one of the possible estimators of the photo-center location. In the Gaia literature, for example, the photo-center location of a realistic, digitized image is named "centroid'' for each estimator used. Nevertheless, in this paper we retain the expression COG for ease of the reader. The photo-center is linearly dependent on the selected wavelength through an asymmetry factor $\epsilon$, representing the difference between the two sides of the PSF, and the chromaticity relation  (1) becomes:

 \begin{displaymath}{\Delta}={\delta \langle y \rangle}= \frac{4\epsilon}{\sqrt{2{\rm\pi}}}\cdot \delta\lambda_{\rm {eff}} . \end{displaymath} (6)

In a more general case, the parameter $\epsilon$ can be considered a slowly varying function of the focal plane coordinates, i.e. $\epsilon(x,y)$, to account for the variation of the optical response (aberration distribution) over the FOV. Also, different location estimators would generate functional forms different from that in Eq.  (6).

   
3.2 Asymmetric PSF with coma

The results of the previous section can be verified, in a more general way, from the Fraunhofer integral for a circular aperture of radius a:

 \begin{displaymath}U(u,v)={C}\!\! \int_0^1\!\!\!\!\int_0^{2{\rm\pi}}\!\!\! \exp[... ...theta - \psi) + u\rho^{2}/2)] \rho {\rm d}\rho {\rm d}\theta , \end{displaymath} (7)

where C is a normalization constant, $(\rho,\theta,z)$ and $(r,\psi,z)$ are the cylindrical coordinates in the exit pupil and focal plane (image) spaces, respectively. Then $\Phi $ is the term of aberration, $0\leq \rho\leq1$, and the dimensionless variables u and v are defined as:

\begin{displaymath}u=\frac{2{\rm\pi}}{\lambda}\frac{a}{R}z \hspace{0.5in} v=\fra... ...\rm\pi}}{\lambda}\frac{a}{R}r \hspace{0.5in} r=\sqrt{x^2+y^2}, \end{displaymath} (8)

R being the radius of the Gaussian sphere (=EFL). Following the treatment in Born & Wolf (1980), we assume working with no piston (u=0) and with the tangential coma as the only aberration term; this type of aberration is expressed in the Nijboer-Zernike representation as $\Phi={A}_{\rm c}(3\rho^3-2\rho)\cos(\theta)$ ( ${A}_{\rm c}$ is a coefficient that quantifies the amount of coma in wavelengths). In this case, it can be shown, that the solution of Eq.  (7) takes the form of a series:

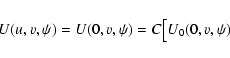
\begin{displaymath}U(u,v,\psi)=U(0,v,\psi)=C\big[U_0(0,v,\psi) \end{displaymath}


 \begin{displaymath}\hspace{0.2in}+({\rm i}\alpha_{031})U_1(0,v,\psi)+(i\alpha_{031})^2U_2(0,v,\psi)+...\big], \end{displaymath} (9)

where $\alpha_{031}= 2{\rm\pi} {A}_{\rm c} /\lambda$ and the functions Ui are given as a combinations of Bessel functions of different orders, $J_{\rm k}$:

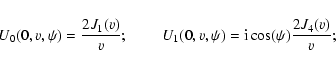
\begin{displaymath}U_0(0,v,\psi)= \frac{2J_1(v)}{v}; \hspace{0.3in} U_1(0,v,\psi)={\rm i}\cos(\psi)\frac{2J_4(v)}{v} ; \end{displaymath}


\begin{displaymath}U_2(0,v,\psi)=\frac{1}{2v}\left[\frac{1}{4}J_1(v)-\frac{1}{20}J_3(v)+\frac{1}{4}J_5(v)\right] \end{displaymath}


 \begin{displaymath}\hspace{0.3in} - \frac{1}{2v}\left\{\frac{9}{20}J_7(v)+\cos(2\psi)\left[\frac{2}{5}J_3(v)+\frac{3}{5}J_7(v)\right]\right\}. \end{displaymath} (10)


  \begin{figure} \par\includegraphics[width=6.8cm,clip]{4180fig2.ps} \end{figure} Figure 2: The LSF obtained from the Fraunhofer integral with the coma term $\Phi $ (see text).
Open with DEXTER

We used Eqs.  (9) and (10) and the value[*] ${A}_{\rm c}=0.3$ (in wavelengths) for the coma coefficient to compute the PSF. Hereafter we use the one-dimensional version, the Line Spread Function (LSF), obtained from the PSF by across-scan integration. The resulting curve is shown in Fig. 2 for the two reference spectral types considered, B3V and M8V in the case of a Gaia-like configuration with $a=0.7\ {\rm m}$ and $R={\rm EFL}=46.7\ {\rm m}$. Note that the intrinsic effective wavelengths of B3V and M8V stars are about 150 nm and 1300 nm, respectively. After taking realistic telescope transmission and detector response (Short & de Bruijne 2003) into account, the effective wavelengths become $\lambda_{{\rm B3V}}=628$ nm and $\lambda_{{\rm M8V}}=756$ nm. Using the discrete representation of the COG:

 \begin{displaymath}y_{{\rm COG}} = \frac{1}{F} \sum y_{n}f_{n}, \end{displaymath} (11)

with fn the signal intensity recorded by the pixel in yn, and $F = \sum f_n$ the total intensity, we verified that the variation of the COG position is linear with wavelength in the range of interest following the relation $\delta y_{{\rm COG}}=-1.0195\lambda + 0.6415$, in agreement to the result derived in Sect. 3.1. The calculation was carried on by making reference to a situation using LSF sampling and focal plane detectors, very similar to one of the options considered for Gaia (Short 2005): single CCD units of about 50 mm in the scan direction, and pixels of $10\ {\rm\mu m}$ in the same direction. The difference between the COG locations of the LSFs of our two reference star types amounts to $\vert{\rm COG_{B3V}}-{\rm COG_{M8V}}\vert= 0.121 {\rm mas}$.

With our PSF modelling and measuring code we were able to investigate the effects of limited detector dimensions (read-out region coincident with the detector dimension) and sampling resolution (pixel size). We went on to extend the detector dimension and to shrink the sampling step by two orders of magnitude (CCD units of 50 cm on a side with $0.1~ {\rm\mu m}$ pixels) and repeated the COG location measurements, which yielded: $\vert{\rm COG_{B3V}}-{\rm COG_{M8V}}\vert=0.122\ {\rm mas}$. This is a variation of only $1\%$ compared to the value above.

These experiments suggest, within the limits probed (the dimension of the "unlikely'' CCD simulated is very large but not infinite, and its pixels small but not infinitesimal), that chromaticity is an intrinsic property of all-reflective optical systems and that it can be approximated by a linear function of source effective wavelength. Therefore whatever the detector geometry and its spatial extension, different spectral type stars, set in the same nominal position in object space, do not have the same estimated position on the FP, even with the simplest possible algorithm; i.e. the same location on the sky is not uniquely mapped on the focal plane.

Chromaticity, a color-dependent position variation, is an important contribution to the systematic error and must be removed to preserve the desired mission accuracy.


  \begin{figure} \par\includegraphics[width=8.1cm,clip]{4180fig3.ps} \end{figure} Figure 3: Upper: PSF for B3V (solid line) and M8V (dashed line) stars in a representative off-axis field position; lower: PSF difference.
Open with DEXTER

4 Chromatic astrometric error

Using our CODE V representation of the Gaia Baseline Configuration, we could derive Gaia-like images of the two B3V and M8V sources (all aberrations terms are now taken into account), for any representative off-axis field position. The sources are always intended to be in the same location in object space, i.e. along the same direction on the sky. An example of the one-dimensional optical signals are shown in the upper panel of Fig. 3, normalized to the peak value; it is apparent that the M8V image (dashed line) is not just a geometrically scaled version of the B3V case (solid line). The different spectral content weighs the design aberrations (i.e. the residual aberrations after final optimization of the optical design), and the diffraction image is also affected by profile variations, in addition to the magnification associated to the intrinsic diffraction factor  $\lambda / D$. The signal difference is shown in Fig. 3 (lower): it is not symmetric, as would be the case for perfect scaling, and reaches 15% of the initial peak value. For consistency with the treatment of the previous section, the coordinate system is defined so that the COG location of an ideal, "non-aberrated'', PSF has abscissa equal to 0; the large common mode displacement (the PSF's do not peak at 0) is mostly due to classical distortion. It can be shown that different algorithms are affected by similar, although not coincident, chromatic effects. Nevertheless, because of the effective image profile of the Gaia telescope, the difference in performance is relatively small (few percent), so that we continue to prefer the simplicity of the COG algorithm throughout this work.

The application of the COG method for centering the Gaia-like PSF's of the two reference stars yielded 20.112  ${\rm\mu m}$ for the blue star and 20.055  ${\rm\mu m}$ for the red star, respectively, a difference of 57 nm. At the optical scale of Gaia, about 4''/mm, this results in more than 200  $\rm {\mu as}$, i.e. comparable with the random location error for stars brighter than ${V = 15 ~ \rm mag}$.

   
4.1 Monochromatic and polychromatic PSF's

It is possible to simplify the formalism used in Sect. 3.2 by recalling that the PSF can be derived by taking the square modulus of the complex amplitude response function (ARF), which in turn is derived as the Fourier transform of the generalized pupil function $P_{\rm g}$ (Goodman 1996), i.e.


 \begin{displaymath}ARF(x,y; \lambda) = q(\lambda) \times F\{P_{{\rm g}}(\rho,\theta)\} , \end{displaymath} (12)

where (x,y) are coordinates on the focal plane and $(\rho, \theta)$are taken on the pupil.

The Fourier integral in Eq. (12) is performed over the rectangular pupil of the Gaia telescope, where the factor $q(\lambda)$ is constant. The pupil function $P_{\rm g}$ is expressed in terms of the wavefront error (WFE) function, $W(\rho,\theta)$, via the relation

 \begin{displaymath}P_{{\rm g}}(\rho,\theta; \lambda) = \exp \left[{\rm i} \frac{2{\rm \pi}}{\lambda}W(\rho,\theta) \right] . \end{displaymath} (13)

Note that Eq. (13) clearly shows how at longer wavelengths the effect of the WFE is reduced, as the phase contribution is a smaller fraction of the period.

The expression for the monochromatic PSF, ${\it PSF}_{\rm m}$, is therefore

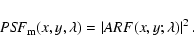\begin{displaymath}{\it PSF}_{\rm m}(x,y,\lambda) = \left\vert ARF(x,y;\lambda) \right\vert^2 . \end{displaymath} (14)

The local polychromatic ${\it PSF}(x,y)$ for a star with a given spectral distribution is

 \begin{displaymath}{\it PSF}(x,y) = \int_{\lambda_1}^{\lambda_2} \omega(\lambda) \times {\it PSF}_m(x,y,\lambda) \ {\rm d}\lambda . \end{displaymath} (15)

The weight function $\omega(\lambda)$ combines the source spectral distribution, the instrument transmission, and the quantum efficiency of the detector; then the polychromatic PSF can be normalized to the expected average number of detected photons.

CODE V can compute the WFE distribution associated to a given field position for a selected optical configuration; it is thus possible to build the PSF for any desired source, using Eqs.  (12)- (15). We use a numeric implementation of this model (Busonero et al. 2005) to provide the description of the imaging performance of the Gaia telescope with all the aberration terms given by CODE V. Additional contributions describing the realistic detector response and the effect of TDI observations can be included, as well as the across-scan binning used for Gaia, to build the recorded signal. For any source of known spectrum, it is possible to derive its effective wavelength, the detected signal, and the chromaticity with respect to the selected reference spectral type using the above expressions. In this way, the measurement of Gaia can, in principle, be made achromatic, as the position estimate is no longer function of the source spectral distribution. This correction requires both color information and knowledge of the local instrument response.

Table 1: Effects of individual Standard Zernike terms vs. the non-aberrated (ideal) case.

4.2 Identification of the critical WFE terms

The source of chromatic errors is the WFE, which is present in any nominal optical design with a finite FOV; manufacturing and alignment may only aggravate the problem. Besides, not every component of WFE contributes to chromaticity: below, we analyze the effect of individual aberrations and the related symmetry properties.

We then investigate how to minimize, by design, the chromatic errors in any given field position, analyzing the effect of partial or total suppression of selected aberration terms. Finally, we proceed to evaluate the overall field properties of chromaticity, verifying the possibility of compensating for it by taking measurements over a complete crossing of the focal plane, a possibility offered by scanning instruments like Gaia.

In optical engineering, typical expansions of the WFE are in terms of Zernike and Fringe Zernike polynomials, orthogonal, and normalized functions, if mapped on a circular pupil (Born & Wolf 1980). In our analysis we have used expansions with 21 Zernike terms; the set of standard Zernike functions are listed in Table 1 (for Fringe Zernike equivalents see Born & Wolf 1980). Note that the representation in Zernike polynomials is not optimal for non-circular pupils and more convenient expansions have been investigated (Gardiol et al. 2005).

In the following, we show how to identify the main individual contributors to chromaticity in the case of a realistic representation of the Gaia telescope regardless of the choice of the Zernike set, and to search for possible correlations between chromaticity and parameters like rms WFE and image rms width[*].

Chromaticity is again evaluated by taking the difference of the COG positions obtained for the adopted reference spectral types B3V and M8V. We used both monochromatic PSFs at the reference wavelengths associated with the two spectral types and the full polychromatic representation of Eq.  (15), assuming the two stars behave like blackbodies. The latter description is more representative from the astrophysical standpoint, whereas the former is computationally much simpler. Preliminary experiments proved that the two methods can be considered equivalent when, as is the case here, the primary goal of the investigation is to evaluate of the properties of chromaticity and not its precise calculation.

The image rms width is derived from the monochromatic PSF at $\lambda = 700\ {\rm nm}$, roughly representative of solar type objects and sort of midway between B3V and M8V types. The image COG displacement is always referred to the ideal, non-aberrated case, which has an image rms width of $8.6425~ {\rm \mu m}$. Each Zernike term is individually evaluated, with the coefficient set to 0.1 (i.e. the small aberrations regime is assumed): then the WFE is built from the selected term, and the PSF computed accordingly to the above model. The results for the first 21 terms are listed in Table 1.


  \begin{figure} \par\includegraphics[width=8.1cm,clip]{4180fig4.ps} \end{figure} Figure 4: Image COG variation ( upper panel) and chromaticity variation ( lower panel) vs. Standard Zernike aberration terms.
Open with DEXTER

In Fig. 4, we show the impact of each individual aberration on the COG (i.e. an effect corresponding to classical distortion) and on chromaticity. Some terms strongly contribute to both, but in general there is little correlation. Similarly, we found that there is no simple relationship between rms WFE, or image rms width (both including the contribution of all aberrations) and chromaticity.

The complex relationship between WFE, image rms width, and chromaticity can be understood in terms of symmetry, since the aberrations are in general bidimensional, whereas the parameters relevant to the Gaia measurement are mostly one-dimensional, i.e. referred to the scan (y-axis) direction. Thus, specific aberration terms may contribute to the WFE significantly, to across-scan image width and across-scan (x-axis) centroid displacement, with little impact on the location, noise and chromaticity, due to the across-scan binning of the images (see Sect. 2).

There is a trend toward increasing image rms width with rms WFE, but this is not a strict relation, and several cases of large WFE and small image width degradation are seen. This could be associated to aberrations inducing significant image degradation in the across scan direction only. The COG, in some cases, is affected by a large displacement associated to low chromaticity values. Thus, the images are translated with respect to the non-aberrated position by an amount that does not depend on the spectral distribution of the source. The case of classical distortion fits this description.

From Fig. 4, we see that significant contributions to chromaticity, i.e. $\geq $ $100\ {\rm\mu as}$, come only from aberrations (Nos. 3, 6, etc.) with a specific functional form: they are all the odd (sinusoidal) functions of the angular coordinate, so that they have odd symmetry on the pupil plane. All of the even (cosinusoidal) terms do not provide net chromaticity; values below $\sim$ $ 30\ {\rm\mu as}$ are the result of limited precision in the calculation scheme that is implemented.

A similar analysis was carried on with the Fringe Zernike polynomials. Again, the critical terms for chromaticity we identified to be those associated to the odd parity portion of the WFE, i.e. the sinusoidal terms, as for the Standard Zernike expansion. Therefore, in the case of Gaia, the terms that should be minimized, by design, manufacturing, and alignment are those with odd parity (anti-symmetric) relative to the across-scan (x) axis.

   
5 Compensation by aberration selection

We now turn our attention to verifying chromaticity with many aberration terms present. The analysis refers to FP position F4 (see Table 2) with coordinates  $0\hbox{$.\!\!^\circ$ }20$ (along-scan) $\times 0\hbox{$.\!\!^\circ$ }33$ (across-scan), which is affected by a significant value of chromaticity[*]. Six cases are considered:
1.
non-aberrated (ideal) PSF;
2.
nominal case (from optical design);
3.
removal of all symmetric terms;
4.
removal of all anti-symmetric terms;
5.
removal of anti-symmetric terms AND scaling of symmetric terms to equivalent rms WFE;
6.
subset of anti-symmetric terms 9 and 10.
The corresponding values of rms WFE, image rms width, and chromaticity are listed in Table 3. The resulting PSF's (monochromatic at the reference wavelength of 700 nm) for four of the cases above are shown in Fig. 5.

Table 2: rms WFE, image rms width (for the two reference spectral types), and chromaticity at different field angle locations over the focal plane.

The nominal case provides an image rms width that is reasonably close to the diffraction limit in spite of non negligible rms WFE (40 nm, i.e. $\lambda / 15$ at $\lambda = 600\ {\rm nm}$); the chromaticity is about 1 mas.

Suppression of the symmetric aberrations provides some improvement to the rms WFE. The variation of the image width is marginal and the initial chromaticity is mostly retained. Conversely, removing the anti-symmetric aberrations completely (case 4), we achieve significant improvement, as in the previous case, on the rms WFE, but not nearly as much on the image rms width; chromaticity, however, is reduced to zero, according to expectations. The rms sum of WFE in cases 3 and 4 restores the nominal value: the mutual orthogonality of symmetric and anti-symmetric function sets is preserved, even if this is no longer true for the individual functions within each set. Even when the symmetric aberrations are scaled to restore the initial WFE level of 40 nm (case 5), the chromaticity is still zero.

Besides, when a random subset of anti-symmetric aberrations (9 and 10) is retained, together with the symmetric terms, with the nominal coefficients (case 6), the result has a value that is comparable to the chromaticity in the nominal case (case 2) but with the opposite sign. Futhermore it leads to a dramatic degradation of both WFE and image quality.

Table 3: Changes in rms WFE, image rms width, and chromaticity for the 6 selected cases discussed in Sect. 5.

This shows that the optimization procedure in the ray tracing code actually achieves some partial compensation among different aberrations, providing some, although limited, benefit to chromaticity. On the other hand, standard optical design optimization procedures are based on improving the general image quality parameters such as WFE and spot diagrams. Therefore, it is possible to introduce custom merit functions in the optimisation procedure, which can include computation of the chromaticity or of the critical anti-symmetric contribution to WFE, with some averaging rule over the field. This does not necessarily modify the actual optical configuration in any significant way, since it is always convenient to start after standard optimization, but chromatic aberrations can be further reduced at the expense of the others and, possibly, of a small increase in overall WFE, which is acceptable in many cases.
  \begin{figure} \par\includegraphics[width=7.4cm,clip]{4180fig5.ps} \end{figure} Figure 5: Modifications of the PSF profile due to the different weight of aberration terms for field position F4 of the Gaia-like astrometric optics considered here.
Open with DEXTER

6 Field distribution of chromaticity

The map of chromaticity over the FOV was derived from the optical representation of the baseline configuration of the astrometric payload. We considered only the nominal design aberrations; manufacturing and alignment errors are not included yet. The result can therefore be considered as a best case.
The analysis used monochromatic PSFs in the set of positions listed in Table 2 that also lists the associated rms WFE in nanometers (nm), the image rms width for the two cases considered (B3V and M8V sources), and the chromaticity. The values were interpolated to cover the field with $0\hbox{$.\!\!^\circ$ }02$ resolution, and the resutling surface is shown in Fig. 6. The distribution is antisymmetric with respect to the y(across scan) axis, due to the intrinsic symmetry of the optical configuration: the mean chromaticity value is $-0.05~ {\rm\mu as}$, with rms value $1.19~ {\rm mas}$ and peak values exceeding $\pm $ $3~ {\rm mas}$, i.e. three orders of magnitude larger than the Gaia measurement goal.

6.1 Transit level compensation

The symmetry of the chromaticity distribution can be exploited to reduce the overall contribution to a set of measurements, at transit-level, in spite of comparably high local values. All targets detected by Gaia are observed in TDI mode on the whole FP, so that the measurements are performed in opposite positions with respect to the symmetry axis; by composition of the photo-center values from exposures in symmetric positions along scan, the residual chromaticity cumulated over a transit drops to values quite close to zero.


  \begin{figure} \par\includegraphics[width=8.4cm,clip]{4180fig6.eps} \end{figure} Figure 6: Chromaticity distribution over the astrometric field in the nominal configuration of the Gaia-like astrometric payload.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.4cm,clip]{4180fig7.eps} \end{figure} Figure 7: Transit level chromaticity vs. across scan field position in the nominal case and for increasing alignment error, (in arcsec).
Open with DEXTER

The average value of the transit chromaticity over the astrometric field is $-0.10\ {\rm\mu as}$, with rms value $0.21\ {\rm\mu as}$. Therefore, chromaticity compensation over the transit appears quite effective in the nominal configuration.

6.2 Partial compensation on misaligned systems

The real configuration used in flight will not retain the design symmetry, due to manufacturing, integration, and re-alignment errors. In order to model the effect, the chromaticity map derived for the nominal configuration is simply shifted by an amount corresponding to the selected offset ranging from one arcsecond to 0.5 arcminute (a fairly large alignment error). The local chromaticity value is mostly preserved, but the transit level combination, which is very close to zero in the nominal (symmetric) case, is affected by a degradation increasing with the error, as shown in Fig. 7. The statistics of transit-level chromaticity across the FP is shown in Table 4. Column 1 lists the offset applied (zero corresponds to the nominal case); in Cols. 2 and 3 we report average and standard deviation of transit-level chromaticity, respectively, as computed across the field.

The transit-level chromaticity remains very close to zero in an across-scan position of about $0\hbox{$.\!\!^\circ$ }55$, which appears to be a chromatic-free section of the field; the residual has opposite signs on either side of this position. This is due to the structure of the local chromaticity distribution (Fig. 6), with alternate signs in each quadrant. The result is that stars of a given spectral type in different regions of the field have nearly opposite residual chromaticity. This aspect may be exploited for further reduction of the residual chromaticity in the data reduction phase. Upon definition of a threshold of acceptable residual chromaticity, at transit level, it is possible to provide a specification for alignment, referred to both initial telescope integration, and in-orbit re-alignment.

Table 4: Transit-averaged chromaticity as a function of re-alignment error.

6.3 Optical engineering aspects

Symmetry considerations can be applied to the contribution from the individual optical components, in particular concerning their figuring error in the manufacturing phase, which can be split in components relevant or not to overall chromaticity. Also, alignment aspects, above referred to the primary mirror, can be applied with appropriate modifications to perturbation of other components. Manufacturing and alignment errors inducing an anti-symmetric residual WFE on a telescope mirror result in increased chromaticity. The on-flight configuration will be affected by manufacturing and alignment errors, which can also be described in terms of symmetric and anti-symmetric aberrations. If the design is optimized in terms of low chromaticity, small perturbations due to manufacturing and alignment are likely to induce a comparably low increase in the chromatic errors, due to larger tolerances. With the configuration considered as representative for Gaia, the relevant values of residual transit chromaticity are on the order of a few arcseconds at the level of the primary mirror, which is challenging for standard optical techniques. However, it is not necessary to perform re-alignment of each optical component: as for many astronomical instruments, when the errors are not too large, a global re-optimization can be achieved by adjusting a small number of degrees of freedom, often localized on a single component (e.g. the secondary mirror). The correction requirements in terms of stroke and resolution are within the range of the actuators considered for Gaia; the main limiting factor is the diagnostics capability, which in any case will benefit from accurate analysis of the image properties over the field.

Quantitative analysis and optimization may be performed on specific optical configurations, including manufacturing and alignment aspects based on realistic WFE data from manufacturers. The resulting minimization of the instrumental chromaticity is an improvement to the overall systematic error budget, which is desirable because correction procedures based on the science data are necessarily limited, and in some ways they subtract information.

7 Conclusions

This paper has discussed the issue of chromaticity in all-reflective optical systems. In spite of common belief, avoiding refractive components is not sufficient for achieving an achromatic instrument response, due to basic diffraction considerations. In the scenario of future space astrometric missions, the impact of systematic errors two or three orders of magnitude larger than the measurement goal is of fundamental importance.

Specific analyses have been performed with reference to the baseline configuration of the Gaia astrometric payload, but the assumptions, principles, and conclusions of our discussion can be applied to any high accuracy astrometric instrument. The chromatic error is defined as the difference in image photo-center location at different wavelengths, and the exact value depends on the selected measurement process, but the effect is unavoidable.

Independently from the selected WFE expansion, the terms relevant to chromaticity are those associated with anti-symmetry of the PSF in the FP and with anti-symmetric WFE contributions on the pupil plane. Symmetric terms only contribute to the astrometric noise by increasing the effective image width in the measurement direction. As the relation between rms WFE and chromaticity is complex, the specification of only the rms WFE is not a sufficient requirement for controlling chromaticity from the optical manufacturing standpoint.

The first prescription to optical manufacturers is to suppress or at least minimize the anti-symmetric terms. However, it is not necessary to set all chromatic terms to zero: an appropriate combination is still able to provide some local balancing. Standard optical design optimization techniques are able to provide reasonable results by applying the conventional image quality merit functions; optimal results on chromaticity require definition of ad hoc criteria, as much as on tolerancing. The distribution of chromaticity over the field inherits some symmetry properties from the optical system; deviations from symmetry are induced e.g. by manufacturing and alignment errors on each optical component.

In case of repeated measurements in different parts of the field, some chromaticity compensation is achieved in the data combination, depending on the symmetry of both instrument and measurement schemes. In the case of Gaia, each object observed by a symmetric (i.e. correctly re-aligned) telescope along a full transit provides a set of astrometric measurements affected by opposite chromatic errors in symmetric positions; transit-level composition is therefore likely to remove a large fraction of the local chromaticity. Any residual chromaticitymust be removed in the science data processing after the best implementation of the astrometric payload, to minimize the initial systematic error. This requires spectral information for each source and a good knowledge of the detailed instrument response (Gai & Cancelliere 2005).

Acknowledgements
We acknowledge the contribution of Dr. D. Carollo to initial investigations of the subject of chromaticity. The ORA team helped in the detailed operation and best usage of their CodeV package. Our activity on Gaia was partially supported by the Italian Space Agency, under research contracts ASI ARS 96-77 and ASI ARS 98-92. M.G.L. acknowledges the support of the Space Telescope Science Institute through the Institute's Visitor Program for 2005.

References

 
Copyright ESO 2006