A&A 448, 843-852 (2006)
DOI: 10.1051/0004-6361:20053409

Relativistic cross sections of mass stripping and tidal disruption of a star by a super-massive rotating black hole

P. B. Ivanov^1,2 - M. A. Chernyakova^3,4,

1 - Astro Space Centre, P. N. Lebedev Physical Institute, 4/32 Profsoyuznaya Street, Moscow 117810, Russia
2 - Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
3 - INTEGRAL Science Data Centre, Chemin d'Écogia 16, 1290 Versoix, Switzerland
4 - Geneva Observatory, 51 ch. des Maillettes, 1290 Sauverny, Switzerland

Received 11 May 2005 / Accepted 28 September 2005

Abstract
Aims. We consider the problem of tidal disruption of a star by a super-massive rotating black hole.
Methods. Using a numerically fast Lagrangian model of a tidally disrupted star developed in our previous works, we survey the parameter space of the problem and find regions where the total disruption of the star or a partial mass loss from the star takes place as a result of fly-by around the black hole. Our treatment is based on General Relativity, and we consider a range of black hole masses where the tidal disruption competes with the relativistic effect of direct capture of stars by the black hole. We model the star as a full polytrope with n=1.5 with the solar mass and radius. We show that our results can also be used to obtain the amount of mass lost by stars with different stellar masses and radii.
Results. We find that the results can be conveniently represented on the plane of specific orbital angular momenta of the star $(j_{\theta }, j_{\phi })$. We calculate the contours of a given mass loss of the star on this plane, for a given black hole mass M, rotational parameter a and inclination of the trajectory of the star with respect to the black hole equatorial plane. In the following such contours are referred to as the tidal cross sections.

It is shown that the tidal cross sections can be approximated as circles symmetric above the axis $j_{\phi}=0$, and shifted with respect to the origin of the coordinates in the direction of negative $j_{\theta}$. The radii and shifts of these circles are obtained numerically for the black hole masses in the range $5\times 10^{5}~M_{\odot}-10^{9}~M_{\odot}$ and different values of a. It is shown that when a=0 tidal disruption takes place for $M < 5\times 10^{7}~M_{\odot}$ and when $a\approx 1$ tidal disruption is possible for $M < 10^{9}~M_{\odot}$.

Key words: black hole physics - relativity - hydrodynamics - stars: mass loss - Galaxy: centre - galaxies: nuclei

1 Introduction

Tidal disruption of stars by a supermassive black hole may be very important in galactic centres. It may provide enough gas to fuel central engines of AGNs, e.g. Hills (1975). It also may account for non-stationary flashes of radiation observed in certain non-active galaxies, see Rees (1988) for theoretical discussion and Komossa et al. (2004) for observations.

Tidal disruption takes place when the periastron of the stellar orbit is smaller than the Roche tidal radius

$$r_{\rm T}=\sqrt[3]{{M\over m}}R_{\rm st}\approx 1.5\times 10^{13}\sqrt[3]{{M_{7}\over m_{*}}}R_{*}~{\rm cm} ,$$ (1)

where M is the black hole mass and m is the mass of star, $R_{\rm st}$ is the stellar radius, $M_{7}=M/10^{7}~M_{\odot}$, $m_{*}=m/M_{\odot}$ and $R_{*}=R_{\rm st}/R_{\odot}$. Since the semi-major axis of the stellar orbit can be as large as a few pc, tidally disrupted stars have highly elongated (technically, parabolic) orbits. Another important process that competes with the process of the tidal disruption is the relativistic process of direct capture of stars by a black hole. The star can be directly captured by the black hole when its periastron is of the order of the black hole gravitational radius

$$r_{\rm g}={2GM\over c^{2}}\approx 3\times 10^{12}M_{7}~{\rm cm}.$$ (2)

Since for a black hole of mass larger than $10^{7}~M_{\odot}$ the ratio $r_{\rm g}/r_{\rm T} > 0.2$, the relativistic treatment of the process of the tidal disruption is important.

We consider problem of tidal disruption of a star, or a partial stripping of mass from the star, by the black hole. Our treatment of the problem is fully based on General Relativity. We determine numerically an amount of mass lost by the star as a result of a tidal encounter, for different parameters of the stellar orbit and of the black hole. Since the initial orbit is assumed to be parabolic and the initial state of the star is assumed to be unperturbed by tidal influence of the black hole, the terminology associated with cross sections is used, see also Beloborodov et al. (1992) (BIIP) and below. As we have mentioned above (and will show quantitatively later on), the relativistic effects are not important when the black hole mass is sufficiently small. On the other hand when the black hole mass is sufficiently large $\sim$ $10^{8}~M_{\odot}{-}10^{9}~M_{\odot}$ the stars can be directly swallowed by the black hole without tidal disruption (see Sect. 3.1.1 and also BIIP and references therein). We obtain numerically approximate expressions for the amount of mass lost by the star for an intermediate mass range of the black hole, where the effects of General Relativity are important and the processes of tidal disruption and tidal stripping of mass compete with the process of direct capture.

The rotating black hole can be characterised by only two parameters, its mass M and the rotational parameter $a=cL_{\rm h}/(GM^{2}) < 1$, where $L_{\rm h}$ is the black hole angular momentum.

To describe the orbit of the star we must specify the orbit's integrals of motion. We introduce the spherical coordinate system $(r, \theta, \phi)$ with $\theta=\pi/2$at the black hole equatorial plane and consider the motion of the star very far from the black hole, $r \rightarrow \infty$. In this case a highly elongated orbit of the star can be characterised by the polar angle $\theta_{\infty}$associated with the semi-major axis of the orbit, and by two projections of specific angular momentum, $j_{\phi}$ and $j_{\theta}$. By definition, these quantities are conserved during the motion of the star. Taking into account that the problem is symmetric with respect to reflection $j_{\phi} \rightarrow -j_{\phi}$ we can consider only positive values of $j_{\phi} > 0$. Alternatively, one can characterise the stellar orbit by projection of the specific angular momentum onto the axis of rotation of the black hole, L_z and the square of the projection of the angular momentum onto the equatorial plane, Q. It is easy to show that the so-defined integral of motion Q coincides with the well-known Carter integral when the gravitational field of the black hole dominates over the gravitational field of the central stellar cluster. The quantities L_z and Q are related to $j_{\phi}$ and  $j_{\theta}$ as

$$L_{z}=j_{\theta}\sin \theta_{\infty}, \quad Q=j_{\phi}^{2}+j_{\theta}^{2}\cos^{2} \theta_{\infty}.$$ (3)

The Carter integral Q is always positive for parabolic orbits, and we will use its square root $q=\sqrt {Q}$ to have the same dimensions for the integrals of motion q and L_z, $j_{\phi}$, $j_{\theta}$. For ${\theta _{\infty }=\pi /2}$ and $j_{\phi} > 0$, $L_{z}=j_{\theta}$ and $q=j_{\phi}$.

It is well known that for a given $\theta_{\infty}$ there is a region, $S_{\rm c}$ in the plane $(j_{\theta }, j_{\phi })$corresponding to capture of the stars by the black hole (e.g. Chandrasekhar 1983; Young 1976). By analogy, we define the cross section of the tidal disruption, $S_{\rm T}$ as a region in the plane $(j_{\theta }, j_{\phi })$ where a partial tidal stripping of mass from the star or a full tidal disruption of the star takes place (BIIP). An alternative definition of the tidal cross sections would be a region in the plane (L_z, q) for a given $\theta_{\infty}$ where a tidal stripping or a tidal disruption takes place. We will call these as the cross sections in the plane (L_z, q). When ${\theta _{\infty }=\pi /2}$ the cross sections in the upper half plane $(j_{\theta}, j_{\phi} > 0)$ and the cross sections in the plane (L_z, q) coincide. It is very important to note that the cross section of direct capture of the stars in the plane (L_z, q) does not depend on the angle $\theta_{\infty}$ (e.g. Chandrasekhar 1983). As we will see (Sect. 3.1.3) this property is also approximately valid for the cross sections of the tidal disruption in the plane (L_z, q) (see the text below). This fact allows us to reduce the dimensionality of the parameter space and obtain the approximate cross sections of tidal disruption for $\theta_{\infty} \ne \pi/2$ by a geometric transform of the cross sections calculated for ${\theta _{\infty }=\pi /2}$.

In order to calculate the cross sections of tidal disruption one should evolve numerically a model of a tidally disrupted star in the relativistic tidal field of the black hole for a sufficiently long time. It should be done for different values $j_{\phi}$, $j_{\theta}$, $\theta_{\infty}$ as well as for different values of M and a. Approximately 10³-10⁵ runs are needed. Taking into account that the present day numerical 3D finite difference or SPH models are rather time consuming it is impossible to survey the whole parameter space with these models. Recently we have proposed another approximate model of a tidally disrupted star which is a one dimensional Lagrangian model from the point of view of numerical calculations, and therefore, it is numerically fast (Ivanov $\&$ Novikov 2001, hereafter IN; Ivanov et al. 2003, hereafter ICN). This model is used in the present Paper.

The model is briefly described in the next section. Section 3 presents the results of our calculations. We discuss our results and present our conclusions in Sect. 4.

We use natural units expressing all quantities related to the star in terms of the characteristic stellar time $t_{\rm st}=\sqrt {R_{\rm st}^{3}/Gm}$, stellar radius $R_{\rm st}$, etc. The parameters related to the stellar orbit are also made dimensionless. We use $\tilde L_{z} =L_{z}/(cr_{\rm g})$, $\tilde q =q/(cr_{\rm g})$, $\tilde j_{\phi} =j_{\phi}/(cr_{\rm g})$ and $\tilde j_{\theta}=j_{\theta}/(cr_{\rm g})$. We do not write tilde below assuming that all quantities mentioned above are dimensionless.

We assume below that the star is a full polytrope with n=1.5 and solar mass and radius. We show how to apply our results to the case of other values of the mass and radius.

We mainly consider the tidal encounters of moderate strength, thus neglecting the possibility of violent tidal disruption and formation of strong shocks in the stellar gas.

2 The model of a tidally disrupted star

The derivation of the basic dynamical equations of our model and detailed comparison of the results with results based on the 3D finite difference models, SPH model and affine models of the tidally disrupted star has been intensively discussed in our previous papers (see IN, ICN).

We assume that summation is performed over all indices appearing in our expression more than once, but summation is not performed if indices are enclosed in brackets. The upper and lower indices describe the rows and columns of matrices.

In our model, in order to reduce the number of degrees of freedom, and accordingly, to significantly reduce the computational time we assume that the star consists of elliptical shells. The parameters and orientation of these shells change with time. This assumption allows us to express the coordinates of some particular gas element in a frame co-moving with the centre of mass of the star, xⁱ in terms of (non-evolving) coordinates of the same gas element xⁱ₀ in the unperturbed spherical state of the star (say, before the tidal field is "switched on'') as

 

xⁱ=Tⁱ_j(t, r₀)e₀^j, (4)

where the radius $r_{0}=\sqrt{x_{0i}x^{i}_{0}}$ is the same for all gas element belonging to a particular shell, and e₀ⁱ=xⁱ₀/r₀ are direction cosines ( e_0ieⁱ₀=1). We represent the position matrix Tⁱ_j and its inverse Sⁱ_j as a product of two rotational matrices Aⁱ_j and Eⁱ_j, and a diagonal matrix Bⁱ_j:

$$T^{i}_{j}=A^{i}_{l}B^{l}_{m}E^{m}_{j}=a_{l}A^{i}_{l}E^{l}_{j}, \quad S^{i}_{j}=a_{l}^{-1}A^{j}_{l}E^{l}_{i},$$ (5)

where $B^{l}_{m}=a_{(l)}\delta^{(l)}_{m}$, and a_l are the principal axes of the elliptical shell.

The evolution equations for the matrix Tⁱ_j follow from the integral consequences of the exact hydrodynamical of motion: the so-called virial relations (e.g. Chandrasekhar 1969) written for a particular elliptical shell of interest, and have the form:

$$\ddot T^{i}_{j}=3S^{j}_{i}\bar {\left({p\over \rho}\right)}-1... ...m d}M} \big\lbrace gS^{l}_{i}T^{k}_{n}{\bar P}^{ln}\big\rbrace$$

$$\qquad-{3\over 2}A^{i}_{k}a_{k}D_{k}E^{k}_{j}{GM\over g}+C^{i}_{k}T^{k}_{j},$$ (6)

where the dot stands for the time derivative. We use the mass enclosed in the shell corresponding to the radius r₀, $M=4\pi \int_{0}^{r_{0}}\rho_{0}r_{1}^{2}{\rm d}r_{1}$ as a new radial variable, and $\rho_{0}$ is the density of the star in its unperturbed spherical state. The matrix Sⁱ_j represents the inverse to the position matrix Tⁱ_j and g is the determinant of the position matrix. The matrix C_i^j represents the relativistic tidal tensor, and therefore it is symmetric and traceless.

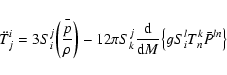
The dimensionless quantities D_k have been described by e. g. Chandrasekhar (1969), p. 41. They have the form:

$$D_{k}=g\int^{\infty}_{0}{{\rm d}u\over \Delta (a_{j}^{2}+u)},$$ (7)

where $\Delta=\sqrt{(a_{1}^{2}+u)(a_{2}^{2}+u)(a_{3}^{2}+u)}$.

The quantities $\bar {({p\over \rho})}$ and ${\bar P}^{ij}$ are determined by distribution of the density $\rho$ and pressure p in the star:

$$\bar {\left({p\over \rho}\right)}={1\over 4\pi}\int {\rm d}\Omega {p\over \rho},$$ (8)

and

$${\bar P}^{ij}={1\over 4\pi}\int {\rm d}\Omega pe_{0}^{i}e_{0}^{j},$$ (9)

where integration is performed over the unit sphere associated with the direction cosines e₀ⁱ.

Obviously, the first two terms in Eq. (6) are due to action of the pressure force on the elliptical shell, and the last two terms describe the self-gravity of the star and action of the tidal forces.

To complete the set of Eq. (6) we should know the distributions of pressure and density over the star. The density distribution

$$\rho(t,x^{i})={\rho_{0}(r_{0})\over D}$$ (10)

is determined by the Jacobian $D=\vert{\partial x^{i} \over \partial x_{0}^{j}}\vert$ of the mapping between the coordinates xⁱ and x₀ⁱ, which can be written as

$$D(x_{0}^{i})={ge_{0i}e_{0k}\over 2 r_{0}^{2}} (S^{i}_{m}(T^{m}_{k})' + S^{k}_{m}(T^{m}_{i})',$$ (11)

where prime stands for differentiation over r₀. We use the standard relation $p=k\rho^{\gamma}$ to find the distribution of pressure over the star. Here k is the entropy constant, and $\gamma$ is the specific heat ratio. $\gamma=5/3$ is used later on.

The dynamical Eq. (6) has the usual integrals of motion: the energy integral and the integral of angular momentum. Their form can be found in ICN. For our discussion it is important that in our model the energy integral can be naturally separated into kinetic, thermal and gravitational parts. In addition to these integrals, the quantities

$$\chi_{jk}(M)=T^{i}_{k}\dot T^{i}_{j}-T^{i}_{j}\dot T^{i}_{k}$$ (12)

are conserved. They represent the conservation of circulation of the fluid over the elliptical shells in our model (IN, ICN).

2.1 Numerical scheme and computational details

Our numerical scheme is described in IN and ICN. The variant of the scheme used in the calculations is a non-conservative explicit numerical scheme, and we use conservation of the integrals of motion to check the accuracy of the calculations. This simple scheme allows us to calculate a single tidal disruption event with a very small computational time. However, as was pointed out in ICN, this variant of the scheme suffers from a slowly growing numerical instability. A radical remedy would be an implicit conservative numerical scheme, but the schemes of this type are much more time consuming. Therefore, in order to suppress this instability we average the dynamical variables over the neighboring grid points once every 200 time steps. We have checked that this procedure leads only to a rather slow numerical leakage of the stellar energy which seems to be non-significant for our purposes.

We use a simple criterion of mass loss. We calculate the sum of kinetic and potential energy (per unit of mass) for each grid point and assume that when this sum is positive the corresponding elliptical shell is gravitationally unbound. This criterion is in good agreement with the results of 3D finite difference computations (see IN and ICN).

In principal one can use other criteria of the amount of mass lost by the star. For example, one can consider the shells with positive total energy (i.e. the sum of the potential, kinetic and thermal energies) as being tidally stripped from the star. For a particular shell the ratio of the thermal energy $E_{\rm th}$ to the potential energy $E_{\rm p}$ is proportional to a power of a characteristic size of the shell, $R_{\rm sh}$: $E_{\rm th}/E_{\rm p} \propto R_{\rm sh}^{-(3\gamma -4)}$. When $\gamma > 4/3$ this ratio decreases with time for an expanding shell. Therefore, taking into account the thermal energy should not make a significant difference to our criterion.

Our model cannot treat shocks which can, in principle, influence the criterion of the mass loss. However, we mainly consider tidal encounters of moderate strength where only a partial mass stripping of the star takes place and the presence of strong shocks is not expected. This statement is confirmed by results of 3D finite difference calculations where no evidence for a strong shock in the star has been found (e.g. Khokhlov et al. 1993; Diener et al. 1997). Note that some shocks may develop after the tidal disruption event in a situation when partial mass stripping takes places. A gravitationally bound part of the stellar gas initially expelled from the star may return and hit the surface of a dense undisrupted stellar core producing a shock there. These shocks only redistribute the energy and momentum of the gravitationally bound part of the stellar gas and therefore cannot influence our criterion.

For the calculation of the stellar orbits we use the usual Boyer-Lindquist coordinates $(r, \theta, \phi)$and the explicit form of the tidal tensor given in Diener et al. (1997).

As follows from the results based on the finite difference scheme (e.g. Diener et al. 1997, and references therein) and our own results (IN, ICN) the stellar structure starts to evolve significantly only when the star approaches the periastron of the orbit, $r_{\rm p}$. Therefore we start our calculations at the radius $r_{0}=1.5r_{\rm p}$ and evolve our numerical scheme during the fly-by around the black hole until a final sufficiently large radius $r_{\rm fin}$ is reached. This radius is taken to be $r_{\rm fin}=4-5r_{\rm p}$ for a sufficiently small mass of the black hole, $M < 8\times 10^{7}~M_{\odot}$. In the opposite case we terminate a single computation when two conditions are satisfied: 1) $r_{\rm fin} > 3r_{\rm p}$; 2) the dimensionless time $\tau=t/t_{*}$ from the beginning of computation is sufficiently large: $\tau > 15$.

3 Results

3.1 The case ${\theta _{\infty }=\pi /2}$

The bulk of our computations has been performed for ${\theta _{\infty }=\pi /2}$. In this case the tidal cross sections in the upper half plane $(j_{\theta}, j_{\phi} > 0)$ and the cross sections in the plane (L_z, q) coincide. For symmetry reasons we can consider only the cross sections in the plane (L_z, q). As it is shown later (see Sect. 3.3) the tidal cross sections in the plane (L_z, q) almost do not depend on the value of $\theta_{\infty}$ and therefore the cross sections in the plane $(j_{\phi}, j_{\theta})$ can be obtained from those corresponding to ${\theta _{\infty }=\pi /2}$ by a geometric transform.

Table 1: The values of the black hole masses and rotational parameters used in the calculations.

Figure 1: The calculated cross sections of tidal disruption for the case a=0.999 and different black hole masses. The levels of the amount of mass lost by the star, $M_{\rm lost}$, are shown by curves of different types corresponding to different masses of the black hole. Three curves of the same type show $M_{\rm lost}=0.1$ (the outer curve), $M_{\rm lost}=0.5$ (the middle curve) and $M_{\rm lost}=1$ (the inner curve). Note that the curves corresponding to the different black hole masses may overlap (e.g. $M_{\rm lost}(M=0.1)=1$ and $M_{\rm lost}(M=0.25)=0.1$). The solid curve shows the cross section of direct capture. Top: the case of small black hole masses is shown, M=0.1, 0.25, 0.5 and 1. The triangle shows the result of 3D finite difference calculations of Diener et al. (1997). They obtained $M^{D}_{\rm lost} \sim 0.5$. Bottom: the case of large black hole masses, M=2, 4, 8, 16, 32, 64 and 100. Note that in the case M=64 and M=100 the curves corresponding to different $M_{\rm lost}$ almost coincide, and we show only the curves corresponding to $M_{\rm lost}=1$.

Open with DEXTER

3.1.1 The form of cross sections

In order to calculate the tidal cross sections we specify the range of the black hole masses and rotational parameters. We calculate the amount of mass lost by the star, $M_{\rm lost}$, for a given value of the black hole mass and rotational parameter. These values are shown in Table 1. We plot the levels of constant $M_{\rm lost}$ in the plane (L_z, q). The black hole mass M is expressed in units of $10^{7}~M_{\odot}$ and $M_{\rm lost}$ is expressed in units of the stellar mass m_* in all figures.

In Figs. 1-4 we show the cross sections for $a\ne 0$. Three levels of $M_{\rm lost}=0.1$, 0.5 and 1 are shown for a given a and M. Since the cross section of direct capture does not depend on M in our dimensionless units, we plot several different tidal cross sections and the cross section of direct capture corresponding to several different black hole masses in the same figure.

	Figure 2: Same as Fig. 1 but a=0.75 Top: M=0.1, 0.25, 0.5 and 1 Bottom: M=2, 4, 8, 16, 32.
Open with DEXTER

	Figure 3: Same as Fig. 1 but a=0.5 Top: M=0.1, 0.25, 0.5 and 1 Bottom: M=2, 4, 8, 16.
Open with DEXTER

	Figure 4: Same as Fig. 1 but a=0.25 Top: M=0.1, 0.25, 0.5 and 1 Bottom: M=2, 4, 8.
Open with DEXTER

Table 2: The values of M_- and M₊ as functions of a.

In the non-relativistic theory of tidal disruption the tidal cross sections are circles centred at the origin of the coordinates (L_z, q) with radius $\propto$M^-1/3 in our units. When the mass of the black hole exceeds a certain value the radius of the tidal cross section becomes smaller than the one corresponding to capture and the tidal disruption can no longer take place. In the fully relativistic treatment of the problem the situation is more complicated. We have checked with an accuracy of the order of 10^-3 that even in this case the levels of the mass loss always have a circular form. However, when a > 0 the centres of these circles are shifted toward negative values of L_z and the radii of these circles do not obey the simple $\propto$M^-1/3 law (see Figs. 7-11 and Sect. 3.1.2).

These effects are most prominent at a high rotational rate of the black hole. In Fig. 1 we show the results of calculations for a=0.9999. When the black hole mass is sufficiently small (see the upper part of this figure), the levels are approximately circular with a small shift toward negative values of L_z. The triangle shows the position of the orbital parameters L_z=2.72945 and q=0 for the case intensively studied by Diener et al. (1997). They obtained $M_{\rm lost}\approx 0.5$ for $M=1.0853\times 10^{7}~M_{\odot}$. This value is in excellent agreement with our results for the mass $M=10^{7}~M_{\odot}$. Note, however, that there is a considerable ambiguity in the results reported by Diener et al. (1997) counting the gas elements leaving the computational box but having velocities less than the parabolic velocity as being stripped away from the star. Provided that these elements are not considered as being stripped, the value of $M_{\rm lost}$ is considerably less, $M_{\rm lost}\approx 0.32$. The lower part of Figure 1 shows the case of high black hole masses. The levels of the amount of mass lost by the star decrease toward the capture cross section with increasing mass. When $M \equiv M_{-} \sim 4\times 10^{7}~M_{\odot}$ the levels of mass loss intersect the capture cross section at the point (q=0, L_z=L_-), where

$$L_{-}(a)=-(1+\sqrt{1-a}),$$ (13)

is a "critical'' negative angular momentum. It is defined for the equatorial orbits with negative angular momenta if the particles on the orbits with |L| < |L_-| are captured by the black hole. When the black hole mass grows further, the intersection point moves toward the positive value of L_z and when $M > 1.6\times 10^{8}~M_{\odot}$ only the stars with positive angular momenta can be tidally disrupted. When $M\equiv M_{+}\sim 10^{9}~M_{\odot}$ the tidal cross section coincides with the capture cross section. In this case only the stars with angular momenta very close to

$$L_{+}=1+\sqrt{1-a}$$ (14)

can be tidally disrupted. Here the "critical'' angular momentum L₊ is defined analogously to L_- for the orbits with positive angular momenta (i.e. the stars with L < L₊ are captured by the black hole). When M> M₊ only the process of capture of the stars is possible. The width of the region in the plane (L_z, q) where a partial stripping of mass takes place decreases with mass. As we will see below this is mainly a relativistic effect.

In Figs. 2-4 we show similar results for smaller values of the rotational parameter, a=0.75 (Fig. 2), 0.5 (Fig. 3), 0.25 (Fig. 4). In general, the behaviour of the levels of $M_{\rm lost}$ looks similar to the previous case and the levels of constant $M_{\rm lost}$ can be well approximated as circles. The shift of the centres of these circles from the origin of the coordinates decreases with the decrease of a. The corresponding values of M_- and M₊ are shown in Table 2. As seen from this table the value of M_- slightly increases and the value of M₊ decreases with decrease of a.

When a=0 the cross sections are circles centred on the origin of the coordinate system, and we can use the dependence of  $M_{\rm lost}$ on $L=\sqrt{L_{z}^{2}+q^{2}}$ to represent our results. This is shown in Fig. 5. In this case $M_{-}=M_{+}\sim 4 \times 10^{7}~M_{\odot}$. Similary to the case of non-zero a the size of the region where a partial stripping takes place decreases with M. To show how important the relativistic effects are we compare our results with simple relations for the amount of mass lost by the star based on the non-relativistic theory of tidal disruption, see Fig. 6. In the non-relativistic theory $M_{\rm lost}$ depends on the periastron distance $r_{\rm p}$, the black hole mass M, the stellar mass m_* and the stellar radius  $R_{\rm st}$ only in combination

$$\eta={(r_{\rm p}/r_{\rm T})}^{3/2},$$ (15)

where $r_{\rm T}$ is the tidal radius given by Eq. (1). We calculate the dependence $M_{\rm lost}(\eta)$ for a very low mass $M=5\times 10^{5}~M_{\odot}$, and use this dependence to calculate $M_{\rm lost}(L)$ for higher masses of the black hole (dot dashed curves in Fig. 6). These curves give a good approximation to the relativistic calculations for a small black hole mass $M=10^{6}~M_{\odot}$. However, the results diverge with increasing mass M. The curves based on the non-relativistic approximation systematically give a larger size of the region where a partial stripping of the mass takes place. We have checked that when $M > 10^{7}~M_{\odot}$ the deviation is very significant and these results are not shown in this figure. To take into account some effects of General Relativity, Diener et al. (1997) have proposed using the relativistic dependence of $r_{\rm p}$ on L in Eq. (15). The curves calculated according to this prescription are shown as dotted curves in Fig. 6. The prescription of Diener et al. (1997) slightly improves the agreement, but the deviation is still rather large. This can be explained by the fact that there are relativistic effects not accounted for by the Diener et al. (1997) prescription, such as a different form of the tidal tensor, a different time spent by the star near the periastron, etc.

Figure 5: The amount of mass lost by the star calculated for the case a=0. Since the cross sections in this case are concentric circles in the plane (Lz, q) we show $M_{\rm lost}$ as a function of the radius $L=\sqrt {q^{2}+L_{z}^{2}}$ for the different black hole masses M=0.1, 0.25, 0.5, 0.75, 1, 2 and 4. Vertical triangles show the position of the radius of the capture cross section $L_{\rm capt}=2$.

Open with DEXTER

	Figure 6: The amount of mass lost by the star compared with the results based on the Newtonian approach to the problem for the case a=0.The dash dotted curves correspond to extrapolation to the higher masses of the results obtained for M=0.05 and the dotted curves take into account the relativistic dependence of the periastron radius $r_{\rm p}$ on L, see the text for details.
Open with DEXTER

3.1.2 Semi-analytic representation of the results obtained

As we discussed above the contours of the amount of mass lost by the star in the plane (L_z, q) can be approximated as circles of a given radius $r_{\rm L}$ shifted toward negative values of L_z. This means that they can be represented in the form:

$$(L_{z}-d)^{2}+q^{2}=r_{\rm L}^{2},$$ (16)

where d < 0 is the shift of the centres of the approximating circles. Therefore, we can describe the levels of $M_{\rm lost}$ with two functions $d_{\rm L}(M,a)$ and r(M,a). We present these functions in Figs. 7-11 for two values of $M_{\rm lost}$: $M_{\rm lost}=0.1$ and $M_{\rm lost}=1$. Since in the non-relativistic approximation the characteristic size of the cross sections scales as M^-1/3, it is convenient to introduce the rescaled radius and shift: d_*=M^1/3d and $r_{*}=M^{1/3}r_{\rm L}$. The change of r_* with mass is a purely relativistic effect.

	Figure 7: The dependence of the shift of the approximating circles d* on mass M for three values of the rotational parameter a=0.9999, 0.9 and 0.75. The lower and upper curves of the same type correspond to the circles approximating the levels $M_{\rm lost}=1$ and $M_{\rm lost}=0.1$, respectively.
Open with DEXTER

In Fig. 7 we present the dependence of d_* with mass for high values of the rotational parameter a=0.9999, 0.9 and 0.75. For any given curve the rightmost value of M is equal to M₊. For a given value of a the shift corresponding to $M_{\rm lost}=1$ is always larger than that corresponding to $M_{\rm lost}=0.1$. In Fig. 8 we show the same results calculated for the case of the small rotational parameters a=0.75, a=0.5 and a=0.25.

	Figure 8: Same as Fig. 7 but a=0.75, 0.5 and 0.25.
Open with DEXTER

Figure 9: The dependence of the radius of the approximating circles r* on mass M for three values of the rotational parameter a=0.9999, 0.9 and 0.75. The curves corresponding to the same value of a and describing two different values of the amount of mass lost by the star $M_{\rm lost}=0.1$ and $M_{\rm lost}=1$ intersect at $M\sim 10$. For black holes of higher masses the radius of the circle corresponding to $M_{\rm lost}=1$ has a radius r* larger than for $M_{\rm lost}=0.1$.

Open with DEXTER

	Figure 10: The ratio f of the length of a segment of the approximating circle lying outside the capture cross section to the total length of the approximating circle as a function of the mass M. All curves correspond to $M_{\rm lost}=0.1$ and different values of a=0.9999, 0.9, 0.75 and 0.5.
Open with DEXTER

	Figure 11: Similar to Fig. 10 but now the ratio f1 of the length of an approximating circle lying outside the capture cross section to the total length of the unit of the tidal cross section and the capture cross section is shown as a function of the mass M.
Open with DEXTER

In Fig. 9 we show the dependence of r_* on mass for a=0.9999, 0.9 and 0.75. Note that all curves are very close to each other. The radius corresponding to the level $M_{\rm lost}=0.1$ is larger than that corresponding to $M_{\rm lost}=1$only for sufficiently small masses $M < M_{\rm intersect} \sim 10^{8}~M_{\odot}$. When $M=M_{\rm intersect}$the curves corresponding to the different levels intersect and when $M > M_{\rm intersect}$ the radius of the cross section corresponding to $M_{\rm lost}=1$ is larger than that corresponding to $M_{\rm lost}=0.1$. However, in the region outside the capture cross section the level corresponding to $M_{\rm lost}=1$ is situated inside the level corresponding to $M_{\rm lost}=0.1$due to a larger negative shift. When $M < M_{\rm intersect}$, the curves with different a coincide. When a < 0.5, we have $M_{+} < M_{\rm intersect}$ and the curves corresponding to smaller values of a coincide with the curves corresponding to the larger values of a. Therefore, we do not show these curves in Fig. 9.

In Fig. 10 we show the ratio f of the length of the circles lying outside the capture cross section to the total length of the circles. The level $M_{\rm lost}=0.1$ is shown for the cases a=0.9999, 0.9, 0.75 and 0.5. For a particular curve, the mass of the black hole corresponding to f=1 is approximately equal to M_- and the mass corresponding to the end of a particular curve is approximately M₊. When a < 0.5, M_- almost coincides with M₊ and the curves are almost vertical. They are not shown in this figure.

Figure 11 is similar to Fig. 10, but here we show the ratio f₁ of length of the circles lying outside the capture cross section to the length of the boundary of unit of the tidal cross section and the capture cross section. This quantity has a direct physical meaning. In a real astrophysical setting where the super-massive black hole is embedded in a stellar cluster, the processes of tidal disruption and capture of the stars typically occur in the so-called regime of the empty loss cone (e.g. Frank $\&$ Rees (1976), BIIP and references therein). In this regime only the stars with orbital parameters close to the boundary of the unit can be either disrupted or captured. So, the quantity f₁ gives the fraction of tidally disrupted stars among all stars with $\Theta_{\infty} \approx \pi/2$that have been destroyed by the black hole (i.e. either tidally disrupted or captured).

3.1.3 The case $\Theta _{\infty }\ne \pi /$2

As follows from Eq. (3) the law of transformation from the coordinates (L_z, q)to the coordinates $(j_{\theta }, j_{\phi })$ has the form

$$j_{\theta}=L_{z}/\cos \Theta_{\infty}, \quad j_{\phi}=\sqrt{q^{2}-L_{z}^{2}\cot^{2} \Theta_{\infty}}.$$ (17)

Since the expression in the square root in Eq. (17) must be positive, only the values of $\Theta_{\infty}$ in the range

$$\Theta_{-}\leq \Theta_{\infty} \leq \Theta_{+}$$ (18)

are allowed, where

$$\Theta_{\pm}=\pi/2 \pm \arctan {\bigg\vert{q\over L_{z}}\bigg\vert}\cdot$$ (19)

In order to check the dependence of our results on $\Theta_{\infty}$ we calculate several tidal cross sections in the plane (L_z, q) for $\Theta _{\infty }=\Theta _{+}$ and compare them to those corresponding to $\Theta _{\infty }=\pi /2$. The results of comparison are presented in Fig. 12. They show that this dependence is practically absent. This may be explained as follows. When the periastron distance $r_{\rm p}$ is sufficiently large, the effects determined by the rotation of the black hole, such as the dependence of the results on $\Theta_{\infty}$, are determined by high order corrections to the non-relativistic results. In the opposite case of a star that has the orbital parameters very close to those corresponding to the capture, the orbit of the star near the periastron is close to a "barrel-like'' critical orbit of constant $r_{\rm p}$. In this case, the angle $\Theta$ changes between two limiting values $\Theta_{-}$ and $\Theta_{+}$ near the periastron, and the dependence of the results on $\Theta_{\infty}$ is averaged out (see also BIIP). Therefore, this dependence appears to be unimportant in the two limiting cases. The results shown in Fig. 12 indicate that this dependence is also small in an intermediate case.

Therefore, for a given value of $\Theta_{\infty}$, we obtain the tidal cross sections in the plane $(j_{\theta }, j_{\phi })$transforming the results obtained for $\Theta _{\infty }=\pi /2$ to the new coordinates according to the transformation law 17. The results are shown in Figs. 13-16. One can see from these figures that the cross sections become more symmetric with respect to the origin of the coordinate system with decreasing of $\Theta_{\infty}$. In the limiting case $\Theta_{\infty}=0$ the cross sections are circles.

Let us consider the situation when the tidal cross section and the capture cross section intersect. The relative position of these cross sections is mainly characterised by their intersection point. Let $L_{z}^{\rm int}$ be the value of the z component of the angular momentum corresponding to the point of intersection on the plane (L_z,q), and $j_{\theta}^{\rm int}$ be the coordinate of the same point on the plane $(j_{\theta }, j_{\phi })$. The values of $L_{z}^{\rm int}$ and $j_{\theta}^{\rm int}$ are connected by Eq. (17). As follows from this equation, when $L^{\rm int}_{z} < 0$, $j_{\theta}^{\rm int}$shifts leftward with decreasing of $\Theta_{\infty}$ from $\pi/2$ to 0. In the opposite case $L^{\rm int}_{z} > 0$, $j_{\theta}^{\rm int}$ shifts to the right. As follows from Fig. 1, we have $L_{z}^{\rm int}\approx 0$ for $M\approx 1.6\times 10^{8}~M_{\odot}$, and as we see from Figs. 13-16 the point of intersection corresponding to this mass has $j_{\theta}\approx 0$ for all $\Theta_{\infty}$.

	Figure 12: The tidal cross sections calculated for $\Theta _{\infty }=\Theta _{+}$ (shown by the circles) in comparison to the tidal cross sections calculated for $\Theta _{\infty }=\pi /2$ for a=0.9999 and $M_{\rm lost}=1$. Note that the case $\Theta _{\infty }=\Theta _{-}$is equivalent to the case shown, by symmetry.
Open with DEXTER

	Figure 13: The tidal cross sections in the plane $(j_{\theta }, j_{\phi })$. The angle $\Theta _{\infty }=\pi /3$ and a=0.9999.
Open with DEXTER

	Figure 14: Same as Fig. 13 but $\Theta _{\infty }=\pi /6$.
Open with DEXTER

	Figure 15: Same as Fig. 13 but $\Theta _{\infty }=\pi /12$.
Open with DEXTER

	Figure 16: Same as Fig. 13 but $\Theta _{\infty }=\pi /24$.
Open with DEXTER

4 Discussion and conclusions

We have obtained the cross sections of the amount of mass lost by a star tidally disrupted by a rotating black hole in the range of black hole masses where the effects of General Relativity are important. Our results can be used in a situation where the process of direct capture of the stars by the black hole and the process of tidal disruption compete with each other. With a high accuracy the tidal cross sections in the plane of angular momenta $(j_{\theta }, j_{\phi })$ are circles shifted toward negative values of $j_{\theta}$ for $a\ne 0$. We have found the values of radius and the shift of these circles as functions of the black hole mass M for several values of the rotational parameter a. The ratio of characteristic size of the tidal cross section to the size of the capture cross sections decreases with the mass M. Since the shift of the capture cross section toward negative values of $j_{\theta}$ is always larger than the shift of the tidal cross sections, the cross sections intersect each other at a certain value of the mass. The intersection point moves toward positive values of $j_{\theta}$ and when the black hole mass is sufficiently large: M > M₊(a), the process of tidal disruption is no longer possible. We estimate $M_{+}(a=0) \sim 4\times 10^{7}~M_{\odot}$ and $M_{+}(a=1) \sim 10^{9}~M_{\odot}$.

We have used the numerical model of a tidally disrupted star developed in our previous work (IN, ICN). Approximately $5\times 10^{3}$ tidal encounters have been considered, the number at least an order of magnitude larger than all results obtained elsewhere.

Our results would be helpful for detailed studies of tidal feeding of the central black holes by the stellar gas.

To model the star we use the simple n=1.5 polytrope. Since the stars are also often approximated by polytropes with larger values of n, it will be interesting to obtain the dependence of the results on n. Such a study lies beyond the scope of the present paper. We note, however, that the polytropes with larger n are more centrally condensed, and therefore, it is more difficult to disrupt them. Accordingly, the mass M₊(a) should be smaller for larger n.

We consider the stars having solar mass $M_{\odot}$ and solar radius $R_{\odot}$. However, our results can be used for stars with different masses m and radii $R_{\rm st}$. Indeed, the stellar mass and the radius enter in our calculations only in combination $t_{\rm st}/t_{\rm gr}$, where $t_{\rm st}=\sqrt {{R_{\rm st}^{3}\over Gm}}$, and $t_{\rm gr}={GM\over c^{3}}$. Therefore, when the stellar mass and radius are not the solar ones, the cross sections obtained for the mass M correspond to the re-scaled mass of the black hole

$$M_{\rm re}=\sqrt{{M_{\odot}\over m}}{\left({R_{\rm st}\over R_{\odot}}\right)}^{3/2}M.$$ (20)

As we have shown there is a rather significant region in the plane $(j_{\theta }, j_{\phi })$ where only a partial stripping of mass from the star takes place. The future of a part of the star that remains gravitationally bound after the tidal stripping depends on many factors. Let us suppose that the orbit of this remainder is unchanged after the tidal encounter. Taking into account that the central density of the remainder is smaller than the density of the unperturbed star and the remainder has significant internal motions and rotation, one can suppose that the remainder would be tidally disrupted during the next tidal encounter. However, the processes of distant gravitational interactions with other stars of the central stellar cluster could increase the value of the orbital angular momentum of the remainder and it could be present in the cluster for a certain period of time. The observational detection of such remainders e.g. in the centre of our own Galaxy would be a very convincing test of the theory of tidal disruptions of stars by a black hole.

Quantitative results obtained above should be taken with caution. From the results of comparison between our "old'' variant of the model of a tidally disrupted star formulated and developed in IN and our "new'' advanced variant formulated and developed in ICN it follows that when the amount of mass lost by the star is large enough the "old'' model gives a larger value of the mass loss, and the difference between these models is of the order of $30\%$. Also, the difference between the 3D hydro-simulations themselves can be as large as $\sim$$50\%$ or even larger depending on particular numerical scheme and criterion for the mass loss (e.g. Diener et al. 1997, and the discussion above). However, we believe that our qualitative conclusions are robust, and future work on improvement of the numerical schemes would mainly lead to corrections of the numerical values characterising the process of the tidal disruption, such as e.g. the value of M₊(a).

We neglect the possibility of formation of strong shocks in the star. Therefore, our results may be changed if future finite difference simulations will show that shocks play a significant role in the range of parameters we consider.

We have calculated only one quantity related to the outcome of the tidal disruption event: the amount of mass lost by the star, $M_{\rm lost}$. As has been pointed out by Lacy et al. (1982) and Rees (1988) the dynamics of the gas lost by the star depends significantly on the distribution of this gas over the orbital energies. The gas elements with negative orbital energies form an eccentric disc and can, in principle, accrete onto the black hole. The gas elements with positive orbital energies may leave the gravitational field of the black hole. Therefore, in a future work it would be interesting to calculate the cross sections characterising the distribution of the gas lost by the star over the orbital integrals of motion. Also, it would be interesting to calculate the cross sections for other quantities, such as the energy, internal angular momentum and average density of the gravitationally bound remainder.

Acknowledgements

PBI thanks the INTEGRAL Science Data Centre for hospitality. This work has been supported in part by RFBR grant 04-02-17444. We are grateful to Alexei Ulyanov and Simon Shaw for useful remarks.

References

• Beloborodov, A. M., Illarionov, A. F., Ivanov, P. B., & Polnarev, A. G. 1992, MNRAS, 259, 209 [NASA ADS] (BIIP) (In the text)
• Chandrasekhar, S. 1969, Ellipsoidal figures of Equilibrium (New Haven: Yale University Press) (In the text)
• Chandrasekhar, S. 1983, The mathematical theory of black holes (New York: Clarendon Press/Oxford: University Press) (In the text)
• Diener, P., Frolov, V. P., Khokhlov, A. M., Novikov, I. D., & Pethick, C. J. 1997, ApJ, 479, 164 [NASA ADS] [CrossRef] (In the text)
• Evans, C. R., & Kochanek, C. S. 1989, 346, L13
• Frank, J., & Rees, M. J. 1976, MNRAS, 176, 633 [NASA ADS] (In the text)
• Hills, J. G. 1975, Nature, 254, 295 [NASA ADS] [CrossRef] (In the text)
• Ivanov, P. B., & Novikov, I. D. 2001, ApJ, 549, 467 [NASA ADS] [CrossRef] (IN) (In the text)
• Ivanov, P. B., Chernyakova, M. A., & Novikov, I. D. 2003, MNRAS, 338, 147 [NASA ADS] [CrossRef] (ICN) (In the text)
• Khokhlov, A. M., Novikov, I. D., & Pethick, C. J. 1993, ApJ, 418, 181 [NASA ADS] [CrossRef] (In the text)
• Komossa, S., Halpern, J., Schartel, N., et al. 2004, ApJ, 603L, 17 [NASA ADS] (In the text)
• Lacy, J. H., Townes, C. H., & Hollenbach, D. J. 1982, ApJ, 262, 120 [NASA ADS] [CrossRef]
• Rees, M. J, 1988, Nature, 333, 523 [NASA ADS] [CrossRef] (In the text)
• Young, P. 1976, Phys. Rev. D, 14, 3281 [NASA ADS] [CrossRef] (In the text)