- ...
![[*]](/icons/foot_motif.gif)
- On leave from Astro Space Center
of the P.N. Lebedev Physical Institute, Moscow, Russia.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
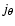
![[*]](/icons/foot_motif.gif)
- Let the velocity components at the orbit apastron be
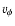 and
and
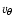 and the apastron distance be
and the apastron distance be 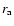 .
Then,
.
Then,
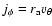 and
and
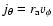 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...1983)
![[*]](/icons/foot_motif.gif)
- Technically, it follows from the fact that the radius of periastron of a parabolic orbit
does not depend on
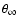 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... models
![[*]](/icons/foot_motif.gif)
- See Ivanov
 Novikov (2001) for an overview of works on tidal disruption and
astrophysical applications.
Novikov (2001) for an overview of works on tidal disruption and
astrophysical applications.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...1997)
![[*]](/icons/foot_motif.gif)
- Note misprints in the Diener et al. (1997)
expression for the components of the tidal tensor.
The sign of all components should be opposite.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... units
![[*]](/icons/foot_motif.gif)
- In physical units the characteristic size of the tidal
cross section
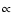 M2/3 and the characteristic size of the
capture cross section
M2/3 and the characteristic size of the
capture cross section 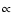 M.
M.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... allowed
![[*]](/icons/foot_motif.gif)
- Note that these inequalities are also valid for the angle
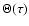 that changes during the fly-by around the black hole:
that changes during the fly-by around the black hole:
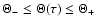 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
hole
![[*]](/icons/foot_motif.gif)
- Note that the fraction of stellar gas eventually accreted
onto the black hole may differ from the fraction of gravitationally
bound gas lost by the star. The physical processes occurring in the gas
after the tidal disruption event have been discussed by e.g. Evans
 Kochanek (1989).
Kochanek (1989).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.