A&A 447, 405-412 (2006)
DOI: 10.1051/0004-6361:20053395
Point source confusion in SZ cluster surveys
J. G. Bartlett1 -
J.-B. Melin2
1 - APC, 11 pl. Marcelin Berthelot, 75231
Paris Cedex 05, France
(UMR 7164 CNRS, Université
Paris 7, CEA, Observatoire de Paris)
2 -
Department of Physics, University of California Davis,
One Shields Avenue, Davis, CA , 95616 USA
Received 10 May 2005 / Accepted 20 September 2005
Abstract
We examine the effect of point source confusion on
cluster detection in Sunyaev-Zel'dovich (SZ) surveys. A filter
matched to the spatial and spectral characteristics of the SZ signal optimally extracts clusters from the astrophysical
backgrounds. We
calculate the expected confusion (point source and primary cosmic
microwave background [CMB]) noise through this
filter and quantify its effect on the detection threshold for both
single and multiple frequency surveys. Extrapolating current radio
counts, we estimate that confusion from sources
below 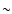
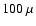 Jy limits single-frequency surveys to
Jy limits single-frequency surveys to
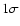 detection thresholds of
detection thresholds of 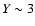
 10-6 arcmin2 at
30 GHz and
10-6 arcmin2 at
30 GHz and
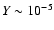 arcmin2 at 15 GHz (for
unresolved clusters in a 2 arcmin beam);
these numbers are highly uncertain, and an
extrapolation with flatter counts leads to much lower confusion limits.
Bolometer surveys must contend with an important population of
infrared point sources. We find that a three-band matched
filter with 1 arcmin resolution (in each band)
efficiently reduces confusion, but does not eliminate it:
residual point source and CMB fluctuations contribute significantly
to the total filter noise. In this light, we find that a 3-band
filter with a low-frequency channel (e.g, 90+150+220 GHz) extracts
clusters more effectively than one with a high frequency channel (e.g,
150+220+300 GHz).
arcmin2 at 15 GHz (for
unresolved clusters in a 2 arcmin beam);
these numbers are highly uncertain, and an
extrapolation with flatter counts leads to much lower confusion limits.
Bolometer surveys must contend with an important population of
infrared point sources. We find that a three-band matched
filter with 1 arcmin resolution (in each band)
efficiently reduces confusion, but does not eliminate it:
residual point source and CMB fluctuations contribute significantly
to the total filter noise. In this light, we find that a 3-band
filter with a low-frequency channel (e.g, 90+150+220 GHz) extracts
clusters more effectively than one with a high frequency channel (e.g,
150+220+300 GHz).
Key words: cosmic microwave background - galaxies: clusters: general - methods: observational
Galaxy cluster surveys based on the Sunyaev-Zel'dovich (SZ) effect
(Sunyaev & Zeldovich 1970, 1972; for comprehensive reviews, see
Birkinshaw 1999 and Carlstrom et al. 2002) will soon supply large, homogeneous catalogs out to redshifts well beyond unity (Barbosa et al. 1996; Eke et al. 1996; Colafrancesco et al. 1997; Holder et al. 2000; Bartlett 2001; Kneissl et al. 2001; Benson et al. 2002). Eagerly awaited, these
surveys will probe dark energy and its evolution, and shed new light
on galaxy formation (Haiman et al. 2001; Weller & Battye 2003; Wang et al. 2004). The instruments designed for these observations are of two types: dedicated
interferometer arrays surveying at a single frequency (e.g., AMI,
AMiBA, and SZA) and bolometer systems operating over several
millimeter bands (e.g., ACBAR, ACT, APEX, Olimpo, Planck,
SPT)![[*]](/icons/foot_motif.gif) . Ground-based and balloon-borne instruments
are expected to find up to several thousands of clusters, while the
Planck mission will produce an essentially all-sky catalog of several
104 clusters by the end of the decade.
. Ground-based and balloon-borne instruments
are expected to find up to several thousands of clusters, while the
Planck mission will produce an essentially all-sky catalog of several
104 clusters by the end of the decade.
An important issue facing these surveys is cluster detection in the
presence of other astrophysical foregrounds/backgrounds. Except for
the very nearby ones, clusters will appear as extended sources over
arcminute scales. Power in diffuse Galactic emission (synchrotron,
free-free and dust emission) and in the primary cosmic microwave
background (CMB) anisotropy falls on these scales and the clusters can
be efficiently extracted using an adapted spatial filter
(Haehnelt & Tegmark 1996; Herranz et al. 2002; Schäfer et al. 2004); fluctuations caused by point
sources (radio and infrared galaxies), on the other hand, are
important on these scales and represent a potentially serious source
of confusion for SZ cluster searches (Knox et al. 2004; White & Majumdar 2004; Aghanim et al. 2005).
The two kinds of SZ survey instruments deal with this problem in
different ways. Single frequency surveys must individually identify
and remove point sources with high angular resolution (better than 1 arcmin) observations, which interferometers achieve by incorporating several long baselines in their antenna array. Operating at relatively low frequencies (15 GHz for AMI, 30 GHz for the SZA and
90 GHz for AMiBA), these surveys will contend with the radio galaxy
population. Bolometer-based instruments will not have the angular
resolution needed to spatially separate point sources from galaxy
clusters; they must instead rely on spectral information. In their
millimeter wavelength bands, these instruments will contend with the
poorly known far-infrared point source population.
In this paper we quantify the effect of point source confusion on
cluster detection in SZ surveys. We shall only consider the effect of
the random field population, but we note that point sources are
expected to preferentially reside in the clusters themselves, locally
raising the effective noise level; we leave examination of this effect
to a future work. White & Majumdar (2004) recently calculated the
expected confusion due to IR point sources as a function of frequency,
while Knox et al. (2004) and Aghanim et al. (2005) studied their
influence on the measurement of SZ cluster parameters. We extend this
work by considering cluster detection with an optimal filter spatially
and spectrally (for multi-frequency surveys) matched to the thermal SZ signal
(Haehnelt & Tegmark 1996; Herranz et al. 2002; Schäfer et al. 2004). Using the matched filter, we quantify the
confusion noise induced by extragalactic point sources for both
single-frequency radio and multi-frequency bolometer SZ surveys.
We begin by briefly describing our matched filter and cluster detection
routine, leaving details to Melin et al. (2005). In Sect. 3 we present our point source model, based on recent
number counts in the radio and far-infrared. We then calculate the
confusion noise through the filter to examine its importance for
future SZ surveys (Sect. 4). In the last section,
we summarize our main results and discuss implications for SZ surveying.
The SZ effect is caused by the hot gas (
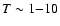 keV) contained in
galaxy clusters known as the intracluster medium (ICM); electrons in
this gas up-scatter CMB photons and create a unique spectral distortion
that is negative at radio wavelengths and positive in the
submillimeter, with a zero-crossing near 220 GHz. The form of this
distortion is universal (in the non-relativistic limit applicable to
most clusters), while the amplitude is given by the Compton y parameter, an integral of the gas pressure along the line-of-sight.
In a SZ survey, clusters will appear as sources extended over
arcminute scales (apart from the very nearby objects, which are
already known) with brightness profile
keV) contained in
galaxy clusters known as the intracluster medium (ICM); electrons in
this gas up-scatter CMB photons and create a unique spectral distortion
that is negative at radio wavelengths and positive in the
submillimeter, with a zero-crossing near 220 GHz. The form of this
distortion is universal (in the non-relativistic limit applicable to
most clusters), while the amplitude is given by the Compton y parameter, an integral of the gas pressure along the line-of-sight.
In a SZ survey, clusters will appear as sources extended over
arcminute scales (apart from the very nearby objects, which are
already known) with brightness profile
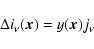 |
(1) |
relative to the mean CMB brightness.
Here
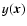 is the Compton y parameter at position
is the Compton y parameter at position 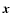 (a 2D vector on the sky) and
(a 2D vector on the sky) and 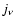 is the SZ spectral function evaluated at the observation frequency
is the SZ spectral function evaluated at the observation frequency 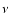 .
.
A SZ survey will produce maps of the sky at one or more
frequencies![[*]](/icons/foot_motif.gif) . We model the survey data as a vector field
. We model the survey data as a vector field
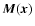 whose components correspond to these maps (for a
single-frequency survey, the data is a scalar field). It is a sum of
cluster profiles at positions
whose components correspond to these maps (for a
single-frequency survey, the data is a scalar field). It is a sum of
cluster profiles at positions 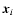 plus noise and foregrounds:
plus noise and foregrounds:
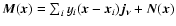 ,
where
,
where
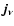 is the column vector with
components given by
is the column vector with
components given by 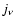 evaluated at the different observation
frequencies. The vector
evaluated at the different observation
frequencies. The vector
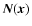 includes all non-SZ
signals as well as instrumental noise; we model it as a stationary
random variable with zero mean:
includes all non-SZ
signals as well as instrumental noise; we model it as a stationary
random variable with zero mean:
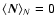 ,
where
the average is taken over realizations of both the instrumental noise and
foreground fields. We thus assume that the mean intensity of the map
is zero, i.e., that the zero mode has been taken out by the
observations
,
where
the average is taken over realizations of both the instrumental noise and
foreground fields. We thus assume that the mean intensity of the map
is zero, i.e., that the zero mode has been taken out by the
observations![[*]](/icons/foot_motif.gif) . Although the model of a stationary random variable applies
to the primary CMB anisotropy and (perhaps) the noise, one may
question its suitability for Galactic foregrounds; it does, all the
same, seem a reasonable approximation for fluctuations around the mean
foreground intensity over angular scales pertinent to galaxy cluster
detection (arcminutes).
. Although the model of a stationary random variable applies
to the primary CMB anisotropy and (perhaps) the noise, one may
question its suitability for Galactic foregrounds; it does, all the
same, seem a reasonable approximation for fluctuations around the mean
foreground intensity over angular scales pertinent to galaxy cluster
detection (arcminutes).
![\begin{figure}
\par\includegraphics[width=15cm,clip]{3395fig1.eps}\end{figure}](/articles/aa/full/2006/08/aa3395-05/Timg25.gif) |
Figure 1:
Radial profiles of single frequency and multiple frequency
matched filters for a cluster of 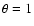 arcmin. In the left-hand
panel we see the spatial weighting used by the single frequency
filter to optimally extract the cluster from the background
(radio point sources + CMB) and noise. The filter is arbitrarily
normalized to unity at the origin and the beam has a 2 arcmin FWHM.
The right-hand panel shows the elements of the 3-band filter
with 150, 220 and 300 GHz channels. The three functions
are arbitrarily normalized to the peak value of the 150 GHz
filter (black curve), and each channel has a 1 arcmin FWHM beam.
In this case we see how the filter uses both spatial
and spectral information to optimally extract the cluster. arcmin. In the left-hand
panel we see the spatial weighting used by the single frequency
filter to optimally extract the cluster from the background
(radio point sources + CMB) and noise. The filter is arbitrarily
normalized to unity at the origin and the beam has a 2 arcmin FWHM.
The right-hand panel shows the elements of the 3-band filter
with 150, 220 and 300 GHz channels. The three functions
are arbitrarily normalized to the peak value of the 150 GHz
filter (black curve), and each channel has a 1 arcmin FWHM beam.
In this case we see how the filter uses both spatial
and spectral information to optimally extract the cluster. |
| Open with DEXTER |
We now wish to use both spatial and spectral information (when
available) to best extract clusters from our survey. Consider a
cluster of characteristic size 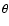 (in the following, we take
this to be the core radius of a
(in the following, we take
this to be the core radius of a 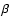 -profile) and central
y-value
-profile) and central
y-value 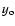 situated at an arbitrary point
situated at an arbitrary point 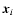 on the
sky. We build a filter
on the
sky. We build a filter
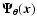 (in general a column
vector in frequency space) that returns an estimate,
(in general a column
vector in frequency space) that returns an estimate,
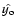 ,
of
,
of 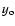 when centered on the cluster:
when centered on the cluster:
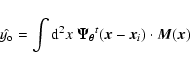 |
(2) |
where superscript t indicates a transpose (with complex conjugation
when necessary). Suppose that clusters of this characteristic size
are described by an average angular form
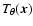 ,
by which we
mean:
,
by which we
mean:
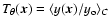 ,
where the
average is over many clusters of size
,
where the
average is over many clusters of size 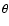 .
We match the
filter to this angular form
.
We match the
filter to this angular form
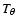 and to the spectral shape of the SZ signal, requiring an unbiased estimate of the central y value:
and to the spectral shape of the SZ signal, requiring an unbiased estimate of the central y value:
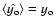 ,
where now the average is over both total noise and cluster (of size
,
where now the average is over both total noise and cluster (of size  )
ensembles. The filter is
then uniquely determined by further demanding a minimum variance estimate.
)
ensembles. The filter is
then uniquely determined by further demanding a minimum variance estimate.
The result expressed in Fourier space (the flat sky approximation is
reasonable on cluster angular scales) is (Haehnelt & Tegmark 1996; Herranz et al. 2002;
Melin et al. 2005, 2006):
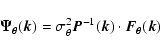 |
(3) |
where
| |
|
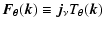 |
(4) |
| |
|
![$\displaystyle \sigma_\theta\equiv \left[\int {\rm d}^2k\;
\vec{F_\theta}^t(\vec{k})\cdot \vec{P}^{-1} \cdot
\vec{F_\theta}(\vec{k})\right]^{-1/2}$](/articles/aa/full/2006/08/aa3395-05/img38.gif) |
(5) |
with
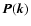 being the noise power spectrum, a matrix in
frequency space with components Pij defined by
being the noise power spectrum, a matrix in
frequency space with components Pij defined by
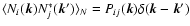 .
Note
that this last expression treats, again, the astrophysical foregrounds
as stationary fields. The quantity
.
Note
that this last expression treats, again, the astrophysical foregrounds
as stationary fields. The quantity
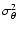 gives the the total noise
variance through the filter. We write the noise power spectrum as a
sum
gives the the total noise
variance through the filter. We write the noise power spectrum as a
sum
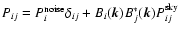 ,
where
,
where
 represents the instrumental noise power,
represents the instrumental noise power,
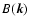 the observational beam and
the observational beam and
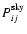 gives the foreground power
(non-SZ signal) between channels i and j. As written, we assume
uncorrelated instrumental noise between observation frequencies.
gives the foreground power
(non-SZ signal) between channels i and j. As written, we assume
uncorrelated instrumental noise between observation frequencies.
Our aim is to quantify the effect of point source confusion on cluster
detection using this filter. To this end, we ignore diffuse Galactic
emission, which is small on cluster scales, and only include primary
CMB temperature anisotropy and point source fluctuations in the sky
power
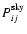 .
For our numerical results, we adopt a standard
flat concordance CMB power spectrum (
.
For our numerical results, we adopt a standard
flat concordance CMB power spectrum (
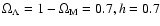 ,
e.g.,
Freedman et al. 2001; Spergel et al. 2003) and employ a cluster template based on the spherically symmetric
,
e.g.,
Freedman et al. 2001; Spergel et al. 2003) and employ a cluster template based on the spherically symmetric 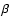 -model with core radius
-model with core radius 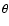 and
and
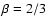 :
:
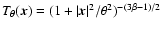 .
.
Two examples of the matched filter for 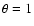 arcmin
are given in Fig. 1, one for a single frequency
survey with a 2 arcmin beam (left-hand panel) and the other for
a 3-band filter with 1 arcmin beams at 150, 220 and 300 GHz (right-hand
panel). The filters are circularly symmetric because we have chosen a
spherical cluster model, and the figure shows their radial profiles.
We clearly see the spatial weighting used by the single frequency filter
to optimally extract the cluster from the noise and from
the point source and CMB backgrounds. The multiple frequency
filter
arcmin
are given in Fig. 1, one for a single frequency
survey with a 2 arcmin beam (left-hand panel) and the other for
a 3-band filter with 1 arcmin beams at 150, 220 and 300 GHz (right-hand
panel). The filters are circularly symmetric because we have chosen a
spherical cluster model, and the figure shows their radial profiles.
We clearly see the spatial weighting used by the single frequency filter
to optimally extract the cluster from the noise and from
the point source and CMB backgrounds. The multiple frequency
filter
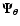 is a 3-element column vector containing
filters for each individual frequency. Their radial profiles are
shown in the right-hand panel arbitrarily normalized to the peak of
the 150 GHz filter. The map from each band is filtered by the
corresponding function and the results are then summed to produce the final
filter output. We see here how the filter uses both spectral and spatial
weighting to optimally extract the cluster signal.
is a 3-element column vector containing
filters for each individual frequency. Their radial profiles are
shown in the right-hand panel arbitrarily normalized to the peak of
the 150 GHz filter. The map from each band is filtered by the
corresponding function and the results are then summed to produce the final
filter output. We see here how the filter uses both spectral and spatial
weighting to optimally extract the cluster signal.
3 Point sources
Two different extragalactic point source populations affect SZ observations (see Fig. 2). At frequencies below
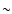 100 GHz, radio galaxies and quasars dominate the source counts,
while at higher frequencies dusty IR galaxies become more important.
The spectral dependence of source flux density in both populations is
often modeled as a power law,
100 GHz, radio galaxies and quasars dominate the source counts,
while at higher frequencies dusty IR galaxies become more important.
The spectral dependence of source flux density in both populations is
often modeled as a power law,
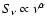 ,
with spectral
index
,
with spectral
index 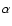 .
Radio sources tend to have falling spectra with
.
Radio sources tend to have falling spectra with
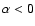 (Herbig & Readhead 1992; Taylor et al. 2001; Mason et al. 2003), but flat and inverted spectra
with
(Herbig & Readhead 1992; Taylor et al. 2001; Mason et al. 2003), but flat and inverted spectra
with
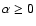 appear more prominent with observing frequency
(Bennett et al. 2003; Trushkin 2003). At millimeter wavelengths we observe the dust
emission of IR galaxies in the Rayleigh-Jeans with rising spectra
characterized by
appear more prominent with observing frequency
(Bennett et al. 2003; Trushkin 2003). At millimeter wavelengths we observe the dust
emission of IR galaxies in the Rayleigh-Jeans with rising spectra
characterized by
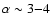 (Vlahakis et al. 2004). As will be seen,
we need information on these extragalactic sources down to mJy
flux densities and below; unfortunately, neither the distribution of
(Vlahakis et al. 2004). As will be seen,
we need information on these extragalactic sources down to mJy
flux densities and below; unfortunately, neither the distribution of 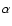 nor the source counts are well known for either population at these flux densities and at frequencies of interest for SZ observations (
nor the source counts are well known for either population at these flux densities and at frequencies of interest for SZ observations (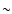 10-300 GHz).
10-300 GHz).
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{3395fig2.ps}\end{figure}](/articles/aa/full/2006/08/aa3395-05/Timg56.gif) |
Figure 2:
Integrated radio and IR source counts.
The lower solid red line results from the differential counts of
Eq. (6), while the dashed red line corresponds to
the model of Eq. (7). Measured counts at
30 GHz from CBI and the VSA are shown as the hashed blue boxes. The
upper solid red line gives the submillimeter source counts from
Eq. (8). The diamonds show the measured counts at
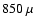 m from the HDF-North (Borys et al. 2003) and the
stars those from the 8 mJy-survey (Scott et al. 2002). m from the HDF-North (Borys et al. 2003) and the
stars those from the 8 mJy-survey (Scott et al. 2002). |
| Open with DEXTER |
Bennett et al. (2003) summarize the radio source counts at 30-40 GHz from
WMAP (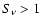 Jy), DASI (
Jy), DASI (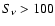 mJy, Kovac et al. 2002), VSA
(
mJy, Kovac et al. 2002), VSA
(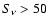 mJy, Taylor et al. 2003; Cleary et al. 2005) and CBI (
mJy, Taylor et al. 2003; Cleary et al. 2005) and CBI (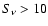 mJy,
Mason et al. 2003). Fitting to these data, Knox et al. (2004) find
mJy,
Mason et al. 2003). Fitting to these data, Knox et al. (2004) find
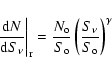 |
(6) |
with
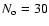 deg-2,
deg-2,
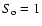 mJy and
mJy and
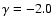 .
The
integrated counts obtained from Eq. (6) are shown in
Fig. 2 as the lower solid red line, together with the
observations from CBI and the VSA. The model fits the CBI counts well,
but lies high relative to the VSA counts at the bright end; as
shown in Bennett et al. (2003), the counts in fact steepen toward higher
flux densities, so a pure power law only matches the data over a limited range.
.
The
integrated counts obtained from Eq. (6) are shown in
Fig. 2 as the lower solid red line, together with the
observations from CBI and the VSA. The model fits the CBI counts well,
but lies high relative to the VSA counts at the bright end; as
shown in Bennett et al. (2003), the counts in fact steepen toward higher
flux densities, so a pure power law only matches the data over a limited range.
We will be interested in the counts at flux densities near
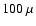 Jy for calculating the expected confusion noise in upcoming
SZ surveys. This requires an extrapolation of the observed counts
using Eq. (6) to much lower flux densities, which
we view with caution. To get a handle on the uncertainty associated
with this extrapolation, we consider an alternate model with a
flattening slope toward the faint end:
Jy for calculating the expected confusion noise in upcoming
SZ surveys. This requires an extrapolation of the observed counts
using Eq. (6) to much lower flux densities, which
we view with caution. To get a handle on the uncertainty associated
with this extrapolation, we consider an alternate model with a
flattening slope toward the faint end:
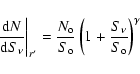 |
(7) |
with the same values of 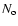 ,
,
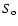 and
and 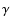 .
These counts are
shown as the red dashed line in Fig. 2, which
clearly provides an equally satisfactory fit to the observations.
Comparing the confusion noise in the two models will give us a sense
of the uncertainty in our estimates.
.
These counts are
shown as the red dashed line in Fig. 2, which
clearly provides an equally satisfactory fit to the observations.
Comparing the confusion noise in the two models will give us a sense
of the uncertainty in our estimates.
We adopt Eq. (6), alternatively
Eq. (7), for the counts at 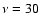 GHz.
Extrapolation to other frequencies suffers from uncertainty in the
spectral index
GHz.
Extrapolation to other frequencies suffers from uncertainty in the
spectral index 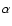 of the emission law. Typically negative,
determinations of
of the emission law. Typically negative,
determinations of 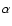 spread over a wide range, including
positive values. Mason et al. (2003), for example, find an average
spread over a wide range, including
positive values. Mason et al. (2003), for example, find an average
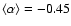 ,
between 1.4 and 30 GHz, with a dispersion
,
between 1.4 and 30 GHz, with a dispersion
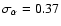 ,
which is roughly consistent with the
observations of Taylor et al. (2001) between 1.4 and 15 GHz. The
brighter sources seen over the higher frequency WMAP bands, on the
other hand, show much flatter spectra, with a distribution centered on
,
which is roughly consistent with the
observations of Taylor et al. (2001) between 1.4 and 15 GHz. The
brighter sources seen over the higher frequency WMAP bands, on the
other hand, show much flatter spectra, with a distribution centered on
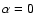 and a dispersion of
and a dispersion of
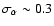 (Bennett et al. 2003; see also Trushkin 2003). There is a pressing need
for better understanding of the radio source population at CMB frequencies.
(Bennett et al. 2003; see also Trushkin 2003). There is a pressing need
for better understanding of the radio source population at CMB frequencies.
Dusty infrared luminous galaxies dominate the source counts at
frequencies near 100 GHz and higher. The dust in these galaxies is
typically heated to temperatures of several tens of Kelvin by their
interstellar radiation field. Its emission can be characterized
with a blackbody spectrum modified by a power-law emissivity:
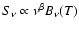 ,
where
,
where
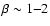 .
In the Rayleigh-Jeans this
leads to a steeply rising power-law with spectral index
.
In the Rayleigh-Jeans this
leads to a steeply rising power-law with spectral index
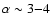 ,
from which we see that source confusion from the IR population
rises rapidly with frequency, the implications of which were recently
discussed by White & Majumdar (2004).
,
from which we see that source confusion from the IR population
rises rapidly with frequency, the implications of which were recently
discussed by White & Majumdar (2004).
Blank field counts around 10 mJy at 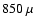 m where obtained by
Scott et al. (2002) and Borys et al. (2003) using the SCUBA instrument.
As discussed by the latter authors, the counts are well described
by a double power-law:
m where obtained by
Scott et al. (2002) and Borys et al. (2003) using the SCUBA instrument.
As discussed by the latter authors, the counts are well described
by a double power-law:
![\begin{displaymath}%
\frac{{\rm d}N}{{\rm d}S_\nu}\bigg\vert _{\rm ir} = \frac{N...
....0} + \left(\frac{S_\nu
}{S_{\rm o}}\right)^{3.3}\right]^{-1}
\end{displaymath}](/articles/aa/full/2006/08/aa3395-05/img76.gif) |
(8) |
with
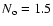
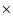 104 deg-2 and
104 deg-2 and
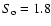 mJy. This model
is shown in Fig. 2 as the upper solid red line,
along with data taken from the two surveys.
mJy. This model
is shown in Fig. 2 as the upper solid red line,
along with data taken from the two surveys.
The SCUBA Local Universe Galaxy Survey (SLUGS, Vlahakis et al. 2004) finds a
broad distribution for the dust emissivity index with
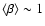 and a dispersion we take to be
and a dispersion we take to be
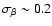 .
According to the SLUGS observations, optical
galaxies tend to have lower spectral indexes than IRAS-selected
objects; we eye-balled the above numbers to be representative of the
population as a whole.
.
According to the SLUGS observations, optical
galaxies tend to have lower spectral indexes than IRAS-selected
objects; we eye-balled the above numbers to be representative of the
population as a whole.
4 Point source confusion
Point source confusion is caused by random fluctuations in the number
of unresolved sources in the filter. We now study the contribution of
this confusion to the overall filter noise,
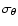 ,
as a function of
filter scale,
,
as a function of
filter scale, 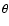 .
As mentioned above, we only consider
uncorrelated instrumental noise, primary CMB anisotropy and point
source terms to the power spectrum matrix
.
As mentioned above, we only consider
uncorrelated instrumental noise, primary CMB anisotropy and point
source terms to the power spectrum matrix 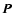 ,
whose
off-diagonal elements are then just sky terms (to be multiplied by
the beam):
,
whose
off-diagonal elements are then just sky terms (to be multiplied by
the beam):
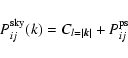 |
(9) |
where Cl is the CMB temperature angular power spectrum and
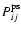 is the point source term. We quote power in units
of CMB temperature equivalent and ignore spatial correlations of the
point sources, which means that
is the point source term. We quote power in units
of CMB temperature equivalent and ignore spatial correlations of the
point sources, which means that
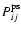 is independent of k.
is independent of k.
To calculate the point source terms
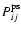 ,
we adopt the counts
of Eq. (6), alternatively
Eq. (7), at
,
we adopt the counts
of Eq. (6), alternatively
Eq. (7), at
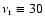 GHz and those of
Eq. (8) at
GHz and those of
Eq. (8) at
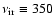 GHz (
GHz (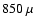 m). Unless
otherwise specified, spectral indexes follow Gaussian distributions
with (
m). Unless
otherwise specified, spectral indexes follow Gaussian distributions
with (
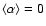 ,
,
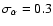 )
for radio
sources, and (
)
for radio
sources, and (
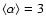 ,
,
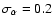 )
for IR galaxies (see previous section). Then we have
)
for IR galaxies (see previous section). Then we have
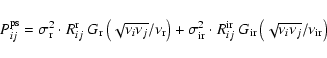 |
(10) |
where (Scheuer 1957; Condon 1974)
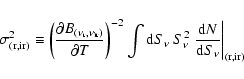 |
(11) |
gives the sky temperature variance due to radio or IR sources
at the fiducial frequencies
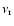 and
and
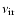 ;
conversion to
CMB temperature units is made with the Planck function
;
conversion to
CMB temperature units is made with the Planck function 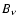 at
at
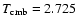 K (Mather et al. 1999). This also appears in
the R-factors:
K (Mather et al. 1999). This also appears in
the R-factors:
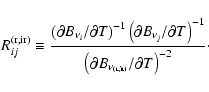 |
(12) |
The function G accounts for spectral variations:
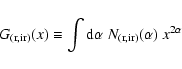 |
(13) |
with
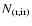 being the normal distribution for radio and
IR spectral indexes, respectively. These results assume that there
is no correlation between flux density
being the normal distribution for radio and
IR spectral indexes, respectively. These results assume that there
is no correlation between flux density 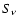 and spectral index,
and spectral index,
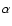 ,
so that the joint distribution is separable.
,
so that the joint distribution is separable.
![\begin{figure}
\par\includegraphics[height=7.9cm,width=8.25cm,clip]{3395fig3a.ep...
...8mm}
\includegraphics[height=7.9cm,width=8.25cm,clip]{3395fig3b.eps}\end{figure}](/articles/aa/full/2006/08/aa3395-05/Timg102.gif) |
Figure 3:
Noise (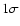 )
on the integrated Compton Y parameter
as a function of filter scale. We assume )
on the integrated Compton Y parameter
as a function of filter scale. We assume 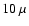 K noise/beam
and adopt 1 arcmin beams in all bands, except for
the green 3-dot-dashed curve in the right-hand panel. At
these frequencies, we only include IR sources
below K noise/beam
and adopt 1 arcmin beams in all bands, except for
the green 3-dot-dashed curve in the right-hand panel. At
these frequencies, we only include IR sources
below
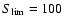 mJy, following the counts of Eq. (8),
and with a spectral index mJy, following the counts of Eq. (8),
and with a spectral index 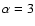 and no dispersion. Left
panel: the black dotted line shows the sensitivity at 150 GHz, where
the instrumental noise and point source confusion are comparable (see
Fig. 4). Confusion is effectively eliminated by a 2-band filter, as demonstrated by the red dot-dashed line lying just above the pure instrumental noise limit (black 3 dot-dashed curve). The upper solid green line shows the result when adding primary CMB anisotropy, in which case the 2-band filter is unable to cleanly
separate the three astrophysical components. Addition of a third band
at 300 GHz (blue dashed line) does not greatly improve the result,
because both the 220 and 300 GHz channels are dominated by point
sources, as shown in Fig. 4 (see text). Right
panel: artificially removing the point sources from the 300 GHz
channel, we see (black dotted line) that the filter gains enough
leverage on the three astrophysical signals to drop its noise to the
instrumental limit (red dot-dashed line). Source confusion being
greatly reduced at lower frequencies, a 3-band filter with 90 GHz
(solid green line) performs better; this remains true even when
we degrade the 90 GHz beam to a more realistic 2 arcmin FWHM (green
3-dot-dashed curve).
and no dispersion. Left
panel: the black dotted line shows the sensitivity at 150 GHz, where
the instrumental noise and point source confusion are comparable (see
Fig. 4). Confusion is effectively eliminated by a 2-band filter, as demonstrated by the red dot-dashed line lying just above the pure instrumental noise limit (black 3 dot-dashed curve). The upper solid green line shows the result when adding primary CMB anisotropy, in which case the 2-band filter is unable to cleanly
separate the three astrophysical components. Addition of a third band
at 300 GHz (blue dashed line) does not greatly improve the result,
because both the 220 and 300 GHz channels are dominated by point
sources, as shown in Fig. 4 (see text). Right
panel: artificially removing the point sources from the 300 GHz
channel, we see (black dotted line) that the filter gains enough
leverage on the three astrophysical signals to drop its noise to the
instrumental limit (red dot-dashed line). Source confusion being
greatly reduced at lower frequencies, a 3-band filter with 90 GHz
(solid green line) performs better; this remains true even when
we degrade the 90 GHz beam to a more realistic 2 arcmin FWHM (green
3-dot-dashed curve). |
| Open with DEXTER |
Single frequency surveys can only use spatial information to control
point source confusion. Operating at 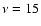 GHz and 30 GHz,
respectively, AMI and SZA will contend primarily with the radio source
population; AMiBA, on the other hand, must deal with both radio and IR sources at
GHz and 30 GHz,
respectively, AMI and SZA will contend primarily with the radio source
population; AMiBA, on the other hand, must deal with both radio and IR sources at 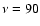 GHz. The former two interferometers include long baselines dedicated to identifying and removing point sources at high spatial frequency on the sky, where they are cleanly
separated from the more extended cluster SZ emission. Point source
confusion is then caused by the residual population below the
subtraction threshold,
GHz. The former two interferometers include long baselines dedicated to identifying and removing point sources at high spatial frequency on the sky, where they are cleanly
separated from the more extended cluster SZ emission. Point source
confusion is then caused by the residual population below the
subtraction threshold,
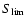 .
.
Apart from the beam convolution, point source confusion contributes to
the filter variance
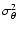 in the same manner as instrumental
noise.
Using the counts of Eq. (6) we find for the
confusion power:
in the same manner as instrumental
noise.
Using the counts of Eq. (6) we find for the
confusion power:
where the numerical value in the last line assumes
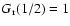 ,
while
it most certainly is larger. These values are comparable to target
sensitivities for interferometer surveys, implying that these
instruments will have to subtract sources down to
,
while
it most certainly is larger. These values are comparable to target
sensitivities for interferometer surveys, implying that these
instruments will have to subtract sources down to 
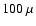 Jy or
better. Assuming a
Jy or
better. Assuming a
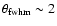 arcmin synthesized beam, we
calculate the confusion limit on the integrated Compton Y parameter
for unresolved clusters. We conclude that confusion from sources
below
arcmin synthesized beam, we
calculate the confusion limit on the integrated Compton Y parameter
for unresolved clusters. We conclude that confusion from sources
below 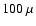 Jy will limit SZ sensitivity to
Jy will limit SZ sensitivity to 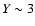
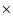 10-6 arcmin2 at 30 GHz and
10-6 arcmin2 at 30 GHz and
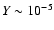 arcmin2 at 15 GHz (both are at
arcmin2 at 15 GHz (both are at 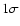 ). The former limit is a factor
). The former limit is a factor
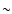 5 greater than the confusion expected from primary CMB anisotropy in the concordence model for unresolved clusters (Melin et al. 2005).
5 greater than the confusion expected from primary CMB anisotropy in the concordence model for unresolved clusters (Melin et al. 2005).
Adopting the alternative model of Eq. (7),
these confusion limits drop by a factor 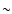 20, and the dependence
of the variance on the source subtraction threshold approaches
20, and the dependence
of the variance on the source subtraction threshold approaches
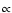
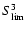 .
There is clearly a large uncertainty associated
with extrapolation of the counts to faint flux densities. In this
light, note that as long as the counts do not steepen toward lower
flux densities, the confusion estimates are, fortunately, dominated by
the counts at
.
There is clearly a large uncertainty associated
with extrapolation of the counts to faint flux densities. In this
light, note that as long as the counts do not steepen toward lower
flux densities, the confusion estimates are, fortunately, dominated by
the counts at
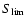 ,
rather than at some unknown cut-off at even
fainter levels.
,
rather than at some unknown cut-off at even
fainter levels.
Planned bolometer-based surveys will operate over several millimeter
and submillimeter bands, allowing them to use spectral information to
extract clusters from the foregrounds. This will in fact be their
only way to reduce the effects of point source confusion, because they
will not have the spatial resolution![[*]](/icons/foot_motif.gif) needed for subtracting point sources from
cluster images. In the multi-frequency case, we refer to the
optimal spatio-spectral filter as a multi-filter.
needed for subtracting point sources from
cluster images. In the multi-frequency case, we refer to the
optimal spatio-spectral filter as a multi-filter.
Specifically, the multi-filter performs a weighted sum designed to
remove foregrounds from the SZ cluster signal, as illustrated in the
right-hand panel of Fig. 1. Figure 3
helps to understand the filter's workings and it will allow us to draw some
important conclusions. The figure shows the filter noise
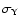 (
(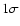 )
in terms of the integrated Compton Y parameter as a
function of filter scale for various band and foreground
combinations. This is calculated from the filter variance as
)
in terms of the integrated Compton Y parameter as a
function of filter scale for various band and foreground
combinations. This is calculated from the filter variance as
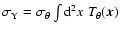 .
We take as representative of planned
observations a survey with
.
We take as representative of planned
observations a survey with 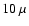 K instrumental noise per 1 arcmin
lobe (FWHM) in all bands. We only include the IR source population
(dominant at these frequencies) below
K instrumental noise per 1 arcmin
lobe (FWHM) in all bands. We only include the IR source population
(dominant at these frequencies) below
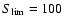 mJy, assuming
brighter sources are explicitly subtracted; this is well above the
knee in the differential counts of Eq. (8). We
further fix, for the present, the spectral index to
mJy, assuming
brighter sources are explicitly subtracted; this is well above the
knee in the differential counts of Eq. (8). We
further fix, for the present, the spectral index to 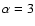 with
zero dispersion (G=1).
with
zero dispersion (G=1).
Consider first the case with just instrumental noise, point sources
(no CMB) and two frequencies, one at 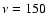 GHz and the other at the
thermal SZ null,
GHz and the other at the
thermal SZ null, 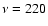 GHz. Point source confusion is severe in
each individual band, as illustrated by Fig. 4. The
dotted line in the left panel of Fig. 3 shows the
total filter noise with just the 150 GHz band. When both bands are
used in the filter, the filter noise
GHz. Point source confusion is severe in
each individual band, as illustrated by Fig. 4. The
dotted line in the left panel of Fig. 3 shows the
total filter noise with just the 150 GHz band. When both bands are
used in the filter, the filter noise
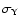 drops considerably (red
dot-dashed line), approaching the pure instrumental noise limit for
the 2-band filter, shown as the black dashed-3 dotted line. It is
straightforward to show under these circumstances that the filter
performs a direct subtraction of the point source signal from the
150 GHz channel by extrapolation of the 220 GHz signal using the
known spectral index
drops considerably (red
dot-dashed line), approaching the pure instrumental noise limit for
the 2-band filter, shown as the black dashed-3 dotted line. It is
straightforward to show under these circumstances that the filter
performs a direct subtraction of the point source signal from the
150 GHz channel by extrapolation of the 220 GHz signal using the
known spectral index 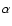 .
What we see here is that the
subtraction is perfect to the instrumental noise limit.
.
What we see here is that the
subtraction is perfect to the instrumental noise limit.
![\begin{figure}
\par\includegraphics[height=7.5cm,width=8.4cm,clip]{3395fig4.eps}\end{figure}](/articles/aa/full/2006/08/aa3395-05/Timg120.gif) |
Figure 4:
Power spectra of the primary CMB anisotropy (solid black line),
point source confusion in different bands (as labeled) and
instrumental noise; the latter corresponds to 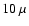 K
noise/1 arcmin lobe, which we take here to be the same in all bands.
Only IR sources with K
noise/1 arcmin lobe, which we take here to be the same in all bands.
Only IR sources with
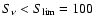 mJy are included, according to
the counts of Eq. (8), and with mJy are included, according to
the counts of Eq. (8), and with 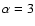 and no
dispersion. The figure shows the that the 300 GHz channel is
dominated by sources, explaining why the 3-band filter with 90 GHz
performs more efficiently than the one with 300 GHz (see
Fig. 3).
and no
dispersion. The figure shows the that the 300 GHz channel is
dominated by sources, explaining why the 3-band filter with 90 GHz
performs more efficiently than the one with 300 GHz (see
Fig. 3). |
| Open with DEXTER |
The sky of course also includes the CMB signal and other foregrounds,
and the point source spectral index has a non-zero distribution,
both of which complicate the subtraction. We discuss the second
effect below and now add CMB anisotropy, keeping 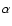 fixed. The
2-band filter is no longer able to separately determine the three sky
signals (SZ, point sources and CMB), with as a consequence a
significant rise in total SZ noise, as shown by the solid green line.
Surprisingly, the situation does not improve even when we include more
information with a third observing band at
fixed. The
2-band filter is no longer able to separately determine the three sky
signals (SZ, point sources and CMB), with as a consequence a
significant rise in total SZ noise, as shown by the solid green line.
Surprisingly, the situation does not improve even when we include more
information with a third observing band at 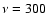 GHz (blue dashed
line).
GHz (blue dashed
line).
This interesting result is due to the fact that both the 220 and
300 GHz bands are dominated by point source confusion (see
Fig. 4) - neither provides good information the CMB anisotropy, so the filter remains unable to completely separate the three sky
signals. We can test this conclusion by artificially removing point
sources from the new channel at 300 GHz. The result is shown in the
right-hand panel of the figure as the black dotted line; the total SZ noise
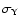 drops to a level comparable to the level induced just by
instrumental noise (red dot-dashed line), indicating that once again
the subtraction is almost perfect.
drops to a level comparable to the level induced just by
instrumental noise (red dot-dashed line), indicating that once again
the subtraction is almost perfect.
This has important consequences for SZ surveying. Observing at high
frequencies, such as 300 GHz, is very difficult from the ground due
to atmospheric effects; moving up in frequency, one approaches strong
water vapor lines. What we have just seen suggests that including
bands beyond the thermal SZ null may not be worth the effort, at least
not for detecting clusters.
To further explore this issue, we replace the 300 GHz channel by a
90 GHz band. At this lower frequency, point source confusion is
greatly reduced and gives the filter a better handle on CMB anisotropy;
in fact, as shown in Fig. 4, point source confusion
is well below the instrumental noise level at 90 GHz. The green solid
line in the right-hand panel of Fig. 3 shows the new
result: this three-band filter with 90 GHz performs significantly
better than the one with 300 GHz. It is, however, unlikely that
all three bands will have the same beam size, which we have taken
as 1 arcmin throughout this discussion. The green 3-dot-dashed
curve in the right-hand panel of the figure shows the result for a
three-band filter with a 2 arcmin beam at 90 GHz. Even with the larger
beam at the lower frequency, the result remains qualitatively the same - the filter with 90 GHz performs better than the one with 300 GHz.
Multi-frequency surveys will
certainly include 150 and 220 GHz bands to cover the maximum decrement
and null of the thermal SZ signal. We conclude here that a 90 GHz
band is a more valuable addition than one at 300 GHz for cluster
extraction, despite a loss in angular resolution at the lower frequency.
As a final note, we consider the effects of dispersion in the source
spectral index 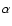 .
With dispersion, the filter can no longer
perform a perfect subtraction by extrapolation across bands; it must
instead find appropriate frequency weights for a statistically optimal
subtraction. In the point source power spectrum matrix
.
With dispersion, the filter can no longer
perform a perfect subtraction by extrapolation across bands; it must
instead find appropriate frequency weights for a statistically optimal
subtraction. In the point source power spectrum matrix
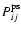 ,
only the self power
,
only the self power
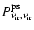 remains unaffected; other
diagonal elements will increase, while correlations between bands
(in the off-diagonal elements) decrease. We therefore expect the filter's
performance to decline.
remains unaffected; other
diagonal elements will increase, while correlations between bands
(in the off-diagonal elements) decrease. We therefore expect the filter's
performance to decline.
We examined the importance of this effect using the function
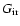 defined in Eq. (13). Dispersions up to
defined in Eq. (13). Dispersions up to
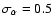 increase matrix elements involving the 150 and
220 GHz bands of the power spectrum matrix by at most 20%, relative
to their values with zero dispersion. The 90 GHz channel is of course
the most affected: the auto-power element
increase matrix elements involving the 150 and
220 GHz bands of the power spectrum matrix by at most 20%, relative
to their values with zero dispersion. The 90 GHz channel is of course
the most affected: the auto-power element
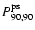 increases by
more than 50% for the same dispersion. Nevertheless, when running
the filter combinations of Fig. 3, we find only a
small change in the filter noise curves, barely perceptible by eye.
We conclude that even rather large variations in the frequency
dependence of individual source spectra does not significantly
increase confusion noise through the filter. In more general terms,
this also suggests that our confusion estimates are not strongly
dependent on the foreground model.
increases by
more than 50% for the same dispersion. Nevertheless, when running
the filter combinations of Fig. 3, we find only a
small change in the filter noise curves, barely perceptible by eye.
We conclude that even rather large variations in the frequency
dependence of individual source spectra does not significantly
increase confusion noise through the filter. In more general terms,
this also suggests that our confusion estimates are not strongly
dependent on the foreground model.
Primary CMB anisotropy and extragalactic point sources are the most
important foregrounds for SZ surveys. Point source confusion is a
particularly critical issue because it rises rapidly on cluster
angular scales. We have quantified its importance for both single
frequency and multiple frequency surveys using current estimates of
the radio and IR source counts and an optimal matched multi-filter
for cluster extraction. Our main conclusion are:
- The expected confusion level from radio point sources
is uncertain due to lack of information on the counts at required flux
densities: a power-law extrapolation of the observed counts
(Eq. (6)) leads to a confusion-limited SZ sensitivity at 30 GHz of
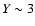
 10-6 arcmin2 from
unresolved sources below
10-6 arcmin2 from
unresolved sources below
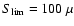 Jy (
Jy (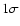 for clusters
unresolved by a 2 arcmin beam); at 15 GHz the corresponding
sensitivity is
for clusters
unresolved by a 2 arcmin beam); at 15 GHz the corresponding
sensitivity is
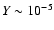 arcmin2. An alternative model in
which the counts flatten at low flux density
(Eq. (7)) predicts much lower confusion limits,
reduced by a factor of
arcmin2. An alternative model in
which the counts flatten at low flux density
(Eq. (7)) predicts much lower confusion limits,
reduced by a factor of 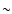 20, in which case CMB confusion becomes
the limiting factor (Melin et al. 2005).
20, in which case CMB confusion becomes
the limiting factor (Melin et al. 2005).
- Currently planned multiple frequency bolometer surveys (e.g.,
10
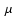 K instrumental noise/ 1 arcmin beam) greatly reduce the
large confusion noise from IR sources and can attain 1
K instrumental noise/ 1 arcmin beam) greatly reduce the
large confusion noise from IR sources and can attain 1 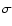 sensitivity
of
sensitivity
of 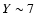
 10-6 arcmin2 for unresolved clusters
(see Fig. 3). Nevertheless, both residual
point source and CMB anisotropy confusion significantly increase the
total filter noise, degrading survey sensitivity from
the ultimate instrumental noise limit.
10-6 arcmin2 for unresolved clusters
(see Fig. 3). Nevertheless, both residual
point source and CMB anisotropy confusion significantly increase the
total filter noise, degrading survey sensitivity from
the ultimate instrumental noise limit.
- For multiple frequency surveys, observation bands below the
thermal SZ null (e.g., 90+150+220 GHz) are more efficient for cluster
extraction than observations at higher frequencies (e.g.,
150+220+300 GHz), despite a potential loss of angular resolution in
the 90 GHz channel (e.g., 2 arcmin beam instead of our fiducial 1 arcmin
beam).
![\begin{figure}
\par\includegraphics[height=7.9cm,width=7.8cm,clip]{3395fig5.eps}\end{figure}](/articles/aa/full/2006/08/aa3395-05/Timg131.gif) |
Figure 5:
Minimum detectable mass as a function of redshift.
The upper solid blue curve shows the result for the 3-band filter
with a 300 GHz channel, while the middle dashed black curve gives the
result when this channel is replaced by a 90 GHz band. For reference,
the lower red dash-dotted curve gives the ideal detector-noise
limited detection mass for the 3-band filter with 90 GHz. The
3-band filter with 90 GHz shows its higher sensitivity (see
Fig. 3), but still suffers from residual foreground
(CMB) contamination. These results follow for 1 arcmin FWHM beams in
all bands. For comparison, the black 3-dot-dashed line gives the mass
limit for the 3-band filter with a 90 GHz beam of 2 arcmin FWHM, which
continues to perform better than the 3-band filter with 300 GHz despite
the loss of angular resolution at the lower frequency. |
| Open with DEXTER |
The minimum detectable cluster mass as a function of redshift,
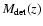 ,
is a key characteristic of a survey. To further
illustrate the last point, we show
,
is a key characteristic of a survey. To further
illustrate the last point, we show
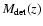 in
Fig. 5 for the 3-band multi-filter. In making
this figure, we adopted simple self-similar relations for Y(M,z)and
in
Fig. 5 for the 3-band multi-filter. In making
this figure, we adopted simple self-similar relations for Y(M,z)and
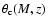 (Melin et al. 2005); given the potentially important
theoretical uncertainty in these relations, the absolute positioning
of the curves should be viewed with caution - more robust and more
pertinent to our discussion are their relative positions. The 3-band
filter with 90 GHz (black dashed line) gains mass sensitivity compared
to the filter with 300 GHz (solid blue line), assuming 1 arcmin beams in
all bands. It does not, however, reach the ideal noise limit
(red dot-dashed line), due to residual point source and CMB confusion
through the filter. A 3-band filter with lower angular resolution at
90 GHz (2 arcmin beam), a more probable observing situation, does
somewhat worse, but still better than the 3-band filter with 300 GHz
(and 1 arcmin beams in all bands). This is an important consideration
given the difficulty imposed by atmospheric effects on observations
at high frequencies.
(Melin et al. 2005); given the potentially important
theoretical uncertainty in these relations, the absolute positioning
of the curves should be viewed with caution - more robust and more
pertinent to our discussion are their relative positions. The 3-band
filter with 90 GHz (black dashed line) gains mass sensitivity compared
to the filter with 300 GHz (solid blue line), assuming 1 arcmin beams in
all bands. It does not, however, reach the ideal noise limit
(red dot-dashed line), due to residual point source and CMB confusion
through the filter. A 3-band filter with lower angular resolution at
90 GHz (2 arcmin beam), a more probable observing situation, does
somewhat worse, but still better than the 3-band filter with 300 GHz
(and 1 arcmin beams in all bands). This is an important consideration
given the difficulty imposed by atmospheric effects on observations
at high frequencies.
With the S/N>5 detection threshold [i.e.,
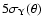 ], we find
15 clusters/deg2 for the filter with 300 GHz (1 arcmin all bands),
30 clusters/deg2 for the filter with 90 GHz and 1 arcmin beams,
and 18 clusters/deg2 for the 3-band filter with a 2 arcmin
beam at 90 GHz.
There are 47 detected clusters/deg2 at the ultimate noise-limit
of the 3-band filter with a 1 arcmin beam at 90 GHz. These numbers
should be compared to the 85 clusters/deg2 with mass >1014 solar masses with our model
parameters.
], we find
15 clusters/deg2 for the filter with 300 GHz (1 arcmin all bands),
30 clusters/deg2 for the filter with 90 GHz and 1 arcmin beams,
and 18 clusters/deg2 for the 3-band filter with a 2 arcmin
beam at 90 GHz.
There are 47 detected clusters/deg2 at the ultimate noise-limit
of the 3-band filter with a 1 arcmin beam at 90 GHz. These numbers
should be compared to the 85 clusters/deg2 with mass >1014 solar masses with our model
parameters.
An important consequence of our results is that SZ survey selection
functions are affected by residual astrophysical confusion and are not
uniquely determined by instrumental properties. Specifically, we have
seen that even a 3-band bolometer survey with good angular resolution
and optimal filter cluster extraction experiences a mixture of residual
point source and primary CMB confusion. Cluster catalog
construction will therefore suffer from uncertaintly in astrophysical
foreground modeling (Melin et al. 2005).
In conclusion, our results support the expectation that future
ground-based SZ surveys will provide rich cluster catalogs for
cosmological studies. Confusion from point sources and primary CMB anisotropy can be greatly reduced by multi-frequency
bolometer surveys, but some residual point source and CMB anistropy
confusion noise will affect cluster detection and catalog construction.
Acknowledgements
We thank G. Evrard and the organizers of the Future of Cosmology
with Clusters of Galaxies conference, where this work began in earnest.
Thanks to J. Mohr for encouragement and to the anonymous referee who
helped improve the clarity of the presentation.
J.-B. Melin was supported at U.C. Davis by the National Science Foundation
under Grant No. 0307961 and NASA under Grant No. NAG5-11098.
- Aghanim, N., Hansen, S.
H., & Lagache, G. 2005, A&A, 439, 901 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Barbosa, D., Bartlett,
J. G., & Blanchard, A. 1996, A&A, 314, 13 [NASA ADS] (In the text)
- Bartlett, J. G. 2001,
review in Tracing cosmic evolution with galaxy clusters (Sesto
Pusteria 3-6 July 2001), ASP Conf. Ser., in press
[arXiv:astro-ph/0111211]
(In the text)
- Bennett, C., Hill, R. S.,
Hinshaw, G., et al. 2003, ApJS, 148, 97 [NASA ADS] [CrossRef] (In the text)
- Benson, A. J., Reichardt,
C., & Kamionkowski, M. 2002, MNRAS, 331, 71 [NASA ADS] [CrossRef] (In the text)
- Birkinshaw, M. 1999,
Proc. 3K Cosmology, 476, American Institute of Physics, Woodbury,
298
(In the text)
- Borys, C., Chapman, S.,
Halpern, M., & Scott, D. 2003, MNRAS, 344, 385 [NASA ADS] [CrossRef] (In the text)
- Carlstrom, J. E., Holder,
G. P., & Reese, E. D. 2002, ARA&A, 40, 643 [NASA ADS] (In the text)
- Cleary, K. A.,
Taylor, A. C., Waldram, E., et al. 2005, MNRAS, 360, 340 [NASA ADS] [CrossRef] (In the text)
- Colafrancesco, S.,
Mazzotta, P., & Vittorio, N. 1997, ApJ, 488, 566 [NASA ADS] [CrossRef] (In the text)
- Condon, J. J. 1974, ApJ,
188, 279 [NASA ADS] [CrossRef] (In the text)
- Eke, V. R., Cole, S.,
& Frenk, C. S. 1996, MNRAS, 282, 263 [NASA ADS] (In the text)
- Freedman, W. L.,
Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [NASA ADS] [CrossRef] (In the text)
- Haehnelt, M. G., &
Tegmark, M. 1996, MNRAS, 279, 545 [NASA ADS] (In the text)
- Haiman, Z., Mohr, J. J.,
& Holder, G. 2001, ApJ, 553, 545 [NASA ADS] [CrossRef] (In the text)
- Herbig, T., &
Readhead, A. C. S. 1992, ApJS, 81, 83 [NASA ADS] [CrossRef] (In the text)
- Herranz, D., Sanz, J. L.,
Hobson, M. P., et al. 2002, MNRAS, 336, 1057 [NASA ADS] [CrossRef] (In the text)
- Holder, G. P., Mohr, J.
J., Carlstrom, J. E., Evrard, A. E., & Leitch, E. M. 2000, ApJ,
544, 629 [NASA ADS] [CrossRef] (In the text)
- Kneissl, R., Jones, M.
E., Saunders, R., et al. 2001, MNRAS, 328, 783 [NASA ADS] [CrossRef] (In the text)
- Knox, L., Holder, G.,
& Church, S. 2004, ApJ, 612, 96 [NASA ADS] [CrossRef] (In the text)
- Kovac, J., Leitch, E. M.,
Pryke, C., et al. 2002, Nature, 420, 772 [NASA ADS] [CrossRef] (In the text)
- Mason, B. S., Pearson, T.
J., Readhead, A. C. S., et al. 2003, ApJ, 591, 540 [NASA ADS] [CrossRef] (In the text)
- Mather, J. C., Fixsen, D.
J., Shafer, R. A., et al. 1999, ApJ, 512, 511 [NASA ADS] [CrossRef] (In the text)
- Melin, J.-B., Bartlett,
J. G., & Delabrouille, J. 2005, A&A, 429, 417 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Melin, J.-B., et al.
2006, in preparation
(In the text)
- Schäfer, B. M.,
Pfrommer, C., Hell, R. M., & Bartelmann, M. 2004
[arXiv:astro-ph/0407090]
(In the text)
- Scheuer, P. A. G. 1957,
Proc. Camb. Phil. Soc., 53, 764 (In the text)
- Scott, S. E., Fox, M. J.,
Dunlop, J. S., et al. 2002, MNRAS, 331, 817 [NASA ADS] [CrossRef] (In the text)
- Spergel, D. N., Verde,
L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] (In the text)
- Sunyaev, R. A., &
Zel'dovich, Ya. B. 1970, Comments Astrophys. Space Phys., 2,
66 [NASA ADS] (In the text)
- Sunyaev, R. A., &
Zel'dovich, Ya. B. 1972, Comments Astrophys. Space Phys., 4,
173 [NASA ADS] (In the text)
- Taylor, A. C., Grainge,
K., Jones, M. E., et al. 2001, MNRAS, 327, L1 [NASA ADS] [CrossRef] (In the text)
- Taylor, A. C., Carreira,
P., Cleary, K., et al. 2003, MNRAS, 341, 1066 [NASA ADS] [CrossRef] (In the text)
- Trushkin, A. S. 2003,
Bull. Spec. Astrophys. Obs. N. Caucasus, 55, 90 [NASA ADS]
[arXiv:astro-ph/0307205]
(In the text)
- Vlahakis, C., Dunne, L.,
& Eales, S. 2004 [arXiv:astro-ph/0411067]
(In the text)
- Wang, S., Khoury, J.,
Haiman, Z., & May, M. 2004, Phys. Rev. D, 70, 123008 [NASA ADS] [CrossRef] (In the text)
- Weller, J., & Battye,
R. A. 2003, NewAR, 47, 775 [NASA ADS] (In the text)
- White, M., & Majumdar,
S. 2004, ApJ, 602, 565 [NASA ADS] [CrossRef] (In the text)
Web pages of various SZ experiments:
- ACBAR http://cosmology.berkeley.edu/group/swlh/acbar/
- ACT http://www.hep.upenn.edu/~angelica/act/act.html
- AMI http://www.mrao.cam.ac.uk/telescopes/ami/index.html
- AMiBA http://www.asiaa.sinica.edu.tw/amiba
- APEX http://bolo.berkeley.edu/apexsz
- SPT http://astro.uchicago.edu/spt/
- SZA http://astro.uchicago.edu/sze
- Olimpo http://oberon.roma1.infn.it/
- Planck http://astro.estec.esa.nl/Planck/
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[width=15cm,clip]{3395fig1.eps}\end{figure}](/articles/aa/full/2006/08/aa3395-05/Timg25.gif)
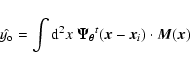
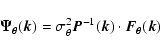
![$\displaystyle \sigma_\theta\equiv \left[\int {\rm d}^2k\;
\vec{F_\theta}^t(\vec{k})\cdot \vec{P}^{-1} \cdot
\vec{F_\theta}(\vec{k})\right]^{-1/2}$](/articles/aa/full/2006/08/aa3395-05/img38.gif)
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{3395fig2.ps}\end{figure}](/articles/aa/full/2006/08/aa3395-05/Timg56.gif)
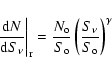
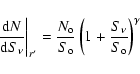
![\begin{displaymath}%
\frac{{\rm d}N}{{\rm d}S_\nu}\bigg\vert _{\rm ir} = \frac{N...
....0} + \left(\frac{S_\nu
}{S_{\rm o}}\right)^{3.3}\right]^{-1}
\end{displaymath}](/articles/aa/full/2006/08/aa3395-05/img76.gif)
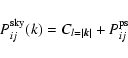
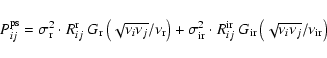
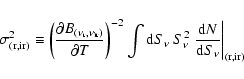
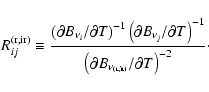
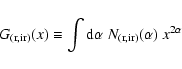
![\begin{figure}
\par\includegraphics[height=7.9cm,width=8.25cm,clip]{3395fig3a.ep...
...8mm}
\includegraphics[height=7.9cm,width=8.25cm,clip]{3395fig3b.eps}\end{figure}](/articles/aa/full/2006/08/aa3395-05/Timg102.gif)
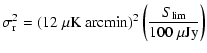
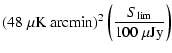
![\begin{figure}
\par\includegraphics[height=7.5cm,width=8.4cm,clip]{3395fig4.eps}\end{figure}](/articles/aa/full/2006/08/aa3395-05/Timg120.gif)
![\begin{figure}
\par\includegraphics[height=7.9cm,width=7.8cm,clip]{3395fig5.eps}\end{figure}](/articles/aa/full/2006/08/aa3395-05/Timg131.gif)