A&A 445, 795-804 (2006)
DOI: 10.1051/0004-6361:20041950
Instituto Nacional de Pesquisas Espaciais, Divisão de Astrofísica, Av. dos Astronautas 1758, 12227-010, São José dos Campos, SP, Brazil
Received 5 September 2004 / Accepted 30 September 2004
Abstract
We present a method to search for large angular-scale
correlations, termed topological signatures, in the angular
distribution of cosmic objects, which does not depend on
cosmological models or parameters and is based only on the
angular coordinates of the objects.
In order to explore Cosmic Microwave Background temperature
fluctuations data, we applied this method to simulated
distributions of objects in thin spherical shells located
in three different multiply-connected Euclidean 3-spaces
(T3, ![]() ,
and G6), and found that the topological
signatures due to these topologies can be revealed even if
their intensities are small.
We show how to detect such signatures for the cases of
full-sky and partial-sky distributions of objects.
This method can also be applied to other ensembles of
cosmic objects, like galaxies or quasars, in order to
reveal possible angular-scale correlations in their
distributions.
,
and G6), and found that the topological
signatures due to these topologies can be revealed even if
their intensities are small.
We show how to detect such signatures for the cases of
full-sky and partial-sky distributions of objects.
This method can also be applied to other ensembles of
cosmic objects, like galaxies or quasars, in order to
reveal possible angular-scale correlations in their
distributions.
Key words: cosmology - cosmology: large-scale structure of Universe - cosmology: cosmic microwave background - methods: data analysis
Homogeneity property refers to the spatial distribution of cosmic objects in the Universe, and to test it one needs to know the angular positions of these objects in the celestial sphere and their distances to us as well. Unfortunately, cosmological distances are not directly measured, as they are calculated through the redshift-distance relationship, which involves cosmological parameters still not known with enough accuracy. So, precise distances to extragalactic objects are not currently available. Isotropy, instead, deals with the angular distribution of objects in the sky. Then, only two angular coordinates for each object are needed to determine whether or not they are isotropically distributed around us. Nowadays such coordinates are accurately measured and there are available catalogs for several types of objects, like quasars, gamma-ray bursts, and the (sky pixels corresponding to the) Cosmic Microwave Background Radiation (CMBR) temperature fluctuations. In analyzing such catalogs, some questions arise: How can we recognize whether a given class of cosmic objects follows an exact or a quasi-exact isotropic distribution? How can we quantify small deviations from a purely isotropic distribution? How can we distinguish a possible cosmological pattern or topological signature imprinted in these catalogs from pure statistical fluctuations?
The study of the large-scale (i.e. global) homogeneity and
isotropy of the Universe encompasses its topology as well,
since topological properties are global properties of
3-spaces.
Multiply-connectedness is a topological property that
tesselates a simply-connected space (like the Euclidean space
![]() )
producing multiple images of a given object.
This property generates distance and angular correlations
(i.e. anisotropies) in the distribution of objects.
The Small Universe hypothesis (Ellis & Schreiber 1986),
which assumes that
the Universe is a compact (i.e. multiply-connected with finite
volume) 3-space that lies inside - at least partially - the
Last Scattering Surface (LSS), has not been discarded by
recent CMBR data.
In view of this situation, we are motivated to study the
anisotropic signatures of topological origin in the angular
distribution of cosmic objects, and for this we consider
simulated ensembles of objects in different Euclidean
multiply-connected 3-spaces.
)
producing multiple images of a given object.
This property generates distance and angular correlations
(i.e. anisotropies) in the distribution of objects.
The Small Universe hypothesis (Ellis & Schreiber 1986),
which assumes that
the Universe is a compact (i.e. multiply-connected with finite
volume) 3-space that lies inside - at least partially - the
Last Scattering Surface (LSS), has not been discarded by
recent CMBR data.
In view of this situation, we are motivated to study the
anisotropic signatures of topological origin in the angular
distribution of cosmic objects, and for this we consider
simulated ensembles of objects in different Euclidean
multiply-connected 3-spaces.
In order to search for these signatures in astronomical data sets, we developed a method based on histograms of angular separations between pairs of cosmic objects. We call it the Pair Angular Separation Histogram (PASH) method. We are particularly interested in studying angular correlations in simulated catalogs of cosmic objects that share the same attributes as the photons of the CMBR temperature fluctuations, i.e., point-like objects located in the (comoving 3-dimensional) thin shell representing the decoupling era, but viewed from Earth as located on the celestial sphere. As we shall show, the correlations originated by the isometry properties of the compact 3-spaces can be revealed by the method we propose here. This method resembles the Cosmic Crystallography (CC) method (Lachièze-Rey & Luminet 1995; Lehoucq et al. 1996; Fagundes & Gausmann 1998a,b; Gomero et al. 2000a,b, 2001, 2002). However, there is a basic difference between them in that here we just look for angular correlations instead of searching for distance correlations as the CC method does. Our method is therefore independent of any cosmological model or parameters, while the CC method depends on this information to calculate the radial distance of cosmic objects from their measured redshifts.
In Sect. 2 we present the basic properties of the
3-spaces representing our Universe in the
Friedmann-Lemaître cosmological models
(Friedmann 1922; Lemaître 1927).
In Sect. 3, we present the geometrical and statistical
method we developed to reveal correlations between pairs
of objects distributed in a 2-dimensional spherical surface.
The treatment of this problem initiates with the theoretical
description of a perfectly isotropic distribution of objects
in a spherical surface
![]() .
For this type of data we construct the normalized expected
probability density for two objects be separated
by a given angle, separation that of course ranges in the
interval
.
For this type of data we construct the normalized expected
probability density for two objects be separated
by a given angle, separation that of course ranges in the
interval ![]() .
This probability gives rise to the Expected Pair Angular
Separation Histogram (EPASH)
.
This probability gives rise to the Expected Pair Angular
Separation Histogram (EPASH)![]() .
We also present the EPASH for partial-sky catalogs containing
objects distributed only in polar-caps.
In Sect. 4, we present the theoretical deduction of the
topological signatures due to pure translational isometries,
also known as Clifford translations, appearing in the PASHs.
We illustrate these results, in Sect. 5, with numerical
simulations using catalogs that contain multiple images of
cosmic objects generated by the isometries of the following
Euclidean compact (i.e. multiply-connected with finite volume)
orientable 3-spaces: T3,
.
We also present the EPASH for partial-sky catalogs containing
objects distributed only in polar-caps.
In Sect. 4, we present the theoretical deduction of the
topological signatures due to pure translational isometries,
also known as Clifford translations, appearing in the PASHs.
We illustrate these results, in Sect. 5, with numerical
simulations using catalogs that contain multiple images of
cosmic objects generated by the isometries of the following
Euclidean compact (i.e. multiply-connected with finite volume)
orientable 3-spaces: T3, ![]() ,
and G6(denoted by
,
and G6(denoted by
![]() ,
,
![]() ,
and
,
and
![]() ,
respectively, in Wolf's classification Wolf 1984).
In this section we also show that performing the mean of
several PASHs (or Mean Pair Angular Separation Histogram -
MPASH) reduces significantly the statistical noise, which
allows us to reveal the anisotropies due to a non-translational
isometry whose tiny signature is present in the angular
distribution of cosmic objects.
We analized this problem considering MPASHs for full-sky
catalogs as well as for polar-cap catalogs.
Finally, in Sect. 6, we discuss our results and also
the problem of finding suitable catalogs of cosmic objects
from the available astronomical data.
,
respectively, in Wolf's classification Wolf 1984).
In this section we also show that performing the mean of
several PASHs (or Mean Pair Angular Separation Histogram -
MPASH) reduces significantly the statistical noise, which
allows us to reveal the anisotropies due to a non-translational
isometry whose tiny signature is present in the angular
distribution of cosmic objects.
We analized this problem considering MPASHs for full-sky
catalogs as well as for polar-cap catalogs.
Finally, in Sect. 6, we discuss our results and also
the problem of finding suitable catalogs of cosmic objects
from the available astronomical data.
The manifold T3, best known as the three-torus, has its
Fundamental Polyhedron (FP) usually -but not necesarily-
represented by an equal-sided cube,
where its three pairs of faces are identified by pure
(or Clifford) translation isometries.
The manifold ![]() has two pairs of faces identified by
pure translation isometries and one pair of faces identified
after a rotation of
has two pairs of faces identified by
pure translation isometries and one pair of faces identified
after a rotation of
![]() ,
the so-called screw-motion
isometry.
The manifold G6 has no pair of faces of its FP identified
by a pure translation
,
the so-called screw-motion
isometry.
The manifold G6 has no pair of faces of its FP identified
by a pure translation![]() .
In analyzing the distributions of objects in these 3-spaces we
shall be considering the effect of not only pure translational
isometries but also translation-with-rotation isometry, or
screw-motion.
For completeness, we find interesting to briefly review here
the basic properties of compact 3-spaces of constant curvature.
.
In analyzing the distributions of objects in these 3-spaces we
shall be considering the effect of not only pure translational
isometries but also translation-with-rotation isometry, or
screw-motion.
For completeness, we find interesting to briefly review here
the basic properties of compact 3-spaces of constant curvature.
The large-scale structure of the Universe is described by
the Friedmann-Lemaître cosmological models.
In these models, the local geometry satisfies the local
homogeneity and isotropy properties and is described by the
Robertson-Walker (RW) line element
![]() ,
where a(t) is the
scale factor, and
d
,
where a(t) is the
scale factor, and
d
![]() is the line element of the
t=constant spatial sections.
The functions
is the line element of the
t=constant spatial sections.
The functions
![]() ,
,
![]() ,
where k is the normalized curvature parameter, which can
take the values +1, 0, -1, corresponding to the spherical,
Euclidean, and hyperbolic geometry, respectively.
It is known that the three-dimensional spatial sections
(hereafter denoted by
,
where k is the normalized curvature parameter, which can
take the values +1, 0, -1, corresponding to the spherical,
Euclidean, and hyperbolic geometry, respectively.
It is known that the three-dimensional spatial sections
(hereafter denoted by
![]() )
are manifolds of constant
curvature obtained from the quotient
)
are manifolds of constant
curvature obtained from the quotient
![]() (see e.g. Wolf 1984), where
(see e.g. Wolf 1984), where ![]() is a discrete group
of isometries of the manifold
is a discrete group
of isometries of the manifold
![]() ,
without fixed points.
The manifold
,
without fixed points.
The manifold
![]() is termed the
universal covering of
is termed the
universal covering of
![]() .
Therefore, while
.
Therefore, while
![]() is a
simply-connected manifold,
is a
simply-connected manifold,
![]() is a multiply-connected
one.
We would like to stress that the values
k = +1, 0, -1 in
the RW line element determines only the local geometry of
is a multiply-connected
one.
We would like to stress that the values
k = +1, 0, -1 in
the RW line element determines only the local geometry of
![]() (equivalently that
of
(equivalently that
of
![]() ).
).
Since the simply-connected
![]() and the
multiply-connected
and the
multiply-connected
![]() manifolds share the assumed
local homogeneity and isotropy properties, we conclude that
both manifolds are good solutions of the RW local geometry,
i.e., the Einstein-Hilbert equations.
Consequently, General Relativity (or any other metrical theory)
can not distinguish between
manifolds share the assumed
local homogeneity and isotropy properties, we conclude that
both manifolds are good solutions of the RW local geometry,
i.e., the Einstein-Hilbert equations.
Consequently, General Relativity (or any other metrical theory)
can not distinguish between
![]() and
and
![]() because they look like each other locally.
because they look like each other locally.
In a Universe with a multiply-connected 3-space
![]() ,
and whenever the horizon scale is greater than half of the
smallest closed geodesic of
,
and whenever the horizon scale is greater than half of the
smallest closed geodesic of
![]() ,
multiple images
of a given cosmic object might exist due to the isometries
of the group
,
multiple images
of a given cosmic object might exist due to the isometries
of the group ![]()
![]() .
These images originate distance correlations between the
mapped cosmic objects and also produce angular
correlations between those distance-correlated objects.
As we shall see, these angular correlations can be revealed
by the PASH method described in the next section.
.
These images originate distance correlations between the
mapped cosmic objects and also produce angular
correlations between those distance-correlated objects.
As we shall see, these angular correlations can be revealed
by the PASH method described in the next section.
In essence, a PASH is a normalized plot of the number of pairs
of objects versus the angular distance between them.
A formal construction of a PASH is as follows:
let
![]() be a ball of radius Rcentered at the origin of coordinates
be a ball of radius Rcentered at the origin of coordinates ![]() ,
and
involving spherical surface
,
and
involving spherical surface
![]() ,
and containing an
ensemble of (cosmic) objects.
We call
,
and containing an
ensemble of (cosmic) objects.
We call
![]() the observable Universe,
the observable Universe, ![]() represents the Earth, R- is the radius of
the LSS,
represents the Earth, R- is the radius of
the LSS,
![]() is the celestial sphere with radius
is the celestial sphere with radius
![]() ,
where
,
where ![]() is
the thickness of the decoupling era.
Since we are interested in analyzing CMB data, our
simulations consider ensembles of objects located in a thin
shell of thickness
is
the thickness of the decoupling era.
Since we are interested in analyzing CMB data, our
simulations consider ensembles of objects located in a thin
shell of thickness ![]() ,
which are after projected
onto the celestial sphere
,
which are after projected
onto the celestial sphere
![]() ignoring their radial
coordinate.
However, we point out that this method can be applied to
any spatial distribution of cosmic objects.
Given a set of well-defined selection rules
ignoring their radial
coordinate.
However, we point out that this method can be applied to
any spatial distribution of cosmic objects.
Given a set of well-defined selection rules![]() ,
a catalog
,
a catalog ![]() is a list of all objects in
is a list of all objects in
![]() which satisfies a sub-set of the whole set of rules.
which satisfies a sub-set of the whole set of rules.
We start the description of the method by firstly showing
how to obtain the PASH.
Let's assume that we have an ensemble of objects that are,
by assumption, isotropically distributed in
![]() (see Eq. (5)).
A full-sky map catalog
(see Eq. (5)).
A full-sky map catalog ![]() is a list of N objects
spreaded out in
is a list of N objects
spreaded out in
![]() with their corresponding angular
coordinates.
We divide the interval
with their corresponding angular
coordinates.
We divide the interval ![]() in m bins of equal length
in m bins of equal length
![]() ,
where each sub-interval has the
form
,
where each sub-interval has the
form
![]()
![]() with center in
with center in
![]() .
Now, we denote by
.
Now, we denote by
![]() the number of pairs of objects
in
the number of pairs of objects
in ![]() separated by a distance
separated by a distance
![]() .
Thus,
.
Thus,
It may occur that some angular correlations of small intensity are present in a given PASH, but are not clearly seen. To reveal them, and since PASH and EPASH are normalized, we subtract the PASH from the EPASH in order to enhance possible angular correlations.
Let us now obtain the EPASH for the simply-connected manifold
![]() .
Let
.
Let
![]() be
an arbitrary pair of objects listed in
be
an arbitrary pair of objects listed in ![]() with
coordinates
with
coordinates
![]() ,
,
![]() ,
respectively.
Then, the probability density that two completely
uncorrelated objects
,
respectively.
Then, the probability density that two completely
uncorrelated objects![]() p and q be separated by an angle
p and q be separated by an angle
![]() ,
is
,
is
![\begin{displaymath}\Lambda(p,q) \equiv \arccos[\cos \theta_p \cos \theta_q +
\sin \theta_p \sin \theta_q \cos(\varphi_p - \varphi_q)],
\end{displaymath}](/articles/aa/full/2006/03/aa1950-04/img72.gif) |
(3) |
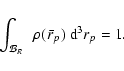 |
(4) |
In Figs. 1 and 2 we show the
EPASH together with the corresponding PASHs obtained
from numerical simulations for full-sky catalogs with
N = 200 and
![]() objects,
respectively.
objects,
respectively.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{figure1.ps}
\end{figure}](/articles/aa/full/2006/03/aa1950-04/Timg85.gif) |
Figure 1:
EPASH (smooth curve) and PASH (noisy curve)
for a full-sky simulated catalog with N = 200 objects
in
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{figure2.ps}
\end{figure}](/articles/aa/full/2006/03/aa1950-04/Timg86.gif) |
Figure 2:
EPASH (smooth curve) and PASH (noisy curve) for a
full-sky simulated catalog with
|
| Open with DEXTER | |
Our galaxy poses a serious problem to the use of full-sky CMBR maps and for other sky catalogs as well, because it contaminates part of the celestial sphere around the Galactic plane. This fact makes somewhat useless the approach we developed studying the angular distribution of cosmic objects listed in full-sky catalogs. For this reason, we also studied the PASHs for catalogs containing objects located in polar-caps (i.e. above or below the equator of a spherical distribution).
Consider a catalog with objects located in a spherical cap
surface
![]() ,
centered, for instance,
around the z-axis, which is assumed to be aligned with the
North Pole. We call this ensemble a polar-cap catalog,
,
centered, for instance,
around the z-axis, which is assumed to be aligned with the
North Pole. We call this ensemble a polar-cap catalog,
![]() .
In this case, any object with coordinates
.
In this case, any object with coordinates
| x | = | ||
| y | = | (9) | |
| z | = |
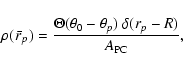 |
(10) |
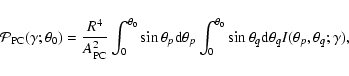 |
(11) |
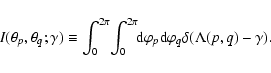 |
(12) |
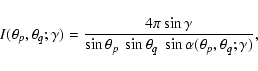 |
(13) |
![\begin{displaymath}\alpha(\theta_p,\theta_q;\gamma) \equiv
\arccos\left[\frac{\c...
...cos\theta_p \cos\theta_q}
{\sin\theta_p\sin\theta_q}\right] ~
\end{displaymath}](/articles/aa/full/2006/03/aa1950-04/img103.gif) |
(14) |
![\begin{displaymath}\frac{\cos\gamma - \cos\theta_p \cos\theta_q}
{\sin\theta_p\sin\theta_q}
~ \in ~ [-1,1] .
\end{displaymath}](/articles/aa/full/2006/03/aa1950-04/img106.gif) |
(15) |
Recently, the analytical expression for the expected
probability density that an arbritary pair
of objects in
![]() be separated by
be separated by ![]() degrees,
i.e. EPASH for polar-caps (EPASHpc), has been found by
Teixeira (2003), who obtained
degrees,
i.e. EPASH for polar-caps (EPASHpc), has been found by
Teixeira (2003), who obtained
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{figure3.ps}
\end{figure}](/articles/aa/full/2006/03/aa1950-04/Timg123.gif) |
Figure 3:
EPASHpc (smooth curve) and PASH (noisy curve) for a
polar-cap simulated catalog with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{figure4.ps}
\end{figure}](/articles/aa/full/2006/03/aa1950-04/Timg124.gif) |
Figure 4:
EPASHpc (smooth curve) and PASH (noisy curve)
for a polar-cap simulated catalog with
|
| Open with DEXTER | |
Suppose that K comparable catalogs
![]() ,
of objects located in the celestial sphere are available for
analysis.
For a given m (common to all the PASHs), we calculate the
functions
,
of objects located in the celestial sphere are available for
analysis.
For a given m (common to all the PASHs), we calculate the
functions
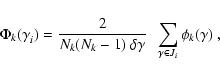 |
(19) |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{figure5.ps}
\end{figure}](/articles/aa/full/2006/03/aa1950-04/Timg131.gif) |
Figure 5:
Difference between PASH and EPASH plotted in
Fig. 1 for a full-sky simulated catalog (K=1)
with N=200 objects and m = 400 bins;
|
| Open with DEXTER | |
In Figs. 5 and 6 we show the
difference between the PASH and the EPASH, already plotted
in Figs. 1 and 2, respectively.
The noise of a PASH, as observed in Figs. 5
and 6, is simply given by
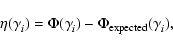 |
(21) |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{figure6.ps}
\end{figure}](/articles/aa/full/2006/03/aa1950-04/Timg134.gif) |
Figure 6:
Difference between PASH and EPASH plotted in
Fig. 2 for a full-sky simulated catalog (K=1)
with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{figure7.ps}
\end{figure}](/articles/aa/full/2006/03/aa1950-04/Timg136.gif) |
Figure 7:
Difference between MPASH (for a
numerical simulation of K= 104 full-sky simulated
catalogs in
|
| Open with DEXTER | |
In Fig. 7, we show the difference between the
MPASH and the EPASH for a numerical simulation of K= 104
full-sky simulated catalogs in
![]() ,
with a mean
number of
,
with a mean
number of
![]() objects per catalog.
The statistical noise is
objects per catalog.
The statistical noise is
![]() .
Fig. 8 shows the difference between a MPASH,
obtained from a numerical simulation of K= 104 full-sky
catalogs with
.
Fig. 8 shows the difference between a MPASH,
obtained from a numerical simulation of K= 104 full-sky
catalogs with
![]() objects each,
and the corresponding EPASH; in this case
objects each,
and the corresponding EPASH; in this case
![]() .
In Fig. 9, we show the difference between a
MPASH and the EPASH, where the MPASH was obtained from a
numerical simulation of K=150 full-sky simulated catalogs
with
.
In Fig. 9, we show the difference between a
MPASH and the EPASH, where the MPASH was obtained from a
numerical simulation of K=150 full-sky simulated catalogs
with
![]() objects each, but with
m=600. In this case
objects each, but with
m=600. In this case
![]() .
.
Thus, when we compare the cases shown in Figs. 6
and 8 (equal m and ![]() ,
different values
for N and K) with the cases shown in Figs. 5
and 7 (equal m and N, different values for
,
different values
for N and K) with the cases shown in Figs. 5
and 7 (equal m and N, different values for
![]() and K), we finally arrive at
and K), we finally arrive at
In Figs. 5 and 6, as well as in
Figs. 3 and 4, we notice the
absence of correlations between pairs of objects for the
exactly isotropic distribution in
![]() generated
using random numbers for the coordinates.
Thus, it is clear from these simulations that as
generated
using random numbers for the coordinates.
Thus, it is clear from these simulations that as
![]() and/or
and/or
![]() the
statistical noise measured by
the
statistical noise measured by
![]() .
The MPASH is related to the statistical noise and this fact
is quantified in Eq. (23).
Although the statistical noise is inherent to any numerical
simulation, it can be controlled in three ways: i) by
obtaining catalogs with a large number of elements, in order
to produce PASHs with a small noise, since the statistical
noise depends on the number of objects;
ii) by computing the MPASH to significantly reduce the
statistical noise;
iii) by choosing a suitable number of bins m.
.
The MPASH is related to the statistical noise and this fact
is quantified in Eq. (23).
Although the statistical noise is inherent to any numerical
simulation, it can be controlled in three ways: i) by
obtaining catalogs with a large number of elements, in order
to produce PASHs with a small noise, since the statistical
noise depends on the number of objects;
ii) by computing the MPASH to significantly reduce the
statistical noise;
iii) by choosing a suitable number of bins m.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{figure8.ps}
\end{figure}](/articles/aa/full/2006/03/aa1950-04/Timg147.gif) |
Figure 8:
Difference between MPASH (for a numerical
simulation of K= 104 full-sky simulated catalogs in
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{figure9.ps}
\end{figure}](/articles/aa/full/2006/03/aa1950-04/Timg148.gif) |
Figure 9:
Difference between MPASH (for a numerical
simulation of K=150 full-sky simulated catalogs in
|
| Open with DEXTER | |
In any multiply-connected 3-space
![]() whose FP lies
inside the ball
whose FP lies
inside the ball
![]() ,
there might exist images of a
given object in a shell of thickness
,
there might exist images of a
given object in a shell of thickness
![]() ,
whenever the horizon scale R is greater than half of the length of the smallest
closed geodesic of
,
whenever the horizon scale R is greater than half of the length of the smallest
closed geodesic of
![]() (Lachièze-Rey & Luminet 1995;
Lehoucq et al. 1996;
Fagundes & Gausmann 1998a,b;
Gomero et al. 2000a,b, 2001,
2002).
These images give extra contributions to the PASH due to
the isometries of
(Lachièze-Rey & Luminet 1995;
Lehoucq et al. 1996;
Fagundes & Gausmann 1998a,b;
Gomero et al. 2000a,b, 2001,
2002).
These images give extra contributions to the PASH due to
the isometries of
![]() .
.
By definition, the probability density for two
objects p, q in ![]() be correlated by a
translational isometry gi (we represent this correlation
by
q=gi(p) ) is
be correlated by a
translational isometry gi (we represent this correlation
by
q=gi(p) ) is
Consider the pure translational isometries in
![]() ,
with a FP represented by a cube of side L.
We know that the distances between pairs correlated by Clifford
translations are independent of the location of the
object (see Gomero et al. 2002), i.e.,
,
with a FP represented by a cube of side L.
We know that the distances between pairs correlated by Clifford
translations are independent of the location of the
object (see Gomero et al. 2002), i.e.,
![]() ,
the distance
,
the distance
![]() is independent of p.
Thus, for this manifold, the translational isometries
gi, i=1,2,... are such that for
is independent of p.
Thus, for this manifold, the translational isometries
gi, i=1,2,... are such that for
![]() we obtain
we obtain ![]() ,
for
,
for
![]() we
obtain
we
obtain
![]() ,
for
,
for
![]() we
obtain
we
obtain ![]() ,
etc.
,
etc.
Let's now apply the above definition to the topological
images correlated by the Clifford translation isometries
gi and located in a thin shell of thickness ![]() .
In this case,
.
In this case,
![\begin{displaymath}\rho({~\bar{\!r}}_p)= \frac{\Theta(R - r_p)~
\Theta(r_p - R_{-})}{\frac{4 \pi}{3} [R^3 - R_{-}^3]} \cdot
\end{displaymath}](/articles/aa/full/2006/03/aa1950-04/img165.gif) |
(25) |
In Euclidean multiply-connected 3-spaces with Clifford
translations, the objects located in a thin shell and
correlated in distance by the Clifford translational isometries
gi (of the covering group ![]() )
give rise to a definite
signature in the PASHs.
In fact, for shells of small thickness (like that corresponding
to the decoupling era where
)
give rise to a definite
signature in the PASHs.
In fact, for shells of small thickness (like that corresponding
to the decoupling era where
![]() ), these
angular correlations between pairs appear in the MPASHs as
small peaks and are approximately located at the angular scales
), these
angular correlations between pairs appear in the MPASHs as
small peaks and are approximately located at the angular scales
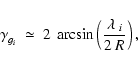 |
(28) |
| (29) | |||
| (30) |
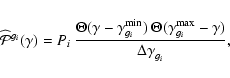 |
(31) |
The effects of the non-translational isometries can also be
calculated using Eq. (24). However, in
such a case, the integrals are cumbersome to handle, so we
prefer to show their effect in MPASHs with plentiful numerical
simulations.
For this reason, we decided to work with the G6 manifold,
which does not present Clifford translations in the histograms
whenever
![]() ,
L being the arista of the
cube representing the FP.
,
L being the arista of the
cube representing the FP.
We performed numerical simulations aiming to reveal topological
signatures due to the isometries of the compact flat manifods
![]() and G6 for full
sky and for polar-cap simulated catalogs.
and G6 for full
sky and for polar-cap simulated catalogs.
It is difficult sometimes to recognize a topological signature
in a single PASH due to the presence of statistical noise.
As a matter of fact, we found that topological signatures due
to Clifford translations appear in PASHs as small triangular
peaks whose heights are inversely proportional to the number
of objects in a given catalog (see Eq. (26)).
We saw that it is convenient to divide a catalog of N objects
in K sub-catalogs of
![]() objects,
where the objects in a sub-catalog share common physical properties,
and then perform the MPASH of the K resulting PASHs.
By doing this, we magnify in two ways the presence of the
topological signatures:
reducing the number of objects per catalog,
objects,
where the objects in a sub-catalog share common physical properties,
and then perform the MPASH of the K resulting PASHs.
By doing this, we magnify in two ways the presence of the
topological signatures:
reducing the number of objects per catalog,
![]() ,
the height of the peak
increases by a factor
,
the height of the peak
increases by a factor
![]() ;
and obtaining K comparable catalogs we can perform the
MPASH to reduce the noise by a factor
;
and obtaining K comparable catalogs we can perform the
MPASH to reduce the noise by a factor
![]() .
The net result is to increase the signal-to-noise ratio
(SNR) of the topological signatures by a factor
.
The net result is to increase the signal-to-noise ratio
(SNR) of the topological signatures by a factor ![]() .
This explains why the strategy of dividing in sub-catalogs
the original catalog with a large N, and performing
the MPASH works better than considering just the PASH of
the original catalog.
For 3D catalogs, that is, when the 3 spatial
coordinates of the objects are provided, the
Collecting Correlated Pairs method
(Uzan et al. 1999) is suitable to enhance the SNR
for the signatures originated by the holonomies
of the 3-space
.
This explains why the strategy of dividing in sub-catalogs
the original catalog with a large N, and performing
the MPASH works better than considering just the PASH of
the original catalog.
For 3D catalogs, that is, when the 3 spatial
coordinates of the objects are provided, the
Collecting Correlated Pairs method
(Uzan et al. 1999) is suitable to enhance the SNR
for the signatures originated by the holonomies
of the 3-space
![]() .
.
In the simulations presented in this section we assume
that the FP is a cube of side L=1, and the origin of
coordinates is in the center of this cube.
Moreover, for T3 and ![]() ,
we consider
,
we consider
![]() ,
i.e.
,
i.e.
![]() .
The case of G6 is doubly special: firstly, in order to
avoid the presence of Clifford translations appearing at
.
The case of G6 is doubly special: firstly, in order to
avoid the presence of Clifford translations appearing at
![]() ,
we assume R = 0.7;
secondly, because the non-translational isometries have a
very small signature in the MPASH, we assume
R- = 0.69,
i.e.
,
we assume R = 0.7;
secondly, because the non-translational isometries have a
very small signature in the MPASH, we assume
R- = 0.69,
i.e.
![]() .
.
In order to normalize and compare the results appearing in
the different MPASHs shown below, we fix the values of m, and consequently that of
![]() ,
in all of them.
Thus, we consider that the interval
,
in all of them.
Thus, we consider that the interval ![]() is divided in
m = 400 bins, each one of width
is divided in
m = 400 bins, each one of width
![]() .
.
In general, to clearly reveal the signatures in the MPASH,
a good SNR is of the order of 10; in particular, regarding
Clifford translational isometries, this implies that the
number of catalogs should be such that
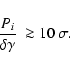 |
(33) |
In this section, we show how to generate full-sky catalogs
in order to construct the MPASHs to reveal topological
signatures in the angular distribution of cosmic objects.
We assume in all the simulations presented here that the FP
is a cube of side L = 1, centered at the origin of
coordinates.
To construct a PASH through a numerical simulation, we first
randomly generate a set of three Euclidean coordinates
![]() for
for
![]() objects located
inside the FP.
objects located
inside the FP.
In order to be sure that the distribution generated in this
way is uniform, we test the randomness of the simulation
using the Pair Separation Histograms for the simply-connected
case
![]() ,
according to the theoretical relationship
expected for such a case given by Bernui & Teixeira (1999).
After that, these
,
according to the theoretical relationship
expected for such a case given by Bernui & Teixeira (1999).
After that, these
![]() objects are mapped to the whole
ball
objects are mapped to the whole
ball
![]() via the translational isometries
via the translational isometries
![]() of T3, giving rise to NT objects (including the
of T3, giving rise to NT objects (including the
![]() objects) in
objects) in
![]() .
Then, we select the N objects located inside the thin
shell, i.e. those objects with radial distance satisfying
.
Then, we select the N objects located inside the thin
shell, i.e. those objects with radial distance satisfying
![]() .
We project them on the involving sphere
.
We project them on the involving sphere
![]() and
calculate all the angular distances between the N (N-1)/2
pairs of objects.
and
calculate all the angular distances between the N (N-1)/2
pairs of objects.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{figure10.ps}
\end{figure}](/articles/aa/full/2006/03/aa1950-04/Timg202.gif) |
Figure 10:
MPASH together with EPASH for K=104 full-sky
simulated catalogs in T3 (the FP is a cube of side 1);
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{figure11.ps}
\end{figure}](/articles/aa/full/2006/03/aa1950-04/Timg203.gif) |
Figure 11: Difference between MPASH and EPASH corresponding to Fig. 10. |
| Open with DEXTER | |
We then count how many of these angular distances are in
the interval
![]() .
Finally, we normalize the PASH and plot the number of
distances versus the angular distance
.
Finally, we normalize the PASH and plot the number of
distances versus the angular distance ![]() .
For the simulations showed in Figs. 10
and 11, where we consider the case
.
For the simulations showed in Figs. 10
and 11, where we consider the case
![]() ,
we use
R = 1, R- = 0.997.
In this case, due to the ratio between the volumes
of
,
we use
R = 1, R- = 0.997.
In this case, due to the ratio between the volumes
of
![]() (=
(=![]() )
and T3 (=1) we should
obtain images corresponding to the first three Clifford
translations:
)
and T3 (=1) we should
obtain images corresponding to the first three Clifford
translations:
![]() ,
,
![]() ,
and
,
and
![]() .
As a consequence of this, the MPASH presents angular
correlations that are approximately located at
.
As a consequence of this, the MPASH presents angular
correlations that are approximately located at
![]() radians,
respectively, with the corresponding peak heights
radians,
respectively, with the corresponding peak heights
![]() ,
and
,
and
![]() .
.
For the simulation showed in Fig. 12, where we
study the case
![]() ,
we also used
R = 1, R- = 0.997.
However, in this case, the Clifford translations contributing
to the topological angular correlations studied in the
previous section are just two:
,
we also used
R = 1, R- = 0.997.
However, in this case, the Clifford translations contributing
to the topological angular correlations studied in the
previous section are just two:
![]() ,
,
![]() ,
which generate only the images
,
which generate only the images
![]() ,
respectively.
According to this, the heights of the 2 peaks appearing in
Fig. 12 are
,
respectively.
According to this, the heights of the 2 peaks appearing in
Fig. 12 are
![]() ,
and are approximately located at
,
and are approximately located at
![]() radians,
for i=1,2 respectively.
In fact, as we can observe in Fig. 13, there
is no peak at
radians,
for i=1,2 respectively.
In fact, as we can observe in Fig. 13, there
is no peak at
![]() because there
is no translational isometry at
because there
is no translational isometry at
![]() in
in
![]() .
.
In Fig. 14 we present the MPASH and the EPASH
for the case of the 3-space
![]() ,
and in
Fig. 15 we show the corresponding difference
between them.
In this case, we assumed again that the FP is a cube of
side 1,
R = 0.7, R-= 0.69, i.e.
,
and in
Fig. 15 we show the corresponding difference
between them.
In this case, we assumed again that the FP is a cube of
side 1,
R = 0.7, R-= 0.69, i.e.
![]() ,
,
![]() objects,
and
objects,
and
![]() .
.
Comparing Figs. 11 and 13 with Fig. 15 we observe that the heights of the peaks are much smaller in the case of screw-motion isometries than in the case of Clifford translation isometries. However, our simulations show that with a suitable number of catalogs, the screw-motions, as well as the pure translational isometries, are revealed in the MPASHs as small peaks.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{figure12.ps}
\end{figure}](/articles/aa/full/2006/03/aa1950-04/Timg220.gif) |
Figure 12:
MPASH together with EPASH for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{figure13.ps}
\end{figure}](/articles/aa/full/2006/03/aa1950-04/Timg221.gif) |
Figure 13: Difference between MPASH and EPASH corresponding to Fig. 12. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{figure14.ps}
\end{figure}](/articles/aa/full/2006/03/aa1950-04/Timg222.gif) |
Figure 14:
MPASH together with EPASH for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{figure15.ps}
\end{figure}](/articles/aa/full/2006/03/aa1950-04/Timg223.gif) |
Figure 15: Difference between MPASH and EPASH corresponding to Fig. 14. |
| Open with DEXTER | |
We present numerical simulations in which the objects are
located in a thin spherical shell of thickness ![]() ;
the radial distance of the object to the origin of coordinates
is
;
the radial distance of the object to the origin of coordinates
is
![]() ,
,
![]() .
We performed these calculations for both T3 and
.
We performed these calculations for both T3 and ![]() 3-spaces.
3-spaces.
A noticeable fact, shown in Figs. 11, 13, and 15 corresponding to the numerical simulations done in the precedent sub-section, is that full-sky catalogs produce small distinguishable peaks in the MPASHs when the isometries are Clifford translations (which appears only in Euclidean and spherical geometries; for details see, e.g., Gomero et al. 2000a,b, 2001, 2002), and even smaller signatures for the non-translational isometries.
For completeness we perform now numerical simulations in order
to test whether these results are valid for partial-sky catalogs,
namely for polar-cap catalogs, and we do this for the cases when
the 3-space is T3 and ![]() .
Observing Figs. 17 and 18, we notice
that the topological information does not disappear when we
consider a suitable polar-cap catalog instead of a full-sky catalog.
.
Observing Figs. 17 and 18, we notice
that the topological information does not disappear when we
consider a suitable polar-cap catalog instead of a full-sky catalog.
Regarding our simulations, we remark that the values assumed for R and L means that the observable Universe includes a small number of multiple images, generated by the isometries of the manifold, for each seed-object present in the FP. This assumption is within the limits imposed by CMBR to the scale of the Small Universe considering a T3 manifold (e.g. Stevens et al. 1993; Starobinsky 1993; de Oliveira-Costa & Smoot 1995; de Oliveira-Costa et al. 1996).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{figure16.ps}
\end{figure}](/articles/aa/full/2006/03/aa1950-04/Timg226.gif) |
Figure 16:
MPASH together with EPASH for a polar-cap
catalog in T3, with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{figure17.ps}
\end{figure}](/articles/aa/full/2006/03/aa1950-04/Timg227.gif) |
Figure 17: Difference between MPASH and EPASH plotted in Fig. 16. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{figure18.ps}
\end{figure}](/articles/aa/full/2006/03/aa1950-04/Timg228.gif) |
Figure 18:
Difference between MPASH and EPASH obtained for
a polar-cap catalog (with
|
| Open with DEXTER | |
We presented a method to study the angular distribution of cosmic objects. It has the great advantage of being independent of cosmological models or parameters. Through the analyses of the PASHs, we investigated the effect that different topological properties, termed Euclidean isometries, produce in the angular distributions of objects. We performed these analyses in full-sky as well as in polar-cap catalogs.
We concentrate on the analysis of objects located in a thin
spherical shell, considering only their angular positions in
the celestial sphere in order to explore CMBR data.
We have considered four different cases regarding the 3-space
where the shell is embedded: the simply-connected
![]() ,
and the three topologically different multiply-connected
flat 3-spaces: T3,
,
and the three topologically different multiply-connected
flat 3-spaces: T3, ![]() ,
and G6.
,
and G6.
In the simply-connected case, topological angular correlations
are clearly absent. This is evinced by plotting the
difference between the MPASH and the EPASH, where only
statistical fluctuations appear, as seen in Figs. 5
to 9, independently of the number of simulated
catalogs used to produce the MPASH.
For the multiply-connected 3-spaces analyzed, angular
correlations due to the isometries involved in each specific
case indeed appear.
Thus, the topological imprints corresponding to translational
isometries manifest themselves as small and independent
peaks, i.e., one peak for each isometry.
On the other hand, the signatures corresponding to the
non-translational isometries (which is the case for the G6 manifold) appear as a less intense but extended angular
correlation: from
![]() radians to
radians to
![]() ,
as can be seen in
Fig. 15.
,
as can be seen in
Fig. 15.
It is also important to notice that the topological information of multiply connected 3-spaces does not disappear when we consider a suitable polar-cap catalog instead of a full-sky catalog, that is, provided that such polar-cap is sufficiently large and conveniently oriented in the sky to map multiple images. This fact is clearly observed in Figs. 17 and 18. This is a very useful result because in general astronomical data are presented in catalogs covering only partial regions of the sky. In order to improve the SNR and reveal small topological imprints in the angular distribution of cosmic objects, the strategy is to divide the original catalog in several sub-catalogs and then perform the MPASH. It could be also useful to divide the full-sky data in a set of antipodal polar-caps and compare them to similar sky patches in a statistically isotropic Universe (Bernui et al. 2004).
We have shown that a topological signature, no
matter how small it is, can always be revealed whenever
one achieves a suitable SNR in the difference between the
MPASH and the EPASH.
As shown in our simulations, the small topological signatures
of T3 and ![]() are clearly revealed when averaging
are clearly revealed when averaging
![]() catalogs with
catalogs with
![]() objects each, from an original catalog of
objects each, from an original catalog of
![]() cosmic objects.
For G6, the numberof cosmic objects should be five times
larger.
For the case of CMBR maps which are always contaminated by
Galactic foregrounds, the polar-cap analysis described in
this paper would be useful to reveal possible angular
correlations in these data sets.
cosmic objects.
For G6, the numberof cosmic objects should be five times
larger.
For the case of CMBR maps which are always contaminated by
Galactic foregrounds, the polar-cap analysis described in
this paper would be useful to reveal possible angular
correlations in these data sets.
Acknowledgements
We thank A.F.F. Teixeira, G.I. Gomero, M.J. Rebouças, and C.A. Wuensche for many fruitful discussions. A.B. thanks CNPq (PCI/DTI7B fellowship) and TWAS for the partial financial support, and the hospitality of the Centro Brasileiro de Pesquisas Físicas visited under the TWAS-Associateship Scheme at Centres of Excellence in the South. T.V. was partially supported by CNPq grant 302266/88-7-FA and FAPESP grant 00/06770-2. We also thank the anonymous referee for the valuable comments on the manuscript.