On leave from Universidad Nacional de Ingeniería, Facultad de Ciencias, Apartado 31 - 139, Lima 31, Peru.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

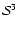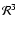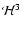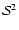This result is independent of the three-dimensional geometry since all three isotropic geometries (i.e. spherical ${\cal S}^3$ , Euclidean ${\cal R}^3$ , and hyperbolic ${\cal H}^3$ ) possess spherical surfaces ${\cal S}^2$ as hypersurfaces.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... translation

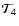A picture of this FP can be seen, for instance, in Bernui et al. (1998), where it is denoted by ${\cal T}_4$ .

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

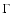
... $\Gamma$

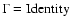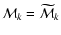Except when $\Gamma=\mbox{Identity}$ , in which case ${\cal M}_k = \widetilde{\cal M}_k$ is a simply-connected manifold.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... rules

i.e. physical properties that are common to the cosmic objects in a given catalog, such as luminosity threshold, redshift, etc.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... objects

This situation corresponds to the monopole term (l = 0) in a multipole decomposition.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.