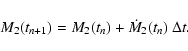 |
(1) |
A&A 445, 647-652 (2006)
DOI: 10.1051/0004-6361:20053288
A. Büning - H. Ritter
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
Received 22 April 2005 / Accepted 24 August 2005
Abstract
Numerical computation of the time evolution of the mass
transfer rate in a close binary can be and, in particular, has been a
computational challenge. Using a simple physical model to calculate
the mass transfer rate, we show that for a simple explicit iteration
scheme the mass transfer rate is numerically unstable unless the time
steps are sufficiently small. In general, more sophisticated explicit
algorithms do not provide any significant improvement since this
instability is a direct result of time discretization. For a typical
binary evolution, computation of the mass transfer rate as a smooth
function of time limits the maximum tolerable time step and thereby
sets the minimum total computational effort required for an
evolutionary computation. By methods of "Controlling Chaos'' it can
be shown that a specific implicit iteration scheme, based on Newton's
method, is the most promising solution for the problem.
Key words: binaries: close - stars: evolution - stars: mass-loss - methods: numerical
To compute the long-term evolution of a semi-detached binary, the
numerically determined mass transfer rate, which is a function of
current stellar and binary parameters, must be a sufficiently smooth
function of time. The simplest approach to obtain the mass M2 of
the mass losing secondary star is an explicit forward integration in time:
Attempts to use a different explicit integration scheme that takes
into account not only
![]() but also
but also
![]() for certain values of j (e.g., for a
particular average over the last m time steps) did not show major
improvements. The reason for this behaviour of the mass transfer rate
has remained unknown.
for certain values of j (e.g., for a
particular average over the last m time steps) did not show major
improvements. The reason for this behaviour of the mass transfer rate
has remained unknown.
The main purpose of this paper is to show analytically why these
numerical instabilities exist, what they are, which methods are
suitable to suppress them, and which ones are not. Even in the case
of the proposed implicit algorithm, calculation of the mass ransfer
rate still limits the maximum tolerable time step in a numerical
computation and thus sets the minimum total computational effort
required for carrying out such a binary evolution. To illustrate this
point: by imposing a fixed mass loss rate on a single low-mass main
sequence star, up to 10% of the total mass of the star can be
removed per time step (eventually after 1 or 2 initial time steps with
a lower rate), and the stellar model still converges. But if the mass
loss rate is coupled to the binary parameters, even in the case of our
proposed implicit iteration scheme, typically no more than a few 10-3 of the stellar mass can be removed per time step without
losing convergence![]() .
When using the explicit algorithm (1), the
corresponding value is much lower: often only about
10-5-10-4
or even less of the total mass can be removed per time step if
fluctuations of the mass transfer rate by up to several orders of
magnitude are to be avoided.
.
When using the explicit algorithm (1), the
corresponding value is much lower: often only about
10-5-10-4
or even less of the total mass can be removed per time step if
fluctuations of the mass transfer rate by up to several orders of
magnitude are to be avoided.
This paper is organized as follows: first, we discuss in
Sect. 2 the necessary input physics before we show in
Sect. 3 that the mass transfer rate in our model is
physically stable. Subsequently, in Sect. 4.1
we prove mathematically that for a simple explicit algorithm the
time-discretized mass transfer rate becomes unstable if ![]() is
greater than a critical value. We also give an estimate of how many
time steps are required to calculate the binary evolution. Next, we
show in Sect. 4.2 that for increasing
is
greater than a critical value. We also give an estimate of how many
time steps are required to calculate the binary evolution. Next, we
show in Sect. 4.2 that for increasing
![]() the mass transfer rate undergoes a Feigenbaum scenario
Feigenbaum 1978,1980; for a more accessible
review see, e.g., Thompson & Stewart 1986 and finally becomes chaotic. In
Sect. 4.3 we discuss how the onset of
chaos can be suppressed in terms of "Controlling Chaos'' and we
present an implicit iteration scheme for the integration of the mass
transfer rate. Finally, in Sect. 5 we discuss
a number of points which have to be considered for a practical
implementation.
the mass transfer rate undergoes a Feigenbaum scenario
Feigenbaum 1978,1980; for a more accessible
review see, e.g., Thompson & Stewart 1986 and finally becomes chaotic. In
Sect. 4.3 we discuss how the onset of
chaos can be suppressed in terms of "Controlling Chaos'' and we
present an implicit iteration scheme for the integration of the mass
transfer rate. Finally, in Sect. 5 we discuss
a number of points which have to be considered for a practical
implementation.
In this paper we use the same nomenclature as in Büning & Ritter (2004),
hereafter called Paper I. For the mass transfer rate we use
Instead of Eq. (2) other relations between
![]() and
and ![]() have also been used in the literature. For example
Tout et al. (1997) have adopted a power-law dependence
have also been used in the literature. For example
Tout et al. (1997) have adopted a power-law dependence
![]() .
However, a mass transfer prescription other
than Eq. (2) results mainly in a different characteristic scale
length
.
However, a mass transfer prescription other
than Eq. (2) results mainly in a different characteristic scale
length
The mass transfer rate ![]() is uniquely invertibly coupled to
is uniquely invertibly coupled to ![]() by Eq. (2). For simplicity, we will consider the
time evolution of
by Eq. (2). For simplicity, we will consider the
time evolution of ![]() instead of
instead of ![]() which is given by
Eq. (36) of Paper I:
which is given by
Eq. (36) of Paper I:
At the stationary value
![]() which is the only fixed
point (FP) of Eq. (6) and which is equivalent to the
stationary mass transfer rate, using Eq. (2) we get
which is the only fixed
point (FP) of Eq. (6) and which is equivalent to the
stationary mass transfer rate, using Eq. (2) we get
(cf. Eq. (44) of Paper I). Since
![]() and
and
![]() ,
DF is negative, not only for
,
DF is negative, not only for
![]() ,
but even for all
,
but even for all
![]() .
This means
that the stationary mass transfer rate, i.e.,
.
This means
that the stationary mass transfer rate, i.e.,
![]() is
stable and that all solutions
is
stable and that all solutions
![]() of Eq. (6)
converge
of Eq. (6)
converge![]() to
to
![]() .
The convergence occurs on a time scale of
.
The convergence occurs on a time scale of
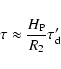 |
(8) |
![\begin{displaymath}%
\Delta R(t) = \overline{\Delta R} +
\left[ \Delta R(0) - \overline{\Delta R} \right]~ {\rm e}^{-DF~t}
\end{displaymath}](/articles/aa/full/2006/02/aa3288-05/img40.gif) |
(9) |
The simplest way to obtain the donor mass numerically as a function
of time is an explicit forward integration of ![]() as given by
Eq. (1). In this time-discretized system the
evolution of
as given by
Eq. (1). In this time-discretized system the
evolution of ![]() is given by an iteration equation which
follows directly from Eq. (6):
is given by an iteration equation which
follows directly from Eq. (6):
Obviously, Eqs. (6) and (10),
i.e., the time-continuous and the time-discretized systems have the
same FP since
![]() if and only if
if and only if
![]() .
But, since
.
But, since
![]() is a map while
is a map while
![]() is
a vector field
is
a vector field![]() , the condition for stability is different: according to the Hartmann-Grobmann theorem (e.g., Guckenheimer & Holmes 1983), a FP
, the condition for stability is different: according to the Hartmann-Grobmann theorem (e.g., Guckenheimer & Holmes 1983), a FP
![]() of a map
of a map
![]() is stable if the absolute
values of all eigenvalues of the Jacobi matrix
is stable if the absolute
values of all eigenvalues of the Jacobi matrix
![]() of
of
![]() at
at ![]() are
less than unity, and
are
less than unity, and ![]() is unstable if at least one
eigenvalue has an absolute value greater than unity.
is unstable if at least one
eigenvalue has an absolute value greater than unity.
In the case of
![]() from Eq. (10) this
means:
from Eq. (10) this
means:
![]() is stable if
is stable if
If the initial value of the iteration is
![]() ,
then in the
linearized system the orbit of
,
then in the
linearized system the orbit of
![]() ,
i.e.,
,
i.e.,
![]() is given by
is given by
The following cases are possible (without proof):
It is now possible to estimate how many time steps an explicit
method like Eq. (1) needs at least for the
computation of a mass transfer phase during which the maximum time
step length
![]() is used. From Eqs. (5)
and (12) it follows that at most the mass
fraction
is used. From Eqs. (5)
and (12) it follows that at most the mass
fraction
The main reason for this increased computational demand in the case of thermally unstable mass transfer can be understood as follows:
The donor star of a binary in which mass transfer is thermally
unstable has a deep radiative envelope. Unperturbed stars with a deep
radiative envelope can be described (to some extent) by a polytropic
stellar structure with a polytropic index ![]() and an
adiabatic index
and an
adiabatic index
![]() (monoatomic ideal gas), see e.g.
Hjellming & Webbink (1987), Table 1. Because for polytropes of index n,
(monoatomic ideal gas), see e.g.
Hjellming & Webbink (1987), Table 1. Because for polytropes of index n,
![]() ,
for radiative stars (with
,
for radiative stars (with ![]() )
)
![]() is a very large, positive number. However, this holds only
for unperturbed stars in thermal equilibrium and only in the limit of
infinitesimally small mass loss (see Hjellming & Webbink (1987), last
paragraph of Sect. II). On the other hand, for finite mass loss
is a very large, positive number. However, this holds only
for unperturbed stars in thermal equilibrium and only in the limit of
infinitesimally small mass loss (see Hjellming & Webbink (1987), last
paragraph of Sect. II). On the other hand, for finite mass loss ![]() decreases rapidly with the amount of mass lost. Yet for such
stars, at least during the initial phases of thermal timescale mass
transfer,
decreases rapidly with the amount of mass lost. Yet for such
stars, at least during the initial phases of thermal timescale mass
transfer, ![]() is still much larger than unity, i.e. typically of
order 10-100 (as shown in Hjellming & Webbink 1987, their Figs. 3 and 4). As a consequence,
is still much larger than unity, i.e. typically of
order 10-100 (as shown in Hjellming & Webbink 1987, their Figs. 3 and 4). As a consequence,
![]() is then also of the
order of 10-100, and
is then also of the
order of 10-100, and
![]() as given in Eq. (14) is smaller and the minimum number of required time steps increases by that factor.
as given in Eq. (14) is smaller and the minimum number of required time steps increases by that factor.
As can be seen from Eq. (15), an artificial
increase of ![]() can significantly reduce the required
number of time steps. This has been used in the past by numerous
authors to speed up the computations (e.g., Hameury 1991).
This approach yields the correct mass transfer rate only when mass
transfer is close to stationary. However, it cannot be used if the
turn-on and turn-off of mass transfer is important, as is the case
for irradiation-induced mass transfer cycles (cf. Paper I).
can significantly reduce the required
number of time steps. This has been used in the past by numerous
authors to speed up the computations (e.g., Hameury 1991).
This approach yields the correct mass transfer rate only when mass
transfer is close to stationary. However, it cannot be used if the
turn-on and turn-off of mass transfer is important, as is the case
for irradiation-induced mass transfer cycles (cf. Paper I).
The linear stability analysis discussed in Sect. 4.1 describes only the system dynamics near the FP, i.e., the local dynamics; we will now briefly discuss the global dynamics.
When going to dimensionless quantities
For
![]() ,
corresponding to
,
corresponding to
![]() ,
the FP becomes unstable and bifurcates into an unstable FP and a stable
cycle of period 2. For increasing values of
,
the FP becomes unstable and bifurcates into an unstable FP and a stable
cycle of period 2. For increasing values of ![]() ,
the 2-cycle also
becomes unstable, and a stable 4-cycle appears, and so on. At a
critical value of
,
the 2-cycle also
becomes unstable, and a stable 4-cycle appears, and so on. At a
critical value of
![]() ,
the system dynamics become
chaotic, and beyond this value the chaotic dynamics are permanently
interrupted by finite windows of regular dynamics which correspond to
the existence of a stable cycle of any period. Figure 1
shows 50 iterations of Eq. (17) of one single
orbit for 5000 different values of
,
the system dynamics become
chaotic, and beyond this value the chaotic dynamics are permanently
interrupted by finite windows of regular dynamics which correspond to
the existence of a stable cycle of any period. Figure 1
shows 50 iterations of Eq. (17) of one single
orbit for 5000 different values of ![]() .
The FP
.
The FP
![]() corresponds to
corresponds to
![]() .
At about
.
At about
![]() ,
a stable orbit of period 3 appears, whose existence is
a mathematical proof for the existence of chaotic dynamics in the
system according to the famous "Period three implies chaos'' by
Li & Yorke (1975). x is a logarithm of
,
a stable orbit of period 3 appears, whose existence is
a mathematical proof for the existence of chaotic dynamics in the
system according to the famous "Period three implies chaos'' by
Li & Yorke (1975). x is a logarithm of ![]() and
and ![]() is
linear in
is
linear in ![]() .
Thus, the transitional region from stable to
chaotic dynamics is rather small.
.
Thus, the transitional region from stable to
chaotic dynamics is rather small.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{3288fig1}
\end{figure}](/articles/aa/full/2006/02/aa3288-05/Timg89.gif) |
Figure 1:
Feigenbaum diagram of map (17).
50 iterations of one orbit for 5000 different values of |
| Open with DEXTER | |
Since chaotic or "random'' values in the mass transfer rate are not
desirable, how can the chaotic dynamics be suppressed? As mentioned
above, an artificial increase of ![]() will increase
will increase
![]() and therefore shift the onset of chaos to higher
values of
and therefore shift the onset of chaos to higher
values of ![]() .
In general, the choice of a mass transfer
prescription which differs from Eq. (2) will only shift the
onset of chaos to different values of
.
In general, the choice of a mass transfer
prescription which differs from Eq. (2) will only shift the
onset of chaos to different values of ![]() but it cannot suppress
it. At least, if
but it cannot suppress
it. At least, if ![]() grows as
grows as ![]() ,
,
![]() basically keeps its behaviour (without proof) for
basically keeps its behaviour (without proof) for
![]() and
this is the case for all physical models for computing mass transfer.
and
this is the case for all physical models for computing mass transfer.
It is possible to suppress chaotic dynamics and to stabilize a given
FP by introducing small pertubations in terms of "Controlling Chaos''![]() .
There are two distinct approaches: the first one varies one system
parameter by a small amount
.
There are two distinct approaches: the first one varies one system
parameter by a small amount
![]() for each time step
to enforce stability of the FP (Ott et al. 1990), but this method
requires the a priori knowledge of the FP, and this is not the case
for our system. The second method adds a small correction
for each time step
to enforce stability of the FP (Ott et al. 1990), but this method
requires the a priori knowledge of the FP, and this is not the case
for our system. The second method adds a small correction
![]() to the new iteration value, i.e.,
to the new iteration value, i.e.,
A nonlinear approach of the form
Since our map (17) is of the form
![]() ,
Eq. (20)
is equivalent to
,
Eq. (20)
is equivalent to
While the explicit iteration scheme is a simple time integration scheme which requires one iteration per time step, the proposed implicit iteration scheme is a fixed point search which requires several iterations per time step until the fixed point is found with sufficiently high accuracy.
Fortunately, the equations of stellar structure are typically solved by Newton's method, more explicitly by the so-called Henyey method (Kippenhahn et al. 1967; Kippenhahn & Weigert 1990). Thus, the best solution is to include the mass transfer rate or the stellar mass itself as an additional variable in the Henyey method and to perform the fixed point search simultaneously with the solution of the equations of stellar structure (Paper I). This has also been done independently by Benvenuto & de Vito (2003). For details of our implementation, see Büning (2003).
Figure 2 shows the mass transfer rate obtained with
our binary evolutionary code as a function of time for one specific
binary system. Since our evolutionary code has not been designed for
the analysis of chaotic dynamics, we have kept ![]() constant and
instead have used the fact that the timescale of thermal relaxation
varies, which is the dominant term in
constant and
instead have used the fact that the timescale of thermal relaxation
varies, which is the dominant term in
![]() for the binary
system in question. When mass transfer starts, the thermal relaxation
of the donor increases (i.e.,
for the binary
system in question. When mass transfer starts, the thermal relaxation
of the donor increases (i.e.,
![]() decreases, cf. Eq. (16)), and, therefore,
decreases, cf. Eq. (16)), and, therefore, ![]() also increases. At
some point, thermal relaxation reaches a maximum and decreases
afterwards, and so does
also increases. At
some point, thermal relaxation reaches a maximum and decreases
afterwards, and so does ![]() .
.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{3288fig2}
\end{figure}](/articles/aa/full/2006/02/aa3288-05/Timg108.gif) |
Figure 2:
Mass transfer rate
|
| Open with DEXTER | |
When using the explicit algorithm (1), the
resulting mass transfer rate undergoes a period doubling bifurcation
before it exhibits chaotic dynamics. Within the chaotic region a
periodic window of period 5 appears. After thermal relaxation and
hence also ![]() has reached its maximum, the Feigenbaum scenario
evolves backwards. Since the decrease of
has reached its maximum, the Feigenbaum scenario
evolves backwards. Since the decrease of ![]() occurs slower than
its increase before, even stable cycles of period 8 and 4 appear
before the secular mass transfer rate finally becomes stable. In
contrast, the result obtained with our implicit algorithm for the
same system and the same system parameters is shown by the dashed
line.
occurs slower than
its increase before, even stable cycles of period 8 and 4 appear
before the secular mass transfer rate finally becomes stable. In
contrast, the result obtained with our implicit algorithm for the
same system and the same system parameters is shown by the dashed
line.
Although the implicit algorithm stabilizes the FP and even provides a
quadratic convergence of the iteration, chaotic dynamics are still
present outside of a neighbourhood of the FP. Therefore, a good
initial value for the iteration is necessary. We used a linear
extrapolation of ![]() and
and ![]() to determine the initial
value for
to determine the initial
value for ![]() by Eq. (2). First, we perform typically
2-4 iterations and keep the preestimated value for
by Eq. (2). First, we perform typically
2-4 iterations and keep the preestimated value for ![]() constant until the solution for the other stellar parameters has
almost converged. Otherwise, even small fluctuations of R2 might
push the next iteration value of
constant until the solution for the other stellar parameters has
almost converged. Otherwise, even small fluctuations of R2 might
push the next iteration value of ![]() out of the basin of
attraction of the FP and prevent convergence. Then, we finish with
mostly 2-6 iterations using the full implicit algorithm to determine
the correct mass transfer rate.
out of the basin of
attraction of the FP and prevent convergence. Then, we finish with
mostly 2-6 iterations using the full implicit algorithm to determine
the correct mass transfer rate.
Furthermore, to calculate the mass transfer rate with a numerical
accuracy of better than ![]() ,
the stellar radius has to be determined
with a very high numerical accurracy. According to Eq. (2),
for a scale height of
,
the stellar radius has to be determined
with a very high numerical accurracy. According to Eq. (2),
for a scale height of
![]() ,
which is
typical for low-mass MS stars, R2 has to be determined with a
relative accuracy of the order of 10-6 in order to get
,
which is
typical for low-mass MS stars, R2 has to be determined with a
relative accuracy of the order of 10-6 in order to get
![]() with a relative accuracy of the order of 10-2. To
compute the radius with such a high accuracy the stellar physics and
especially the equation of state must be a very smooth function of its
variables. Every small discontinuity, especially in the outer layers
of the star, can cause small jumps in the stellar radius which appear,
magnified by the factor
with a relative accuracy of the order of 10-2. To
compute the radius with such a high accuracy the stellar physics and
especially the equation of state must be a very smooth function of its
variables. Every small discontinuity, especially in the outer layers
of the star, can cause small jumps in the stellar radius which appear,
magnified by the factor
![]() ,
as significant jumps in the
mass transfer rate.
,
as significant jumps in the
mass transfer rate.
We have used a simple analytical model, a 1d autonomous ordinary
differential equation to describe the time evolution of the mass
transfer rate. We have shown that, while the FP in the time-continuous
system, i.e., the "physical'' mass transfer rate is stable, the FP in
the time-discretized system, i.e., the "numerical'' mass transfer
rate becomes unstable if the length of the time step ![]() exceeds a critical value
exceeds a critical value
![]() given by
Eq. (12). We have estimated that even in the ideal
case where
given by
Eq. (12). We have estimated that even in the ideal
case where
![]() at least several thousand
time steps are necessary to reduce the donor mass in a low-mass binary
system by a factor of two. For systems with thermally unstable mass
transfer, it is even worse.
at least several thousand
time steps are necessary to reduce the donor mass in a low-mass binary
system by a factor of two. For systems with thermally unstable mass
transfer, it is even worse.
We outline a mathematical proof that the iteration equation for the
time-discretized system shows a behaviour similar to that of the
logistic map and, for
![]() ,
undergoes a
series of period doublings which finally leads to chaotic dynamics,
i.e., to apparently random values of the computed mass transfer rate.
The choice of a different explicit prescription to calculate the
mass transfer rate results only in a shift of the critical time step
length
,
undergoes a
series of period doublings which finally leads to chaotic dynamics,
i.e., to apparently random values of the computed mass transfer rate.
The choice of a different explicit prescription to calculate the
mass transfer rate results only in a shift of the critical time step
length
![]() which, in turn, depends on the
characteristic scale length H at the FP
which, in turn, depends on the
characteristic scale length H at the FP
![]() ,
i.e., at the secular mass transfer rate.
,
i.e., at the secular mass transfer rate.
In terms of "Controlling Chaos'' we have briefly discussed several
methods to stabilize the FP. Various modified iteration schemes which
are equivalent to different explicit iteration schemes have been
discussed in the literature, but they all do not show sufficient
stabilization. Therefore, we suggest that using a different explicit
iteration scheme may shift
![]() to higher values but
will not solve the problem. An implicit scheme, Newton's method, is
the most promising solution because it stabilizes the FP formally for
to higher values but
will not solve the problem. An implicit scheme, Newton's method, is
the most promising solution because it stabilizes the FP formally for
![]() ,
although for this to be the case a
sufficiently good initial value for the iteration is required.
,
although for this to be the case a
sufficiently good initial value for the iteration is required.
In practice, the implicit algorithm reduces the number of required
time steps by at least a factor of 10. Another advantage is that the
implicit algorithm either yields the "correct'' mass transfer rate or
does not converge at all, whereas the explicit algorithm provides a
result in every case, even if it is random. Therefore, in our binary
evolutionary calculations we reject results of the last time step if
convergence is not reached and restart it with a smaller ![]() .
.
Acknowledgements
We thank A. Weiss and H. Schlattl for providing their stellar evolutionary code, and H. Schlattl for valuable support and helpful discussions about numerics. We also thank U. Kolb for providing unpublished details about his numerical calculations.