- ... convergence
![[*]](/icons/foot_motif.gif)
- This upper limit of about 10-3 varies and depends on the
starting value for the iteration, on the "smoothness'' of the stellar
input physics, and on the "smoothness'' of the stellar structure. In
principle, this is not a limitation of the implicit mass transfer algorithm.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
converge
![[*]](/icons/foot_motif.gif)
- This can be proven by using the fact that F is continuous and has
only one FP. Thus,
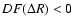 for all
for all
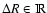 together with
together with
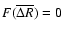 implies
implies
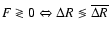 so that from (6) the convergence of all solutions
to
so that from (6) the convergence of all solutions
to
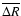 can be concluded.
can be concluded.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... field
![[*]](/icons/foot_motif.gif)
- For details on maps, vector fields an their related nomenclature,
the reader is referred to, e.g., Guckenheimer & Holmes (1983).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... functions
![[*]](/icons/foot_motif.gif)
- Unimodal functions and their system dynamics are discussed in detail by Collet & Eckmann (1980). For an overview about topological conjugacy and
the Feigenbaum scenario see, e.g., Jackson (1989); Thompson & Stewart (1986).
For some background about topological conjugacy and topological
equivalence of maps, see Wiggins (1990); Arnold (1983). A more
in-depth discussion of map (17) can also
be found in Büning (2003).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... parameter
![[*]](/icons/foot_motif.gif)
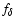 is not topologically conjugated to a full family of
is not topologically conjugated to a full family of 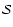 -unimodal functions. Hence, unlike the logistic map,
-unimodal functions. Hence, unlike the logistic map,
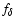 formally does not undergo a complete Feigenbaum scenario.
formally does not undergo a complete Feigenbaum scenario.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Chaos''
![[*]](/icons/foot_motif.gif)
- The term "Controlling Chaos'' comes from an article of the same title
by Ott et al. (1990) who suggested to control chaotic motion in nonlinear
systems by small perturbations. The keyword "Controlling Chaos'' or
"Control of Chaos'' later became common in that special field of
research. In their introduction to The Control of Chaos: Theory
and Applications, Boccaletti et al. (2000) gave a short historical
overview of that topic.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.