A&A 445, 747-758 (2006)
DOI: 10.1051/0004-6361:20053238

3D-radiation hydro simulations of disk-planet interactions

I. Numerical algorithm and test cases

H. Klahr1,2 - W. Kley1


1 - Universität Tübingen, Institut für Astronomie und Astrophysik, Abt. Computational Physics, Auf der Morgenstelle 10, 72076 Tübingen, Germany
2 - Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany

Received 13 April 2005 / Accepted 16 August 2005

Abstract
We study the evolution of an embedded protoplanet in a circumstellar disk using the 3D-Radiation Hydro code TRAMP, and treat the thermodynamics of the gas properly in three dimensions. The primary interest of this work lies in the demonstration and testing of the numerical method. We show how far numerical parameters can influence the simulations of gap opening. We study a standard reference model under various numerical approximations. Then we compare the commonly used locally isothermal approximation to the radiation hydro simulation using an equation for the internal energy. Models with different treatments of the mass accretion process are compared. Often mass accumulates in the Roche lobe of the planet creating a hydrostatic atmosphere around the planet. The gravitational torques induced by the spiral pattern of the disk onto the planet are not strongly affected in the average magnitude, but the short time scale fluctuations are stronger in the radiation hydro models.

An interesting result of this work lies in the analysis of the temperature structure around the planet. The most striking effect of treating the thermodynamics properly is the formation of a hot pressure-supported bubble around the planet with a pressure scale height of $H/R \approx 0.5$ rather than a thin Keplerian circumplanetary accretion disk.

Key words: accretion, accretion disks - hydrodynamics - solar system: formation - radiative transfer - planets and satellites: formation

1 Introduction

During their formation process, massive, gaseous planets are believed to undergo a phase of evolution where they are still embedded in the protoplanetary disk. The gravitational influence of the planet onto the ambient disk leads to such features as spiral arms and, for planets sufficiently massive, an annular gap at the planetary radius. The back-reaction of the perturbed disk onto the planet generates torques, which induce a change of the orbital elements (semi-major axis and eccentricity) of the planet. The linear phase for small planetary masses has been studied for two-dimensional flat disks by Goldreich & Tremaine (1980) and Ward (1997), and more recently in three dimensions by Tanaka et al. (2002). Analytical formulae for the (inward) radial migration rate have been obtained. These linear (local) analyses have been supplemented by a variety of numerical simulations that also consider the global disk and larger planetary masses. Two-dimensional flat disks with planets were modeled by Bryden et al. (1999); Kley (1999) and Lubow et al. (1999) applying a locally isothermal assumption for the radial temperature distribution. Later, global three-dimensional simulations of embedded planets were performed on equidistant grids (Kley et al. 2001), with nested grids (D'Angelo et al. 2003b) and by applying local grid refinement (Bate et al. 2003). They confirmed the linear results for very small planets as well as the estimates for gap opening large planets. In these simulations the planet is held on a fixed circular orbit and the mass accretion and migration rate are estimated from the obtained density distribution. Simulations with a moving single planet (Nelson et al. 2000) are again in agreement with the inward migration scenario.

These hydrodynamical simulations have been extended recently to full 3D-MHD calculations though neglecting vertical gravity (Winters et al. 2003; Papaloizou & Nelson 2003; Nelson & Papaloizou 2003). Here, the turbulent state of the disk is modeled directly, and the migration rate is found to fluctuate strongly around a mean value.

All the above mentioned simulations treat the disk as isothermal locally, although polytropic disks have been considered in Kley (1999). Recently, D'Angelo et al. (2003a) added thermodynamical effects in a two-dimensional model. They assume that the dissipation produced in the disk (by viscosity) is radiated locally, while the equation of state includes dissociation and ionization effects. Using this method in addition to nested grid refinement around the planet it also has been possible for the first time to obtain an estimate of the two-dimensional temperature structure in the disk's midplane in the vicinity of the planet. However, these simulations still suffer from their two-dimensionality.

In the present paper we extend the radiation hydrodynamical planet-disk calculations to three dimensions, by applying a flux-limited diffusion approximation for the radiation. This allows us to study directly the dynamical influence of the planetary accretion luminosity and to determine the three-dimensional temperature structure in the vicinity the planet.

Here, we focus on numerical issues, and study the effects of the radiation transport, of resolution and mass accretion. By introducing radiation and opacities the model is no longer scale-free, as it is in the isothermal case. Hence, there is a difference, whether the planet is located at 5 AU or 0.5 AU, say. In addition to influencing the gravitational torques acting on the planet, the disk mass now has an effect on the temperature structure as well, because it provides the optical depth.

We find that for the test parameters (1 Jupiter mass at 5 AU) and the low numerical resolution that we apply, there is no significant acceleration or breaking of the mean radial drift in comparison to the isothermal approximation. However, the fluctuations in the radial drift appear an order of magnitude larger in the radiative models with realistic accretion than in the isothermal models.

We find the circumplanetary "accretion disk'' to be rather thick, i.e. the pressure scale height is $H/R \approx 0.5$ in our models, which is even thicker than the results from 2D simulations (D'Angelo et al. 2003a). The deviation from a Keplerian profile in this "disk'' is about $50\%$, which also indicates the strong support from the thermal pressure. Under such conditions the thin disk approximation breaks down and one has to deal with a circumplanetary cloud filling a sizable fraction of the Roche lobe rather than a disk.

The detailed modeling of the observational appearance of a planet interacting with a disk and a detailed parameter study are left to follow up studies.

In the next section we describe our model setup, the boundary and initial conditions. In Sect. 3 we present an analysis of our models, and we conclude in Sect. 4.

2 Model characterization

We consider a Jupiter sized protoplanet embedded in a protoplanetary disk in three dimensions, where we use a spherical polar coordinate system ( $r, \theta, \varphi$). The central star lies at the origin of the coordinate system and the disk midplane coincides with the $\theta=0$ plane. We work in a coordinate frame corotating with the planet, and use a special formulation avoiding explicit source terms to conserve angular momentum locally and globally, see Kley (1998).

2.1 Physical setup

All models we consider in this paper have a radial extent from 1.25 AU to 20 AU, where a Jupiter mass planet is located at 5 AU. The vertical extent is from $-10^{\circ}$ below the midplane to $+10^{\circ}$ above the midplane of the disk. In the azimuthal $\varphi$-direction we consider a complete annulus from 0 to $2\pi$. The initial temperature distribution is proportional to r-1and "vertically'' (i.e. in the polar direction) constant. This temperature is chosen to reproduce a local pressure scale height H/r = 0.05 for all radii. The actual vertical extent of the computational domain is then approximately ${\pm}3.5 \times H/r$. The initial density distribution is radially proportional to r-1.5 with a midplane density at 5 AU of $\rho({\rm 5~ AU},~\theta = 0) = 10^{-11}$ g cm-3. This corresponds approximately to a local surface density $\Sigma = 2 H \rho = 75~[{\rm g~ cm}^{-2}]$ at 5 AU, i.e. the location of the planet. This is similar to the value used by Bryden et al. (1999); Kley (1999); Lubow et al. (1999).

Due to the assumed local vertical isothermal disk as initial setup, the vertical density structure is given to first order by a Gaussian:

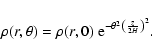\begin{displaymath}\rho(r,\theta)= \rho(r,0) ~ {\rm e}^{- \theta^2\left(\frac{z}{2H} \right)^{2}}. \end{displaymath} (1)

The vertical $v_\theta$ and radial $v_{\rm r}$ velocities vanish initially. The initial azimuthal velocity is given by the equilibrium of gravity, centrifugal acceleration and the radial pressure gradient. This is not an exact solution because the Gaussian density distribution is only valid in the thin disk approximation. Thus, as we resolve the disk out to $\pm 10^{\circ}$ a small discrepancy appears. Nevertheless, the model is only slightly out of equilibrium and will relax quickly into a more stable state, which deviates only marginally from the initial state.

In the models we do not use any explicit physical disk viscosity and model the ideal hydrodynamical equations. However, we use an artificial bulk viscosity in the form of von Neumann & Richtmyer (1950), see Stone & Norman (1992). Applying an explicit viscosity, e.g. $\alpha$-viscosity would have introduced one further free parameter, which we seek to avoid. Although MHD turbulence is a good candidate to produce an $\alpha$-like viscosity (Shakura & Sunyaev 1973), it is not obvious that $\alpha$ would be a constant in time and space (see e.g. Wünsch et al. 2005). It is also unclear in how far the magneto-rotational instability would operate in the gap region and in the circumplanetary bubble.

A second reason for not using an explicit viscosity is that it would have led to additional heating on top of the adiabatic contraction of the circumplanetary bubble, thus making it more difficult to identify the importance of the heating by the accretion onto the planet.

2.2 Gravitational potential

The Roche lobe around the planet determines the region where mass is gravitationally bound to the planet. The Roche lobe is pear-shaped with a sharp edge at the side towards the star and thus is usually approximated by the Hill sphere. This sphere is centered at the location of the planet and completely includes the Roche lobe. We will usually refer to the Roche lobe and its approximate size given by the Hill radius.

To calculate the potential due to a planet of mass $M_{\rm p}$ at the radius $r_{\rm p}$ in the midplane of the accretion disk, we determine the radius $a_{\rm h}$ of the Hill sphere around the planet, which is a function of the reduced mass $\mu = \frac{M_{\rm p}}{M_\odot + M_{\rm p}}$ of the system

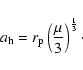\begin{displaymath}a_{\rm h} = r_{\rm p} \left(\frac{\mu}{3}\right)^{\frac{1}{3}}\cdot \end{displaymath} (2)

For distances from the planet larger than a critical fraction $q_{\rm g}$ of the Hill radius $a_{\rm h}$ we use the exact gravitational potential $\Phi$ as the sum of stellar $\Phi_\odot$ and planetary $\Phi_{\rm p}$ potential

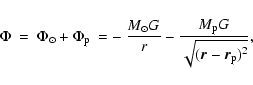\begin{displaymath}\Phi ~ = ~ \Phi_\odot + \Phi_{\rm p} ~ = - ~ \frac{M_\odot G}{r} - \frac{M_{\rm p} G}{\sqrt{({\vec r}-{\vec r}_{\rm p})^2}}, \end{displaymath} (3)

where ${\vec r}$ is the radius vector pointing from the star to a specific location in the disk. For closer distances we use a cubic expansion which is 2${\rm nd }$ order accurate at a critical distance $a_{\rm g} = q_{\rm g} ~ a_{\rm h}$ (i.e. it agrees with the outer potential in its 1${\rm st}$ and 2${\rm nd }$ derivative) and then becomes shallower towards the center with a vanishing gradient at the planet location:

\begin{displaymath}\Phi_{\rm p}^* = - M_{\rm p} G \left[\frac{\left(r-r_{\rm p... ...m p}\right)^2}{a_{\rm g}^3} + \frac{2}{a_{\rm g}} \right]\cdot \end{displaymath} (4)

The benefit of such a treatment for the smoothing is that the potential is accurate down to the critical distance, whereas using the more classical approach

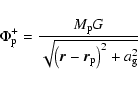\begin{displaymath}\Phi_{\rm p}^+ = \frac{M_{\rm p} G}{\sqrt{\left({\vec r}-{\vec r}_{\rm p}\right)^2+a^2_{\rm g}}} \end{displaymath} (5)

leads to a significant underestimation of the potential depth already at $a_{\rm g}$.

In our models we test the influence the parameter $q_{\rm g}$ has on the mass of gas that accumulates in the Roche lobe of the planet.

2.3 Accretion

Accretion is treated as in Kley (1999), where a certain fraction of mass is taken out per time step within a given accretion radius $a_{\rm acc} = q_{\rm acc} a_{\rm h}$ around the planet. Here, we take this fraction $q_{\rm acc}$ of the Hill radius as a free parameter and study its influence on the gas density and temperature in the vicinity of the planet. We believe that our models that treat accretion and conserve the total energy (DR and DR4) have the highest relevance for the temperature structure of the circumplanetary cloud. These models yield a lower estimate for the temperatures, because using a deeper potential might still increase the temperatures. We also measure the mass contained in the Roche lobe and the mass change in the Roche lobe per time unit, which is a good tool to show that the planet is accreting at a steady rate and that the system is in equilibrium, i.e. no mass is piling up in the Roche lobe any longer.

2.4 Numerical scheme

We use the TRAMP hydro code as described in Klahr et al. (1999). TRAMP is a versatile 3D radiation hydro package that can use various advection schemes. For the purpose of this paper we apply a monotonic transport scheme (van Leer 1977). The radiation transport in TRAMP is treated in the flux-limited diffusion approximation using the flux limiters of Levermore & Pomraning (1981), see also Kley (1989), and dust opacities typical for the solar nebula (Bell & Lin 1994). The scheme to treat internal energy and radiation energy density is as in Kley & Lin (1996). Adding the equations for internal and radiation energy and assuming that the latter is much smaller than the internal energy, which is certainly a very good approximation for protostellar disks we arrive at the following evolution equation for the internal energy

 \begin{displaymath} \partial_t e + \nabla \cdot \left({\vec u} e \right) = - p \nabla \cdot {\vec u} + \Phi - \nabla \cdot {\vec F} \end{displaymath} (6)

where ${\vec u}$ is the velocity vector, p the thermal pressure, $\Phi$is the dissipation by viscosity. Here we use only artificial viscosity in shocks to achieve the proper entropy generation but no explicit physical viscosity in the smooth flow. Nevertheless, tensor viscosity is fully implemented in TRAMP and we can use it in future simulations of gap opening. For this paper containing test simulations we avoid the additional effects of viscous heating in order to study more carefully the accretional heating in the vicinity of the planet.

Table 1: Parameters chosen in the different simulations and their results. These parameters are the dimensioning of the grid ( $n_r, n_\vartheta ,n_\varphi $), the kind of spacing (lc = logarithmically centered around the planet), the thermodynamics (iso = locally isothermal, rad = ideal gas plus radiation transport, rad+ = ideal gas, radiation transport and conservation of total energy for gas accreted onto planet), the gravitational smoothing radius ($q_{\rm g}$ = fraction of the Hill radius over that smoothing is applied), the accretion radius ( $q_{\rm acc}$ = fraction of the Roche lobe (respectively Hill radius) that mass is taken out of), the type of the initial model (G: starting with an existing gap), and the total number of orbits calculated ( $t_{\rm int}$). The results we give are the accretion rate onto the Planet ($\dot M$) in units of Jupiter masses per orbit, the mass contained in the Roche lobe ( $M_{\rm Roche}$), the maximum density and temperature in the Roche lobe ( $\rho _{\rm max}, T_{\rm max}$) and the migration time-scale that we determined ( $\tau _{\rm mig}$).

The radiation flux ${\vec F}$ is calculated in flux-limited diffusion approximation

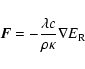\begin{displaymath}{\vec F} = - \frac{\lambda c}{\rho \kappa} \nabla E_{\rm R} \end{displaymath} (7)

with the Rosseland mean opacity $\kappa$ and the speed of light c. The flux limiter $\lambda$ is defined according to Levermore & Pomraning (1981). Here we assume local thermal equilibrium and set

 \begin{displaymath} E_{\rm R} = a T^4 . \end{displaymath} (8)

Numerically, the radiative diffusion part is solved separately as part of an operator splitting technique. The diffusion equation for $E_{\rm R}$

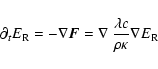\begin{displaymath}\partial_t E_{\rm R} = - \nabla {\vec F} = \nabla ~ \frac{\lambda c}{\rho \kappa} \nabla E_{\rm R} \end{displaymath} (9)

is solved implicitly to avoid time step limitations using e.g. the standard SOR (successive over-relaxation) scheme. The new temperature is then calculated from Eq. (8).

The code has been extensively tested in the context of accretion disks (Klahr et al. 1999). The new part that is implemented to the code is the inclusion and modification of the gravitational potential of the planet as described above.

2.5 Boundary conditions

The boundary conditions are chosen to minimize the effects of wave reflections at the boundaries. In the polar and radial direction these are outflow conditions not allowing for inflow. Thus, for pressure, density and orthogonal velocities, we apply a zero gradient condition, while the normal velocity components have a vanishing gradient only if the direction of the flow is outward of the computational domain. For inward directed flow the normal velocities components are set to zero. For the angular velocity we assume a Keplerian flow. No sponge layer as in Klahr & Bodenheimer (2003) is used. In the azimuthal direction we apply periodic boundary conditions.

  
3 The models

The purpose of all the different models using the same physical parameters, i.e. stellar, planetary and disk mass as well as planet location, is to study the influence of the numerical treatment of the problem and to find the numerical parameters suited to study the gap opening as realistically as possible.

In Table 1 we give an overview of all the models we compare in the following. The second column (grid) states the numerical resolution ( $n_r, n_\vartheta ,n_\varphi $) of the grid. There are low resolution (100$\times$20$\times$200) models with a logarithmic radial spacing and equidistant in the azimuthal and vertical direction. We also calculated some high resolution models, where the grid is in all dimensions logarithmically concentrated (indicated by lc) towards the location of the planet, which results in a resolution in the Roche lobe up to four times higher than in the low resolution case. In these models there are about 2400 grid points within the Roche lobe. We tested the influence of the logarithmically distorted high resolution grid on a disk without a perturbing planet. Despite the grid refinement around the planet and quite distorted grid cells towards the edges of the grid, there are no unstable growing modes.

Some models are calculated in the standard locally isothermal approximation (EOS = iso), some treat the internal energy equation plus flux-limited radiation transport (EOS = rad). We also state the parameters for the smoothing of the gravitational potential $q_{\rm g}$ and for the mass accretion onto the planet $q_{\rm acc}$. Some models start with no gap initially, others use an axisymmetric initial model with a gap (ini = G).

After briefly mentioning a test model for the non-equidistant high resolution grid, we will go through our models in the following order: first isothermal models, then radiative models, followed by non-accreting models, and finally accreting and energy conserving models.

3.1 Isothermal models

3.1.1 The axisymmetric model CI

This model uses only one grid-cell in the azimuthal direction but it includes the full potential of the planet, and mass is taken out of the grid from the center of the Roche lobe. It is used to run a model quickly into an initial state with a gap, which forms here not due to the gravitational torques by the planet but rather by the perturbation in gravity as it would result from a massive ring. However, as we shall see the obtained gap size and shape are in reasonable agreement with the realistic 3D case.

In Fig. 1 we introduce the kind of plot that we will subsequently use for some of the following models. It shows quantities measured in the midplane at the azimuthal position of the planet. Thus, it is one-dimensional data. We plot 10 snapshots, which are taken at equal time intervals, e.g. in the case of Fig. 1 every 26 orbits from t=60 to t=320 orbits. First we plot the density $\rho$. One clearly sees how the gap forms and how stable it is. Most of the disk is still at the initial values, which are given by the dashed line. The next plot shows the azimuthally averaged surface density $\Sigma$. This value is slightly higher than $75~[{\rm g}~{\rm cm}^{-2}]$ at 5 AU, because here we integrate over the total height of the computational domain and not only over $\pm H$. The temperature T in the third plot does not fluctuate as this run is isothermal.


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{3238fig1.ps} \end{figure} Figure 1: Model CI: snapshots taken every 26 orbits from t=60 to t=320 orbits, which is after the convergence of model CI. The radial slices of the density, temperature and azimuthal velocity are taken in the midplane at the location of the planet. Model CI defines the initial values for all the models that start off with an axisymmetric gap.
Open with DEXTER

The deviation of the local azimuthal velocity ( $v_\phi/v_{\rm K}$) from the Keplerian value is significant only in the vicinity of the "planet''. The shape of the rotational profile is determined by the gradient in the surface density and thus has no physical relevance for the real gap case where the gravitational torques are determining the shape of the gap. We also have to mention that this artificial gap structure is not unique, but there is a family of solutions, where either the surface density profile or the azimuthal velocity profile is a free parameter. Still this method generates a gap structure that is not too unrealistic to serve as an initial model for our simulations.

The stationary state of model CI is given by the balance of centrifugal forces, radial pressure gradients and the attraction of the combined stellar and ring potential, is used as the initial setup in all of the subsequent models that include a C in their names (see Table 1). Models without a C are started from the same initial condition as model CI is started, which is a disk without a gap.

3.1.2 Model CDI
This is the standard isothermal three-dimensional model. Mass is taken out of the Roche lobe. Thus, the model is directly comparable to the ones in Kley et al. (2001). The radial midplane profiles (see Fig. 2) are measured at equal times between 164 and 184 orbits. The profile only changes very slowly. In the inner part of the disk one recognizes a decrease in density, which is related to two effects: first, the accretion process triggered by the tidal forces of the planet, which "drives'' the material through the inner boundary simulating accretion onto the star. This is possible because we use non-reflecting boundary conditions at the radial boundaries, which allow for outflow but not for inflow. As an effect also the most outer grid cells loose a lot of mass, which shows at most in the high resolution models, e.g. model CD4I.


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{3238fig2.ps} \end{figure} Figure 2: Model CDI: snapshots taken every 2 orbits from t=164 to t=184 orbits. The radial slices of the density are taken in the midplane at the location of the planet. The surface density is azimuthally averaged.
Open with DEXTER

The second reason for the mass depletion is the accretion process onto the planet, which occurs from both sides, from the inner as well as from the outer part of the disk. But the mass reservoir in the outer part of the disk is much larger, thus the decrease in mass is not visible over the span of the simulation. In comparison to the simulations by Bryden et al. (1999), Kley (1999), and Lubow et al. (1999) the gap in the surface density is shallower. Those simulations used explicit tensor viscosity and started already with a wider gap than we used. So in our case it will take many hundreds of orbits before the gap will reach a comparable depth. In terms of computational time such a run would take several months of computation time on our fastest available workstations. The code in its present version is not parallelized, due to the implicit solver of the radiation part. In the future we will consider runs with a much longer evolution time.


  \begin{figure} \par\includegraphics[width=8.2cm,clip]{3238fig3.ps} \end{figure} Figure 3: Model CDI: ( upper row) accreted mass $m_{\rm a}$ and accretion rate onto the planet $\dot m_{\rm a}$ over time; ( lower row) evolution of the mass contained in the Roche lobe $m_{\rm Ro}$ and mass change in the Roche lobe $\dot m_{\rm Ro}$ in units of Jupiter masses and orbital periods of the planet.
Open with DEXTER

Plotting the mass accreted onto the planet and the mass accumulated in the Roche lobe (see Fig. 3) also shows that we are only slowly approaching a steady state of the solution. There is a mass of $2.2\times10^{-5}$ Jupiter masses in the Roche lobe and the accretion rate, i.e. the mass taken off the grid, is $1.5\times10^{-4}$ Jupiter masses per orbit. The time that mass resides in the Roche lobe in this model is only about a tenth of an orbital period. The non-zero accretion rate is interesting because we include no viscosity in our model. One might expect that planets opening a gap in an inviscid disk could not accrete any more mass. There is the possibility that the planet-disk torques together with the induced Reynolds stresses provide enough angular momentum transport to feed the planet via the circumplanetary accretion disk. Nevertheless, to clarify this issue of the accretion rate onto the planet the simulations will have to be continued for many more orbits at high resolution. It may still be possible that accretion will stop after a thousand orbits, which is the case in non-viscous 2D simulations of gap opening.

We also calculate the gravitational torques acting on the planet and translate them into the typical radial migration time (Kley et al. 2001). We measure the torques in three ways: excluding the mass contained in the inner half Hill radius of the Roche lobe (in the following the dashed curves), excluding all the Roche lobe (solid curves) and excluding 1.5 times the Hill radius (dotted curves). Bate et al. (2003) have used this method to give error bars to the measurements of the torques from the numerical simulations. This procedure is also very useful to study the relative importance of the torques generated from gas close to the planet. In Fig. 4 we see that the torques vary over time but the mean drift rate corresponds to the 105 yrs observed in other simulations and which fit the results from linear theory (Ward 1997; Tanaka et al. 2002; Goldreich & Tremaine 1980). It is remarkable how close the three measurements of the torques are at each time. This is a consequence of the fact that we take the mass out of a significant part of the Roche lobe producing a very clean gap. There is not enough matter left, to exert a torque on the planet. This changes in the models that do not treat mass accretion onto the planet ( $q_{\rm acc}=0.0$) or remove gas from a smaller part of the Roche lobe ( $q_{\rm acc}=0.2$).

3.1.3 Model CD4I


  \begin{figure} \par\includegraphics[width=8cm,clip]{3238fig4.ps} \end{figure} Figure 4: Model CDI: evolution of planet migration rate in terms of migration time. The solid curve is based on the torques excluding the Roche lobe and the solid horizontal line is the time average. In addition we plot the torques based on an exclusion of 1.5 and 0.5 Hill radii (dotted and dashed lines respectively). In this particular model the gap is very clean, such that all three torques mostly coincide.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{3238fig5.ps} \end{figure} Figure 5: Model CD4I: snapshots taken each orbit from t=71 to t=81 orbits. The radial slices of the density are taken in the midplane at the location of the planet. The surface density is azimuthally averaged. The dotted line indicates the values for model CDI for comparison.
Open with DEXTER

We also have performed simulations with the same parameters as for model CDI but with a higher resolution due to logarithmic concentration of grid cells around the planet. Now the gravitational smoothing length is set to a value of only 20% of the Hill radius ( $q_{\rm g} = 0.2$), and the accretion radius to the same small region ( $q_{\rm acc}=0.2$). The radial slices (all orbits from t=71 to t=81 orbits) through the planet (see Fig. 5) show that more mass has accumulated in the Roche lobe than in model CDI (the values from model CDI are given by the dotted line). This result can be expected because of the deeper gravitational potential of the planet; the increase of density towards the planet is clearly visible. The inner disk is less depleted than in model CDI, but this indicates the earlier evolutionary step (81 orbits for model CD4I vs. 184 orbits for model CDI). This model apparently loses more mass at the outer boundary, but this is mainly due to the very coarse grid in combination with the open boundary conditions there.

Nevertheless, the overall structure of the gap has not changed substantially. This model takes about 5 times more computational time than the low resolution case. This is mainly due to the fine resolution in the azimuthal direction, i.e. the Courant condition for the azimuthal velocity component. Table 1 shows that there is a little more mass accumulating in the Roche lobe (which was empty initially) than in the low resolution case. The torques are now strongly fluctuating while the average values are very similar to those of model CDI (see Table 1). The fluctuations are so strong that they even change their sign. Again the time averaged torques are insensitive to the radius around the planet, which has been excluded from the calculation of the torque. We suspect that the oscillations might be an effect of the high density concentration near the planet (see Fig. 5), because small density asymmetries induce large torque variation. Similar findings have been obtained for nested grid simulations by D'Angelo et al. (2002).

In future work we will return to mesh refinement around the planet to study these effects in more detail.

3.2 Radiative models

3.2.1 Model CD


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{3238fig6.ps} \end{figure} Figure 6: Model CD4: snapshot at t=5 orbits after the refinement of the grid. Radial slices of density and temperature are taken in the midplane at the location of the planet, while surface density is the azimuthal average. (solid line = Model CD4; dotted line = Model CD; dashed line = Model CDS).
Open with DEXTER

The isothermal approach used in the previous models is a strong simplification of the thermodynamics of the disk near the planet and may not be well suited for studying the gap opening problem. For the radiative model CD we keep all parameters identical to model CDI, but use the equation for internal energy including flux-limited radiation transport, see Eq. (6). Again, mass is removed from within the Roche lobe, which means that energy is taken out without releasing its accretion energy (this will be treated differently in models DR and DR4). The temperature and density structure of this model are displayed together with other models in Fig. 6 with dotted lines. In contrast to model CDI the disk has cooled dramatically because there is no internal heating in our inviscid model, while the region around the planet has become slightly hotter than in the isothermal gap case (Fig. 6). The rest of the gap is much cooler. There is also three times more mass piling up in the Roche lobe than in Model CDI (see also Table 1). This is a direct consequence of the radiative cooling. If the matter within the Roche lobe cools down it will contract leading to a higher density. The mass accretion rate onto the planet is roughly three to four times larger than for the corresponding isothermal model. Thus, there is more mass stored in the Roche lobe, which also influences the torque (see Fig. 7). While the overall average migration time is only 10% less than in model CDI, there are now variations between the torques measured by excluding more or less mass from the Roche lobe. Excluding either the entire Roche lobe or even 1.5 times the Hill radius gives very similar results, while excluding only 0.5 of the Hill radius doubles the amplitude of the fluctuations.


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{3238fig7.ps} \end{figure} Figure 7: Model CD: evolution of the planet migration rate in terms of migration time. The solid curve is based on the torques excluding the Roche lobe and the solid horizontal line is the time average. In addition we plot the torques based on an exclusion of 0.5 Hill radii (dotted lines) and 1.5 Hill radii (dashed lines). The horizontal lines refer to the time averaged values.
Open with DEXTER

This is the first hint that radiative cooling changes the structure of matter in the Roche lobe and consequently the resulting torques on the planet.

3.2.2 Model CDS
The following model is identical to the previous one but this time mass is taken out of only 20% of the Hill radius. Thus we can study the effect of the arbitrary size of this mass removal zone. As a result more mass accumulates in the Roche lobe close to the planet and the temperature around the planet is even higher (Fig. 6 dashed line). Nevertheless, the model is already strongly limited by resolution as 20% of the Hill radius means only two grid cells.

The accretion rate is also close to the one in model CD. The average torques are still the same as in the isothermal case, model CDI. It also shows that the migration times are the longest if one excludes only half the Hill radius. This indicates the importance of the proper treatment of mass in the Roche lobe and its potential capability of altering the radial drift rate. This model is also used for comparison to model CD4 and CD in Fig. 6.

3.2.3 Model CD4

Here, we increase the resolution and decrease the gravitational smoothing again to 20% of the Hill radius (cf. model CD4I). The radius out of which mass may be taken is decreased in the same fashion. Otherwise this model (see Fig. 6) is identical to models CD (dotted line) and CDS (dashed line).

The most striking effect of the higher resolution is the higher temperature at the planet's location. Temperatures three times higher than in model CD are reached.

This can be explained by two effects which are: 1. a deeper potential well leading to stronger compression and release of accretion energy; 2. the much higher densities near the planet leading to higher optical depth and lower cooling rates.

Again the accretion rate is similar to model CD and the average torques are also not very different (see Table 1).

3.3 Non-accreting models

In all of the previous models mass has been taken out from the grid in the vicinity of the planet. In the isothermal models this might be a tolerable simplification as the average torques are not different between the high and low resolution cases.

However, in the models with radiation transport one introduces a large error if one simply takes mass off the grid: internal energy is removed from the simulation along with the mass, but the accretion energy released during final accretion phase onto the planet is neglected. One can now either construct a model for this process and re-adjust the energy content of the gas after some mass has been taken away (see Models DR and DR4) or simply refrain from accreting mass and study the effects of the mass piling up. The first approach has one more free parameter than the second, which is the relative accretion rate (i.e. the fraction of the mass removed from the grid per orbit).

We will first study more closely the effect of taking mass arbitrarily from the grid. Therefore, we go back to the isothermal model CDI but do not remove any mass this time.

3.3.1 Model CDNI

In comparison to model CDI the lack of accretion leads to a slightly higher concentration of mass around the planet, similar to the models with a deeper potential (see Table 1). The mass in the Roche lobe is now three times greater than in model CDI.

The major effect of not taking mass off the grid and letting it pile up in the Roche lobe is the introduction of strong fluctuations in the migration rate. The torques calculated including half of the Hill radius especially showed large fluctuations. Nevertheless, the time averaged migration rate is still dominated by the structures outside the Roche lobe and thus are of the same magnitude as in all the previous models (see Table 1).


  \begin{figure} \par {\includegraphics[width=17cm]{3238fig8C.ps} }% % \end{figure} Figure 8: Model DR4: early stage of gap opening. Temperature in the $r-\theta $ plane of the protoplanetary disk at the azimuthal location of the planet. This snapshot is taken after 12 orbits, thus the gap is not completely empty yet. In this early phase the heating by the accretion onto the planet drives a strong convectional flow in the still optically thick disk material above the planet. Brightness is logarithmic temperature (lighter = warmer) ranging from 38 K to 1060 K and vectors give the logarithmic mass flux. We also plot iso-density lines with labels giving values in g cm-3. Density ranges from 1015 g cm-3 up to $1.3 \times 10^{10}$ g cm-3. See the online edition for a color version of this plot.
Open with DEXTER

3.3.2 Model CDN and CDN4

In these models we start with a gap, do not remove any mass and perform the full radiation step. Models starting with a gap eventually converge to models without an initial gap. This convergence can be demonstrated for the low resolution models (see Table 1), while the high resolution models are too expensive in computational effort to show this in a reasonable computation time. The general trend can be seen in Table 1. Density and temperature increase with the resolution of the Roche lobe while the torques are not much different in the high and low resolution cases.

3.3.3 Model DN and DN4
Instead of beginning with an artificial gap and then slowly filling the Roche lobe to accumulate mass around the planet, we start here with an unperturbed axisymmetric disk without a gap. The main result is that now a pressure supported atmosphere builds up around the planet, which becomes very hot. Both models become stationary and we observe maximum temperatures of about 600 K for model DN and 1150 K for the high resolution case DN4 (see Table 1). The radial profiles for these models along with the models DR and DR4 are displayed in Fig. 9. We remove no mass from the grid but treat the full radiative dynamics. The fact that the temperature is constant can be interpreted with a self regulated accretion process into the Roche lobe. The mass accretion rate balances the contraction of the cooling planetary envelope and this contraction releases potential energy in the planetary gravitational field. Thus we have a balance between mass flux and radiation flux over the surface of the Roche lobe. The equilibrium between cooling and accretion now yields a temperature that only depends on the depth of the potential well. This leads us to assume that the temperatures will be even higher if we can avoid the artificial smoothing of the potential well. This is partly tested by model DN4 with higher resolution and a smaller smoothing parameter (see Table 1). Interestingly there is also a good agreement in temperature structure with the models that conserve total energy during accretion (see Fig. 9).


  \begin{figure} \par\includegraphics[width=7.2cm,clip]{3238fig9.ps} \end{figure} Figure 9: Model DR: snapshot taken after t=121 orbits (solid line). Model DR4: after t=141 orbits (dotted line). Model DN: after t=121 orbits (dashed line). Model DN4: snapshot taken after t=55 orbits (dash dotted line). Radial slices of density and temperature are taken in the midplane at the location of the planet, while surface density is the azimuthal average.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{3238fig10.ps} \end{figure} Figure 10: Model DR: ( upper row) accreted mass $m_{\rm a}$ and accretion rate  $\dot m_{\rm a}$onto the planet over time; ( lower row) evolution of the mass contained in the Roche lobe $m_{\rm Ro}$ and mass change in the Roche lobe  $\dot m_{\rm Ro}$ in units of Jupiter masses and orbital periods of the planet.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{3238fig11.ps} \end{figure} Figure 11: Model DR: evolution of planet migration rate in terms of migration time. The solid curve is based on the torques excluding the Roche lobe and the solid horizontal line is the time average. In addition we plot the torques based on an exclusion of 0.5 Hill radii (dotted lines) and 1.5 Hill radii (dashed lines), plus the time averaged values.
Open with DEXTER

3.4 Accreting and energy conserving models

3.4.1 Model DR and DR4
This model is similar to model CD in the sense that we accrete mass from the Roche lobe. But this time it is started without a gap and we conserve the total energy locally in the grid cells where the gas is removed from the grid. Hence, the kinetic energy and the potential energy that can be released when the gas is accreted onto the planet are added locally to the internal energy. The radius of such a young planet probably will be about two times the current size of Jupiter (Bodenheimer, private communication).

First we show the flow situation in model DR4 after 12 orbits past the initial set up. The gap has not cleared completely and the heating by accretion onto the planet drives strong vertical convection in the optically thick disk material above the planet (see Fig. 8). This "fountain'' flow is subsonic and will not escape from the disk because the velocity is too low in comparison to the escape velocity. Nevertheless, the effect might be very important for observations because even embedded planets still too small to open a gap will probably produce this effect, which shows as an extended bubble of hot gas to the planet thus raising the local pressure scale height in the disk.

Model DR approaches a quasi steady state after 100 orbits (see Fig. 9), which can also be inferred from the almost constant Roche lobe mass of $5\times 10^{-4}~ M_{\rm Jup}$ and the accretion rate onto the planet of $6\times 10^{-4}~ M_{\rm Jup}$ per orbit (see Fig. 10). Nevertheless, there are also short time scale fluctuations in the Roche lobe mass, which again show up in the fluctuations of the torques (see Fig. 11). Based on non-viscous 2D runs we know that it will take up to a thousand orbits before the gap is so deep that no accretion onto the planet occurs any longer. In 3D with radiation transport we presently cannot afford such long runs. The resulting maximal temperature in the Roche lobe is 800 K for model DR and 1500 K for model DR4. A finer grid resolution might even lead to higher temperatures.


  \begin{figure} \par {\includegraphics[width=8.2cm]{VERSION_COULEUR/fig12.EPS.eps} }\end{figure} Figure 12: Model DR: density in the midplane of the protoplanetary disk after 121 orbits. Dark means low, light means high density. The density ranges from $2.4 \times 10^{-13}~{\rm g}~{\rm cm}^{-3}$ to $8.3 \times 10^{-11}~{\rm g}~{\rm cm}^{-3}$. See the online edition for a color version of this plot.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.2cm]{VERSION_COULEUR/fig13.EPS.eps} \end{figure} Figure 13: Model DR: temperature in the midplane of the protoplanetary disk after 121 orbits. Brightness corresponds to the logarithm of temperature. Black indicates 10 K and white 800 K. See the online edition for a color version of this plot.
Open with DEXTER


  \begin{figure} \par {\includegraphics[width=6.5cm,clip]{3238fig14.ps} }\end{figure} Figure 14: Model DR4: pressure scale height in the midplane of the circumplanetary cloud after 141 orbits. Radial location is given in units of Hill radii.
Open with DEXTER

For model DR we also display the density structure that results in the midplane (see Fig. 12) after 122 orbits. The gap has clearly formed but still mass is left in the horseshoe orbit. This mass will decrease gradually over time. The density structure does not change significantly from any isothermal simulation, but the temperature of course does (see Fig. 13). The planet is the hottest spot in the simulation. We adopted a grey approximation for the radiation transport, thus continuum (wavelength dependent) radiation transport simulations (using our temperature and density structure) will show whether this hot circumplanetary gas-dust mixture will be observable. The extent of the warm gas around the planet as well as the two mass feeding streams of warm gas hitting the circumplanetary cloud are clearly visible now. We do not resolve any circumplanetary accretion disk yet, for two reasons: first our resolution is too low and second the pressure dominates the hot gas around the planet strongly enough so that no Keplerian disk forms, and one is left with a pressure-supported planetary envelope filling most of the Roche lobe.

In Fig. 14 we display the pressure scale height of the gas in the midplane around the planet. In the circumplanetary "disk'' $H_{\rm p}/R_{\rm p}$ is the inverse Mach number $1/M = c_{\rm s} / v_k$ of the flow around the planet. Due to the high temperatures the relative vertical thickness is about 0.5, which is larger than those values typically used in thin Keplerian accretion disks with H/R < 0.1. In the case of $H_{\rm p}/R_{\rm p} = 0.5$ this structure is better described by a rotating envelope which additionally shows strong deviations from a Keplerian rotation law of about $50\%$.

For model DR4 we display some details of the flow onto the planet (see Fig. 15). We plot the temperature in the $r-\theta $ plane of the protoplanetary disk at the azimuthal location of the planet. The temperature is hottest around the planet and the gas in the gap is also heated by the accretion luminosity of the planet. The flow indicates that accretion mainly occurs via the poles of the planet and that there is convection in the envelope around the planet. We can see no inflow along the equatorial plane. The mass falling onto the central region around the planet originates only in part from the gap material above the planet. The largest contribution in mass is via the convective flow in the upper part of the circumplanetary cloud.

This simulation also suggests that at least at this stage of gap opening and planet disk interaction there is no formation of moons from the circumplanetary material possible. The reason is simple: with $H_{\rm p}/R_{\rm p} = 0.5$and the resulting strongly sub-Keplerian rotation, all solid material will quickly rain down onto the planet. The maximum radial drift velocity is given by the difference between the actual azimuthal velocity and and the Keplerian value (Weidenschilling 1977). Thus before solid material has orbited the planet once, it will fall onto the planet. The fastest drifting solids are given by unity in the parameter $\Omega_{\rm p} \tau_{\rm f} =1$, with $\Omega_{\rm p}$ the Keplerian frequency and $\tau_{\rm f}$ the friction time of the solid body. For the physical conditions in our model DR4 (e.g. density and temperature) the fastest drifting objects would be 1 m sized boulders, which drift into Jupiter in about a month if released at 0.1 Roche radii. Thus the drift problem for the formation of moons from circumplanetary material is even more crucial than in the case of planet formation. We conclude that at least for the time when Jupiter is accreting its mass there can be no formation of a satellite system.

4 Conclusions

We have performed full 3D radiation hydrodynamical simulations of embedded protoplanets in disks, and compare the results in detail to the standard isothermal approach.

Mean torques and migration rates are not strongly affected by the treatment of the thermodynamics in the case of Jupiter mass planets. This might change for lower mass planets, which are more embedded in the disk. The fluctuations of the torques on the other hand are much stronger, in particular in higher resolution cases. Similar effects have been observed in high resolution nested grid simulations (D'Angelo et al. 2003b,2002) and also MHD simulations of planet-disk interactions (Winters et al. 2003; Papaloizou & Nelson 2003; Nelson & Papaloizou 2003). In some cases the torques even change their sign for a short period.

We find that planets are most likely to form a circumplanetary pressure-supported envelope rather than an accretion disk around them, with strong convective vertical flows. The relative pressure scale height in the circumplanetary material is at least 0.5, in which case the approximations for a thin Keplerian accretion disk are no longer valid. What results is a cloud which rotates at only 50 percent of the Keplerian value.

This slow rotation of the circumplanetary gas makes it impossible to form the moons of Jupiter from circumplanetary material as the solid content will rain down the planet in less than an orbit around Jupiter.


  \begin{figure} \par {\includegraphics[width=17cm]{3238fig15C.ps} }% \par % \end{figure} Figure 15: Model DR4: Temperature in the $r-\theta $ plane of the protoplanetary disk at the azimuthal location of the planet after 141 orbits. Brightness is logarithmic temperature (lighter = warmer) between 30 K and 1500 K, contours are equi-density lines (in g cm-3) and vectors give the logarithmic mass flux. See the online edition for a color version of this plot.
Open with DEXTER

How does this thick and slowly rotating envelope behave with respect to magneto-centrifugal wind as discussed for a circumplanetary disk by Fendt (2003)? The high thermal pressure could be beneficial for launching the magneto-centrifugal wind, but on the other hand we observe a strong mass infall onto the poles of the planet and the surface of the circumplanetary cloud, thus a wind might be suppressed. Detailed investigations on that issue are needed.

The deviation from symmetry with respect to the midplane is very small in our simulations. Some convection cells show eventual overshooting across the midplane but in general, treating only one hemisphere would have led to the same results.

We observe strong vertical flows in the early gap opening phase. Considering the entire mass accretion phase of the young planet starting from a few earth masses (Pollack et al. 1996), one finds that these vertical fountains may last for hundred-thousands of years before the planet opens its gap, making the effect clearly relevant for observations. As a result there would be locally a stronger flaring of the disk, and more radiation could interact with the small dust grains in the surface layer above the planet. Future instruments like SIM should be able to observe this asymmetry in the scattered light from disks in which planets are forming (Geoffrey Bryden, personal communication). On the other hand, the effect might be weaker if we allow for a gradual buildup of the planet. This has to be investigated in future simulations.

We do not observe the formation of vortices at the edges of the gap, which can often be found in the equivalent 2D simulations (Kley 1999; Koller et al. 2003). Further investigations will have to show whether this is related to the 3D nature of our simulations or a consequence of the comparable low resolution of the grid.

Finally, we speculate that the extended warm gas and dust which fills most of the Roche lobe should be detectable in the far infrared. Investigations such as by Wolf & D'Angelo (2005) indicate this already for 2D flat simulations that include radiative cooling. Similar studies using 3D density and temperature distributions will follow in the near future.

Acknowledgements

The authors wish to thank Geoff Bryden for fruitful discussions. This work was sponsored by the European Community's Research Training Networks Programme The Origin of Planetary Systems under contract HPRN-CT-2002-00308.

References

 
Copyright ESO 2005