A&A 445, 361-372 (2006)
DOI: 10.1051/0004-6361:20053694
Theoretical calculations of excited rovibrational levels of HD. Term values and transition probabilities of VUV electronic bands![[*]](/icons/foot_motif.gif)
H. Abgrall
-
E. Roueff
Laboratoire Univers et Théorie, UMR 8102 du CNRS,
Observatoire de Paris, Section de Meudon, Place Jules Janssen, 92195
Meudon, France
Received 24 June 2005 / Accepted 12 July 2005
Abstract
In this paper, we derive the theoretical properties of rovibrational levels belonging to excited B, C, B', and D electronic states of HD. We compute the eigenvalues and eigenfunctions of the nuclear coupled Schroedinger equations using ab initio electronic molecular properties available in the literature. Transition wavenumbers and spontaneous emission probabilities are calculated for all transitions belonging to B-X, C-X, B'-X, and D-X electronic band systems of HD when the upper rotational quantum number is below or equal to 10. We compare our results with available experimental values: the accuracy in the wavenumbers is on the order of 3 reciprocal centimetres, whereas the intensity properties are satisfactorily reproduced. The origin of the remaining discrepancies is analyzed.
Key words: molecular processes -
molecular data - line: identification - radiation mechanisms: general
1 Introduction
HD is the simplest 2-electron system to consider after H2. There have been few spectroscopic studies of this molecule since the VUV absorption analysis of HD by Dabrowski & Herzberg (1976) that followed the study by Monfils (1965). Ubachs and colleagues (Reinhold et al. 1999; Hinnen et al. 1995; de Lange et al. 2000) have performed specific experimental studies at very short wavelengths and discussed the nonadiabatic coupling effects in the Rydberg excited electronic levels of HD. Symmetry-breaking effects between u and g electronic excited levels have been inferred from these experiments.
On the other hand, HD has been detected in VUV absorption in diffuse and translucent clouds thanks to the Copernicus mission (Wright & Morton 1979) and FUSE (Far Ultra-violet Spectroscopic Explorer), both in galactic and extragalactic environments (Lacour et al. 2005; André et al. 2004). The derivation of comprehensive column densities of HD requires precise knowledge of the absorption oscillator strengths or emission transition probabilities.
These observations motivated us to undertake systematic calculations of the electronic spectrum of HD using the same approach that we used for H2 (Abgrall et al. 1993,1999,2000,1994). These results extend the systematic calculations by Allison & Dalgarno (1969) in a one-dimensional approximation for the excited and ground electronic states involved in the Lyman (B-X) and Werner (C-X) band systems, without considering centrifugal barrier effects.
The theoretical aspects are summarized in Sect. 2, including the derivation of the coupled Schroedinger equations and the molecular data required to derive the wavefunctions and matrix elements of the dipole transition moments. We report our results of transition wavenumbers, emission transition probabilities, and total radiative lifetimes in Sect. 3. Comparison of our calculations of both transition wavenumbers and intensities and the available experimental results is discussed in Sect. 4, and the summary of our results given in Sect. 5.
2 Theoretical context
We consider the transitions between the upper B (
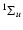 ), C (
), C (
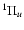 ), B' (
), B' (
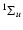 ), D (
), D (
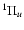 )
electronic rovibrational levels and
those corresponding to the ground electronic states of HD.
The ground X
)
electronic rovibrational levels and
those corresponding to the ground electronic states of HD.
The ground X
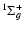 electronic state is isolated from the other excited electronic state, so the different rotational and vibrational eigenfunctions and their eigenvalues are obtained
by solving the one dimensional Schroedinger equation without introducing any coupling. The repulsive centrifugal barrier potential is introduced in addition to the ground electronic potential computed by Wolniewicz (1993) including relativistic and adiabatic corrections
for H2 and introducing the reduced mass of HD,
electronic state is isolated from the other excited electronic state, so the different rotational and vibrational eigenfunctions and their eigenvalues are obtained
by solving the one dimensional Schroedinger equation without introducing any coupling. The repulsive centrifugal barrier potential is introduced in addition to the ground electronic potential computed by Wolniewicz (1993) including relativistic and adiabatic corrections
for H2 and introducing the reduced mass of HD, 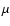 = 1223.8988 a.u. according to Senn et al. (1988).
= 1223.8988 a.u. according to Senn et al. (1988).
2.1 General considerations
The rovibronic upper states are obtained by including the non-adiabatic couplings between the four B, B', C, and D excited electronic states.
We expand the total electronic and nuclear wave function
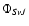 characterized by the electronic S label, the total parity (+, -), and the vibrational v and rotational J nuclear quantum numbers over the electronic Born-Oppenheimer (B.O.) wavefunctions corresponding to a single electronic state:
characterized by the electronic S label, the total parity (+, -), and the vibrational v and rotational J nuclear quantum numbers over the electronic Born-Oppenheimer (B.O.) wavefunctions corresponding to a single electronic state:
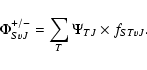 |
(1) |
Each 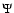 wave function is the product
of the electronic B.O.
wavefunction, corresponding to a particular electronic state referred by T index, and the pure rotational nuclear wavefunction. When the electronic state has a
wave function is the product
of the electronic B.O.
wavefunction, corresponding to a particular electronic state referred by T index, and the pure rotational nuclear wavefunction. When the electronic state has a 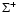 symmetry, the parity of the total wave function is given by the parity of J (e levels). In the case of doubly degenerate
symmetry, the parity of the total wave function is given by the parity of J (e levels). In the case of doubly degenerate 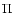 electronic states, no definite parity holds. However, non-adiabatic coupling between different electronic states may split the electronic potential curves according to the parity. For example, levels belonging to C+ and D+ have a parity given by (-1)J and labelled e-levels, whereas levels belonging to C- and D- have a parity given by
(-1)J+1 and labelled f-levels.
electronic states, no definite parity holds. However, non-adiabatic coupling between different electronic states may split the electronic potential curves according to the parity. For example, levels belonging to C+ and D+ have a parity given by (-1)J and labelled e-levels, whereas levels belonging to C- and D- have a parity given by
(-1)J+1 and labelled f-levels.
We calculate the rovibrational wave functions fSTvJ and the corresponding energy levels
EvjJj
by searching the eigenvalues of the coupled equations (split according to their total parity and total angular momentum J), obtained when writing the Schroedinger equation of the total wave function as described by Senn et al. (1988).
The diagonal terms are given by the adiabatic electronic potentials, and the off-diagonal terms are rotational (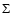 -
-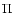 )
and radial (
)
and radial (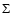 -
-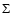 or
or 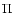 -
-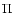 )
electronic coupling matrix elements.
)
electronic coupling matrix elements.
Table 1:
Molecular ab initio properties used in the calculations.
HD is not a homonuclear molecule, whereas inversion symmetry applies for pure B.O. electronic states. Then, gerade and ungerade labels are not completely exact
good quantum numbers for the rovibronic states. Indeed, very faint electric dipole transitions between so-called g electronic levels (as EF-X, GK-X, etc.)
have been observed (see for example Hinnen et al. 1995; Dabrowski & Herzberg 1976), whereas they are completely forbidden if inversion symmetry holds.
However, the rovibrational coupling between the u and g B.O. states
is very weak for the majority of states, so we neglect it in our calculations. The lack of accuracy resulting from this assumption will be discussed when we compare our results with experimental data.
We introduce the weight of each T electronic state in the expansion of the rovibrational wave function:
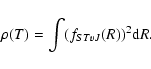 |
(2) |
The normalization is such
that
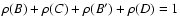 .
Except for very specific cases, one value of T is
preponderant, which allows us to define an electronic label S for the total wave function that, by convention, corresponds to the state of greatest weight.
The spontaneous emission probability or Einstein A coefficient, expressed in s-1, is given by the expression:
.
Except for very specific cases, one value of T is
preponderant, which allows us to define an electronic label S for the total wave function that, by convention, corresponds to the state of greatest weight.
The spontaneous emission probability or Einstein A coefficient, expressed in s-1, is given by the expression:
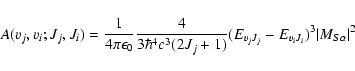 |
(3) |
EvJ is the energy of the level (v,J),
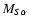 ,
the electric
transition dipole matrix element between wavefunctions of excited
S(vj,Jj), and
ground electronic
X(vi,Ji) states, while
,
the electric
transition dipole matrix element between wavefunctions of excited
S(vj,Jj), and
ground electronic
X(vi,Ji) states, while 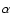 indicates whether the
spectroscopic branch label is P, Q, or R corresponding to
indicates whether the
spectroscopic branch label is P, Q, or R corresponding to
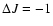 ,
0, 1, respectively.
When the emission takes place in the X continuum states, the expression is modified in order to acount for the energy normalization of the continuum wave function:
,
0, 1, respectively.
When the emission takes place in the X continuum states, the expression is modified in order to acount for the energy normalization of the continuum wave function:
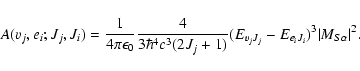 |
(4) |
The continuum index of the kinetic energy of dissociating atoms ei replaces the vibrational label vi.
The total emission probability, which produces dissociation from one specific excited level (vj; Jj), is obtained by performing the integration of the emission probability over all possible kinetic energies and by summing over the different rotational quantum numbers of the lower states with appropriate selection rules:
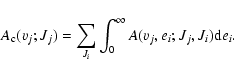 |
(5) |
The radiative lifetime of one specific excited (vj; Jj) level is given by the inverse of the total emission probability A
t(vj;Jj) which is expressed as:
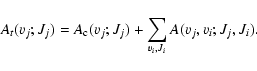 |
(6) |
The transition dipole matrix elements
 appearing in Eq. (2) are given by the following expressions:
appearing in Eq. (2) are given by the following expressions:
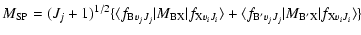 |
|
|
|
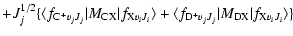 |
|
|
(7) |
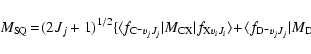 |
(8) |
where
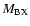 ,
,
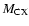 ,
,
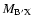 ,
and
,
and
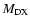 are
the real values of the electronic transition moments calculated
for each internuclear distance in the B.O. approximation, and P, Q, R refer to the different branches of the transitions. We see that the P and R branches connect e-levels belonging to B, B', C+, and D+ electronic states, whereas Q branches connect f-levels involving C- and D- electronic states.
are
the real values of the electronic transition moments calculated
for each internuclear distance in the B.O. approximation, and P, Q, R refer to the different branches of the transitions. We see that the P and R branches connect e-levels belonging to B, B', C+, and D+ electronic states, whereas Q branches connect f-levels involving C- and D- electronic states.
The absorption oscillator strengths can be derived from the spontaneous emission probabilities via the following expressions:
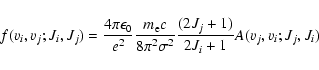 |
(10) |
where 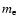 is the electron mass,
is the electron mass, 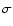 the wavenumber of the transition. This expression has a very convenient numerical value when
the wavenumber of the transition. This expression has a very convenient numerical value when 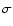 is expressed in reciprocal centimetres:
is expressed in reciprocal centimetres:
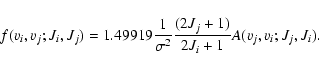 |
(11) |
2.2 Numerical method and molecular properties
The integrations are performed by using atomic units (the atomic unit of energy is 219 474.631 cm-1 from the latest definitions).
We solve the nuclear coupled equations by using the Numerov method as described by
Johnson (1978), similarly to our previous calculations of H2 or D2. We
take an integration step length of 0.01 au, an outer integration limit of 30 au, and use a spline interpolation to calculate the electronic matrix elements at the integration grid points.
In the absence of g-u coupling, the dissociating limits of the B, C, and B' states corresponding to H(1s)+D(2s, 2p) or D(1s)+H(2s, 2p) are not distinguished. The values labelled D(2), relative to the ground state of the neutral molecules, X
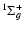 (v=0, J=0) are adopted from Table IX of Dressler & Wolniewicz (1986).
The dissociation limit of the D state involves n =3 of H or D and is labelled D(3). We take the theoretical value derived from the adiabatic approximation (Senn et al. 1988).
The corresponding values are
D(2) = 118 676.087 cm-1 and
D(3) = 133 911.154 cm-1.
The ab initio data used in our calculations are displayed in Table 1.
(v=0, J=0) are adopted from Table IX of Dressler & Wolniewicz (1986).
The dissociation limit of the D state involves n =3 of H or D and is labelled D(3). We take the theoretical value derived from the adiabatic approximation (Senn et al. 1988).
The corresponding values are
D(2) = 118 676.087 cm-1 and
D(3) = 133 911.154 cm-1.
The ab initio data used in our calculations are displayed in Table 1.
When considering the non-adiabatic effects within the four excited states for which the coupling is most important, we expect that the accuracy is several reciprocal centimeters, due to the neglect of the other weakly coupled states combined with the uncertainties involved in the ab initio data themselves.
Our former calculations on H2and D2 transition wavenumbers (Abgrall et al. 1999,1993,1994) were closer to the
experimental rovibronic levels up to the higher J, as we were able to make slight adjustments of the diagonal potential data for the unperturbed levels involved (J=0 or J=1). The discrepancy in the energy terms was less than 1 cm-1,
even for the higher rotational levels. The transition probability is less sensitive to the molecular potentials, except for the
few perturbed levels where the energy difference between adiabatic values is critical.
We were not able to use this semi-empirical procedure in the case of HD, since there are not enough published experimental levels
for J=0 or 1 and because the g-u coupling induces shifts in a random way
in the rovibrational level energy values (see discussion in Sect. 4.1.2 and lower part of Fig. 1). The recent ab initio data used in the present work are given for a large number of internuclear distances and are much more accurate than the values used in our previous calculations of H2 and D2.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{3694fig1.ps}\end{figure}](/articles/aa/full/2006/01/aa3694-05/Timg35.gif) |
Figure 1:
Upper plot: o-c of H2 versus v' for the levels B(v', 1). Lower plot: o-c of HD versus v' for the levels B(v', 1).
|
| Open with DEXTER |
3 Results
We have solved the nuclear coupled Schroedinger equations up to J = 10 and obtained the corresponding discrete eigenfunctions and eigenvalues for
the excited electronic states B, C, B' and D below the dissociation limit D(2) in the non-adiabatic approximation.
As the D long range potential converges towards the H(3p) or D(3p) state, discrete levels belonging to D may occur between D(2) and
D(3). In the case of H2 and D2, the e levels belonging to D+ are strongly predissociated by B' (u-u rotational coupling),
and only f-levels belonging to D- are seen in emission. This does not hold for HD, as g-u coupling takes place between f-levels belonging to
D
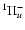 and I
and I
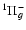 (Dehmer & Chupka 1983). However, as we neglegt the g-u coupling, we also calculate the Q branches corresponding to
(Dehmer & Chupka 1983). However, as we neglegt the g-u coupling, we also calculate the Q branches corresponding to
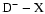 transitions for excited level energies
between D(2) and D(3) in the adiabatic approximation.
transitions for excited level energies
between D(2) and D(3) in the adiabatic approximation.
Neglecting non-adiabatic corrections for the X lower rovibrational levels may also produce up to a 5 cm-1 discrepancy in the energy terms when compared to experimental values (Wolniewicz 1993,1995). So, as in our previous work on H2 and D2, we introduce, if available, the experimental energy levels (Dabrowski & Herzberg 1976) corresponding to the electronic X ground state to derive the transition energies involved in the various electronic bands.
Thus, the accuracy of the transition wavenumbers reported here depends only on the uncertainties involved in the calculations of excited level energies.
3.1 Excited level properties: energy terms, electronic weight factors, total radiative decay probability, radiative dissociation probability
Tables 5-10 give the presently calculated rovibrational
energy terms obtained with the origin at the rovibrational ground level v=0, J=0 of the X electronic state,
the total spontaneous emission probabilities
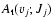 ,
and the emission probability towards the continuum
,
and the emission probability towards the continuum
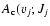 expressed in s-1 as described in Eqs. (3)-(5) for the different excited levels included, i.e. B, C, B', and D for rotational quantum number values from 0 to 10.
The tables also include the
electronic weight factors
expressed in s-1 as described in Eqs. (3)-(5) for the different excited levels included, i.e. B, C, B', and D for rotational quantum number values from 0 to 10.
The tables also include the
electronic weight factors
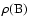 ,
,
 ,
,
 ,
,
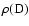 of the B.O. states
for each rovibrational level of definitive parity, as defined in Sect. 2.
Tables 5-8 present the e manifold which involves only P and R branches in radiative transitions with the ground electronic state.
When J > 0, we include the coupling between the four B, C+, B', D+ states that incorporate both a significant rotational
coupling between
of the B.O. states
for each rovibrational level of definitive parity, as defined in Sect. 2.
Tables 5-8 present the e manifold which involves only P and R branches in radiative transitions with the ground electronic state.
When J > 0, we include the coupling between the four B, C+, B', D+ states that incorporate both a significant rotational
coupling between 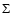 and
and 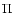 states and a weak radial coupling between
states and a weak radial coupling between
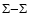 ,
on the one hand and
,
on the one hand and 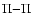 ,
on the other. The rotational coupling does not occur when J=0, as the
,
on the other. The rotational coupling does not occur when J=0, as the 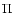 levels have no rotational quantum number below 1, and rovibrational levels with J = 0 belonging to B and B' are coupled by the corresponding weak radial coupling.
Tables 9-10 present the f manifold that involves only Q branches in radiative transitions with the ground electronic state.
The C- and D- are coupled by a weak non-adiabatic u-u radial coupling. Above the energy corresponding to D(2), the calculations are only performed
in the adiabatic approximation in a single potential approach, as stated before.
levels have no rotational quantum number below 1, and rovibrational levels with J = 0 belonging to B and B' are coupled by the corresponding weak radial coupling.
Tables 9-10 present the f manifold that involves only Q branches in radiative transitions with the ground electronic state.
The C- and D- are coupled by a weak non-adiabatic u-u radial coupling. Above the energy corresponding to D(2), the calculations are only performed
in the adiabatic approximation in a single potential approach, as stated before.
We display in Table 2 an example of the data given in Tables 5-10 for the states with a rotational quantum number J = 1 belonging mainly to B. These levels are attained in absorption from the electronic ground state via the R(0) transitions of the Lyman band system and can only be perturbed by levels of 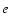 parity.
One value of
parity.
One value of 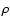 is dominant (corresponding to state B in Table 2), which is also true in most cases, and justifies using the classification B, C, B' or D
and labelling the levels with the name of the B.O. state of greatest electronic weight factor,
is dominant (corresponding to state B in Table 2), which is also true in most cases, and justifies using the classification B, C, B' or D
and labelling the levels with the name of the B.O. state of greatest electronic weight factor, 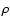 .
It may, however, happen that one value of
.
It may, however, happen that one value of 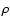 becomes close to 0.5 for a specific rovibrational level, in which case the
classification in terms of B.O. states becomes arbitrary. It is thus necessary to include an extra label, noted
becomes close to 0.5 for a specific rovibrational level, in which case the
classification in terms of B.O. states becomes arbitrary. It is thus necessary to include an extra label, noted 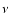 ,
to give
the order of the level in ascending energies within a given parity (
,
to give
the order of the level in ascending energies within a given parity (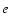 or
or 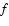 )
starting from
)
starting from 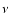 = 1.
In the example reported in Table 2, the B v= 9, J= 1 level energy is not directly after the B, v=8, J=1 level. We also notice that the probability of dissociating into the continuum increases with the energy term values, and the photodissociation probability (ratio between the probability to fluorescence towards the continuum and the total emission probability) is almost 1 for the higher terms so that the corresponding levels are not seen in spectroscopic experiments.
= 1.
In the example reported in Table 2, the B v= 9, J= 1 level energy is not directly after the B, v=8, J=1 level. We also notice that the probability of dissociating into the continuum increases with the energy term values, and the photodissociation probability (ratio between the probability to fluorescence towards the continuum and the total emission probability) is almost 1 for the higher terms so that the corresponding levels are not seen in spectroscopic experiments.
Table 2:
Properties of the v', J = 1 levels belonging to the B
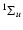 electronic state. See text for explanations of the various columns.
electronic state. See text for explanations of the various columns.
3.2 Tables of transitions and line emission probabilities
Emission transition probabilities are displayed in Tables 11-16 for excited rotational quantum numbers less than 11.
We also indicate, when available, the discrepancies with the experimental determinations. The labels (mn) of the last column indicate how the transition wavenumbers have been derived:
- m = 1
- if the X energy terms are taken from experiments((Dabrowski & Herzberg 1976);
- m = 2
- if the X energy terms are theoretical values form Wolniewicz (1995);
- m = 3
- if we use our own calculations in the absence of any other information;
- n = 0
- indicates that no experimental information is available for the transition;
- n = 1
- corresponds to the transition wavenumber given by Dabrowski & Herzberg (1976);
- n = 2
- corresponds to the experimental values of Dehmer & Chupka (1983);
- n = 3
- corresponds to the experimental values of Takezawa & Yanaka (1972);
- n = 4
- corresponds to the experimental values of Monfils (1965).
4 Comparison with experiments and discussion
A few transition energies have been derived recently by Hinnen et al. (1995) in the region between 102 040 cm-1 and 108 700 cm-1 with a claimed accuracy of 0.035 cm-1.
We collect the corresponding values in Table 3 and compare our calculated
values with those of Dabrowski & Herzberg (1976) and those of Hinnen et al. (1995). The discrepancies in the B levels are usually less than 3 cm-1 and less than 1 cm-1 for C states.
Table 3:
Comparison of present calculations of the transition wavenumbers of B-X, C+-X, and C--X electronic band systems of HD with the high-resolution experimental determinations of Hinnen et al. (1995) (o1-c) and Dabrowski & Herzberg (1976) (o2-c).
In Tables 3, 11 to 16, o-c (observed-calculated) is generally
negative and goes from about -0.5 cm-1 to about -5 cm-1. The shift is only due to the uncertainty in the
excited rovibrational levels. This discrepancy is, however, higher
and irregular for some specific cases. Four main sources can be invoked for these differences:
- 1.
- the ab initio electronic matrix elements are not accurate enough or
the number of coupled u electronic states should be increased to more states;
- 2.
- the coupling between u and g states is neglected, so the corresponding approximation fails;
- 3.
- the transition labelling of Dabrowski & Herzberg (1976) is different from ours;
- 4.
- there are misprints in the data of Dabrowski & Herzberg (1976).
The corresponding examples are given below.
4.1.1 Discrepancies due to rotational or radial coupling between u states
We test the effect of the couplings by performing equivalent calculations but including H2 parameters. In the upper part of Fig. 1, we display the o-c values of H2 taken from experimental determinations of Abgrall et al. (1993) and concerning the energy terms of B(v', 1) versus the vibrational quantum numbers implied. We report both our previous results derived by semi-empirical fitting of the excited potential curves (Abgrall et al. 1994) and the results obtained by using pure ab initio data used for HD (cf. Table 1), but including the reduced mass of H2.
We note first that the o-c values reported from our previous work are within a 0.5 reciprocal centimetre. With pure ab initio data, there is a regular increase of
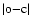 from 0.5 to 3 cm-1 with the vibrational quantum number, as other excited electronic levels get close and may perturb the calculated term. This means that the expansion of the total wave function should include supplementary electronic states of u symmetry such as B'', D' etc. However, two extra features appear for v' = 14 and 31. We infer from our previous studies that the perturbation of the B(14, 1) level by the C(3, 1) level is not fully calculated from ab initio calculations. An additional coupling has to be introduced to improve the calculation corresponding to B(31, 1), where the coupling with B'' should be taken into account.
from 0.5 to 3 cm-1 with the vibrational quantum number, as other excited electronic levels get close and may perturb the calculated term. This means that the expansion of the total wave function should include supplementary electronic states of u symmetry such as B'', D' etc. However, two extra features appear for v' = 14 and 31. We infer from our previous studies that the perturbation of the B(14, 1) level by the C(3, 1) level is not fully calculated from ab initio calculations. An additional coupling has to be introduced to improve the calculation corresponding to B(31, 1), where the coupling with B'' should be taken into account.
4.1.2 Discrepancies due to g-u coupling
The lower part of Fig. 1 displays the o-c values of the same B(v', 1) transition wavenumbers for HD obtained in the present work without taking the g-u coupling into account. The values are also negative and show a slight increase of
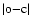 up to v' = 10. For higher values of v', the points are significantly random, and we tentatively explain the deviations as due to coupling with the EF
up to v' = 10. For higher values of v', the points are significantly random, and we tentatively explain the deviations as due to coupling with the EF
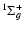 electronic state.
For example, in the case of B(11, 1), o-c = -6.5 cm-1, i.e. 4 cm-1 below the value obtained for B(10, 1).
electronic state.
For example, in the case of B(11, 1), o-c = -6.5 cm-1, i.e. 4 cm-1 below the value obtained for B(10, 1).
Table 4:
Experimental term values of Dabrowski & Herzberg (1976) for J=1 sorted in ascending order of energy.
We display in Table 4 the different experimental terms corresponding to 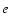 parity levels reported in Dabrowski & Herzberg (1976) with a rotational quantum number J = 1 for any electronic band system. The B(11, 1) term has been measured 8.76 cm-1 below the EF(4,1) term. We thus conclude that a significant perturbation occurs between these two levels. In order to evaluate the order of magnitude for this coupling, we use a two-state
perturbation approximation and estimated the borrowing effect, which accounts for the
emission probability of the EF state towards X. We find in this way that the emission probability lost by B(11,1) when we incorporate
g-u coupling is 4/8.76, i.e. about 40%. However, such coincidences are not frequent, as shown in Table 4, and the 2-state approximation is usually not valid.
parity levels reported in Dabrowski & Herzberg (1976) with a rotational quantum number J = 1 for any electronic band system. The B(11, 1) term has been measured 8.76 cm-1 below the EF(4,1) term. We thus conclude that a significant perturbation occurs between these two levels. In order to evaluate the order of magnitude for this coupling, we use a two-state
perturbation approximation and estimated the borrowing effect, which accounts for the
emission probability of the EF state towards X. We find in this way that the emission probability lost by B(11,1) when we incorporate
g-u coupling is 4/8.76, i.e. about 40%. However, such coincidences are not frequent, as shown in Table 4, and the 2-state approximation is usually not valid.
Table 5:
Properties of B
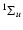 rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
Table 6:
Properties of C+ 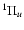 rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
Table 7:
Properties of B'
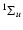 rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
Table 8:
Properties of D+ 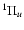 rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
Table 9:
Properties of C- 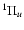 rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
Table 10:
Properties of D- 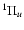 rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
Table 11:
Spontaneous emission probabilities and transition wavenumbers of B-X (Lyman) band transitions of HD. Full table available in electronic form at the CDS.
Table 12:
Spontaneous emission probabilities and transition wavenumbers of C+-X (Werner) band transitions (P and R branches) of HD. Full table available in electronic form at the CDS.
Table 13:
Spontaneous emission probabilities and transition wavenumbers of B'-X band transitions of HD. Full table available in electronic form at the CDS.
Table 14:
Spontaneous emission probabilities and transition wavenumbers of D+-X bands of HD. Full table available in electronic form at the CDS.
Table 15:
Spontaneous emission probabilities and transition wavenumbers of C--X (Werner) band transitions (Q branches) of HD. Full table available in electronic form at the CDS.
Table 16:
Spontaneous emission probabilities and transition wavenumbers of D--X bands of HD. Full table available in electronic form at the CDS.
The wavenumbers of the transitions C-X (5-10) R(5) and C-X (5-0) R(5) reported in Table 6 have -85.51 and -86.35 cm-1 differences, respectively, with Dabrowski & Herzberg (1976) data, whereas the wavenumbers of the B-X (20-0) R(5) transition reported in Table 2
display a difference of 81.55 cm-1. The corresponding o-c values become -2.92, -2.09, and -1.88 cm-1 if we exchange the assignments of C(5, 6) and B(20, 6) levels.
We may justify these assumptions by considering the electronic weight factors of the levels involved, i.e. C(5, 6) and B(20, 6). Indeed, C(5, 6) has an electronic weight factor for state B of 0.269
and an electronic weight factor for state C of 0.731, whereas B(20, 6) has an electronic weight factor for state B of 0.739 and an electronic weight factor for state C of 0.261.
There is also a change of assigment between C(4, 7) and B(18, 7) levels, as well as between
(C11-5) and B(33, 5) levels.
Some significant discrepancies between calculations and experiments are still present. We suspect a misprint for the R(1), R(2), R(3) transitions belonging to the B-X (9-8) band, because a change of the wave number of 2000 cm-1 in the Dabrowski & Herzberg (1976) values gives an o-c value of
-2.4, -2.41, -2.53 cm-1, comparable to the other o-c values involving B, v=9 levels. The same conjecture applies for the C-X (12-16) band
concerning the P and Q transitions reported in Tables 6 and 9, respectively. An o-c value of
153.73 cm-1 also occurs for the B'-X (3-0) R(5) in Table 7, for which no obvious explanation can be found.
Ajello et al. (2005) have recently measured the intensity of a fluorescence experimental spectrum at a 0.16 Å FWHM spectral resolution, obtained by exciting HD molecules at a temperature of 300 K, with a monoenergetic 100 ev electron beam.
The aim of this experiment was the determination of the electronic excitation cross sections of HD by electrons through a comparison of experimental and simulated spectra using the calculations reported here.
As for H2 (Liu et al. 2002) and D2 (Abgrall et al. 1999), the most important path is the direct excitation in which the electrons excite HD via the electric-dipole transitions towards B, C, B', and D states of u symmetry.
The simulated and experimental spectra generally agree very satisfactorily when a direct excitation mechanism is invoked. The differences are discussed below and arise from an additional excitation process.
In some wavenumber regions, experimental peaks are not reproduced by the calculations (see for example Fig. 4 of Ajello et al. 2005).
These peaks correspond to transitions emitted by the low vibrational levels of B (v=0-3) and involve an indirect excitation mechanism via the so-called EF g electronic states. This mechanism has already been described for H2 (Liu et al. 2002,2003) and D2 (Abgrall et al. 1999).
In addition, as discussed in Ajello et al. (2005), the EF states are perturbed by some states of u character and may thus be excited by electrons via allowed electric dipole transitions. Then the EF levels fluoresce mainly towards B(v=0-3) levels via infrared emission, which finally emit UV photons towards the X electronic ground state.
Figure 4 in Ajello et al. (2005), displays examples of such features, which are reproduced when the excitation in the EF states is taken into account (Fig. 5 of the same paper). A detailed description of this treatment will be reported in a future paper.
We do not systematically calculate the direct de-excitation from EF, GK, towards X, as comparison with experiments shows that the corresponding effect is weak at the resolution in Ajello et al. (2005). However we do notice some rare features where the calculated intensity is above the experimental value, which may be explained by the borrowing effect described in Sect. 4.1.2.
We discuss here the feature at 1333 Å displayed
in Fig. 2e of Ajello et al. (2005). The 1333.24054 Å wavelength corresponds to the B-X (11-9) P(2) transition (Table 5 and Dabrowski & Herzberg 1976). However, there is a close transition belonging to EF-X (4-9) P(2) band system (reported in Dabrowski & Herzberg (1976) at 1333.08485). The term values of the upper levels involved, B(11, 1) and EF(4, 1), are reported in Table 4 and separated by 8.76 reciprocal centimeters as already emphasised in Sect. 4.1.2. This suggests that some coupling between B and EF can take place and induce intensity anomalies.
We then use a 2-state approximation and derive the coupling from the difference between the level energies. We may then evaluate the electronic weight factors corresponding to each state and derive the intensity of the two transitions: 60% of the total intensities are attributed to the B-X (11-9) P(2) and 40% to EF-X (4-9) P(2). This simple treatment allows the experimental fluorescence spectrum around 1333 Å to be explained. Other anomalies implying these same upper levels are expected in the whole spectrum.
5 Conclusion and summary
We give below a detailed description of the tables whose numerical data may be obtained in electronic form. The transition wavenumbers are accurate within a few wavenumbers, and experimental values should be used when available. The transition probabilities are probably accurate within a few percent, and they update the previous calculations of Allison & Dalgarno (1969).
Tables 5-8 display the properties of the excited rovibronic levels of 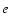 - parity states linked by rotational and radial coupling,
i.e. B
- parity states linked by rotational and radial coupling,
i.e. B
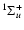 ,
C
,
C
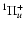 ,
B
,
B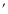
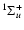 and D
and D
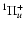 .
As these states are coupled, we have labelled them according to the B.O. state of greatest electronic weight factor. Note that there is no coupling
with C+ and D+ when J=0, as the corresponding levels do not occur in
.
As these states are coupled, we have labelled them according to the B.O. state of greatest electronic weight factor. Note that there is no coupling
with C+ and D+ when J=0, as the corresponding levels do not occur in 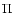 electronic symmetry.
electronic symmetry.
Column 1 gives the vibrational number.
Column 2 gives the energy order of the 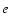 -parity levels of the same J value irrespective of the
label B, C, B', or D.
-parity levels of the same J value irrespective of the
label B, C, B', or D.
Column 3 gives the rotational quantum number.
Columns 4-8 give the fractions of B.O. state as defined in Sect. 2, Eq. (1).
Column 8 gives the term value.
Column 9 gives the total emission probability towards X ground electronic state in s-1.
Column 10 gives the total dissociation probability towards X continuum in s-1.
Tables 9-10 display the properties of the excited rovibronic levels of
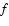 - parity states that are coupled via radial coupling only between C
- parity states that are coupled via radial coupling only between C
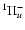 and D
and D
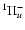 .
As for
.
As for 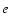 levels, we have labelled them according to the B.O. state of greatest electronic weight factor.
levels, we have labelled them according to the B.O. state of greatest electronic weight factor.
Column 1 gives the vibrational number.
Column 2 gives the energy order of the 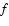 -parity levels of the same J value irrespective of the
label C or D.
-parity levels of the same J value irrespective of the
label C or D.
Column 3 gives the rotational quantum number.
Columns 4-5 give the fractions of B.O. state as defined in Sect. 2, Eq. (1).
Column 6 gives the term value.
Column 7 gives the total emission probability towards X ground electronic state in s-1.
Column 8 gives the total dissociation probability towards X continuum in s-1.
Tables 11 to 16 display the transition emission probabilities and transition wavenumbers towards X states for upper rotational quantum numbers less than 11. Comparison with experimental wavenumbers are given when available. The conventions to experimental references have been defined in Sect. 3.2.
The 14414 R and P transitions of the Lyman system (B-X) are displayed in Table 11,
the 4778 R and P transitions of the Werner system (C-X) in Table 12,
the 3213 R and P transitions of the B'-X system in Table 13,
the 933 R and P transitions of the D-X system in Table 14,
the 2482 Q transitions of the Werner system (C-X) in Table 15 and the 3257 Q transitions of the D-X system in Table 16.
Column 1 gives the upper vibrational quantum number v'.
Column 2 gives the upper rotational quantum number J'.
Column 3 gives the lower vibrational quantum number v''.
Column 4 gives the lower rotational quantum number J''.
Column 5 gives the presently calculated emission probabilities in s-1.
Column 6 gives our obtained transition energies in cm-1.
Column 7 gives o-c in cm-1 when available.
Column 8 is a code mn, defined in Sect. 3.2, specifying which experimental reference has been used.
- Abgrall, H., Roueff, E.,
Launay, F., Roncin, J. Y., & Subtil, J. L. 1993, J.
Molec. Spectrosc., 157, 512 [NASA ADS] [CrossRef]
- Abgrall, H., Roueff, E.,
Launay, F., & Roncin, J. 1994, Canadian J. Phys., 72, 856 [NASA ADS]
- Abgrall, H., Roueff, E.,
Liu, X., Shemansky, D. E., & James, G. K. 1999, J.
Phys. B Atom. Molec. Phys., 32, 3813 [NASA ADS]
- Abgrall, H., Roueff, E.,
& Drira, I. 2000, A&AS, 141, 297 [EDP Sciences] [NASA ADS]
- Ajello, J., Vatti
Palle, P., Abgrall, H., Roueff, E., Bhardwaj, A., &
Gustin, J. 2005, ApJS, 159, 314 [NASA ADS] [CrossRef] (In the text)
- Allison,
A. C., & Dalgarno, A. 1969, Atomic Data, 1, 289 (In the text)
- André,
M. K., Le Petit, F., Sonnentrucker, P., et al. 2004,
A&A, 422, 483 [EDP Sciences] [NASA ADS] [CrossRef]
- Dabrowski, I., &
Herzberg, G. 1976, Canadian J. Phys., 54, 525 [NASA ADS] (In the text)
- de Lange, A.,
Reinhold, E., Hogervorst, W., & Ubachs, W. 2000, Canadian
Journal of Physics, 78, 567 [NASA ADS] [CrossRef]
- Dehmer, P. M.,
& Chupka, W. A. 1983, J. Chem. Phys., 79,
1569 [NASA ADS] [CrossRef] (In the text)
- Dressler, K.,
& Wolniewicz, L. 1986, J. Chem. Phys., 85, 2821 [NASA ADS] [CrossRef] (In the text)
- Hinnen, P. C.,
Werners, S. E., Stolte, S., Hogervorst, W., & Ubachs, W.
1995, Phys. Rev. A, 52, 4425 [NASA ADS] [CrossRef]
- Johnson, B. R.
1978, J. Chem. Phys., 69, 4678 [NASA ADS] [CrossRef] (In the text)
- Lacour, S.,
André, M. K., Sonnentrucker, P., et al. 2005,
A&A, 430, 967 [EDP Sciences] [NASA ADS] [CrossRef]
- Liu, X., Shemansky,
D. E., Abgrall, H., et al. 2002, ApJS, 138, 229 [NASA ADS] [CrossRef] (In the text)
- Liu, X., Shemansky,
D. E., Abgrall, H., et al. 2003, J. Phys. B Atom.
Molec. Phys., 36, 173 [NASA ADS]
- Monfils, A. 1965, J.
Molecular Spectroscopy, 15, 265 [NASA ADS] (In the text)
- Reinhold, E.,
Hogervorst, W., Ubachs, W., & Wolniewicz, L. 1999,
Phys. Rev. A, 60, 1258 [NASA ADS] [CrossRef]
- Senn, P., Quadrelli,
P., & Dressler, K. 1988, J. Chem. Phys., 89,
7401 [NASA ADS] [CrossRef] (In the text)
- Staszewska, G., &
Wolniewicz, L. 2002, J. Molec. Spectrosc., 212, 208 [NASA ADS] [CrossRef]
- Takezawa, S., &
Yanaka, Y. 1972, J. Chem. Phys., 56, 6125 [CrossRef] (In the text)
- Wolniewicz, L. 1993,
J. Chem. Phys., 99, 1851 [NASA ADS] [CrossRef] (In the text)
- Wolniewicz, L. 1995,
J. Chem. Phys., 103, 1792 [NASA ADS] [CrossRef]
- Wolniewicz, L., &
Dressler, K. 1988, J. Chem. Phys., 88, 3861 [NASA ADS] [CrossRef]
- Wolniewicz, L., &
Staszewska, G. 2003a, J. Molec. Spectrosc., 217, 181 [NASA ADS] [CrossRef]
- Wolniewicz, L., &
Staszewska, G. 2003b, J. Molec. Spectrosc., 220, 45 [NASA ADS] [CrossRef]
- Wright, E. L., &
Morton, D. C. 1979, ApJ, 227, 483 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2005
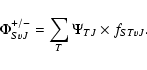
![]() -
-![]() )
and radial (
)
and radial (![]() -
-![]() or
or ![]() -
-![]() )
electronic coupling matrix elements.
)
electronic coupling matrix elements.
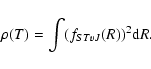
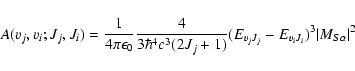
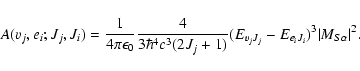
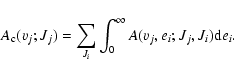
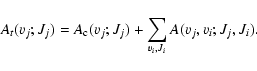
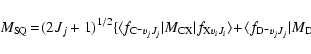
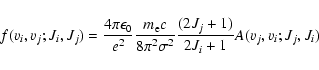
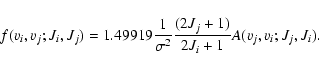
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{3694fig1.ps}\end{figure}](/articles/aa/full/2006/01/aa3694-05/Timg35.gif)
![]() and I
and I
![]() (Dehmer & Chupka 1983). However, as we neglegt the g-u coupling, we also calculate the Q branches corresponding to
(Dehmer & Chupka 1983). However, as we neglegt the g-u coupling, we also calculate the Q branches corresponding to
![]() transitions for excited level energies
between D(2) and D(3) in the adiabatic approximation.
transitions for excited level energies
between D(2) and D(3) in the adiabatic approximation.
![]() parity.
One value of
parity.
One value of ![]() is dominant (corresponding to state B in Table 2), which is also true in most cases, and justifies using the classification B, C, B' or D
and labelling the levels with the name of the B.O. state of greatest electronic weight factor,
is dominant (corresponding to state B in Table 2), which is also true in most cases, and justifies using the classification B, C, B' or D
and labelling the levels with the name of the B.O. state of greatest electronic weight factor, ![]() .
It may, however, happen that one value of
.
It may, however, happen that one value of ![]() becomes close to 0.5 for a specific rovibrational level, in which case the
classification in terms of B.O. states becomes arbitrary. It is thus necessary to include an extra label, noted
becomes close to 0.5 for a specific rovibrational level, in which case the
classification in terms of B.O. states becomes arbitrary. It is thus necessary to include an extra label, noted ![]() ,
to give
the order of the level in ascending energies within a given parity (
,
to give
the order of the level in ascending energies within a given parity (![]() or
or ![]() )
starting from
)
starting from ![]() = 1.
In the example reported in Table 2, the B v= 9, J= 1 level energy is not directly after the B, v=8, J=1 level. We also notice that the probability of dissociating into the continuum increases with the energy term values, and the photodissociation probability (ratio between the probability to fluorescence towards the continuum and the total emission probability) is almost 1 for the higher terms so that the corresponding levels are not seen in spectroscopic experiments.
= 1.
In the example reported in Table 2, the B v= 9, J= 1 level energy is not directly after the B, v=8, J=1 level. We also notice that the probability of dissociating into the continuum increases with the energy term values, and the photodissociation probability (ratio between the probability to fluorescence towards the continuum and the total emission probability) is almost 1 for the higher terms so that the corresponding levels are not seen in spectroscopic experiments.
![]() electronic state. See text for explanations of the various columns.
electronic state. See text for explanations of the various columns.![]() rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.![]() rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
![]() rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
![]() rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
![]() rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
![]() rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
rovibrational states: electronic weight factors, term value, total spontaneous emission probability (s-1) and total dissociation probability (s-1). Full table available in electronic form at the CDS.
![]() -parity levels of the same J value irrespective of the
label B, C, B', or D.
-parity levels of the same J value irrespective of the
label B, C, B', or D. ![]() - parity states that are coupled via radial coupling only between C
- parity states that are coupled via radial coupling only between C
![]() and D
and D
![]() .
As for
.
As for ![]() levels, we have labelled them according to the B.O. state of greatest electronic weight factor.
levels, we have labelled them according to the B.O. state of greatest electronic weight factor.
![]() -parity levels of the same J value irrespective of the
label C or D.
-parity levels of the same J value irrespective of the
label C or D.