National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, PR China
A&A 444, L25-L28 (2005)
DOI: 10.1051/0004-6361:200500200
Hong Sheng Zhao
SUPA, School of Physics and Astronomy, University of St Andrews, KY16 9SS, Fife, UK![]()
National Astronomical Observatories, Chinese Academy of
Sciences, Beijing 100012, PR China![]()
Received 3 May 2005 / Accepted 7 October 2005
Abstract
MOdified Newtonian Dynamics survived the test over two decades,
fitting the ups and downs of a variety of galaxy
velocity curves without fine tuning (Sanders & McGaugh 2002, ARA&A, 40, 263).
MOND is also evolving from an empirical to a decent theory respecting
fundamental physics after Bekenstein (2004, Phys. Rev. D, 70, 3509)
showed that lensing and Hubble expansion can be modeled rigourously
in a Modified Relativity.
However, many properties of MOND are obscured by its non-linear Poisson's equation.
Here we study the effect of tides for a binary
stellar system or a baryonic satellite-host galaxy system.
We show that the Roche lobe is more squashed than the Newtonian case
due to the anisotropic dilation effect in deep-MOND.
We prove analytically that the Roche lobe volume
scales linearly with the "true'' baryonic mass ratio
in both Newtonian and deep-MOND regimes,
insensitive to the modification to the inertia mass.
Hence accurate Roche radii of satellites can break
the degeneracy of MOND and dark matter theory.
Globular clusters and dwarf galaxies of comparable luminosities
and distances show a factor of ten scatter in limiting radii; this
is difficult to explain in any "mass-tracing-light'' universe.
Key words: dark matter - galaxy kinematics and dynamics - gravitation - galaxies: dwarf - globular clusters
The alternative gravity theory of Modified Newtonian Dynamics
(MOND) (Milgrom 1983) has been doing very well in fitting
kinematic data on galaxy scales, often better than the standard
cold dark matter theory. Baryonic matter alone is sufficient to
account for the gravity in such theory. The predictive power of
this 20-year-old classical theory with virtually no free
parameters (Bekenstein & Milgrom 1984) is recently highlighted by
the astonishingly good fits to contemporary kinematic data of a
wide variety of high and low surface brightness spiral and
elliptical galaxies; even the fine details of the ups and downs of
velocity curves are elegantly reproduced without fine tuning of
the baryonic model (Sanders & McGaugh 2002; Milgrom & Sanders
2003). Originally it was proposed empirically (Milgrom 1983) that
rotation curves of axisymmetric disk galaxies could be fit by an
acceleration
![]() which is stronger
than the Newtonian gravity GM/r2 by a spatially varying factor
which is stronger
than the Newtonian gravity GM/r2 by a spatially varying factor
![]() in the weak regime defined by
in the weak regime defined by
![]() ;
e.g.,
;
e.g.,
![]() .
This empirical MOND relation can be elevated
to a theory for an arbitrary baryon density distribution
.
This empirical MOND relation can be elevated
to a theory for an arbitrary baryon density distribution
![]() ,
where
a curl-free gravity field
,
where
a curl-free gravity field
![]() is the gradient of
a conservative potential
is the gradient of
a conservative potential
![]() and satisfies an equation
(Bekenstein & Milgrom 1984)
and satisfies an equation
(Bekenstein & Milgrom 1984)
![\begin{displaymath}-L = \int {\rm d}{\vec R}^3
\left[ \rho \Phi + {\bar{\mu} \v...
...],
\qquad {\vec g}({\vec R}) = - {\vec \nabla}\Phi({\vec R}), \end{displaymath}](/articles/aa/full/2005/47/aahe021/img27.gif) |
(2) |
In the past this non-relativistic formulation of MOND has been criticized for being incomplete for modelling the bending of light (but see Qin et al. 1995). This, too, has changed since its generalization into a respectable relativistic theory (christened TeVeS by Bekenstein 2004), which includes Hubble expansion, and passes standard tests to check General Relativity (Skordis et al. 2005; Chiu et al. 2005); GR is merely one limitting case of TeVeS.
Nevertheless, a main challenge of working on MOND is its essential
subtle non-linearity and scale-dependency, which makes it
unreliable to extrapolate Newtonian intuitions. As a result, there are very
few predictions of MOND in the literature in dynamical situations
where the non-sphericity of the potential is essential. It is
encouraging that the recent work of Ciotti & Binney (2004) shows
surprisingly simple analytical scaling relations exist even for
the highly non-linear and non-spherical two-body relaxation
problem in MOND. Here we show a surprisingly simple scaling of
tides or the Roche lobe of a binary system (on either stellar or
galaxy scales) if it is in the non-linear deep-MOND regime. A
subtle difference from a naive Newtonian extrapolation is also
pointed out. We compare the predicted Roche lobe sizes with the observed
limiting sizes of Milky Way satellites (globular clusters and dwarf galaxies)
of
![]() .
.
One way to reach the deep-MOND regime so that
![]() is to be at a distance R
sufficiently far way from an isolated galaxy of total baryonic
mass M so that the gravity
is to be at a distance R
sufficiently far way from an isolated galaxy of total baryonic
mass M so that the gravity
![]() .
Here g(R) and the spherical galaxy potential
.
Here g(R) and the spherical galaxy potential ![]() are approximately related to the Newtonian gravity GM/R2 by
are approximately related to the Newtonian gravity GM/R2 by
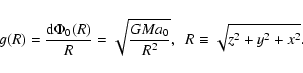 |
(3) |
The above formulation allows us to approximate the potential of,
e.g., the Milky Way galaxy with a satellite. Substitute in the
expressions for ![]() ,
g(R), R and
,
g(R), R and ![]() ,
the combined
potential is then given by
,
the combined
potential is then given by
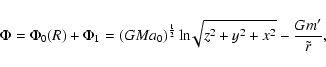 |
(6) |
Let the low-mass satellite with ![]() rotate around the
galaxy centre (fixed) with an angular velocity
rotate around the
galaxy centre (fixed) with an angular velocity
![]() ,
then particles in the corotating frame conserve the Jacobi
energy with an effective (triaxial) potential
,
then particles in the corotating frame conserve the Jacobi
energy with an effective (triaxial) potential
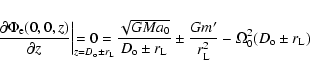 |
(9) |
The shape of the Roche lobe is defined by the contour of the
effective potential (Eq. (8)) passing through the Lagrange
point. Finding the roots analytically yields (Zhao & Tian 2005)
![\begin{displaymath}r = \left[ 1,{\sqrt{2} \over 3},
(\sqrt{10}+\!\!\sqrt{2})^{1 ...
... \right]
\left({m \over 2 M}\right)^{1 \over 3}\!\! D_{\rm o}, \end{displaymath}](/articles/aa/full/2005/47/aahe021/img69.gif) |
(11) |
If MOND is correct the Roche lobe would act as Nature's balance to
weigh the relative baryonic content of a secondary vs. a primary star,
or a satellite vs. its host galaxy. Interestingly the Roche lobe
satisfies the same scaling relation
![]() ,
but the
,
but the
![]() in strong gravity regime (Binney & Tremaine 1987)
while
in strong gravity regime (Binney & Tremaine 1987)
while
![]() in deep-MOND. E.g., in a gedanke experiment where
we take the solar system out of the Galaxy, and
increase the Earth-Sun distance from 1AU to 0.1 pc
(the separation of the widest known binary stars) so that near the
inner Lagrangian point of the system the gravity drops from the
strong regime to the weak regime.
Fixing the Earth-Sun mass ratio
in deep-MOND. E.g., in a gedanke experiment where
we take the solar system out of the Galaxy, and
increase the Earth-Sun distance from 1AU to 0.1 pc
(the separation of the widest known binary stars) so that near the
inner Lagrangian point of the system the gravity drops from the
strong regime to the weak regime.
Fixing the Earth-Sun mass ratio
![]() ,
the rescaled intermediate Roche lobe radius
,
the rescaled intermediate Roche lobe radius
![]() should decreases slowly by a subtle amount from
should decreases slowly by a subtle amount from
![]() radian (for strong gravity) to
radian (for strong gravity) to
![]() radian (for weak gravity);
cf. Eqs. (10) and (12) and see Fig. 1.
Likewise the aspect ratios of the Roche lobe evolves from
1:2/3:91/3-31/3=1:0.667:0.638 (Binney & Tremaine 1986)
to about
1:0.471:0.456, and the volume of Roche lobe evolves from
radian (for weak gravity);
cf. Eqs. (10) and (12) and see Fig. 1.
Likewise the aspect ratios of the Roche lobe evolves from
1:2/3:91/3-31/3=1:0.667:0.638 (Binney & Tremaine 1986)
to about
1:0.471:0.456, and the volume of Roche lobe evolves from
![]() to
to
![]() .
The Roche lobe is more squashed in MOND than in Newtonian gravity
(cf. Fig. 1).
.
The Roche lobe is more squashed in MOND than in Newtonian gravity
(cf. Fig. 1).
![\begin{figure}
\par {\includegraphics[width=8.8cm,clip]{He021fig1.ps} } \end{figure}](/articles/aa/full/2005/47/aahe021/Timg80.gif) |
Figure 1:
shows the
re-scaled Roche lobes (contours of the effective potential) in the
equatorial xz plane ( lower half) and in the vertical yz plane
( upper half) of a hypothetical isolated Earth-Sun binary with a
mass ratio
|
| Open with DEXTER | |
Interestingly, the same rescaled Roche radius can be predicted if we
substitute the Earth-Sun binary by a satellite (either a dwarf
spheroidal or a globular cluster) of a typical luminosity
![]() orbiting a luminous host galaxy of
orbiting a luminous host galaxy of
![]() so that the baryonic mass ratio is about Earth-Sun
mass ratio. The self-gravity around an extended object of mass
distribution m(r) becomes weak compared to a0 outside a
radius
so that the baryonic mass ratio is about Earth-Sun
mass ratio. The self-gravity around an extended object of mass
distribution m(r) becomes weak compared to a0 outside a
radius
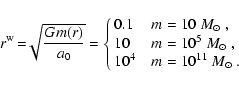 |
(13) |
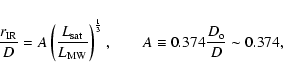 |
(14) |
The actual direct observable is the limiting angular size
![]() of a satellite
seen from the Sun's perspective. If a satellite fills the MONDian Instantaneous Roche Lobe,
we expect to observe an angular size
of a satellite
seen from the Sun's perspective. If a satellite fills the MONDian Instantaneous Roche Lobe,
we expect to observe an angular size
![]() perpendicular to the line of sight.
From these observables we can construct an observable "filling factor''
perpendicular to the line of sight.
From these observables we can construct an observable "filling factor''
![\begin{figure}
\par {\includegraphics[width=8.2cm,clip]{He021fig2.ps} } \end{figure}](/articles/aa/full/2005/47/aahe021/Timg97.gif) |
Figure 2:
shows the MONDian "filling factor''
for outer Galactic satellites (20-200 kpc), i.e., the ratio of
the observed limiting radius
|
| Open with DEXTER | |
These expectations, however, are not borne out by Fig. 2, which shows
surprisingly large scatter of the observed
![]() for
distant Milky Way satellites with comparable luminosities (
for
distant Milky Way satellites with comparable luminosities (
![]() ).
It is also difficult to understand why our expectation
).
It is also difficult to understand why our expectation
![]() (cf. Eq. (15))
is contradicted most strikingly by systems of larger tidal radii (larger symbols).
Surely observations carry errors.
The distance factor A is insensitive to the typical 10% distance error.
Satellites often change profiles at
(cf. Eq. (15))
is contradicted most strikingly by systems of larger tidal radii (larger symbols).
Surely observations carry errors.
The distance factor A is insensitive to the typical 10% distance error.
Satellites often change profiles at
![]() ,
so
,
so
![]() is well-defined with very little error.
Finally many satellites are in mild MOND regime with a Roche lobe size more rigorously given by (Zhao & Tian 2005)
is well-defined with very little error.
Finally many satellites are in mild MOND regime with a Roche lobe size more rigorously given by (Zhao & Tian 2005)
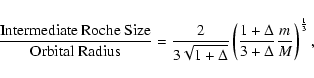 |
(16) |
In short, it is likely challenging for any theory of structure formation of a baryonic MOND universe to explain the puzzling large scatter in the rescaled Roche radius without fine-tuning of satellite orbits and mass-to-light ratios. It is less challenging for dark matter theories; 105-star satellite objects could form either inside or outside a small dark halo. The scatter of satellite sizes echos with similar scatter of Einstein ring sizes around high-redshift lens galaxies (see lensing models of Zhao et al. 2005), highlighting possible difficulties of mass-trace-light models.
Acknowledgements
H.S.Z. thanks the referee for constructive comments, LanLan Tian and Huanyuan Shan for help, and partial support from Chinese NSF grant 10428308.