- ... UK
![[*]](/icons/foot_motif.gif)
- PPARC Advanced Fellow.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... China
![[*]](/icons/foot_motif.gif)
- Outstanding Young Overseas
Scholar.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... factor
![[*]](/icons/foot_motif.gif)
- The "dielectric index''
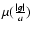 is more sensitive to perturbation along
the external field
is more sensitive to perturbation along
the external field
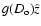 direction than perpendicular because
direction than perpendicular because
![$\vert{\vec g}+{\rm d}{\vec g}\vert=\left[(g_{D_{\rm o}}+{\rm d} g_z)^2
+({\rm d} g_x)^2 + ({\rm d} g_y)^2\right]^{1 \over 2}$](/articles/aa/full/2005/47/aahe021/img44.gif) depends on the perturbation
depends on the perturbation
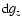 to first order, and
to first order, and
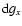 and
and
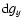 to second order.
to second order.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... masses
![[*]](/icons/foot_motif.gif)
- Dimensional analysis
only cannot tell whether the dimensionless
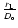 scales like
scales like
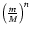 or
or
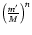 ,
where
,
where
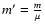 is the modified inertia (cf. Eq. (4)).
is the modified inertia (cf. Eq. (4)).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.