A&A 443, 781-791 (2005)
DOI: 10.1051/0004-6361:20053025
SALT: a spectral adaptive light curve template for type Ia supernovae
J. Guy - P. Astier - S. Nobili - N. Regnault - R. Pain
Laboratoire de Physique Nucléaire et des Hautes Énergies,
IN2P3, CNRS, Universités Paris VI et Paris VII,
4 place Jussieu,
Tour 33, Rez de chaussée,
75252 Paris Cedex 05, France
Received 8 March 2005 / Accepted 23 June 2005
Abstract
We present a new method to
parameterize type Ia Supernovae (SN Ia) multi-color light curves.
The method was developed in order to analyze the large number of
SN Ia multi-color light curves measured in current high-redshift projects.
The technique is based on empirically modeling SN Ia luminosity variations as a function of phase,
wavelength, a shape parameter, and a color parameter. The model is trained with a sample of
well-measured nearby SN Ia and then tested with an independent set of supernovae by
building an optimal luminosity distance estimator that combines the supernova rest-frame luminosity,
shape parameter, and color reconstructed with the model. The distances we measure using B-
and V-band data show a dispersion around the Hubble line comparable or lower than obtained
with other methods. With this model, we are able to measure distances using U- and B-band
data with a dispersion of
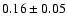 around the Hubble line.
around the Hubble line.
Key words: supernovae: general - cosmology: observations
Type Ia supernovae (SNe Ia) are a powerful tool for studying the evolution
of the luminosity distance as a function of redshift and for subsequently constraining the
cosmological parameters. SNe Ia are indeed very luminous and "standardizable'' candles, and
have lead to the discovery of the acceleration of the Universe (Riess et al. 1998; Perlmutter et al. 1999).
Although often described as a homogeneous class of objects, SNe Ia exhibit variability in
light curve shapes, colors, intrinsic luminosity, and spectral features. Finding
correlations among SN Ia observables is motivated by improving
the estimation of their intrinsic luminosity on an event-by-event basis, in
order to reduce the scatter in luminosity distance estimates.
The main correlations observed in photometric measurements are:
The case of the brighter-bluer relation is interesting.
Even if authors fully agree neither on the origin of the effect nor on the
strength of the correlation, most, if not all, recent attempts to build a SN Ia Hubble
diagram have made use of color in their distance
estimator![[*]](/icons/foot_motif.gif) .
Riess et al. (1996b) summarizes previous work on the subject and proposes
a way to reconcile divergent interpretations of data by taking into account
the correlation between light curve shape and color.
New methods using color information have also been recently
proposed to estimate luminosity
distances (see for example Wang et al. 2003,2005).
We will bring to the
debate our own estimations of the correlation strength and its
wavelength dependence.
.
Riess et al. (1996b) summarizes previous work on the subject and proposes
a way to reconcile divergent interpretations of data by taking into account
the correlation between light curve shape and color.
New methods using color information have also been recently
proposed to estimate luminosity
distances (see for example Wang et al. 2003,2005).
We will bring to the
debate our own estimations of the correlation strength and its
wavelength dependence.
Cosmological measurements using SNe Ia are based on comparing
nearby and distant objects. In order to reduce the sources of
systematic uncertainties, it is important that all distances are
derived using the same procedure, especially when considering
large samples such as those being collected by the
ESSENCE![[*]](/icons/foot_motif.gif) or
SNLS
or
SNLS![[*]](/icons/foot_motif.gif) projects. To analyze
these data sets, the following constraints have to be taken into
account:
projects. To analyze
these data sets, the following constraints have to be taken into
account:
- High redshift objects often lack late-time photometric data
(or have one of too poor quality)
which makes it impracticable to estimate color from late-time
data as proposed by
Lira et al. (1998).
- Above redshifts
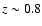 ,
rest-frame U-band measurements have to be used
because of the limitation of silicon
detectors.
Incorporating rest-frame U-band measurements on the same footing
as the commonly used rest-frame B- and V-band data is hence highly
desirable.
,
rest-frame U-band measurements have to be used
because of the limitation of silicon
detectors.
Incorporating rest-frame U-band measurements on the same footing
as the commonly used rest-frame B- and V-band data is hence highly
desirable.
- Applying cuts on light curve parameters should be prohibited since
the resolution on these parameters follows the photometric resolutions and
hence degrades with redshift, therefore biasing the event sample.
In particular, cuts on
colors to eliminate reddened events are to be avoided.
Various techniques have been used to estimates distances.
Phillips (1993) and
Perlmutter et al. (1997) fit one band at a time, and derive distances
from light curve parameters measured in different bands (usually B and V bands), sometimes relying on late time measurements to measure host
galaxy extinction. A recent and refined version of this approach can
be found in Wang et al. (2005), and in Wang et al. (2003) it is proposed to fit B-Vas a function of B. These methods do not make use of rest-frame U-band
measurements.
Nugent et al. (2002)
discuss in detail the problems associated with SN Ia
U-band photometry. They mention in particular the apparent large intrinsic
variations of the UV luminosity among similar supernovae as well as
our lack of understanding of the SN Ia UV photometry - principally due
the uncertainties which affect the large extinction corrections which
have to be applied to the data. Nevertheless, it is important to try and
incorporate rest-frame U-band data to estimate distances.
An extension of Perlmutter et al. (1997) to rest-frame U-band data was
developed in Knop et al. (2003), but at the expense of adding a large distance
systematic (and probably statistical) uncertainty. Similarly, the MLCS method
(Riess et al. 1996a,1995) has been extended to
include U-band measurements
under the name of MLCS2k2 (Jha 2002) and used in Riess et al. (2004), but
also at the expense of a worsened distance resolution (Jha 2002).
We will show that our model predicts
light curves for any band located between rest-frame U and R bands and
that we are
able to get a similar or better distance resolution
with both rest-frame (B,V) and (U,B) band pairs.
We propose here to parameterize the
light curve model with a minimal parameter set: a luminosity parameter,
a decline rate parameter and a single color parameter. Our approach
will be to build a phenomenological model of the expected SN flux,
continuously varying with phase, wavelength, decline rate and color,
in order to capture all these features at once.
This approach offers
several practical advantages which make it easily applicable to
high-redshift SNe Ia currently measured in large projects.
First, the k-corrections are built into the model and not applied to
the data. This allows one to propagate all the uncertainties directly
from the measurement errors.
More importantly, when needed, we make use of the SN rest-frame
U-band fluxes to estimate the supernova distances.
In Sect. 2 we describe the semi-analytic model used.
We then describe, in Sect. 3, how the coefficients of the model are determined
by an iterative training based
on a set of well-sampled nearby SNe Ia taken from the literature. We also
highlight some properties of the resulting model. At this stage, the aim
is to model multi-color light curves and not to estimate luminosity distances.
The model is tested in Sect. 4 with an independent set of SNe Ia in the Hubble flow.
A luminosity distance estimate is then constructed from the fitted parameters of the
light curve model. It is used
to build Hubble diagrams successively from (B,V) and (U,B)
light curve pairs.
In order to assess the precision of this approach, we compare
distance estimates of the same events obtained from
the (U,B) and (B,V) band pairs and
with other distance estimators.
2 The light curve model
As already mentioned, we choose to parameterize light curves (more precisely
light curve pairs or light curve triplets when available) using a single
luminosity,
a single shape parameter and a single color.
The choice among possible implementations is largely arbitrary. We
choose the following parameters, which enable comparisons to be made with previous works:
- f0: a global intensity parameter which varies with redshift like
the inverse of the luminosity distance squared,
- s: a time stretch factor as the decline rate indicator (Perlmutter et al. 1997).
In Goldhaber et al. (2001), this parameter is shown to apply to the
rising part of the light curve as well. However, while the stretch paradigm
describes
well the bright part of the B light curve, it does poorly
at late time. It also fails to capture
the shape variations in the other bands. This is why our model
uses the stretch parameter as an index rather than the stretch paradigm itself.
As described below, by construction our model follows exactly the
stretch paradigm in the B band.
- c =
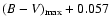 ,
where
,
where
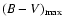 is measured
at B maximum, and -0.057 is the chosen reference color (Vega magnitudes)
of a SN Ia.
is measured
at B maximum, and -0.057 is the chosen reference color (Vega magnitudes)
of a SN Ia.
-
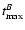 :
the date of maximum in the rest-frame B band.
:
the date of maximum in the rest-frame B band.
With these definitions, the expected counting rate
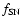 in a given pass-band T, of a supernova
at redshift z, and at a phase
in a given pass-band T, of a supernova
at redshift z, and at a phase
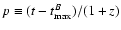 ,
can be written:
,
can be written:
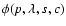 is a model of the SN Ia energy luminosity per
unit wavelength. It may vary with the supernova stretch and color.
Note that the potential extinction by dust in the host galaxy is not explicit
in the equation. Instead, we choose to incorporate it in the model
is a model of the SN Ia energy luminosity per
unit wavelength. It may vary with the supernova stretch and color.
Note that the potential extinction by dust in the host galaxy is not explicit
in the equation. Instead, we choose to incorporate it in the model
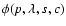 as discussed below.
as discussed below.
Building an
average spectral template 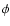 as a function of phase, wavelength, color and
stretch from observations is complicated because of the inhomogeneity and
incompleteness of published
data. Although some spectral features have been correlated with
stretch, we do not have yet a complete knowledge of spectral
diversity as a function of phase. In most of the approaches to SN Ia
light curve fitting, the limited knowledge of spectral variability
impacts on the accuracy of cross-filter k-corrections, defined as
expected ratios of fluxes in different bands at the same phase
(Kim et al. 1996; Nugent et al. 2002).
as a function of phase, wavelength, color and
stretch from observations is complicated because of the inhomogeneity and
incompleteness of published
data. Although some spectral features have been correlated with
stretch, we do not have yet a complete knowledge of spectral
diversity as a function of phase. In most of the approaches to SN Ia
light curve fitting, the limited knowledge of spectral variability
impacts on the accuracy of cross-filter k-corrections, defined as
expected ratios of fluxes in different bands at the same phase
(Kim et al. 1996; Nugent et al. 2002).
In Nugent et al. (2002), it was shown that the variation in
k-corrections from one supernova to another depends
primarily on the supernova color,
and to a lesser extent on spectral
features![[*]](/icons/foot_motif.gif) .
Hence we neglected the variability of those spectral features
in the modeling of light curves.
.
Hence we neglected the variability of those spectral features
in the modeling of light curves.
In order to implement stretch dependent light curve shapes and colors
we therefore used the following approximation:
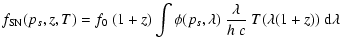 |
|
|
|
![$\displaystyle \times \ \exp \left[ -0.4 ~ \ln(10) \times {\cal K}(p_s, \lambda_T, s, c) \right]$](/articles/aa/full/2005/45/aa3025-05/img20.gif) |
|
|
(1) |
where
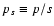 is a stretch-corrected phase. This functional
form defines the light curve model.
is a stretch-corrected phase. This functional
form defines the light curve model.
In Eq. (1), 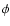 no longer depends explicitly on s and c, and
no longer depends explicitly on s and c, and
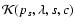 is a smooth "correction'' function of our four
variables.
is a smooth "correction'' function of our four
variables. 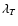 is the central wavelength of the filter T.
is the central wavelength of the filter T. 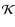 enables one to implement light curve shape variations
that are more complicated than simple dilation of the time scale,
along with stretch dependent colors.
As described below,
enables one to implement light curve shape variations
that are more complicated than simple dilation of the time scale,
along with stretch dependent colors.
As described below, 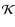 varies smoothly
with
varies smoothly
with 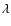 ;
this justifies placing it outside the
integral over wavelength. We also
considered
keeping
;
this justifies placing it outside the
integral over wavelength. We also
considered
keeping
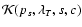 inside
the integral. It changed the results of the fits by less than 1%,
while the computing time was multiplied by a factor of 10.
inside
the integral. It changed the results of the fits by less than 1%,
while the computing time was multiplied by a factor of 10.
Equation (1) implements
k-corrections for an average SN Ia, conforming to the common
practice. The approach proposed here will be easy to
adapt when constructing a stretch-dependent spectral
template becomes possible.
The k-corrections are usually applied to data. Here, they are
incorporated into the model. This offers a few practical advantages:
first, light curves can be generated for arbitrary pass-bands (within
the spectral coverage of 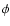 and
and 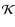 ); light curves in the observed
pass-bands can be directly fitted to the data.
Second, the light curve parameter
uncertainties extracted from the fit incorporate all uncertainties
propagated from measurement uncertainties; for example, uncertainties
introduced in the k-corrections by the possibly poor determination
of the date of maximum and/or color are propagated into the
parameters uncertainties.
); light curves in the observed
pass-bands can be directly fitted to the data.
Second, the light curve parameter
uncertainties extracted from the fit incorporate all uncertainties
propagated from measurement uncertainties; for example, uncertainties
introduced in the k-corrections by the possibly poor determination
of the date of maximum and/or color are propagated into the
parameters uncertainties.
The functions 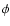 and
and 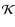 define the model. Once they are determined, one can fit
the supernova photometric data points, measured in a minimum of
two pass-bands,
to estimate f0, s, c, and a date of B maximum light,
which is a nuisance parameter. With only one passband, c must be held fixed.
define the model. Once they are determined, one can fit
the supernova photometric data points, measured in a minimum of
two pass-bands,
to estimate f0, s, c, and a date of B maximum light,
which is a nuisance parameter. With only one passband, c must be held fixed.
For
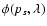 ,
we use a template spectrum
assembled by Nugent (Nugent et al. 2002 and private communication)
smoothed along the phase (time) axis, and normalized as a function of phase
to the B-band light curve template "Parab -18'' of Goldhaber et al. (2001).
Any smooth variation of the template
,
we use a template spectrum
assembled by Nugent (Nugent et al. 2002 and private communication)
smoothed along the phase (time) axis, and normalized as a function of phase
to the B-band light curve template "Parab -18'' of Goldhaber et al. (2001).
Any smooth variation of the template 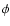 with phase or wavelength is irrelevant
at this level, since it may be changed by the function
with phase or wavelength is irrelevant
at this level, since it may be changed by the function
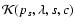 .
The only important quantities in
.
The only important quantities in
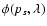 are the SN Ia spectral features,
intended to be realistic on average.
are the SN Ia spectral features,
intended to be realistic on average.
The empirical correction function 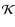 is implemented as a sum of two polynomials:
is implemented as a sum of two polynomials:
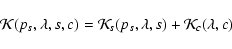 |
(2) |
where we explicitly separate the corrections associated with the parameters s and c to
clarify their interpretation.
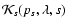 modifies the shape of light curves and absorbs
any stretch-color relation except for the
modifies the shape of light curves and absorbs
any stretch-color relation except for the
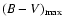 color.
Indeed we want c to describe exactly the
color.
Indeed we want c to describe exactly the
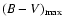 color.
color.
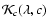 is then a color correction as a function of wavelength and color.
is then a color correction as a function of wavelength and color.
In order to remove all degeneracies among coefficients, the model
must fulfill the following constraints:
where 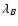 and
and 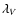 refer to the mean wavelengths of the B and V filters.
The first constraint ensures that the parameter s actually defines the stretch
in B band, since the template is not modified for
refer to the mean wavelengths of the B and V filters.
The first constraint ensures that the parameter s actually defines the stretch
in B band, since the template is not modified for
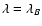 .
The
remaining constraints define c as the B-V color (relative to the spectral
template) at maximum B, for all stretches. Note that other colors may
(and in fact will) depend on s at fixed c.
f0 describes the actual peak flux in B. It is in no way "corrected''
for the brighter-slower relation.
.
The
remaining constraints define c as the B-V color (relative to the spectral
template) at maximum B, for all stretches. Note that other colors may
(and in fact will) depend on s at fixed c.
f0 describes the actual peak flux in B. It is in no way "corrected''
for the brighter-slower relation.
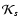 is implemented as a polynomial of degree Dp in phase,
is implemented as a polynomial of degree Dp in phase,
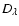 in
in 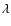 and Ds in stretch respectively. Similarly,
and Ds in stretch respectively. Similarly,
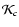 is a polynomial of degree Dp in phase and Dc in color. In
this study, we chose for the degrees of polynomials
is a polynomial of degree Dp in phase and Dc in color. In
this study, we chose for the degrees of polynomials
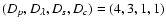 .
The large degree in phase permits a
detailed adaptation of the model light curve shapes to the actual
data. The other degrees correspond to the minimal number of
coefficients (a degree 3 in wavelength is chosen to adapt colors in
.
The large degree in phase permits a
detailed adaptation of the model light curve shapes to the actual
data. The other degrees correspond to the minimal number of
coefficients (a degree 3 in wavelength is chosen to adapt colors in
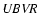 ,
independently). The
,
independently). The 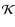 polynomials are then defined by 48
coefficients, but
the constraints reduce the number of independent coefficients to 34. There are 32 free coefficients for
polynomials are then defined by 48
coefficients, but
the constraints reduce the number of independent coefficients to 34. There are 32 free coefficients for
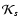 and 2 free
coefficients for
and 2 free
coefficients for
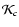 .
We
will call "training'' the determination of these coefficients from
measurements of nearby SNe Ia.
.
We
will call "training'' the determination of these coefficients from
measurements of nearby SNe Ia.
The value of f0 depends on the normalization of the spectral
template 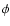 .
This is not an issue
when comparing nearby and distant supernovae to measure cosmological
parameters, since only flux ratios matter: all objects have to be
fitted using the same model. For H0measurements, one would need to normalize
.
This is not an issue
when comparing nearby and distant supernovae to measure cosmological
parameters, since only flux ratios matter: all objects have to be
fitted using the same model. For H0measurements, one would need to normalize 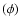 using SNe Ia at known
distances, but we will not perform this here.
using SNe Ia at known
distances, but we will not perform this here.
More important is the apparent dependence of the value of f0 with respect
to the normalization
of the transmission T (Eq. (1)). Since we aim at fitting multi-color
light curves, observed with different
instruments, with a single set of parameters (f0,s,c), it is mandatory to
remove this dependence.
All photometric data are expressed in units of the integrated flux
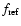 (deduced from the zero point) of a known standard spectrum
(deduced from the zero point) of a known standard spectrum
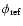 (e.g. Vega).
While the functional form of
(e.g. Vega).
While the functional form of
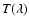 is
determined by optical transmission measurements its normalization
can be determined from
is
determined by optical transmission measurements its normalization
can be determined from
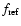 and
and
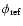 via the relation
via the relation
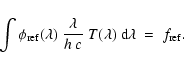 |
(3) |
The filter transmissions are usually published as series of numbers
(as in Bessell 1990), and this leads to ambiguities: for example,
Suntzeff et al. (1999) writes "Note that Bessell (1990)
defines the sensitivity function as the product of the quantum
efficiency of the detector+telescope, the filter transmission curve,
the atmospheric extinction, and a linearly increasing function of
wavelength.''. The ambiguity is whether the transmission refers to
signal per unit energy, or signal per photon flux.
Attributing dimensions to transmissions solves the ambiguity.
There have also been concerns about the relative weights of the
different wavelengths in the integrals over wavelength (Nugent et al. 2002),
namely whether one should sum photons or energies.
If one aims at reproducing the instrument response to an arbitrary
spectral energy density, the mathematical integrals should mimic
the physical integration process of the instrument (Fukugita et al. 1996).
For example, if one considers a CCD-based
observing system, the effective transmission
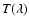 will be proportional to
a number of photo-electrons per photon.
So one should not integrate photon counts
nor energies, but charge on the detector (or ADC counts).
will be proportional to
a number of photo-electrons per photon.
So one should not integrate photon counts
nor energies, but charge on the detector (or ADC counts).
Since f0 describes the observed luminosity in the B band (because of the constraints applied to the corrections), the
model only incorporates stretch-shape and stretch-color relations, but
no correlation involving luminosity. This option was chosen in order
to allow us to train the model with objects at unknown distances, in
particular the nearby objects in the sample of Jha (2002) measured
in the U band. If one offsets all magnitudes of each training
object by an arbitrary amount, possibly different for each object, the
resulting model will not change. One could then consider incorporating
high redshift objects into the training,
but we choose not to do it here.
The model was trained and tested using a sample of published nearby
supernova light curves. We collected 122
SNe Ia for which B- and V-band light curves are available in
the literature, including data from Riess et al. (1996b); Hamuy et al. (1996b) and
Jha (2002) for a total of 94 objects, and 28 additional supernovae
collected from various sources (see the caption of
Table 1).
Objects were then selected based on two main criteria.
First, we kept
supernovae with at least two measurements before
the maximum in the B or the V band. This is necessary to ensure
that the date of maximum is well defined and that the measurements
can safely be used as a function of phase.
Out of the whole sample, 56 SNe satisfied this criterion. Then
under-luminous peculiar supernovae:
SN 1991bg,
SN 1998bp, SN 1998de and SN 1999by (Howell 2001; Li et al. 2001b), and the
peculiar objects SN 2000cx and SN 2002er
(Pignata et al. 2004; Li et al. 2001a) were rejected from our sample.
There are a number of reasons for this
choice; the most important one being the spectral difference between normal
and SN 1991bg-like SNe Ia. Since our model is built using a spectral
template describing the features of the average normal SN Ia, it is
not well suited for describing very different objects, such as
SN 1991bg-like events. We note that, this is not a constraint for
cosmological studies since, so far, no under-luminous SNe have been
found in distant SN searches. Furthermore, if present at high-redshift,
these objects would easily be
identified both from spectroscopy and from their B-V color
evolution (see for instance Phillips et al. 1999; Garnavich et al. 2004).
SN 1991T-like events were kept in
the sample. This "sub-class'' of over-luminous SNe Ia is
spectroscopically identified by the presence of unusually weak
absorption lines during the pre-maximum phase. These are more
difficult to identify than their under-luminous counterparts in low
signal-to-noise spectra, such as those usually available for high
redshift SNe.
Moreover, the B-V color evolution is not particularly
different from the one of normal SNe. Ideally, one should use a
different spectral template for fitting this kind of events. We
estimate the errors introduced in the k-corrections using a standard
SN Ia spectral template
to be of a few percent in the
worst cases, and well within the final dispersion in the peak
luminosity of SNe Ia. We further note that, the uncertainty due to
using a non optimal spectral template is analogous to the
uncertainty in the cross filter k-corrections used in standard methods.
The resulting sample of 50 SNe was then split into two sets: a training
sample and a test sample. The training sample was used to adjust the
coefficients of the polynomials of the model. It contains all the
supernovae with redshifts smaller than 0.015 (not in the Hubble flow)
and 6 supernovae at
redshifts above 0.015, for which with U-band data was available, in order
to improve the model in this wavelength region. The training sample
contains the 34
supernovae listed in Table 1.
The test sample contains 26 supernovae (Table 2).
Note that the two samples are not completely independent. Indeed, they
share ten supernovae with U-band light curves, since such events are
rather scarce.
Table 1:
The training sample of type Ia supernovae light curves.
Table 2:
The test sample of type Ia supernovae light curves.
The data was not pre processed in any way prior to fitting. To account
for the Milky Way extinction, we incorporate it into the instrument
transmission, using the law from Cardelli et al. (1989) with a color
excess E(B-V) obtained from Schlegel et al. (1998) dust maps at the
position of the object to fit.
All the published nearby supernova magnitudes are expressed in the
Johnson-Cousins
 system. In Eq. (1), we use models
of the instrument transmissions as a function of wavelength. We
adopted the transmission functions published by Bessell (1990),
and interpreted them as
system. In Eq. (1), we use models
of the instrument transmissions as a function of wavelength. We
adopted the transmission functions published by Bessell (1990),
and interpreted them as
 (see Eq. (1)),
i.e. counts per unit energy, following a footnote of Suntzeff et al. (1999).
(see Eq. (1)),
i.e. counts per unit energy, following a footnote of Suntzeff et al. (1999).
Training the model consists in determining the
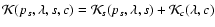 correction function
(Eq. (2)) using the training sample data
in the
correction function
(Eq. (2)) using the training sample data
in the
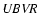 bands. The R band was introduced to avoid relying
on extrapolation for measurements beyond rest-frame V band.
We start with a first guess:
bands. The R band was introduced to avoid relying
on extrapolation for measurements beyond rest-frame V band.
We start with a first guess:
and we use an iterative algorithm which can be sketched as follows:
- 1.
- Fit the light curves using the current determination of
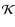 .
.
- 2.
- Fit
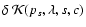 ,
an instance of the
,
an instance of the 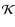 function, on the light curve residuals.
During this step, identify and remove the outliers data points.
function, on the light curve residuals.
During this step, identify and remove the outliers data points.
- 3.
-
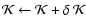 .
.
- 4.
- GOTO step 1, until
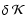 becomes negligible.
becomes negligible.
All the available data, i.e. the
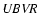 residuals, up to large
phases were used to determine the
residuals, up to large
phases were used to determine the 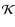 function (step 2). However, not all the data points were used to fit the light
curves (step 1):
the R-band data was not used
and
only
function (step 2). However, not all the data points were used to fit the light
curves (step 1):
the R-band data was not used
and
only 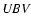 photometric points with phases ranging from -15 days to
+35 days were used since we are mostly interested in describing the
rest-frame
photometric points with phases ranging from -15 days to
+35 days were used since we are mostly interested in describing the
rest-frame 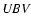 central part of the supernova light curves.
central part of the supernova light curves.
3.3 Results of the training
The fit converged after four iterations.
2480 measurement points were fitted, and 39 were discarded as
outliers (at the 3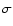 level). Compared to the number of free coefficients
of the model, we can safely conclude that the model is not over-trained.
The standard deviations of the residuals
to the model in
level). Compared to the number of free coefficients
of the model, we can safely conclude that the model is not over-trained.
The standard deviations of the residuals
to the model in
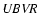 are respectively of
0.09, 0.09, 0.06, 0.07 mag.
Figure 1 shows the final U, B, V and R templates
obtained at the end of the process as a function of stretch.
By construction, the rest-frame B and V-band magnitudes at maximum
do not vary with stretch.
We find a strong dependence of
are respectively of
0.09, 0.09, 0.06, 0.07 mag.
Figure 1 shows the final U, B, V and R templates
obtained at the end of the process as a function of stretch.
By construction, the rest-frame B and V-band magnitudes at maximum
do not vary with stretch.
We find a strong dependence of
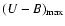 with
stretch (
with
stretch (
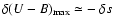 ,
compatible with Jha 2002),
which is an essential feature for the model to reproduce in order to
estimate a reliable color in the wavelength range
between U and B. The model also manages to reproduce a
a stretch-dependent secondary shoulder in the R band. We also notice
that the R-band light curves cross each-other for different values of the
stretch. This reproduces well the fact that the brighter slower relation
is weaker in the redder pass-bands, as noted by Phillips et al. (1999).
The residuals to the light curve fit are shown Fig. 2.
,
compatible with Jha 2002),
which is an essential feature for the model to reproduce in order to
estimate a reliable color in the wavelength range
between U and B. The model also manages to reproduce a
a stretch-dependent secondary shoulder in the R band. We also notice
that the R-band light curves cross each-other for different values of the
stretch. This reproduces well the fact that the brighter slower relation
is weaker in the redder pass-bands, as noted by Phillips et al. (1999).
The residuals to the light curve fit are shown Fig. 2.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{3025f8.eps}
\end{figure}](/articles/aa/full/2005/45/aa3025-05/Timg58.gif) |
Figure 1:
The UBVR template light curves obtained after the training
phase for different values of the stretch and null color.
Note the strong variations of the U-band maximum with
the stretch.
Note also the after max shoulders in the V and R bands.
The model also reproduces well the fact that
the brighter-slower relation is weaker in the R band than in the B or V bands.
The model does not incorporate the brighter-slower correlation.
The apparent brighter-slower correlation for the U band is, in fact, a stretch-color correlation. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{3025f7.eps}
\end{figure}](/articles/aa/full/2005/45/aa3025-05/Timg59.gif) |
Figure 2:
Residuals to the light curve fit as a function of phase, for supernovae from the training sample (open symbols) and the test sample (filled symbols).
There is no significant difference between the distributions obtained with both samples which proves that the model is not over-trained.
The systematic residuals as a function of phase are a direct consequence of the limited number of parameters (5) used to implement the corrections
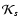 as a function of phase. Increasing this number would remove this systematic trend in residuals, but some parameters would be poorly constrained in the U band where photometric data is scarce.
as a function of phase. Increasing this number would remove this systematic trend in residuals, but some parameters would be poorly constrained in the U band where photometric data is scarce. |
| Open with DEXTER |
Figure 3 represents the color correction
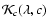 for c=0.1 compared to the dust extinction law
from Cardelli et al. (1989). Interestingly enough, the law we obtain follows
pretty well that of Cardelli in the R band but not
in the U band where we get a stronger dependence on c. Also
shown (shaded area) is the uncertainty on
for c=0.1 compared to the dust extinction law
from Cardelli et al. (1989). Interestingly enough, the law we obtain follows
pretty well that of Cardelli in the R band but not
in the U band where we get a stronger dependence on c. Also
shown (shaded area) is the uncertainty on
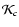 derived from the
derived from the 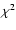 increment (normalized to the number of supernovae)
of the fit to the light curve residuals.
The Cardelli law in the U band is at 3.7 standard deviation from the best fit value.
increment (normalized to the number of supernovae)
of the fit to the light curve residuals.
The Cardelli law in the U band is at 3.7 standard deviation from the best fit value.
As a consequence, we deduce that the relation between E(B-V) and E(V-R) are
very similar (i.e. indistinguishable) to the ones expected from
reddening by dust. This similarity, noted by Riess et al. (1996b), does not prove however
that c can be interpreted as reddening by dust; an additional requirement for this
hypothesis to be valid would be that the peak B-band magnitude increases with c
by a value of
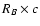 .
We will see that this is not the case in the next
section.
Let us also emphasize that the stretch dependent part of the U-B and V-R
colors are included in the stretch dependent term
.
We will see that this is not the case in the next
section.
Let us also emphasize that the stretch dependent part of the U-B and V-R
colors are included in the stretch dependent term
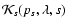 ,
and
not in the color curve of Fig. 3.
,
and
not in the color curve of Fig. 3.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3025f4.eps}
\end{figure}](/articles/aa/full/2005/45/aa3025-05/Timg62.gif) |
Figure 3:
The color correction
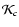 as a function of wavelength for a value
of c of 0.1 (thick line). The shaded area corresponds to one standard deviation
to the best fit value. The dashed curve represents the extinction with respect
to B band,
as a function of wavelength for a value
of c of 0.1 (thick line). The shaded area corresponds to one standard deviation
to the best fit value. The dashed curve represents the extinction with respect
to B band,
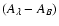 ,
from Cardelli et al. (1989) with RV=3.1
and
E(B-V)=0.1. The curves are compatible in the R band but not in
the U band (by construction they match in B and V bands as illustrated with
the open circles). ,
from Cardelli et al. (1989) with RV=3.1
and
E(B-V)=0.1. The curves are compatible in the R band but not in
the U band (by construction they match in B and V bands as illustrated with
the open circles). |
| Open with DEXTER |
4 Performance study
Once the correction function
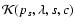 is determined, we can
fit the model on the sample of nearby SN Ia light curves
listed in Table 2.
This allows us to perform various consistency checks, in order to make
sure that the model describes well the
is determined, we can
fit the model on the sample of nearby SN Ia light curves
listed in Table 2.
This allows us to perform various consistency checks, in order to make
sure that the model describes well the 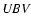 photometry of SNe Ia.
photometry of SNe Ia.
A first test consists in checking the ability of the model to reproduce the
shape and color features of the independent set of SNe Ia. This is
demonstrated in Fig. 2 which shows the residuals to
the fits of light curves of SNe from the test sample.
The global intensity parameter f0 is proportional to
dL(z)-2
and inversely
proportional to the normalization of 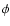 .
One can define a rest-frame B
magnitude m*B (Perlmutter et al. 1997) which removes this artificial
dependence on the model normalization,
.
One can define a rest-frame B
magnitude m*B (Perlmutter et al. 1997) which removes this artificial
dependence on the model normalization,
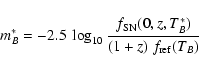 |
(4) |
where
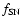 and
and
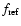 are respectively defined by Eqs. (1)
and (3), TB is the transmission of the B filter and
are respectively defined by Eqs. (1)
and (3), TB is the transmission of the B filter and
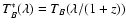 is a redshifted B transmission. One can check
that m*B varies as
is a redshifted B transmission. One can check
that m*B varies as
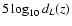 with redshift and that
with redshift and that
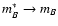 for
for 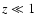 ,
where mB is the conventional B magnitude.
,
where mB is the conventional B magnitude.
We incorporate the Hubble parameter dependence of dL in a constant parameter
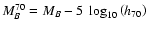 ,
which is the average absolute
magnitude of a SN Ia with s=1 and c=0, for a value of the Hubble
parameter of 70 km s-1 Mpc-1.
,
which is the average absolute
magnitude of a SN Ia with s=1 and c=0, for a value of the Hubble
parameter of 70 km s-1 Mpc-1.
As mentioned in the introduction, the peak luminosity of SNe Ia is
correlated to stretch and color, so we may build a distance estimator
that accounts
for those correlations and as a result reduces the dispersion.
Following Tripp (1998), we adopt linear corrections of
coefficients 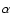 and
and 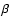 respectively
for stretch and color. The distance estimator is then
respectively
for stretch and color. The distance estimator is then
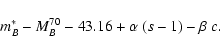 |
(5) |
Its expectation value for a supernova at redshift z is
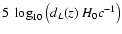 .
Since our goal is here to test the distance estimator rather than actually perform
a cosmological fit, we impose the "concordance'' cosmological parameters
(
.
Since our goal is here to test the distance estimator rather than actually perform
a cosmological fit, we impose the "concordance'' cosmological parameters
(
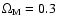 and
and
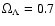 )
when fitting MB70,
)
when fitting MB70, 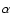 and
and 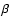 and
apply the method to build low-z Hubble diagrams using
successively (B,V) only and (U,B) only light curves of supernovae from the test sample
(Table 2). In general, rest-frame (U,B,V) light curve triplets
should be used, when available, to determine the light curve parameters.
and
apply the method to build low-z Hubble diagrams using
successively (B,V) only and (U,B) only light curves of supernovae from the test sample
(Table 2). In general, rest-frame (U,B,V) light curve triplets
should be used, when available, to determine the light curve parameters.
4.1.1 Hubble diagram in BV only
Using B- and V-band only light curves of supernovae
with redshifts larger than 0.015 from the test sample, we obtain:
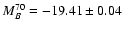 ,
,
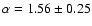 and
and
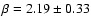 .
The standard deviation of residuals is
.
The standard deviation of residuals is
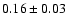
![[*]](/icons/foot_motif.gif) .
Uncertainties on mB,s,c along with their covariance were included in
the fit
.
Uncertainties on mB,s,c along with their covariance were included in
the fit![[*]](/icons/foot_motif.gif) , we also considered an uncertainty on
redshifts due to peculiar velocities of 300 km s-1; an additional
"intrinsic'' dispersion of 0.13
is needed in order to get a
, we also considered an uncertainty on
redshifts due to peculiar velocities of 300 km s-1; an additional
"intrinsic'' dispersion of 0.13
is needed in order to get a 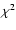 per degree of
freedom of 1.
The resulting Hubble diagram as well as the
observed brighter-slower and brighter-bluer relations are shown
Fig. 4.
per degree of
freedom of 1.
The resulting Hubble diagram as well as the
observed brighter-slower and brighter-bluer relations are shown
Fig. 4.
![\begin{figure}
\par\includegraphics[width=6.1cm,clip]{3025f3.eps}\vspace*{3mm}
\...
...f5.eps}\vspace*{3mm}
\includegraphics[width=5.9cm,clip]{3025f9.eps}
\end{figure}](/articles/aa/full/2005/45/aa3025-05/Timg80.gif) |
Figure 4:
From top to bottom: residuals to the Hubble diagram as a function of
redshift, stretch s and color c indexes for supernovae of the test sample
fitted in B and V bands. SNe with redshifts smaller than 0.015 are labeled
with opened symbols. |
| Open with DEXTER |
Our approach to estimating distances easily compares to the
one adopted in Tripp (1998): the main differences are the light curve
model and the brighter-slower parameterization. When we fit
the same SNe sample (The Calán-Tololo sample from Hamuy et al. 1996a),
a value of
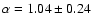 and
and
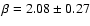 are obtained, which
compare well to
are obtained, which
compare well to
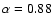
![[*]](/icons/foot_motif.gif) ,
,
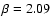 of Tripp (1998),
based on peak luminosity, color, and decline rate estimates from
Hamuy et al. (1996a). We conclude that our model correctly reproduces
basic parameter estimations of previous works.
of Tripp (1998),
based on peak luminosity, color, and decline rate estimates from
Hamuy et al. (1996a). We conclude that our model correctly reproduces
basic parameter estimations of previous works.
Concerning the interpretation of the brighter-bluer correlation,
we find a value of 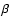 which is
incompatible with RB=4.1, expected for extinction by dust analogous
to the observed law in the Milky Way. The value we find is compatible with
those found in previous works (see Tripp 1998 and references therein).
However, as stressed in Riess et al. (1996b),
the color excess (or deficit) at maximum should not be interpreted
as entirely due to extinction but be corrected for the
part of this excess that is correlated with stretch . We measure
a stretch-color slope of about 0.2, similar to the relation
proposed in Phillips et al. (1999)
which is
incompatible with RB=4.1, expected for extinction by dust analogous
to the observed law in the Milky Way. The value we find is compatible with
those found in previous works (see Tripp 1998 and references therein).
However, as stressed in Riess et al. (1996b),
the color excess (or deficit) at maximum should not be interpreted
as entirely due to extinction but be corrected for the
part of this excess that is correlated with stretch . We measure
a stretch-color slope of about 0.2, similar to the relation
proposed in Phillips et al. (1999)![[*]](/icons/foot_motif.gif) and can redefine our parameters to account for this correlation:
and can redefine our parameters to account for this correlation:
| c' |
= |
c + 0.2 (s-1) |
|
| s' |
= |
s |
|
so that s' and c' are uncorrelated. The correlation coefficients
then become
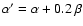 and
and
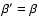 ,
which
means that
redefining the color excess to explicitly assign to stretch the
color variations correlated to stretch does not change
the brighter-bluer correlation strength.
,
which
means that
redefining the color excess to explicitly assign to stretch the
color variations correlated to stretch does not change
the brighter-bluer correlation strength.
The two-parameter (stretch and color) pragmatic approach we followed
can accommodate both reddening by dust and any intrinsic color effect
dependent or not on stretch. One may reasonably assume that
reddening by dust and stretch independent intrinsic colors mix
(as proposed in Nobili et al. 2003), and
that disentangling the contributions would improve the distance
resolution. Our distance indicator is however independent of the
interpretation of the color variations. Since the low value of 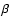 may indicate that some intrinsic effect plays a role, we did
not interpret color as only due to reddening by dust and hence
accepted negative c values as such.
may indicate that some intrinsic effect plays a role, we did
not interpret color as only due to reddening by dust and hence
accepted negative c values as such.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{3025f1.eps}
\end{figure}](/articles/aa/full/2005/45/aa3025-05/Timg92.gif) |
Figure 5:
68% joint confidence regions for
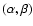 fitted
using either UB or BV light curves of the test sample.
The crosses show the best fitted values with
fitted
using either UB or BV light curves of the test sample.
The crosses show the best fitted values with 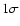 uncertainties.
uncertainties. |
| Open with DEXTER |
4.1.2 Hubble diagram in UB only
We applied the same procedure as in the previous section to fit the U and B-band light curves of the sub-sample of Table 2
for which U-band measurements are available and redshifts larger than 0.015 (9 supernovae).
We obtain
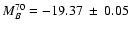 ,
,
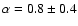 ,
,
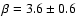 ,
and the standard deviation of residuals is
,
and the standard deviation of residuals is
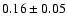 .
As expected,
these results are consistent with the fit using B and V, as
shown by the confidence contours for
.
As expected,
these results are consistent with the fit using B and V, as
shown by the confidence contours for 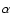 and
and 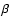 fitted using either UB or BV light curves shown Fig. 5.
Note the covariance between the estimated values
of
fitted using either UB or BV light curves shown Fig. 5.
Note the covariance between the estimated values
of 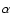 and
and 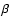 ,
particularly in the U+B band case,
which simply reflects the correlation between the parameters c and s in the test sample.
,
particularly in the U+B band case,
which simply reflects the correlation between the parameters c and s in the test sample.
One of the SN present in this sample (1996bo) show a large statistical uncertainty
due to its limited U-band photometry. Removing this point from the fit has the
effect of bringing down the U,B contour
to the point
that it contains almost all of the B,V contour, bringing the two determinations
of 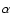 and
and 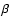 closer to each other.
closer to each other.
Figure 6
presents the residuals to the Hubble diagram as a function of redshift, stretch and
color using the values of
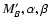 fitted with B- and V-band light
curves in the previous section. Note the large uncertainty affecting 1996bo, which
appears as a
fitted with B- and V-band light
curves in the previous section. Note the large uncertainty affecting 1996bo, which
appears as a 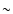 2 sigma outlier in the 3 plots.
Fitting the Hubble diagram with the values of
2 sigma outlier in the 3 plots.
Fitting the Hubble diagram with the values of 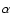 and
and 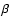 obtained with B- and V-band light curves, the standard
deviation of residuals is
obtained with B- and V-band light curves, the standard
deviation of residuals is
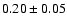 .
.
Comparisons of the fitted values of s and c fitted using either UB
or BV data are shown Fig. 7.
The error bars only reflect the propagation
of photometric errors and do not account for any intrinsic dispersion.
There is no significant bias between the two estimates.
![\begin{figure}
\par\includegraphics[width=5.9cm,clip]{3025f6.eps}\par\vspace*{2m...
...ps}\par\vspace*{2mm}
\includegraphics[width=5.8cm,clip]{3025f2.eps}
\end{figure}](/articles/aa/full/2005/45/aa3025-05/Timg97.gif) |
Figure 6:
From top to bottom: residuals to the Hubble diagram as a function
of redshift, stretch s and color c indexes for supernovae of the test sample
fitted in U and B bands. The values of
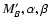 used here are
those fitted using B and V bands as described in the text. SNe with
redshifts smaller than 0.015 are labeled with opened symbols.
Note the large uncertainty affecting one SN (1996bo)
due to its limited U-band photometry, and which also
appears as a
used here are
those fitted using B and V bands as described in the text. SNe with
redshifts smaller than 0.015 are labeled with opened symbols.
Note the large uncertainty affecting one SN (1996bo)
due to its limited U-band photometry, and which also
appears as a 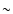 2 sigma outlier in the 3 plots. 2 sigma outlier in the 3 plots. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{3025f12.eps}\par\vspace*{3mm}
\includegraphics[width=6cm,clip]{3025f11.eps}
\end{figure}](/articles/aa/full/2005/45/aa3025-05/Timg98.gif) |
Figure 7:
Differences of s and c values fitted with
either UB or BV light curves of supernovae from the training and the test
sample (respectively opened and filled symbols).
The error bars only reflect the propagation
of photometric errors and do not account for any intrinsicdispersion. |
| Open with DEXTER |
We compare our method with various estimators of SN Ia distances
by examining the dispersions about the Hubble line of a sample of nearby
supernovae. The comparison is made on distances measured in B and V bands only
for which we obtain a dispersion of
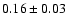 .
Our U- plus B-band distances
estimates could not be compared with other estimate
due to the lack of published distances measured
in these 2 bands.
.
Our U- plus B-band distances
estimates could not be compared with other estimate
due to the lack of published distances measured
in these 2 bands.
As shown in many papers (e.g. Wang et al. 2003, 2005),
testing luminosity distance indicators on "low-extinction sample''
greatly improves their performance. As said in the introduction,
cutting on color estimate measured with a redshift
dependent accuracy is a source of systematic errors which we need
to avoid for
cosmological applications. We hence compare our resolutions to "full-sample''
resolutions, for distance indicators involving rest-frame U, B and V bands.
The MLCS method was originally presented in Riess et al. (1996a),
quoting a distance resolution of 0.12. Its
latest development is presented
in Jha (2002), with a distance resolution of 0.18,
and used in Riess et al. (2004).
From the latter, we collected the distance measurements
to the 20 objects in common with our test sample, and compute
a Hubble diagram dispersion of 0.24 (0.22 with the low-redshift
"golden sample'')
to be compared with our value of 0.16 when measured on the
same 20 events.
The CMAGIC method of Wang et al. (2003) finds a weighted dispersion of 0.08
for a sub-sample of SNe with
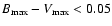 .
With a weaker
cut on color,
.
With a weaker
cut on color,
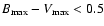 ,
the dispersion rises to about 0.15, which is consistent with our result. Similarly, the
,
the dispersion rises to about 0.15, which is consistent with our result. Similarly, the
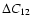 method presented in Wang et al. (2005), also present an exquisite
distance resolution of 0.07 in the V band based on a low-extinction subsample.
However, when considering the full sample, the distance resolution degrades
to 0.18.
A more detailed comparison with CMAGIC and
method presented in Wang et al. (2005), also present an exquisite
distance resolution of 0.07 in the V band based on a low-extinction subsample.
However, when considering the full sample, the distance resolution degrades
to 0.18.
A more detailed comparison with CMAGIC and
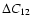 would require comparing the distances of the same sample of SNe
(due to the limited statistics) but their distances
are not published.
Note also that in these papers,
the test and training samples are not separated.
would require comparing the distances of the same sample of SNe
(due to the limited statistics) but their distances
are not published.
Note also that in these papers,
the test and training samples are not separated.
In summary, the method we propose gives a dispersion on distances
measured using B- and V-band data only comparable or lower than obtained
with other methods while also providing, for the first time, comparable dispersion
values for distances measured using U- and B-band data only.
We have proposed a new method to fit broadband light curves of type Ia
supernovae. It allows us to determine simultaneously the SN Ia rest-frame B magnitude
at maximum, stretch and color excess (or deficit) using any measured multi-color
light curve within the wavelength range of rest-frame 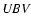 bands.
This technique is particularly well-suited to the treatment of high-redshift
SNe Ia for which limited coverage is obtained in both wavelength and phase.
bands.
This technique is particularly well-suited to the treatment of high-redshift
SNe Ia for which limited coverage is obtained in both wavelength and phase.
The k-corrections, which allow the observer to
transform the observed magnitudes into the standard rest-frame magnitudes,
are built-in; the model
includes the dependence on stretch and color of the spectrum template needed
to estimate those corrections. In particular, the well-known correlation between
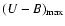 and stretch is reproduced.
and stretch is reproduced.
The (B-V) and (V-R) stretch-independent colors
we obtain are extremely similar to the ones expected from reddening by dust. The (U-B)
color departs from this law. We find a relation between (B-V) color and
observed B luminosity incompatible with RB = 4.1, at more than 3 standard
deviations, even when accounting for the stretch-color correlation.
We have tested this fitting procedure on an independent sample
of SNe Ia. Alternatively using B- and V-band data and U- and B-band data,
we are able to retrieve consistent parameters and hence build Hubble
diagrams with both sets of data. The dispersions
about the Hubble line were found to be
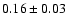 and
and
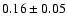 in the B plus V and U plus B bands only, respectively.
This method is particularly well adapted
to reliably measure SN Ia distances in the full redshift range
and in particular beyond redshift
in the B plus V and U plus B bands only, respectively.
This method is particularly well adapted
to reliably measure SN Ia distances in the full redshift range
and in particular beyond redshift 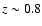 for which rest-frame
V-band measurements are often not available.
for which rest-frame
V-band measurements are often not available.
Acknowledgements
It is always a pleasure to acknowledge the stimulating discussions among the
FROGS (FRench Observing Group of Supernovae), especially with G. Garavini, J. Rich
and R. Taillet whom we would also like to thank for their critical reading
of the manuscript. We thank P. Nugent for providing us with his template spectrum time series.
- Altavilla,
G., Fiorentino, G., Marconi, M., et al. 2004, MNRAS, 349,
1344 [NASA ADS] [CrossRef]
- Barris, B. J.,
Tonry, J. L., Blondin, S., et al. 2004, ApJ, 602,
571 [CrossRef]
- Benetti, S.,
Meikle, P., Stehle, M., et al. 2004, MNRAS, 348, 261 [NASA ADS] [CrossRef]
- Bessell, M. S.
1990, PASP, 102, 1181 [NASA ADS] [CrossRef] (In the text)
- Buta, R. J., &
Turner, A. 1983, PASP, 95, 72 [NASA ADS] [CrossRef]
- Cardelli,
J. A., Clayton, G. C., & Mathis, J. S. 1989,
ApJ, 345, 245 [NASA ADS] [CrossRef] (In the text)
- Filippenko,
A. V., Richmond, M. W., Matheson, T., et al. 1992,
ApJ, 384, L15 [NASA ADS] [CrossRef]
- Fukugita, M.,
Ichikawa, T., Gunn, J. E., et al. 1996, AJ, 111,
1748 [NASA ADS] [CrossRef] (In the text)
- Garavini, G.,
Aldering, G., Amanullah, R., et al. 2005, to be submitted
- Garavini, G.,
Folatelli, G., Goobar, A., et al. 2004, AJ, 128, 387 [NASA ADS] [CrossRef]
- Garnavich,
P. M., Bonanos, A. Z., Krisciunas, K., et al. 2004,
ApJ, 613, 1120 [NASA ADS] [CrossRef]
- Goldhaber,
G., Groom, D. E., Kim, A., et al. 2001, ApJ, 558,
359 [NASA ADS] [CrossRef] (In the text)
- Hamuy, M.,
Phillips, M. M., Suntzeff, N. B., et al. 1996a, AJ,
112, 2408 [NASA ADS] [CrossRef] (In the text)
- Hamuy, M.,
Phillips, M. M., Suntzeff, N. B., et al. 1996b, ApJ,
112, 2391 [NASA ADS]
- Howell, D. A.
2001, ApJ, 554, L193 [NASA ADS] [CrossRef]
- Jha, S. 2002, Ph.D.
Thesis, University of Washington
(In the text)
- Kim, A., Goobar, A.,
& Perlmutter, S. 1996, PASP, 108, 190 [NASA ADS] [CrossRef]
- Kimeridze,
G. N., & Tsvetkov, D. I. 1986, Astrofiz., 25,
279 [NASA ADS]
- Knop, R. A.,
Aldering, G., Amanullah, R., et al. 2003, ApJ, 598, 102 [NASA ADS] [CrossRef]
- Krisciunas,
K., Hastings, N. C., Loomis, K., et al. 2000, ApJ, 539,
658 [NASA ADS] [CrossRef]
-
Krisciunas, K., Phillips, M. M., Suntzeff, N. B.,
et al. 2004, AJ, 127, 1664 [NASA ADS] [CrossRef]
- Krisciunas,
K., Suntzeff, N. B., Candia, P., et al. 2003, AJ, 125,
166 [NASA ADS] [CrossRef]
-
Krisciunas, K., Suntzeff, N. B., Phillips, M. M., et al. 2004,
[arXiv:astro-ph/0409036]
- Leibundgut,
B., Kirshner, R. P., Filippenko, A. V., et al. 1991,
ApJ, 371, L23 [NASA ADS] [CrossRef]
- Li, W., Filippenko,
A. V., Gates, E., et al. 2001a, PASP, 113, 1178 [NASA ADS] [CrossRef]
- Li, W., Filippenko,
A. V., Treffers, R. R., et al. 2001b, ApJ, 546,
734 [NASA ADS] [CrossRef]
- Lira, P., Suntzeff,
N. B., Phillips, M. M., et al. 1998, AJ, 116,
1006 [NASA ADS] [CrossRef] (In the text)
- Meikle,
W. P. S., Cumming, R. J., Geballe, T. R.,
et al. 1996, MNRAS, 281, 263 [NASA ADS]
- Nobili, S., Goobar,
A., Knop, R., & Nugent, P. 2003, A&A, 404, 901 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Nugent, P., Kim,
A., & Perlmutter, S. 2002, PASP, 114, 803 [NASA ADS] [CrossRef] (In the text)
- Parodi, B. R.,
Saha, A., Sandage, A., & Tammann, G. A. 2000, ApJ, 540,
634 [NASA ADS] [CrossRef]
- Patat, F., Benetti,
S., Cappellaro, E., et al. 1996, MNRAS, 278, 111 [NASA ADS]
- Perlmutter,
S., Gabi, S., Goldhaber, G., et al. 1997, ApJ, 483, 565 [NASA ADS] [CrossRef]
- Perlmutter,
S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517,
565 [NASA ADS] [CrossRef]
- Phillips,
M. M. 1993, ApJ, 413, L105 [NASA ADS] [CrossRef]
- Phillips,
M. M., Lira, P., Suntzeff, N. B., et al. 1999, AJ,
118, 1766 [NASA ADS] [CrossRef]
- Phillips,
M. M., Phillips, A. C., Heathcote, S. R.,
et al. 1987, PASP, 99, 592 [NASA ADS] [CrossRef]
- Pignata, G.,
Patat, F., Benetti, S., et al. 2004
[arXiv:astro-ph/0408234]
- Pskovskii,
I. P. 1977, Soviet Astron., 21, 675 [NASA ADS]
- Richmond,
M. W., Treffers, R. R., Filippenko, A. V.,
et al. 1995, AJ, 109, 2121 [NASA ADS] [CrossRef]
- Riess, A. G.,
Filippenko, A. V., Challis, P., et al. 1998, AJ, 116,
1009 [NASA ADS] [CrossRef]
- Riess, A. G.,
Kirshner, R. P., Schmidt, B. P., et al. 1999, AJ,
117, 707 [NASA ADS] [CrossRef]
- Riess, A. G.,
Press, W. H., & Kirshner, R. P. 1995, ApJ, 438,
L17 [NASA ADS] [CrossRef]
- Riess, A. G.,
Press, W. H., & Kirshner, R. P. 1996a, ApJ, 473,
88 [NASA ADS] [CrossRef]
- Riess, A. G.,
Press, W. H., & Kirshner, R. P. 1996b, ApJ, 473,
588 [NASA ADS] [CrossRef] (In the text)
- Riess, A. G.,
Strolger, L., Tonry, J., et al. 2004, ApJ, 607, 665 [NASA ADS] [CrossRef] (In the text)
- Schlegel,
D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500,
525 [NASA ADS] [CrossRef] (In the text)
-
Stritzinger, M., Hamuy, M., Suntzeff, N. B., et al. 2002,
AJ, 124, 2100 [NASA ADS] [CrossRef]
- Strolger,
L.-G., Smith, R. C., Suntzeff, N. B., et al. 2002,
AJ, 124, 2905 [NASA ADS] [CrossRef]
- Suntzeff, N.
1992, IAU Coll., ed. R. McCray (Cambridge: Cambridge University
Press), 145
- Suntzeff,
N. B., Phillips, M. M., Covarrubias, R., et al.
1999, AJ, 117, 1175 [NASA ADS] [CrossRef] (In the text)
- Tonry, J. L.,
Schmidt, B. P., Barris, B., et al. 2003, ApJ, 594, 1 [NASA ADS] [CrossRef]
- Tripp, R. 1998,
A&A, 331, 815 [NASA ADS]
- Tripp, R., &
Branch, D. 1999, ApJ, 525, 209 [NASA ADS] [CrossRef]
- Valentini,
G., Di Carlo, E., Massi, F., et al. 2003, ApJ, 595, 779 [NASA ADS] [CrossRef]
- Vinkó, J.,
Bíró, I. B., Csák, B., et al. 2003,
A&A, 397, 115 [EDP Sciences] [NASA ADS] [CrossRef]
- Wang, L., Goldhaber,
G., Aldering, G., & Perlmutter, S. 2003, ApJ, 590, 944 [NASA ADS] [CrossRef]
- Wang, X., Wang, L.,
Zhou, X., Lou, Y., & Li, Z. 2005, ApJ, 620, L87 [NASA ADS] [CrossRef]
- Zapata, A. A.,
Candia, P., Krisciunas, K., Phillips, M. M., & Suntzeff,
N. B. 2003, Am. Astron. Soc. Meeting Abstracts, 203
Copyright ESO 2005
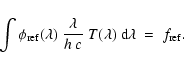
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{3025f8.eps}
\end{figure}](/articles/aa/full/2005/45/aa3025-05/Timg58.gif)
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{3025f7.eps}
\end{figure}](/articles/aa/full/2005/45/aa3025-05/Timg59.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3025f4.eps}
\end{figure}](/articles/aa/full/2005/45/aa3025-05/Timg62.gif)
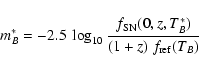
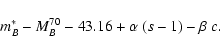
![\begin{figure}
\par\includegraphics[width=6.1cm,clip]{3025f3.eps}\vspace*{3mm}
\...
...f5.eps}\vspace*{3mm}
\includegraphics[width=5.9cm,clip]{3025f9.eps}
\end{figure}](/articles/aa/full/2005/45/aa3025-05/Timg80.gif)
![\begin{figure}
\par\includegraphics[width=5.9cm,clip]{3025f6.eps}\par\vspace*{2m...
...ps}\par\vspace*{2mm}
\includegraphics[width=5.8cm,clip]{3025f2.eps}
\end{figure}](/articles/aa/full/2005/45/aa3025-05/Timg97.gif)
![\begin{figure}
\par\includegraphics[width=6cm,clip]{3025f12.eps}\par\vspace*{3mm}
\includegraphics[width=6cm,clip]{3025f11.eps}
\end{figure}](/articles/aa/full/2005/45/aa3025-05/Timg98.gif)