G. P. Szokoly
Max-Planck-Institut für extraterrestrische Physik, Giessenbachstraße, 85748 Garching, Germany
Received 17 December 2004 / Accepted 20 June 2005
Abstract
Historically, long-slit spectroscopic observations
were carried out using the parallactic angle for the slit orientation
if slit loss was an important consideration (either to maximize
the signal-to-noise or to do spectrophotometry). This
requires periodic realignment of the slit position angle as the parallactic
angle changes. This is not possible for multi-slit
observations where one slit position angle must be chosen for
the entire exposure. Common wisdom suggests using the parallactic
angle at the meridian (
![]() ). In this paper, I examine what
the best strategy is for long, multi-slit exposures. I find that in
extreme cases (very long exposure time) the best choice is
to orient the slit perpendicular to the parallactic
angle at the meridian. There are two effects to consider: the increasing
dispersion with increasing airmass
and the changing angle between the parallactic angle and the slit.
In the case of traditional slit orientation, the two
effects amplify each other, thus rendering a significant
fraction of the observation useless. Using the perpendicular orientation,
the two processes work against each other, thus most of the
observation remains useful.
I will use, as an example, our 8 h Lockman Hole observations
using the Keck telescope, but generic methods are given to
evaluate a particular observation.
I also make the tools available to the community.
). In this paper, I examine what
the best strategy is for long, multi-slit exposures. I find that in
extreme cases (very long exposure time) the best choice is
to orient the slit perpendicular to the parallactic
angle at the meridian. There are two effects to consider: the increasing
dispersion with increasing airmass
and the changing angle between the parallactic angle and the slit.
In the case of traditional slit orientation, the two
effects amplify each other, thus rendering a significant
fraction of the observation useless. Using the perpendicular orientation,
the two processes work against each other, thus most of the
observation remains useful.
I will use, as an example, our 8 h Lockman Hole observations
using the Keck telescope, but generic methods are given to
evaluate a particular observation.
I also make the tools available to the community.
Key words: atmospheric effects - instrumentation: spectrographs - techniques: spectroscopic
The introduction of multi-object spectrographs (MOS) in optical spectroscopy is quite often thought of as just a set of traditional long-slit spectrographs (LS) and some consequences are overlooked. The main difference between MOS and LS spectroscopy is the constraints imposed by the geometry of the instrument. While in LS spectroscopy, the slit orientation can be chosen arbitrarily, this is no longer the case in MOS spectroscopy: slit position angles cannot be changed during a set of observations.
As observers tend to concentrate on very faint objects (typical R-band magnitude of 23-24 with 8-10 m class telescopes), the integration times are longer and longer. Sometimes a whole night (8-10 h or more) is spent on a single mask. These observations require a rethinking of the optimal observation strategy.
Since many MOS instruments lack an atmospheric dispersion corrector (e.g. VIMOS on VLT, DEIMOS on Keck), atmospheric dispersion is a serious problem. Long observations (many hours) span a large range of zenith distance. Thus, a differential refraction of a few arc seconds is quite common.
As most observations require high signal to noise ratios or good spectral resolution, using sufficiently wide slits to compensate for this effect is not acceptable. Very wide slits have a devastating effect on background-limited exposures (since the sky background grows linearly with slit width, while the object signal grows much more slowly) and a wide slit also blurs the spectra.
For short exposures, one can observe "close to the parallactic angle'', i.e. align the slit with the atmospheric dispersion direction. This way the photons from the object enter the slit, the dispersion only introduces an additional tilt in the resulting spectra, which is easy to correct for for most applications. If the goal of the observation is to extract spatial information, too, then extra care is required to correct for this effect.
In the case of longer observations, the direction of dispersion projected on the sky, i.e. the parallactic angle, varies with time. For single object observations (i.e. long slit spectroscopy), one can compensate by periodically realigning the slit. For MOS exposures, this is not possible. For masks, a single slit orientation must be chosen for the whole exposure.
In this paper, I examine how the effective slit loss can be estimated and I demonstrate the effect using our sample observation of the Lockman Hole using the Keck telescope. I also describe how to use our Web-based service to find the best strategy for a particular observation.
I will start with the current best determination of the atmospheric refraction. I also work out a simplified formula that is sufficient in many applications. I simulate different observational strategies and show the effect of atmospheric refraction on the efficiency of observations.
The importance of atmospheric refraction in spectroscopic observations was emphasized by Filippenko (1982). The paper discusses the optimal strategy (and the effect of non-optimal strategies) for short long-slit spectroscopic observations. Even though the paper uses a formula to calculate the index of refraction that became obsolete, it is still the strategy to be followed for short integrations. The refined formula to calculate the refraction introduces only negligible changes. On the other hand, the paper does not discuss the optimal strategy for long integrations.
Cohen & Cromer (1988) calculate the magnitude of differential refraction for the Keck and the Norris spectrographs for realistic observing scenarios. The paper determines the limits beyond which the atmospheric dispersion degrades the data, but does not discuss how to optimize observations that go beyond these limits.
Donnelly et al. (1989) discusses optimal observational strategies for fiber spectrographs for long exposures. Unfortunately these results cannot be directly applied to slit spectrographs: in many (but not all) projects, the slit orientation can be chosen arbitrarily, thus, there is an extra degree of freedom to minimize the effect of atmospheric refraction. This is not possible for fiber spectrographs, thus, this is not discussed in this paper.
Table 1: Current and future 8 m class telescopes and MOS instruments.
In Table 1 I review all current and known future 8 m telescopes and optical MOS spectrographs. There are only 2 instruments without an ADC in operation or in planning:
DEIMOS on Keck is heavily red optimized, thus, atmospheric dispersion is not a significant issue for many projects. The DEIMOS Slitmask design page (http://www.ucolick.org/~phillips/deimos_ref/masks.html) provides preliminary tools to evaluate the effect of atmospheric dispersion on slit loss for short integrations. No guidelines are provided for long integrations.
The VIMOS manual (2005) discusses the effect of
atmospheric dispersion in MOS mode. They arrive at the
conclusion that the only generic way to minimize slit losses is
to orient the slits North-South and observe within ![]() 2 h
of the meridian. Even though the detailed study of the effect of
atmospheric dispersion on VIMOS (Cuby et al. 1998)
makes no explicit statement about deviating from these
constraints, a casual reading of the manual by an inexperienced
observer may leave the impression that this slit orientation is
the only valid strategy.
2 h
of the meridian. Even though the detailed study of the effect of
atmospheric dispersion on VIMOS (Cuby et al. 1998)
makes no explicit statement about deviating from these
constraints, a casual reading of the manual by an inexperienced
observer may leave the impression that this slit orientation is
the only valid strategy.
This conclusion is clearly valid for the sample observation used in the manual: observing between airmasses of 1.7 and 1.4 in the UV/blue. On the other hand, for some observing projects, e.g. limiting UV/blue spectroscopy to low airmass, the advantage of N-S orientation diminishes. Thus, an additional freedom (slit orientation) is available in some cases to maximize scientific return of the observations.
Throughout this paper, I will use a sample observation of the
Lockman Hole (
![]() :35:25.0, J2000) using the Keck telescope
(latitude of +19:46:36). I assume multislit spectroscopy
with 1.0'' slit width and 1.2'' seeing. I assume an ambient
temperature of 2.5 degrees C, ambient pressure of 61.5 kPa (615 mbar) and
a relative humidity of 40%.
:35:25.0, J2000) using the Keck telescope
(latitude of +19:46:36). I assume multislit spectroscopy
with 1.0'' slit width and 1.2'' seeing. I assume an ambient
temperature of 2.5 degrees C, ambient pressure of 61.5 kPa (615 mbar) and
a relative humidity of 40%.
The observations consist of 1 night long integration on a mask, which for this field implies an hour angle range between 18 h and 3 h (the asymmetry is due to the mechanical constraints of the telescope), which covers an airmass range of 1.27 (hour angle of 0) to 3.5 (hour angle of 18 h). I will concentrate on the DEIMOS multiobject spectrograph, which is red-optimized. Thus, I will concentrate on the 4500...9500 Å wavelength range.
In the calculation I assume that the seeing does not depend on the wavelength and I also assume that the alignment and guiding is done in the R-band (approximately 7000 Å).
The most up-to-date atmospheric dispersion determination, the Ciddor formula (1996) is reviewed in the Appendix. The most important formulas are:
The differential refraction (as a function of wavelength, relative
to the alignment/guiding effective wavelength, ![]() )
in radians is:
)
in radians is:
| (1) |
![\begin{figure}
\par\includegraphics[width=8cm]{2565fig1.eps} \end{figure}](/articles/aa/full/2005/44/aa2565-04/Timg16.gif) |
Figure 1:
Differential refraction as a function of wavelength
at different airmasses: Solid line -
|
| Open with DEXTER | |
The index of refraction,
![]() of standard air is
of standard air is
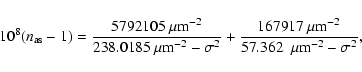 |
(2) |
If we are only interested in differential refraction, we can write
a simpler formula that is
sufficiently accurate for many applications:
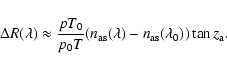 |
(3) |
![\begin{figure}
\par\includegraphics[width=8cm]{2565fig2.eps}\end{figure}](/articles/aa/full/2005/44/aa2565-04/Timg22.gif) |
Figure 2:
The error introduced by our approximate formula (solid line) and the
old Edlén formula (dotted line) in the atmospheric refraction assuming
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm]{2565fi3a.eps}\includegraphics[width=8cm]{2565fi3b.eps}\end{figure}](/articles/aa/full/2005/44/aa2565-04/Timg23.gif) |
Figure 3: Slit loss as a function of wavelength at different airmasses. I used our sample observation of the Lockman Hole using Keck (see Sect. 1 for details). Notice the different scales used on the plots. |
| Open with DEXTER | |
Now that we have the atmospheric dispersion, we can also calculate
the slit loss. I assume a point source that has a surface brightness
profile of
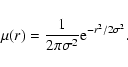 |
(4) |
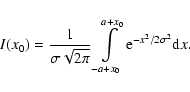 |
(5) |
As we can see, the N-S slit orientation results in a low slit loss at hour angle of 0 (minimal airmass) that does not depend on wavelength (as we are observing close to the parallactic angle). On the other hand, as we are moving away from the optimal configuration, the situation deteriorates rapidly. This is due to the fact that the atmospheric dispersion increases as the airmass increases and the slit orientation is moving away from the ideal, parallactic angle - both effects increase the slit loss.
In the alternative configuration, i.e. East-West slit orientation, the slit loss is never optimal. Even at low airmass, a significant fraction of the light is lost (e.g. slit loss is 42% at 5000 Å, instead of 33%), but the slit loss does not deteriorate very quickly. This is due to the fact that as the airmass increases, the dispersion increases, but the slit is getting closer to the parallactic angle, thus the projected dispersion is not increasing very rapidly. In fact, in our particular configuration (Lockman Hole and Keck), the slit loss is actually smaller at high airmass (42%, 38% and 39% at 5000 Å at the airmass of 1.27, 1.56 and 3.50, respectively).
To evaluate the overall effect of the slit orientation on the signal level achievable, we can also calculate the "average'' slit loss of a long exposure. This is shown in Fig. 4.
![\begin{figure}
\par\includegraphics[width=5.5cm]{2565fig4.eps}\end{figure}](/articles/aa/full/2005/44/aa2565-04/Timg26.gif) |
Figure 4: Average slit loss at different slit orientations. Solid line indicates East-West slit orientation, dotted lines shows North-South orientation. I used our sample observation of the Lockman Hole using Keck (see Sect. 1 for details). |
| Open with DEXTER | |
In Fig. 5 I show the effect of sky position angle on average slit loss at 4500 Å, using my example observations and a southern field (Chandra Deep Field South). As we can see, for short exposures around meridian passage, the N-S orientation is optimal. As we go to longer integration times, the effect of slit orientation becomes smaller, while at extremely long integration times, the E-W orientation becomes ideal for the Lockman Hole field. For asymmetric cases (for example our actual observations between hour angles 18 and 3) the optimal slit orientation is neither E-W nor N-S.
In contrast, for the southern field, the optimal slit orientation remains North-South. This is due to the fact that for the CDFS field the airmass is never below 1.48 from Keck, thus, the differential refraction is comparable to the slit width even at meridian passing.
All results presented so far only hold for objects in the center of
the field of view of the instrument.
For wide-field spectrographs, an additional effect is important:
the zenith distance is not constant across the field of view, thus
the differential refraction is not constant, either. This is
an achromatic effect, which we can calculate using Eq. (A.4):
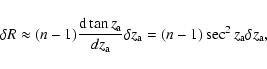 |
(6) |
![\begin{figure}
\par\includegraphics[width=12.6cm]{2565fig5.eps} %
\end{figure}](/articles/aa/full/2005/44/aa2565-04/Timg32.gif) |
Figure 5: Average slit loss at 4500 Å at different slit orientations. I used our sample observation of the Lockman Hole using Keck (see Sect. 1 for details - left panel) and a southern field (CDFS, -27:48:30 declination - right panel). I show the effect of slit sky position angle at different hour angle ranges. For sky position angle I use the (unusual) DEIMOS definition, where 90 degree is E-W, 0 degree is N-S. |
| Open with DEXTER | |
I make our code used in our calculations available to the community in both source code and web application form at http://www.xray.mpe.mpg.de/~szgyula/slitloss/. The program uses the full Ciddor formula to evaluate the slit loss, but for comparison all three formulas are available to calculate the differential refraction.
I demonstrated that choosing the optimal slit orientation for multiobject spectroscopy, using long exposure times, requires care and should be evaluated individually for each project. For each field and expected duration, one has to find a balance.
I reviewed the most recent determination of atmospheric dispersion. For typical cases, I found that a simplified version of the most up-to-date Ciddor formula can be used, due to the fact that alignment/guiding removes the effect of dispersion in zeroth order. The simplified formula only depends on pressure and temperature. The effect of relative humidity and CO2 concentration is very small. Furthermore, the differential refraction follows very simple scaling rules, i.e. it scales linearly with pressure and the inverse of temperature (in Kelvins).
For short exposures, the optimal strategy is, as expected, still to orient the slits with the parallactic angle. On the other hand, for longer exposures, this is not always the right strategy. There are two effects to consider, the increasing differential refraction and the changing angle between the slits and the parallactic angle. Depending on the configuration, these effects can work against each other, thus resulting in a long, relatively stable observation that is never optimal or these effects can amplify each other, thus resulting in an optimal short observation that deteriorates very fast.
Alignment/guiding is crucial. One has to select the effective wavelength of these to maximize the science output. It is worthwhile to spend a few extra minutes every few hours using some standard filters instead of using no filters at all, especially with alignment stars with unknown spectral types. This latter approach runs the risk of using very blue stars for alignment, thus the alignment will only be optimal in the blue, where one may not be observing.
Naturally, in the long run, the use of atmospheric dispersion correctors should be considered. As I have shown, these can improve the throughput by as much as a factor of two for instruments operating in the blue. The cost of these from an observational point of view is small (few photons are lost in the extra optical elements) as only two very weak prisms are sufficient in most cases to produce a "tunable'' prism to compensate for differential refraction in the first order. This can solve the problem of differential refraction, but does not eliminate the slit loss completely. Finite slit widths will always "cut'' the object signal. As the seeing can be wavelength dependent(this effect was completely ignored in this paper), so can the slit loss. Thus, accurate spectrophotometry still requires very wide slits, and consequently, very low spectral resolution and a significantly degraded signal to noise ratio.
Finally, I provide a web-based service to the community and release the software developed.
Acknowledgements
Part of this work was supported by the German DLR project number 50 OX0001.
Atmospheric dispersion (i.e. the apparent displacement of object), R,
is defined as
| (A.1) |
Assuming that the index of refraction depends only on height, using
Snell's law, we can write that
| (A.2) |
| (A.3) |
As a consequence, the absolute magnitude of
atmospheric refraction is irrelevant, since alignment/guiding
automatically compensates for it. The relevant quantity, the
differential refraction (as a function of wavelength, relative
to the alignment/guiding effective wavelength, ![]() )
in radians is:
)
in radians is:
| (A.5) |
The index of refraction,
![]() of standard air, i.e. dry air at 15
of standard air, i.e. dry air at 15 ![]() C,
using the International Temperature Scale of 1990
(Saunders 1990), 101 325 Pa pressure
and 450 ppm (part per million) CO2 concentration, is
C,
using the International Temperature Scale of 1990
(Saunders 1990), 101 325 Pa pressure
and 450 ppm (part per million) CO2 concentration, is
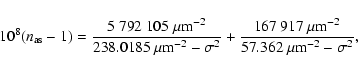 |
(A.6) |
If the CO2 concentration is ![]() ppm instead of 450 ppm, the
index of refraction,
ppm instead of 450 ppm, the
index of refraction,
![]() ,
is
,
is
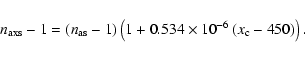 |
(A.7) |
For water vapor at the "standard conditions'', i.e. at 20 ![]() C and
1333 Pa, the index of refraction,
C and
1333 Pa, the index of refraction,
![]() ,
is
,
is
| |
|||
| (A.8) |
The saturation vapor pressure of water vapor,
![]() ,
at temperature T(in Kelvins), over liquid water is
,
at temperature T(in Kelvins), over liquid water is
| |
|||
| (A.9) |
The enhancement factor of water vapor in air is
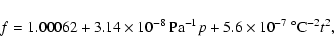 |
(A.10) |
The molar fraction of water vapor in moist air is
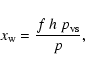 |
(A.11) |
The compressibility of the moist air, Z is
| Z | 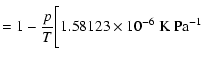 |
||
![$\displaystyle +\left(1.9898\times10^{-4}~{\rm K}~{\rm Pa}^{-1}-2.376\times10^{-6}~{\rm Pa}^{-1}t\right)x_w^2\Bigg]$](/articles/aa/full/2005/44/aa2565-04/img66.gif) |
|||
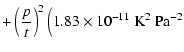 |
|||
| (A.12) |
At standard conditions (p=101 325 Pa, t=15 ![]() C, dry air), the
standard compressibility is
C, dry air), the
standard compressibility is
| (A.13) |
| (A.14) |
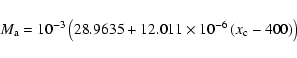 |
(A.15) |
The density of air, ![]() (in kg/m3 units) is
(in kg/m3 units) is
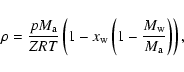 |
(A.16) |
At standard conditions (
p0=101 325 Pa and t0=15 ![]() C) the
density of dry air (
C) the
density of dry air (
![]() )
only depends on the CO2 concentration
)
only depends on the CO2 concentration
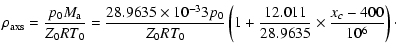 |
(A.17) |
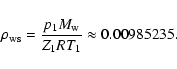 |
(A.18) |
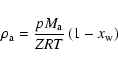 |
(A.19) |
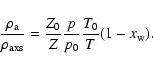 |
(A.20) |
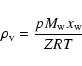 |
(A.21) |
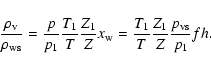 |
(A.22) |
Finally, the refractive index is
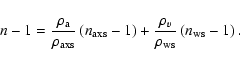 |
(A.23) |
As I have shown, the variation in
![]() introduced by CO2concentration variation is less than 10-7. Thus, the
differential refraction variation introduced is 0.03 arcsec
or less. For most applications, this is negligible.
introduced by CO2concentration variation is less than 10-7. Thus, the
differential refraction variation introduced is 0.03 arcsec
or less. For most applications, this is negligible.
If we are only interested in differential refraction and are considering
these approximations, we can write a much simpler formula that is
sufficiently accurate for many applications:
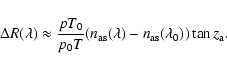 |
(A.24) |
Table A.1:
The effect of different environmental parameters on the differential
refraction. The effects of changes in the atmospheric parameters
on the differential refraction are shown using our observations of the
Lockman hole with Keck. As a reference point, 2.5 ![]() C
temperature, 61.5 kPa ambient pressure, 40% relative humidity
and 450 ppm CO2 concentration is used. The effect of changing one of
these four parameters (while keeping the other three at the nominal
value) is shown below. Only the differential refraction for 3500 Å
is shown,
C
temperature, 61.5 kPa ambient pressure, 40% relative humidity
and 450 ppm CO2 concentration is used. The effect of changing one of
these four parameters (while keeping the other three at the nominal
value) is shown below. Only the differential refraction for 3500 Å
is shown,
![]() in arc seconds. The hour angle is
18 h.
in arc seconds. The hour angle is
18 h.