A&A 443, 231-241 (2005)
DOI: 10.1051/0004-6361:20052824

Cygnus X-3 and the problem of the missing Wolf-Rayet X-ray binaries

D. Lommen1,2 - L. Yungelson1,3,4 - E. van den Heuvel1 - G. Nelemans5 - S. Portegies Zwart1,6


1 - Astronomical Institute "Anton Pannekoek'', University of Amsterdam, and Center for High Energy Astrophysics, Kruislaan 403, 1098 SJ Amsterdam, The Netherlands
2 - Sterrewacht Leiden, Niels Bohrweg 2, 2333 CA Leiden, The Netherlands
3 - Institute of Astronomy of the Russian Academy of Sciences, 48 Pyatniskaya Str., 119017 Moscow, Russia
4 - Isaac Newton Institute, Moscow Branch, 12 Universitetskii Pr., Moscow, Russia
5 - Astronomy Department, IMAPP, Radboud Universiteit Nijmegen, Toernooiveld 1, 6525 ED Nijmegen, The Netherlands
6 - Informatics Institute, University of Amsterdam, Kruislaan 403, 1098 SJ, Amsterdam, The Netherlands

Received 6 February 2005 / Accepted 7 July 2005

Abstract
Cygnus X-3 is a strong X-ray source ( $L_{\rm X} \approx 10^{38}$ erg s-1) which is thought to consist of a compact object accreting matter from a helium star. We analytically find that the estimated ranges of mass-loss rate and orbital-period derivative for Cyg X-3 are consistent with two models: i) the system is detached and the mass loss from the system comes from the stellar wind of a massive helium star, of which only a fraction that allows for the observed X-ray luminosity is accreted, or ii) the system is semidetached and a Roche-lobe-overflowing low- or moderate-mass helium donor transfers mass to the compact object, followed by ejection of its excess over the Eddington rate from the system. These analytical results appear to be consistent with evolutionary calculations. By means of population synthesis we find that currently in the Galaxy there may exist $\sim$1 X-ray binary with a black hole that accretes from a $\ga$$7~M_\odot$ Wolf-Rayet star and $\sim$1 X-ray binary in which a neutron star accretes matter from a Roche-lobe-overflowing helium star with mass $\la$ $1.5~M_\odot$. Cyg X-3 is probably one of these systems.

Key words: accretion, accretion disks - stars: individual: Cyg X-3 - stars: binaries: close - stars: binaries: general - stars: Wolf-Rayet

   
1 Introduction

Cygnus X-3 was discovered as an X-ray source by Giacconi et al. (1967). It is a strong X-ray source ( $L_{\rm X} \approx 10^{38}$ erg s-1, assuming a distance of 9 kpc), and the X-rays are expected to be due to accretion of matter onto a compact object (c.o.), presumably a black hole (BH) or a neutron star (NS) (see, e.g., Predehl et al. 2000; Kitamoto et al. 1987). The X-ray and infrared (IR) emission show a periodicity of 4.8 h, which is believed to be the orbital period P of the system (see, e.g., Parsignault et al. 1972). Van den Heuvel & de Loore (1973) suggested that Cyg X-3 consists of a NS with a helium (He) star companion, as a later evolutionary product of a high-mass X-ray binary. Tutukov & Yungelson (1973a) independently considered a NS accompanied by a He star as a stage in an evolutionary scenario leading from a pair of main-sequence stars to a binary NS. There is too much interstellar obscuration towards the source to observe it optically, but observations in the IR wave bands in the 1990's by van Kerkwijk & coauthors (1992, 1993, 1996) identified a Wolf-Rayet (WR) spectrum with Cyg X-3. Both the observations of van Kerkwijk and coauthors and high-resolution spectroscopy by Fender et al. (1999) revealed hydrogen depletion of the mass donor. Furthermore, phase-to-phase variations in the X-ray spectra can be explained by a strong (factor 10-100) overabundance of carbon, nitrogen, or oxygen (Terasawa & Nakamura 1994), consistent with classification of the Cyg-X-3 companion as a WN-type star. This added credibility to van den Heuvel & de Loore's and Tutukov & Yungelson's prediction.

The aims of this paper are twofold.

1.
We determine what combinations of stellar masses and what mass-transfer/mass-loss mechanisms are consistent with the observed $\dot{P}/P$ values and observed mass-loss rates $\dot{M}$ from the Cyg-X-3 system (the observations are taken from the literature and summarised in Sect. 2). For this we make analytical estimates and carry out evolutionary calculations for systems consisting of a He star and a c.o. (Sects. 3 and 4).
2.
We study how many X-ray sources with these (Cyg-X-3-like) parameters are expected to exist in the Galaxy at present. To do this, we carry out a population synthesis for He-star plus c.o. (He+c.o.) binaries in the Galaxy and apply disk-formation criteria to estimate the number of observable X-ray binaries with Cyg-X-3-like parameters in the Galaxy (Sect. 5). We try to explain why Cyg X-3 is the only X-ray binary with a He-star companion we observe in our galaxy (Sect. 6.1), and briefly discuss two other binary systems that were recently suggested to consist of a c.o. and a WR star (Sect. 6.2). Conclusions follow in Sect. 7.

   
2 Observed and inferred properties of Cygnus X-3

   
2.1 Masses of the components

Tavani et al. (1989) and later Mitra (1998,1996) argued that the companion in Cyg X-3 should be a very-low-mass ( $0.01{-}0.03~M_\odot$) He star. However, this is hard to reconcile with the high IR luminosity of the system (Hanson et al. 2000). Our calculations (Sects. 3.2 and 4) and population synthesis (Sect. 5) also exclude a donor less massive than $\sim$ $0.8~M_\odot$.

Terasawa & Nakamura (1994) found, from the ionisation structure of the wind in Cyg X-3, that the mass of the wind-supplying component has to be moderate: $7^{+3}_{-2}~M_\odot$.

Schmutz et al. (1996) conclude that the variations in the profiles of several near-IR emission lines are due to the orbital motion of the WR star and derive a mass function for the donor  $f(m_{\rm d})=2.3~M_\odot$. For the range of assumed Wolf-Rayet masses 5 to 20 $M_\odot $ and a range of possible inclinations  $30^\circ \leq i \leq 90^\circ$, they get a mass in the range  $(7{-}40)~M_\odot$ for the c.o., from which they infer that it is a BH.

Hanson et al. (2000) found a sinusoidal absorption feature originating in the wind in the 2.06 $\mu$m spectral region of Cyg X-3, which allowed them to derive a mass function $f(m)=0.027~M_\odot$. They considered two options: an origin of the absorption in the accretion disk or other material centred on the compact object, or association of absorption with the donor. The first option is consistent with low- or moderate-mass ($\la$$8~M_\odot$) donors, but requires a low orbital inclination of the system ($\la$$20^\circ$). Association of the absorption feature with the donor limits the mass of the WR companion to $\la$ $10~M_\odot$ if the accretor is a NS. For BH accretors the mass of the secondary may be as high as $70~M_\odot$.

Stark & Saia (2003) studied the modulation of X-ray emission lines from Cyg X-3. Based on a discussion of the location of the regions of emission of highly-ionised silicon, sulfur, and iron, they assume that the iron line is produced in the wind captured by the c.o. or in an accretion disk around it. They then use the fact of non-detection of a modulation of the iron lines to derive an upper limit to the mass function for the accretor: $f(m_{\rm a}) \le 0.22~M_\odot$. For an accretor of $1.4~M_\odot$ or $10~M_\odot$, the minimum mass of the donor is then $\sim$ $1.1~M_\odot$ and $\sim$ $ 3.4~M_\odot$, respectively. We furthermore note that in the case of Roche-lobe overflow (RLOF) a mass ratio $m_{\rm d}/m_{\rm a} > 1.39$ is inconsistent with the observed increase in the period (see below), which then also implies an inclination $\ga$$20^\circ$ in this case.

The early models of Cyg X-3 that assumed an elliptic orbit for the system (Ghosh et al. 1981) may be discarded now, since no signs of an apsidal motion were found in $\simeq$30 yr of observations (Singh et al. 2002). One implication of not discovering any apsidal motion is the irrelevance of values found by Ghosh et al. (1981) for the orbital inclination, which are often used in the literature.

To summarise, an ambiguity still exists in the interpretation of the radial-velocity curves of Cyg X-3, mostly related to different locations of spectral features that serve as the basis for radial-velocity determinations. However, at the moment it seems likely that Stark & Saia (2003) really measure emission originating in the vicinity of the c.o. Then their results suggest a rather moderate mass for the companion to the c.o., if the c.o. is a neutron star or a stellar-mass black hole.

   
2.2 Orbital period and its derivative

The period P of Cyg X-3 has been extensively monitored over the years (e.g., van der Klis & Bonnet-Bidaud 1981; Kitamoto et al. 1987), and is found to be increasing on a relatively short time scale of $\sim$106 yr. There are also indications of a second derivative on the order of -10-10 yr-1 to the period (van der Klis & Bonnet-Bidaud 1989; Kitamoto et al. 1995). A summary of the estimates of $\dot{P}/P$ for Cyg X-3 is presented in Table 1.

Table 1: The values for $\dot{P}/P$ of Cyg X-3, derived by fitting two different models to the observations. A parabolic ephemeris assumes $\ddot{P} = 0$, whereas in the cubic ephemeris a second derivative of the period unequal to zero is also taken into account.

   
2.3 Mass-loss rate

The mass-loss rate for Cyg X-3 was estimated from IR observations, usually using the Wright & Barlow (1975, W & B) model for the emission of a spherical, homogeneous, constant-velocity, isothermal wind. Stars have an accelerating wind with a temperature gradient, but W & B note that observations show spectrum flattenings in the near-IR similar to those predicted by their constant-temperature, constant-velocity model.

Waltman et al. (1996) and Miller-Jones et al. (2005) use another method to estimate $\dot{M}$. They also assume the mass outflow to be spherically symmetric and then use the fact that a (post-outburst) jet becomes observable with different delays after the burst at different frequencies (see Waltman et al. 1996, for details). Note that this method gives $\dot{M}$ in the wind, not $\dot{M}$ in the jet itself, which is assumed to be much smaller.

The estimated mass-loss rates for Cyg X-3, varying from $0.5 \times 10^{-6}~M_\odot$ yr-1 up to $2.9 \times 10^{-4}~M_\odot$ yr-1, are presented in Table 2. All estimates except one assume spherical symmetry. Note that deviations from spherical symmetry will most probably result in a higher mass-loss rate in the estimates from time delays (Waltman et al. 1996; Miller-Jones et al. 2005), whereas deviations from spherical symmetry in the other cases will result in a lower effective mass-loss rate from the system (see, e.g., Koch-Miramond et al. 2002).

If the increase in the orbital period is considered to be the result of a high-velocity wind from the system that takes away specific angular momentum of the donor (e.g., Kitamoto et al. 1995; Ergma & Yungelson 1998), the formula $\dot{P}/(2 P) = - \dot{M_{\rm t}}/M_{\rm t}$ yields $\dot{M_{\rm t}} \approx -5 \times 10^{-7} (M_{\rm t}/M_\odot) M_\odot$ yr-1, where $M_{\rm t}$is the total mass in the system.

Table 2: Values for $\dot{M}$ from the literature. We only show values that are obtained from observations of the mass loss from the system, hence not those inferred from the evolution of the orbital period. All estimates except Ogley et al. (2001)d assume spherical symmetry. See the main text for details.

   
3 The models

We consider two possible mechanisms that may cause variations of the orbital period in a binary system consisting of a c.o. and a companion. In the first model the companion loses mass in a wind which is directly lost from the system, except a tiny fraction that may be accreted (we assume accretion at the Eddington limit). This is the model assumed by, e.g., Kitamoto et al. (1995) and Ergma & Yungelson (1998), see previous section. In the second model the companion in a semidetached system transfers mass to the c.o., which then may eject (part of) the transferred mass from the system. A similar qualitative model was first suggested for Cyg X-3 by Vanbeveren et al. (1998a) and later for both SS 433 and Cyg X-3 by Fuchs et al. (2004,2002a). In this model the transferred matter forms an envelope around the c.o., resembling a stellar atmosphere. A small thin accretion disk may be present around the c.o. The envelope is ionised by X-ray emission from the vicinity of the c.o. and expelled from the system by radiation pressure. The whole process mimics the formation of a WR-star wind and consequently of a WR-like spectrum. Note that a disk-like wind from the system would give the same observed spectrum as a direct spherical wind from the donor. Following Fuchs et al. (2004,2002a), one may speak about a "WR phenomenon'' in this case. The line-emission region may then really be associated with the c.o. as suggested by, e.g., Fender et al. (1999) and Stark & Saia (2003). The details of this qualitative picture remain to be elaborated upon and verified by observations.

In principle the observed mass loss may be a combination of a direct wind and re-ejection of transferred mass. However, since in the case of Roche-lobe overflow (RLOF), the mass-loss rate considerably exceeds the mass-loss rate of a direct wind (see Sect. 3.2), we consider only the extreme cases, one being only wind mass loss (with only so much mass transfer as to allow the c.o. to accrete at the Eddington rate), the other being no direct wind and only mass transfer from the He star followed by re-ejection from the compact star.

   
3.1 Equation for the period derivative

We consider a binary system containing a mass-losing star (the donor) with mass $m_{\rm d}$ and a c.o. (the accretor) with mass $m_{\rm a}$. The donor loses an amount of mass  ${\rm d}m_{\rm d}$ of which a fraction $\alpha$ is directly lost from the system, carrying away the specific orbital angular momentum of the donor. A fraction $\beta$ is first transferred to the accretor and then lost through re-ejection, carrying away  $\beta {\rm d}m_{\rm d}$in mass with the specific orbital angular momentum of the accretor. We can then find $\dot{P}/P$ as a direct function of $\alpha$, $\beta$, $m_{\rm d}$, $m_{\rm a}$, and  $\dot{m}_{\rm d}$ (see Appendix A):
 
$\displaystyle \frac{\dot{P}}{P}$ = $\displaystyle \frac{\dot{m_{\rm d}}}{m_{\rm a} m_{\rm d} (m_{\rm a} + m_{\rm d}... ...t)\alpha - 2 m_{\rm a} m_{\rm d} \beta + 3 m_{\rm d}^2 - 3 m_{\rm a}^2 \right].$ (1)

We assume the c.o. to accrete at the Eddington rate, which leaves four free parameters to deal with to obtain a time scale for orbital-period variations in the range of observed values for  $\dot{P}/P$ (see Table 1). Note that the cubic ephemerides ( $\ddot{P} \neq 0$, in all those cases $\ddot{P} < 0$) fit the observations (slightly) better than the parabolic ephemerides. Although the cubic ephemerides of van der Klis & Bonnet-Bidaud (1989) and Kitamoto et al. (1995) are not confirmed - according to both ephemerides the period P should have stopped increasing and started decreasing by now, which is not observed - we note that $\ddot{P} < 0$ may indicate a decrease in the mass-loss rate. Discarding the unconfirmed cubic models in Table 1, the observed $\dot{P}/P$ values are in the range $1.0 \times 10^{-6}$ yr-1 to $2.2 \times 10^{-6}$ yr-1. We note here that in the extreme case in which there is only re-ejection and no direct WR wind (i.e., $\alpha = 0, \beta = 1$), only ratios of $m_{\rm d}/m_{\rm a} < 1.39$ give an increase of the orbital period and are thus consistent with the observed $\dot{P}$ of Cyg X-3.

  
3.2 Limits on the component masses derived from the rate of mass transfer and mass loss

  
3.2.1 Mass loss due to a direct wind
The presence of relativistic jets (e.g., Mioduszewski et al. 2001) shows that there must be an accretion disk around Cyg X-3. This accretion disk may be formed either through wind accretion or through RLOF. We first consider the case where the He star loses mass in a wind and the compact object accretes part of this wind, presumably at the Eddington rate. For the wind mass-loss rate of a He star we use

 \begin{displaymath} \dot{M} = \left\{ \begin{array}{ll} 2.8 \times 10^{-13}... ...bf\textrm{~~if} } & \log{L/L_\odot} < 4.5 \end{array} \right. \end{displaymath} (2)

in $M_\odot $ yr-1 (see Dewi et al. 2002,  and references therein). We take the luminosity of a He star on the He main-sequence (HeMS) from Hurley et al. (2000), who only did calculations for He stars up to  $10~M_\odot$; but Nugis & Lamers (2000) find that when the Hurley et al. results are extrapolated up to He-star masses of $M_{\rm He} = 40~M_\odot$ they are consistent with the results of Schaerer & Maeder (1992), which are valid for WNE[*]/WC stars up to  $40~M_\odot$. In Fig. 1 we plot the thus obtained mass-loss rate for a He star as a function of its mass  $M_{\rm He}$at the beginning and at the end of the HeMS.
  \begin{figure} \psfrag{Helium-star mass (MSun)}[t][c][3][0]{{\sf M$_{\sf He}$ /... ...} \resizebox{8.8cm}{!}{\includegraphics[angle=270]{2824fig4.ps}} \end{figure} Figure 1: Mass-loss rates of He stars: a) wind mass-loss rate for a homogeneous He star; b) wind mass-loss rate for a He star at He terminal-age main sequence; c) rough estimate of the mass-loss rate of a star that overflows its Roche lobe on a thermal time scale after completion of core He burning.
Open with DEXTER

Observed population I WR stars are more massive than $\sim$$7~M_\odot$ (see, e.g., Nugis & Lamers 2000); lower-mass He stars will probably not show a WR spectrum, nor will they produce a wind that could explain the mass-loss rate observed in the Cyg-X-3 system. Nugis & Lamers do not report any WR stars with mass-loss rates below $4 \times 10^{-6}~M_\odot$ yr-1, whereas Miller-Jones et al. (2005) find that the mass-loss rate from Cyg X-3 may be below $4 \times 10^{-6}~M_\odot$ yr-1. This might be an indication that the WR spectrum observed from Cyg X-3 is due to the re-ejection of Roche-lobe-overflowed material that mimics the WR phenomenon. Another explanation, however, may be that the outflow is not spherically symmetric in the case of Cyg X-3 (Sect. 2).

  
3.2.2 Mass transfer due to RLOF

Evolutionary calculations of Paczynski (1971), Tutukov & Yungelson (1973b), and Iben & Tutukov (1985) showed that He stars with $M_{\rm He} \la 0.8~M_\odot$ do not expand during core He burning and later evolutionary stages. Also He stars with $M_{\rm He} \ga 8~M_\odot$ hardly expand before carbon (C) ignition in their cores, later stages are so short that they may be neglected. For intermediate-mass He stars, inspection of the summary figure of Dewi et al. (2002, their Fig. 1) shows that in a binary with P = 0.2 days containing a NS and a He star, the latter may overflow its Roche lobe in the He-shell-burning stage if $M_{\rm He} \la 5.8~M_\odot$ or in the core-C-burning stage if $M_{\rm He} \la 7.4~M_\odot$. However, the expected number of systems in the Galaxy that experience RLOF in the C-burning stage is negligibly small since this stage is very short, and we are left with (0.8-5.8) $M_\odot $ He stars, overflowing their Roche lobe in the He-shell-burning stage (so-called BB case of evolution). If RLOF occurs after core He burning is completed, the mass-exchange time scale is on the order of the thermal one:

 \begin{displaymath} \tau_{\rm th} = \frac{G M^2}{R L}, \end{displaymath} (3)

with M, R, and L the mass, radius, and luminosity of the donor. In Fig. 1 we also plot the mass-transfer rate from the He star given by Eq. (3), with R and L at the end of the He main-sequence from Hurley et al. (2000).We see that if in a system containing a rather low-mass He star, matter is transferred to the c.o. via RLOF in a thermal time scale, the rate of loss of the re-ejected matter from the system would cover the same range in $\dot{M}$ as that for the winds of WR stars. Notice that Fig. 1 justifies considering only the two extreme cases of mass loss (stellar wind vs. RLOF+re-ejection): in a system with a given He-star mass that experiences RLOF, the mass transfer rate due to RLOF is two orders of magnitude higher than the wind mass-loss rate of a He star with the same mass would be.

  
3.2.3 Analytical results for the Cyg-X-3 system


  \begin{figure} \resizebox{8.8cm}{!}{\includegraphics[clip]{2824fig5.eps}} \end{figure} Figure 2: Schematic representation of possible system configurations that are consistent with $\dot{P}/P$ and $\dot{M}$ as observed in Cyg X-3. RLOF solutions give a very narrow range of possible combinations of $m_{\rm a}$ and $m_{\rm d}$ (the two narrow strips in the lower left; the gap is due to the presumed gap between the masses of NSs and those of BHs). For wind-accretion solutions, the range of possible combinations of $m_{\rm a}$ and $m_{\rm d}$ is much larger (hatched areas). Population synthesis shows that RLOF systems with NSs are formed in sufficiently large numbers to produce an observable Cyg-X-3 system. On the other hand, Roche-lobe overflowing BH systems are formed so rarely with P similar to the period of Cyg X-3 that the probability of observing them is negligible. See Figs. 5 and 4 and text.
Open with DEXTER

We can now insert the estimated values of RLOF and wind mass-loss rates given by Eqs. (2) and (3) and the observed $\dot{P}/P$ into Eq. (1) and solve it for all possible combinations of masses of the components $m_{\rm a}$ and $m_{\rm d}$ that satisfy the observations for Cyg X-3. The result of this is shown in Fig. 2. The narrow strips in the lower left show the possible combinations, assuming that mass transfer in the system is due to RLOF in a thermal time scale. The strips are shown here to exemplify their narrowness: the width of the strip is typically less than  $0.05~M_\odot$. When one uses mass-transfer rates for RLOF obtained from real binary-stellar-evolution calculations, the position of the strip may be somewhat displaced, but it remains narrow. The larger areas to the right show the possible mass combinations, assuming that mass-transfer in the system is due to wind accretion. We note that the much larger areas for the wind-accretion solutions do not mean that wind accretion is the most probable means of mass transfer in the Cyg-X-3 system. It merely shows that, if wind accretion is the mass-transfer mechanism in Cyg X-3, the space of possible  $m_{\rm a}$-$m_{\rm d}$ combinations is still quite large, whereas RLOF as the mass-transfer mechanism leaves only a few possible combinations of $m_{\rm a}$ and $m_{\rm d}$. However, results of population synthesis (see below) show that under the assumptions leading to the formation of He-star+BH (He+BH) systems, only a minor part of the "allowed'' area is populated. Figure 2 shows that the observed mass-loss rate from the system and the observed $\dot{P}/P$ are hard to reconcile with the suggestions of donor masses of several  $10~M_\odot$.

  
4 Evolutionary calculations

Analytical estimates for the Roche-lobe-overflowing systems presented above suggest that the "observed'' $\dot{M}$ range of Cyg X-3 may be typical for moderate-mass (up to several $M_\odot $) He stars overflowing their Roche lobes after completion of core He burning. The results of our population synthesis also suggest that most He companions to compact objects are of moderate mass, see Sect. 5.

To verify the inferences in the previous section, we carried out several evolutionary calculations of semidetached systems consisting of He stars accompanied by a c.o. We assumed that the latter can accrete matter at $\dot{M} \le \dot{M}_{\rm Edd}$ and that the excess of the transferred mass is lost from the system, taking away the specific angular momentum of the accretor. Prior to RLOF, mass loss by stellar wind was computed according to formulae (2). Accretion prior to RLOF was neglected. In the RLOF stage wind mass loss directly from the He star was neglected (see Fig. 1). The adopted ranges of initial masses were $1.0~M_\odot{-}4.1~M_\odot$ for the He stars and $1.4~M_\odot{-}5.0~M_\odot$ for the c.o.'s. Computations were carried out using P. Eggleton's evolutionary code (priv. comm. 2003, see also Eggleton & Kiseleva-Eggleton 2002,  and references therein). A selection of the results are presented graphically in Fig. 3. The systems had the following combinations of component masses at the onset of mass transfer: $m_{\rm d} = 3.0~M_\odot$, $m_{\rm a} = 5.0~M_\odot$ (Fig. 3a, b), $m_{\rm d} = 1.46~M_\odot$, $m_{\rm a} = 1.4~M_\odot$(Fig. 3c, d), and $m_{\rm d} = 1.0~M_\odot$, $m_{\rm a} = 1.4~M_\odot$(Fig. 3e, f). In all the computed systems the He stars started RLOF at $P \approx 0.2$ day.

  \begin{figure} \par\includegraphics[angle=270,width=15cm,clip]{2824fig7.eps} \end{figure} Figure 3: $\dot{M}$ and $\dot{P}/P$ as function of $M_{\rm He}$ for systems with Roche-lobe overflowing He-star donors and compact accretors. Masses $(m_{\rm d}, m_{\rm a})$ at the onset of mass transfer are: (3.0, 5.0), (1.46, 1.4), (1.0, 1.4) $M_\odot $ (from top to bottom). Roche-lobe overflow starts at $P \approx 0.2$ day. In all panels thick solid lines show results of computations. In panels for $\dot{P}/P$ thin solid lines show the limits of observed $\dot{P}/P$ in Cyg X-3. Dotted curves show rough estimates for $\dot{M}$ and $\dot{P}/P$ based on Eq. (3), derived with the approximations to R and L at the terminal-age He main-sequence from Hurley et al. (2000).
Open with DEXTER

We find that the systems with He-star donors $\ga$ $3.0~M_\odot$ traverse the range of $\dot{P}/P$ observed for Cyg X-3 in $\sim$102 yr. We do note, however, that the typical value of $\dot{P}/P$ in the RLOF phase decreases with the mass of the donor (for a given mass of the compact star) and that the time spent close to the observed $\dot{P}/P$ range increases for lower-mass systems. A system that at the onset of mass transfer consists of a $1.46~M_\odot$ He star and a $1.4~M_\odot$ c.o. (Figs. 3c, d) spends about $5 \times 10^3$ yrs in the $\dot{P}/P$ range observed in Cyg X-3, and stays some $6 \times 10^4$ yrs at $\dot{P}/P$ values less than twice those in the observed range. A system of a $1.0~M_\odot$ He star and a $1.4~M_\odot$ c.o. stays within the observed range throughout RLOF (Fig. 3e, f).

  
5 Population synthesis

We carried out a population synthesis to determine the current number of He+c.o. binaries in the Galaxy. The details of the population synthesis are briefly described in Appendix B. We used the approximations of Pols (1993) to the computations of Paczynski (1971) and Habets (1986) to estimate the core-He-burning times. In Figs. 4 and 5 we plot the masses of the components and the orbital periods of the He+c.o. systems that have He components in the core-He-burning stage. We find that there are currently $\sim$200 He+BH and $\sim$540 He+NS binaries in the Galaxy[*].

5.1 Wind-fed X-ray systems

As noted in Sect. 3.2.1 we expect an accretion disk in the Cyg-X-3 system. The systems shown in Figs. 4 and 5 may form a disk through wind accretion if the wind matter carries enough angular momentum as realised first by Illarionov & Sunyaev (1975); see, e.g., Livio (1994) for later work on this subject.

  \begin{figure} \par\includegraphics[angle=-90,width=8.65cm]{2824fig6.ps} \includ... ...fig2.eps} \includegraphics[angle=-270,width=8.65cm]{2824fig3.eps} \end{figure} Figure 4: Current population of core-He-burning He+BH binaries in the Galaxy. Upper panel - distribution in $M_{\rm He} - P$ plane; middle panel - distribution in $M_{\rm BH} - P$ plane; lower panel - distribution in $M_{\rm He} - M_{\rm BH}$ plane. The dash-dotted vertical lines in the upper and lower panel show the lower-mass boundary for He stars identified as WR stars. Systems that satisfy the disk-formation criterion for wind-fed objects (Eq. (4)) are marked by open circles; the subset of them with $3.6 \leq P/{\rm hr} \leq 6.0$ is marked by stars.
Open with DEXTER

5.1.1 Helium-star/black-hole binaries
Following the derivation in Ergma & Yungelson (1998) for systems with Kerr BHs, we applied the disk-formation criterion

 \begin{displaymath}P \la 0.2 (M_{\rm BH}/M_\odot) v^{-4}_{1000}~{\rm day}, \end{displaymath} (4)

where $M_{\rm BH}$ is the BH mass, and v1000 is the magnitude of the radial velocity of the wind in the vicinity of the c.o. in units of 1000 km s-1. It appears then that for v1000=1 there are currently $\sim$30 wind-fed disk-forming systems in the Galaxy, 5 of them with orbital periods similar to that of Cyg X-3. However, only 9 out of the 30 systems have $M_{\rm He} \ga 7~M_\odot$ donors and would be identified as WR stars. Only one of these systems has an orbital period close to that of Cyg X-3. The remaining four systems with P in the observed range have $M_{\rm He} \approx (2{-}4)~M_\odot$; according to Eq. (2) their wind mass-loss rate will be below $\sim$ $10^{-7}~M_\odot$ yr-1 and they probably will not produce the WR phenomenon[*]. There are 8 systems with $M_{\rm He} \ga 7~M_\odot$ and $P \ga 10$ h that fulfil the disk-formation criterion. Note, however, that criterion (4) has a very steep dependence on v1000; if we assume, e.g., that v1000=1.5, only 3 systems remain out of the 30 able to form disks, all of them with P < 0.15 day and with $M_{\rm He} \approx 3~M_\odot$. Since known WR stars have $v_{1000} \approx (0.7{-}5.0)$ (Nugis & Lamers 2000), we claim that Cyg X-3 may well be the only wind-fed WR+BH system in the Galaxy.

As already noted by Iben et al. (1995) and Ergma & Yungelson (1998), with $v_{1000} \approx 1.5$, Cyg X-3 may have a wind-fed disk if $M_{\rm BH} \approx 5~M_\odot$. The latter value fits well into the model range of expected black-hole masses in wind-fed systems with disks and orbital periods close to that of Cyg X-3 (the star symbols in Fig. 4). An additional reason why only a WR system with $P \la 0.25$ days shows up as a WR X-ray binary may have to do with the velocity profile of the wind. In such a close system the wind will, at the orbit of the compact object, not yet have reached its terminal velocity (of for example 1500 km s-1), whereas in the wider systems it may have, such that no disk forms in the wider systems.


  \begin{figure} {\includegraphics[angle=270,width=8.8cm,clip]{2824fig8.ps} } \end{figure} Figure 5: Current population of core-He-burning He+NS binaries in the Galaxy. The dash-dotted vertical line shows the lower-mass boundary for He stars identified with WR stars. The four dashed lines show the critical periods below which according to criterion (5) disk formation through wind accretion is possible, if v1000 = 1, 1.5, 2, and 3 (highest to lowest), respectively.
Open with DEXTER

5.1.2 Helium-star/neutron-star binaries

Figure 5 shows the population of He+NS binaries, which can be divided into two subpopulations. The first and larger subpopulation consists of systems with $P \la 1$ day and $M_{\rm He} \la 2~M_\odot$. The short period is due to their previous common-envelope (CE) phase; the large number of low-mass He-star systems is due to the initial-mass function and to the fact that low-mass He stars live much longer than higher-mass He stars. The other systems form through a "double spiral-in'' in which two giants go through a CE phase, producing two He stars. This formation channel only occurs for nearly-equal-mass binaries, and since the most massive He star collapses into a c.o., there is a lower limit to the mass of the other He star (see Brown 1995).

As shown by Illarionov & Sunyaev (1975) and Ergma & Yungelson (1998), an accretion disk will form in a He+NS binary if the rotation period of the NS is longer than the equilibrium period that was established during the CE episode that accompanied the formation of the He star. Assuming that the wind-mass-loss rate may be described by a formula $\dot M = k M_{\rm He}^{\alpha}$ (e.g. Nelemans & van den Heuvel 2001), one derives as the disk-formation criterion

 \begin{displaymath}P \la 1.5 \times 10^5 k^{0.75} M_{\rm NS}^{1.5} M_{\rm t}^{-0.5} M_{\rm He}^{0.75 \alpha} v_{1000}^{-3}~{\rm h}. \end{displaymath} (5)

(This is equivalent to Eq. (9) of Ergma & Yungelson (1998), but with a more general expression for $\dot{M}$.) We assume $k=1.38 \times 10^{-8}$, $\alpha=2.87$ after Nelemans & van den Heuvel (2001), which gives practically the same $\dot{M}$ values as Eq. (2). Limiting periods for v1000 = 1, 1.5, 2, and 3 are plotted in Fig. 5 (dashes). We find $\sim$5 systems that may be identified as WR+NS systems with accretion disks. However, the very steep dependence on the wind velocity may reduce this number to 0. Thus, as already noted by Ergma & Yungelson (1998), the low angular momentum of WR-star winds may completely preclude the formation of wind-fed Cyg-X-3-like systems with NS companions.

One should note, however, that the mass-loss rates for He stars quoted above were derived from observational data on WR stars. Data on mass-loss rates for lower-mass He stars are not available. It is therefore not clear whether $\dot{M}$ may be extrapolated to below $\sim$$7~M_\odot$. Hence, the validity of criterion (5) below this mass is uncertain.

5.2 X-ray systems powered by RLOF

Another possibility for Cyg X-3 is that the system contains a He star of $\la$$7~M_\odot$ which transfers mass in the case BB of RLOF. Then the WR spectrum arises in re-ejected matter. Also in the RLOF case, we can estimate the number of systems we should currently observe as WR X-ray binaries. As mentioned in Sect. 4, the RLOF systems that can provide a $\dot{P}/P$ close to the observed range must initially have had a low-mass ($\la$1.5 $M_\odot $) He-star donor. From the population-synthesis calculations we expect $\sim$500 such systems in the Galaxy at any time. Typically these systems live $\sim$ $1.5 \times 10^7$ yrs, of which they spend $\sim$105 yrs in the phase of Roche-lobe overflow. We thus expect only of order 1 such system in the Galaxy to be in the phase of Roche-lobe overflow at any time.

As indicated by Fig. 5, the bulk of these systems has $P \le 10$ h. The typical mass-transfer rates in these systems are in the range $(1{-}3) \times 10^{-6}~M_\odot$ yr-1, and most of the transferred mass will be lost from the system through re-ejection. These rates are consistent with the lowest observational estimates of $\dot{M}$ for Cyg X-3.

6 Discussion

  
6.1 The "missing'' He+c.o. binaries

Our population synthesis shows that there are several core-He-burning He+NS binaries and a few dozen core-He-burning He+BH binaries with He-star masses $\ga$$7~M_\odot$ in our Galaxy. If we assume that all matter that passes through the so-called accretion radius $r_{\rm a} = 2 G m_{\rm a} / c^2$ (G the gravitational constant, c the speed of light) is accreted by the c.o., and that the gravitational potential energy of the accreted matter is converted into luminosity, all wind-accreting He-star binaries with $M_{\rm He} > 3~M_\odot$ in our model population will have an intrinsic luminosity $\ga$1036 erg s-1 and should be observable as He-star X-ray sources. In this we also assume that Eq. (2) holds down to low-mass He stars.

Apart from Cyg X-3, a few WR+c.o. candidates are reported: e.g., HD 197406/WR 148 (Marchenko et al. 1996), HD 191765/WR 134 (Morel et al. 1999), HD 104994/WR 46 (Marchenko et al. 2000). However, it is still unclear whether the companions to these WR stars really have a relativistic nature, as the systems lack the X-ray luminosity expected in such a case. A low $L_{\rm X}$ can be reconciled with, e.g., a spinning pulsar, that deflects the flow.

The fact that we do not observe several tens of He-star X-ray binaries in the Galaxy may be due to self-absorption of the X-ray photons by the wind of the donor. It turns out that for the binaries in our population-synthesis sample, the minimum column density between the c.o. and Earth due to the He-star wind depends mainly on  $M_{\rm He}$. This column density is $\ga$10 g cm-2 for all sources with $M_{\rm He} > 4~M_\odot$, rendering these sources unobservable in X-rays at energies below 20 keV. We do note that INTEGRAL has discovered several sources at energies >20 keV, of which $\sim$40 are still unidentified (Ubertini 2005). These hard sources might well be the missing He+c.o. binaries.

The derivation for the column density also applies to RLOF-accreting sources that spherically symmetrically throw out overflowing matter in excess of the Eddington rate. We saw in Sect. 3 that the mass-transfer rate for RLOF systems is $\ga$ $5 \times 10^{-6}~M_\odot$ yr-1, well above the Eddington rate for a solar-mass c.o. ( $\dot{M}_{\rm Edd} \approx 8 \times 10^{-8}~M_\odot$ yr-1 for a 1.4 $M_\odot $ NS accreting pure He) and good enough for a minimum column density of $\sim$102 g cm-2. This may support the suggestion of a model for Cyg X-3 in which the excess matter is thrown out of the system equatorially instead of spherically symmetrically (Sect. 3), together with a very low inclination for the system.

  
6.2 IC10 X-1 and SS 433, two other Wolf-Rayet X-ray binaries?

  
6.2.1 IC10 X-1

Bauer & Brandt (2004) and Clark & Crowther (2004) find that the luminous X-ray source IC10 X-1 [ $L_{0.1{-}2.5~{\rm keV}}=(2{-}4)\times 10^{38}$ erg s-1] in the starburst galaxy IC10 is spatially coincident with WNE star [MAC92] 17-A (notation adopted from Crowther et al. 2003). Assuming [MAC92] 17-A to be the most probable optical counterpart to IC10 X-1, Clark & Crowther (2004) fit a model with a stellar temperature of 85 000 K, log ( $L/L_\odot) = 6.05$, $\dot{M} = 4 \times 10^{-6}~M_\odot$ yr-1, and a terminal wind velocity of 1750 km s-1 to the observed He II  $\lambda4686$ and N V  $\lambda\lambda$4603-20 emission. They infer a mass for the WR star of $\sim$ $35~M_\odot$, using the WR mass - luminosity relations of Schaerer & Maeder (1992). Allowing for clumping, Clark & Crowther find that $\dot{M}$ is equivalent to a homogeneous mass-loss rate of $\sim$ $1 \times 10^{-5}~M_\odot$ yr-1.

Bauer & Brandt (2004) note that IC10 X-1 is quite similar to Cyg X-3 in terms of X-ray luminosity, spectrum, and variability. Thus, IC10 X-1 may be the first extragalactic example of a short-lived WR X-ray binary similar to Cyg X-3. Identification of the optical counterpart to IC10 X1 with a massive WR star suggests that the system is wind-fed[*].

Note, however, that in the field of IC10 X-1 there are three other candidate optical counterparts, with O- or B-spectral types, to the X-ray source. Clark & Crowther (2004) suggest that their wind mass loss is insufficient to explain the observed X-ray luminosity with wind accretion. From this Clark & Crowther argue that, if one of those three candidates is the optical counterpart to IC10 X-1, the system is Roche-lobe-overflow fed similar to LMC X-4 or LMC X-3.

  
6.2.2 SS 433

The variable X-ray and radio source SS 433 was also suggested to be a WR X-ray binary (van den Heuvel et al. 1980; Fuchs et al. 2004,2002a). Van den Heuvel et al. suggested that SS 433 contains an evolved early-type star or a WR star, based on the nature of its stationary spectrum, the size of the emitting region, the necessary presence of a strong wind for the production of the IR emission, and the large outflow velocity of the wind.

In one of the latest attempts to identify the optical counterpart of SS 433, Fuchs et al. (2002b,a) compared its mid-IR spectrum to WR stars of the WN subtype. They found the spectrum of SS 433 to resemble that of WR 147, a WN8+B0.5V binary with colliding wind. Using the formulae of Wright & Barlow (1975) and taking wind clumping into account, Fuchs et al. (2004) obtain $\dot{M}=(5{-}7)\times 10^{-5}~M_\odot$ yr-1, compatible to a strong late-WN wind.

Fuchs et al. (2004) proposed that the material surrounding the c.o. forms a thick torus or envelope around it rather than a classic thin accretion disk. They argue that the material is ionised by X-rays emitted from the vicinity of the c.o. and expelled by radiation pressure, which results in the imitation of a WR star. As mentioned above, this model needs further elaboration, especially the formation of the WR spectrum and the self-absorption of the X-rays.

On the other hand, King et al. (2000) suggested that SS 433 is a mass-transferring system in which the formation of a CE may be avoided if radiation pressure expels the transferred matter in excess of the Eddington rate, i.e., a re-ejection model with a hydrogen-rich donor. For this model the donor mass must be in the range of  $(4{-}12)~M_\odot$. The model has received support from the discovery of A-type super-giant features in the spectrum of SS 433 observable at certain orbital phases (Hillwig et al. 2004; Gies et al. 2002). Estimated masses of the components are $10.9 \pm 3.1$ and $2.9 \pm 0.7~M_\odot$, fitting the King et al. model. As noted by Fuchs et al. (2004), if the results of Gies et al. (2002) and Hillwig et al. (2004) are confirmed, one needs to resolve an apparent contradiction of the simultaneous presence of A-star and WR-star features in the spectrum.

If the presence of an A-type star is not confirmed, however, it may appear that SS 433 really is a WR X-ray binary, the second one known in the Galaxy after Cyg X-3.

   
7 Conclusions

We find in Sect. 5 that there are in principle two possible He-star binary configurations which may explain the observed $\dot{P}/P$ and $\dot{M}$ of Cyg X-3, and for which population-synthesis calculations combined with disk-formation criteria predict the existence of $\sim$1such system in the Galaxy.

The first possibility is a system consisting of a massive ($\ga$$7~M_\odot$) helium (i.e., WR) star and a BH around which a disk is formed through wind accretion. Population synthesis predicts that at any time $\sim$1 such system with an orbital period similar to that of Cyg X-3 is present in the Galaxy, provided that the wind velocity near the orbit of the c.o. is $\la$1000 km s-1. In this case the system will have a lifetime of several times 105 yrs (the lifetime of the He star), and the secular orbital-period increase is simply due to stellar-wind mass loss.

The second possibility is a system consisting of a He star with a mass $\la$ $1.5~M_\odot$ and a NS, which is powered by mass transfer due to RLOF at a rate in the range $(1{-}3) \times 10^{-6}~M_\odot$ yr-1. Population synthesis predicts that also $\sim$1 such system with P < 10 h may be present in the Galaxy at any time. In this case the system will have a lifetime of about 105 yrs, and the secular orbital-period increase is due to the combined effects of the mass transfer and subsequent mass loss - at a rate close to the transfer rate - from the accretion disk around the NS.

In view of the population-synthesis results, we deem both configurations equally likely for Cyg X-3. We note that, though the first of the solutions implies the presence of a "real'' WR star in the system, its mass is probably not extremely high, $\la$ $12~M_\odot$. Thus, both solutions are consistent with the conclusion of a relatively moderate mass for the companion in Cyg X-3, which follows from identification of the emission region with the vicinity of the compact object (Stark & Saia 2003; Fender et al. 1999).

We now speculate on the fate of these configurations. In the "wind'' case, if the WR star loses sufficient mass, it might terminate as a NS, such that a system consisting of a BH plus a young radio pulsar would emerge. In view of the likely mass of $\sim$$5~M_\odot$ for the BH (a value well within the range of BH masses in confirmed BH binaries, see, e.g., McClintock & Remillard 2004), disruption of the system in the supernova explosion seems unlikely. Alternatively, the WR star might collapse to a black hole, producing a double-BH binary.

The fate of the "RLOF'' configuration is most likely a binary consisting of a massive white dwarf (composed of CO or ONeMg), together with a recycled neutron star. Several such systems are known in our galaxy as fast-spinning binary radio pulsars with massive white-dwarf companions in circular orbits (see, e.g., Stairs 2004).

Acknowledgements
We are grateful to P. Eggleton for providing the latest version of his evolutionary code. We would like to thank our colleagues at the "Anton Pannekoek'' Astronomical Institute and at the Institute of Astronomy of the Russian Academy of Sciences for useful discussions. In particular we would like to thank T. Maccarone for discussions on X-ray binaries, J. Miller-Jones for sharing preliminary results on Cyg X-3, and K. van der Hucht, A. de Koter, and N.N. Chugai for useful discussions on the properties of WR stars. LRY acknowledges the warm hospitality of the Astronomical Institute "Anton Pannekoek,'' where part of this work was accomplished. LRY is supported by RFBR grant 03-02-16254, the Russian Ministry of Science and Education Program "Astronomy'', NWO, and NOVA. SPZ is supported by KNAW.

Appendix A

We derive below the dependence of $\dot{P}/P$ on the masses of the donor and the accretor $m_{\rm d}$ and $m_{\rm a}$, the mass-loss rate from the donor  $\dot{m}_{\rm d}$, the fraction of  $\dot{m}_{\rm d}$ that goes in a direct wind $\alpha$, and the fraction of  $\dot{m}_{\rm d}$ that is re-ejected after transfer to the accretor $\beta$. Early similar derivations are given in e.g. Huang (1963) and Tutukov & Yungelson (1971).

The total orbital angular momentum of the system is

 \begin{displaymath} J = \frac{2 \pi}{P} \left[ \frac{m_{\rm a} m_{\rm d}}{(m_{\rm a}+m_{\rm d})} \right] a^2. \end{displaymath} (6)

From Eq. (6) we have

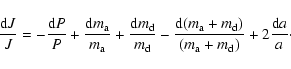\begin{displaymath}\frac{{\rm d}J}{J} = - \frac{{\rm d}P}{P} + \frac{{\rm d}m_{\... ...m_{\rm d})}{(m_{\rm a}+m_{\rm d})} + 2 \frac{{\rm d}a}{a}\cdot \end{displaymath} (7)

We then use Kepler's third law and definitions

 \begin{displaymath}{\rm d}m_{\rm a} = - (1-\alpha-\beta) {\rm d}m_{\rm d} \end{displaymath} (8)


 \begin{displaymath}{\rm d}(m_{\rm a}+m_{\rm d}) = (\alpha+\beta) {\rm d}m_{\rm d} \end{displaymath} (9)

(by definition, $\alpha + \beta \le 1$) to derive

 \begin{displaymath} \frac{{\rm d}P}{P} = 3 \frac{{\rm d}J}{J} + 3 \frac{(1-\alp... ...c{(\alpha+\beta) {\rm d}m_{\rm d}}{(m_{\rm a}+m_{\rm d})}\cdot \end{displaymath} (10)

The logarithmic derivative of the orbital angular momentum due to mass loss from the system is given by

 \begin{displaymath} \frac{{\rm d}J}{J} = \frac{\alpha m_{\rm a}^2 + \beta m_{\r... ...m_{\rm d})} \frac{{\rm d} m_{\rm d}}{m_{\rm a} m_{\rm d}}\cdot \end{displaymath} (11)

Inserting this into (10), we obtain
 
$\displaystyle \frac{{\rm d}P}{P} = \frac{{\rm d}m_{\rm d}}{m_{\rm a} m_{\rm d} ... ...-\!2 m_{\rm a} m_{\rm d} \beta\! +\! 3 m_{\rm d}^2 \!- \!3 m_{\rm a}^2 \right].$     (12)

We note that our Eq. (12) is not consistent with the expressions for variations of a and P in a similar model given by Soberman et al. (1997, their Eqs. (30) and (31)). The correct equations in their notation are:
  
$\displaystyle \frac{\partial \ln{a}}{\partial \ln{q}}$ = $\displaystyle 2(\mathscr{A}_w - 1) + (1 - 2 \mathscr{B}_w) \frac{q}{1 + q} + (3 + 2 \mathscr{C}_w) \epsilon \frac{q}{1 + \epsilon q},$  
$\displaystyle \frac{\partial \ln{P}}{\partial \ln{q}}$ = $\displaystyle 3(\mathscr{A}_w - 1) + (1 - 3 \mathscr{B}_w) \frac{q}{1 + q} + (5 + 3 \mathscr{C}_w) \epsilon \frac{q}{1 + \epsilon q}\cdot$ (13)

Appendix B


  \begin{figure} \par {\includegraphics[angle=0,width=8.8cm,clip]{2824fig1.ps} } \end{figure} Figure 6: Summary of the evolution of the mass of single stars or components of wide binaries ( top panel) and of stars in binaries experiencing RLOF ( bottom panel). As a function of initial mass, the lines give: the mass at the end of the main-sequence ( $M_{\rm tams}$, solid line), the initial mass of the He-core ( $M_{\rm core, i}$, dotted line), the mass just before the supernova explosion or the formation of the white dwarf ( $M_{\rm pre-SN}$, dashed line), and the mass of the final c.o. ( $M_{\rm comp. obj}$, black-white-black line). The bottom panel shows the masses for a primary that loses its hydrogen envelope soon after the end of the main sequence, before the He-core burning starts.
Open with DEXTER

We used the Nelemans et al. (2004) realisation of the SeBa program (Portegies Zwart & Verbunt 1996) to carry out our population-synthesis calculations. The effects of stellar wind and c.o. formation are shown in Fig. 6. The most important assumptions about the evolution of massive stars in binaries relevant to this paper are as explained in Portegies Zwart & Yungelson (1999); Nelemans et al. (2001); Portegies Zwart & Yungelson (1998) with the following two differences:

1.
WR stellar winds are modelled by the fit to observed WR mass-loss rates derived by Nelemans & van den Heuvel (2001).

2.
It is assumed that stars with more massive carbon-oxygen cores than 6.5 $M_\odot $ collapse into a BH (for single stars this means stars with an initial mass above 25 $M_\odot $, in close binaries stars with an initial mass above 28 $M_\odot $, see Fig. 6). The mass of the resulting BH is 65 per cent of the mass of the exploding object (based on, e.g., Nelemans et al. 1999). The lowest-mass BH (for an exploding naked carbon-oxygen core) thus has a mass of 4.2 $M_\odot $.
The bottom panel of Fig. 6 summarises the evolution of binaries in which RLOF occurs. The period for which this happens is a function of the mass of the primary. As can be seen from the figure, we skip RLOF for any case-B period for initial masses > $80~M_\odot$. Note that RLOF may be omitted for much lower primary masses due to the occurrence of an LBV phase (e.g., Vanbeveren et al. 1998b). However, a detailed discussion of this matter is beyond the scope of this paper.

References

 
Copyright ESO 2005