A&A 442, 579-586 (2005)
DOI: 10.1051/0004-6361:20053143
The coughing pulsar magnetosphere
I. Contopoulos![[*]](/icons/foot_motif.gif)
200 Akti Themistokleous Str., Piraeus 18539, Greece
Received 28 March 2005 / Accepted 28 June 2005
Abstract
Polar magnetospheric gaps consume a fraction of the electric
potential that develops
across open field lines. This effect modifies significantly
the structure of the axisymmetric pulsar magnetosphere.
We present numerical
steady-state solutions for various values of the
gap potential.
We show that a charge starved magnetosphere contains significantly
less electric current than one with freely
available electric charges.
As a result, electromagnetic neutron star braking becomes
inefficient.
We argue that the magnetosphere may spontaneously rearrange
itself to a lower energy configuration through
a dramatic release of electromagnetic field energy
and magnetic flux. Our results might be relevant
in understanding the recent December 27, 2004 burst observed in
SGR 1806-20.
Key words: magnetohydrodynamics (MHD) - pulsars: general - stars: magnetic fields - gamma ray: bursts
The magnetosphere of a rotating neutron star with
polar magnetic field B*, mass
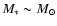 ,
radius
,
radius
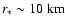 ,
magnetic dipole moment
,
magnetic dipole moment
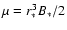 ,
and angular velocity
,
and angular velocity 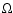 is expected
to radiate electromagnetic energy at a rate
is expected
to radiate electromagnetic energy at a rate
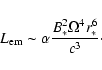 |
(1) |
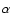 is a factor of order unity (Beskin 1997)
is a factor of order unity (Beskin 1997)![[*]](/icons/foot_motif.gif) .
The source of the radiation is the neutron star rotational
kinetic energy which is lost at a rate
.
The source of the radiation is the neutron star rotational
kinetic energy which is lost at a rate
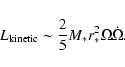 |
(2) |
It is usual to equate Eqs. (1) and (2) and thus obtain
an estimate of the stellar magnetic field B*.
In general, however, the two do not have to be equal.
As we shall see below, in the case of axisymmetry,
electromagnetic torques need to be significantly revised.
In the context of ideal axisymmetric MHD,
electric charges are available
in copious amounts and move freely along magnetic field lines,
shorting out any component of the electric field that might
arise along
the magnetic field. As a result, magnetic flux surfaces become
equipotentials, and an electric field 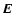 develops
across magnetic field lines (
develops
across magnetic field lines (
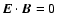 )
with magnitude
)
with magnitude
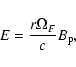 |
(3) |
where, 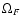 ,
a constant along magnetic flux surfaces
(see below), can be thought of as the
angular velocity of rotation of magnetic field lines (r is
the cylindrical radius;
,
a constant along magnetic flux surfaces
(see below), can be thought of as the
angular velocity of rotation of magnetic field lines (r is
the cylindrical radius; 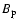 is
the poloidal component of the magnetic field).
The source of the electric potential across magnetic
field lines is obviously the rotating magnetized conducting
surface of the neutron star which acts as a unipolar inductor.
For the sake of simplicity, most studies of the axisymmetric
pulsar magnetosphere have assumed that the full potential drop
induced across field lines along the surface
of the star continues to manifest itself all along those
field lines, i.e.
is
the poloidal component of the magnetic field).
The source of the electric potential across magnetic
field lines is obviously the rotating magnetized conducting
surface of the neutron star which acts as a unipolar inductor.
For the sake of simplicity, most studies of the axisymmetric
pulsar magnetosphere have assumed that the full potential drop
induced across field lines along the surface
of the star continues to manifest itself all along those
field lines, i.e.
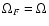 .
It has been pointed out, however,
(e.g. Ruderman & Sutherland 1975) that
"open magnetic field lines play a role analogous to that
of conducting wires in ordinary circuits. If the wire is broken
near the pulsar surface, a potential drop develops across the gap''.
The presence
of such gaps obviously reduces the electric potential available
across open field lines, and thus the electromagnetic energy
power radiated at large distances.
Models of particle acceleration and pair creation
above the polar cap of rotation-powered pulsars yield
potential drops near the surface of the star
of the order of 1012 Volts (e.g. Hibschman & Arons 2001; Arons,
personal communication),
and therefore, in general,
.
It has been pointed out, however,
(e.g. Ruderman & Sutherland 1975) that
"open magnetic field lines play a role analogous to that
of conducting wires in ordinary circuits. If the wire is broken
near the pulsar surface, a potential drop develops across the gap''.
The presence
of such gaps obviously reduces the electric potential available
across open field lines, and thus the electromagnetic energy
power radiated at large distances.
Models of particle acceleration and pair creation
above the polar cap of rotation-powered pulsars yield
potential drops near the surface of the star
of the order of 1012 Volts (e.g. Hibschman & Arons 2001; Arons,
personal communication),
and therefore, in general,
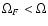 .
.
Beskin & Malyshkin 1998
took the above well known effect into account
in their calculation of the modified magnetospheric structure
inside the light cylinder.
In the present paper we obtain the first global
solution of this problem.
In Sect. 2 we formulate the problem and the numerical method
that we implement for its solution.
In Sect. 3 we obtain the structure of the magnetosphere
for various values of 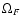 in the range
in the range
![$[0,\Omega]$](/articles/aa/full/2005/41/aa3143-05/img43.gif) and argue that the magnetosphere
may switch between solutions, releasing
energy in the process.
In Sect. 4 we discuss the relevance of our results in
understanding the recent December 27, 2004 SGR-1806-20 burst.
Our conclusions are summarized in Sect. 5.
and argue that the magnetosphere
may switch between solutions, releasing
energy in the process.
In Sect. 4 we discuss the relevance of our results in
understanding the recent December 27, 2004 SGR-1806-20 burst.
Our conclusions are summarized in Sect. 5.
We will work in cylindrical spatial coordinates 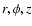 ,
and will consider only the axisymmetric case where
the magnetic dipole axis is aligned with the axis of rotation.
This simplification allows us
to introduce the magnetic flux function
,
and will consider only the axisymmetric case where
the magnetic dipole axis is aligned with the axis of rotation.
This simplification allows us
to introduce the magnetic flux function 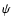 (
(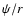 is the
is the 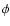 -component of the magnetic
vector potential),
the poloidal electric current function
-component of the magnetic
vector potential),
the poloidal electric current function 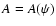 (the poloidal electric current contained within
the magnetic flux surface
(the poloidal electric current contained within
the magnetic flux surface 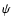 is equal to Ac/2;
is equal to Ac/2;
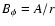 ),
and the magnetic field line
"rotational velocity''
),
and the magnetic field line
"rotational velocity''
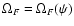 .
The various
magnetospheric physical quantities are obtained as follows:
.
The various
magnetospheric physical quantities are obtained as follows:
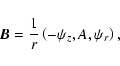 |
(4) |
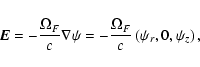 |
(5) |
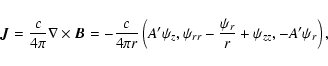 |
(6) |
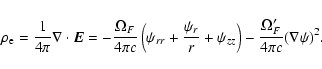 |
(7) |
Here, and in what follows,
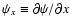 .
Also,
.
Also,
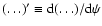 .
When we neglect inertia, force balance requires that
.
When we neglect inertia, force balance requires that
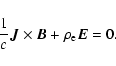 |
(8) |
Following Gruzinov (2005), we take
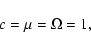 |
(9) |
and thus Eq. (8) becomes
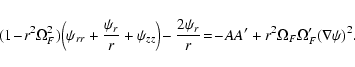 |
(10) |
This is a more general form of the pulsar equation than
the one considered in Contopoulos, Kazanas & Fendt (hereafter CKF)
where
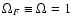 everywhere.
everywhere.
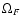 is related to the magnetospheric
potential drop VF between
the axis and any magnetic flux surface
is related to the magnetospheric
potential drop VF between
the axis and any magnetic flux surface 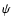 (Eq. (5)), namely
(Eq. (5)), namely
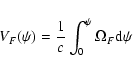 |
(11) |
(in units
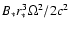 ). This is in general
different from the stellar potential drop between the pole and
the footpoint on the surface of the star
of the magnetic flux surface
). This is in general
different from the stellar potential drop between the pole and
the footpoint on the surface of the star
of the magnetic flux surface 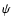 ,
namely
,
namely
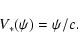 |
(12) |
The difference
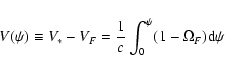 |
(13) |
is just the particle acceleration gap potential which devolops
along the magnetic field near
the footpoint of the magnetic flux surface (e.g. Beskin 1997).
In the region of closed field lines (hereafter the "dead zone''),
there is no particle flow, and
therefore there is no need for the formation of
particle acceleration gaps. We can thus express
 |
(14) |
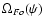 is determined by the particle acceleration gap
microphysics and by the supply of charge carriers
at the base of the magnetosphere (see discussion in Sect. 4).
In our present discussion,
is determined by the particle acceleration gap
microphysics and by the supply of charge carriers
at the base of the magnetosphere (see discussion in Sect. 4).
In our present discussion,
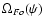 is essentially a free function.
For the sake of simplicity, we take
is essentially a free function.
For the sake of simplicity, we take
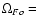 const.,
as in Beskin & Malyshkin (1998).
The magnetospheric gap potential is, therefore, given by
const.,
as in Beskin & Malyshkin (1998).
The magnetospheric gap potential is, therefore, given by
 |
(15) |
V is minimal at the center of the polar cap and increases
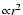 as we move away from the axis.
as we move away from the axis.
Observational manifestation of the differential magnetospheric
rotation is thought to be found in the sub-pulse slow drifts across
the pulse profile in almost aligned pulsars (e.g. Rankin & Wright 2003).
Interpretation of such drifts remains still rather sketchy.
We speculate that the sub-pulses are
associated with the above mentioned magnetospheric gaps
present around the separatrix between open and closed
field lines where the need for electric charge carriers
is the greatest (as we discuss below, this is where
closes the electric circuit of the
poloidal electric current that flows through the polar cap).
In most cases with observed sub-pulse drifts
(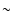 1 s period pulsars)
1 s period pulsars)
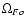 is expected to
be much smaller than
is expected to
be much smaller than 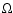 .
These gaps are
probably carried around the axis of rotation
by the "friction'' between the differentially rotating
open and closed line regions, and thus
their observed angular velocity is found to be
close to
.
These gaps are
probably carried around the axis of rotation
by the "friction'' between the differentially rotating
open and closed line regions, and thus
their observed angular velocity is found to be
close to 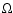 .
.
As we mentioned before, solutions of the pulsar equation
exist only for the simplest case
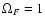 and
and
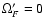 .
Even
in that case, though, a strong mathematical singularity,
the so called "light cylinder''
.
Even
in that case, though, a strong mathematical singularity,
the so called "light cylinder''
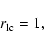 |
(16) |
makes the problem non-trivial.
Note that this is just the force-free Alfven surface,
and only very recently
has a numerical method been presented which allowed us
to obtain a "smooth'' solution that fills all space (CKF).
The main features of that numerical solution
(further refined in Gruzinov 2005) are:
- 1.
- The region of open field lines, the so called "polar cap'',
is slightly larger than
the region of static dipolar field lines which cross the equator
beyond the distance r=1, namely
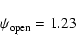 |
(17) |
(present calculation![[*]](/icons/foot_motif.gif) ).
We remind the reader that
).
We remind the reader that
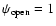 for a static dipole,
and therefore we see that
rotation "pulls'' dipolar magnetic field lines out.
for a static dipole,
and therefore we see that
rotation "pulls'' dipolar magnetic field lines out.
- 2.
- The distribution of poloidal electric current along
the open field lines is very close to the one in the
Michel (1974) relativistic split monopole solution, namely
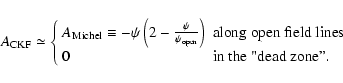 |
(18) |
The electric current distribution deviates slightly from the above
near
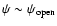 where field lines follow
the singular shape of the separatrix between the open and closed
line regions (see Fig. 6 below).
where field lines follow
the singular shape of the separatrix between the open and closed
line regions (see Fig. 6 below).
- 3.
- The return current of the above current distribution,
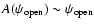 ,
flows
along the separatrix.
This implies the presence of magnetic and electric field
discontinuities across the separatrix.
,
flows
along the separatrix.
This implies the presence of magnetic and electric field
discontinuities across the separatrix.
- 4.
- In general, the equatorial extent
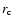 of the "dead zone''
may be taken as a free parameter (see Sect. 5, Appendix).
It is very natural, however, to assume that the "dead zone''
extends all the way to the light cylinder
of the "dead zone''
may be taken as a free parameter (see Sect. 5, Appendix).
It is very natural, however, to assume that the "dead zone''
extends all the way to the light cylinder![[*]](/icons/foot_motif.gif) .
.
- 5.
- Open field lines become monopole-like around and beyond
the light cylinder.
- 6.
-
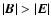 everywhere
everywhere![[*]](/icons/foot_motif.gif) .
.
We are now ready to address the physically more interesting
case
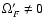 ,
in the simplest possible case
where
,
in the simplest possible case
where
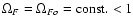 in the open field line
region, and
in the open field line
region, and
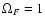 in the dead zone (Eq. (14)).
When
in the dead zone (Eq. (14)).
When
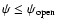 ,
we can rewrite Eq. (10) in
the new spatial coordinates
,
we can rewrite Eq. (10) in
the new spatial coordinates
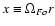 and
and
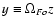 ,
,
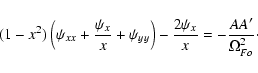 |
(19) |
Equation (19) is the same as our original equation in CKF.
We thus expect that solutions of Eq. (10) will be very similar
to the ones obtained in CKF. We would like to emphasize the
following interesting features:
- 1.
- As in CKF, it is natural to assume that
the corotating "dead zone'' extends all the way to the
light cylinder distance, i.e.
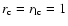 .
The real mathematical singularity, however, is not at the light
cylinder, but at a certain distance outside, the
"open field light cylinder''
.
The real mathematical singularity, however, is not at the light
cylinder, but at a certain distance outside, the
"open field light cylinder''
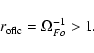 |
(20) |
This is where we will apply the numerical iteration routine
developed in CKF.
- 2.
- We also expect
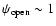 as in previous solutions.
as in previous solutions.
- 3.
- As in CKF, we expect to encounter similar
magnetic and electric field discontinuities across the separatrix
between open and closed field lines.
- 4.
- The r.h.s. of Eq. (19)
is obtained through a numerical iteration
along the open field light cylinder that guarantees smooth
crossing of the singularity. Based on our experience, we expect this
function to be very close to
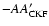 .
Therefore, to a good approximation,
.
Therefore, to a good approximation,
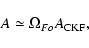 |
(21) |
i.e.
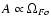 .
Obviously, as
.
Obviously, as
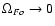 ,
,
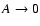 .
As
we will see, this result has very interesting implications
for the electromagnetic torques
on the surface of the neutron star.
.
As
we will see, this result has very interesting implications
for the electromagnetic torques
on the surface of the neutron star.
Equation (10) is elliptic with mixed
boundary conditions inside and outside the open
field light cylinder
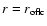 :
:
- 1.
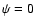 along r=0, and
along r=0, and
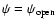 along the equator beyond r=1 (Dirichlet boundary
conditions)
along the equator beyond r=1 (Dirichlet boundary
conditions)![[*]](/icons/foot_motif.gif) .
.
- 2.
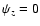 (i.e. Br=0) along the equator in the closed
line region r< 1 (Newman boundary condition).
(i.e. Br=0) along the equator in the closed
line region r< 1 (Newman boundary condition).
- 3.
-
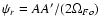 along the open field light cylinder
along the open field light cylinder
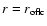 (Newman boundary condition).
(Newman boundary condition).
- 4.
- Finally, as in CKF,
boundary conditions at infinity are irrelevant as long
as we rescale our spatial coordinates to new ones that map the full
![$(r,z)=([0,\infty],[0,\infty])$](/articles/aa/full/2005/41/aa3143-05/img97.gif) space to our finite grid size
space to our finite grid size
![$(r_{\rm new},z_{\rm new})=([0,2],[0,1])$](/articles/aa/full/2005/41/aa3143-05/img98.gif) .
Note that this is not
the case for other numerical schemes where the integration is
constrained within finite spatial extent (Ogura & Kojima 2003;
Goodwin et al. 2004; Gruzinov 2005).
.
Note that this is not
the case for other numerical schemes where the integration is
constrained within finite spatial extent (Ogura & Kojima 2003;
Goodwin et al. 2004; Gruzinov 2005).
The above show that the problem is well defined inside and
outside the open field light cylinder, and therefore one
can obtain solutions for a general current distribution 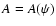 .
The two problems are, however, independent, and in general
the solution will be discontinuous at the open field
light cylinder, unless one chooses the one poloidal electric
current distribution
.
The two problems are, however, independent, and in general
the solution will be discontinuous at the open field
light cylinder, unless one chooses the one poloidal electric
current distribution 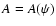 that will guarantee
that will guarantee
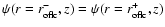 .
Continuity will also result in the smoothness of the
solution (see above boundary condition # 3).
.
Continuity will also result in the smoothness of the
solution (see above boundary condition # 3).
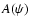 is obtained as described in CKF
by iteratively correcting to a new function
is obtained as described in CKF
by iteratively correcting to a new function
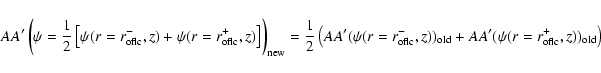 |
(22) |
for all grid points along the open field light cylinder.
In the present work
the relaxation inside each grid proceeds
together with the iteration along the open field light cylinder.
This improvement over the CKF method allowed for a
much greater numerical resolution and a much faster
speed of numerical convergence!
Our numerical scheme consists of an elliptic solver
with Chebyshev acceleration (Press et al. 1988) over
two
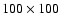 numerical grids joined along the open field
light cylinder.
The discontinuities of
numerical grids joined along the open field
light cylinder.
The discontinuities of 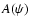 and
and
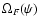 across the separatrix between the open and closed line regions
are smoothed out numerically
over a distance
across the separatrix between the open and closed line regions
are smoothed out numerically
over a distance
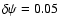 inside the dead zone.
inside the dead zone.
![\begin{figure}
\par\includegraphics[angle=270,width=6cm,clip]{3143fig1.eps}\end{figure}](/articles/aa/full/2005/41/aa3143-05/Timg105.gif) |
Figure 1:
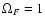 everywhere (CKF; Gruzinov 2005).
Thin lines correspond to
everywhere (CKF; Gruzinov 2005).
Thin lines correspond to
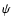 intervals of 0.1.
intervals of 0.1. 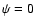 along the axis.
The dotted line shows the separatrix
along the axis.
The dotted line shows the separatrix
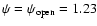 .
The mathematical singularity is at .
The mathematical singularity is at
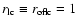 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=270,width=6cm,clip]{3143fig3.eps}\end{figure}](/articles/aa/full/2005/41/aa3143-05/Timg107.gif) |
Figure 3:
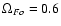 in the open line region.
Thin lines correspond to
in the open line region.
Thin lines correspond to
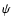 intervals of 0.1. intervals of 0.1. 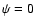 along the axis.
The dotted line shows the separatrix
along the axis.
The dotted line shows the separatrix
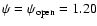 .
The mathematical singularity is at .
The mathematical singularity is at
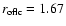 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=270,width=6cm,clip]{3143fig4.eps}\end{figure}](/articles/aa/full/2005/41/aa3143-05/Timg108.gif) |
Figure 4:
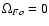 in the open line region.
in the open line region.
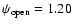 . .
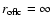 ,
i.e.
the mathematical singularity is absent in this
limiting case. ,
i.e.
the mathematical singularity is absent in this
limiting case. |
| Open with DEXTER |
The various types of solutions of Eq. (10)
are shown in Figs. 1-4 and B.1.
Thin lines correspond to 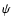 intervals of 0.1.
intervals of 0.1. 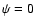 along the axis. The
dotted line represents the separatrix
along the axis. The
dotted line represents the separatrix
 .
Figure 1 shows the CKF case
.
Figure 1 shows the CKF case
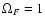 .
Here,
.
Here,
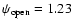 within
the accuracy of our numerical simulation.
Figures 2 and 3 show intermediate cases
with
within
the accuracy of our numerical simulation.
Figures 2 and 3 show intermediate cases
with
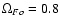 and 0.6
in the open line region respectively.
and 0.6
in the open line region respectively.
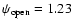 and 1.20 respectively.
Figure 4 shows the limiting case with
and 1.20 respectively.
Figure 4 shows the limiting case with
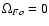 .
In that case there is no light cylinder singularity that
would yield the poloidal electric current distribution
.
In that case there is no light cylinder singularity that
would yield the poloidal electric current distribution 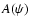 .
However, we showed previously that
the poloidal electric current disappears, since it is obtained
as a limit of solutions with
.
However, we showed previously that
the poloidal electric current disappears, since it is obtained
as a limit of solutions with
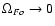 in the open line region. Here,
in the open line region. Here,
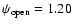 .
.
The various magnetospheres show a similar poloidal
magnetic field distribution.
This result is understood since
Bz is approximately
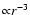 in the equatorial
dipole-like closed line region, and therefore an approximate
estimate for
in the equatorial
dipole-like closed line region, and therefore an approximate
estimate for
 is
is
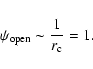 |
(23) |
However, they
differ significantly in the amount of electric charge and
electric current
they contain in the open field line region, since
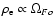 and
and
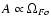 .
As a result,
they differ in the amount of electromagnetic
field energy they contain in the azimuthal component of the magnetic
field
.
As a result,
they differ in the amount of electromagnetic
field energy they contain in the azimuthal component of the magnetic
field 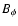 and in the electric field E, namely
and in the electric field E, namely
Here, the integration distance r extends to distances
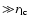 .
Any evolution between the different
solutions will require the release (or buildup) of the corresponding
energy difference (see discussion in the next section).
.
Any evolution between the different
solutions will require the release (or buildup) of the corresponding
energy difference (see discussion in the next section).
We discovered that, as
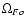 varies from
varies from
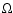 to 0, the open field region decreases
to a minimum value of about
to 0, the open field region decreases
to a minimum value of about
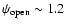 (see Fig. 5).
In the next section we will see that this numerical
result might have interesting physical implications
in understanding the SGR phenomenon.
(see Fig. 5).
In the next section we will see that this numerical
result might have interesting physical implications
in understanding the SGR phenomenon.
![\begin{figure}
\par\includegraphics[angle=270,width=5.6cm,clip]{3143fig5.eps}\end{figure}](/articles/aa/full/2005/41/aa3143-05/Timg120.gif) |
Figure 5:
Summary of our numerical solutions
applied in the case of SGR 1806-20. We show here
 (continuous line),
the accelerating potential
(continuous line),
the accelerating potential
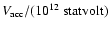 (dashed line), and the spindown rate (dashed line), and the spindown rate
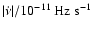 (short dashed line).
On the plot are shown
our estimates for the magnetospheric configuration before
and after the December 27, 2004 burst.
(short dashed line).
On the plot are shown
our estimates for the magnetospheric configuration before
and after the December 27, 2004 burst. |
| Open with DEXTER |
Figure 6 shows the corresponding rescaled
electric current distribution
 ,
and the rescaled distribution
,
and the rescaled distribution
 ,
(obtained numerically) as functions of the
normalized magnetic flux
,
(obtained numerically) as functions of the
normalized magnetic flux
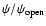 .
.
![\begin{figure}
\par\includegraphics[angle=270,width=7.3cm,clip]{3143fig6.eps}\end{figure}](/articles/aa/full/2005/41/aa3143-05/Timg121.gif) |
Figure 6:
The rescaled electric current distribution
 and the rescaled distribution and the rescaled distribution
 ,
as functions of the rescaled magnetic flux ,
as functions of the rescaled magnetic flux
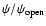 in the open line region, for in the open line region, for
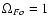 ,
0.8 and 0.6 (from
the lower curves up respectively).
The upper curves (dotted) are the ones that correspond to the
Michel split monopole expression. ,
0.8 and 0.6 (from
the lower curves up respectively).
The upper curves (dotted) are the ones that correspond to the
Michel split monopole expression. |
| Open with DEXTER |
We see that indeed the electric current
distributions are very similar and proportional to
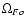 .
Let us now see how this result affects our estimation of
stellar magnetic fields B*. As we mentioned in the introduction,
it is customary to estimate B* by equating the observed
stellar spindown energy loss to the estimated electromagnetic
spindown torque. As we show in the Appendix,
.
Let us now see how this result affects our estimation of
stellar magnetic fields B*. As we mentioned in the introduction,
it is customary to estimate B* by equating the observed
stellar spindown energy loss to the estimated electromagnetic
spindown torque. As we show in the Appendix,
(in real units).
In general, 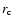 introduces one more free parameter
in the problem (see Sect. 5). Let us here consider
only the natural case
introduces one more free parameter
in the problem (see Sect. 5). Let us here consider
only the natural case
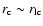 and discuss the physical significance
of
and discuss the physical significance
of
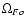 .
Equation (25)
implies that stellar magnetic
field estimates need to be revised upwards
over the canonical value obtained when one
compares Eqs. (1) and (2). Note that when
.
Equation (25)
implies that stellar magnetic
field estimates need to be revised upwards
over the canonical value obtained when one
compares Eqs. (1) and (2). Note that when
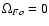 ,
,
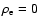 ,
J= 0, i.e. no currents flow
through the magnetosphere, and therefore the star will not
spin down. In most cases,
,
J= 0, i.e. no currents flow
through the magnetosphere, and therefore the star will not
spin down. In most cases,
![$\Omega_{Fo}\sim [80,95]\%\Omega$](/articles/aa/full/2005/41/aa3143-05/img128.gif) (Romani, personal communication), and therefore, the correction
introduced in the stellar magnetic field estimate is
in most cases practically insignificant.
The correction is significant and should be taken into
serious consideration for slow pulsars near the pulsar death-line,
where
(Romani, personal communication), and therefore, the correction
introduced in the stellar magnetic field estimate is
in most cases practically insignificant.
The correction is significant and should be taken into
serious consideration for slow pulsars near the pulsar death-line,
where
 Volts
Volts
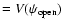 and
and
 (Eq. (13)).
(Eq. (13)).
The solutions presented in the previous section are
all steady-state solutions characterized by one parameter,
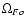 ,
which, as we argued, is determined
by the particle acceleration gap microphysics.
Let us imagine first that
charge carriers are freely available at the base
of the magnetosphere.
In that case, the gap is shorted out, and the magnetosphere
is described by a steady-state solution with
,
which, as we argued, is determined
by the particle acceleration gap microphysics.
Let us imagine first that
charge carriers are freely available at the base
of the magnetosphere.
In that case, the gap is shorted out, and the magnetosphere
is described by a steady-state solution with
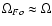 (CKF). Let us imagine next that
the supply of charge carriers is somehow suddenly depleted.
The gap will suddenly grow, and the magnetosphere
will quickly evolve towards a different steady-state
solution with
(CKF). Let us imagine next that
the supply of charge carriers is somehow suddenly depleted.
The gap will suddenly grow, and the magnetosphere
will quickly evolve towards a different steady-state
solution with
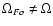 .
We are now going to discuss how,
in our opinion, the magnetosphere may evolve from
the one steady-state solution to the other.
We will base our discussion on the particular
example of SGR 1806-20, and its December 27, 2004 burst.
.
We are now going to discuss how,
in our opinion, the magnetosphere may evolve from
the one steady-state solution to the other.
We will base our discussion on the particular
example of SGR 1806-20, and its December 27, 2004 burst.
We will argue that, when the particle acceleration gap
at the base of the magnetosphere suddenly grows,
the magnetosphere will spontaneously
evolve from a configuration with a larger open
field line region and a larger poloidal electric current,
to one with a smaller open field line
region and a smaller poloidal electric current.
One way to achieve this might be through north-south reconnection
at the distance of the light cylinder.
We expect a significant amount of
magnetic flux (
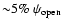 )
to "snap'' and move equatorially outward similarly
to a solar coronal mass ejection (plasmoid).
At the same time, the magnetosphere will release the
excess energy contained in the azimuthal component
of the magnetic field
)
to "snap'' and move equatorially outward similarly
to a solar coronal mass ejection (plasmoid).
At the same time, the magnetosphere will release the
excess energy contained in the azimuthal component
of the magnetic field 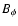 and in the electric field Ethrough a spherical electromagnetic wave
sweeping through the open field region at the speed of light
and in the electric field Ethrough a spherical electromagnetic wave
sweeping through the open field region at the speed of light![[*]](/icons/foot_motif.gif) .
As is shown in Eq. (24), the energy contained in
that wave would grow with distance. We would like to characterize this
dramatic evolution as "magnetospheric coughing''
(see Fig. 7 for a schematic description).
.
As is shown in Eq. (24), the energy contained in
that wave would grow with distance. We would like to characterize this
dramatic evolution as "magnetospheric coughing''
(see Fig. 7 for a schematic description).
![\begin{figure}
\par\includegraphics[angle=270,width=5.5cm,clip]{3143fig7.eps}\end{figure}](/articles/aa/full/2005/41/aa3143-05/Timg134.gif) |
Figure 7:
Schematic magnetospheric evolution characterized
as "magnetospheric coughing'' (clockwise from upper left corner).
In the upper left corner
is shown a steady-state solution with
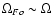 .
Conditions at the base of the magnetosphere changed suddenly
towards a different steady-state solution with .
Conditions at the base of the magnetosphere changed suddenly
towards a different steady-state solution with
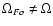 ,
and a spherical electromagnetic wave
(shown with dotted line)
sweeps through the open field line region at the speed of
light. When the wave reaches
the light cylinder region, reconnection allows the expulsion
of the amount of magnetic flux required for the magnetosphere
to evolve towards the new steady-state solution that corresponds
to the new value of ,
and a spherical electromagnetic wave
(shown with dotted line)
sweeps through the open field line region at the speed of
light. When the wave reaches
the light cylinder region, reconnection allows the expulsion
of the amount of magnetic flux required for the magnetosphere
to evolve towards the new steady-state solution that corresponds
to the new value of
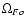 (upper right corner).
The detached magnetic flux forms a "plasmoid'' that escapes
in the equatorial region (lower right corner).
The system reaches a final steady-state shown schematically
in the lower left corner, and will remain there for
as long as the physical conditions that sustained the new value
of
(upper right corner).
The detached magnetic flux forms a "plasmoid'' that escapes
in the equatorial region (lower right corner).
The system reaches a final steady-state shown schematically
in the lower left corner, and will remain there for
as long as the physical conditions that sustained the new value
of
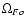 at the base of the magnetosphere persist.
at the base of the magnetosphere persist. |
| Open with DEXTER |
As long as the depletion of charges persists, the
magnetosphere will remain in the low
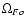 state.
The magnetosphere might return to
a higher
state.
The magnetosphere might return to
a higher
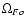 state
where angular momentum is removed more efficiently
only if charge carriers become freely available
again at the base of the magnetosphere.
We speculate that in such case, the magnetosphere
will evolve through differential rotation
between the star and the light cylinder region, and therefore
the evolution will be less dramatic than the magnetospheric
coughing described above.
state
where angular momentum is removed more efficiently
only if charge carriers become freely available
again at the base of the magnetosphere.
We speculate that in such case, the magnetosphere
will evolve through differential rotation
between the star and the light cylinder region, and therefore
the evolution will be less dramatic than the magnetospheric
coughing described above.
In our example (see Fig. 5),
let us choose the solution with
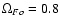 as the pre-burst solution. Our numerical analysis yielded
as the pre-burst solution. Our numerical analysis yielded
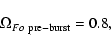 |
(26) |
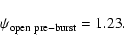 |
(27) |
Based on our detailed axisymmetric ideal MHD model, and given the
observed pre-burst spindown rate
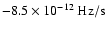 ,
we obtain
,
we obtain
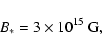 |
(28) |
and a corresponding
accelerating potential in the magnetospheric gaps
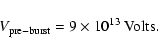 |
(29) |
We know that, after the burst, the spindown rate was 2.7 times
smaller (Woods et al. 2005). This allows us to take
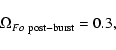 |
(30) |
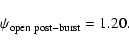 |
(31) |
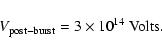 |
(32) |
We see that both before and after the burst, the accelerating
potential is of the order of 1014 Volts.
Indeed, the magnetosphere
is emitting pulsed radiation in both cases, only after
the burst, pulsed radiation is observed to be weaker. We attribute this
difference to the smaller radiation cone (due to the smaller
open field line region) which might thus avoid our line of sight.
According to Eq. (24),
the energy difference between the two magnetospheres is of the
order of
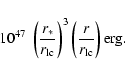 |
(33) |
According to 33, the energy contained in the
spherical blast wave will be
comparable to the apparent burst luminosities observed
on earth (e.g. Yamazaki et al. 2005)
at distances
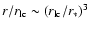 .
We would like to defer a more detailed discussion of the burst
energetics to a future work.
.
We would like to defer a more detailed discussion of the burst
energetics to a future work.
In our present work we presented global numerical solutions
of the generalized pulsar equation
that describe the steady-state structure of axisymmetric
rotating neutron star magnetospheres.
We have introduced
two new parameters besides the neutron star angular velocity
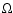 ,
,
-
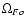 ,
the angular velocity of rotation of
open field lines. This quantity is related to the particle
acceleration gaps at the base of the magnetosphere (the closer
,
the angular velocity of rotation of
open field lines. This quantity is related to the particle
acceleration gaps at the base of the magnetosphere (the closer
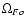 is to
is to 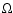 ,
the smaller the gap), and is determined
by gap microphysics outside the context of our present ideal MHD
formulation.
,
the smaller the gap), and is determined
by gap microphysics outside the context of our present ideal MHD
formulation.
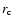 ,
the maximum equatorial extent of the closed line region
(see Appendix).
We speculate that
,
the maximum equatorial extent of the closed line region
(see Appendix).
We speculate that 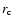 might be determined by inertial effects outside
the context of our present ideal MHD formulation.
might be determined by inertial effects outside
the context of our present ideal MHD formulation.
Note that, in our global solutions,
 (the amount of open field lines)
is determined self-consistently, and consequently it is not
a free parameter (see, however,
Goodwin et al. 2004, for a different point of view).
Similarly to CKF, the poloidal electric current distribution
that guarantees smoothness and continuity at the open field light cylinder
is obtained iteratively, and an approximate analytic expression is given.
Our results generalize the solution presented in CKF;
Gruzinov (2005).
(the amount of open field lines)
is determined self-consistently, and consequently it is not
a free parameter (see, however,
Goodwin et al. 2004, for a different point of view).
Similarly to CKF, the poloidal electric current distribution
that guarantees smoothness and continuity at the open field light cylinder
is obtained iteratively, and an approximate analytic expression is given.
Our results generalize the solution presented in CKF;
Gruzinov (2005).
We also obtained a generalized expression for the
steady-state spindown magnetospheric energy losses (Eq. (25)),
which is different from the canonical one for a misalingned magnetic
rotator. Magnetospheres with different values of
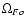 and/or
and/or 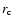 contain different amounts of electric currents, and therefore
spin down differently. This changes slightly our estimates of stellar magnetic
fields B* (see also Harding et al. 1999, for a relevant discussion
in the case of magnetar magnetic field estimates).
More importantly, however, this might have serious
implication in the calculation of the magnetic braking index
contain different amounts of electric currents, and therefore
spin down differently. This changes slightly our estimates of stellar magnetic
fields B* (see also Harding et al. 1999, for a relevant discussion
in the case of magnetar magnetic field estimates).
More importantly, however, this might have serious
implication in the calculation of the magnetic braking index
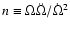 .
One can easily check
(Eq. (25)) that any functional dependence of
.
One can easily check
(Eq. (25)) that any functional dependence of
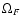 and
and
 different from the
canonical one
different from the
canonical one
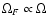 ,
and
,
and
 will yield a braking index
will yield a braking index
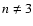 as obtained observationally (Contopoulos & Spitkovsky,
in preparation).
as obtained observationally (Contopoulos & Spitkovsky,
in preparation).
Finally, we argued that the magnetosphere may spontaneously
evolve between steady-state configurations characterized by different
values of
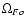 and/or
and/or 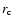 .
The evolution from
a high to low value of
.
The evolution from
a high to low value of
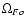 and/or low to high value of
and/or low to high value of 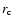 will result in the dramatic
release of a significant amount of electromagnetic field
energy and magnetic flux. The return to the former configuration
will be less dramatic, since it will require the
buildup of the corresponding electromagnetic field energy
difference. Our results might be relevant in understanding
the SGR burst phenomenon.
will result in the dramatic
release of a significant amount of electromagnetic field
energy and magnetic flux. The return to the former configuration
will be less dramatic, since it will require the
buildup of the corresponding electromagnetic field energy
difference. Our results might be relevant in understanding
the SGR burst phenomenon.
Acknowledgements
We would like to thank
Christos Eftymiopoulos and Demos Kazanas
for their support in reviving this intriguing problem.
We would also like to thank Jonathan Arons,
Roger Blandford, Roger Romani, and Anatoly Spitkovsky
for interesting discussions and comments. We would finally like to
acknowledge the contribution of the unknown referee
in improving the presentation of our ideas.
When a neutron star is not surrounded by vacuum,
the rotating charged relativistic Goldreich-Julian-type
magnetosphere is threaded by poloidal and toroidal electric currents.
We will consider only the axisymmetric case for simplicity.
Two large scale poloidal electric current circuits
(north & south) are generated. These flow only along
open field lines, and
close along the surface of the star at the two polar caps where
they generate electromagnetic torques antiparallel
to the angular momentum of the neutron star
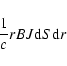 |
(A.1) |
through any stellar cross section 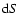 threaded
by poloidal electric current density J. One can easily check
that the stellar kinetic energy loss
through the above torques is given by
threaded
by poloidal electric current density J. One can easily check
that the stellar kinetic energy loss
through the above torques is given by
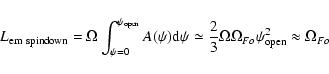 |
(A.2) |
(our expression accounts for the two hemispheres, north & south).
We made use of the numerical result
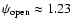 .
At the same time, the magnetosphere radiates electromagnetic
energy
.
At the same time, the magnetosphere radiates electromagnetic
energy
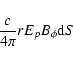 |
(A.3) |
through any cross section 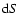 in the
region of open field lines. One can easily check
that the total electromagnetic energy loss
through the above Poynting flux is given by
in the
region of open field lines. One can easily check
that the total electromagnetic energy loss
through the above Poynting flux is given by
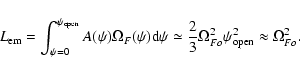 |
(A.4) |
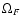 is in general smaller than
is in general smaller than 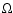 ,
and therefore,
,
and therefore,
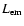 is in general less than
is in general less than
 .
The difference between the two is consumed in the
particle acceleration gaps that develop along open
field lines, namely
.
The difference between the two is consumed in the
particle acceleration gaps that develop along open
field lines, namely
The above expressions are normalized to the
Goldreich-Julian value
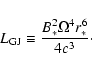 |
(A.6) |
In solving Eq. (10),
we have all along argued that nature will choose the most natural
solution, namely the one with the maximum extent of the "dead zone''.
A competing to the above scenario might be one where
the extent of the "dead zone'' is
a free parameter 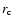 (Goodwin et al. 2004).
Since
(Goodwin et al. 2004).
Since
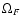 introduces one more free parameter
in the problem, we will consider only one representative
case with
introduces one more free parameter
in the problem, we will consider only one representative
case with
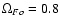 .
Equation (10)
can be solved numerically as described before.
In this scenario, solutions with
a smaller "dead zone'' are also more efficient in removing
angular momentum from the spinning star (Eq. (A.2)).
As an example, we take
.
Equation (10)
can be solved numerically as described before.
In this scenario, solutions with
a smaller "dead zone'' are also more efficient in removing
angular momentum from the spinning star (Eq. (A.2)).
As an example, we take
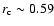 and obtain
and obtain
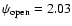 (Fig. B.1).
This solution may evolve rapidly
through reconnection towards the solution shown
in Fig. 2
with
(Fig. B.1).
This solution may evolve rapidly
through reconnection towards the solution shown
in Fig. 2
with
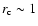 ,
,
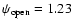 ,
and thus yield a spindown rate 2.7 times lower, releasing
at the same time a significant amount of magnetic field
energy. Note that the system is an efficient
radiator through particle acceleration processes both
before and after the burst (
,
and thus yield a spindown rate 2.7 times lower, releasing
at the same time a significant amount of magnetic field
energy. Note that the system is an efficient
radiator through particle acceleration processes both
before and after the burst (
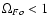 ).
).
![\begin{figure}
\par\includegraphics[angle=270,width=6cm,clip]{3143fig8.eps}\end{figure}](/articles/aa/full/2005/41/aa3143-05/Timg167.gif) |
Figure B.1:
A solution with 2.7 times more efficient spindown
than the solution shown in Fig. 2.
The "dead zone'' extends up to
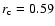 . .
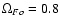 . .
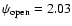 . . |
- Beskin, V. S. 1997,
Physics-Uspekhi, 40, 659 (In the text)
- Beskin, V. S., &
Malyshkin, L. M. 1998, MNRAS, 298, 847 [NASA ADS] [CrossRef] (In the text)
- Contopoulos, I., Kazanas, D.,
& Fendt, C. 1999, ApJ, 511, 351 [NASA ADS] [CrossRef]
- Goldreich, P., &
Julian, W. H. 1969, ApJ, 157, 869 [NASA ADS] [CrossRef]
- Goodwin, S. P.,
Mestel, J., Mestel, L., & Wright, G. A. E. 2004, MNRAS, 349,
213 [NASA ADS] [CrossRef] (In the text)
- Gruzinov, A.
2005, Phys. Rev. Lett., 94
- Harding, A. K., Contopoulos,
I., & Kazanas, D. 1999, ApJ, 525, 125 [NASA ADS] [CrossRef] (In the text)
- Hibschman, J. A.,
& Arons, J. 2001, ApJ, 554, 624 [NASA ADS] [CrossRef] (In the text)
- Lyubarskii,
Y. E. 1990, Sov. Astron. Lett., 16, 16 [NASA ADS]
- Michel, F. C. 1974,
ApJ, 192, 713 [NASA ADS] [CrossRef] (In the text)
- Ogura, J., &
Kojima, Y. 2003, Progr. Theor. Phys., 109, 619 [NASA ADS] (In the text)
- Palmer, D. M.,
Barthelmy, S., Gehrels, N., et al. 2005
[arXiv:astro-ph/0503030]
- Press, W. H.,
Flamery, B. P., Teukolsky, S. A., & Vetterling, W. T. 1988,
Numerical Recipes (Cambridge: Cambridge Univ. Press)
(In the text)
- Rankin, J. M.,
& Wright, G. A. E. 2003, A&ARv, 12, 43 [NASA ADS] (In the text)
- Ruderman, M. A., &
Sutherland, P. G. 1975, ApJ, 196, 51 [NASA ADS] [CrossRef]
- Spitkovsky,
A. 2004, IAUS, 218, 357 [NASA ADS]
- Uzdensky, D. A.
2003, ApJ, 598, 446 [NASA ADS] [CrossRef]
- Woods, P. M.,
Kouveliotou, C., Gogus, E., et al. 2005, Astronomer's Telegram, No.
407
(In the text)
- Yamazaki, R.,
Ioka, K., Takahara, F., & Shibazaki, N. 2005
[arXiv:astro-ph/0502320]
(In the text)
Copyright ESO 2005
![]() ,
radius
,
radius
![]() ,
magnetic dipole moment
,
magnetic dipole moment
![]() ,
and angular velocity
,
and angular velocity ![]() is expected
to radiate electromagnetic energy at a rate
is expected
to radiate electromagnetic energy at a rate
![]() develops
across magnetic field lines (
develops
across magnetic field lines (
![]() )
with magnitude
)
with magnitude
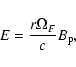
![]() in the range
in the range
![]() and argue that the magnetosphere
may switch between solutions, releasing
energy in the process.
In Sect. 4 we discuss the relevance of our results in
understanding the recent December 27, 2004 SGR-1806-20 burst.
Our conclusions are summarized in Sect. 5.
and argue that the magnetosphere
may switch between solutions, releasing
energy in the process.
In Sect. 4 we discuss the relevance of our results in
understanding the recent December 27, 2004 SGR-1806-20 burst.
Our conclusions are summarized in Sect. 5.
![]() ,
and will consider only the axisymmetric case where
the magnetic dipole axis is aligned with the axis of rotation.
This simplification allows us
to introduce the magnetic flux function
,
and will consider only the axisymmetric case where
the magnetic dipole axis is aligned with the axis of rotation.
This simplification allows us
to introduce the magnetic flux function ![]() (
(![]() is the
is the ![]() -component of the magnetic
vector potential),
the poloidal electric current function
-component of the magnetic
vector potential),
the poloidal electric current function ![]() (the poloidal electric current contained within
the magnetic flux surface
(the poloidal electric current contained within
the magnetic flux surface ![]() is equal to Ac/2;
is equal to Ac/2;
![]() ),
and the magnetic field line
"rotational velocity''
),
and the magnetic field line
"rotational velocity''
![]() .
The various
magnetospheric physical quantities are obtained as follows:
.
The various
magnetospheric physical quantities are obtained as follows:
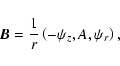
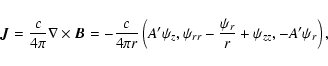
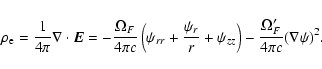
![]() is related to the magnetospheric
potential drop VF between
the axis and any magnetic flux surface
is related to the magnetospheric
potential drop VF between
the axis and any magnetic flux surface ![]() (Eq. (5)), namely
(Eq. (5)), namely
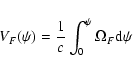
![]() 1 s period pulsars)
1 s period pulsars)
![]() is expected to
be much smaller than
is expected to
be much smaller than ![]() .
These gaps are
probably carried around the axis of rotation
by the "friction'' between the differentially rotating
open and closed line regions, and thus
their observed angular velocity is found to be
close to
.
These gaps are
probably carried around the axis of rotation
by the "friction'' between the differentially rotating
open and closed line regions, and thus
their observed angular velocity is found to be
close to ![]() .
.
![]() and
and
![]() .
Even
in that case, though, a strong mathematical singularity,
the so called "light cylinder''
.
Even
in that case, though, a strong mathematical singularity,
the so called "light cylinder''
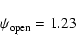
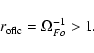
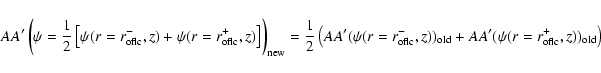
![\begin{figure}
\par\includegraphics[angle=270,width=6cm,clip]{3143fig1.eps}\end{figure}](/articles/aa/full/2005/41/aa3143-05/Timg105.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=6cm,clip]{3143fig2.eps}\end{figure}](/articles/aa/full/2005/41/aa3143-05/Timg106.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=6cm,clip]{3143fig3.eps}\end{figure}](/articles/aa/full/2005/41/aa3143-05/Timg107.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=6cm,clip]{3143fig4.eps}\end{figure}](/articles/aa/full/2005/41/aa3143-05/Timg108.gif)
![]() intervals of 0.1.
intervals of 0.1. ![]() along the axis. The
dotted line represents the separatrix
along the axis. The
dotted line represents the separatrix
![]() .
Figure 1 shows the CKF case
.
Figure 1 shows the CKF case
![]() .
Here,
.
Here,
![]() within
the accuracy of our numerical simulation.
Figures 2 and 3 show intermediate cases
with
within
the accuracy of our numerical simulation.
Figures 2 and 3 show intermediate cases
with
![]() and 0.6
in the open line region respectively.
and 0.6
in the open line region respectively.
![]() and 1.20 respectively.
Figure 4 shows the limiting case with
and 1.20 respectively.
Figure 4 shows the limiting case with
![]() .
In that case there is no light cylinder singularity that
would yield the poloidal electric current distribution
.
In that case there is no light cylinder singularity that
would yield the poloidal electric current distribution ![]() .
However, we showed previously that
the poloidal electric current disappears, since it is obtained
as a limit of solutions with
.
However, we showed previously that
the poloidal electric current disappears, since it is obtained
as a limit of solutions with
![]() in the open line region. Here,
in the open line region. Here,
![]() .
.
![]() in the equatorial
dipole-like closed line region, and therefore an approximate
estimate for
in the equatorial
dipole-like closed line region, and therefore an approximate
estimate for
![]() is
is
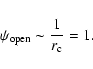
![]() varies from
varies from
![]() to 0, the open field region decreases
to a minimum value of about
to 0, the open field region decreases
to a minimum value of about
![]() (see Fig. 5).
In the next section we will see that this numerical
result might have interesting physical implications
in understanding the SGR phenomenon.
(see Fig. 5).
In the next section we will see that this numerical
result might have interesting physical implications
in understanding the SGR phenomenon.
![\begin{figure}
\par\includegraphics[angle=270,width=5.6cm,clip]{3143fig5.eps}\end{figure}](/articles/aa/full/2005/41/aa3143-05/Timg120.gif)
![]() ,
and the rescaled distribution
,
and the rescaled distribution
![]() ,
(obtained numerically) as functions of the
normalized magnetic flux
,
(obtained numerically) as functions of the
normalized magnetic flux
![]() .
.
![\begin{figure}
\par\includegraphics[angle=270,width=7.3cm,clip]{3143fig6.eps}\end{figure}](/articles/aa/full/2005/41/aa3143-05/Timg121.gif)
![]() ,
which, as we argued, is determined
by the particle acceleration gap microphysics.
Let us imagine first that
charge carriers are freely available at the base
of the magnetosphere.
In that case, the gap is shorted out, and the magnetosphere
is described by a steady-state solution with
,
which, as we argued, is determined
by the particle acceleration gap microphysics.
Let us imagine first that
charge carriers are freely available at the base
of the magnetosphere.
In that case, the gap is shorted out, and the magnetosphere
is described by a steady-state solution with
![]() (CKF). Let us imagine next that
the supply of charge carriers is somehow suddenly depleted.
The gap will suddenly grow, and the magnetosphere
will quickly evolve towards a different steady-state
solution with
(CKF). Let us imagine next that
the supply of charge carriers is somehow suddenly depleted.
The gap will suddenly grow, and the magnetosphere
will quickly evolve towards a different steady-state
solution with
![]() .
We are now going to discuss how,
in our opinion, the magnetosphere may evolve from
the one steady-state solution to the other.
We will base our discussion on the particular
example of SGR 1806-20, and its December 27, 2004 burst.
.
We are now going to discuss how,
in our opinion, the magnetosphere may evolve from
the one steady-state solution to the other.
We will base our discussion on the particular
example of SGR 1806-20, and its December 27, 2004 burst.
![]() )
to "snap'' and move equatorially outward similarly
to a solar coronal mass ejection (plasmoid).
At the same time, the magnetosphere will release the
excess energy contained in the azimuthal component
of the magnetic field
)
to "snap'' and move equatorially outward similarly
to a solar coronal mass ejection (plasmoid).
At the same time, the magnetosphere will release the
excess energy contained in the azimuthal component
of the magnetic field ![]() and in the electric field Ethrough a spherical electromagnetic wave
sweeping through the open field region at the speed of light
and in the electric field Ethrough a spherical electromagnetic wave
sweeping through the open field region at the speed of light![]() .
As is shown in Eq. (24), the energy contained in
that wave would grow with distance. We would like to characterize this
dramatic evolution as "magnetospheric coughing''
(see Fig. 7 for a schematic description).
.
As is shown in Eq. (24), the energy contained in
that wave would grow with distance. We would like to characterize this
dramatic evolution as "magnetospheric coughing''
(see Fig. 7 for a schematic description).
![\begin{figure}
\par\includegraphics[angle=270,width=5.5cm,clip]{3143fig7.eps}\end{figure}](/articles/aa/full/2005/41/aa3143-05/Timg134.gif)
![]() state.
The magnetosphere might return to
a higher
state.
The magnetosphere might return to
a higher
![]() state
where angular momentum is removed more efficiently
only if charge carriers become freely available
again at the base of the magnetosphere.
We speculate that in such case, the magnetosphere
will evolve through differential rotation
between the star and the light cylinder region, and therefore
the evolution will be less dramatic than the magnetospheric
coughing described above.
state
where angular momentum is removed more efficiently
only if charge carriers become freely available
again at the base of the magnetosphere.
We speculate that in such case, the magnetosphere
will evolve through differential rotation
between the star and the light cylinder region, and therefore
the evolution will be less dramatic than the magnetospheric
coughing described above.
![]() as the pre-burst solution. Our numerical analysis yielded
as the pre-burst solution. Our numerical analysis yielded
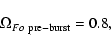
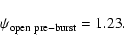
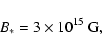
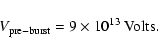
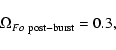
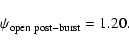
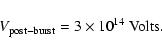
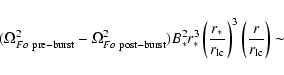
![]() ,
,
![]() and/or
and/or ![]() contain different amounts of electric currents, and therefore
spin down differently. This changes slightly our estimates of stellar magnetic
fields B* (see also Harding et al. 1999, for a relevant discussion
in the case of magnetar magnetic field estimates).
More importantly, however, this might have serious
implication in the calculation of the magnetic braking index
contain different amounts of electric currents, and therefore
spin down differently. This changes slightly our estimates of stellar magnetic
fields B* (see also Harding et al. 1999, for a relevant discussion
in the case of magnetar magnetic field estimates).
More importantly, however, this might have serious
implication in the calculation of the magnetic braking index
![]() .
One can easily check
(Eq. (25)) that any functional dependence of
.
One can easily check
(Eq. (25)) that any functional dependence of
![]() and
and
![]() different from the
canonical one
different from the
canonical one
![]() ,
and
,
and
![]() will yield a braking index
will yield a braking index
![]() as obtained observationally (Contopoulos & Spitkovsky,
in preparation).
as obtained observationally (Contopoulos & Spitkovsky,
in preparation).
![]() and/or
and/or ![]() .
The evolution from
a high to low value of
.
The evolution from
a high to low value of
![]() and/or low to high value of
and/or low to high value of ![]() will result in the dramatic
release of a significant amount of electromagnetic field
energy and magnetic flux. The return to the former configuration
will be less dramatic, since it will require the
buildup of the corresponding electromagnetic field energy
difference. Our results might be relevant in understanding
the SGR burst phenomenon.
will result in the dramatic
release of a significant amount of electromagnetic field
energy and magnetic flux. The return to the former configuration
will be less dramatic, since it will require the
buildup of the corresponding electromagnetic field energy
difference. Our results might be relevant in understanding
the SGR burst phenomenon.
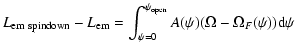
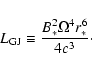
![]() (Goodwin et al. 2004).
Since
(Goodwin et al. 2004).
Since
![]() introduces one more free parameter
in the problem, we will consider only one representative
case with
introduces one more free parameter
in the problem, we will consider only one representative
case with
![]() .
Equation (10)
can be solved numerically as described before.
In this scenario, solutions with
a smaller "dead zone'' are also more efficient in removing
angular momentum from the spinning star (Eq. (A.2)).
As an example, we take
.
Equation (10)
can be solved numerically as described before.
In this scenario, solutions with
a smaller "dead zone'' are also more efficient in removing
angular momentum from the spinning star (Eq. (A.2)).
As an example, we take
![]() and obtain
and obtain
![]() (Fig. B.1).
This solution may evolve rapidly
through reconnection towards the solution shown
in Fig. 2
with
(Fig. B.1).
This solution may evolve rapidly
through reconnection towards the solution shown
in Fig. 2
with
![]() ,
,
![]() ,
and thus yield a spindown rate 2.7 times lower, releasing
at the same time a significant amount of magnetic field
energy. Note that the system is an efficient
radiator through particle acceleration processes both
before and after the burst (
,
and thus yield a spindown rate 2.7 times lower, releasing
at the same time a significant amount of magnetic field
energy. Note that the system is an efficient
radiator through particle acceleration processes both
before and after the burst (
![]() ).
).
![\begin{figure}
\par\includegraphics[angle=270,width=6cm,clip]{3143fig8.eps}\end{figure}](/articles/aa/full/2005/41/aa3143-05/Timg167.gif)