Present address: Research Center for Astronomy & Applied Mathematics, Academy of Athens.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

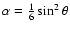$\alpha=\frac{1}{6}\sin^2\theta$ for a misaligned dipole rotating in vacuum. In that scenario, an aligned magnetic rotator ( $\theta\approx 0$ ) does not radiate. However, when the neutron star is not surrounded by vacuum, one needs to consider the structure of its rotating charged relativistic Goldreich-Julian-type magnetosphere (Goldreich & Julian 1969). In that case, the electric currents that flow through the magnetosphere lead to electromagnetic energy losses comparable to the ones for a misaligned magnetic rotator. See the Appendix for a general calculation.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... calculation

In CKF, with a much lower numerical resolution, we obtained a value of 1.36. Gruzinov 2005 obtained a value of 1.27 with a numerical resolution comparable to our present one.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... cylinder

Gruzinov (2005) shows that this solution requires infinite magnetic fields at the point r=1,z=0 (in the limit of infinitesimal grid size). Uzdensky (2003) and Lyubarskii (1990) argue against infinite fields and thus conclude that the dead zone should end at some finite distance inside the light cylinder.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... everywhere

This observation counteracts criticism that the assumptions of ideal MHD may break down beyond the light cylinder (Ogura & Kojima 2003; Spitkovsky 2004). We believe that the source of the opposite result presented in Ogura & Kojima (2003) (their Fig. 5) is due to their numerical boundary condition, Eq. (3.3) and Fig. 1, namely that field lines become horizontal at large radial distances.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... conditions)

As is shown in the Appendix we are in general allowed to arbitrarily choose the equatorial extent 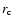$r_{\rm c}$ of the closed line region. In that case, $\psi _{\rm open}$ is obtained as a solution of Eq. (10) inside the open field light cylinder, i.e. it is not an extra free parameter (see Goodwin et al. 2004 for a different point of view).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... light

In general, this will be a spherical Alfven wave moving outward at the Alfven speed.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.