A&A 442, 567-578 (2005)
DOI: 10.1051/0004-6361:20042476
Gravitational-darkening of Altair from interferometry
A. Domiciano de Souza 1 - P. Kervella2 - S. Jankov 3,4 - F. Vakili 3 - N. Ohishi 5 - T. E. Nordgren 6 - L. Abe 5
1 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel
69, 53121 Bonn, Germany
2 - LESIA, UMR 8109, Observatoire de
Paris-Meudon, 5 place Jules Janssen, 92195 Meudon Cedex, France
3 - Lab. Univ. d'Astrophysique de Nice (LUAN), UMR 6525, UNSA,
Parc Valrose, 06108 Nice Cedex 02, France
4 - Astronomical
Observatory Belgrade, MNTRS 1940, Volgina 7, 11050 Beograd, Serbia
and Montenegro
5 - National Astronomical Observatory of Japan,
2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
6 - Department of
Physics, University of Redlands, 1200 East Colton Avenue,
Redlands, CA 92373, USA
Received 3 December 2004 / Accepted 13 June 2005
Abstract
Interferometric observations have revealed that the
rapid rotator Altair is a flattened star with a non-centrally
symmetric intensity distribution. In this work we perform for the
first time a physically consistent analysis of all interferometric
data available so far, corresponding to three different
interferometers operating in several spectral bands. These
observations include new data (squared visibilities in the H and K bands from VLTI-VINCI) as well as previously published data
(squared visibilities in the K band from PTI and squared
visibilities, triple amplitudes, and closure phases in the visible
between 520 nm and 850 nm from NPOI). To analyze these data we
perform a  minimization using an interferometry-oriented
model for fast rotators, which includes Roche approximation,
limb-darkening, and von Zeipel-like gravity-darkening. Thanks to
the rich interferometric data set available and to this physical
model, the main uniqueness problems were avoided. As a result, we
show that the observations can only be explained if Altair has a
gravity-darkening compatible with the expected value for hot
stars, i.e., the von Zeipel effect (
minimization using an interferometry-oriented
model for fast rotators, which includes Roche approximation,
limb-darkening, and von Zeipel-like gravity-darkening. Thanks to
the rich interferometric data set available and to this physical
model, the main uniqueness problems were avoided. As a result, we
show that the observations can only be explained if Altair has a
gravity-darkening compatible with the expected value for hot
stars, i.e., the von Zeipel effect (
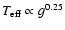 ).
).
Key words: techniques: high angular resolution -
techniques: interferometric - methods: data analysis - stars:
rotation - stars: individual: Altair
Altair ( Aql, HR 7557, HD 187642) is a bright
(V=0.77), rapidly rotating A7IV-V star, which has been
studied by many authors. For example, Buzasi et al. (2005)
recently detected several oscillating frequencies in Altair and
proved that this star is a variable of the
Aql, HR 7557, HD 187642) is a bright
(V=0.77), rapidly rotating A7IV-V star, which has been
studied by many authors. For example, Buzasi et al. (2005)
recently detected several oscillating frequencies in Altair and
proved that this star is a variable of the  Scuti type, as
expected by its location within the instability strip. Several
basic physical parameters of Altair are summarized by Buzasi et al. (2005) in their introduction. One important characteristic of
Altair is its fast rotation. Spectroscopic and interferometric
observations indicate a
Scuti type, as
expected by its location within the instability strip. Several
basic physical parameters of Altair are summarized by Buzasi et al. (2005) in their introduction. One important characteristic of
Altair is its fast rotation. Spectroscopic and interferometric
observations indicate a
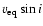 value between
value between
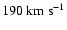 and
and
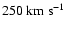 (Abt & Morrell 1995; van Belle et al. 2001; Royer et al. 2002; among others); most recently Reiners & Royer (2004)
determined
(Abt & Morrell 1995; van Belle et al. 2001; Royer et al. 2002; among others); most recently Reiners & Royer (2004)
determined
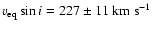 from spectroscopy.
from spectroscopy.
Theories foresee that such a high rotation velocity can lead to
many modifications in the physical structure of a star like
Altair. In particular, the star is expected (1) to be oblate
because of a strong centrifugal force and (2) to exhibit
gravity-darkening (after the seminal work of von Zeipel 1924).
These theoretically expected modifications are now measured by
modern observing techniques, notably those based on long baseline
interferometry. See, for example, Domiciano de Souza et al. (2003)
for the case of another rapidly rotating star (Achernar).
For Altair, van Belle et al. (2001) measured the rotational
flattening projected onto the sky-plane using the Palomar Testbed
Interferometer (PTI, Colavita et al. 1999). By adopting an
equivalent limb-darkened ellipse model these authors derived major
and minor axes of
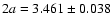 mas and
mas and
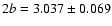 mas, respectively, which means an axial ratio
of
mas, respectively, which means an axial ratio
of
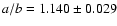 .
van Belle et al. (2001) used a
Roche model (solid body rotation and mass M concentrated in a
point at the center of the star) without gravity-darkening to
analyze their observations of Altair. However, even with this
relatively simplified model their analysis encountered several
uniqueness problems caused by the limited coverage of spatial
frequencies (observations inside the first visibility lobe only)
and spectral information (only one broadband near-IR filter used).
The important issue of uniqueness problems in interferometric
studies of rapidly rotating stars is discussed by Domiciano de
Souza et al. ().
.
van Belle et al. (2001) used a
Roche model (solid body rotation and mass M concentrated in a
point at the center of the star) without gravity-darkening to
analyze their observations of Altair. However, even with this
relatively simplified model their analysis encountered several
uniqueness problems caused by the limited coverage of spatial
frequencies (observations inside the first visibility lobe only)
and spectral information (only one broadband near-IR filter used).
The important issue of uniqueness problems in interferometric
studies of rapidly rotating stars is discussed by Domiciano de
Souza et al. ().
More recently, Ohishi et al. (2004) used the Navy
Prototype Optical Interferometer (NPOI, Armstrong et al. 1998) to
observe Altair. In particular, they obtained closure phases and
squared visibilities around the first minimum. These observations
suggest that Altair is not only oblate but also that it is a
gravity-darkened star with a non-centrally symmetric intensity
distribution. The nature of these data largely diminishes the
uniqueness problems associated with the analysis of rapid
rotators.
Even though the observations indicate that Altair is an oblate and
gravity-darkened star, previous works did not adopt physically
consistent models including these two effects. In the present work
we use our interferometry-oriented model for fast rotators
(Domiciano de Souza et al. 2002) to perform a  minimization including all interferometric data available
up-to-date: new squared visibilities in the H and K bands from the
Very Large Telescope Interferometer (VLTI, e.g., Glindemann et al.
2003); (2) squared visibilities in the K band from PTI; and (3)
squared visibilities, triple amplitudes, and closure phases in the
visible from NPOI.
minimization including all interferometric data available
up-to-date: new squared visibilities in the H and K bands from the
Very Large Telescope Interferometer (VLTI, e.g., Glindemann et al.
2003); (2) squared visibilities in the K band from PTI; and (3)
squared visibilities, triple amplitudes, and closure phases in the
visible from NPOI.
In Sect. 2 we summarize the observations used here,
and in Sect. 3 we describe the adopted model, which
includes Roche approximation, a limb-darkening law compatible with
Altair's effective temperature distribution, and a von Zeipel-like
gravity-darkening law. In Sect. 4 we present the main
results of our  analysis of the interferometric data. A
critical discussion of our results is given in
Sect. 5, while the conclusions of this work are
summarized in Sect. 6.
analysis of the interferometric data. A
critical discussion of our results is given in
Sect. 5, while the conclusions of this work are
summarized in Sect. 6.
2 Interferometric observations
The first attempt to measure the geometrical deformation of Altair
was carried out with the Narrabri intensity interferometer
(Hanbury Brown 1974). However, these observations remained too
marginal to allow unambiguous conclusions to be drawn by the
Australian group. Recent observations by at least three modern
interferometers have resulted in several high-quality measurements becoming
available. In the following section we briefly describe the three
interferometric data sets (one new and two previously published
and analyzed) used in this work to constrain a number of unknown
physical parameters of Altair.
We first describe the new near-IR observations of Altair performed
with the VLTI. These new data were obtained with two test
siderostats (0.35 m aperture) and the VINCI![[*]](/icons/foot_motif.gif) instrument
(Kervella et al. 2000 and Kervella et al. 2003a). The visibility
measurements were all recorded on the E0-G1 baseline of the VLTI
(ground length of 66 m). We combined the stellar light using a
classical fiber-based triple coupler (MONA) for the K band
observations, and an integrated optics beam combiner (IONIC,
Lebouquin et al. 2004) in the H band. Standard K(
instrument
(Kervella et al. 2000 and Kervella et al. 2003a). The visibility
measurements were all recorded on the E0-G1 baseline of the VLTI
(ground length of 66 m). We combined the stellar light using a
classical fiber-based triple coupler (MONA) for the K band
observations, and an integrated optics beam combiner (IONIC,
Lebouquin et al. 2004) in the H band. Standard K(
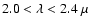 m) and H (
m) and H (
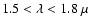 m) band
filters were used for these observations. The effective wavelength
of the observations changes slightly depending on the spectral
type of the observed target. For Altair, we determined
m) band
filters were used for these observations. The effective wavelength
of the observations changes slightly depending on the spectral
type of the observed target. For Altair, we determined
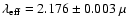 m and
m and
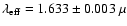 m, respectively in
the K and H bands.
m, respectively in
the K and H bands.
Table 1:
VLTI-VINCI observations of Altair performed in the H and K bands.
The raw data processing has been achieved using a wavelet-based
algorithm, integrated in an automated data reduction pipeline
(Kervella et al. 2004a). The general principle is similar to the
original FLUOR algorithm (Coudé du Foresto et al. 1997), but
instead of the classical Fourier analysis, we implemented a
wavelet-based time-frequency analysis (Ségransan et al. 1999). The
two calibrated output interferograms are subtracted to correct for
residual photometric fluctuations. The output of the pipeline is a
single value of the squared coherence factor 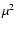 for each
series of 500 interferograms and the associated bootstrapped error
bar. We obtained a total of 5500 interferograms of Altair in the
K band and 4500 in the H band, among which 2749 and 1949
were reduced by the pipeline, respectively. All the VINCI data
were obtained between July and September 2002. The final
normalized squared visibilities V2 and other observational
information are given in Table 1.
for each
series of 500 interferograms and the associated bootstrapped error
bar. We obtained a total of 5500 interferograms of Altair in the
K band and 4500 in the H band, among which 2749 and 1949
were reduced by the pipeline, respectively. All the VINCI data
were obtained between July and September 2002. The final
normalized squared visibilities V2 and other observational
information are given in Table 1.
We used three stars as calibrators for the K band observations
(24 Cap, 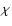 Phe, and 70 Aql) and one for the H band
(
Phe, and 70 Aql) and one for the H band
(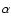 Ind). These stars were selected from Cohen et al. (1999) for their stability, and we took their sizes from the
Bordé et al. (2002) catalogue. To obtain their equivalent
uniform-disk diameters, we applied the broadband limb-darkening
corrections provided by Claret (2000a), based on the ATLAS models
(Kurucz 1992). In absence of data in the literature, the
metallicity of the calibration stars was taken as solar. Note,
however, that in the H and K bands the influence of metallicity on
the limb-darkening is very weak. The relevant properties of the
calibrators used for VINCI observations are listed in
Table 2.
Ind). These stars were selected from Cohen et al. (1999) for their stability, and we took their sizes from the
Bordé et al. (2002) catalogue. To obtain their equivalent
uniform-disk diameters, we applied the broadband limb-darkening
corrections provided by Claret (2000a), based on the ATLAS models
(Kurucz 1992). In absence of data in the literature, the
metallicity of the calibration stars was taken as solar. Note,
however, that in the H and K bands the influence of metallicity on
the limb-darkening is very weak. The relevant properties of the
calibrators used for VINCI observations are listed in
Table 2.
The choice of the calibrators is an important step for preparing
interferometric observations, since significant departures of
their actual visibilities from the expected model can propagate
into biases on the calibrated visibilities of the scientific
target. Among the possible reasons for such departures, binarity
(or multiplicity in general) and deviations from spherical
symmetry (due, for instance, to fast rotation or gravitational
interaction) are the most critical. All stars in the Cohen et al. (1999) catalogue were carefully scrutinized by these authors
for the presence of companions and are currently regarded as
single stars. With respect to fast rotation, the value of
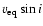 is only available for one star, 70 Aql,
which is also the most sensitive star to potential deformations as
it is a bright giant. With
is only available for one star, 70 Aql,
which is also the most sensitive star to potential deformations as
it is a bright giant. With
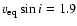 km s-1,
km s-1,
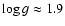 ,
and a radius of
,
and a radius of 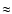 200
200 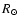 ,
a first
order approximation of its flattening ratio (Roche model) is given
by the following relation (e.g. Domiciano de Souza et al. 2002):
,
a first
order approximation of its flattening ratio (Roche model) is given
by the following relation (e.g. Domiciano de Souza et al. 2002):
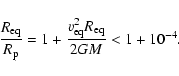 |
(1) |
The effect of the rotation on the shape of this star is therefore
taken as negligible. Measurements of the projected rotational
velocities are not available for the other calibrators of our
sample, but as they are giant stars, we assume that they are small
enough so that their rotational deformation can be neglected. Our
four calibrators are significantly resolved by the interferometer,
but the a priori uncertainty on their angular diameters was
carefully propagated to the final error bars on the calibrated
squared visibilities of Altair. The errors in the calibrated V2(statistical, systematic, and total) are also listed in
Table 1. The uncertainties in V2 are
dominated by the statistical errors.
Table 2:
Relevant parameters of the calibrators used
for VINCI observations of Altair.
Another data set used in this paper was obtained with PTI and was
previously reported and analyzed by van Belle et al. (2001,
hereafter vB2001). This data set corresponds to 27 measurements of
V2 on Altair performed in the K band for two distinct baselines
(ground lengths of 85 m and 110 m).
The third data set used in this work, which was previously
reported and analyzed by Ohishi et al. (2004,
hereafter ONH2004), corresponds to interferometric observations in
the visible obtained with NPOI. These observations of Altair were
recorded simultaneously using three baselines forming a triangle
(ground lengths of 30, 37, and 64 m), allowing measurements of
V2, triple amplitudes, and closure phases. In this work we use
the NPOI observations of Altair performed on May 25 2001 (see
Table 2 of ONH2004), which consist of 7 scans (Hummel et al. 1998). We use 18 spectral channels covering wavelengths from
520 to 850 nm; the data for
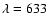 nm are not used because
they contain light from the metrology laser, and the data for
nm are not used because
they contain light from the metrology laser, and the data for
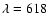 nm are not used because they are not available for
all NPOI observables.
nm are not used because they are not available for
all NPOI observables.
3 Modeling Altair
Since previous interferometric observations (vB2001 and ONH2004)
indicate that Altair's flattening is compatible with uniform
rotation, in this paper we adopt the classical Roche model. This
model is described in more detail, for example, by Domiciano de
Souza et al. (), who developed an interferometry-oriented
model for rapid rotators. Once the surface equipotential (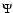 )
and the corresponding local effective surface gravity
(
)
and the corresponding local effective surface gravity
(
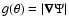 ,
where
,
where 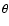 is the
colatitude) in the Roche approximation are defined, the local
effective temperature is given by the following von Zeipel-like
gravity-darkening law (e.g. Collins 1965):
is the
colatitude) in the Roche approximation are defined, the local
effective temperature is given by the following von Zeipel-like
gravity-darkening law (e.g. Collins 1965):
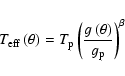 |
(2) |
where 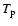 and
and 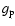 are the polar
effective temperature and gravity, respectively. In this paper we
adopt two theoretical limits for the gravity-darkening coefficient
are the polar
effective temperature and gravity, respectively. In this paper we
adopt two theoretical limits for the gravity-darkening coefficient
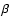 ,
namely,
,
namely,
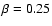 for hot stars with radiative
external layers (von Zeipel 1924) and
for hot stars with radiative
external layers (von Zeipel 1924) and
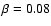 for cold stars
with convective external layers (Lucy 1967).
for cold stars
with convective external layers (Lucy 1967).
To compute our models of Altair the code BRUCE (Townsend 1997) is
used to obtain a stellar grid (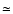 25 500 visible points)
for the local values of effective temperature and gravity,
velocity field, projected surface, and surface normal direction.
25 500 visible points)
for the local values of effective temperature and gravity,
velocity field, projected surface, and surface normal direction.
3.2 Intensity maps
Because of the geometrical deformation and gravity-darkening, the
intensity maps are highly dependent on the inclination of the
rotation axis i (Domiciano de Souza et al. 2002). In order to
evaluate the intensity maps for Altair we first used Kurucz (1992)
model atmospheres![[*]](/icons/foot_motif.gif) as input for the SYNSPEC code
(Hubeny 1988 and Hubeny & Lanz 1995) to generate a grid of
synthetic specific intensities normal to the surface
as input for the SYNSPEC code
(Hubeny 1988 and Hubeny & Lanz 1995) to generate a grid of
synthetic specific intensities normal to the surface
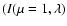 ,
where
,
where 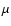 and
and 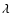 have their usual
meanings). This grid corresponds to different values of
have their usual
meanings). This grid corresponds to different values of
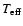 and
and 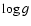 in steps of 250 K and 0.5 dex,
respectively. To be consistent with recent spectroscopic
observations the grids of
in steps of 250 K and 0.5 dex,
respectively. To be consistent with recent spectroscopic
observations the grids of
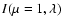 were calculated for
microturbulent velocity
were calculated for
microturbulent velocity
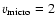 km s-1 and solar
abundance, except for 14 elements between C and Cu (Erspamer &
North 2002, 2003).
km s-1 and solar
abundance, except for 14 elements between C and Cu (Erspamer &
North 2002, 2003).
Since interferometric observations of Altair were performed within
wide spectral bands, we integrated
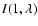 over the
corresponding spectral channel/band to obtain a grid of integrated
intensities normal to the surface I(1). Before performing this
integration we multiply
over the
corresponding spectral channel/band to obtain a grid of integrated
intensities normal to the surface I(1). Before performing this
integration we multiply
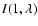 by the atmospheric and
instrumental transmissions. Because the computation of I(1)influences the calculations of interferometric observables, we
present further details of this integration procedure in
Sect. 3.3.
by the atmospheric and
instrumental transmissions. Because the computation of I(1)influences the calculations of interferometric observables, we
present further details of this integration procedure in
Sect. 3.3.
Once I(1) is defined, we can obtain the intensity at every 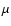 (
(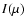 )
through an appropriate limb-darkening law. Accurate
modeling of limb-darkening is crucial to determine precise stellar
diameters, in particular for rapidly rotating stars where we
expect a non-uniform surface brightness distribution. To model
Altair we adopted the four-parameter non-linear limb-darkening law
proposed by Claret (2000a,b):
)
through an appropriate limb-darkening law. Accurate
modeling of limb-darkening is crucial to determine precise stellar
diameters, in particular for rapidly rotating stars where we
expect a non-uniform surface brightness distribution. To model
Altair we adopted the four-parameter non-linear limb-darkening law
proposed by Claret (2000a,b):
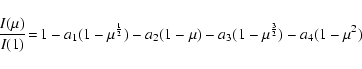 |
(3) |
where tabulated values of a1, a2, a3, and a4are given by Claret for 12 commonly used photometric bands. For
Altair we used those for the H and K bands to simulate PTI and
VLTI-VINCI observations and those for the V (for
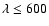 nm) and R (for
nm) and R (for
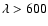 nm) bands to
simulate NPOI observations.
nm) bands to
simulate NPOI observations.
Claret (2000a,b) argues that Eq. (3) is
valid across the whole HR diagram, which is, in fact, an important
requirement for a consistent modeling of Altair since this star
could present an effective temperature distribution in the
transition range between hot (radiative envelope) and cold
(convective envelope) stars (e.g., Panzera et al. 1999).
Finally, we can now define the intensity maps 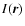 ,
i.e.,
the visible stellar surface brightness distribution on the
two-dimensional sky-plane at a position
,
i.e.,
the visible stellar surface brightness distribution on the
two-dimensional sky-plane at a position 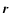 .
To obtain
.
To obtain
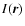 we thus perform a linear interpolation of the
predefined grids of integrated intensities I(1) and the
limb-darkening coefficients a1, a2, a3, and a4, for
each visible point of the stellar grid.
we thus perform a linear interpolation of the
predefined grids of integrated intensities I(1) and the
limb-darkening coefficients a1, a2, a3, and a4, for
each visible point of the stellar grid.
3.3 Complex visibilities
Once the intensity map is defined, the computation of complex
visibilities is straightforward. Normalized complex visibilities
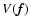 are obtained by the numerical counterpart of the
following equation (for further details see Domiciano de Souza et al. 2002):
are obtained by the numerical counterpart of the
following equation (for further details see Domiciano de Souza et al. 2002):
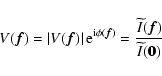 |
(4) |
where |V| and 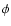 are the visibility amplitude and
phase,
are the visibility amplitude and
phase,
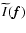 is the Fourier transform of the
intensity map
is the Fourier transform of the
intensity map 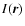 ,
and
,
and 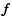 is the spatial frequency
coordinate associated with
is the spatial frequency
coordinate associated with 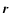 .
From Eq. (4) we can
directly obtain the interferometric observables: squared
visibilities V2, triple amplitudes
.
From Eq. (4) we can
directly obtain the interferometric observables: squared
visibilities V2, triple amplitudes
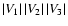 ,
and closure phases
,
and closure phases
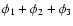 .
These observables are functions of the
spatial frequency
.
These observables are functions of the
spatial frequency 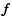 ,
and the indices 1, 2, and 3 denote the
three interferometric baselines in a triangular configuration.
,
and the indices 1, 2, and 3 denote the
three interferometric baselines in a triangular configuration.
For each pair of telescopes, 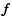 is given by the ratio between
the vector baseline projected onto the sky
is given by the ratio between
the vector baseline projected onto the sky
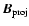 and the effective wavelength
and the effective wavelength
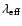 of the considered spectral channel:
of the considered spectral channel:
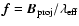 .
This dependence of
the spatial frequency on
.
This dependence of
the spatial frequency on
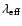 is responsible for
an observational effect known as bandwidth smearing
(e.g., Kervella et al. 2003b; and Wittkowski et al. 2004). Indeed, the wide spectral coverage in the H(
is responsible for
an observational effect known as bandwidth smearing
(e.g., Kervella et al. 2003b; and Wittkowski et al. 2004). Indeed, the wide spectral coverage in the H(
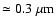 )
and K (
)
and K (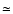
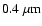 )
bands implies
that several spatial frequencies are simultaneously observed by
the interferometer (VLTI-VINCI and PTI in our case).
)
bands implies
that several spatial frequencies are simultaneously observed by
the interferometer (VLTI-VINCI and PTI in our case).
To account for the bandwidth smearing in the near-IR we divided
the H and K bands into N=20 spectral sub-channels and computed
the stellar intensity distributions Ij integrated over each
spectral sub-channel j. The corresponding Fourier transforms
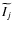 are then calculated, and the final normalized
squared visibilities in the H and K bands are given by:
are then calculated, and the final normalized
squared visibilities in the H and K bands are given by:
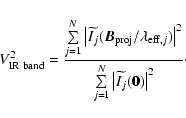 |
(5) |
The bandwidth smearing is negligible for the relatively narrow
spectral channels of the NPOI observations.
4 Results from the  analysis
analysis
In this section we perform a  analysis to constrain a
number of unknown physical parameters in our model for Altair from
the available interferometric observations.
analysis to constrain a
number of unknown physical parameters in our model for Altair from
the available interferometric observations.
We investigate two test models corresponding to the theoretical
limits for the gravity-darkening parameter 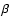 ,
namely, 0.08
(convective atmospheres) and 0.25 (radiative atmospheres). To
obtain a mean effective temperature compatible with previous works
(between
,
namely, 0.08
(convective atmospheres) and 0.25 (radiative atmospheres). To
obtain a mean effective temperature compatible with previous works
(between  7500 K and
7500 K and  8000 K; see for example
Esparmer & North 2003, vB2001; and Ferrero et al. 1995) the
adopted polar temperatures
8000 K; see for example
Esparmer & North 2003, vB2001; and Ferrero et al. 1995) the
adopted polar temperatures 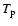 for the test models are
8000 K and 8500 K, corresponding to
for the test models are
8000 K and 8500 K, corresponding to
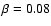 and 0.25,
respectively. The chosen stellar mass
and 0.25,
respectively. The chosen stellar mass
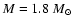 is given by
Malagnini & Morossi (1990). Other slightly different mass
estimates exist since determining the mass of a single star,
particularly a rapid rotator, is not a simple task, but the main
results of this work do not critically depend on this value. We
adopted the projected equatorial velocity
is given by
Malagnini & Morossi (1990). Other slightly different mass
estimates exist since determining the mass of a single star,
particularly a rapid rotator, is not a simple task, but the main
results of this work do not critically depend on this value. We
adopted the projected equatorial velocity
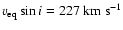 determined by Reiners & Royer (2004) from high
spectral resolution observations. Their value is compatible with
other recent measurements of
determined by Reiners & Royer (2004) from high
spectral resolution observations. Their value is compatible with
other recent measurements of
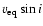 within their
error bars (e.g. vB2001; and Royer et al. 2002).
within their
error bars (e.g. vB2001; and Royer et al. 2002).
In addition to the fixed physical parameters described above, the
equatorial radius
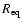 (or the polar one
(or the polar one
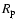 )
is also needed to calculate the models of Altair.
However,
)
is also needed to calculate the models of Altair.
However,
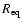 is related to the equatorial angular
diameter
is related to the equatorial angular
diameter
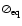 by means of the stellar distance
(
by means of the stellar distance
(
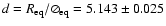 pc from Hipparcos; Perryman
et al. 1997). Since
pc from Hipparcos; Perryman
et al. 1997). Since
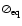 is one important output from our
interferometric data analysis,
is one important output from our
interferometric data analysis,
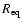 has to be updated
accordingly to each
has to be updated
accordingly to each
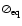 value tested during the
value tested during the  minimization procedure. To avoid calculating a large number of
models we performed a preliminary
minimization procedure. To avoid calculating a large number of
models we performed a preliminary  minimization using a
fixed
minimization using a
fixed
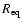 in order to constraint the range of
in order to constraint the range of
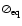 close to the minimum
close to the minimum  .
In the final
.
In the final  analysis,
analysis,
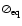 (and the corresponding
(and the corresponding
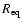 )
varies with steps
of 0.01 mas within a range corresponding to the uncertainty in
)
varies with steps
of 0.01 mas within a range corresponding to the uncertainty in
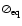 .
Since this uncertainty is rather small (
.
Since this uncertainty is rather small (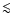 2%),
2%),
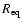 could be kept constant without introducing any
significant changes in our modeling and results.
could be kept constant without introducing any
significant changes in our modeling and results.
Additionally, the major axis orientation (position angle) on the
sky-plane 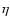 is allowed to vary in steps of
is allowed to vary in steps of
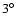 .
The
inclination of the rotation axis i can vary between
.
The
inclination of the rotation axis i can vary between
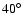 and
and
 (steps of
(steps of
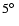 ). For
). For
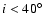 the equatorial
rotation velocity becomes higher than
the equatorial
rotation velocity becomes higher than 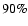 of the critical limit
(
of the critical limit
(
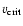 )
leading to unrealistically low equatorial
temperatures as a consequence of the von Zeipel effect.
)
leading to unrealistically low equatorial
temperatures as a consequence of the von Zeipel effect.
We thus have two test models (corresponding to
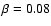 and
and
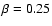 )
with three free parameters (i,
)
with three free parameters (i,
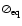 ,
and
,
and 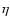 )
for our
)
for our  analysis whose results are presented below.
analysis whose results are presented below.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{2476fig1.eps} %
\end{figure}](/articles/aa/full/2005/41/aa2476-04/Timg148.gif) |
Figure 1:
Reduced  (
(
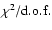 )
as a function of
the stellar inclination i computed from all interferometric
observations described in Sect. 2 for the two test
models (radiative and convective limits for the
gravity-darkening). These values correspond to the best
equatorial angular diameter )
as a function of
the stellar inclination i computed from all interferometric
observations described in Sect. 2 for the two test
models (radiative and convective limits for the
gravity-darkening). These values correspond to the best
equatorial angular diameter
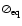 and major axis orientation
and major axis orientation
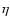 for a given i. Models with
for a given i. Models with
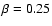 (solid
curve) are preferred compared to models with
(solid
curve) are preferred compared to models with
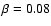 (dashed
curve). The minimum
(dashed
curve). The minimum
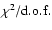 ( (
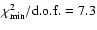 )
is obtained for )
is obtained for
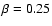 and
and
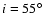 .
Further physical parameters for this
best model from all data (BMAD) and the corresponding error bars
are given in Table 3, together with the results
of other .
Further physical parameters for this
best model from all data (BMAD) and the corresponding error bars
are given in Table 3, together with the results
of other  analyses.
analyses. |
| Open with DEXTER |
 |
Figure 2:
Squared visibilities V2 and corresponding errors
versus the wavelength for the seven NPOI scans (see
Sect. 2). Solid curves correspond to theoretical
values obtained from our best model from the  analysis of
all interferometric data (BMAD; see also
Fig. 1). Plots for scans 2 to 7 were
progressively shifted for better visualization.
analysis of
all interferometric data (BMAD; see also
Fig. 1). Plots for scans 2 to 7 were
progressively shifted for better visualization. |
| Open with DEXTER |
 |
Figure 3:
Triple amplitudes
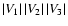 ,
closure phases ,
closure phases
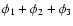 ,
and corresponding errors versus the
wavelength for the seven NPOI scans (Sect. 2).
Solid curves correspond to theoretical values obtained from our
best model from the ,
and corresponding errors versus the
wavelength for the seven NPOI scans (Sect. 2).
Solid curves correspond to theoretical values obtained from our
best model from the  analysis of all interferometric data
(BMAD; see also Fig. 1). The closure phase
is very sensitive to the stellar intensity distribution.
Therefore, a comparison between a strong (
analysis of all interferometric data
(BMAD; see also Fig. 1). The closure phase
is very sensitive to the stellar intensity distribution.
Therefore, a comparison between a strong (
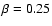 ;
solid
curves) and a weak ( ;
solid
curves) and a weak (
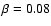 ;
dashed curves) gravity-darkened
model shows that a highly non-uniform surface brightness
distribution is mandatory to reproduce the observed closure
phases. Note that the closure phases have small error bars ( ;
dashed curves) gravity-darkened
model shows that a highly non-uniform surface brightness
distribution is mandatory to reproduce the observed closure
phases. Note that the closure phases have small error bars (
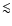 0.03 rad). Plots for scans 2 to 7 were progressively shifted for
better visualization. The picture in the right is the effective
temperature map for the BMAD (Table 3). 0.03 rad). Plots for scans 2 to 7 were progressively shifted for
better visualization. The picture in the right is the effective
temperature map for the BMAD (Table 3). |
| Open with DEXTER |
We present the results of our  analysis applied to
all available interferometric data on Altair (cf.
Sect. 2). This consists of 47 near-IR V2observations (VLTI-VINCI and PTI) together with 630 visible
observations (NPOI). Figure 1 shows the
reduced
analysis applied to
all available interferometric data on Altair (cf.
Sect. 2). This consists of 47 near-IR V2observations (VLTI-VINCI and PTI) together with 630 visible
observations (NPOI). Figure 1 shows the
reduced  (
(
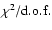 ,
where the degree of
freedom (d.o.f.) is 674) as a function of the inclination icomputed from all interferometric observations for the two test
models. The values in Fig. 1 correspond
to the best
,
where the degree of
freedom (d.o.f.) is 674) as a function of the inclination icomputed from all interferometric observations for the two test
models. The values in Fig. 1 correspond
to the best
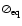 and
and 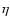 for a given i.
for a given i.
An important result seen in Fig. 1 is that
all models with a gravity-darkening coefficient for hot stars
(
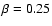 )
are preferred, i.e., have lower
)
are preferred, i.e., have lower  in
comparison to models with a gravity-darkening coefficient for cold
stars (
in
comparison to models with a gravity-darkening coefficient for cold
stars (
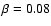 ). This is model-dependent but still the first
direct determination of the gravity-darkening coefficient for a
rapid rotator, obtained thanks to a physically coherent modeling
dedicated to stellar interferometry.
). This is model-dependent but still the first
direct determination of the gravity-darkening coefficient for a
rapid rotator, obtained thanks to a physically coherent modeling
dedicated to stellar interferometry.
The minimum
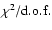 is
is
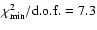 obtained for an inclination
obtained for an inclination
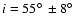 .
This best model obtained from the
.
This best model obtained from the  analysis of all data is hereafter refereed as BMAD (best model for
all data). All free parameters (
analysis of all data is hereafter refereed as BMAD (best model for
all data). All free parameters (
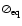 ,
,
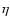 ,
and i) and
uncertainties corresponding to the BMAD are given in
Table 3 together with some selected dependent
parameters. In Table 3 we also list the results
from additional
,
and i) and
uncertainties corresponding to the BMAD are given in
Table 3 together with some selected dependent
parameters. In Table 3 we also list the results
from additional  analyses described in the following
sections.
analyses described in the following
sections.
In order to avoid an underestimation of the uncertainties on the
free parameters, we computed the limits of the confidence domain
by searching for the region between
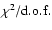 and
and
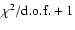 .
We used the reduced
.
We used the reduced  and not the
total
and not the
total  as we found it difficult to account for possible
correlations between the error bars on each measurement, in
particular for the NPOI data. By adopting
as we found it difficult to account for possible
correlations between the error bars on each measurement, in
particular for the NPOI data. By adopting
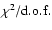 ,
we chose the conservative approach to consider that all
measurements are fully correlated with each other, i.e. that their
error bars cannot be diminished by averaging in the fitting
process. This means that our derived error bars may be
overestimated, but this will avoid an over-interpretation of the
data.
,
we chose the conservative approach to consider that all
measurements are fully correlated with each other, i.e. that their
error bars cannot be diminished by averaging in the fitting
process. This means that our derived error bars may be
overestimated, but this will avoid an over-interpretation of the
data.
In Figs. 2 and 3 we compare the
five NPOI observables (V2 for three baselines, triple
amplitudes, and closure phases) with the corresponding theoretical
values derived from the BMAD. We note in particular that, although
the uncertainties in the closure phases are quite small
(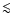 0.03 rad), there is a rather good agreement between the
observed closure phases and those obtained from the BMAD (solid
curves). Clearly, models with
0.03 rad), there is a rather good agreement between the
observed closure phases and those obtained from the BMAD (solid
curves). Clearly, models with
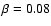 (plotted as dashed
curves for comparison) cannot reproduce these data, leading to
(plotted as dashed
curves for comparison) cannot reproduce these data, leading to
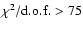 in Fig. 1. In
Fig. 4 we compare the theoretical
squared visibilities V2 from the BMAD with the observed V2and corresponding errors from VLTI-VINCI (H and K bands) and PTI
(K band), as described in Sect. 2.
in Fig. 1. In
Fig. 4 we compare the theoretical
squared visibilities V2 from the BMAD with the observed V2and corresponding errors from VLTI-VINCI (H and K bands) and PTI
(K band), as described in Sect. 2.
Considering all these distinct interferometers, observables,
wavelengths, and baselines (lengths and position angles),
Figs. 2 to 4 show a
good general agreement between observations and the BMAD,
particularly for the closure phases. However, some discrepancies
between theoretical and observed V2 exist, leading to a
relatively a high
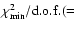 7.3). This
issue is discussed hereafter.
7.3). This
issue is discussed hereafter.
The high
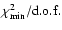 obtained in the last
section from the analysis of all interferometric data is partially
due to an underestimation of long-term errors for the NPOI
visibility amplitudes. This calibration problem is clearly present
in Figs. 2 and 3 as a scatter
of the observed V2 and triple amplitudes relative to the model.
The observations for a given scan are shifted in the same
direction for all wavelengths. On the other hand, the closure
phase is a more stable interferometric observable, being
unaffected by this calibration problem as shown by the excellent
agreement between observation and model in
Fig. 3.
obtained in the last
section from the analysis of all interferometric data is partially
due to an underestimation of long-term errors for the NPOI
visibility amplitudes. This calibration problem is clearly present
in Figs. 2 and 3 as a scatter
of the observed V2 and triple amplitudes relative to the model.
The observations for a given scan are shifted in the same
direction for all wavelengths. On the other hand, the closure
phase is a more stable interferometric observable, being
unaffected by this calibration problem as shown by the excellent
agreement between observation and model in
Fig. 3.
We have thus performed another  analysis including only
the (7 scans)*(18 wavelengths) closure phases from NPOI, together
with the 47 near-IR V2 from PTI and VINCI. The
analysis including only
the (7 scans)*(18 wavelengths) closure phases from NPOI, together
with the 47 near-IR V2 from PTI and VINCI. The
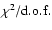 behavior is similar to that seen in
Fig. 1, but the minimum reduced
behavior is similar to that seen in
Fig. 1, but the minimum reduced  is
now
is
now 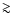 2 times smaller than before, namely,
2 times smaller than before, namely,
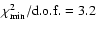 .
In agreement with the
analysis of all data presented in the last section, we obtained
.
In agreement with the
analysis of all data presented in the last section, we obtained
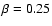 and
and
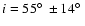 .
Further physical
parameters for this best model determined from the near-IR V2and closure phases (BMIRCP) are given in
Table 3.
.
Further physical
parameters for this best model determined from the near-IR V2and closure phases (BMIRCP) are given in
Table 3.
Even though this analysis showed that
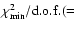 3.2) diminishes when the NPOI
V2 and triple amplitudes are removed, the value obtained
indicates that some non negligible discrepancies between model and
observations still exist. Such discrepancies come from the fact
that the near-IR V2 for the BMAD and the BMIRCP systematically
underestimate the observations from PTI and VINCI, as we can see
in Fig. 4.
3.2) diminishes when the NPOI
V2 and triple amplitudes are removed, the value obtained
indicates that some non negligible discrepancies between model and
observations still exist. Such discrepancies come from the fact
that the near-IR V2 for the BMAD and the BMIRCP systematically
underestimate the observations from PTI and VINCI, as we can see
in Fig. 4.
![\begin{figure}
\par\includegraphics*[width=12.5cm,clip]{2476fig4.eps} %
\end{figure}](/articles/aa/full/2005/41/aa2476-04/Timg160.gif) |
Figure 4:
Squared visibilities V2 (triangles) and corresponding
error bars from VLTI-VINCI (H and K bands) and PTI (K band;
baselines 85 m and 110 m) as described in Sect. 2.
The abscissa is an index (integer number) to label each group of
V2 data. The crosses correspond to theoretical V2 obtained
from the model with minimum  (best model; cf.
Fig. 1). The abscissas of the V2 data
are slightly shifted to the right compared to those of the
theoretical V2 for better visualization.
(best model; cf.
Fig. 1). The abscissas of the V2 data
are slightly shifted to the right compared to those of the
theoretical V2 for better visualization. |
| Open with DEXTER |
Table 3:
Input and derived parameters obtained from a
 minimization procedure applied to several data sets: all
data (BMAD), near-IR V2 and closure
phases (BMIRCP), closure phases alone (BMCP), and near-IR V2alone (BMIR). There is no uncertainty associated to
minimization procedure applied to several data sets: all
data (BMAD), near-IR V2 and closure
phases (BMIRCP), closure phases alone (BMCP), and near-IR V2alone (BMIR). There is no uncertainty associated to 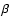 and
and
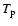 because they define two test models based on
theoretical limits for the gravity darkening (see text for
details). Selected dependent parameters for the best models are
also listed.
because they define two test models based on
theoretical limits for the gravity darkening (see text for
details). Selected dependent parameters for the best models are
also listed.
 |
Figure 5:
The left panel shows the closure phases
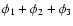 and corresponding errors versus the
wavelength for the seven NPOI scans (Sect. 2).
Solid curves correspond to theoretical values obtained from our
best model from the
and corresponding errors versus the
wavelength for the seven NPOI scans (Sect. 2).
Solid curves correspond to theoretical values obtained from our
best model from the  analysis of closure phases alone
(BMCP; see Table 3). Dashed curves correspond to
the theoretical closure phases obtained by fixing
analysis of closure phases alone
(BMCP; see Table 3). Dashed curves correspond to
the theoretical closure phases obtained by fixing
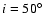 , ,
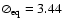 mas, and mas, and
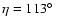 .
These parameters were
derived from the .
These parameters were
derived from the  analysis of near-IR V2 alone (BMIR).
The solid curves provide a much better fit to the observed closure
phases because they correspond to an angular equatorial diameter
larger (
analysis of near-IR V2 alone (BMIR).
The solid curves provide a much better fit to the observed closure
phases because they correspond to an angular equatorial diameter
larger (
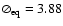 mas) than the value for the dashed curves
( mas) than the value for the dashed curves
(
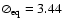 mas). On the other hand, a model (BMIR) with mas). On the other hand, a model (BMIR) with
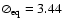 mas nicely fits the near-IR V2 as shown in the
right panel (see also Fig. 4). mas nicely fits the near-IR V2 as shown in the
right panel (see also Fig. 4). |
| Open with DEXTER |
Because these near-IR V2 include data from two distinct
interferometers using different calibrators, one can hardly invoke
some kind of calibration problem, such as those found on the NPOI
data. These low theoretical near-IR V2 seem to be due to the
rather large equatorial angular diameter deduced from the  minimization, namely,
minimization, namely,
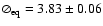 mas for the BMAD and
mas for the BMAD and
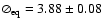 mas for the BMIRCP
(Table 3). To investigate this point we
performed two additional
mas for the BMIRCP
(Table 3). To investigate this point we
performed two additional  analyses: one for the (7
scans)*(18 wavelengths) closure phases alone (NPOI data) and
another for the 47 near-IR V2 alone (VLTI-VINCI and PTI data).
These results are also summarized in Table 3.
analyses: one for the (7
scans)*(18 wavelengths) closure phases alone (NPOI data) and
another for the 47 near-IR V2 alone (VLTI-VINCI and PTI data).
These results are also summarized in Table 3.
Our analysis result in
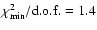 for
the best model for the closure phases alone (BMCP). The
for
the best model for the closure phases alone (BMCP). The
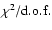 behavior is once more similar to that seen
in Fig. 1, resulting in
behavior is once more similar to that seen
in Fig. 1, resulting in
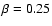 and
and
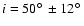 .
The derived equatorial diameter
(
.
The derived equatorial diameter
(
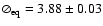 mas) is compatible with those from the two
previous analyses (BMAD and BMIRCP).
mas) is compatible with those from the two
previous analyses (BMAD and BMIRCP).
Before analyzing the near-IR V2 alone, we should note that
since VLTI-VINCI and PTI data correspond to observations in the
first visibility lobe far from the first minimum and in a limited
range of baseline position angles, this analysis suffers from a
significant uniqueness problem (Domiciano de Souza et al. 2002).
This means, in particular, that the stellar inclination cannot be
derived from these data. Thus, we fixed
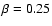 and
and
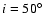 ,
compatibly with the values derived for the BMCP. The
obtained
,
compatibly with the values derived for the BMCP. The
obtained
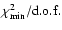 is 0.50 for the best
model for the near-IR V2 alone (BMIR). As expected, the derived
equatorial diameter is significantly smaller (
is 0.50 for the best
model for the near-IR V2 alone (BMIR). As expected, the derived
equatorial diameter is significantly smaller (
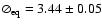 mas) than all previous analyses, which included visible data
from NPOI.
mas) than all previous analyses, which included visible data
from NPOI.
Figure 5 shows the fit to the closure phase
for the BMCP (solid curves in the left panel) and the fit to the
near-IR V2 for the BMIR (right panel). Individually, these fits
are rather good as one can see in Fig. 5 and
also as indicated by the corresponding
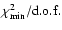 (1.4 for the BMCP and 0.5 for
the BMIR). However, it is clear that the large
(1.4 for the BMCP and 0.5 for
the BMIR). However, it is clear that the large
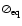 from the
analyses including the closure phases cannot fit the near-IR V2(as already shown in Fig. 4).
from the
analyses including the closure phases cannot fit the near-IR V2(as already shown in Fig. 4).
Conversely, the smaller
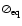 derived from the near-IR V2alone (BMIR) cannot fit the closure phases. This is shown as
dashed curves in Fig. 5 (left panel), where
we plotted the theoretical closure phases obtained by a model with
fixed
derived from the near-IR V2alone (BMIR) cannot fit the closure phases. This is shown as
dashed curves in Fig. 5 (left panel), where
we plotted the theoretical closure phases obtained by a model with
fixed
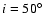 ,
,
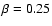 ,
,
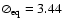 mas, and
mas, and
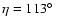 (values from the BMIR). Although this model
certainly leads to a high
(values from the BMIR). Although this model
certainly leads to a high  ,
we note that models with
,
we note that models with
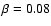 and free i,
and free i,
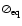 ,
and
,
and 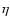 ,
lead to an even
higher
,
lead to an even
higher  .
Thus, the identification of the von Zeipel effect
on Altair (
.
Thus, the identification of the von Zeipel effect
on Altair (
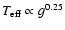 ), which is the main
result of this work, is not affected or hampered by this
discrepancy between the angular sizes derived from the visible and
near-IR data.
), which is the main
result of this work, is not affected or hampered by this
discrepancy between the angular sizes derived from the visible and
near-IR data.
In the following section we investigate this discrepancy and
discuss some physical consequences of our results, in particular
concerning the von Zeipel effect.
Table 4:
Apparent and absolute magnitudes of Altair, using the Hipparcos parallax
(
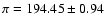 mas).
mas).
5 Discussion
5.1 The size of Altair
The results described in the last section and summarized in
Table 3 reveal a discrepancy between the stellar
angular diameters required to fit the visible and near-IR
interferometric data. This discrepancy also appears when we
compare the results obtained in the visible by ONH2004 (NPOI data)
and in the K band by vB2001 (PTI data).
To investigate this issue we estimate the angular size of Altair
using an independent method: the average surface brightness. Using
the surface brightness relations from Kervella et al. (2004b), we
can derive the mean equivalent limb-darkened angular diameter of
Altair using only its photometric properties (Table
4). We adopted the apparent magnitudes in the
visible and near-IR from Hipparcos (Perryman et al. 1997), Morel & Magnetat (1978), Ducati (2002), and the recent infrared
catalogue from Kidger & Martín-Luis (2003). The error bars from
the original authors on the apparent magnitudes are given for each
band, except for the U, R, and I bands, where a conservative
0.05 mag error has been assumed. No interstellar extinction is
taken into account for this nearby star (
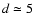 pc).
pc).
We obtain consistent limb-darkened disk angular diameters for all
the visible-infrared colors, with, for instance,
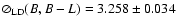 mas. Considering
the Hipparcos parallax of
mas. Considering
the Hipparcos parallax of
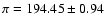 mas (distance
mas (distance
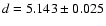 pc), this translates into a photometric
equivalent linear radius of
pc), this translates into a photometric
equivalent linear radius of
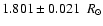 .
Erspamer &
North (2003) obtain an effective temperature of
.
Erspamer &
North (2003) obtain an effective temperature of
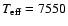 K, averaged over the disk of Altair. The
K, averaged over the disk of Altair. The
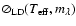 relations from
Kervella et al. (2004b) give the same LD angular diameter using
the H, K, and L apparent magnitudes.
relations from
Kervella et al. (2004b) give the same LD angular diameter using
the H, K, and L apparent magnitudes.
Let us compare the photometric-average angular size derived above
(
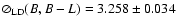 mas) with an
equivalent angular disk diameter leading to the same area of the
stellar surface projected onto the sky-plane
mas) with an
equivalent angular disk diameter leading to the same area of the
stellar surface projected onto the sky-plane
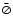 obtained from our models. For BMIR we obtain
obtained from our models. For BMIR we obtain
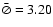 mas, while for BMAD, BMIRCP, and BMCP we
obtain
mas, while for BMAD, BMIRCP, and BMCP we
obtain
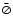 between 3.53 and 3.58 mas. This comparison
points towards a smaller size of Altair since there is a better
agreement between the sizes estimated by the surface brightness
method and by the
between 3.53 and 3.58 mas. This comparison
points towards a smaller size of Altair since there is a better
agreement between the sizes estimated by the surface brightness
method and by the  analysis including near-IR V2 alone,
with the latter still being slightly smaller.
analysis including near-IR V2 alone,
with the latter still being slightly smaller.
From the present data it is not possible to determine whether the
discrepancy between the stellar angular diameters in the visible
and near-IR has a physical or an instrumental origin. Bias in the
wavelength calibration could lead to a larger or smaller size
since it affects the spatial frequency. Previous comparisons
between stellar angular diameters measured by NPOI and other
interferometers show no sign of systematic differences (Nordgren
et al. 2001). On the other hand, the large angular size in the
visible could also be explained, for example, by an extended
emission only seen in the visible. To further investigate the
origin of this discrepancy, more precise interferometric
observations of Altair are required, preferably in the near-IR at
the second visibility lobe and/or with phase closures. These
observations should be made in such a way that the quality and the
nature of the data in the visible and near-IR are similar and,
thus, better comparable. Such observations are expected to be
performed with the instrument VLTI-AMBER (e.g., Petrov et al. 2003).
5.2 Rotation and gravity darkening laws
In the present paper we consistently adopted the Roche
approximation and a von Zeipel-like gravity-darkening
(Eq. (2)). Nevertheless, other more subtle
possibilities exist and should be considered in the future when
more precise interferometric observations of Altair will be
available.
For example, our results indicate that the effective temperature
at Altair's equator could be low enough that the star
presents convection in its external equatorial regions
(
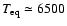 K for the models with minimum
K for the models with minimum
 ). Such low
). Such low
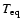 requires a gravity-darkening
exponent
requires a gravity-darkening
exponent
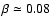 (Lucy 1967; Claret 2000c), so that a
latitudinal dependent
(Lucy 1967; Claret 2000c), so that a
latitudinal dependent 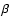 parameter should be more convenient
for Altair (e.g., a continuous variation from the radiative limit
parameter should be more convenient
for Altair (e.g., a continuous variation from the radiative limit
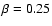 to the convective limit
to the convective limit
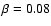 between the
poles and the equator). The hypothesis of a convective equatorial
region is supported by several works showing that Altair has a
chromosphere and a corona, possibly linked to subphotospheric
convective zones (e.g., Ferrero et al. 1995).
between the
poles and the equator). The hypothesis of a convective equatorial
region is supported by several works showing that Altair has a
chromosphere and a corona, possibly linked to subphotospheric
convective zones (e.g., Ferrero et al. 1995).
Other possibilities for a variable parameter 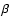 or even for
an alternative gravity-darkening law is the presence of
differential rotation (e.g., Connon Smith & Worley 1974;
Kippenhahn 1977). Although Reiners & Royer (2004) found no
signatures of external latitudinal-dependent differential rotation
in Altair, we think that one cannot exclude internal differential
rotation and/or external differential rotation not detected by the
Fourier transform method used by those authors. In fact, the
method used by Reiners & Royer (2004) is not very sensitive to
differential rotation laws where polar regions rotate faster than
layers closer to the equator (anti solar-like or negative
differential rotation; e.g., Reiners & Schmitt 2002).
or even for
an alternative gravity-darkening law is the presence of
differential rotation (e.g., Connon Smith & Worley 1974;
Kippenhahn 1977). Although Reiners & Royer (2004) found no
signatures of external latitudinal-dependent differential rotation
in Altair, we think that one cannot exclude internal differential
rotation and/or external differential rotation not detected by the
Fourier transform method used by those authors. In fact, the
method used by Reiners & Royer (2004) is not very sensitive to
differential rotation laws where polar regions rotate faster than
layers closer to the equator (anti solar-like or negative
differential rotation; e.g., Reiners & Schmitt 2002).
Interestingly enough, Stoekley (1968) found evidence of an
anti-solar-like differential rotation in Altair. The presence of
negative surface differential rotation is in fact compatible with
the hypothesis of a convective equatorial region. For such cool
regions, characteristic of F and later type stars, it is possible
that some braking mechanism (magnetic effects and/or viscosity due
to the onset of convection) could act preferentially close to
Altair's equator, slowing these regions relative to those closer
to the poles.
This important issue concerning the presence of differential
rotation in Altair, and the corresponding gravity-darkening law,
should be investigated in the future by additional studies,
preferably with distinct and complementary techniques. For
example, Domiciano de Souza et al. (2004) proposed a technique to
detect both solar-like and anti-solar-like differential rotation
by combining high angular resolution with high spectral resolution
(differential interferometry). The forthcoming VLTI-AMBER will be
able to operate in a differential interferometry mode in the
near-IR (e.g., Petrov et al. 2003).
The results presented in Sect. 4 suggest an
intermediate inclination for Altair (see
Table 3). These results seem to disagree with
the analysis from Reiners & Royer (2004), which points towards
higher inclinations (
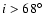 on a
on a 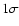 level). However,
this discrepancy disappears if we consider
level). However,
this discrepancy disappears if we consider 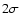 confidence
levels in the results from Reiners & Royer (2004), which implies
confidence
levels in the results from Reiners & Royer (2004), which implies
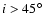 .
Additionally, Stoeckley (1968) derived an inclination
angle between
.
Additionally, Stoeckley (1968) derived an inclination
angle between
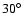 and
and
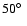 from the analysis of line
profiles of Mg II 4481 and Ca II 3934, which is in
agreement with our results as well.
from the analysis of line
profiles of Mg II 4481 and Ca II 3934, which is in
agreement with our results as well.
It is important that further studies investigate how subtle
effects, such as differential rotation and gravity-darkening,
influence the interferometric observables and, in particular, the
line profiles. It would thus be possible to consistently combine
interferometry and spectroscopy in order to determine the stellar
inclination more precisely.
Once i,
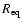 ,
and
,
and
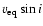 are known,
the rotation frequency can be determined, in the uniform rotation
approximation, by:
are known,
the rotation frequency can be determined, in the uniform rotation
approximation, by:
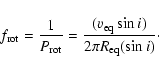 |
(6) |
The rotation frequencies computed from the equation above and
corresponding to our  analyses are listed in
Table 3. Recently, Buzasi et al. (2005) detected
several pulsation modes in WIRE (Wide-field InfraRed Explorer)
observations, indicating that Altair is a low-amplitude
analyses are listed in
Table 3. Recently, Buzasi et al. (2005) detected
several pulsation modes in WIRE (Wide-field InfraRed Explorer)
observations, indicating that Altair is a low-amplitude
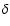 Scuti star. The authors suggest that the two
low-frequency modes found (
Scuti star. The authors suggest that the two
low-frequency modes found (
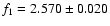 cycles/day and
cycles/day and
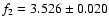 cycles/day) may be associated with the stellar
rotation frequency.
cycles/day) may be associated with the stellar
rotation frequency.
The theoretical
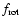 values listed in
Table 3 suggest that the frequency f1measured by Buzasi et al. (2005) is a better candidate for
values listed in
Table 3 suggest that the frequency f1measured by Buzasi et al. (2005) is a better candidate for
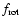 .
However, more precise measurements should be
acquired before we can unambiguously identify
.
However, more precise measurements should be
acquired before we can unambiguously identify
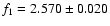 cycles/day as the rotation frequency of Altair.
cycles/day as the rotation frequency of Altair.
This work, along with previous ones, has proven that long baseline
interferometry is a powerful technique for studying rapidly
rotating stars. In particular, this technique can provide
important clues to the many unanswered questions concerning the
structure and evolution of rapid rotators. For example, placing an
intermediate-mass star like Altair in its evolutionary history is
an interesting but difficult task requiring as much information as
possible.
The age of a star can be derived using different indicators.
Lachaume et al. (1999) have used five different methods to study
main-sequence stars in the solar neighborhood: isochrones in the
HR diagram, rotation, calcium emission lines, kinematics in the
Galaxy, and iron abundance. Unfortunately, due to Altair's rapid
rotation, its spectral lines are very broad, and this prevents the
application of the Ca emission line and kinematic methods. The
rotational velocity of a hot, fast rotator is not an accurate
indicator of its age, because of the uncertainties on the initial
rotational velocity and on the braking mechanisms possibly
present.
To estimate the age of Altair, we took advantage of the recent
models from Girardi et al. (2002). We read the tables of these
authors for the following parameters:
![$[{\rm Fe/H}]=-0.34$](/articles/aa/full/2005/41/aa2476-04/img219.gif) ,
,
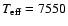 K,
K,
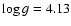 (Erspamer & North 2003), and
Z=0.008. We adopted the absolute magnitudes presented in
Table 4, derived using the parallax from Hipparcos
(Perryman et al. 1997):
(Erspamer & North 2003), and
Z=0.008. We adopted the absolute magnitudes presented in
Table 4, derived using the parallax from Hipparcos
(Perryman et al. 1997):
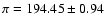 mas. The bolometric
magnitude was estimated using the corrections provided by Girardi
et al. (2002). The best fit of the models with the observed
absolute magnitudes of Altair is obtained for an age between 1.2
and 1.4 Gyr.
mas. The bolometric
magnitude was estimated using the corrections provided by Girardi
et al. (2002). The best fit of the models with the observed
absolute magnitudes of Altair is obtained for an age between 1.2
and 1.4 Gyr.
The relatively old age of Altair suggests that it has kept a high
rotation velocity for a long time, well into its lifetime on the
main sequence. It does not seem that an efficient braking
mechanism is acting to slow down the rotation velocity of this
intermediate-mass star. Altair was searched for the presence of a
debris disk by Kuchner et al. (1998) in the
mid-infrared, without success. The absence of a disk could be one
of the factors that prevented an efficient slow down of the star
by magnetic coupling or turbulent friction. In any case we believe
that further studies should be performed on the evolution of an
intermediate-mass and fast rotating star such as Altair.
6 Summary and conclusions
We performed a physically consistent analysis of all available
interferometric data on Altair using our interferometry-oriented
model for fast rotators. This model includes Roche approximation,
limb-darkening from Claret (2000a,b), and a von
Zeipel-like gravity-darkening law, as described in
Sect. 3 and also by Domiciano de Souza et al. (2002).
The rich observational set analyzed here includes new data from
VLTI-VINCI (V2 in the H and K bands), as well as published data
from PTI (V2 in the K band) and NPOI (V2, triple amplitudes,
and closure phases in the visible between 520 nm and 850 nm).
In particular, and as already pointed out by ONH2004, the presence
of gravity-darkening in Altair is revealed by the NPOI
observations showing (1) a non-zero V2 in the first minimum and
(2) a smooth variation of the closure phase between 0 and 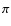 rad. Thanks to our interferometry-oriented model we were able, for
the first time, to provide a physical interpretation of all
observations from NPOI, PTI, and VLTI-VINCI combined. In particular,
we could show that Altair exhibits a gravity-darkening
compatible with the theoretically expected value for hot stars
(von Zeipel effect):
rad. Thanks to our interferometry-oriented model we were able, for
the first time, to provide a physical interpretation of all
observations from NPOI, PTI, and VLTI-VINCI combined. In particular,
we could show that Altair exhibits a gravity-darkening
compatible with the theoretically expected value for hot stars
(von Zeipel effect):
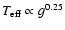 .
.
Moreover, with the parameters and models considered here we were
able to show that the observations of Altair are better reproduced
by models with an intermediate inclination (between
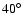 and
and
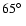 including the error bars).
including the error bars).
Our analysis also reveals a possible discrepancy between visible
and near-IR angular diameters derived from the data that should be
further investigated by visible and near-IR observations of high
quality, preferably within the second visibility lobe and/or with
closure phases.
Further observations should also be performed to investigate the
presence of differential rotation on Altair and the corresponding
gravity-darkening laws. Precise interferometric observations in
the near-IR, allowing us to study differential rotation in
particular (Domiciano de Souza et al. 2004), are soon expected for
the VLTI spectro-interferometer AMBER (e.g., Petrov et al. 2003).
Acknowledgements
This work has been supported by a postdoctoral fellowship at the
Max-Planck-Institut für Radioastronomie (Infrared
Interferometry Group). We acknowledge Drs. G. Weigelt and
T. Driebe for their invaluable suggestions that allowed us to
improve the quality of this work.
- Abt, H. A., &
Morrell, N. I. 1995, ApJS, 99, 135 [NASA ADS] [CrossRef] (In the text)
-
Armstrong, J. T., Mozurkewich, D., Rickard, L. J., et al. 1998,
ApJ, 496, 550 [NASA ADS] [CrossRef] (In the text)
- Bordé, P.,
Coudé du Foresto, V., Chagnon, G., & Perrin, G. 2002,
A&A, 393, 183 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Buzasi, D. L.,
Bruntt, H., Bedding, T. R., et al. 2005, ApJ, 619, 1072 [NASA ADS] [CrossRef] (In the text)
- Cayrel de Strobel, G., Soubiran,
C., Friel, E. D., Ralite, N., & Francois, P. 1997, A&AS,
124, 299 [EDP Sciences] [NASA ADS]
- Cayrel de Strobel G., Soubiran C.,
& Ralite N. 2001, A&A, 373, 159 [EDP Sciences] [NASA ADS] [CrossRef]
- Claret, A.
2000a, A&A, 363, 1081 [NASA ADS] (In the text)
- Claret, A.
2000b, VizieR Online Data Catalog, 336, 31081 [NASA ADS]
- Claret, A.
2000c, A&A, 359, 289 [NASA ADS] (In the text)
- Cohen, M.,
Walker, R. G., Carter, B., et al. 1999, AJ, 117, 1864 [NASA ADS] [CrossRef] (In the text)
- Colavita,
M. M., Wallace, J. K., Hines, B. E., et al. 1999, ApJ, 510,
505 [NASA ADS] [CrossRef] (In the text)
- Collins, G.
W. 1965, ApJ, 142, 265 [NASA ADS] [CrossRef] (In the text)
-
Connon Smith, R., & Worley, R. 1974, MNRAS, 167, 199 [NASA ADS] (In the text)
-
Coudé du Foresto, V., Ridgway, S., & Mariotti, J.-M. 1997,
A&AS, 121, 379 [EDP Sciences] [NASA ADS] (In the text)
- Domiciano de Souza, A., Vakili,
F., Jankov, S., Janot-Pacheco, E. & Abe, L. 2002, A&A, 393,
345 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Domiciano de Souza, A., Kervella,
P., Jankov, S., et al. 2003, A&A, 407, L47 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Domiciano de Souza, A., Zorec,
J., Jankov, S., et al. 2004, A&A, 418, 781 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Ducati, J. R.
2002, NASA Ref. Pub. 1294
(In the text)
- Erspamer,
D., & North, P. 2002, VizieR Online Data Catalog, 339,
81121 [NASA ADS]
- Erspamer,
D., & North, P. 2003, A&A, 398, 1121 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Ferrero, R.
F., Gouttebroze, P., Catalano, S., et al. 1995, ApJ, 439, 1011 [NASA ADS] [CrossRef] (In the text)
- Girardi, L.,
Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Glebocki,
R., Gnacinski, P., & Stawikowski, A. 2000, Acta Astron., 50,
509 [NASA ADS]
-
Glindemann, A., Algomedo, J., Amestica, R., et al. 2003, Proc.
SPIE, 4838, 89 [NASA ADS] (In the text)
-
Hanbury Brown, R. 1974, in The Intensity Interferometer (London:
Taylor & Francis LTD), 151
- Hubeny, I.
1988, Comp. Phys. Comm., 52, 103 [NASA ADS] (In the text)
- Hubeny, I.,
& Lanz, T. 1995, ApJ, 439, 875 [NASA ADS] [CrossRef] (In the text)
- Hummel, C. A.,
Mozurkewich, D., Armstrong, J. T., et al. 1998, AJ, 116, 2536 [NASA ADS] [CrossRef] (In the text)
- Kervella,
P., Coudé du Foresto, V., Glindemann, A., & Hofmann, R.
2000, SPIE, 4006, 31 [NASA ADS] (In the text)
- Kervella,
P., Gitton, Ph., Ségransan, D., et al. 2003a, SPIE, 4838,
858 [NASA ADS] (In the text)
- Kervella,
P., Thévenin, F., Morel, P., Bordé, P., & Di Folco,
E. 2003b, A&A, 408, 681 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Kervella,
P., Ségransan, D., & Coudé du Foresto, V. 2004a,
A&A, 425, 1171 [NASA ADS] (In the text)
- Kervella,
P., Thévenin, F., Di Folco, E., & Ségransan, D.
2004b, A&A, 426, 297 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Kidger, M. R.,
& Martín-Luis, F. 2003, AJ, 125, 3311 [NASA ADS] [CrossRef] (In the text)
-
Kippenhahn, R. 1977, A&A, 58, 267 [NASA ADS] (In the text)
- Kuchner, M.
J., Brown, M. E., & Koresko, C. D. 1998, PASP, 110, 1336 [NASA ADS] [CrossRef] (In the text)
- Kurucz, R. L.
1992, The Stellar Populations of Galaxies, IAU Symp. 149, 225
(In the text)
- Lachaume,
R., Dominik, C., Lanz, T., & Habing, H. J. 1999, A&A, 348,
897 [NASA ADS] (In the text)
-
Lebouquin, J. B., Rousselet-Perraut, K., Kern, P., et al. 2004,
A&A, 424, 719 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Lucy, L. B. 1967,
Z. Astrophys., 65, 89 [NASA ADS] (In the text)
-
Malagnini, M. L., & Morossi, C. 1990, A&AS, 85, 1015 [NASA ADS] (In the text)
- Morel, M., &
Magnetat, P. 1978, A&AS, 34, 477 [NASA ADS]
- Nordgren,
T. E., Sudol, J. J., & Mozurkewich, D. 2001, AJ, 122, 2707 [NASA ADS] [CrossRef] (In the text)
- Ohishi, N.,
Nordgren, T. E., & Hutter, D. J. 2004, ApJ, 612, 463 [NASA ADS] [CrossRef] (In the text)
- Panzera, M.
R., Tagliaferri, G., Pasinetti, L., & Antonello, E. 1999,
A&A, 348, 161 [NASA ADS] (In the text)
- Perryman,
M. A. C., Lindegren, L., Kovalevsky, J., et al., The Hipparcos
Catalogue, 1997, A&A, 323, 49 [NASA ADS] (In the text)
- Petrov, R. G.,
& Amber Consortium, The 2003, EAS Publications Series,
Observing with the VLTI, ed. G. Perrin and F. Malbet, 6, 111
(In the text)
- Reiners, A.,
& Schmitt, J. H. M. M. 2002, A&A, 384, 155 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Reiners, A.,
& Royer, F. 2004, A&A, 428, 199 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Royer, F.,
Grenier, S., Baylac, M.-O., Gómez, A. E., & Zorec, J.
2002, A&A, 393, 897 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Ségransan, D., Forveille, T., Millan-Gabet, C. P. R., &
Traub, W. A. 1999, in ASP Conf. Ser. 194, 290
(In the text)
-
Stoeckley, T. R. 1968, MNRAS, 140, 121 [NASA ADS] (In the text)
- Townsend,
R. H. D. 1997, MNRAS, 284, 839 [NASA ADS] (In the text)
- van Belle,
G. T., Ciardi, D. R., Thompson, R. R., Akeson, R. L., & Lada,
E. A. 2001, ApJ, 559, 1155 [NASA ADS] [CrossRef] (In the text)
- von
Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] (In the text)
-
Wittkowski, M., Aufdenberg, J. P., & Kervella, P. 2004,
A&A, 413, 711 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2005
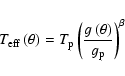
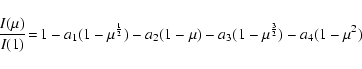
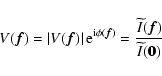
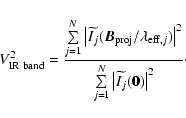
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{2476fig1.eps} %
\end{figure}](/articles/aa/full/2005/41/aa2476-04/Timg148.gif)


![\begin{figure}
\par\includegraphics*[width=12.5cm,clip]{2476fig4.eps} %
\end{figure}](/articles/aa/full/2005/41/aa2476-04/Timg160.gif)