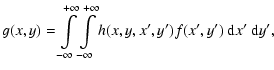 |
(1) |
A&A 442, 397-403 (2005)
DOI: 10.1051/0004-6361:20053414
R. Vio1 - J. Bardsley2 - M. Donatelli3 - W. Wamsteker4
1 - Chip Computers Consulting s.r.l., Viale Don L. Sturzo 82,
S.Liberale di Marcon, 30020 Venice, Italy
2 -
Department of Mathematical Sciences, The University of Montana,
Missoula, MT 59812-0864, USA
3 -
Dipartimento di Fisica e Matematica, Università dell'Insubria,
via Valleggio 11, 22100 Como, Italy
4 -
INTA/LAEFF, Apartado 50727, 28080 Madrid, Spain
Received 12 May 2005/ Accepted 11 July 2005
Abstract
It is well-known that when an astronomical image is
collected by a telescope, the measured intensities at pixels near
the edge of the image may depend on the intensity of the object
outside of the field of view (FOV) of the instrument. This makes
the deconvolution of astronomical images troublesome. Standard
approaches for solving this problem artificially extend the object
outside the FOV via the imposition of boundary conditions (BCs).
Unfortunately, in many instances the artificially extended object
has little in common with the object itself outside of the FOV.
This is most pronounced in the case of objects close to the
boundary of the image and/or extended objects not completely
contained in the image domain. In such cases, an inaccurate
extension of the image outside of the FOV can introduce
non-physical edge effects near the boundary that can degrade the
quality of the reconstruction. For example, if the BCs used result
in an extended image that is discontinuous at the boundary, these
edge effects take the form of ripples (Gibbs oscillations). In
this paper, we extend to least-squares (LS) algorithms a method
recently proposed by Bertero & Boccacci (2005, A&A, 437, 369) in the context of the
Richardson-Lucy (RL) algorithm for the restoration of images
contaminated by Poissonian noise. The most important
characteristic of the proposed approach is that it does not impose
any kind of artificial BCs and is therefore free from edge
effects. For this reason it can be considered the natural method
for the restoration of images via LS algorithms.
Key words: methods: data analysis - methods: statistical - techniques: image processing
When a two-dimensional object f(x,y) in outer-space is viewed
through a telescope, the observed image g(x,y) is related to fvia the integral equation
The image deblurring, or deconvolution, problem is to obtain an
approximate solution of the linear system (3). A
very common approach is the least-squares (LS) method, where the
restored image is obtained by approximately solving
The standard approach that is used to avoid this problem is to
impose a priori boundary conditions (BCs) on ![]() .
The BCs that
are most often used force a functional dependency between the
elements of
.
The BCs that
are most often used force a functional dependency between the
elements of ![]() external to the FOV and those internal to this
area. This has the effect of extending
external to the FOV and those internal to this
area. This has the effect of extending ![]() outside of the FOV
without adding any unknowns to the associated image deblurring
problem. Because of this, problem (4) can be
reformulated in terms of an
outside of the FOV
without adding any unknowns to the associated image deblurring
problem. Because of this, problem (4) can be
reformulated in terms of an
![]() unknown array
unknown array ![]() ,
and
,
and ![]() can be written as an
can be written as an
![]() square matrix
whose structure can be exploited by fast algorithms.
square matrix
whose structure can be exploited by fast algorithms.
The following BCs and associated extensions of ![]() are by far
the most common choices in image processing:
are by far
the most common choices in image processing:
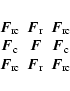
| F(1-i,j) = 2 F(1,j) - F(i+1,j) | |||
| F(i,1-j) = 2 F(i,1) - F(i,j+1) | |||
| F(N+i,j) = 2 F(N,j) - F(N-i,j) | |||
| F(i,N+j) = 2 F(i,N) - F(i,N-j) | |||
Formally, the minimum norm solution of problem (4)
is given by
The benefit of the approach set forth in the previous paragraph is
that it allows for the use of the fast DFT. Unfortunately it does
not, by itself, work well. The reason is that the matrix ![]() in
(3) maps
in
(3) maps
![]() arrays into
arrays into
![]() arrays, whereas
arrays, whereas ![]() works in the opposite direction. However,
because of the zero-padding operation, the matrices
works in the opposite direction. However,
because of the zero-padding operation, the matrices
![]() and
and
![]() are artificially forced to map
are artificially forced to map
![]() arrays into
arrays into
![]() arrays. Thus, one might expect that if the zero-extended
model is modified in such a way that the domains in which
arrays. Thus, one might expect that if the zero-extended
model is modified in such a way that the domains in which ![]() and
and ![]() operate are preserved, things should work. This
simple observation was recently made by Bertero & Boccacci (2005) in the
context of the restoration of images contaminated by Poissonian
noise, and led to the development of a modified version of the
Richardson-Lucy (RL) algorithm that has proved to provide superb
results
operate are preserved, things should work. This
simple observation was recently made by Bertero & Boccacci (2005) in the
context of the restoration of images contaminated by Poissonian
noise, and led to the development of a modified version of the
Richardson-Lucy (RL) algorithm that has proved to provide superb
results![]() .
.
The extension of the arguments of
Bertero & Boccacci (2005) to the LS case leads us to rewrite problem (4)
in the equivalent form
Problem (6) can be rewritten in the revealing form
The prototypical iterative regularization algorithm for least
squares problems is the Landweber method (LW). This is a
gradient descent algorithm for solving problem (4). In
particular, it creates a sequence of iterates that, provided
![]() has full column rank, converges to the solution in
Eq. (5) (see Engl et al. 1996). Because of its slow
convergence, it is not frequently used in practical applications.
However, because of its simplicity, it is often utilized in the
theoretical analysis of the potential performance of the LS
approach.
has full column rank, converges to the solution in
Eq. (5) (see Engl et al. 1996). Because of its slow
convergence, it is not frequently used in practical applications.
However, because of its simplicity, it is often utilized in the
theoretical analysis of the potential performance of the LS
approach.
If
![]() is the starting image, then the iterations take the form
is the starting image, then the iterations take the form
Applying LW to the problem of solving (6) yields the
modified Landweber iteration
For the sake of clarity and completeness, we now provide a
detailed analysis of the convergence of (10). The
analogue of Eq. (9) in this case is
![\begin{displaymath}[\vec{\widetilde\Lambda}_k]_{ii}= 1-(1-\omega s_i^2)^k,
\end{displaymath}](/articles/aa/full/2005/40/aa3414-05/img84.gif) |
(14) |
![\begin{displaymath}[\vec{\Lambda}^\dagger]_{ii}= \left\{\begin{array}{cr} s_i^{-1} & \qquad s_i>0, \\
0 & \qquad s_i = 0.\end{array}\right.
\end{displaymath}](/articles/aa/full/2005/40/aa3414-05/img85.gif) |
(15) |
| |
= | (16) | |
| = | (17) |
A DFT-based coding of the modified LW is trivial.
In fact, since
![]() ,
,
![]() ,
and
,
and
![]() ,
it is not difficult to see that the
iterate (10) can be rewritten in the form
,
it is not difficult to see that the
iterate (10) can be rewritten in the form
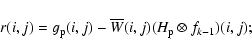 |
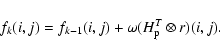 |
For each iteration this procedure requires the computation of four
![]() DFTs, versus the two
DFTs, versus the two
![]() DFTs required by
the classic algorithm based on P-BCs.
DFTs required by
the classic algorithm based on P-BCs.
We now present some numerical experiments in which the performance of the modified LW algorithm is compared with the performance of classical LW when R-BCs and AR-BCs are imposed. Actually, we have used a projected version of LW that constrains the solution to be nonnegative. We do this because in the experiments we have used as a benchmark the modified RL algorithm as proposed by Bertero & Boccacci (2005) which also imposes a nonnegativity constraint on the solution.
In all of the experiments, the adopted PSF is a Gaussian with
circular symmetry and dispersion set to 6 pixels. We have
deliberately chosen non-astronomical objects. In fact, because of
the more important contribution of the high frequency components,
objects with sharp outline are much more difficult to restore than
those typical of astronomical observations. Hence, we have
considered a rectangular function and a very sharply structured
object. For each object we have considered three different
situations concerning noise, i.e., no-noise, Gaussian noise and
Poissonian noise. In the last two cases an
![]() and a peak
and a peak
![]()
![]() , respectively,
have been adopted. This is to ensure that the performance of the
modified LW does not depend on the particular kind of noise that
contaminates the images. In order to avoid pixels with zero
values, a sky-background has been added whose intensity, in the
blurred image, is set to
, respectively,
have been adopted. This is to ensure that the performance of the
modified LW does not depend on the particular kind of noise that
contaminates the images. In order to avoid pixels with zero
values, a sky-background has been added whose intensity, in the
blurred image, is set to ![]() of the maximum value of the image.
Figures 1-10 clearly indicate the
supremacy of the modified LW over classical LW with both R-BCs and
AR-BCs.
of the maximum value of the image.
Figures 1-10 clearly indicate the
supremacy of the modified LW over classical LW with both R-BCs and
AR-BCs.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{3414fg1.eps}\end{figure}](/articles/aa/full/2005/40/aa3414-05/Timg116.gif) |
Figure 1: Rectangular function used in the first experiment. No noise has been added. The delimited area corresponds to the image used in the deblurring operation. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{3414fg2.eps} \end{figure}](/articles/aa/full/2005/40/aa3414-05/Timg118.gif) |
Figure 2:
Relative restoration error (RRE)
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{3414fg3.eps} \end{figure}](/articles/aa/full/2005/40/aa3414-05/Timg119.gif) |
Figure 3: Results obtained from deblurring for the experiment with the object in Fig. 1. The displayed RREs correspond to the best value obtained during the iterations. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{3414fg4.eps} \end{figure}](/articles/aa/full/2005/40/aa3414-05/Timg120.gif) |
Figure 4:
As in Fig. 2 but in the case of Gaussian noise with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{3414fg5.eps} \end{figure}](/articles/aa/full/2005/40/aa3414-05/Timg121.gif) |
Figure 5:
As in Fig. 2 but in the case of Poissonian noise with peak
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{3414fg6.eps} \end{figure}](/articles/aa/full/2005/40/aa3414-05/Timg122.gif) |
Figure 6: Sharply structured object used in the second experiment. No noise has been added. The delimited area corresponds to the image used in the deblurring operation. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{3414fg7.eps} \end{figure}](/articles/aa/full/2005/40/aa3414-05/Timg123.gif) |
Figure 7:
Relative restoration error (RRE)
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.48cm,clip]{3414fg8.eps} \end{figure}](/articles/aa/full/2005/40/aa3414-05/Timg124.gif) |
Figure 8: Results obtained from deblurring for the experiment with the object in Fig. 6. The displayed RREs corresponds to the best value obtained during the iterations. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.48cm,clip]{3414fg9.eps} \end{figure}](/articles/aa/full/2005/40/aa3414-05/Timg125.gif) |
Figure 9:
As in Fig. 7 but in the case of Gaussian noise with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.48cm,clip]{3414fg10.eps} \end{figure}](/articles/aa/full/2005/40/aa3414-05/Timg126.gif) |
Figure 10:
As in Fig. 7 but in the case of Poissonian noise with peak
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.48cm,clip]{3414fg11.eps} \end{figure}](/articles/aa/full/2005/40/aa3414-05/Timg128.gif) |
Figure 11:
Rectangular function used in the third experiment. Noise is Poissonian with
peak
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.48cm,clip]{3414fg12.eps} \end{figure}](/articles/aa/full/2005/40/aa3414-05/Timg129.gif) |
Figure 12:
Relative restoration error (RRE)
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{3414fg13.eps} \end{figure}](/articles/aa/full/2005/40/aa3414-05/Timg130.gif) |
Figure 13: Results obtained from deblurring for the experiment with the object in Fig. 11. The displayed RREs corresponds to the best value obtained during the iterations. |
| Open with DEXTER | |
As shown by Figs. 11-13, this result does
not change when an experiment based on a typical astronomical
object is considered. Apart from the fact that the noise is
Poissonian with a peak
![]() ,
the other
conditions of the experiment are identical to those in the
previous cases. The only point worth noting is that AR-BC is able
to provide a reconstruction whose quality is similar to that of
the modified LW and RL algorithms. This is a consequence of the
fact that in the object the contribution of the high frequency
components (i.e., those that determine the edge effects) is
negligible.
,
the other
conditions of the experiment are identical to those in the
previous cases. The only point worth noting is that AR-BC is able
to provide a reconstruction whose quality is similar to that of
the modified LW and RL algorithms. This is a consequence of the
fact that in the object the contribution of the high frequency
components (i.e., those that determine the edge effects) is
negligible.
The theoretical arguments and numerical experiments presented above lead one to conclude that in the case of objects close to the boundaries of an image and/or extended objects not completely contained in the image domain, the imposition of artificial BCs is not, in general, the optimal approach. This is due to the fact that imposing BCs can alter the original problem in a way that is not compatible with physical reality. Much better results are obtained by solving the under-determined LS problem (6).
Three more points have to be stressed. The first one is that there are indications that the solution of problem (6) permits one to obtain remarkably good restorations even in the case of Poissonian noise, where model (3) no longer holds. Given the limited number of experiments carried out in this paper, we cannot justifiably make the claim that this will hold in general. However, in a recent work, Vio et al. (2005) have shown that the LS deblurring algorithms are remarkably insensitive to the nature of the noise. Hence, it can be safely expected that modified LS algorithms will also work well in the case of non-Gaussian noises.
A second point to note is the fact that, in spite of inferior
performance in terms of reconstruction quality when compared to
the approach that we advocate in this paper, AR-BCs work
surprisingly well. This could be useful in the case of very large
images. In fact, when the PSF is doubly symmetric, the deblurring
algorithms can be implemented using the discrete sine transform
(DST-I). In this case, LW requires two
![]() DST-Is
and a few computations of lower order for the edges (Donatelli & Serra-Capizzano 2005),
whereas with an asymmetric PSF, it requires two DFTs of size
DST-Is
and a few computations of lower order for the edges (Donatelli & Serra-Capizzano 2005),
whereas with an asymmetric PSF, it requires two DFTs of size
![]() (extending the image with an antireflective padding).
Therefore, in the case of a generic PSF, one LW iteration with
AR-BCs shows a computational cost about one half of modified LW.
(extending the image with an antireflective padding).
Therefore, in the case of a generic PSF, one LW iteration with
AR-BCs shows a computational cost about one half of modified LW.
As a final comment, we note that although we have considered only
the Landweber algorithm, all of the LS algorithms that make use of
the matrices ![]() and
and ![]() can be similarly modified.
can be similarly modified.