A&A 442, 1-10 (2005)
DOI: 10.1051/0004-6361:20052983

Discovery of the binary pulsar PSR B1259-63 in very-high-energy gamma rays around periastron with HESS

F. Aharonian1 - A. G. Akhperjanian2 - K.-M. Aye3 - A. R. Bazer-Bachi4 - M. Beilicke5 - W. Benbow1 - D. Berge1 - P. Berghaus6,[*] - K. Bernlöhr1,7 - C. Boisson8 - O. Bolz1 - I. Braun1 - F. Breitling7 - A. M. Brown3 - J. Bussons Gordo9 - P. M. Chadwick3 - L.-M. Chounet10 - R. Cornils5 - L. Costamante1,20 - B. Degrange10 - A. Djannati-Ataï6 - L. O'C. Drury11 - G. Dubus10 - D. Emmanoulopoulos12 - P. Espigat6 - F. Feinstein9 - P. Fleury10 - G. Fontaine10 - Y. Fuchs13 - S. Funk1 - Y. A. Gallant9 - B. Giebels10 - S. Gillessen1 - J. F. Glicenstein14 - P. Goret14 - C. Hadjichristidis3 - M. Hauser12 - G. Heinzelmann5 - G. Henri13 - G. Hermann1 - J. A. Hinton1 - W. Hofmann1 - M. Holleran15 - D. Horns1 - O. C. de Jager15 - S. Johnston21 - B. Khélifi1 - J. G. Kirk1 - Nu. Komin7 - A. Konopelko1,7 - I. J. Latham3 - R. Le Gallou3 - A. Lemière6 - M. Lemoine-Goumard10 - N. Leroy10 - O. Martineau-Huynh16 - T. Lohse7 - A. Marcowith4 - C. Masterson1,20 - T. J. L. McComb3 - M. de Naurois16 - S. J. Nolan3 - A. Noutsos3 - K. J. Orford3 - J. L. Osborne3 - M. Ouchrif16,20 - M. Panter1 - G. Pelletier13 - S. Pita6 - G. Pühlhofer1,12 - M. Punch6 - B. C. Raubenheimer15 - M. Raue5 - J. Raux16 - S. M. Rayner3 - I. Redondo10,20,[*] - A. Reimer17 - O. Reimer17 - J. Ripken5 - L. Rob18 - L. Rolland16 - G. Rowell1 - V. Sahakian2 - L. Saugé13 - S. Schlenker7 - R. Schlickeiser17 - C. Schuster17 - U. Schwanke7 - M. Siewert17 - O. Skjæraasen22 - H. Sol8 - R. Steenkamp19 - C. Stegmann7 - J.-P. Tavernet16 - R. Terrier6 - C. G. Théoret6 - M. Tluczykont10,20 - G. Vasileiadis9 - C. Venter15 - P. Vincent16 - H. J. Völk1 - S. J. Wagner12


1 - Max-Planck-Institut für Kernphysik, Heidelberg, Germany
2 - Yerevan Physics Institute, Yerevan, Armenia
3 - University of Durham, Department of Physics, Durham, UK
4 - Centre d'Étude Spatiale des Rayonnements, CNRS/UPS, Toulouse, France
5 - Universität Hamburg, Institut für Experimentalphysik, Hamburg, Germany
6 - APC, Paris, France[*]
7 - Institut für Physik, Humboldt-Universität zu Berlin, Berlin, Germany
8 - LUTH, UMR 8102 du CNRS, Observatoire de Paris, Meudon, France
9 - Groupe d'Astroparticules de Montpellier, IN2P3/CNRS, Université Montpellier II, Montpellier, France
10 - Laboratoire Leprince-Ringuet, IN2P3/CNRS, École Polytechnique, Palaiseau, France
11 - Dublin Institute for Advanced Studies, Dublin, Ireland
12 - Landessternwarte, Königstuhl, Heidelberg, Germany
13 - Laboratoire d'Astrophysique de Grenoble, INSU/CNRS, Université Joseph Fourier, Grenoble, France
14 - DAPNIA/DSM/CEA, CE Saclay, Gif-sur-Yvette, France
15 - Unit for Space Physics, North-West University, Potchefstroom, South Africa
16 - Laboratoire de Physique Nucléaire et de Hautes Énergies, IN2P3/CNRS, Universités Paris VI & VII, Paris, France
17 - Institut für Theoretische Physik, Lehrstuhl IV: Weltraum und Astrophysik, Ruhr-Universität Bochum, Germany
18 - Institute of Particle and Nuclear Physics, Charles University, Prague, Czech Republic
19 - University of Namibia, Windhoek, Namibia
20 - European Associated Laboratory for Gamma-Ray Astronomy, jointly supported by CNRS and MPG
21 - School of Physics, University of Sydney, Australia
22 - Institute of Theoretical Astrophysics, University of Oslo, Norway

Received 3 March 2005 / Accepted 2 June 2005

Abstract
We report the discovery of very-high-energy (VHE) $\gamma $-ray emission of the binary system PSR B1259-63/SS 2883 of a radio pulsar orbiting a massive, luminous Be star in a highly eccentric orbit. The observations around the 2004 periastron passage of the pulsar were performed with the four 13 m Cherenkov telescopes of the HESS experiment, recently installed in Namibia and in full operation since December 2003. Between February and June 2004, a $\gamma $-ray signal from the binary system was detected with a total significance above $13\sigma$. The flux was found to vary significantly on timescales of days which makes PSR B1259-63 the first variable galactic source of VHE $\gamma $-rays observed so far. Strong emission signals were observed in pre- and post-periastron phases with a flux minimum around periastron, followed by a gradual flux decrease in the months after. The measured time-averaged energy spectrum above a mean threshold energy of 380 GeV can be fitted by a simple power law $F_0(E/1~\rm TeV)^{-\Gamma}$ with a photon index $\Gamma = 2.7\pm0.2_{\rm stat}\pm0.2_{\rm sys}$ and flux normalisation $F_0 = (1.3 \pm 0.1_{\rm stat} \pm 0.3_{\rm sys}) \times 10^{-12}~\rm TeV^{-1}~\rm cm^{-2}~\rm s^{-1}$. This detection of VHE $\gamma $-rays provides unambiguous evidence for particle acceleration to multi-TeV energies in the binary system. In combination with coeval observations of the X-ray synchrotron emission by the RXTE and INTEGRAL instruments, and assuming the VHE $\gamma $-ray emission to be produced by the inverse Compton mechanism, the magnetic field strength can be directly estimated to be of the order of 1 G.

Key words: gamma-rays: observations - stars: pulsars: individual: PSR B1259-63

1 Introduction

PSR B1259-63 / SS 2883 is a binary system consisting of a $\sim $48 ms pulsar in orbit around a massive B2e companion star (Johnston et al. 1992b,a). The highly eccentric orbit of the pulsar places it just $\sim $ $10^{13}~ \rm cm$ from the companion during periastron every $\sim $3.4 years. Be stars are known to have non-isotropic stellar winds forming an equatorial disk with enhanced mass outflow (e.g. Waters et al. 1988). In the case of PSR B1259-63, timing measurements suggest that the disk is inclined with respect to the orbital plane (Wex et al. 1998), probably because the neutron star received a substantial birth kick, causing the pulsar to cross the disk two times near periastron. These unique properties make the binary system PSR B1259-63 an excellent laboratory for the study of pulsar winds interacting with a changing environment in the presence of an extremely intense photon field. The synchrotron origin of optically thin unpulsed radio emission detected from this source, in particular during the periastron passage (e.g. Johnston et al. 1999; Connors et al. 2002), indicates acceleration of electrons to relativistic energies. The acceleration process has been argued to be most efficient when the pulsar passes through the equatorial disk (Ball et al. 1999). The basic features of such a system ("binary plerion'') in the context of higher energy X- and $\gamma $-radiation components have been comprehensively discussed by Tavani & Arons (1997).

The intense photon field provided by the companion star not only plays an important role in the cooling of relativistic electrons but also serves as a perfect target for the production of high energy $\gamma $-rays through inverse Compton (IC) scattering (Murata et al. 2004; Ball & Dodd 2001; Kirk et al. 1999; Tavani et al. 1996; Ball & Kirk 2000). Some of these emission models predict wind-powered shock acceleration of electrons to multi-TeV energies, radiating predominantly through the synchrotron and IC channels, with the main energy release in the X- and high energy $\gamma $-ray bands, respectively.

The unpulsed non-thermal X-ray emission detected from PSR B1259-63 throughout its orbital phase in 1992 to 1996 by the ROSAT and ASCA satellites (Cominsky et al. 1994; Hirayama et al. 1996; Kaspi et al. 1995) generally supports the synchrotron origin of X-rays. The spectrum of the synchrotron radiation seems to extend to hard X-rays/low energy $\gamma $-rays as shown by OSSE (Grove et al. 1995) and recently confirmed by observations with the INTEGRAL satellite (Shaw et al. 2004).

Since the companion star provides the dominant source of photons for IC scattering, the target photon density is well known throughout the entire orbit. Therefore, the ratio of X-ray flux to high energy $\gamma $-ray flux depends only on the strength of the ambient magnetic field. Although the latter can be estimated within a general magneto-hydrodynamic treatment of the problem, it contains large uncertainties which affect the estimate of the IC $\gamma $-ray flux as $F_\gamma \propto B^{-2}$.

Kirk et al. (1999) studied the light curves of very-high-energy (VHE) $\gamma $-rays under the assumption of a 1/r dependence of the magnetic field which implies that the ratio of the energy density of the photon field to that in the magnetic field B is independent of orbital phase. They also assumed that the position of the termination shock as well as the strength of the magnetic field is not affected by the disk of the B2e star. Under such assumptions, they predicted an asymmetric $\gamma $-ray light curve with respect to periastron (because of the inclination of the orbit with respect to the line of sight and the dependence of the inverse Compton $\gamma $-ray emissivity on the scattering angle), with an increase towards periastron and monotonic decrease after the passage of periastron. However, one might possibly expect significant deviation from such a simplified picture given the apparent strong impact of the disk on the pulsar wind termination as seen in the X-ray light curve (Tavani & Arons 1997). Moreover, during the time periods of interaction of the pulsar wind with the equatorial disk one may expect, in addition to the IC $\gamma $-rays, a new component of $\gamma $-radiation associated with interactions of accelerated electrons and possibly also protons with the dense ambient gas (Kawachi et al. 2004). Up to now, the theoretical understanding of the properties of this complex system, involving pulsar and stellar winds interacting with each other, is quite limited because of the lack of constraining observations.

Nevertheless, the fortunate combination of: (1) the high spin-down luminosity of the pulsar, $L=8.3~\times~ 10^{35}~\rm erg/s$, which is partially converted into populations of ultra-relativistic particles, (2) the presence of the intense target photon field provided by the companion star with energy density $\approx$ $0.9~(R(t)/10^{13}~\rm cm)^{-2}~\rm erg/cm^3$ (where R(t) is the spatial separation between the pulsar and the companion star), and (3) the relatively small distance to the source ( $d \approx 1.5~\rm kpc$) makes this object a very attractive candidate for VHE $\gamma $-ray emission.

Previous observations of PSR B1259-63 in VHE $\gamma $-rays, apart from its periastron passage were performed using the CANGAROO I and CANGAROO II detectors, but did not result in significant signals and provided upper limits at $13\%$ of the flux from the Crab Nebula (see Kawachi et al. 2004, and references therein). The first significant detection in VHE $\gamma $-rays based on preliminary analysis results was reported in Beilicke et al. (2004) a few days prior to the periastron passage in February 2004 by the High Energy Stereoscopic System (HESS) to allow for target of opportunity observations of other instruments. The analysis of the data from this initial detection and the data obtained in the subsequent HESS observation campaign on PSR B1259-63 is presented in this paper.

2 VHE $\gamma $-ray observations and results

2.1 Observations and analysis

The observations from February to June 2004 were performed with the High Energy Stereoscopic System (HESS), consisting of four imaging atmospheric Cherenkov telescopes (Hinton 2004) located in Namibia, at $23\hbox{$^\circ$ }16'$ S $16\hbox{$^\circ$ }30'$ E in 1800 m above sea level. Each telescope has a tesselated spherical mirror with 13 m diameter and $107~\rm m^2$ area (Cornils et al. 2003; Bernlöhr et al. 2003) and is equipped with a camera of 960 $0.16\hbox{$^\circ$ }$-photomultiplier tubes providing a total field of view of $5\hbox{$^\circ$ }$ in diameter (Vincent et al. 2003). During the stereoscopic observations, an array trigger requires the simultaneous detection of air-showers by several telescopes at the hardware level, allowing a suppression of background events (Funk et al. 2004).

All observations were carried out in moonless nights tracking sky positions with an alternating offset of typically $\pm0.5^\circ$ in declination relative to the source (the wobble mode) in time intervals of 28 min duration. This allows to determine the background from the same field of view and one can omit off-source observations, effectively doubling the observation time. Due to the serendipitous discovery of another source in the field of view around PSR B1259-63 (see Aharonian et al. 2005a), for all observations subsequent to the 14th of May 2004 (MJD 53 139) the array pointing was changed to a position $\sim $0.6$^\circ$ north of PSR B1259-63 and an alternating wobble offset of 0.5$^\circ$ in right ascension (instead of declination) was used.

The data set, selected on the basis of standard quality criteria, has a dead time corrected exposure (live time) of 48.6 h and a mean zenith angle of 42.7 $\hbox{$^\circ$ }$. The corresponding mean threshold energy defined by the peak $\gamma $-ray detection rate for a source with a Crab-like spectrum (Aharonian et al. 2000) after selection cuts was estimated to be 380 GeV. In the phase prior to the periastron passage (7.8 h live time), due to technical problems, data from only three telescopes were considered, and for the post-periastron phase (41.9 h live time) data from the full telescope array were used.

After the calibration of the recorded air shower data (Aharonian et al. 2004), each telescope image was parametrised by its centre of gravity and second moments (Hillas 1985) followed by the stereoscopic reconstruction of the shower geometry providing an angular resolution of $\sim $ $0.1\hbox{$^\circ$ }$ for individual $\gamma $-rays. The $\gamma $-ray energy was estimated from the image intensity and the shower geometry with a typical resolution of $\sim $$15\%$. In order to reject the vast background of cosmic-ray showers, $\gamma $-ray candidates are selected using cuts on image shape scaled with their expectation values obtained from Monte Carlo simulations. The cuts used for this analysis were optimised on simulations of a $\gamma $-ray point source with a flux level of 10% of the Crab Nebula VHE $\gamma $-ray flux, allowing 41.2% of the $\gamma $-rays to be retained while rejecting more than 99.9% of the cosmic-ray air showers. A more detailed description of the analysis techniques can be found in Aharonian et al. (2005b).

2.2 Detection

Figure 1 shows the distribution of the squared angular distance $\theta ^2$ of excess events relative to the position of PSR B1259-63 for the whole data set. The circle with a radius corresponding to the angular cut $\theta^2_{\rm cut}=0.02~{\rm deg}^2$ in the field of view around the source position was considered as the on-region. The background was estimated from several non-overlapping circles of the same radius (off-regions) with the same angular distance from the camera centre, allowing corrections due to the varying camera acceptance to be omitted (Aharonian et al. 2001). The clear excess in the direction of the pulsar has a significance of 13.8 $\sigma$ and is consistent with a distribution obtained from a simulated $\gamma $-ray point source. The $\gamma $-ray signal from the direction of PSR B1259-63 was detected in most of the darkness periods from February to June 2004, for which the results are summarised in Table 1.


  \begin{figure} \par\includegraphics[width=8.2cm,clip]{2983fig1.eps} \end{figure} Figure 1: Main figure: distribution of background-subtracted $\gamma $-ray candidates in $\theta ^2$ where $\theta $ is the angular distance between the reconstructed shower direction and the pulsar position for the complete 2004 data set. The solid line indicates the distribution expected for a point source of $\gamma $-rays. Inset: distributions in $\theta ^2$ for "on-source'' $\gamma $-ray candidates relative to the source position (full points) and for all background control regions (histogram, scaled with the background normalisation factor $\alpha $). An uniform background results in a flat distribution in $\theta ^2$. The dashed vertical line indicates the angular cut applied ( $\theta^2 < \theta^2_{\rm cut} = 0.02~\rm deg^2$).
Open with DEXTER

Table 1: Results of HESS observations on PSR B1259-63. For each darkness period the number of telescopes used in the analysis $N_{{\rm tel}}$, the live time $t_{{\rm live}}$, the significance S calculated according to Li & Ma (1983), the number of counts within the on-source ( $N_{{\rm on}}$) and off-source ( $N_{{\rm off}}$) region(s), the background normalisation $\alpha $, and the number of detected $\gamma $-rays ( $N_{{\rm\gamma }}$) are listed. The background normalisation $\alpha $ was determined by the number of off-regions, which do not coincide with other $\gamma $-ray sources in the field of view. Therefore $\alpha $ is not the same for all data subsets because it depends on the distribution of wobble offsets used when obtaining the data.

A 2D-analysis of the HESS field of view around PSR B1259-63 was performed using the ring background technique as alternative background estimation method. In this method, for each bin, the number of on-events $N_{{\rm on}}$ was derived by integrating the bin content within a circle of radius $\theta_{\rm cut}$(on-region). The number of background events $N_{{\rm off}}$ was estimated from a ring around the bin position with mean radius  $ 0.6\hbox {$^\circ $ }$ and an area 7 times larger than the area of the on-region. The normalisation $\alpha $ was corrected for the decrease of the radial acceptance of the cameras towards the edge of the field of view. Figure 2 shows the significance sky-map of a $2.3\hbox{$^\circ$ }$ field of view around PSR B1259-63 for the February data. The excess at the pulsar position ( $N_{\rm\gamma}=N_{\rm on}-\alpha N_{\rm off}=227~\pm~27$, with a significance $S=9.1\sigma$) is consistent with the excess given in Table 1. The additional broad excess $\sim $ $ 0.6\hbox {$^\circ $ }$ north of the pulsar is the unidentified TeV source HESS J1303-631 discovered in the same field of view (Aharonian et al. 2005a). The resulting bias in the background estimation due to both sources was corrected in the analysis by excluding events from a circle with radius  $0.4\hbox{$^\circ$ }$ around each source from the background estimation.

In order to derive the position of the pulsar excess and to check for possible source extension, the data was reanalysed using hard cuts requiring a minimal camera image intensity of 200 photo-electrons which significantly improves the angular resolution and drastically reduces the cosmic ray background at the expense of a higher energy threshold of 750 GeV. The uncorrelated two dimensional excess distribution for the whole data set was fitted assuming a radially symmetric, Gaussian source intensity profile

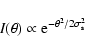
\begin{displaymath}I(\theta) \propto {\rm e}^{-\theta^2/2 \sigma_{\rm s}^2} \end{displaymath}

convolved with the point spread function of the detector. A possible bias from the second source within the field of view was corrected for by including an additional non-symmetric two dimensional Gaussian excess distribution in the fit, centred at the position of HESS J1303-631 and allowing the orientation and width to vary freely. The resulting pulsar excess position of $\rm RA~13^{\rm h}2^{\rm m}49\hbox{$.\!\!^{\rm s}$ }3 \pm 2\hbox{$.\!\!^{\rm s}$ }3_{\rm stat}$, $\rm Dec~-63\degr49\hbox{$^\prime$ }53\hbox{$^{\prime\prime}$ }\pm 17\hbox{$^{\prime\prime}$ }_{\rm stat}$ is consistent with the position of PSR B1259-63 ( $\Delta{\rm RA} = 9\hbox{$^{\prime\prime}$ }\pm 15\hbox{$^{\prime\prime}$ }_{\rm stat}$, $\Delta{\rm Dec} = 16\hbox{$^{\prime\prime}$ } \pm 17\hbox{$^{\prime\prime}$ }_{\rm stat}$) within statistical errors. The systematic uncertainty on the absolute pointing of the telescopes has been estimated in Gillessen (2003) to be $\sim $ $20\hbox{$^{\prime\prime}$ }$. A limit for the source extension $\sigma_{\rm s}$ was found to be < $33\hbox{$^{\prime\prime}$ }$ at $95\%$ confidence level which corresponds to 0.24 pc at an assumed distance of 1.5 kpc. Note that a possible source confusion with the variable hard X-ray source 1RXP J130159.6-635806 (Kaspi et al. 1995), located  $9\hbox{$^\prime$ }$ southeast from the pulsar, can be firmly excluded.
  \begin{figure} \par\includegraphics[width=8.3cm,clip]{2983fig2.eps} \end{figure} Figure 2: Significance sky-map centred on the position of PSR B1259-63 for the HESS February data. The excess $\sim $ $ 0.6\hbox {$^\circ $ }$ north of the pulsar is the newly discovered unidentified TeV source HESS J1303-631 (Aharonian et al. 2005a). The bins are correlated within a circle of radius $\theta_{\rm cut} = 0.02~\rm deg^2$. The background for each position in the field of view was estimated from a ring around this position correcting for the radial acceptance of the instrument within the field of view and background contamination from the two $\gamma $-ray sources.
Open with DEXTER

2.3 Energy spectra

The measured differential energy spectrum derived from all darkness periods with a significant detection of the source (February to May) is shown in Fig. 3. A power-law fit

 \begin{displaymath} F(E)={\rm d}N/{\rm d}E = F_0\left(\frac{E}{{\rm 1~TeV}}\right)^{-\Gamma} \end{displaymath} (1)

of this spectrum yields a photon index $\Gamma=2.7~\pm~0.2_{\rm stat}$and $F_0 = (1.3~\pm~0.1_{\rm stat})\times 10^{-12}~\rm cm^{-2}\rm ~s^{-1}~\rm TeV^{-1}$. The integral flux above the mean threshold energy is $F(E>380~\rm GeV) = (4.0\pm0.4_{\rm stat})\times 10^{-12}~\rm cm^{-2}\rm ~s^{-1}$, equivalent to $\sim $$4.9\%$ of the Crab Nebula flux (Aharonian et al. 2000) above this threshold.
  \begin{figure} \par\includegraphics[width=8.4cm,clip]{2983fig3.eps} \end{figure} Figure 3: Differential energy spectrum ${\rm d}N$/${\rm d}E$ of $\gamma $-rays from PSR B1259-63 using HESS 2004 data from the periods with significant detection of the pulsar (February-May). The solid line shows the power-law fit to the spectrum (see also Table 2).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.6cm,clip]{2983f4_1.eps}\vspace*{3mm}... ....eps}\vspace*{3mm} \includegraphics[width=7.6cm,clip]{2983f4_3.eps} \end{figure} Figure 4: Differential energy spectra of $\gamma $-rays from PSR B1259-63 for data of the periods February, March and April (from top to bottom). The straight line in each plot indicates the power-law fit to the particular spectrum for which the results are listed in Table 2. Note, that the photon index $\Gamma $ is constant within the statistical errors.
Open with DEXTER

For each darkness period for which the significance of the observed $\gamma $-ray excess exceeded $6\sigma$ (February, March, and April) a differential spectrum was derived (see Fig. 4) and the results of the corresponding power law fit according to Eq. (1) are listed in Table 2. Within statistical errors, there is no indication of time variability of the photon index. However, the changing flux normalisation F0 indicates source flux variability (see next section). Systematic errors were estimated to be $\delta \Gamma \approx 0.2$ and $\delta F/F\approx 30\%$, dominated by the precision of the energy calibration of the instrument and variations in the atmospheric extinction of the Cherenkov light.

2.4 Flux variability

The daily integral flux of $\gamma $-rays above the mean threshold of 380 GeV is shown in Fig. 5 (lower panel). Since the spectrum cannot be derived on a daily basis due to limited statistics, the integral flux $F(E>E_{\rm th}=380~\rm GeV)$ was obtained by integrating Eq. (1) assuming the spectral index of the time-averaged spectrum $\Gamma = 2.7$. The flux normalisation F0 was calculated using the measured excess of $\gamma $-rays $N_\gamma$ given by

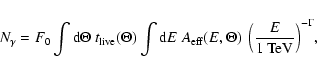
\begin{displaymath}N_\gamma = F_0 \int{{\rm d}\Theta~t_{\rm live}(\Theta)} \int{... ...eff}(E,\Theta)~\left( \frac{E}{{\rm 1~TeV}}\right)^{-\Gamma}}, \end{displaymath}

with the daily live time $t_{\rm live}(\Theta)$ as a function of the zenith angle $\Theta$, and the effective area $A_{\rm eff}(E,\Theta)$after selection cuts obtained from simulations. Note that this method does not depend on the energy reconstruction and so the complete sample of excess events can be used. An alternative method, using the energy reconstruction to calculate the flux based on the effective area for each event above the energy threshold $E_{\rm th}$ according to

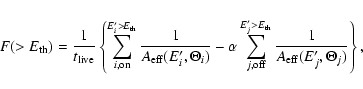
\begin{displaymath}F(>E_{\rm th}) = \frac{1}{t_{\rm live}} \left\{ \sum^{E^\prim... ...rm off} {\frac{1}{A_{\rm eff}(E^\prime_j,\Theta_j)}} \right\}, \end{displaymath}

with $E^\prime$ as the reconstructed energy and $\alpha $ as the background normalisation, yields consistent results but introduces a bigger statistical error since only events above the threshold are considered.

The daily light curve in Fig. 5 clearly indicates a variable flux. This can be quantified by a fit of a constant flux to the data yielding a $\chi ^2$ of 90.9 per 35 degrees of freedom corresponding to a $\chi ^2$ probability of $1.2\times 10^{-7}$.

Table 2: Parameters of the power law fit to the differential spectrum for the different darkness periods of HESS observations on PSR B1259-63. For the periods May and June 2004, no spectrum could be derived due to insufficient statistics. Shown are the photon index $\Gamma $ and the flux normalisation $F_{\rm0}$ (with statistical error only), the $\chi ^2$ per number of degrees of freedom $\chi ^2/{\rm ndf}$ and the $\chi ^2$ probability  $P_{\chi ^2}$ for the power law fit of the spectrum, and the corresponding mean threshold energy $E_{\rm th}$ (rounded to 10 GeV).


  \begin{figure} \par\includegraphics[width=17.2cm,clip]{2983fig5.eps} \end{figure} Figure 5: VHE $\gamma $-ray and radio light curves of PSR B1259-63 around its periastron passage (epoch $\tau =0$, dotted vertical line). Upper panel, open points: flux density of the transient unpulsed radio emission at 1.4 GHz (Johnston et al. 2005). The pulsed radio emission was eclipsed in the time interval between $\sim $$\tau -18$ days and $\sim $$\tau +15$ days, indicated by the two dashed vertical lines. Lower panel, full points: daily integral flux above 380 GeV as measured by HESS Note that the moonlight prohibits HESS observations for $\sim 10$ days between each darkness period.
Open with DEXTER

In order to investigate the flux trend in each darkness period, the individual light curves were fitted separately by a straight line and the significance for an increasing or decreasing flux is listed in Table 3. The low flux state after periastron is followed by a distinct rise beginning at $\tau\sim+15$ days and a slow decrease until $\tau\sim+75$ days where the observed excess is no longer significant.

Table 3: Light curve properties of the HESS 2004 data. The integrated flux F(> $380~{\rm GeV})$ was calculated assuming a photon index $\Gamma = 2.7$ (see text). For the daily integral flux light curve of each period the following properties are given: the $\chi ^2$/${\rm ndf}$for a fit to a constant flux, and the slope a and significance $S_a = \left \vert a\right \vert$/$\sigma _a$ of an increasing or declining flux after fitting a straight line $F(t_{\rm MJD})=a t_{\rm MJD} + F(0)$ ( $t_{\rm MJD}$ is the Modified Julian Date), together with the corresponding $\chi ^2_{\rm line}/{\rm ndf}$.

The upper panel of Fig. 5 shows the light curve of the transient unpulsed radio emission obtained from 2004 observations of PSR B1259-63 (Johnston et al. 2005) for the same time range as for the TeV band. There is some correlation visible between the radio and the TeV bands, especially a low flux state around periastron and a high flux state at $\sim $$\tau+20$ days. The pulsed radio emission from the pulsar was eclipsed during the periastron passage (Johnston et al. 1992a), interpreted as due to scattering in the dense disk material and allowing the dates of the disk crossings to be estimated, in particular $\sim $$\tau-16$ days and $\sim $$\tau+13$ days for the 2004 periastron passage (Johnston et al. 2005). The observed dates of enhanced VHE $\gamma $-ray flux roughly correspond to orbital phases a few days after the assumed disk crossings. However, the coverage of the considered time interval by HESS observations is limited and does not allow firm conclusions about VHE $\gamma $-ray flux maxima, especially pre-periastron.

3 Discussion and conclusions

The detection of VHE $\gamma $-rays from PSR B1259-63 gives the first unambiguous and model-independent evidence of particle acceleration to multi-TeV energies in this unique binary system. The (most likely) synchrotron origin of X-rays (e.g. Tavani & Arons 1997) also indicates the presence of ultra-relativistic particles, in the form of electrons, but other possible explanations of the X-radiation, e.g. due to the bulk motion Comptonisation of the stellar photons by the pulsar wind with a moderate Lorentz factor of 10-100 (Chernyakova & Illarionov 1999), cannot be firmly excluded.

In contrast to the X-ray emission, the extension of the $\gamma $-ray spectrum to several TeV necessarily implies that the parent particles, electrons and/or protons, are accelerated to at least 10 TeV. The point-like feature of the detected signal constrains the extension of the $\gamma $-ray production region to $R \leq 0.24~\rm pc = 7.4~\times~10^{17}~cm$. The information contained in the time variability of the signal on timescales of days provides a hundred times more stringent upper limit on the size of the $\gamma $-ray source of about $10^{16}~\rm cm$.

The most likely scenario of particle acceleration and radiation in this system is a variation of the standard model of Pulsar Driven Nebulae (see e.g. Rees & Gunn 1974; Kennel & Coroniti 1984) which postulates that the deceleration of the ultra-relativistic pulsar wind (with a bulk motion Lorentz factor of 106-107) by the pressure forces of the external medium enforces a termination shock. In this context electrons are accelerated to multi-TeV energies. These electrons radiate in the magnetic and photon fields in which they propagate and thus produce synchrotron and Inverse-Compton nebulae with a typical size exceeding 0.1 pc, commonly called plerions.

The mean energy flux contained in the VHE $\gamma $-ray emission derived from the time-averaged energy spectrum is $EF_E \approx 3 \times 10^{-12}\rm ~erg~cm^{-2}~s^{-1}$ which represents a $\gamma $-ray luminosity of $L_\gamma \approx 8 \times 10^{32}\rm ~erg~s^{-1}$ for an assumed distance of the binary system of 1.5 kpc. This corresponds to $\approx$$0.1\%$ of the pulsar spin-down luminosity. Interestingly, this value matches the typical ratio between the pulsed and unpulsed component of X-ray radiation from isolated pulsars with associated pulsar windnebulae and their spin-down luminosity (see e.g. Cheng et al. 2004), supporting the suggestion that the energy for the observed $\gamma $-rays is provided by the pulsar.

However, in the case of PSR B1259-63 both the spatial and temporal scales are expected to be rather different from those in plerions around isolated pulsars. Also, dynamical flow effects can play a different role since the pulsar moves through the stellar wind and the photon field of the massive companion star. Due to the high pressure of the stellar wind, the pulsar wind terminates very close to the pulsar and thus the electrons are accelerated well within the binary system. Moreover, because of severe adiabatic and radiative losses, the TeV electrons have a very short lifetime. As a result, the radiation is emitted in a rather compact region not far from the acceleration site, and for any given time the emission originates from a quite short sector of the pulsar trajectory.

In the following we summarise the physical processes expected to be at work, and put our observational results into this perspective.

3.1 Characteristic cooling times

The synchrotron loss time

 \begin{displaymath}t_{\rm sy}=6 \pi \frac{m_{\rm e}^2 c^4}{\sigma_{\rm T} c \eps... ...B^2} \simeq 400~\epsilon_{\rm TeV}^{-1} B_{\rm G}^{-2}~\rm s~, \end{displaymath} (2)

of an electron with energy $\epsilon$ depends on the local magnetic field strength B (where BG = B / 1 G) which is not known a priori. We shall estimate B below by combining the INTEGRAL X-ray data and our HESS TeV $\gamma $-ray data. In contrast, we can estimate the inverse Compton cooling rate of electrons with very good accuracy at any given time, i.e. at any location of the pulsar in its orbit (Kirk et al. 1999; Tavani & Arons 1997).

Indeed, the inverse Compton losses are dominated by the scattering of electrons on the light of the companion star with luminosity $L_{\rm star}=3.3 \times 10^{37}~\rm erg/s$ and effective blackbody temperature $T_{\rm eff}=2.3 \times 10^4~\rm K$. At any distance R, the black-body radiation decreases by a factor of $(R/R_\star)^{-2}$, where $R_\star=4 \times 10^{11}~\rm cm$ is the radius of the companion star. Thus at the distance of the pulsar to the star $R_{13}=R/10^{13}~\rm cm$, the energy density of the radiation is

 \begin{displaymath}w_{\rm r}= \frac{L_{\rm star}}{4 \pi R^2 c} \simeq 0.87 R_{13}^{-2}~\rm erg/cm^3 , \end{displaymath} (3)

and correspondingly the electron cooling time is determined in the deep relativistic Klein-Nishina regime which applies here for TeV energies, given the high energies of the seed photons. For a Planckian seed photon spectrum, and using the formalism of Blumenthal & Gould (1970), one obtains

 \begin{displaymath}t_{\rm KN}=3.2 \times 10^3 \frac{\epsilon_{\rm TeV} R_{13}^2}{\ln ~ (30.6 \epsilon_{\rm TeV}) -1.4}~\rm s . \end{displaymath} (4)

For PSR B1259-63, with its environment of a strong stellar wind and a strong radiative flow from the companion, we must in addition consider the adiabatic losses of the accelerated pulsar particles. This has already been noted by Tavani & Arons (1997). Indeed, the plasma flow beyond the pulsar wind termination shock differs strongly from the spherically symmetric configuration of an isolated pulsar in a static pressure environment. Rather than being decelerated in a spherically symmetric fashion while compressing the post-shock magnetic field, the actual flow will stagnate at the sub-stellar point at a distance $l\sim 10^{12}$ cm and expand relativistically into the downstream direction, which roughly points away from the Be star. The surface of separation between the interior flow of the pulsar particles and the exterior stellar wind flow is indicated as "Wind interface'' in Fig. 6.


  \begin{figure} \par\includegraphics[width=8.2cm,clip]{2983fig6.eps} \end{figure} Figure 6: Sketch of the orbit of PSR B1259-63 with respect to the line of sight (adapted from Johnston et al. 1999). The pulsar approaches the equatorial disk prior to periastron while it is "behind'' the companion star and turns towards the observer before it crosses the disk after periastron for the second time. Note that the orientation of the disk with respect to the orbital plane is not precisely known. The colour gradient bars along the orbit indicate the periods of HESS observations and show the integral VHE $\gamma $-ray flux using a smoothed light curve based on the data points from Fig. 5.
Open with DEXTER

The expansion of the relativistic, shocked pulsar wind gas will proceed with a flow velocity of magnitude $\vert\underline{u}\vert$, roughly equal to the relativistic magnetosonic speed $\varepsilon v_{\rm ms,\perp}$, where $v_{\rm ms,\perp}\simeq c\!\sqrt{2/3}$, over a distance $\Delta l$, where $\Delta l$ is a few $\times l$. The factor  $\varepsilon$ ranges between $\sqrt{2}/2$ and 1, if the direction of the postshock MHD flow ranges between a perpendicular and a parallel orientation with respect to the magnetic field direction, respectively. Assuming the pitch angle scattering mean free path of the accelerated pulsar wind particles to be small compared to l, their adiabatic loss time is then given by

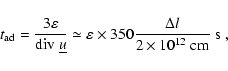\begin{displaymath}t_{\rm ad} = \frac{3 \varepsilon}{{\rm div}~\underline{u}} \s... ...n \times 350 \frac{\Delta l}{2\times 10^{12}~{\rm cm}}~\rm s~, \end{displaymath} (5)

with $0.71 < \varepsilon < 1$, depending on the details of the post-shock MHD flow.

In this picture the adiabatic losses proceed about as fast as the synchrotron losses if $B \approx 1$ G (compare with Eq. (2)) - while both are faster than the inverse Compton losses - and the energy spectrum of the radiating electrons is close to their source spectrum produced during acceleration at the termination shock. We shall consider neither electron Bremsstrahlung nor $\gamma $-ray production in interactions of relativistic protons with the ambient gas via decay of secondary $\pi^0$-mesons (see e.g. Kawachi et al. 2004) here, since the accelerated pulsar wind particles are hydromagnetically constrained to the magnetic field lines of the pulsar outflow and will hardly interact individually with the stellar wind particles, except in a thin boundary layer at the Wind interface far downstream.

The missing quantity in our cooling considerations is the value of B. We shall use the contemporaneous INTEGRAL results and our HESS fluxes to estimate it as follows: Since there is little doubt that the detected TeV $\gamma $-rays are produced in the Klein-Nishina regime, we may conclude that they are emitted by electrons of the same energy, $\epsilon_{\rm e} \approx E_\gamma$. This allows to set up a direct relation between $\gamma $-rays and X-rays produced by the same electrons,

 \begin{displaymath} E_{\rm X} > 20 B_{\rm G} E_{\rm TeV}^2~\rm keV . \end{displaymath} (6)

The Compton losses with $E_{\rm TeV}$ take place in a spatial region that is larger than that of synchrotron losses, and therefore adiabatic losses have already occurred there.

An experimental estimate of B is possible by comparing the energy fluxes of the detected X- and $\gamma $-rays. The post-periastron data obtained in March by RXTE and INTEGRAL in the X-ray band from 1 keV to 100 keV (see Shaw et al. 2004) show a relatively flat spectral energy distribution $\nu F_\nu \sim E^2 {\rm d}N$/${\rm d}E$ at the level of $3\times 10^{-11}~\rm erg/c m^2~s$. The VHE $\gamma $-ray flux for the same period was $\approx$ $ 2~ \times~ 10^{-12}~\rm erg/s$. This implies that in the TeV energy regime the synchrotron losses of electrons proceed an order of magnitude faster than the inverse Compton losses. Therefore, from the comparison of the synchrotron cooling time, given by Eq. (2), with the Klein-Nishina cooling time given by Eq. (4), and taking into account that two weeks after the periastron the separation between the pulsar and the companion star was approximately $1.5 \times 10^{13}~\rm cm$, we find

 \begin{displaymath}B \approx 1 E_{\rm TeV}^{-1}~\rm G. \end{displaymath} (7)

Our experimentally determined fields of the order of 1 G agree rather well with the theoretical estimate of the field derived from the MHD treatment of the pulsar wind (Tavani & Arons 1997; Ball et al. 1999), and the value deduced from the observed unpulsed radio emission near periastron (Connors et al. 2002).

   
3.2 Spectral and temporal characteristics of the TeV radiation

Let us assume that the accelerated electrons enter the $\gamma $-ray production region with a rate $Q~(\epsilon) \propto \epsilon^{-\alpha_0}$. As a consequence, in the case of dominant synchrotron or inverse Compton losses in the Thompson regime, a steeper electron spectrum is established in the $\gamma $-ray production region with power-law index $\alpha=\alpha_0+1$, while dominating adiabatic (or Bremsstrahlung losses) will not change the initial electron spectrum, i.e. $\alpha=\alpha_0$, both for $\alpha_0>1$.

Let us conversely assume that the radiating electrons have a power law distribution ${\rm d} N/\rm d \epsilon \propto \epsilon^{-\alpha}$. Then the inverse Compton scattering in the Klein-Nishina regime leads to a $\gamma $-ray spectrum (Blumenthal & Gould 1970)

 \begin{displaymath} \frac{{\rm d} N}{{\rm d}E} \propto E^{-(\alpha+1)} \left(\ln\frac{k_{\rm B}T~E}{m_{\rm e}^2 c^4} + C\right). \end{displaymath} (8)

Using the HESS results, the photon index of the radiating electrons can therefore be estimated from the observed $\gamma $-ray spectrum ${\rm d} N/{\rm d}E \propto E^{-\Gamma_\gamma}$ with $\Gamma_{\gamma} = 2.7 \pm 0.2_{\rm stat}$ by equating it with the expected Klein-Nishina spectrum of Eq. (8). A more detailed numerical evaluation of the IC $\gamma $-ray spectrum shows that in our energy range the average photon spectral index can be approximated as $\Gamma_\gamma \approx \alpha+0.5$. Therefore we find $\alpha \approx 2.2$. In the scenario in which adiabatic losses dominate, this is, within errors, compatible with an acceleration process giving $\alpha_0=2$. If radiation losses dominate, this requires an injection spectrum significantly harder than $\alpha_0=2$.


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{2983fig7.eps} \end{figure} Figure 7: Spectral energy distribution from Kirk et al. (1999) assuming the electron cooling to be dominated by radiative (dashed lines) or adiabatic losses (solid lines) for a magnetic field strength of 0.32 G at an orbital phase 12 days prior to periastron. The spectra were calculated by Kirk et al. (1999) for different electron injection spectra with the power law indices $\alpha _0=1.4$ and $\alpha _0=2.4$, respectively. For illustration, the predicted spectrum for adiabatic losses for B=3.2 G is also shown (dotted line). Data points represent the measured energy flux from HESS observations in February 2004.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=17cm,clip]{2983fig8.eps} \end{figure} Figure 8: Comparison of the light curves predicted by different models of VHE $\gamma $-ray emission with HESS data. The solid line was taken from Kawachi et al. (2004), for a misaligned disk geometry, model (iii) in Fig. 7, and scaled by a factor of 0.3. The dashed and dotted lines represents the curves given in Kirk et al. (1999), for dominant adiabatic and radiative energy losses, respectively. The full points represent the corresponding light curve obtained from the HESS data using a bin width of 2 days.
Open with DEXTER

The relevant photon spectral index range $1.6 < \Gamma_X < 1.8$ in the $1 \leq E_X \leq 10$ keV energy range from the 1994 ASCA observations (Hirayama et al. 1996), although not coeval, would also indicate a rather hard spectrum of the radiating electrons $2.2 \leq \alpha \leq 2.6$ which would again be difficult to reconcile with dominant synchrotron cooling. This 1994 synchrotron photon spectral index is consistent with a preliminary spectral fit with $\Gamma_X = 1.82 \pm 0.34$ derived from the coeval INTEGRAL observations (Shaw 2004). In this paper we shall ultimately rely on the HESS spectrum.

Within the scheme of dominant adiabatic cooling, the strong variability of the VHE $\gamma $-ray emission might be explainable by a varying spatial confinement of the accelerated pulsar wind particles by the kinetic and thermal pressure of the stellar mass outflow. In Fig. 6 the variations of the measured VHE $\gamma $-ray flux are illustrated within the context of the orbital parameters and environment of the binary system with respect to the line of sight. The enhanced mass outflow in the equatorial disk will result in a more compact emission region - and therefore weaker adiabatic cooling - during the pulsar disk passages compared to the other regions of the orbit, in particular the periastron phase, where the expected stronger adiabatic cooling could lead to a minimum of the $\gamma $-ray flux. A second flow aspect would be a Doppler modulation due to the relativistic bulk flow velocity away from the stagnation point of the shocked pulsar wind. Considering Fig. 6, this could again lead to a flux minimum during periastron. However, a detailed consideration of this overall physical picture is beyond the scope of the present paper.

A minimum in the X-ray flux, observed for previous periastron passages, has been interpreted as being due to increased IC losses (Tavani & Arons 1997). However, HESS measurements indicate a minimum in the IC flux around periastron, which would rule out such an interpretation for this periastron passage. Unfortunately, due to the full moon and bad weather conditions we were not able to take data during the periastron passage of the pulsar.

The predicted pre-periastron spectrum from Kirk et al. (1999) is compared to the corresponding HESS data in Fig. 7. The model curves, taken from Kirk et al. (1999) (Figs. 2, 6), were computed for the two scenarios of dominant radiative losses and dominant adiabatic losses, and matched the archival X-ray data for electron injection spectra with $\alpha _0=1.4$ and $\alpha _0=2.4$, respectively. They agree well with the TeV data, assuming a magnetic field strength of B=0.32 G supporting the estimate of the order of 1 G obtained from the HESS data. Despite the spectral agreement, the models fail to describe the TeV light curve as can be seen in Fig. 8 (dashed and dotted lines). In particular, neither the minimum around nor the high flux states before and after periastron are described by the model. This is perhaps not surprising, because the model assumed that the ratio between the energy densities of the magnetic field and the photon field does not change throughout the full orbit, and that the effects related to the pulsar passage through the stellar disk can be neglected.

Interestingly, the observed light curve seems to be qualitatively similar to the prediction made by the model of Kawachi et al. (2004) which is also shown in Fig. 8 (solid line). In this model, hadronic interactions and $\pi^0$production in the misaligned stellar disk plays a dominant role in the $\gamma $-ray production mechanism. However, present data do not allow safe conclusions concerning the interpretation of the TeV light curve. Studies of the most interesting part of the pulsar orbit have to be postponed until multi-wavelength observations during periastron become possible.

In summary, the detection of VHE $\gamma $-ray emission from the binary pulsar PSR B1259-63 by HESS provides the first model-independent evidence of particle acceleration in this object. The results clearly demonstrate the power of $\gamma $-ray observations for the study of the properties and the nature of high energy processes in this unique cosmic accelerator. Further observations at VHE $\gamma $-ray energies are necessary to derive spectra on a daily basis also during periastron passage.

Acknowledgements

The support of the Namibian authorities and of the University of Namibia in facilitating the construction and operation of HESS is gratefully acknowledged, as is the support by the German Ministry for Education and Research (BMBF), the Max Planck Society, the French Ministry for Research, the CNRS-IN2P3 and the Astroparticle Interdisciplinary Programme of the CNRS, the UK Particle Physics and Astronomy Research Council (PPARC), the IPNP of the Charles University, the South African Departmentof Science and Technology and National Research Foundation, and by the University of Namibia. We appreciate the excellent work of the technical support staff in Berlin, Durham, Hamburg, Heidelberg, Palaiseau, Paris, Saclay, and in Namibia in the construction and operation of the equipment. We also thank S. Shaw for informations on the photon spectral index from the INTEGRAL X-ray observations.

References

 
Copyright ESO 2005