A&A 439, 309-315 (2005)
DOI: 10.1051/0004-6361:20052804

Abundances from disentangled component spectra: the eclipsing binary V578 Mon[*]

K. Pavlovski1 - H. Hensberge2


1 - Department of Physics, University of Zagreb, Bijenicka 32, 10 000 Zagreb, Croatia
2 - Royal Observatory of Belgium, Ringlaan 3, 1180 Brussel, Belgium

Received 2 February 2005 / Accepted 1 April 2005

Abstract
Chemical abundances of the early-B type components of the binary V578 Mon are derived from disentangled component spectra. This is a pilot study showing that, even with moderately high line-broadening, metal abundances can be derived from disentangled spectra with a precision of 0.1 dex, differential to sharp-lined single stars of the same spectral type. This binary is well-suited to such an assessment because of its youth as a member of the Rosette Nebula cluster NGC 2244, strengthening the expectation of an unevolved ZAMS chemical composition. The method is useful for studying rotationally driven mixing in main-sequence stars, since fundamental stellar parameters are known with higher accuracy in (eclipsing) binaries. This paper also evaluates of the bias that might be present in disentangled spectra.

Key words: techniques: spectroscopic - stars: abundances - stars: binaries: spectroscopic - stars: individual: V578 Mon (HDE 259 135) - open clusters and associations: individual: NGC 2244

  
1 Introduction

Besides the time-evolution of global parameters like effective temperature, luminosity, etc., stellar evolutionary models also predict changes in chemical composition. Recent theoretical computations of stellar evolutionary tracks for rotating stars suggest that the chemical composition of surface layers already changes when the star evolves on the main sequence (Meynet & Maeder 2000; Heger & Langer 2000). Observational support has come in the last decade from helium overabundances of stars in late stages of hydrogen-core burning (cf. Maeder & Meynet 2000, and references therein).

More controversial than these were results from components in close binaries. The first systematic study of the chemical composition of high-mass stars in close binaries was undertaken by Leushin (1984). He noticed substantial helium enrichment for components still on the main-sequence (hereafter: MS) from analysis of two dozen bright components of binaries. His studies of carbon (Leushin 1998a) and nitrogen (Leushin 1998b) disclosed carbon underabundances and nitrogen overabundances, as expected in the CNO bi-cycle. These studies had to deal with rather low-resolution, noisy photographic spectra, and the dilution effect of the less-luminous secondary component. His results and those of Lyubimkov and co-workers (cf. Lyubimkov 1998, and references therein) were contrary to the traditional view that mixing of the CNO bi-cycle products does not occur before hydrogen-shell burning. Lyubimkov (1998) claimed a dependence of helium enrichment on the fraction of the stellar MS life-time. A recent review of abundance determinations using components of close binaries is given by Pavlovski (2004).

Chemical analysis of binary components with precisely known fundamental stellar parameters allows a powerful comparison with theory. However, the precision of empirical abundances from double-lined binaries is hampered by increased line blending and by dilution of the spectral lines in the composite spectra. Spectral disentangling and tomographic techniques (Bagnuolo & Gies 1991; Simon & Sturm 1994; Hadrava 1995; cf. Gies 2004; and Hadrava 2004, for recent reviews) overcome these difficulties by separating the individual component spectra using a time-series of spectra taken over the orbital cycle.

In this paper, the first abundance analysis of disentangled B-type spectra is presented. It is based on the disentangled spectra obtained by Hensberge et al. (2000, hereafter Paper  I) when deriving the orbit and the fundamental stellar parameters of the eclipsing, detached, double-lined binary V578 Mon (HDE 259 135; NGC 2244 #J8, Johnson 1962; NGC 2244 #200, Ogura & Ishida 1981) in the stellar cluster NGC 2244, which is embedded in the Rosette Nebula. V578 Mon consists of very young ( $2.3\pm 0.2 \times 10^6$ yr) high mass stars, $M_{\rm A} = 14.54\pm0.08$ $M_{\odot}$ and $M_{\rm B} = 10.29\pm0.06$ $M_{\odot}$. Hence, no abundance anomalies were expected. Moreover, the stars rotate moderately fast ($\simeq$100 km s-1). V578 Mon is thus well-suited for evaluate whether an abundance analysis of disentangled spectra will be feasible for a large amount of early-B stars in close binaries. Following the work of Vrancken et al. (1997, hereafter Paper  II), the analysis was performed differential to a sharp-lined B1V star in the same cluster. First, the analysis method is outlined and the dominant error sources discussed (Sect. 2). Then, the spectral differences between the components are described and their disentangled spectra are compared to single star spectra (Sect. 3). The quantitative abundance analysis is presented in Sect. 4 and results summarized in Sect. 5.

  
2 Method

While applying spectral disentangling with the purpose of deriving orbits is common practice, analysis of the component spectra is often not included. No metal abundance studies have been made yet of disentangled spectra of OB stars, presumably because the progression of systematic errors to the disentangled spectra and the definition of their continua was not sufficiently understood.

V578 Mon A and V578 Mon B rotate synchronously with the orbital revolution and have projected rotational velocities of 117 km s-1 and 94 km s-1. A robust analysis technique is then to determine abundances differential to a template spectrum obtained by blurring the spectrum of a sharp-lined star of similar spectral type, as shown in Paper  II. The detailed mathematics for deriving the differential abundances from the comparison of lines and line blends in observed and model spectra is given in the appendix of that paper. It was shown that differential abundances derived in such a way for single stars rotating at more than 200 km s-1 can have an accuracy better than 0.1 dex if the stellar atmospheres are sufficiently similar.

An important ingredient in the analysis was the care taken to eliminate systematic errors in the normalisation of the spectra with respect to the template. Figure 6 in Paper  II shows that flux normalisation errors with an amplitude of 1% and low frequency in wavelengths exist, even when all spectra were consistently normalised using the same continuum windows. While such errors are small at first glance, they are not negligible compared with the depth of the relevant spectral lines in rotating early-B stars. Systematic normalisation errors were estimated and eliminated by applying the normalisation procedure to the (not yet normalised) artificially broadened sharp-lined star and comparing that with the spectrum obtained by broadening the normalised sharp-lined spectrum. Figure 7 in Paper  II shows that the spectra of fast rotating stars of the same spectral type are then within the noise identical to the broadened template taking the effects of a small difference in temperature into account.

  
2.1 Data

For analysis of V578 Mon, we use the same template star as in Paper  II, NGC 2244 #201 (B1V, $v \sin i = 22$ km s-1). It has the same spectral type as V578 Mon B and is less than 1 $.\mkern-4mu^\prime$5 away from V578 Mon in the SE part of the cavity in the Rosette Nebula. A hotter sharp-lined member, NGC 2244 #180 (O9.5V, $v \sin i = 24$ km s-1), is still a better match to V578 Mon A. #180 has recently been analysed in detail by Daflon et al. (2004b), who derive $T_{\rm eff}$  = 31 500 K and $\log g$  = 4.2 from high-dispersion spectra taken with the FEROS echelle spectrograph at the 1.5 m ESO telescope at La Silla. From Walraven photometry, Verschueren (1991) estimated $T_{\rm eff}$  = 32 060 K and $\log g$  = 4.25. Hence, V578 Mon A ( $T_{\rm eff}$  = 30 000 K) is well bracketed between the two comparison stars. The template spectra were obtained with CASPEC at the 3.6 m ESO telescope, as was the V578 Mon spectra, and reduced in the same way. Details of observations and data reduction are mentioned in Paper  I, Paper  II, and references therein. The impact of data reduction errors on disentangled spectra is discussed in Hensberge (2004).

  
2.2 Error progression

The observed composite spectra reflect the characteristics of two different stars, and the lines, roughly twice as numerous and twice less deep, are Doppler-shifted according to the orbital movement. Continuum windows are thus scarcer than in single-star spectra and are phase-dependent. Although this did not prevent normalising all the composite spectra in a consistent way (Sect. 4.1 in Paper  I), application of the method used in Paper  II, to eliminate differential normalisation errors between the spectra of the binary and the template is not evident. The fact that both the spectra of V578 Mon are double-lined and spectral disentangling was applied is a source of systematic normalisation errors which need consideration.

The disentangling process in general determines the contribution  $s_{\rm A,B} $ of each component to the observed spectra up to additive constants $ c_{\rm A} = - c_{\rm B}$. The latter indeterminacy follows from the fact that a pure continuum cannot be uniquely disentangled, as it contains no time-dependent Doppler information. The observed composite spectra $O(\lambda; \Delta\lambda_{\rm A}, \Delta\lambda_{\rm B})$ were recovered as

\begin{displaymath}O(\lambda; \Delta\lambda_{\rm A}, \Delta\lambda_{\rm B}) = s... ...}) + s_{\rm B}(\lambda; \Delta\lambda_{\rm B}) + c_{\rm obs} \end{displaymath} (1)

where the average values of $s_{\rm A}$ and $s_{\rm B}$ are zero, $c_{\rm obs}$ is the average value of  $O(\lambda)$ over the considered wavelength range, $1 - c_{\rm obs}$ the line-blocking coefficient  $b_{\rm obs}$ over the considered wavelength range, and  $\Delta\lambda_{\rm A,B}$ are the time-dependent orbital Doppler shifts. While this disentangling gives the shape of the spectral features in  $s_{\rm A}(\lambda)$ and  $s_{\rm B}(\lambda)$, the sum of  $s_{\rm A}(\lambda) + 0.5 c_{\rm obs} + c_{\rm A}$ and  $s_{\rm B}(\lambda) + 0.5 c_{\rm obs} - c_{\rm A}$ reproduces the composite spectra irrespective of the value of $c_{\rm A}$.

Only when composite spectra are available in which the components contribute with time-dependent light fractions  $\ell_{\rm A,B} $, i.e.

$\displaystyle O(\lambda; \Delta\lambda_{\rm A}, \Delta\lambda_{\rm B}, t) = \el... ...ta\lambda_{\rm A}) + \ell_{\rm B}(t) S_{\rm B}(\lambda; \Delta\lambda_{\rm B}),$     (2)

the disentangling process can uniquely recover the component spectra. Here  $S_{\rm A,B} $ are the component spectra normalised to their intrinsic continuum, and $\ell(t) $ are relative light fractions in the continuum (with a slow dependence on wavelength), such that  $\ell_{\rm A}(t) + \ell_{\rm B}(t) = 1 $. As an example, a spectrum in total eclipse straightforwardly reveals one of the component spectra. But any factor that makes the depth of the spectral features of one of the components substantially time-variable in the composite spectra suffices to remove the indeterminacy discussed above. In that case, the $\ell(t) $ are treated either as free parameters in the disentangling process, or specified in the input when information from light curves is considered more robust than adding free parameters. The latter was applied for the eclipsing binary V578 Mon.

For time-independent $ \ell $, the zero-points and scaling of the  $S_{\rm A,B} $ are not determined uniquely. Ilijic et al. (2004) show how the zero-points of the normalised, intrinsic component spectra are coupled by the observed line-blocking in the composite spectra. In the notation introduced here, this coupling may be expressed as

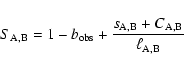\begin{displaymath}S_{\rm A,B} = 1 - b_{\rm obs} + \frac{s_{\rm A,B} + C_{\rm A,B}}{\ell_{\rm A,B}} \end{displaymath} (3)

with

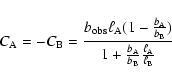\begin{displaymath}C_{\rm A} = - C_{\rm B} = { {b_{\rm obs} \ell_{\rm A} ( 1 -... ... {b_{\rm A}}{ b_{\rm B}} {\ell_{\rm A} \over \ell_{\rm B}}} }} \end{displaymath} (4)

where $ b_{\rm A} $ and $ b_{\rm B} $ are the line-blocking coefficients in the intrinsic component spectra. Without additional astrophysical constraints, they are only coupled by the requirement to reproduce the observed line-blocking,

\begin{displaymath}\ell_{\rm A} b_{\rm A} + \ell_{\rm B} b_{\rm B} = b_{\rm obs}, \end{displaymath} (5)

such that one of them (or e.g. their ratio) can be chosen freely in the case of time-independent light fractions. Astrophysical constraints may apply in some cases. An evident condition is that the flux in the deepest absorption lines should be non-negative. This constraint is useful for late spectral type components (see e.g. Griffin 2002), where e.g. the core of the Ca  II K line is very deep, quite independently of temperature, but not in our specific case.

The key point in our discussion here is that the $S_{\rm A,B} $ are obtained through a linear transformation of the $s_{\rm A,B} $ that involves an additive as much as a multiplicative operation. The latter amplifies random and systematic errors by a factor inversely proportional to  $\ell_{\rm A,B} $, i.e. a factor 1.45 for V578 Mon A and 3.2 for V578 Mon B. This amplification allows us to recognize low-frequency systematic errors best in the normalised spectra of the fainter component. For random errors, this amplification is counteracted by the use of several observed spectra. With 12 input spectra with a typical S/N-ratio of 125-250 in the 4000-4700 Å wavelength region, the S/N-ratio in the normalised component spectra is about 360 for V578 Mon A and 160 for V578 Mon B.

The difference in the additive terms reflects the difference in the line-blocking for the two components, so that from the viewpoint of an abundance analysis, an error in these coupled additive terms would bias the abundances of one component in the opposite direction from the other. Additive terms are not a dominant error source, because the very similar line-blocking in the spectra of the components of V578 Mon allows us to determine $\ell_{\rm A,B} $ from photometry. Only minor corrections apply to derive the light ratio in the continuum.

Turning toward the effect of small phase-dependent normalisation errors in the composite spectra, we note that they may transform after Fourier space disentangling into undulations in the continuum of the disentangled spectra (Ilijic 2004). The disentangled V578 Mon B spectrum is 2.2 times more sensitive to these than the V578 Mon A spectrum. Inspection of the component spectra showed a posteriori marginal evidence for low frequency errors, at a level of 1%, in the continua of the composite spectra compared with the continuum definition of the template star #201. We eliminated these by straightening each disentangled region in  $S_{\rm A,B} $ by a low-amplitude sinusoidal function, properly scaled and phased for $ S_{\rm B}$ relative to $ S_{\rm A} $, such that the predicted composite spectrum is not affected. This procedure is subjective. Independent trials suggest that spurious low-frequency patterns have been removed up to the level of 1% in the intrinsic V578 Mon B spectrum and better in regions with weaker metal lines.

Finally, the presence of an unrecognised third component in the composite spectra, be it of astrophysical origin (another star, or e.g. diffuse interstellar bands or telluric lines) or of instrumental origin (due to detector blemishes), may lead to complex disturbances. We removed the interstellar CH $\lambda$4233 line from the observed spectra before disentangling and did not disentangle the spectra around the diffuse interstellar bands (DIBs) at $\lambda$4430 and $\lambda$4505. In the $\lambda$4565-4610 region, a broad absorption feature centered at $\lambda$4580 with a central depth of 1.2% in the observed spectra may be present; it "grows'' in the intrinsic V578 Mon B spectrum to almost 4%, which makes it easy recognisable. The feature discussed here appears too far off in wavelength to attribute it to the 27.6 Å wide (fwhm) DIB at $\lambda$4594 (Jenniskens & Désert 1994; Tuairisg et al. 2000). We do not exclude that such a shallow feature is the result of a non-linear reacting detector column crossing the extraction slit of the echelle order. Since this "blemish'' affects the region of the Si  III triplet at  $\lambda\lambda$4553, 4568, 4575 Å and the O  II line at  $\lambda\lambda$4590, 4596 Å, this feature was removed from the observed spectra requiring that no spurious broad feature should appear in the disentangled spectra (Fig. 1). Re-defining the continuum on the observed spectra is more consistent than the alternative of locally defining a pseudo-continuum for the equivalent width measurements on the affected Si  III and O  II lines in the biased component spectra (shown in Fig. 1, down-shifted spectrum A and B). It preserves the coupling between the corrections in the two component spectra in a natural way. Figure 1 suggests that the remaining bias in the continuum is an order of magnitude smaller than in the original component spectra.


   \begin{figure} \par\includegraphics[width=8.8cm,clip]{2804fig1.ps} \end{figure} Figure 1: Extract of the disentangled component spectra around a blemish in the input spectra. The original result is shifted down by 0.02 relative to the one obtained from improved input spectra. The spectra of V578 Mon B are shifted down 0.09 relative to V578 Mon A.
Open with DEXTER


   \begin{figure} \includegraphics[width=8.8cm,clip]{2804fig2.ps} \end{figure} Figure 2: Six spectral regions containing temperature-dependent lines and line blends. Each panel shows, from top to bottom: the sharp-lined O9.5 #180 and an artificially blurred version mimicking the rotational broadening in V578 Mon A; the spectra of V578 Mon A and V578 Mon B; and the sharp-lined B1V #201 and an artificially blurred version mimicking the rotational broadening in V578 Mon B. The most important absorbers are identified. The applied vertical shift to the spectra is indicated by dashed lines representing the continuum levels.
Open with DEXTER

  
3 Component spectra

In order to evaluate to which level the intrinsic component spectra can be interpreted, a detailed comparison was made with the sharp-lined stars #201 and #180. We compared blended features whose shape changes with temperature as a consequence of the behaviour of its constituents in the B1V-O9.5V spectral range. Six examples in Fig. 2 illustrate that the disentangling process successfully reproduces the temperature-dependent morphology of the broad line blends:

-
$\lambda$4169 is a blend of He  I $\lambda$4169.0 and O  II $\lambda$4169.28, whose effective wavelength shifts to the blue with higher temperature. Nearby, the C  III line at $\lambda$4162.86 and the line at $\lambda$4164.8 form a blend whose morphology depends highly on temperature.

-
$\lambda$4186 is a blend of O  II $\lambda$4185.46 and C  III $\lambda$4186.90 with the oxygen line weakening with increasing temperature and the carbon line strengthening.

-
$\lambda$4641 is a blend of O  II lines, N  II, and N  III, with N  III $\lambda$4640.64 filling in the central dip in the blend at higher temperature, and N  II $\lambda$4643.09 extending the blend to longer wavelengths at lower temperature.

-
the ratio of the strength of Si  IV $\lambda$4116.10 and He  I $\lambda$4120.9 (the latter blended with several O  II lines) is very sensitive to temperature.

-
complex blends of, mainly, O  II and C  III are seen in the blue wing of H $\delta$ and near $\lambda$4650, producing wide features whose morphology and/or position of maximum absorption changes with temperature.
As a result the blended line profiles in the disentangled spectra contain trustworthy information, and the main limitation in interpreting disentangled spectra lies in the occurrence of low-level low-frequency patterns as discussed in Sect. 2.1. As in the case of single stars, line blending due to rotational broadening remains a factor limiting the information on abundances in complex blends.

We now briefly describe the aspects in which the intrinsic component spectra differ. The Balmer hydrogen lines and the helium lines have been discussed extensively in Paper  I, Sect. 6.3.2/3 and Figs. 8-9. We pointed out that the hydrogen lines of V578 Mon A are slightly stronger than expected considering the dynamically derived gravity and the temperature-sensitive He and Si lines from different ionisation stages. The He  I lines are slightly stronger in the spectrum of V578 Mon B than in V578 Mon A, but the difference is somewhat less than expected. The spectroscopic temperatures of $30~000 \pm 500$ K and $26~400 \pm 400$ K are a compromise. Carbon is present in two ionisation stages. Numerous C  III lines contribute to blends in which O  II is generally the main contributor. C  II $\lambda$4267 is prominent and unblended. The C  II line is significantly stronger in the cooler component. Nitrogen is present in two ionisation stages, but N  II is the dominant ion in V578 Mon B, while N  III is dominant in V578 Mon A. This is seen very clearly in the feature just longward of $\lambda$4630. In the cooler component N  II $\lambda$4630.55 dominates over Si  IV $\lambda$4631.24 and N  III $\lambda$4634.16, but the last two contributors shift the feature to longer wavelength in the hotter component. Another example is the complex blend near $\lambda$4640 shown in Fig. 2. The fact that N  II still contributes to the spectrum of the hotter component is obvious around $\lambda$4040, where the absorption in both stars is dominated by four lines of ionized nitrogen ($\lambda$$\lambda$4035.08, 4041.31, 4043.53, 4044.78), around $\lambda$4240 ( $\lambda\lambda$4237.0, 4241.79), and in the strong, relatively isolated line N  II $\lambda$3995.00. Many lines of ionized oxygen are seen at these temperatures, and several are unblended or are the main contributor to slightly blended features, even at these appreciable rotation velocities. Lines of ionized neon are too weak to allow meaningful analysis, but are suspected to be giving a minor contribution to some features. The doublet of ionized magnesium at $\lambda$4481 is prominent and weakly blended with lines of Al  III and O  II. Aluminium contributes to some features, mainly Al  III $\lambda$4529.19 in a blend with N  II $\lambda$4530.41 and, in the hotter component, with N  III  $\lambda\lambda$4527.89, 4530.86. Silicon has prominent lines from two ionisation stages, namely the triplet of Si  III at  $\lambda\lambda$4552.616, 4567.82, 4574.76 and the Si  IV lines at $\lambda$4088.85, 4116.10. More Si  IV lines are visible, e.g. at $\lambda$4212.41 and $\lambda$4631.24 (at least in V578 Mon A) and $\lambda$4654.32. Sulphur and iron contribute at these rotation velocities at best in a subtle way to blends.

Table 1: Spectral features used in the abundance analysis. Main contributing ions are indicated. For each binary component, the equivalent width W of all the absorption over the spectral interval specified in Cols. 2 and 4 is given in Cols. 3 and 5. The values between brackets are the corresponding W measured in the #201 spectrum blurred to the rotation velocity of component A resp. B (and in #180, behind the semicolon in the fourth column).

  
4 Quantitative abundance analysis

LTE line-blanketed atmosphere models were calculated for a relevant grid of effective temperatures and gravities, in steps of 1000 K and 0.1 dex respectively, for solar composition and a depth-independent microturbulent velocity of 2 km s-1, with the ATLAS 9 code (Kurucz 1992). Non-LTE line formation and spectrum synthesis computations were then performed as explained in Paper  II using codes DETAIL and SURFACE developed and maintained by Keith Butler. The Mg  II atom model is due to Przybilla et al. (2001). The use of the same models as in Paper  II allows consistent differential analysis.

The spectral features used in the quantitative analysis are listed in Table 1. Differential abundances with respect to #201 are listed in Table 2 and converted to relative-to-solar values using the results of Paper  II for the template star. Solar abundances are the same as in Daflon et al. (2004a). None of the V578 Mon abundances differs significantly from those of the template star. The tendency for  $\Delta \epsilon_A$ and  $\Delta \epsilon_B$ to have opposite signs (4 cases out of 5) might hint at coupled normalisation errors as discussed in Sect. 2.2, but has low statistical significance. The consistency of the results instead shows that disentangled component spectra can be normalised sufficiently well to obtain abundances with an accuracy of 0.1 dex.

With #201, #80, and #128 analyzed by Vrancken et al. (1997) and the components of V578 Mon, we have five early-B type stars in NGC 2244 ( $T_{\rm eff} = 26~300{-}30~000$ K), for which abundances are derived in a consistent way. They include slow and fast rotators ( $v \sin~i = 22{-}260$ km s-1). The abundances averaged over these five stars and the corresponding rms values are listed in Table 3. Within the achieved accuracy, the stars have an identical chemical composition. No correlation with projected rotation velocity is noticed. In passing, we note that evidence of an anomalous abundance pattern in the atmosphere of the young stars of NGC 2244 is found in the strongly magnetic, less massive mid-B star #334 (Bagnulo et al. 2004) and in #180. #334 shows an abundance pattern typical of chemical peculiar stars of the He-weak Si subclass. Some stars may thus modify their atmospheric chemical composition early in their youth, probably even before arriving on the main sequence. #180 has been found by Daflon et al. (2004b) to have lower metallicity. It is actually the star that deviates most from the average relation of metallicity versus galactocentric distance (Daflon & Cunha 2004). Unfortunately, it is the only member of NGC 2244 in their sample. The reason for this discrepancy deserves attention but this falls outside the scope of this paper; Daflon et al. (2004b) derive e.g. a much higher microturbulent velocity than for the stars our group analysed. We used #180 only to visualise the dependence of the morphology of temperature-sensitive line blends, but did not use the star in the quantitative abundance analysis in view of the possible break-down of the LTE line-blanketed atmosphere models at higher temperatures. At present we conclude that there is no compelling evidence against the hypothesis that the young early-B stars of NGC 2244 all have a chemical composition similar to the stars in the large inner-disk sample of Daflon et al. (2004a, see Table 3).

No study of the chemical abundances in the Rosette Nebula using H  II region recombination or collisionally excited emission lines has been undertaken so far. Using the results from several other H  II regions and the relation with galactocentric distance derived by Esteban et al. (2005) suggests [C/H] = 8.43 and [O/H] = 8.63, similar to modern solar abundances. The abundances of the early-B stars in NGC 2244, as well as those of early-B stars in general, are slightly lower than the solar abundances and those derived from H  II regions. Daflon & Cunha (2004) find agreement between abundances derived in massive stars and the accompanying H  II region within 0.1 to 0.2 dex. With the recent lesson learned from the sensitivity of solar abundances to sophisticated atmosphere modeling, one should probably not overinterpret difference on this level between abundance determinations derived with very different techniques. It may indicate limitations in one or several of the techniques rather than being astrophysically significant.

Table 2: Abundances for both components of V578 Mon, $\Delta \epsilon $ with respect to #201, and [X/H] relative to solar. Solar abundances are as listed in Table 3.

Table 3: Abundances [X/H] for the early-B stars in NGC 2244 (2nd column) compared to the inner-disk early-B abundances (3rd column). Also, stellar abundances for CNO elements could be compared to abundances derived for Orion Nebula (4th column), and with solar abundances (5th column).

  
5 Discussion and conclusions

We performed a detailed spectral line analysis of disentangled component spectra of the eclipsing early-B binary V578 Mon in the open cluster NGC 2244. Both spectra have rotationally broadened lines. By comparison with spectra of single stars in the same open cluster, temperature-dependent, faint spectral features are shown to reproduce well in the disentangled spectra, which validates a detailed quantitative analysis of these component spectra. As a main concern in the error budget the (coupled) undulations in the continua of disentangled spectra have to be eliminated with care.

An abundance analysis differential to a sharp-lined single star, as applied earlier in this cluster to single stars rotating faster than the components of V578 Mon, revealed abundances in agreement with the cluster stars studied by Vrancken et al. (1997) and the large inner-disk sample of Daflon et al. (2004a). We conclude that methods applicable to observed single star spectra perform well on disentangled spectra, given that the latter are carefully normalised to their intrinsic continua. Since the fundamental stellar and atmospheric parameters of eclipsing binaries can be known more precisely than in the case of single stars, this opens interesting possibilities for studying physical processes evolving during the main-sequence lifetime of the stars.

Acknowledgements

In particular, our thanks go to Dr. Keith Butler for his cooperation in implementing his computer codes for NLTE analysis. Also, we are indebted to Prof. Philip Dufton, referee of our paper, for his constructive comments. This research was carried out in the framework of the project "IUAP P5/36'' financed by the Belgian Federal Science Policy Office. K.P. acknowledges financial support from the Croatian Ministry of Science and Technology through research grant #0119254. He extends his thanks to ROB for hospitality in July/August 2002 and June/July 2003.

References

 
Copyright ESO 2005