All Tables
- Table 1:
Properties of a radiative shock for gas with a ratio
of specific heats,
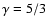 .
.
- Table 2:
Cooling length of a radiative shock for gas with a ratio
of specific heats,
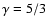 ,
and cooling exponent,
,
and cooling exponent, 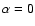 .
.
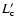 in appropriate units can be obtained by multiplying by
the numerical values of
in appropriate units can be obtained by multiplying by
the numerical values of
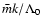 (note that in this
work we also specify that
(note that in this
work we also specify that
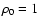 and v0=1).
There is convergence in the value of
and v0=1).
There is convergence in the value of 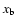 as M increases.
as M increases.
- Table 3:
Critical value of
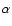 for damping of the fundamental mode, and
angular frequency (when
for damping of the fundamental mode, and
angular frequency (when
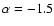 )
as a function of the Mach number.
For
)
as a function of the Mach number.
For
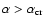 the
fundamental mode is damped, though the shock may still be unstable to
higher order modes, such as the first overtone ( cf. Chevalier & Imamura
1982; Strickland & Blondin 1995).
the
fundamental mode is damped, though the shock may still be unstable to
higher order modes, such as the first overtone ( cf. Chevalier & Imamura
1982; Strickland & Blondin 1995).
- Table 4:
The initial behaviour of the M=5 and M=10 simulations
shown in Fig. 9 can be determined from the
solution to a Riemann problem, which yields the resulting wave
velocities in the system (
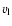 ,
,
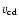 ,
and
,
and 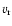 being the
velocity into the left state, the velocity of the contact discontinuity, and
the velocity into the right state).
The left state is defined as the CDL, while
the right state is defined as the pre-shock flow (see
Fig. 3). While the values quoted are for the initial
conditions, they should be a good representation of the conditions
which exist at the exact moment that the cooling layer disappears when
being the
velocity into the left state, the velocity of the contact discontinuity, and
the velocity into the right state).
The left state is defined as the CDL, while
the right state is defined as the pre-shock flow (see
Fig. 3). While the values quoted are for the initial
conditions, they should be a good representation of the conditions
which exist at the exact moment that the cooling layer disappears when
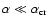 .
.
- Table 5:
Critical value of
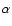 for damping of the fundamental mode
as a function of the Mach number and
for damping of the fundamental mode
as a function of the Mach number and 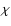 ,
the ratio of the temperature
of the CDL to the pre-shock temperature. This table is an extension of
Table 3 where
,
the ratio of the temperature
of the CDL to the pre-shock temperature. This table is an extension of
Table 3 where
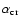 is listed for
is listed for 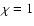 .
.
- Table 6:
Reflection coefficient, R, as a function of the Mach number
and
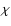 ,
the ratio of the temperature
of the CDL to the pre-shock temperature.
,
the ratio of the temperature
of the CDL to the pre-shock temperature.
- Table 7:
Approximate properties of SNR blast waves at the transition into the
pressure-driven snowplough stage for different values of
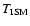 and n0, chosen to demonstrate the
conditions under which SNRs in the pressure-driven snowplough stage
have low Mach number forward shocks which are susceptible to the
radiative overstability. The age of the SNR at the onset of shell
formation,
and n0, chosen to demonstrate the
conditions under which SNRs in the pressure-driven snowplough stage
have low Mach number forward shocks which are susceptible to the
radiative overstability. The age of the SNR at the onset of shell
formation,
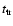 ,
the shock velocity,
,
the shock velocity,
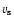 ,
and the Mach number, M, at this time, are given. The values
illustrate that overstable low Mach
number radiative shocks in SNRs will exist.
For
,
and the Mach number, M, at this time, are given. The values
illustrate that overstable low Mach
number radiative shocks in SNRs will exist.
For
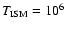 K and
K and
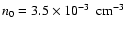 the blast wave becomes subsonic before transition to
the pressure-driven snowplough stage.
the blast wave becomes subsonic before transition to
the pressure-driven snowplough stage.