L. Ciotti1 - G. Bertin2
1 - Dipartimento di Astronomia, Università di Bologna,
via Ranzani 1, 40127 Bologna, Italy
2 -
Dipartimento di Fisica, Università di Milano,
via Celoria 16, 20133 Milano, Italy
Received 6 October 2004 / Accepted 30 March 2005
Abstract
We start from a study of the density-potential relation for
classical homeoids in terms of an asymptotic expansion for small
deviations from spherical symmetry. We then show that such expansion
is a useful device that allows us to construct a variety of exact
density-potential pairs with spheroidal, toroidal, or triaxial shapes
for which the deviation from spherical symmetry is finite. As
concrete analytical applications, we describe: (1) The construction of
a family of toroidal axisymmetric density-potential pairs one of which
is associated with a perfectly flat rotation curve (for a member of
this family, the supporting two-integral phase-space distribution
function is obtained in closed form); (2) The determination of the
aperture velocity dispersion in a wide class of two-integral
axisymmetric models not stratified on homeoids with central black
hole, which may be useful for the discussion of the dynamical
contributions to the characteristics of the Fundamental Plane of
early-type galaxies; and (3) For such class of models, the
construction of the ![]() -ellipticity relation, often considered
to assess the role of rotation in the structure of elliptical
galaxies.
-ellipticity relation, often considered
to assess the role of rotation in the structure of elliptical
galaxies.
Key words: galaxies: kinematics and dynamics - galaxies: structure
For the discussion of many astrophysical problems where gravity is important, a major difficulty is set by the potential theory. In general, to calculate the gravitational potential associated with a given density distribution one has to evaluate a three-dimensional integral. Except for special circumstances, where a solution can be found in terms of elementary functions, one has to resort to numerical techniques and sophisticated tools, such as expansions in orthogonal functions or integral transforms.
Under spherical symmetry, the density-potential relation can be reduced to a one-dimensional integral, while for axisymmetric systems one is left in general with a (usually non-trivial) two-dimensional integral. As a result, the majority of explicit density-potential pairs refers to spherical symmetry and only a handful of axially symmetric pairs are known (e.g., see Binney & Tremaine 1987, hereafter BT87). In few special cases (in particular, when a density-potential pair is available in a suitable parametric form) there exist systematic procedures to generate new non-trivial density-potential pairs (e.g., see the case of Miyamoto & Nagai 1975 and the related Satoh 1980 disks; see also Evans & de Zeeuw 1992).
For non-axisymmetric systems the situation is worse. One class of triaxial density distributions for which the potential can be expressed in a tractable integral form is that of the stratified homeoids, such as the Ferrers (1887) distributions (e.g., see Pfenniger 1984; Lanzoni & Ciotti 2003, hereafter LC03) and special cases of the family considered by de Zeeuw & Pfenniger (1988). Additional explicit density-potential pairs are given by the Evans (1994) models and by those constructed with the Kutuzov-Osipkov (1980) method (see also Kutuzov 1998).
In this paper we draw attention to an elementary yet curious property of the asymptotic expansion for small flattening of the homeoidal potential quadrature formula. Such expansion can be traced back to the treatise on geodesy by Sir H. Jeffreys (1970, and references therein; see also Hunter 1977). Recently, it has been applied to the modeling of gaseous halos in clusters (Lee & Suto 2003, 2004) and to the study of the dynamics of elliptical galaxies (Muccione & Ciotti 2003, 2004, hereafter MC03, MC04). The apparently unnoticed property of the expansion is that it offers a device to construct, in a systematic way, density-potential pairs with finite deviations from spherical symmetry. In turn, these can be used to carry out a number of calculations explicitly, thus allowing for a variety of interesting applications to stellar dynamics.
The paper is organized as follows. In Sect. 2 we present the basic asymptotic expansions and we outline the method. In Sect. 3 we study the Jeans equations for axisymmetric fluid models associated with density distributions obtained from our method. In Sect. 4 we focus on three significant applications. In Sect. 5 we make some concluding remarks. In Appendix A we address the issue of the relevant parameter space. In Appendix B we clarify the relation between the homeoidal expansion and the expansion in spherical harmonics. In Appendix C we summarize the intrinsic kinematical profiles of a family of axisymmetric galaxy models with central black hole.
We start by assuming a density distribution stratified on homeoidal
surfaces,
![]() ,
where
,
where
![]() ,
,
![]() is
a density scale, and
is
a density scale, and
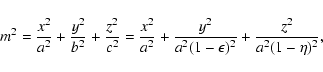 |
(1) |
It is well known (e.g., see Kellogg 1953; Chandrasekhar 1969) that the
(inner) potential associated with a homeoidal density distribution can
be written as
By ordering arguments and by the linearity of the Poisson equation, it
follows that the truncation of Eqs. (4) and (5) to
first order in the flattening parameters produces exact
density-potential pairs independently of the value of ![]() and
and ![]() .
In order to be physically acceptable, the density distribution
truncated to first order in
.
In order to be physically acceptable, the density distribution
truncated to first order in ![]() and
and ![]() must be positive
definite (see Appendix A). Density-potential pairs belonging to the
families thus constructed can be non-spherical at the "non-linear''
level, because the values of the flattening parameters can differ
significantly from zero. On the other hand, the truncated potential
is also the approximate potential for the density
must be positive
definite (see Appendix A). Density-potential pairs belonging to the
families thus constructed can be non-spherical at the "non-linear''
level, because the values of the flattening parameters can differ
significantly from zero. On the other hand, the truncated potential
is also the approximate potential for the density
![]() when
when
![]() and
and ![]() .
.
Now we proceed one step further and use
Eqs. (4) and (5) to construct new density-potential
pairs, independent of the ellipticities ![]() and
and ![]() defining the homeoidal expansion. In fact, by the same ordering
argument used above, it is immediate to see that
defining the homeoidal expansion. In fact, by the same ordering
argument used above, it is immediate to see that
![]() is the potential associated with
the "density''
is the potential associated with
the "density''
![]() .
For radially declining density
distributions
.
For radially declining density
distributions
![]() ,
we can thus consider the (dimensionless)
pair
,
we can thus consider the (dimensionless)
pair
That Eqs. (7)-(10) indeed identify explicit
density-potential pairs can be checked a posteriori by deriving
the potential ![]() from the density
from the density ![]() by means of a standard
expansion in spherical harmonics (Appendix B). Note however that, if
we started with a seemingly simpler idea, i.e., to transform the
density
by means of a standard
expansion in spherical harmonics (Appendix B). Note however that, if
we started with a seemingly simpler idea, i.e., to transform the
density
![]() in spherical coordinates and then to expand it in
spherical harmonics, we would have discarded all the expansion terms
above the monopole as candidates for acceptable density distributions
because the related mass vanishes. In contrast, the present method
works because, at least to first order, it is possible to isolate a
density term with constant (in our case, negative) sign over all
the space.
in spherical coordinates and then to expand it in
spherical harmonics, we would have discarded all the expansion terms
above the monopole as candidates for acceptable density distributions
because the related mass vanishes. In contrast, the present method
works because, at least to first order, it is possible to isolate a
density term with constant (in our case, negative) sign over all
the space.
In the approach followed so far, we have considered the density
![]() as given: in this way, several density-potential
pairs can be easily obtained, for example by starting from well known
seeds for
as given: in this way, several density-potential
pairs can be easily obtained, for example by starting from well known
seeds for
![]() ,
such as the density of the
,
such as the density of the ![]() -models
(Dehnen 1993; Tremaine et al. 1994, see also Appendix A). However,
the generated density profiles given in Eqs. (7)-(10) remain largely out of control.
-models
(Dehnen 1993; Tremaine et al. 1994, see also Appendix A). However,
the generated density profiles given in Eqs. (7)-(10) remain largely out of control.
On the other hand, it is possible to specify the spherically symmetric
factor
![]() in Eqs. (7),
(8), and (10): the potentials
in Eqs. (7),
(8), and (10): the potentials
![]() ,
,
![]() ,
and
,
and
![]() required to complete the non-spherical
density-potential pair are recovered by inserting in
Eq. (6) the supporting density
required to complete the non-spherical
density-potential pair are recovered by inserting in
Eq. (6) the supporting density
Another way to specify the supporting density
![]() (and
so
(and
so
![]() )
is by imposing a given rotation curve in the equatorial
plane, that is a circular velocity
)
is by imposing a given rotation curve in the equatorial
plane, that is a circular velocity
![]() defined from the
relation
defined from the
relation
![]() at z=0. In fact, by considering the
dimensionless potential
at z=0. In fact, by considering the
dimensionless potential ![]() in Eq. (10) and by assigning the
function
in Eq. (10) and by assigning the
function
![]() ,
one gets and can solve the following
(inhomogeneous Euler) differential equation for
,
one gets and can solve the following
(inhomogeneous Euler) differential equation for
![]() :
:
In this section, in view of applications to galactic dynamics, we study the Jeans equations for axisymmetric density-potential pairs either in the form of Eqs. (7) and (10), or in the axisymmetric cases of Eqs. (4) and (5). In our study we can also include the case in which the density distributions mentioned above are added to a separate spherically symmetric density distribution.
In all the axisymmetric cases described above, the pair
![]() belongs to the general family of density-potential
pairs
belongs to the general family of density-potential
pairs![]()
Let us assume that the density-potential pair defines the equilibrium
configuration of a stellar dynamical system for which the underlying
distribution function (DF) depends on the two classical integrals Eand Jz (star energy and z-component of the angular momentum, per unit mass), so that the velocity dispersion tensor
![]() is
diagonal and
is
diagonal and
![]() ;
we will denote
by
;
we will denote
by
![]() the dispersion
the dispersion
![]() .
Along the
azimuthal direction, part of the kinetic energy can be stored in
systematic motions
.
Along the
azimuthal direction, part of the kinetic energy can be stored in
systematic motions![]() , so that
, so that
![]() .
.
Given the form of the density-potential pair in Eq. (13),
the Jeans equations (e.g., see LC03, Eqs. (7) and (8)) can be easily
solved as
The general expression of projection integrals for axisymmetric
systems can be found in LC03. For simplicity, in this paper we focus
on the case when the system is observed edge-on (i.e. from a
line-of-sight where the contribution of rotation is expected to be
largest), even though for density distributions as in
Eq. (13) explicit projection formulae can be obtained for any
inclination of the line-of-sight direction ![]() .
Thus, we project
along the x axis, so that
.
Thus, we project
along the x axis, so that
![]() and the projection plane is
the (y,z) plane. The projected density is given by
and the projection plane is
the (y,z) plane. The projected density is given by
![]() ,
while the mass-weighted
projected streaming velocity field is given by
,
while the mass-weighted
projected streaming velocity field is given by
![]() ,
where
,
where
![]() and
and
![]() ;
similarly, the projection of the square of the streaming velocity
field is
;
similarly, the projection of the square of the streaming velocity
field is
![]() .
Finally, the line-of-sight velocity dispersion field is
.
Finally, the line-of-sight velocity dispersion field is
![]() ,
where
,
where
![]() ,
and
,
and
![]() (see Eqs. (B5) in LC03).
(see Eqs. (B5) in LC03).
At the end of this section, we may ask whether it would be possible to
reconstruct the phase-space DF for the general family of densities
given in Eq. (10). As is well known, the DF
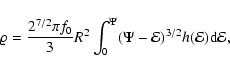 |
(17) |
Following the normalization introduced at the beginning of Sect. 2, in
this section and in Appendix C, the density ![]() ,
the relevant
radii, and the potential
,
the relevant
radii, and the potential ![]() are meant to be normalized to
are meant to be normalized to ![]() ,
to the scale-length a, and to
,
to the scale-length a, and to
![]() ,
respectively. It
follows that masses, projected densities, and velocities are
normalized to
,
respectively. It
follows that masses, projected densities, and velocities are
normalized to ![]() ,
,
![]() ,
and
,
and
![]() ;
for
simplicity, we omit the tilde above these quantities.
;
for
simplicity, we omit the tilde above these quantities.
In this subsection we describe a toroidal stellar system belonging to
the family associated with Eq. (10), for which the general
methods outlined in Sect. 3 allow us to obtain explicitly the relevant
kinematical profiles (and their projections on the plane of the sky),
even in the presence of a central black hole. For simplicity, we focus
here on the fully self-gravitating case, i.e. on the case when no
black hole is present. The simplest model is that of a power-law
torus, defined by the (normalized) density distribution
For
![]() and
and
![]() the circular velocity in the
equatorial plane is
the circular velocity in the
equatorial plane is
In the isotropic case (k=1), Eq. (22) gives the square of
the streaming velocity
![]() ;
in this case in the equatorial plane
(where r=R), the ratios
;
in this case in the equatorial plane
(where r=R), the ratios
![]() ,
,
![]() ,
and
,
and
![]() are constant. The isotropic case can also be
interpreted as the description of a toroidal fluid structure for which
the velocity
are constant. The isotropic case can also be
interpreted as the description of a toroidal fluid structure for which
the velocity
![]() is not constant over cylinders (corresponding to
the fact that the system is baroclinic; e.g., see Tassoul 1978): the
asymmetric drift
is not constant over cylinders (corresponding to
the fact that the system is baroclinic; e.g., see Tassoul 1978): the
asymmetric drift
![]() on the equatorial plane presented
by all the models scales as
on the equatorial plane presented
by all the models scales as
![]() ,
vanishes for
,
vanishes for ![]() ,
and is negative for lower values of
,
and is negative for lower values of ![]() .
Along the z axis
(where R=0), according to Eq. (21) the pressure vanishes,
and so does the quantity
.
Along the z axis
(where R=0), according to Eq. (21) the pressure vanishes,
and so does the quantity
![]() :
while this
latter behavior is a common property of two-integral axisymmetric
systems (e.g., see Ciotti & Pellegrini 1996, LC03), the former is a
peculiarity of the present toroidal model. Along the major axis in
the edge-on projection plane (i.e., along the y axis, at z=0),
:
while this
latter behavior is a common property of two-integral axisymmetric
systems (e.g., see Ciotti & Pellegrini 1996, LC03), the former is a
peculiarity of the present toroidal model. Along the major axis in
the edge-on projection plane (i.e., along the y axis, at z=0),
![]() ,
while
,
while
![]() ,
where the
proportionality constants are simple functions of
,
where the
proportionality constants are simple functions of ![]() that can be
easily computed for
that can be
easily computed for
![]() ;
below this value of
;
below this value of ![]() the
projected velocity dispersion diverges. The properties of two
toroidal models associated with Eq. (18) are illustrated in Fig. 1.
the
projected velocity dispersion diverges. The properties of two
toroidal models associated with Eq. (18) are illustrated in Fig. 1.
From the solution of Eq. (12) with
![]() ,
one can
prove that the
,
one can
prove that the ![]() power-law torus is the only model of this
class characterized by a perfectly flat rotation curve. For a generic
value of k, along the major axis in the edge-on projection, we have
power-law torus is the only model of this
class characterized by a perfectly flat rotation curve. For a generic
value of k, along the major axis in the edge-on projection, we have
![]() ,
and
,
and
![]() .
.
A more general family of power-law tori with flat rotation curves can
be obtained by expansion of the oblate spheroid
![]() (the so-called "isothermal'' spheroid) to higher orders in the
flattening, beyond Eqs. (4) and (5). In fact, such
oblate spheroid is characterized by a flat rotation curve on the
equatorial plane (for any flattening; e.g., see BT87,
Chap. 2). Therefore, following the arguments presented in Sect. 2.1 we
find that the tori
(the so-called "isothermal'' spheroid) to higher orders in the
flattening, beyond Eqs. (4) and (5). In fact, such
oblate spheroid is characterized by a flat rotation curve on the
equatorial plane (for any flattening; e.g., see BT87,
Chap. 2). Therefore, following the arguments presented in Sect. 2.1 we
find that the tori
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2123fig1.eps}
\end{figure}](/articles/aa/full/2005/26/aa2123-04/Timg157.gif) |
Figure 1:
Isodensity ( top), constant projected density ( middle),
and isopotential ( bottom) contours (in arbitrary units) for
the toroidal model described by Eq. (18) with
|
| Open with DEXTER | |
We conclude by noting that fully self-consistent, self-gravitating
toroidal stellar systems corresponding to the density-potential pair (18)-(19) with
![]() do not exist. In
fact, for
do not exist. In
fact, for
![]() the zero-velocity curves in the
meridional plane (R,z) are open. Surprisingly, the Jeans equations
would lead to apparently "innocent'' solutions even for
the zero-velocity curves in the
meridional plane (R,z) are open. Surprisingly, the Jeans equations
would lead to apparently "innocent'' solutions even for
![]() .
This concrete example illustrates the risks
that are taken when stellar systems are modeled by means of the Jeans
equations without a final check on the physical viability of the
solutions found from the formal analysis.
.
This concrete example illustrates the risks
that are taken when stellar systems are modeled by means of the Jeans
equations without a final check on the physical viability of the
solutions found from the formal analysis.
The general considerations presented in Sect. 3.1 can be elaborated in
greater detail for the family of power-law tori. In the case of
non-self gravitating power-law tori, the distribution function in the
presence of a dominant massive central black hole of mass
![]() can
be explicitly written as a Fricke distribution function by adopting
can
be explicitly written as a Fricke distribution function by adopting
![]() (with
(with
![]() )
and
)
and
![]() in
Eq. (16), where
in
Eq. (16), where
![]() is the standard Euler complete
Beta function.
is the standard Euler complete
Beta function.
As noted at the end of Sect. 3.1, by combining Eqs. (18) and (19), the function
![]() can be obtained
explicitly. In addition, for the entire family of power-law tori (with
can be obtained
explicitly. In addition, for the entire family of power-law tori (with
![]() ), the envelope and the dynamical window
(relevant to such method) can be expressed in terms of elementary
functions: for example, the envelope is defined by the relation
), the envelope and the dynamical window
(relevant to such method) can be expressed in terms of elementary
functions: for example, the envelope is defined by the relation
![]() when
when ![]() ,
while
,
while
![]() in all the other cases, where
in all the other cases, where ![]() is
the energy per unit mass of a star orbiting on the circular orbit.
Finally, for two members of this family it is possible to construct
the function
is
the energy per unit mass of a star orbiting on the circular orbit.
Finally, for two members of this family it is possible to construct
the function
![]() explicitly, thus
providing analytically all the required ingredients for a numerical
implementation of the Hunter-Qian method (Qian et al. 1995). In
particular,
explicitly, thus
providing analytically all the required ingredients for a numerical
implementation of the Hunter-Qian method (Qian et al. 1995). In
particular,
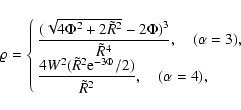 |
(24) |
| f(E,Jz) | = | 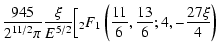 |
|
![$\displaystyle -{143\xi\over 256}
{_2F_1}\left({17\over 6},{19\over 6};5,-{27\xi\over 4}\right)\Big]$](/articles/aa/full/2005/26/aa2123-04/img176.gif) |
|||
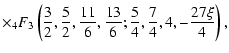 |
(25) |
We now apply the formulae derived in Sect. 2.1 to the family of
power-law oblate (
![]() )
spheroids. Thus, we start from
)
spheroids. Thus, we start from
![]() ,
where the range
,
where the range
![]() is such that
the density profile is radially decreasing and the central mass
remains finite.
is such that
the density profile is radially decreasing and the central mass
remains finite.
Several properties of these models have been investigated by Qian et al. (1995), who reconstructed their phase-space properties; in addition, Evans (1994) and Evans & de Zeeuw (1994) studied the observational properties that would result from a decomposition similar (but not identical) to the Satoh (1980) decomposition for a similar class of models (which they called "power-law'' models, in their scale-free limit).
Here we study the relevant Jeans equations on the basis of the Satoh decomposition, which has found widespread applications to elliptical galaxies (e.g., see Binney et al. 1990; van der Marel et al. 1990; van der Marel 1991). We are then able to provide expressions for the intrinsic and projected kinematical profiles in a form that may be useful to model the observations. These expressions can be easily generalized to the case in which a central black hole or a power-law dark matter halo with different flattening are present.
For ![]() the potential vanishes at infinity and is negative
divergent at the origin. For
the potential vanishes at infinity and is negative
divergent at the origin. For
![]() an upper truncation
must be applied to some integrals appearing in Eq. (6); in
Eq. (27) an additive constant has then been set to zero, so
that the potential diverges at infinity and vanishes at the origin.
Finally, for
an upper truncation
must be applied to some integrals appearing in Eq. (6); in
Eq. (27) an additive constant has then been set to zero, so
that the potential diverges at infinity and vanishes at the origin.
Finally, for ![]() the model is characterized by a flat rotation
curve, as the seed density distribution. In fact,
the model is characterized by a flat rotation
curve, as the seed density distribution. In fact,
The fully nonlinear (i.e., up to ![]() terms included) Jeans
Eqs. (14) and (15) for the assumed density-potential
pair can be solved without difficulty. Here, for simplicity, we use
the solution up to first order in
terms included) Jeans
Eqs. (14) and (15) for the assumed density-potential
pair can be solved without difficulty. Here, for simplicity, we use
the solution up to first order in ![]() ;
the analytical expressions
of the intrinsic and (edge-on) projected kinematical fields are given
in Appendix C. In Appendix C we also show that the projection of all
the quadratic (intrinsic) kinematical profiles can be obtained
explicitly even for
;
the analytical expressions
of the intrinsic and (edge-on) projected kinematical fields are given
in Appendix C. In Appendix C we also show that the projection of all
the quadratic (intrinsic) kinematical profiles can be obtained
explicitly even for
![]() .
Unfortunately, the streaming
velocity field cannot be obtained in explicit form when
.
Unfortunately, the streaming
velocity field cannot be obtained in explicit form when
![]() ;
for this case we can only provide asymptotic expressions for small
values of the projected radius. Close to the origin, independently of
the value of
;
for this case we can only provide asymptotic expressions for small
values of the projected radius. Close to the origin, independently of
the value of ![]() ,
the dynamical effects of
,
the dynamical effects of
![]() are always
dominant.
are always
dominant.
For
![]() ,
the analysis presented in Appendix C gives (for
,
the analysis presented in Appendix C gives (for
![]() )
)
| |
= | 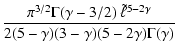 |
|
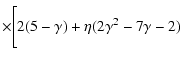 |
|||
![$\displaystyle -{4k^2\eta\Gamma^2(3\gamma/4-1/2)\Gamma (\gamma/2)\Gamma (\gamma)\over
\Gamma^2(3\gamma /4)\Gamma (\gamma/2-1/2)\Gamma (\gamma -3/2)}
\Bigg],$](/articles/aa/full/2005/26/aa2123-04/img203.gif) |
(29) |
For
![]() and
and ![]() (that is, in practice, for apertures
not larger than the sphere of influence of the black hole)
(that is, in practice, for apertures
not larger than the sphere of influence of the black hole)
![$\displaystyle M_{\rm p}~\sigma_{\rm a}^2 ={\mu_{\rm BH}\pi^{3/2}\Gamma (\gamma/...
...a\gamma (\gamma^2-1)\Gamma^2(\gamma +1/4)\over
\Gamma^2(\gamma/2 +3/4)}
\right]$](/articles/aa/full/2005/26/aa2123-04/img207.gif) |
(30) |
By combining the two formulae above we obtain an expression for the
aperture velocity dispersion which is asymptotically correct for small
and large apertures when
![]() .
.
In LC03, the problem of projection effects on the tilt and thickness of the Fundamental Plane (FP) of elliptical galaxies was investigated by means of a novel approach, introduced by Bertin et al. (2002). In particular, it was shown that rotation has no significant effects on the value of the measured "central'' velocity dispersion (consistent with the results obtained by van Albada et al. 1995 for cuspier models), and thus has a negligible effect on the FP tilt and thickness. However, the models used suffered from possessing unrealistically flat density profiles in their central regions. Here we illustrate how such legitimate concern can be resolved with our method, for simplicity restricting our discussion to the edge-on case, where the effect of rotation is maximum.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2123fig2.eps}
\end{figure}](/articles/aa/full/2005/26/aa2123-04/Timg214.gif) |
Figure 2:
Relative displacement of galaxy models induced by
different amounts of rotational support with respect to the edge-on FP
for different slopes |
| Open with DEXTER | |
In Fig. 2 we show the position of our models with respect to the edge-on FP. The models are first (arbitrarily) placed on the FP (the diagonal solid line) in the isotropic case (i.e., k=1); the two dotted lines parallel to the diagonal show the 1-rms dispersion of real galaxies around the FP. We refer to the FP coefficients measured by Jørgensen et al. (1996; for Coma cluster ellipticals and H0= 50 km s-1 Mpc-1).
The models are then "moved'' horizontally by letting their
"observed'' velocity dispersion ![]() vary with the Satoh
parameter k down to k=0, while their scale-length and mean surface
brightness are kept constant. To better illustrate our point, in Fig. 2 we place different models at different values
of
vary with the Satoh
parameter k down to k=0, while their scale-length and mean surface
brightness are kept constant. To better illustrate our point, in Fig. 2 we place different models at different values
of ![]() .
.
Because of the scale-free nature of the models considered the relative
effects are independent of the adopted aperture (cf. Eqs. (29) and (30)).
In all models ![]() increases for decreasing k, i.e., as the
flattening becomes more and more supported by the azimuthal velocity
dispersion. However, the displacement depends on the density slope
increases for decreasing k, i.e., as the
flattening becomes more and more supported by the azimuthal velocity
dispersion. However, the displacement depends on the density slope ![]() and on the model flattening. Note how cuspier models are
more affected by rotation than softer ones. The effect of flattening
at fixed
and on the model flattening. Note how cuspier models are
more affected by rotation than softer ones. The effect of flattening
at fixed ![]() is then shown by the line labeled
(2.4, 1/4.8):
for this model the density slope is
is then shown by the line labeled
(2.4, 1/4.8):
for this model the density slope is
![]() ,
but the flattening
is only half of the maximum allowed. The effect of rotation for
models with a dominant central black hole is apparently weaker.
,
but the flattening
is only half of the maximum allowed. The effect of rotation for
models with a dominant central black hole is apparently weaker.
The behavior of cuspy models, even in the presence of a massive central black hole, is not very different from that of the Ferrers models in LC03, thus confirming the findings of van Albada et al. (1995) and the statistical results of LC03.
One important property of a family of models characterized by
different degrees of flattening, is the way it covers the so-called
![]() -ellipticity plane. In fact, such plane is a simple tool
often used to investigate to what extent the observed flattening of
galaxies should be ascribed to rotation (e.g., Illingworth 1977;
Binney 1978). For the purpose, the observed quantities (
-ellipticity plane. In fact, such plane is a simple tool
often used to investigate to what extent the observed flattening of
galaxies should be ascribed to rotation (e.g., Illingworth 1977;
Binney 1978). For the purpose, the observed quantities (![]() ,
a
measurement of the ratio of observed rotation to velocity dispersion,
and the observed ellipticity) are usually compared to a curve
associated with the behavior of classical spheroids (see Chandrasekhar
1969). However, such a comparison may be misleading, because (1) galaxies need not conform to the properties of classical spheroids
with density stratified on homeoidal surfaces (Roberts 1962), and (2) the observations sample the central regions and may thus provide
insufficient information for a proper comparison with the theoretical
expectations. Indeed, Evans & de Zeeuw (1994), in the study of their
"power-law'' models, noted that their nearly isotropic models are
associated with points in the
,
a
measurement of the ratio of observed rotation to velocity dispersion,
and the observed ellipticity) are usually compared to a curve
associated with the behavior of classical spheroids (see Chandrasekhar
1969). However, such a comparison may be misleading, because (1) galaxies need not conform to the properties of classical spheroids
with density stratified on homeoidal surfaces (Roberts 1962), and (2) the observations sample the central regions and may thus provide
insufficient information for a proper comparison with the theoretical
expectations. Indeed, Evans & de Zeeuw (1994), in the study of their
"power-law'' models, noted that their nearly isotropic models are
associated with points in the ![]() -ellipticity plane
systematically below the curve of the classical spheroids, which is
obtained from virial (and therefore integrated) quantities.
-ellipticity plane
systematically below the curve of the classical spheroids, which is
obtained from virial (and therefore integrated) quantities.
Here we address this issue by studying the behavior of the family of
models introduced in Sect. 4.2. Note that, even though our models are
indeed obtained from a seed density distribution stratified on
homeoidal surfaces, their density distribution is not stratified on
homeoids, being the sum of a spherical density distribution and a
(negative) toroidal density. To stay closer to the issue of the
relevant observed quantities we define ![]() in terms of the
aperture velocity dispersion (Eqs. (29) and (30)) and v in terms of the
major axis projected streaming velocity (obtained from Eq. (C8)).
Note that, because of the scale-free nature of the present
models, the rotational parameter is independent of the aperture radius
adopted, when both the streaming velocity and the aperture velocity
dispersion are measured at the same radius.
in terms of the
aperture velocity dispersion (Eqs. (29) and (30)) and v in terms of the
major axis projected streaming velocity (obtained from Eq. (C8)).
Note that, because of the scale-free nature of the present
models, the rotational parameter is independent of the aperture radius
adopted, when both the streaming velocity and the aperture velocity
dispersion are measured at the same radius.
In Fig. 3 we show the model position in the
ellipticity-rotational parameter (![]() )
space for edge-on,
isotropic stellar systems. For the n=0 model described in LC03 the
major axis projected rotational velocity increases linearly with
radius and thus, following Evans & de Zeeuw (1994) (footnote 2
there), we adopt as reference value of v the value
)
space for edge-on,
isotropic stellar systems. For the n=0 model described in LC03 the
major axis projected rotational velocity increases linearly with
radius and thus, following Evans & de Zeeuw (1994) (footnote 2
there), we adopt as reference value of v the value ![]() measured
at the "core'' radius (i.e. at
measured
at the "core'' radius (i.e. at
![]() ,
where Rt is the
ellipsoid semimajor axis). The aperture velocity dispersion
,
where Rt is the
ellipsoid semimajor axis). The aperture velocity dispersion ![]() referred to an elliptical aperture of core radius (curve "c''). It is
thus clear that the rotational parameter
referred to an elliptical aperture of core radius (curve "c''). It is
thus clear that the rotational parameter ![]() can stay above or
below the locus of classical spheroids. In fact, it can be easily
proved that for the constant density spheroid the line-of-sight
velocity dispersion and the projected velocity dispersion coincide
(Eq. (C.10) in LC03), and so from the projected virial theorem (e.g.
Ciotti 1994) the aperture velocity dispersion over the whole object
coincides with the virial velocity dispersion (in the isotropic
case). Also, the streaming velocity, projected for the edge-on
isotropic case, evaluated along the major axis at
can stay above or
below the locus of classical spheroids. In fact, it can be easily
proved that for the constant density spheroid the line-of-sight
velocity dispersion and the projected velocity dispersion coincide
(Eq. (C.10) in LC03), and so from the projected virial theorem (e.g.
Ciotti 1994) the aperture velocity dispersion over the whole object
coincides with the virial velocity dispersion (in the isotropic
case). Also, the streaming velocity, projected for the edge-on
isotropic case, evaluated along the major axis at
![]() coincides with the rotational velocity obtained from the virial
ordered kinetic energy. For example, curve "0'' refers to the n=0 model where v is taken at
coincides with the rotational velocity obtained from the virial
ordered kinetic energy. For example, curve "0'' refers to the n=0 model where v is taken at
![]() ,
while
,
while ![]() is the
central projected velocity dispersion.
is the
central projected velocity dispersion.
The result we wish to point out here is associated with the dashed
lines, which correspond to our models with (long-dashed) and without
(short-dashed) a dominant central black hole, for density slopes near
the limits of the acceptable range (labels near the curves give the
value of ![]() for the assumed
for the assumed
![]() of
Sect. 4.2).
of
Sect. 4.2).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2123fig3.eps}
\end{figure}](/articles/aa/full/2005/26/aa2123-04/Timg219.gif) |
Figure 3:
The |
| Open with DEXTER | |
Thus, while our analysis confirms the importance of aperture effects even for the classical spheroids, we are also able to show that in general models different from classical spheroids may be found well below the classical locus, with deviations increasing at larger ellipticities.
The applications addressed in some detail in Sect. 4 are only a small sample of the many applications that can grow out of the general method introduced in this paper. Among other applications not addressed here, we may mention the following. MC04 adopt the method to calculate stellar orbits in triaxial elliptical galaxies, while Barnabé et al. (2005) investigate the properties of exploratory models for the low-rotation, extraplanar gas in spiral galaxies. Finally, we should recall that the interest in the study of toroidal structures is also motivated by the fact that centrally depressed surface brightness profiles need not always be associated with the projection of spherically symmetric, non-monotonic density profiles (Ciotti 2000), but may trace instead the presence of truly toroidal structures.
When considering homeoidal expansions we have to impose that the
density distribution thus obtained be positive-definite, which then
sets limits on the maximum values of ![]() and
and ![]() as a
function of the seed density profile. Without loss of generality we
take
as a
function of the seed density profile. Without loss of generality we
take
![]() .
In the case of the expansion at fixed total
mass (see MC04, Eq. (C.1)) we require
.
In the case of the expansion at fixed total
mass (see MC04, Eq. (C.1)) we require
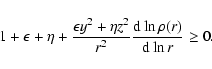 |
(A.1) |
| (A.2) |
To illustrate these conclusions, let us consider the density profile
A particularly interesting case of expansion at fixed total mass is
represented by the so-called ![]() -models (Dehnen 1993; Tremaine et al. 1994), for which
-models (Dehnen 1993; Tremaine et al. 1994), for which ![]() ,
b=1,
,
b=1,
![]() .
The
.
The
![]() -models received much attention not only for their analytical
simplicity, but also because the projected density distribution of the
-models received much attention not only for their analytical
simplicity, but also because the projected density distribution of the
![]() model (Jaffe 1983) is well fitted by the de Vaucouleurs
(1948) R1/4 law. Curiously, the positivity condition for the
oblate case is
model (Jaffe 1983) is well fitted by the de Vaucouleurs
(1948) R1/4 law. Curiously, the positivity condition for the
oblate case is
![]() ,
i.e., the expansion must be limited
to models rounder than E7. For the
,
i.e., the expansion must be limited
to models rounder than E7. For the ![]() models we have
models we have
![]() ,
and so, from Eq. (C.1) of MC04
,
and so, from Eq. (C.1) of MC04
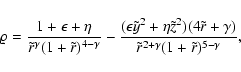 |
(A.4) |
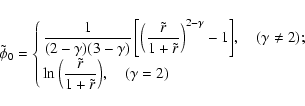 |
(A.5) |
 |
(A.6) |
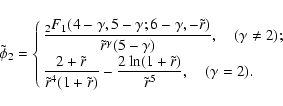 |
(A.7) |
Equation (7) can be recovered also from a study based on
spherical harmonics. Let us assume that the density distribution is
given in spherical coordinates by
![]() .
In a standard expansion in spherical harmonics
.
In a standard expansion in spherical harmonics
![]() (e.g., Jackson 1999); for our case
we thus have
(e.g., Jackson 1999); for our case
we thus have
![\begin{displaymath}D_{lm}(r) = -\rho_0r\tilde\rho'(r) {\sqrt{4\pi}\over 3}\delta_{m0}
\left[\delta_{l0}+{2\over\sqrt{5}}\delta_{l2}\right].
\end{displaymath}](/articles/aa/full/2005/26/aa2123-04/img249.gif) |
(B.1) |
In the seminal paper describing the numerical set-up of the "Schwarzschild![]() method'' for the construction of triaxial models of elliptical
galaxies (Schwarzschild
method'' for the construction of triaxial models of elliptical
galaxies (Schwarzschild![]() 1979), the (dimensionless) density distribution was
chosen of the form
1979), the (dimensionless) density distribution was
chosen of the form
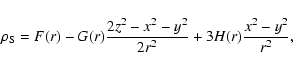 |
(B.2) |
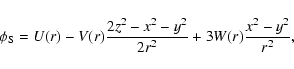 |
(B.3) |
Several authors constructed triaxial density-potential pairs starting
from Eqs. (B2) and (B3), through a potential-priority variation of the
Schwarzschild![]() method (e.g., de Zeeuw & Merritt 1983; Hernquist & Quinn 1989;
de Zeeuw & Carollo 1996). We wish to emphasize that the approach
based on homeoidal expansions developed in this paper to construct
analytically tractable density-potential pairs leads to new solutions.
For example, models constructed from an expansion of triaxial
method (e.g., de Zeeuw & Merritt 1983; Hernquist & Quinn 1989;
de Zeeuw & Carollo 1996). We wish to emphasize that the approach
based on homeoidal expansions developed in this paper to construct
analytically tractable density-potential pairs leads to new solutions.
For example, models constructed from an expansion of triaxial
![]() -models are different from those studied by de Zeeuw &
Carollo (1996).
-models are different from those studied by de Zeeuw &
Carollo (1996).
Here we record the expressions for the intrinsic and projected kinematical profiles associated with the density profile in Eq. (26), derived from the Jeans equations under the assumption that the underlying DF depends on E and Jz. We adopt the same normalization procedure mentioned at the beginning of Sect. 4.
We first note that for ![]() the edge-on projected density
("surface brightness'') is
the edge-on projected density
("surface brightness'') is
![\begin{displaymath}\Sigma = {\sqrt{\pi}\Gamma (\gamma/2 -1/2)\over
\Gamma (\ga...
...}
\left[1-{(\gamma -1)\eta\tilde z^2\over\tilde\ell^2}\right]
\end{displaymath}](/articles/aa/full/2005/26/aa2123-04/img256.gif) |
(C.1) |
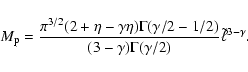 |
(C.2) |
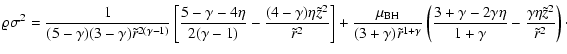 |
(C.3) |
![\begin{displaymath}\varrho(\overline{{v}_{\varphi}^2}-\sigma^2)={2\eta\tilde R^2...
...ma\mu_{\rm BH}\over (3+\gamma)\tilde r^{3-\gamma}}\right]\cdot
\end{displaymath}](/articles/aa/full/2005/26/aa2123-04/img260.gif) |
(C.4) |
| |
= | ||
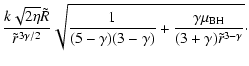 |
(C.5) |
![$\displaystyle \Sigma V_{\rm p}^2= {2\eta k^2\sqrt{\pi}\tilde y^2\over\tilde\ell...
...\tilde\ell^{3-\gamma}}
{\Gamma (\gamma/2 +1)\over 2\Gamma(\gamma/2+5/2)}
\Big],$](/articles/aa/full/2005/26/aa2123-04/img266.gif) |
(C.6) |
| |
= | ![$\displaystyle {\sqrt{\pi}\Gamma(\gamma-1/2)\over
(5-\gamma)(3-\gamma)\Gamma(\ga...
...gamma-4\eta\over 2\gamma-3}-
{(4-\gamma)\eta\tilde z^2\over\tilde\ell^2}\right]$](/articles/aa/full/2005/26/aa2123-04/img269.gif) |
|
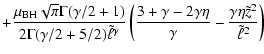 |
|||
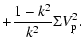 |
(C.7) |
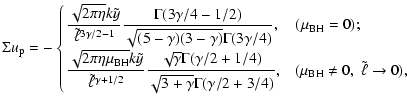 |
(C.8) |
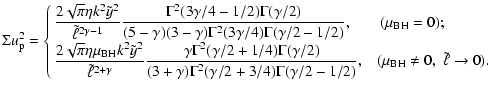 |
(C.9) |