M. Wolf1 - M. Zejda2
1 - Astronomical Institute, Charles University Prague,
180 00 Praha 8, V Holesovickách 2, Czech Republic
2 - Nicholas Copernicus Observatory and Planetarium, 616 00 Brno,
Czech Republic
Received 20 August 2004 / Accepted 20 February 2005
Abstract
Several new times of minimum light have been observed photoelectricaly
for the early-type double-lined eccentric eclipsing binaries
V539 Ara (
![]() ),
GG Lup (
),
GG Lup (
![]() ),
V526 Sgr (
),
V526 Sgr (
![]() )
and
AO Vel (
)
and
AO Vel (
![]() ).
The
).
The ![]() diagrams are analysed using all reliable timings found
in the literature and improved values for the elements of the
apsidal motion are computed. We find more precise, relatively short
periods of apsidal motion of about
162, 102, 155 and 54 years for
V539 Ara, GG Lup, V526 Sgr and AO Vel, respectively.
The corresponding internal structure
constants, log k2, are then found to be -2.33, -2.16, -2.36 and -2.24
under the assumption that the component stars rotate pseudosynchronously.
The relativistic effects are negligible, being about 6-7% of the total
apsidal motion rate in all systems.
Using the light-time effect solution, for V539 Ara we have found a
third component orbiting with a period of about 42 years, for AO Vel
we confirmed the third body with an orbital period of 33 years.
diagrams are analysed using all reliable timings found
in the literature and improved values for the elements of the
apsidal motion are computed. We find more precise, relatively short
periods of apsidal motion of about
162, 102, 155 and 54 years for
V539 Ara, GG Lup, V526 Sgr and AO Vel, respectively.
The corresponding internal structure
constants, log k2, are then found to be -2.33, -2.16, -2.36 and -2.24
under the assumption that the component stars rotate pseudosynchronously.
The relativistic effects are negligible, being about 6-7% of the total
apsidal motion rate in all systems.
Using the light-time effect solution, for V539 Ara we have found a
third component orbiting with a period of about 42 years, for AO Vel
we confirmed the third body with an orbital period of 33 years.
Key words: stars: binaries: eclipsing - stars: individual: V539 Ara - stars: individual: GG Lup - stars: individual: V526 Sgr - stars: individual: AO Vel - stars: fundamental parameters
Eccentric eclipsing binaries with apsidal motion are useful sources of knowledge about the internal structure of stars. The motion of the apsis of a binary star is a direct consequence of the finite size of its components. This effect has been well known for decades (Cowling 1938; Sterne 1939). The rate of motion of the apsis is dependent on the internal structure of each component. The study of the apsidal motion thus provides an important observational test of the theoretical models of stellar structure and evolution.
We are interested in an analysis of the light-time effect of multiple stellar systems. The combination of apsidal motion with a light-time effect in such multiple systems serves as an excellent laboratory of celestial mechanics to study a wide variety of processes in stellar astrophysics.
In this paper, we report new results from our project to monitor eclipsing binaries with eccentric orbits (see f.e. Wolf et al. 1999; Wolf 2000). Here we analyse the observational data and rates of apsidal motion for four well-known eclipsing systems, all relatively bright southern-hemisphere objects, known with eccentric orbit and that exhibit apsidal motion. With the exception of AO Vel, spectroscopic observations have been published for all these binary systems.
Our previous photometric study of apsidal motion in southern eccentric
eclipsing binaries was published by Wolf (2000). Current ![]() diagrams
for GG Lup, V526 Sgr and AO Vel were given in Kreiner et al. (2001).
diagrams
for GG Lup, V526 Sgr and AO Vel were given in Kreiner et al. (2001).
The aim of our photometric measurements was to secure several new,
well-covered primary and secondary minima for all variables.
Our new photoelectric ![]() observations were obtained with
modular photometer utilizing a Hamamatsu EA1516
photomultiplier on the 0.5-m telescope at the Sutherland site
of the South Africa Astronomical Observatory (SAAO) during
two weeks in April/May 2004. Each observation of an eclipsing binary
was accompanied by observation of a local comparison star
(see Table 1).
The photoelectric measurements were done in the
observations were obtained with
modular photometer utilizing a Hamamatsu EA1516
photomultiplier on the 0.5-m telescope at the Sutherland site
of the South Africa Astronomical Observatory (SAAO) during
two weeks in April/May 2004. Each observation of an eclipsing binary
was accompanied by observation of a local comparison star
(see Table 1).
The photoelectric measurements were done in the ![]() filters
of the Johnson's photometric system with a 10 s integration
time. All observations were carefully reduced to the
Cousins E-region standard system (Menzies et al. 1989)
and corrected for differential extinction using the
reduction program HEC 22 rel. 14 (Harmanec & Horn 1998).
The standard errors of these measurements were about 0.008,
0.006 and 0.005 mag in U, B and V filters, respectively.
filters
of the Johnson's photometric system with a 10 s integration
time. All observations were carefully reduced to the
Cousins E-region standard system (Menzies et al. 1989)
and corrected for differential extinction using the
reduction program HEC 22 rel. 14 (Harmanec & Horn 1998).
The standard errors of these measurements were about 0.008,
0.006 and 0.005 mag in U, B and V filters, respectively.
Table 1: Selected local comparison stars and their colour indexes.
Table 2: New times of minimum light.
The new times of primary and secondary minima and their errors were determined using a least squares fit of the data and by the bisecting chord method. Only the bottom parts of the eclipses were used. The given errors represent the third order polynomial fitting mean error for each light curve. In the case of SAAO measurements the mean value and error from the individual filter bands are given. The new times of minima are included in Table 2. In this table, the epochs are calculated from the light elements given in the text, the other columns being self-explanatory.
The apsidal motion in all system was studied by an ![]() diagram
analysis. For an accurate calculation of the apsidal motion rate
the method described by Giménez & García-Pelayo (1983),
with equations revised by Giménez & Bastero (1995), was routinely used.
Our relation for the prediction of the times of minimum caused
by the apsidal motion is also given in Wolf & Sarounová (1995).
diagram
analysis. For an accurate calculation of the apsidal motion rate
the method described by Giménez & García-Pelayo (1983),
with equations revised by Giménez & Bastero (1995), was routinely used.
Our relation for the prediction of the times of minimum caused
by the apsidal motion is also given in Wolf & Sarounová (1995).
We have collected all reliable times of minimum light available in the literature and current databases. The ASAS-3 (Pojmanski 2002), Hipparcos (Perryman et al. 1997) and Northern Sky Variability Survey (NSVS, Wozniak et al. 2004) databases have been used to find new times of minimum light. The NSVS observations were collected by the ROTSE-1 experiment using a robotic system of four unfiltered telephoto lenses equipped with CCD cameras. All photoelectric and CCD times of minima were used with a weight of 10 in our computation. Earlier, less accurate photographic or visual measurements were assigned weights of 3 or 1. We tested the stability of the results with respect to our - somewhat arbitrarily chosen - weighting scheme. It turned out that the results for the well-covered phase curves of all binaries are insensitive to the weighting scheme used.
The detached double-lined eclipsing binary V539 Ara
(also HD 161783, HR 6622A, HIP 87314, CD
![]() 7423,
CPD
7423,
CPD
![]() 8799, BV 420, FL 2271;
8799, BV 420, FL 2271;
![]() ,
,
![]() 36
36![]() 45
45
![]() ,
,
![]()
![]() 71; Sp. B3V+B4V)
is a frequently studied early-type binary with a slightly eccentric orbit
(e = 0.055) and an orbital period of about 3.17 days.
The double-line spectrum was discovered by Neubauer (1930a),
eclipses were later detected by Strohmeier (1964).
See also history of work on this binary in Clausen (1996).
The secondary component belongs to the slowly pulsating B stars with
periods of 1.36, 1.78 and possibly 1.08 days.
V539 Ara has a close fainter visual companion HR 6622B (
71; Sp. B3V+B4V)
is a frequently studied early-type binary with a slightly eccentric orbit
(e = 0.055) and an orbital period of about 3.17 days.
The double-line spectrum was discovered by Neubauer (1930a),
eclipses were later detected by Strohmeier (1964).
See also history of work on this binary in Clausen (1996).
The secondary component belongs to the slowly pulsating B stars with
periods of 1.36, 1.78 and possibly 1.08 days.
V539 Ara has a close fainter visual companion HR 6622B (
![]() )
which may be physically connected to the eclipsing pair.
A circular diaphragm of 35'' was used in our photometric
measurements, so this visual companion was included.
Clausen (1996) derived the apsidal motion period to be
)
which may be physically connected to the eclipsing pair.
A circular diaphragm of 35'' was used in our photometric
measurements, so this visual companion was included.
Clausen (1996) derived the apsidal motion period to be
![]() years with a remark that it is not possible to describe all available
times of minima through normal apsidal motion.
years with a remark that it is not possible to describe all available
times of minima through normal apsidal motion.
Table 3: Apsidal motion elements of V539 Ara, GG Lup, V526 Sgr and AO Vel.
All photoelectric times of minimum light given in
Clausen (1996, his Table 2) were incorporated in our calculation.
The epochs in Table 2 were computed according
to the ephemeris given in that paper:
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1868fig1.eps}\end{figure}](/articles/aa/full/2005/26/aa1868-04/Timg24.gif) |
Figure 1:
The
|
| Open with DEXTER | |
Three new times were derived using the Hipparcos photometry
(Perryman et al. 1997).
A total of 34 photoelectric times of minimum light were used
in our analysis, with 16 secondary eclipses among them.
The orbital inclination was adopted to be
![]() based
on the photometric analysis (Clausen 1996).
As was generally found, the apsidal motion solution is
insensitive to relatively large changes in i, but strongly
depends on the orbital eccentricity. Analysing the preliminary
based
on the photometric analysis (Clausen 1996).
As was generally found, the apsidal motion solution is
insensitive to relatively large changes in i, but strongly
depends on the orbital eccentricity. Analysing the preliminary
![]() diagram, we solved the apsidal motion and the light-time
effect (LITE) simultaneously.
The deviation of the observed values
diagram, we solved the apsidal motion and the light-time
effect (LITE) simultaneously.
The deviation of the observed values
![]() from the
linear ephemeris is given by a superposition of the apsidal motion
of the eccentric binary system and by the LITE caused
by a presence of a third body:
from the
linear ephemeris is given by a superposition of the apsidal motion
of the eccentric binary system and by the LITE caused
by a presence of a third body:
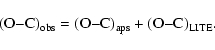
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1868fig2.eps}\end{figure}](/articles/aa/full/2005/26/aa1868-04/Timg28.gif) |
Figure 2:
The
|
| Open with DEXTER | |
Subtracting the influence of apsidal motion, the
![]() diagram
in Fig. 2 can be plotted. The sinusoidal variation of
these values are remarkable and could be caused by a LITE.
A preliminary analysis of the third body orbit gives the following
parameters:
diagram
in Fig. 2 can be plotted. The sinusoidal variation of
these values are remarkable and could be caused by a LITE.
A preliminary analysis of the third body orbit gives the following
parameters:
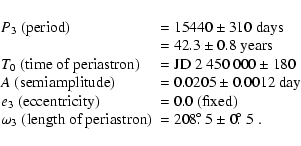
Assuming a coplanar orbit (
![]() )
and a total mass
of the eclipsing pair
M1 + M2 = 11.55
)
and a total mass
of the eclipsing pair
M1 + M2 = 11.55 ![]() (Clausen 1996), we can obtain a lower limit for the mass of the
third component
(Clausen 1996), we can obtain a lower limit for the mass of the
third component
![]() .
The value of the mass function
is
f(M) = 0.025
.
The value of the mass function
is
f(M) = 0.025 ![]() ,
from which the minimum mass
of the third body follows as 1.63
,
from which the minimum mass
of the third body follows as 1.63 ![]() .
A possible third component of spectral type A8 with the bolometric
magnitude of about +2.75 mag would be barely detectable in the system
with a B3 primary (
.
A possible third component of spectral type A8 with the bolometric
magnitude of about +2.75 mag would be barely detectable in the system
with a B3 primary (
![]() mag, Harmanec 1988).
For a total mass of this triple system
mag, Harmanec 1988).
For a total mass of this triple system
![]()
![]() and given the value of P3 one can obtain
a3 = 28.7 AU.
The close fainter visual companion HR 6622B (mV = 9.3 mag,
sep. = 12.6
and given the value of P3 one can obtain
a3 = 28.7 AU.
The close fainter visual companion HR 6622B (mV = 9.3 mag,
sep. = 12.6
![]() )
at a distance of about 3200 AU from the
eclipsing pair (
)
at a distance of about 3200 AU from the
eclipsing pair (
![]() mas, Perryman et al. 1997)
clearly cannot be this third body.
Therefore, new high-accuracy timings of this eclipsing binary are
necessary in order to confirm the LITE in this system.
mas, Perryman et al. 1997)
clearly cannot be this third body.
Therefore, new high-accuracy timings of this eclipsing binary are
necessary in order to confirm the LITE in this system.
The detached eclipsing binary GG Lup (also HD 135876,
HR 5687, HIP 74950, CD
![]() 9496, BV 448, FL 1762;
9496, BV 448, FL 1762;
![]() ,
,
![]() 47
47![]() 18
18
![]() ,
,
![]()
![]() 589; Sp. B7V+B9V)
is a relatively less-studied early-type binary with an eccentric orbit
(e = 0.15) and a period of about 1.85 days.
It was discovered to be a spectroscopic binary by Neubauer (1930b)
and eclipses were later independently discovered by Smith (1966)
and Strohmeier (1967).
Photometric orbits and apsidal motion parameters were derived by
Andersen et al. (1993), who found a relatively short period of apsidal
motion of about
589; Sp. B7V+B9V)
is a relatively less-studied early-type binary with an eccentric orbit
(e = 0.15) and a period of about 1.85 days.
It was discovered to be a spectroscopic binary by Neubauer (1930b)
and eclipses were later independently discovered by Smith (1966)
and Strohmeier (1967).
Photometric orbits and apsidal motion parameters were derived by
Andersen et al. (1993), who found a relatively short period of apsidal
motion of about
![]() years.
The epochs in Table 2 were computed according
to the following linear ephemeris given in that paper:
years.
The epochs in Table 2 were computed according
to the following linear ephemeris given in that paper:
All photoelectric times of minimum light given in
Andersen et al. (1993) were incorporated in our calculation.
Using the Hipparcos photometry (Perryman et al. 1997), we were able
to derive one additional time of minimum light.
A total of 40 photoelectric times of minimum light were used in our
analysis, with 18 secondary eclipses among them.
The orbital inclination was adopted to be
![]() based
on the photometric analysis (Andersen et al. 1993). The computed
apsidal motion parameters and their internal errors of the least
squares fit are given in Table 3.
The
based
on the photometric analysis (Andersen et al. 1993). The computed
apsidal motion parameters and their internal errors of the least
squares fit are given in Table 3.
The
![]() diagram is shown in Fig. 3.
diagram is shown in Fig. 3.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1868fig3.eps}
\end{figure}](/articles/aa/full/2005/26/aa1868-04/Timg42.gif) |
Figure 3:
The |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1868fig4.eps}\end{figure}](/articles/aa/full/2005/26/aa1868-04/Timg43.gif) |
Figure 4:
The
|
| Open with DEXTER | |
The detached eclipsing binary V526 Sgr
(also HD 177994, CD
![]() ,
CPD
,
CPD
![]() ,
FL 2634;
,
FL 2634;
![]() ,
,
![]() 20
20![]() 55.0
55.0
![]() ,
,
![]()
![]() 805; Sp. B9.5V+A2V) is a classical example
of apsidal motion. It was one of the first binaries recognized
to show the effects of apsidal motion in the times of its eclipses.
It was discovered photographically to be a variable star in 1934
by O'Connell (1935) on plates taken at Riverview Observatory.
The early history of this binary is described in detail in O'Connell (1967),
where the following linear light elements are also given
805; Sp. B9.5V+A2V) is a classical example
of apsidal motion. It was one of the first binaries recognized
to show the effects of apsidal motion in the times of its eclipses.
It was discovered photographically to be a variable star in 1934
by O'Connell (1935) on plates taken at Riverview Observatory.
The early history of this binary is described in detail in O'Connell (1967),
where the following linear light elements are also given
The improved photometric orbit and apsidal motion parameters were
derived by Lacy (1993). He found a period of apsidal motion of
![]() years. Absolute dimensions and masses of
V526 Sgr were later derived spectroscopicaly by Lacy (1997).
The epochs in Table 2 were computed according
to the ephemeris given in that paper:
years. Absolute dimensions and masses of
V526 Sgr were later derived spectroscopicaly by Lacy (1997).
The epochs in Table 2 were computed according
to the ephemeris given in that paper:
A total of 77 times of minimum light were used in our
analysis, with 39 secondary eclipses among them.
The orbital inclination was adopted to be
![]() based
on the photometric analysis (Lacy 1993). The computed
apsidal motion parameters and their internal errors of the least
squares fit are given in Table 3.
The
based
on the photometric analysis (Lacy 1993). The computed
apsidal motion parameters and their internal errors of the least
squares fit are given in Table 3.
The
![]() diagram is shown in Fig. 4.
diagram is shown in Fig. 4.
The detached eclipsing binary AO Vel
(also HD 68826, CD
![]() ,
CPD
,
CPD
![]() ,
FL 932;
,
FL 932;
![]() ,
,
![]() 44
44![]() 46.0
46.0
![]() ,
,
![]()
![]() 34; Sp. B9III/Ap)
is a relatively seldom-investigated early-type
binary with a short period of 1.58 days in a multiple stellar system.
It was discovered to be variable by Hertzsprung (1937).
Apsidal motion with a short period of about 50 years was first detected
by Oosterhoff & van Houten (1949). Four-colour uvby photometry was
obtained by Grønbech (1987). Clausen et al. (1995) presented the
first photometric analysis and derived an apsidal motion period of
34; Sp. B9III/Ap)
is a relatively seldom-investigated early-type
binary with a short period of 1.58 days in a multiple stellar system.
It was discovered to be variable by Hertzsprung (1937).
Apsidal motion with a short period of about 50 years was first detected
by Oosterhoff & van Houten (1949). Four-colour uvby photometry was
obtained by Grønbech (1987). Clausen et al. (1995) presented the
first photometric analysis and derived an apsidal motion period of
![]() yr.
They also discovered a third body in this system orbiting with the period
of
yr.
They also discovered a third body in this system orbiting with the period
of
![]() yr and contributing about 30% of the total
light. As far as we know, radial velocity observations of this system
are not available. AO Vel is also mentioned as one of several known
Ap eclipsing binaries and the only example of the Si-type (Clausen et al. 1995).
yr and contributing about 30% of the total
light. As far as we know, radial velocity observations of this system
are not available. AO Vel is also mentioned as one of several known
Ap eclipsing binaries and the only example of the Si-type (Clausen et al. 1995).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1868fig5.eps}\end{figure}](/articles/aa/full/2005/26/aa1868-04/Timg59.gif) |
Figure 5:
The
|
| Open with DEXTER | |
All photoelectric times of minimum light given in
Clausen et al. (1995, their Table 2) were included in our analysis.
The older photographic minima (Oosterhoff & van Houten 1949)
have not been included in this apsidal motion study due to their
large uncertainties of at least 0.05 days.
The epochs in Table 2 were computed according
to the ephemeris given by Clausen et al. (1995):
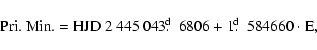
A total of 33 photoelectric times of minimum light were used in our
analysis, with 14 secondary eclipses among them.
The orbital inclination was adopted to be
![]() based
on the photometric analysis (Clausen et al. 1995).
As in the case of V539 Ara we solved the apsidal motion and the LITE
simultaneously.
The computed apsidal motion parameters and their internal errors
of the least squares fit are given in Table 3.
The
based
on the photometric analysis (Clausen et al. 1995).
As in the case of V539 Ara we solved the apsidal motion and the LITE
simultaneously.
The computed apsidal motion parameters and their internal errors
of the least squares fit are given in Table 3.
The
![]() diagram is shown in Fig. 5.
An analysis of the third body orbit gives the following parameters:
diagram is shown in Fig. 5.
An analysis of the third body orbit gives the following parameters:
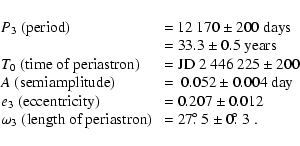
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1868fig6.eps}\end{figure}](/articles/aa/full/2005/26/aa1868-04/Timg64.gif) |
Figure 6: The LITE for AO Vel after subtraction of the apsidal motion. The curve represents the third body orbit with a period of 33 years and an eccentricity of e = 0.2. See legend to Fig. 2. |
| Open with DEXTER | |
Assuming a coplanar orbit (
![]() )
and a total mass
of the eclipsing pair
M1 + M2 = 8.0
)
and a total mass
of the eclipsing pair
M1 + M2 = 8.0 ![]() (Clausen et al. 1995),
we obtained the value of the mass function of
f(M) = 0.692
(Clausen et al. 1995),
we obtained the value of the mass function of
f(M) = 0.692 ![]() ,
from which the minimum mass of the third body is
,
from which the minimum mass of the third body is
![]()
![]() .
The third component of spectral type B5 with bolometric magnitude
of about -2.7 mag can produce more than 30% of the total light
in the system with a B9III primary (
.
The third component of spectral type B5 with bolometric magnitude
of about -2.7 mag can produce more than 30% of the total light
in the system with a B9III primary (
![]() mag,
Schmidt-Kaler 1982).
mag,
Schmidt-Kaler 1982).
Table 4: Adopted basic physical properties of the binary components and the internal structure constant.
The internal structure constant (ISC) k2, which is related to the
variation of the density within the star, is an important parameter
of stellar evolution models. However, the period of rotation
of the periastron in eccentric eclipsing binaries does not allow us to
derive the individual internal stellar constant of the component stars.
The observed average value of
![]() can be derived using the
following expression:
can be derived using the
following expression:
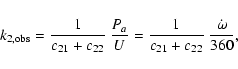 |
(1) |
where c21 and c22 are functions of the orbital eccentricity,
fractional radii, the masses of the components and the ratio between
rotational velocity of the stars and Keplerian velocity (Kopal 1978).
We also assume that the component stars rotate pseudosynchronously
with the same angular velocity as the maximum orbital value
at periastron.
Taking into account the value of the eccentricity and the masses
of the components, one has to subtract from
![]() a relativistic correction
a relativistic correction
![]() (Levi-Civita 1937;
Giménez 1985):
(Levi-Civita 1937;
Giménez 1985):
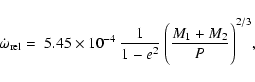 |
(2) |
where Mi denotes the individual masses of the
components in solar units and P is the orbital period in days.
The values of
![]() and the resulting mean internal
structure constants
and the resulting mean internal
structure constants
![]() are given in Table 4.
Their errors were evaluated according to the following relation
are given in Table 4.
Their errors were evaluated according to the following relation
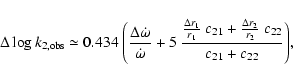 |
(3) |
where
![]() and
and
![]() are standard
errors of the apsidal motion rate and fractional radii of binary components.
The uncertainities in the mass and in the eccentricity were neglected due
to the presence of higher terms in the eccentricity.
The complete formula for the calculation of the ISC error is given
in the paper of Tudose at al. (2000).
are standard
errors of the apsidal motion rate and fractional radii of binary components.
The uncertainities in the mass and in the eccentricity were neglected due
to the presence of higher terms in the eccentricity.
The complete formula for the calculation of the ISC error is given
in the paper of Tudose at al. (2000).
The presence of a third component with orbital period P3 perturbs the
orbit of a close binary system. One of the most sensitive elements is the
longitude of the periastron. The acceleration of the rate of apsidal
motion for coplanar orbits and small eccentricities caused by the presence
of the third body
![]() can be approximated by (Martynov 1948):
can be approximated by (Martynov 1948):
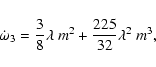 |
(4) |
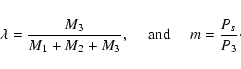 |
(5) |
This correction for the apsidal motion is negligible in both systems
(V539 Ara and AO Vel) due to the relatively long period P3 of the
third body orbit.
Theoretical values
![]() according to available theoretical
models for the internal stellar structure computed by Claret & Giménez
(1992) for given masses of components are presented in Table 4.
The metal abundance Z for X = 0.7 is also given.
according to available theoretical
models for the internal stellar structure computed by Claret & Giménez
(1992) for given masses of components are presented in Table 4.
The metal abundance Z for X = 0.7 is also given.
The photometric study of triple or multiple stellar systems with
apsidal motion of the eclipsing pair is a relatively poorly studied
field of celestial mechanics.
This study provides accurate information on the apsidal motion rates
and internal structure constants of the three main-sequence binary
systems V539 Ara, GG Lup and V526 Sgr and possible B9III/Ap system
AO Vel.
None of the analysed binaries present an important relativistic contribution.
The obtained values of the internal structure constant
![]() are compared to their theoretical values
are compared to their theoretical values
![]() according
to available theoretical models for the internal stellar structure along
the main sequence computed by Claret & Giménez (1992) for a variety
of masses and chemical compositions (Fig. 7).
according
to available theoretical models for the internal stellar structure along
the main sequence computed by Claret & Giménez (1992) for a variety
of masses and chemical compositions (Fig. 7).
The apsidal motion in eccentric eclipsing binaries has been used for
decades to test evolutionary stellar models.
Extensive comparison between theoretical models of stellar structure,
including moderate core overshooting and mass loss, and the best available
data of apsidal motion rates for double-lined eclipsing binaries was done
by Claret & Giménez (1993), using the opacities published by Rogers &
Iglesias (1992).
They concluded that there were no systematic deviations between observational
and theoretical values of ![]() .
The previous discrepancies between theory and observations have been reduced
to an acceptable level with the introduction of modern stellar models
including the effects of dynamic tides (Claret & Willems 2002).
Recently, new grids of stellar models based on updated opacities, expanded
nuclear network and mass loss rates were published by Claret (2004).
.
The previous discrepancies between theory and observations have been reduced
to an acceptable level with the introduction of modern stellar models
including the effects of dynamic tides (Claret & Willems 2002).
Recently, new grids of stellar models based on updated opacities, expanded
nuclear network and mass loss rates were published by Claret (2004).
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{1868fig7.eps}\end{figure}](/articles/aa/full/2005/26/aa1868-04/Timg83.gif) |
Figure 7: Comparison between observed and predicted average values of log k2 using models of stellar evolution. |
| Open with DEXTER | |
With the exception of the system AO Vel, where the stellar masses are probably estimated incorrectly, the agreement between the theoretical and observed value of the ISC is very good for V539 Ara and GG Lup and satisfactory for V526 Sgr.
For V539 Ara we derived a slightly longer apsidal motion period
of about
![]() years then was given in Clausen (1996).
For GG Lup we have confirmed the apsidal motion period
of
years then was given in Clausen (1996).
For GG Lup we have confirmed the apsidal motion period
of
![]() years, which is in excellent agreement with
the results obtained by Andersen et al. (1993).
Our results for the apsidal motion of V526 Sgr are practical identical
to the parameters derived in Lacy (1993).
years, which is in excellent agreement with
the results obtained by Andersen et al. (1993).
Our results for the apsidal motion of V526 Sgr are practical identical
to the parameters derived in Lacy (1993).
For AO Vel we substantially improved the apsidal motion and LITE
parameters. The third component which has a wide orbit (
![]() AU) probably contributes more than 30% of the total light
of this multiple system.
It is also highly desirable to obtain new, high-dispersion
and high-S/N spectroscopic observations for this system and to apply modern
disentangling methods to them to obtain the radial-velocity curves
of both binary components and, therefore, derive accurate masses for
this important system. This massive system with its relatively short orbital
period could be attractive for spectroscopists. The radial velocity curve
should have a semi-amplitude of more than 200 km s-1.
AU) probably contributes more than 30% of the total light
of this multiple system.
It is also highly desirable to obtain new, high-dispersion
and high-S/N spectroscopic observations for this system and to apply modern
disentangling methods to them to obtain the radial-velocity curves
of both binary components and, therefore, derive accurate masses for
this important system. This massive system with its relatively short orbital
period could be attractive for spectroscopists. The radial velocity curve
should have a semi-amplitude of more than 200 km s-1.
Moreover, V539 Ara and AO Vel belong to the important group of triple eccentric eclipsing binaries with apsidal motion (f.e. V889 Aql, TV Cet, RU Mon, U Oph, YY Sgr, DR Vul) described recently in Wolf et al. (2001). New high-accuracy timings of these eclipsing binaries are necessary to improve the LITE parameters derived in this paper.
Acknowledgements
This investigation was supported by the Grant Agency of the Czech Republic, grant No. 205/04/2063 and by allocation of SAAO observing time. The research of MW was also supported by the plan J13/98: 113200004 of Ministry of Education, Youth and Sports. MW wish to thank the staff at SAAO for their warm hospitality and help with the equipment and Dr. Petr Harmanec for help with the photometric reductions. We are indebted to the referee Dr. J. V. Clausen for his helpful comments that improved the paper. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France, and of NASA's Astrophysics Data System Bibliographic Services.