A&A 436, 127-143 (2005)
DOI: 10.1051/0004-6361:20042185
Determination of stellar ages from isochrones:
Bayesian estimation versus isochrone fitting
B. R. Jørgensen
- L. Lindegren
Lund Observatory, Lund University, Box 43, 221 00 Lund, Sweden
Received 15 October 2004 / Accepted 19 February 2005
Abstract
We present a new method, using Bayesian estimation, to determine stellar
ages and their uncertainties from observational data and theoretical
isochrones. The result for an individual star is obtained as the relative
posterior probability density as function of the age ("G function''). From
this can be derived the most probable age and confidence intervals.
The convoluted morphology of isochrones and strong non-linearities make
the age determination by any method difficult and susceptible to
statistical biases, and as a result age uncertainties havee
often been underestimated in the literature. From simulations we find
that the G functions provide a general, robust and reliable way to quantify
age information. Resulting age estimates are at least as accurate as those
obtained with conventional isochrone fitting methods, and in some cases much
better, especially when the observational uncertainties are large. We also
find that undetected binaries, on the whole, have a surprisingly small effect
on the age determinations. For a stellar sample, the individual G functions
can be combined to derive the star formation history of the population;
this will be developed in a forthcoming paper. For a
coeval population the combination simplifies to computing the product of
the individual G functions, and we apply that method to estimate the
ages of the two open clusters IC 4651 and M 67, using Padova isochrones
and photometric data from the literature. For IC 4651 we find an estimated
age of
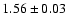 Gyr, assuming a true distance modulus of 9.80.
For M 67 we find
Gyr, assuming a true distance modulus of 9.80.
For M 67 we find
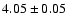 Gyr for true distance modulus 9.48. The
small formal errors of these age estimates do not include the (much larger)
uncertainties from calibration and model errors, but illustrate the
statistical power of combining G functions. Our statistical approach
to the age determination problem is well suited for the mass treatment
of data resulting from large-scale surveys such as the Gaia mission.
Gyr for true distance modulus 9.48. The
small formal errors of these age estimates do not include the (much larger)
uncertainties from calibration and model errors, but illustrate the
statistical power of combining G functions. Our statistical approach
to the age determination problem is well suited for the mass treatment
of data resulting from large-scale surveys such as the Gaia mission.
Key words: stars: fundamental parameters - stars: evolution -
solar neighbourhood - methods: data analysis - methods: statistical
1 Introduction
Determination of stellar ages is crucial in observational studies aiming
to understand stellar and galactic evolution (e.g., Fuhrmann 2004).
The use of theoretical stellar evolutionary sequences, or equivalently
isochrone fitting, is one of the few methods available for this purpose,
and possibly the only one that can be applied on a large scale to the full
range of stellar ages. When
studying evolution on galactic timescales (e.g., the star formation history
and age-metallicity relations of the solar neighbourhood), or the ages of
individual field stars, the method is mainly applied to late A-type, F and
G dwarfs, whose main-sequence life times range from below 1 Gyr up to the age
of the universe. Examples of such studies include
Edvardsson et al. (1993),
Gómez et al. (1997),
Ng & Bertelli (1998),
Lachaume et al. (1999),
Chen et al. (2000),
Liu & Chaboyer (2000),
Feltzing et al. (2001),
Ibukiyama & Arimoto (2002),
Lastennet & Valls-Gabaud (2002),
Laws et al. (2003),
Reddy et al. (2003),
Pont & Eyer (2004), and
Nordström et al. (2004).
In spite of the considerable practical importance of ages determined from
isochrones,
relatively little attention has been given to quantifying their statistical
reliability in view of the observational uncertainties. Although it is
recognized (e.g., Lachaume et al. 1999) that the uncertainties
of isochrone ages are often underestimated in the literature, there has been
little systematic study of the reasons for this phenomenon, or of the possible
statistical biases introduced by the estimation procedure. Aspects of the
problem were recently discussed by Pont & Eyer (2004) from the
viewpoint of Bayesian probability theory.
In the present paper we use Bayesian theory to derive stellar ages based
on a comparison of observed data with theoretical isochrones. The basic
assumptions are given in Sect. 2, while in Sect. 3
we derive the relative posterior probability density G as function of the
age 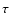 .
Under the given assumptions the G function
.
Under the given assumptions the G function![[*]](/icons/foot_motif.gif) specifies the available age information on an individual star. From this
it is possible to assign a unique (most probable) age to the star, as well as
confidence intervals (CI) at any given confidence level, but for many applications
the complete G function is required rather than a single value or interval
for the age. The effects of binaries on the age estimates are also studied
(Sect. 3.8).
specifies the available age information on an individual star. From this
it is possible to assign a unique (most probable) age to the star, as well as
confidence intervals (CI) at any given confidence level, but for many applications
the complete G function is required rather than a single value or interval
for the age. The effects of binaries on the age estimates are also studied
(Sect. 3.8).
In Sect. 4 we contrast the Bayesian age estimates with those
obtained using classical methods of isochrone fitting, where the uncertainties
may be obtained by classical error propagation or Monte Carlo techniques. The
properties of the estimators are studied by means of numerical simulations.
Section 5 describes the application of the method to the
determination of the ages of nearby field stars, in particular the sample
of more than 13 000 F and G dwarfs by Nordström et al. (2004).
Moreover, we derive the ages of the two open clusters IC 4651 and M 67 by
statistically combining the G functions for member stars. Finally, in
Sect. 6, we discuss the present method in relation to
some other methods described in the literature,
as well as some of the limitations implied by the adopted model.
2 Problem formulation and assumptions
2.1 Model parameters and observational data
Determination of ages from isochrones depends on comparing observed data with
theoretically computed values obtained from stellar models, where age (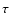 )
is one of the free parameters, but not the only one: at least the initial
stellar mass (m) and initial chemical composition (Z and possibly more
parameters) must also be considered. Quite generally we may summarize the
relevant model parameters in a vector
)
is one of the free parameters, but not the only one: at least the initial
stellar mass (m) and initial chemical composition (Z and possibly more
parameters) must also be considered. Quite generally we may summarize the
relevant model parameters in a vector 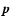 .
.
The observational data for a given object are similarly collected
in a vector 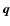 to which observational uncertainties are attached. Since
isochrone fitting is traditionally linked to the HR or colour-magnitude diagram,
the observational data are often taken to be quantities associated with the axes
of the HR diagram, such as
to which observational uncertainties are attached. Since
isochrone fitting is traditionally linked to the HR or colour-magnitude diagram,
the observational data are often taken to be quantities associated with the axes
of the HR diagram, such as
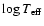 and MV. These are of course
derived from more basic photometric, spectroscopic and astrometric data and
therefore, strictly speaking, not directly observed quantities; however, in the
present context they can be regarded as such.
and MV. These are of course
derived from more basic photometric, spectroscopic and astrometric data and
therefore, strictly speaking, not directly observed quantities; however, in the
present context they can be regarded as such.
The theoretical models provide a mapping from the parameter space 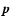 to
the data space
to
the data space 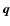 .
Determination of stellar ages is a special case of
the inverse problem, i.e., to find a mapping from
.
Determination of stellar ages is a special case of
the inverse problem, i.e., to find a mapping from 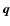 to
to 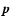 ,
which
is possible if
,
which
is possible if
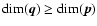 and the mapping is
non-degenerate.
and the mapping is
non-degenerate.
In the following, the model parameters are taken to be the age 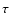 ,
initial mass m, and initial metallicity, for which we introduce the
parameter
,
initial mass m, and initial metallicity, for which we introduce the
parameter
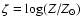 (with
(with
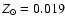 ). The helium content (Y) and the mixture of heavier elements are regarded as known functions of
Z, so that the stellar evolutionary models are uniquely labelled by the
parameter vector
). The helium content (Y) and the mixture of heavier elements are regarded as known functions of
Z, so that the stellar evolutionary models are uniquely labelled by the
parameter vector
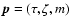 .
Similarly, we usually take the
observational data to be
.
Similarly, we usually take the
observational data to be
![$\vec{q} = (\mbox{[Me/H]},\log T_{\rm eff},M_V)$](/articles/aa/full/2005/22/aa2185-04/img32.gif) ,
although an application using the colour index (V-I)0 instead of
,
although an application using the colour index (V-I)0 instead of
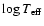 is given in Sect. 5.2.2. However, it should be
noted that the estimation method described in Sect. 3 in no way
is limited to this particular choice of variables, but is generally applicable
as long as the model provides a unique mapping from
is given in Sect. 5.2.2. However, it should be
noted that the estimation method described in Sect. 3 in no way
is limited to this particular choice of variables, but is generally applicable
as long as the model provides a unique mapping from 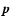 to
to 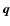 .
.
The age determination can thus be understood as the problem to invert the
function
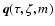 ,
and in particular to calculate
,
and in particular to calculate
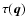 .
The problem can basically be approached either by direct numerical inversion
(isochrone fitting), or using probabilistic methods (Bayesian estimation).
We discuss variants of both approaches in Sects. 3 and 4.
.
The problem can basically be approached either by direct numerical inversion
(isochrone fitting), or using probabilistic methods (Bayesian estimation).
We discuss variants of both approaches in Sects. 3 and 4.
2.2 Choice of stellar isochrone data
The function
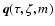 is in practice realized by numerical
interpolation in a set of pre-computed stellar evolutionary tracks or isochrones.
We have chosen to use the the Padova evolutionary models by Girardi et al. (2000), including convective overshooting, for all numerical examples
and simulations in this paper. Although any of the recent sets of models
(e.g., the Geneva models, Mowlavi et al. 1998; or the
Yonsei-Yale models, Yi et al. 2003) could in principle equally well
have been used to illustrate and compare age determination methods, our
choice was mainly guided by convenience: the Padova models cover sufficient
ranges in parameter space with a reasonably dense grid for realistic test
cases, and broad-band magnitudes are provided for every model.
is in practice realized by numerical
interpolation in a set of pre-computed stellar evolutionary tracks or isochrones.
We have chosen to use the the Padova evolutionary models by Girardi et al. (2000), including convective overshooting, for all numerical examples
and simulations in this paper. Although any of the recent sets of models
(e.g., the Geneva models, Mowlavi et al. 1998; or the
Yonsei-Yale models, Yi et al. 2003) could in principle equally well
have been used to illustrate and compare age determination methods, our
choice was mainly guided by convenience: the Padova models cover sufficient
ranges in parameter space with a reasonably dense grid for realistic test
cases, and broad-band magnitudes are provided for every model.
The Padova isochrones span the age interval
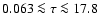 Gyr, the
metallicity range
Gyr, the
metallicity range
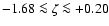 ,
and initial masses
,
and initial masses
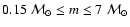 .
The applications require that the
observational quantities (
.
The applications require that the
observational quantities (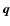 )
can be computed for any valid combination
of
)
can be computed for any valid combination
of
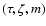 within these ranges.
within these ranges.
2.3 Computing interpolated isochrones
A special interpolation method was devised to calculate
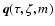 while ensuring that no significant artifacts are introduced by the extremely
non-linear relation between m and the quantities along any isochrone.
Briefly, we defined a continuous parameter u along each isochrone by
identifying a set of equivalent evolutionary points: the foot of the isochrone
at
while ensuring that no significant artifacts are introduced by the extremely
non-linear relation between m and the quantities along any isochrone.
Briefly, we defined a continuous parameter u along each isochrone by
identifying a set of equivalent evolutionary points: the foot of the isochrone
at
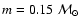 (u=0), the core H exhaustion (u=1), the point of maximum
(u=0), the core H exhaustion (u=1), the point of maximum
 before the RGB (u=2), the start of the RGB (u=3), etc.
Between these points u was taken to be proportional to the curve length of
the isochrone, using the (somewhat arbitrary) line element
before the RGB (u=2), the start of the RGB (u=3), etc.
Between these points u was taken to be proportional to the curve length of
the isochrone, using the (somewhat arbitrary) line element
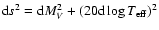 .
Linear
interpolation was then carried out in the
.
Linear
interpolation was then carried out in the
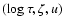 space
with m regarded as a dependent variable like
space
with m regarded as a dependent variable like
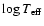 and MV.
This procedure ensures that the general morphology of the isochrones is preserved
so that, for example, the interpolated isochrones do not intersect where they
should not do so.
and MV.
This procedure ensures that the general morphology of the isochrones is preserved
so that, for example, the interpolated isochrones do not intersect where they
should not do so.
2.4 Metallicity parameter
The observational quantity [Me/H] is theoretically related to 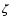 through the formula:
through the formula:
![\begin{displaymath}
\begin{array}{rcl}
\mbox{[Me/H]} &=& \log\left(Z/Z_\odot\rig...
...\zeta - \log\left[1-k\left(10^\zeta-1\right)\right]
\end{array}\end{displaymath}](/articles/aa/full/2005/22/aa2185-04/img44.gif) |
(1) |
assuming that Me represents the same mixture of elements (weighted by
atomic weight) as Z.
Here
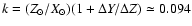 for
for
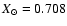 ,
,
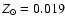 ,
and
,
and
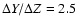 (e.g., Pagel & Portinari 1998).
For
(e.g., Pagel & Portinari 1998).
For
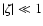 we have
we have
![$\mbox{[Me/H]}\simeq 1.094\zeta$](/articles/aa/full/2005/22/aa2185-04/img49.gif) while
for
while
for
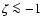 there is an almost constant offset
there is an almost constant offset
![$\mbox{[Me/H]}\simeq \zeta-0.04$](/articles/aa/full/2005/22/aa2185-04/img51.gif) .
The actual relation
between
.
The actual relation
between 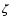 and the observational quantity is much more
complicated because the relative abundances of elements in Z may
vary (in particular the
and the observational quantity is much more
complicated because the relative abundances of elements in Z may
vary (in particular the 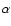 elements versus other elements).
These complications are however beyond the scope of this paper and we
simply assume
elements versus other elements).
These complications are however beyond the scope of this paper and we
simply assume
![\begin{displaymath}
\mbox{[Me/H]} \simeq \zeta.
\end{displaymath}](/articles/aa/full/2005/22/aa2185-04/img53.gif) |
(2) |
This is a reasonable approximation for the present purpose of
exploring the methodology of age determination by isochrones.
In real applications, considering that typical observational
uncertainties in [Me/H] are (at least) of order 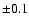 dex,
this relation is still useful for stars of about solar metallicity,
but should not be used for metal-poor stars.
dex,
this relation is still useful for stars of about solar metallicity,
but should not be used for metal-poor stars.
2.5 Assumed observational errors
In simulations and for illustration purposes we usually assume the
following standard errors, which are fairly representative of what
can be achieved for F and G dwarfs in the solar neighbourhood
(Nordström et al. 2004): 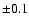 dex in [Me/H],
dex in [Me/H],
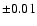 dex in
dex in
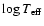 ,
and
,
and 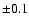 mag in MV.
We call these nominal errors. However, we shall sometimes
consider observational errors that are half or twice the nominal ones.
mag in MV.
We call these nominal errors. However, we shall sometimes
consider observational errors that are half or twice the nominal ones.
3 Bayesian estimation of stellar ages
3.1 The posterior probability density function
In Bayesian estimation the parameters to be determined (in this case
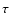 ,
,
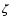 and m) are regarded as random variables and their
(posterior) joint probability density function is given by
and m) are regarded as random variables and their
(posterior) joint probability density function is given by
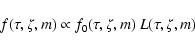 |
(3) |
where f0 is the prior probability density of the parameters
(Sect. 3.3) and L the likelihood function
(Sect. 3.2). The probability density function (pdf) fis defined such that
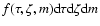 is the fraction
of stars with ages between
is the fraction
of stars with ages between 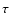 and
and
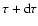 ,
metallicities between
,
metallicities between 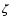 and
and
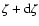 ,
and initial
masses between m and
,
and initial
masses between m and
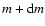 .
The constant of proportionality
in Eq. (3) must be chosen to make
.
The constant of proportionality
in Eq. (3) must be chosen to make
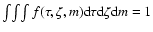 .
.
Integrating f with respect to m gives
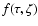 ,
which is
the posterior joint pdf of
,
which is
the posterior joint pdf of 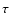 and
and 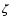 .
This function is of
interest when studying the age-metallicity relation, since it
summarizes the available information concerning these two parameters,
given the observational data. Integrating once more with respect to
.
This function is of
interest when studying the age-metallicity relation, since it
summarizes the available information concerning these two parameters,
given the observational data. Integrating once more with respect to
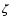 gives
gives 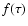 ,
the posterior pdf of
,
the posterior pdf of 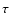 ,
which similarly
summarizes the available information concerning the age of the star.
,
which similarly
summarizes the available information concerning the age of the star.
In the next sections we discuss in some detail the two
functions L and f0 that together define the posterior probability
density.
3.2 The likelihood function
The likelihood function L equals the probability of getting the
observed data 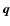 for given parameters
for given parameters 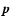 .
Regarded as
a function of
.
Regarded as
a function of 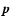 it is not a pdf - for instance, its
integral may be infinite. We assume independent Gaussian observational
errors in each of the
it is not a pdf - for instance, its
integral may be infinite. We assume independent Gaussian observational
errors in each of the
 observed quantities, with
standard errors
observed quantities, with
standard errors 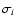 .
The likelihood function is then
.
The likelihood function is then
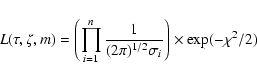 |
(4) |
where
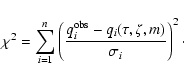 |
(5) |
A maximum-likelihood (ML) estimate of the stellar parameters
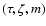 may be obtained by finding the maximum of this function,
which (in the case of Gaussian errors) is equivalent to minimizing
may be obtained by finding the maximum of this function,
which (in the case of Gaussian errors) is equivalent to minimizing
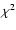 .
ML estimators are in general good estimators and in many
cases nearly optimal (Casella & Berger 1990), so why not
simply adopt the ML age estimate?
.
ML estimators are in general good estimators and in many
cases nearly optimal (Casella & Berger 1990), so why not
simply adopt the ML age estimate?
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm,clip]{2185f01.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg73.gif) |
Figure 1:
HR diagram showing the location of two hypothetical observations
at
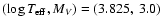 and
(3.800, 3.0), with nominal
uncertainties as in Sect. 2.5 (error bars show
and
(3.800, 3.0), with nominal
uncertainties as in Sect. 2.5 (error bars show
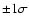 ).
The zero-age main sequence (ZAMS) and selected isochrones for ).
The zero-age main sequence (ZAMS) and selected isochrones for
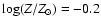 (
(
![${\simeq} \mbox{[Me/H]}$](/articles/aa/full/2005/22/aa2185-04/img71.gif) )
are also shown.
The symbols along the isochrones show where the initial mass is a
multiple of )
are also shown.
The symbols along the isochrones show where the initial mass is a
multiple of
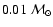 .
See text for further explanation. .
See text for further explanation. |
| Open with DEXTER |
The difficulty with the ML estimate in the present case has to do with
the complex morphology of the isochrones, i.e., of the highly non-linear
mapping from 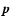 to
to 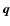 .
Effectively, it means that more
information is needed to make a good estimate of the age than provided
by the likelihood function alone. An illustration is given in
Fig. 1, where we consider the hypothetical
observation of two isolated field stars. The observed data are
depicted together with a selection of isochrones. All isochrones and
data are for
.
Effectively, it means that more
information is needed to make a good estimate of the age than provided
by the likelihood function alone. An illustration is given in
Fig. 1, where we consider the hypothetical
observation of two isolated field stars. The observed data are
depicted together with a selection of isochrones. All isochrones and
data are for
![$\mbox{[Me/H]}\simeq\zeta=-0.2$](/articles/aa/full/2005/22/aa2185-04/img74.gif) .
.
For the left data point (
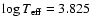 ,
MV=3.0) there is only one
isochrone going exactly through the observed point, namely
,
MV=3.0) there is only one
isochrone going exactly through the observed point, namely 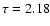 Gyr.
This is then the best-fitting age in terms of the
Gyr.
This is then the best-fitting age in terms of the 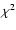 in Eq. (5)
and consequently also the ML estimate of the age based on the given data. For
the second point (
in Eq. (5)
and consequently also the ML estimate of the age based on the given data. For
the second point (
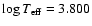 ,
MV=3.0), there are three
distinct isochrones going exactly through the data point:
,
MV=3.0), there are three
distinct isochrones going exactly through the data point: 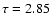 ,
3.27 and 3.82 Gyr. There are thus three points in parameter space where
,
3.27 and 3.82 Gyr. There are thus three points in parameter space where
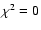 and where consequently
and where consequently
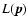 attains its global maximum.
Which of the three solutions should be chosen? In the absence of any additional
information, a reasonably experienced astronomer, forced to make a choice,
would probably select the youngest isochrone (2.85 Gyr) as the most reasonable
solution. Why? Because at that age the star would still be in the slowly
evolving stage of core hydrogen burning. If any of the higher ages were adopted,
we would have to assume that the star is in a more advanced and rapid evolutionary
stage, which is less probable for a (normal) star picked at random
attains its global maximum.
Which of the three solutions should be chosen? In the absence of any additional
information, a reasonably experienced astronomer, forced to make a choice,
would probably select the youngest isochrone (2.85 Gyr) as the most reasonable
solution. Why? Because at that age the star would still be in the slowly
evolving stage of core hydrogen burning. If any of the higher ages were adopted,
we would have to assume that the star is in a more advanced and rapid evolutionary
stage, which is less probable for a (normal) star picked at random![[*]](/icons/foot_motif.gif) .
This is an example where the astronomer, consciously or not, makes use of prior
information. The Bayesian approach offers a systematic way to quantify and make
use of this information by means of the prior pdf f0 in Eq. (3).
.
This is an example where the astronomer, consciously or not, makes use of prior
information. The Bayesian approach offers a systematic way to quantify and make
use of this information by means of the prior pdf f0 in Eq. (3).
3.3 Choice of prior distributions
The prior density of the model parameters in Eq. (3) can be written
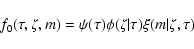 |
(6) |
where
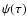 is the a priori star-formation rate (SFR)
history,
is the a priori star-formation rate (SFR)
history,
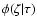 the a priori metallicity distribution as
function of age, and
the a priori metallicity distribution as
function of age, and
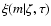 the a priori initial
mass function (IMF) as function of metallicity and age.
the a priori initial
mass function (IMF) as function of metallicity and age.
To proceed further it is necessary to make specific assumptions about
the functions 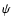 ,
,
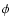 and
and 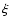 .
Inevitably, the end result will
to some extent depend on these assumptions. However, if the observations
are good enough there will only be a weak such dependence.
On the other hand, if the data are poor, it is important to make
only the most non-committal assumptions concerning the prior statistics.
For example, it makes sense to assume that
.
Inevitably, the end result will
to some extent depend on these assumptions. However, if the observations
are good enough there will only be a weak such dependence.
On the other hand, if the data are poor, it is important to make
only the most non-committal assumptions concerning the prior statistics.
For example, it makes sense to assume that 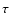 ,
,
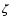 and
and 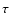 are
independent, so that
are
independent, so that
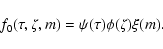 |
(7) |
A contrary assumption, e.g. that there is a priori a correlation
between 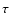 and
and 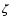 ,
would clearly be unreasonable if the
objective of the study is to determine a possible age-metallicity
relation. For a similar reason, we assume that the prior SFR
,
would clearly be unreasonable if the
objective of the study is to determine a possible age-metallicity
relation. For a similar reason, we assume that the prior SFR
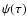 is flat.
is flat.
The choice of the prior metallicity distribution
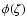 is less obvious. On one hand, the actual metallicity distribution of
nearby field stars is known to be strongly peaked at around
is less obvious. On one hand, the actual metallicity distribution of
nearby field stars is known to be strongly peaked at around
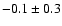 dex
(e.g., Nordström et al. 2004), which might indeed be
a useful a priori assumption e.g. in the absence of any metallicity measurement
at all for a given (field) star. If the true metallicity happens to be much
different from this assumption, it would of course result in a biased age
estimate, but that may still be preferable to no estimate at all. On the
other hand, if a metallicity measurement is available, one would
probably not want to prejudice the age determination by making an
additional assumption about what the metallicity should have been.
Thus, provided a metallicity measurement of adequate precision is at hand,
we think that a flat prior is generally the most reasonable choice.
It could still be debated whether it should be flat in the logarithmic
variable
dex
(e.g., Nordström et al. 2004), which might indeed be
a useful a priori assumption e.g. in the absence of any metallicity measurement
at all for a given (field) star. If the true metallicity happens to be much
different from this assumption, it would of course result in a biased age
estimate, but that may still be preferable to no estimate at all. On the
other hand, if a metallicity measurement is available, one would
probably not want to prejudice the age determination by making an
additional assumption about what the metallicity should have been.
Thus, provided a metallicity measurement of adequate precision is at hand,
we think that a flat prior is generally the most reasonable choice.
It could still be debated whether it should be flat in the logarithmic
variable 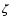 or in the linear variable Z; we have chosen the former
alternative (cf. below). For a more extensive
discussion of the role and importance of the prior distributions we refer
to Pont & Eyer (2004).
or in the linear variable Z; we have chosen the former
alternative (cf. below). For a more extensive
discussion of the role and importance of the prior distributions we refer
to Pont & Eyer (2004).
For the IMF, finally, there can be no doubt
that underlying star formation processes generate a decreasing function
at least for the relevant mass range (
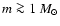 ), for which we
assume a power-law
), for which we
assume a power-law
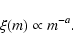 |
(8) |
An exponent a of order 2 to 3 would be representative for the empirical
IMF at around
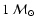 (Kroupa et al. 1993). For the
simulations described below we normally use a=2.7.
(Kroupa et al. 1993). For the
simulations described below we normally use a=2.7.
3.4 Calculating the G function
With the assumptions from Sect. 3.3 we find, after
inserting Eq. (6) into Eq. (3) and integrating with respect
to m and 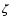 ,
that the posterior pdf of
,
that the posterior pdf of 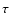 can be written
can be written
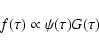 |
(9) |
where
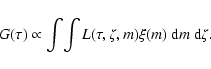 |
(10) |
For the IMF 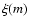 we use Eq. (8).
We normalize (10) such that
we use Eq. (8).
We normalize (10) such that 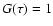 at its maximum.
Comparison with Eq. (3) suggests that
at its maximum.
Comparison with Eq. (3) suggests that 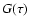 can be interpreted
as the relative likelihood of
can be interpreted
as the relative likelihood of 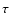 after elimination of m and
after elimination of m and 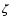 .
.
Numerically, we evaluate Eq. (10) for each age value (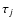 )
as a double sum along a set of isochrones at the required age that are
equidistant in metallicity (
)
as a double sum along a set of isochrones at the required age that are
equidistant in metallicity (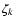 ). (In practice we use pre-computed
isochrones for a step size of 0.04 dex in
). (In practice we use pre-computed
isochrones for a step size of 0.04 dex in 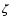 ,
and consider only those
within
,
and consider only those
within
![$\pm 3.5\sigma_{\rm [Me/H]}$](/articles/aa/full/2005/22/aa2185-04/img100.gif) of the observed metallicity.)
Let
of the observed metallicity.)
Let
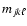 be the initial-mass values along each isochrone (
be the initial-mass values along each isochrone (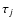 ,
,
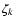 ); then
); then
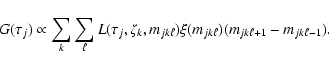 |
(11) |
Discretization and interpolation errors sometimes produce a slight
raggedness of the computed G function which we eliminate by numerical
smoothing. This is mainly needed in order to compute reliably the mode
of the G function (Sect. 3.7).
The solid line in Fig. 2 shows the G function for the right data
point in Fig. 1, assuming nominal
observational errors (Sect. 2.5). The dashed and dotted
curves show the G functions computed for the same data but assuming half
or double the nominal errors. These functions have a global maximum around
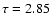 Gyr, corresponding to the most probable age according to the
discussion of this example in Sect. 3.2. Around the alternative
age 3.82 Gyr there are lower peaks, suggesting that this solution is
less probable. Around 3.27 Gyr there is no visible peak at all.
Gyr, corresponding to the most probable age according to the
discussion of this example in Sect. 3.2. Around the alternative
age 3.82 Gyr there are lower peaks, suggesting that this solution is
less probable. Around 3.27 Gyr there is no visible peak at all.
This behaviour of the G functions can be understood with reference to
Fig. 1. Along each isochrone in that diagram we have
marked off the models that are equidistant in initial mass
(
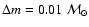 ). From the markings it is clear that the
error ellipse around the observed point covers a much wider range of masses
along the 2.85 Gyr isochrone than along the 3.82 Gyr isochrone, and a very
small mass range for the intermediate isochrone. When performing the
integration over m in Eq. (10) there is a correspondingly larger
contribution to the G function at
). From the markings it is clear that the
error ellipse around the observed point covers a much wider range of masses
along the 2.85 Gyr isochrone than along the 3.82 Gyr isochrone, and a very
small mass range for the intermediate isochrone. When performing the
integration over m in Eq. (10) there is a correspondingly larger
contribution to the G function at 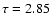 Gyr than at 3.82 Gyr, and
a very small contribution at the intermediate age. The varying density
of markings reflects the changing speed of stellar evolution. Thus, by
performing the integration over m in Eq. (10) we automatically
take into account the different evolutionary time scales.
Gyr than at 3.82 Gyr, and
a very small contribution at the intermediate age. The varying density
of markings reflects the changing speed of stellar evolution. Thus, by
performing the integration over m in Eq. (10) we automatically
take into account the different evolutionary time scales.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.7cm,clip]{2185f02.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg105.gif) |
Figure 2:
Plot of the relative posterior probability density, 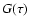 ,
for
the observed data point ( ,
for
the observed data point (
![$\mbox{[Me/H]}=-0.2$](/articles/aa/full/2005/22/aa2185-04/img104.gif) , ,
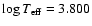 ,
MV=3.0).
The three curves are for the nominal uncertainties (thick solid line), half the
nominal values (dashed) and twice the nominal (dotted); see Sect. 2.5.
The vertical bars indicate the ages for the three isochrones in
Fig. 1 that go though the observed data point. ,
MV=3.0).
The three curves are for the nominal uncertainties (thick solid line), half the
nominal values (dashed) and twice the nominal (dotted); see Sect. 2.5.
The vertical bars indicate the ages for the three isochrones in
Fig. 1 that go though the observed data point. |
| Open with DEXTER |
Note that the assumed IMF has only a marginal impact on the shape of
the G functions compared with the varying speed of stellar evolution.
For example, changing the exponent a in Eq. (8) from 2.7 to 0
(i.e., a flat IMF) only reduces the secondary peak in Fig. 2
from 0.59 to 0.45 for the nominal errors. Similarly the assumed prior
in 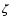 is normally uncritical. For example, it could be argued
that it is more reasonable to assume a flat prior density in
is normally uncritical. For example, it could be argued
that it is more reasonable to assume a flat prior density in
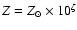 than in the logarithmic parameter
than in the logarithmic parameter 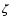 .
Using a flat prior in Z implies
.
Using a flat prior in Z implies
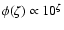 .
Including this factor in the integrand of Eq. (10) would
reduce the secondary peak in Fig. 2 from 0.59 to 0.51.
The corresponding effects on the estimated age are on the 1% level
for the nominal errors, but increase quickly with the observational
errors.
.
Including this factor in the integrand of Eq. (10) would
reduce the secondary peak in Fig. 2 from 0.59 to 0.51.
The corresponding effects on the estimated age are on the 1% level
for the nominal errors, but increase quickly with the observational
errors.
3.5 Age determination from the G function
Assuming a flat prior pdf in 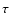 we have
we have
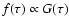 and the age determination can be entirely based on the G function.
As discussed in Sect. 3.7 we will adopt the mode (maximum)
of the G function,
and the age determination can be entirely based on the G function.
As discussed in Sect. 3.7 we will adopt the mode (maximum)
of the G function,
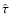 ,
as our "best'' estimate
of a stellar age, based exclusively on the given observational data.
,
as our "best'' estimate
of a stellar age, based exclusively on the given observational data.
It may happen that the observed data point falls well outside
all the isochrones. In this case it is obviously not possible to infer
anything about the age. Although the G function can still be computed
and even may show a well-defined peak, it is clearly meaningless and
should not be used. We adopt (somewhat arbitrarily) the criterion
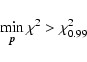 |
(12) |
for such a "no solution'' condition. The left hand side is the minimum of
Eq. (5)
for any combination of model parameters, and
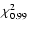 is the
99th percentile value of the chi-square distribution for
is the
99th percentile value of the chi-square distribution for
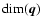 degrees of freedom - in our case
degrees of freedom - in our case
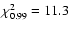 for 3 d.o.f. This
means that there is less than 1% probability for a data point falling
that far from the isochrones purely by chance, rather than for some
technical or astrophysical reason (peculiar star, bad data, etc.).
for 3 d.o.f. This
means that there is less than 1% probability for a data point falling
that far from the isochrones purely by chance, rather than for some
technical or astrophysical reason (peculiar star, bad data, etc.).
3.6 Confidence intervals
In addition to the single age estimate
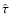 it is often
desirable to provide a confidence interval (CI) at some specified
confidence level
it is often
desirable to provide a confidence interval (CI) at some specified
confidence level 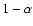 (say, 68% or 95%). The meaning of the
confidence level is that we expect the true age to be inside the
CI in a fraction
(say, 68% or 95%). The meaning of the
confidence level is that we expect the true age to be inside the
CI in a fraction 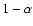 of all the cases. The usual
of all the cases. The usual
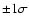 is a CI at 68% confidence level if the errors are Gaussian.
is a CI at 68% confidence level if the errors are Gaussian.
Since 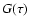 is proportional to the posterior pdf of
is proportional to the posterior pdf of 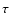 ,
one
could use the following equation to construct a confidence interval
,
one
could use the following equation to construct a confidence interval
![$[\tau_1,\tau_2]$](/articles/aa/full/2005/22/aa2185-04/img115.gif) for any given confidence level
for any given confidence level 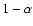 :
:
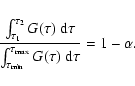 |
(13) |
Here,
 ,
,
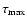 are the extreme ages considered,
e.g., as covered by the isochrones. The fractional area below
are the extreme ages considered,
e.g., as covered by the isochrones. The fractional area below 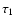 and above
and above 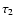 need not be the same, but could be chosen to minimize the
length of the confidence interval.
need not be the same, but could be chosen to minimize the
length of the confidence interval.
However, we have not adopted this method to compute a confidence
interval, mainly
for the following reason. Suppose that the data give very little information
about the age so that the G function is essentially flat.
Then any sub-interval of length
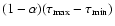 would be a formally correct confidence interval at the chosen confidence
level, without carrying any useful information at all, but with an
obvious risk of misinterpretation.
would be a formally correct confidence interval at the chosen confidence
level, without carrying any useful information at all, but with an
obvious risk of misinterpretation.
We have therefore adopted a different procedure to derive a CI from the G function. As suggested in connection with Eq. (10), 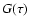 can be regarded as the relative likelihood function with
can be regarded as the relative likelihood function with
 at the mode
at the mode
 .
For any other age,
.
For any other age, 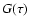 is therefore the likelihood
ratio obtained by constraining one parameter (
is therefore the likelihood
ratio obtained by constraining one parameter (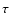 )
to a given value.
It is well known (e.g., Casella & Berger 1990) that the
likelihood ratio, under certain regularity conditions, has a simple
asymptotic distribution which in our case suggests that
)
to a given value.
It is well known (e.g., Casella & Berger 1990) that the
likelihood ratio, under certain regularity conditions, has a simple
asymptotic distribution which in our case suggests that
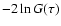 has
a chi-square distribution with 1 degree of freedom. Thus,
has
a chi-square distribution with 1 degree of freedom. Thus,
![\begin{displaymath}
1-\alpha = \mbox{Pr}[G(\tau)\ge G_{\rm lim}] \simeq 2\Phi\left(\!\sqrt{-2\ln G_{\rm lim}}\right)-1
\end{displaymath}](/articles/aa/full/2005/22/aa2185-04/img124.gif) |
(14) |
where
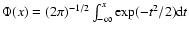 is the
standard normal distribution. The reasoning behind this expression
is admittedly weak, but we will substantiate the result below by means of
numerical simulations.
is the
standard normal distribution. The reasoning behind this expression
is admittedly weak, but we will substantiate the result below by means of
numerical simulations.
Assuming that Eq. (14) holds, we compute for the given confidence
level 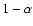 the corresponding value
the corresponding value
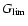 and then define the CI
and then define the CI
![$[\tau_1,\tau_2]$](/articles/aa/full/2005/22/aa2185-04/img115.gif) to be the shortest interval such that
to be the shortest interval such that
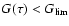 outside the interval. (Since
outside the interval. (Since 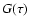 can have multiple maxima, it may
happen that
can have multiple maxima, it may
happen that 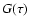 is locally below
is locally below
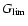 inside the interval
as well.) The 68, 90 and 95% confidence levels correspond respectively
to
inside the interval
as well.) The 68, 90 and 95% confidence levels correspond respectively
to
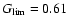 ,
0.26 and 0.15.
,
0.26 and 0.15.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.7cm,clip]{2185f03.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg129.gif) |
Figure 3:
Representative locations in the HR diagram used in the Monte Carlo
experiments (Sect. 3.6) to test the validity of the approximation (14). The isochrones are for
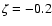 and and 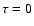 ,
1, 2, ,
1, 2, 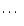 ,
8, 10, 12 and 15 Gyr. The points at the
centres of the error ellipses indicate the true observational data,
to which independent Gaussian errors are added with nominal errors.
Note the behavior of the points marked A, B, C and D in Fig. 4. ,
8, 10, 12 and 15 Gyr. The points at the
centres of the error ellipses indicate the true observational data,
to which independent Gaussian errors are added with nominal errors.
Note the behavior of the points marked A, B, C and D in Fig. 4. |
| Open with DEXTER |
We have made extensive Monte Carlo simulations to test whether Eq. (14)
holds to a reasonable accuracy in practical situations. For representative
points in the HR diagram (Fig. 3) we generated "observed'' data
with nominal uncertainties (Sect. 2.5), computed the resulting Gfunctions and derived the confidence intervals corresponding to
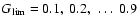 .
We then counted the number of cases when
the true age fell within the derived confidence interval. Figure 4
shows the fraction of such cases as function of
.
We then counted the number of cases when
the true age fell within the derived confidence interval. Figure 4
shows the fraction of such cases as function of
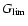 for each set of
1000 experiments. The solid curve is the theoretically expected relation
from Eq. (14). It is seen that the experiments follow the theoretical
relation rather well for most of the selected points in the HR diagram.
for each set of
1000 experiments. The solid curve is the theoretically expected relation
from Eq. (14). It is seen that the experiments follow the theoretical
relation rather well for most of the selected points in the HR diagram.
Exceptions are the points marked A and B in Fig. 3, and to a
smaller degree points C and D. The problem at points A and B can be understood
as an effect of the multiply overlapping isochrones on the upper part of the
giant branch, especially when also the uncertainty in metallicity is considered,
while it is not so obvious what happens at C and D. Nevertheless, we conclude
that the simple recipe of using a fixed threshold value
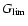 is in
general quite reasonable and should produce realistic confidence intervals
under the given assumptions.
is in
general quite reasonable and should produce realistic confidence intervals
under the given assumptions.
In the following we always use a confidence level of 68% (corresponding
to the usual
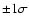 for Gaussian errors), or
for Gaussian errors), or
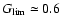 .
.
It will often happen that 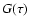 exceeds
exceeds
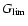 at one (or both) of
the extreme ages considered. In that case the confidence interval is
correspondingly truncated. Thus, if
at one (or both) of
the extreme ages considered. In that case the confidence interval is
correspondingly truncated. Thus, if
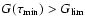 we set
we set
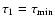 ,
while if
,
while if
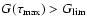 we set
we set
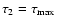 .
Effectively, this means that only an upper or lower
bound to the age can be set at the chosen confidence level, or possibly no
bound at all. In contrast, when the confidence interval is entirely within the
considered range (i.e., when
.
Effectively, this means that only an upper or lower
bound to the age can be set at the chosen confidence level, or possibly no
bound at all. In contrast, when the confidence interval is entirely within the
considered range (i.e., when
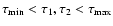 ),
we call our age estimate well-defined
(Nordström et al. 2004).
),
we call our age estimate well-defined
(Nordström et al. 2004).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.7cm,clip]{2185f04.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg138.gif) |
Figure 4:
Results of the Monte Carlo experiments described in
Sect. 3.6.
Each circle represents the statistics from 1000 experiments. The ordinate
is the fraction of experiments in which the true age falls within the
confidence interval defined by
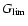 .
The solid curve is the
relation expected if .
The solid curve is the
relation expected if 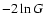 follows the chi-square distribution with
1 d.o.f., Eq. (14).
The experiments follow the theoretical relation rather well
except those for the points marked A, B, C and D in Fig. 3.
follows the chi-square distribution with
1 d.o.f., Eq. (14).
The experiments follow the theoretical relation rather well
except those for the points marked A, B, C and D in Fig. 3. |
| Open with DEXTER |
Having defined a confidence interval
![$[\tau_1,\tau_2]$](/articles/aa/full/2005/22/aa2185-04/img115.gif) it is also useful to
have a measure of the relative precision (
it is also useful to
have a measure of the relative precision (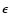 )
of the age
estimate. We define
)
of the age
estimate. We define
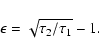 |
(15) |
This definition was chosen in order to cope with the whole
range of confidence intervals encountered in practice.
For small 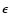 it agrees with any sensible representation of relative
precision, e.g.,
it agrees with any sensible representation of relative
precision, e.g.,
![$[\tau_1,\tau_2] = [0.99,~1.01]$](/articles/aa/full/2005/22/aa2185-04/img140.gif) gives
gives
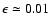 .
However, confidence intervals like
[0.5, 2.0] are much more typical for
age determinations, and it is then not obvious if the relative precision should be
expressed relative to the lower limit, the upper limit, or some mid-point of
the confidence interval. In this particular example our definition
leads to a relative precision of 100% (
.
However, confidence intervals like
[0.5, 2.0] are much more typical for
age determinations, and it is then not obvious if the relative precision should be
expressed relative to the lower limit, the upper limit, or some mid-point of
the confidence interval. In this particular example our definition
leads to a relative precision of 100% (
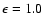 ).
).
It should be noted that a large value of the relative precision, e.g.
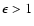 ,
does not imply the absence of age information; for
example,
,
does not imply the absence of age information; for
example,
![$[\tau_1,\tau_2] = [0,~1]$](/articles/aa/full/2005/22/aa2185-04/img144.gif) Gyr corresponds to infinite
Gyr corresponds to infinite 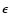 but would still provide a very meaningful upper limit on the age.
but would still provide a very meaningful upper limit on the age.
3.7 Defining the "best'' age estimate from the G function
As already emphasized, we need the complete G function to characterize
the available age information on a given star. Compressing this to a single
age estimate and confidence interval inevitably results in a loss of
information. For example, in Fig. 2, knowing the location
of the maximum and 68% confidence interval (i.e., where G>0.6) may
be enough to characterize the main peak, but completely ignores the
secondary maximum. When defining a "best'' age estimate the goal should be to
minimize the loss of relevant information in practical situations.
There are at least three natural choices for computing a unique age estimate
from the G function: the mean value (centre of gravity of the area under the
G curve), the median value (bisecting the area under the G curve), and the
mode (the position of the global maximum in G). We compared the behaviour
of the three estimates through Monte Carlo simulations of (initially) 7080
single stars. A constant SFR was assumed, with a Kroupa et al. (1993)
IMF in the range
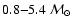 and a constant metallicity of
and a constant metallicity of
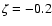 .
As it turns out, 4112 of the stars evolve out of the range of
the isochrones, leaving a sample of 2968 stars. For these we generated observed
data [Me/H],
.
As it turns out, 4112 of the stars evolve out of the range of
the isochrones, leaving a sample of 2968 stars. For these we generated observed
data [Me/H],
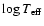 and MV with errors of 0.1 dex, 0.01 dex and
0.15 mag, respectively; see Fig. 5. For each star we then
calculated the G function and hence the age estimates corresponding to the
mean, median and mode.
and MV with errors of 0.1 dex, 0.01 dex and
0.15 mag, respectively; see Fig. 5. For each star we then
calculated the G function and hence the age estimates corresponding to the
mean, median and mode.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm,clip]{2185f05.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg146.gif) |
Figure 5:
HR diagram for the synthetic sample of 2968 stars generated as
described in the text. The assumed observational uncertainties in
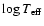 and MV are indicated in the lower-left corner
(in addition there is a
and MV are indicated in the lower-left corner
(in addition there is a 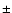 0.1 dex uncertainty in metallicity).
The isochrones are for 0, 1, 2, ..., 8, 10, 12 and 15 Gyr. 0.1 dex uncertainty in metallicity).
The isochrones are for 0, 1, 2, ..., 8, 10, 12 and 15 Gyr. |
| Open with DEXTER |
In Fig. 7 we compare the three age estimates with the true
ages for the 2968 stars in the synthetic data set. It is seen that the mean and
median behave similarly while the mode exhibits a different pattern. The
difference between the mode and the other estimators is mainly due to stars with
ages not well-defined in the sense of Sect. 3.6. These stars often
have very broad G functions that are cut off at the minimum and/or maximum
isochrone age, which tends to move the mean and median toward the center of the
age interval. The mode, on the other hand, may be located anywhere in the age
interval, but very often at the extreme ages (producing the "lines'' at the
top and bottom of the panel for the mode). Thus, while the mean and median
superficially appear to be better estimates than the mode (in the sense that
there are much fewer such points far away from the 1:1 line), they tend to be
deviously biased towards the middle of the full age range.
Considering only the subset of 937 stars with well-defined ages, much of these
differences between the three estimators disappear, and this is even more true
for the 193 stars that in addition obtain a relative precision
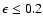 .
The left panels in Figs. 8 and 9 show
the mode versus true age for these subsets; we do not show the rather similar
plots for the mean and median.
.
The left panels in Figs. 8 and 9 show
the mode versus true age for these subsets; we do not show the rather similar
plots for the mean and median.
Although it is not easily seen in the scatter plots, there is a slight bias
towards lower ages in all the (sub-) samples and for all three estimators.
To estimate the size of this bias we fitted a bisector to each scatter plot,
i.e., a straight line through the origin dividing the stars into two equally
large groups. For well-defined ages the bisector slope is
between 0.93 and 0.95, depending on the estimator. In the
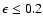 case the bisector slope is between 0.95 and 0.98. This 2-7% bias
towards lower ages is caused by the strongly asymmetric non-linearity of the mapping
from
case the bisector slope is between 0.95 and 0.98. This 2-7% bias
towards lower ages is caused by the strongly asymmetric non-linearity of the mapping
from 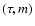 to
to
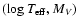 .
For any given position in the HR
diagram above the main sequence, the younger isochrones in a region around the
observed
position cover a wider mass interval than the older isochrones on the opposite
side (cf. Fig. 1). There are therefore more young
.
For any given position in the HR
diagram above the main sequence, the younger isochrones in a region around the
observed
position cover a wider mass interval than the older isochrones on the opposite
side (cf. Fig. 1). There are therefore more young 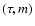 combinations that can "explain'' the observed data than old combinations.
combinations that can "explain'' the observed data than old combinations.
When a single value is required for the estimated age, we strongly
recommend to use the mode rather than the mean or median, because it avoids the
tendency of the latter to assign an age in the middle of the permitted range.
By contrast, the mode tends to assign an extreme age in such cases, which
clearly signals a bad estimate. Furthermore, when a confidence interval
is computed as in Sect. 3.6, the mode will always be within that
confidence interval, while this (highly desirable!) property cannot be
guaranteed for the mean or median.
Figure 6 is an HR diagram for the 937 stars in the synthetic
sample for which the ages are well-defined. Comparison with the full synthetic
sample in Fig. 5 shows that well-defined ages are normally
obtained for data points that are at least 1-2 standard deviations above
the isochrones for the most extreme ages considered. A relative precision
better than 20% (large dots in Fig. 6) is mainly achieved
in a band some 1-2 mag above the zero-age main sequence.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm,clip]{2185f06.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg149.gif) |
Figure 6:
Same as Fig. 5 but showing only the data for the
937 stars with well-defined ages according to the criterion in
Sect. 3.6. Large dots show the subset having a relative precision
(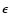 )
in age better than 20%. )
in age better than 20%. |
| Open with DEXTER |
3.8 Influence of undetected binaries
Thus far we have always assumed that we are dealing with single stars.
Binary (and multiple) stars are however the norm rather than the exception,
and it is important to quantify how this affects the age determinations.
Known binary systems can be removed from a sample or dealt with in other
manners, but a certain fraction of undetected binary systems is unavoidable
in most samples and could pose a problem.
An unresolved secondary
affects the observed parameters of a star in different ways depending on
the mass ratio (
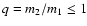 )
of the components and their evolutionary
status. On or near the main sequence, a small q means that the primary
completely dominates the light and there will be no perceptible change in
the observational data. For systems with comparable masses the effects may
be quite large, and in the worst case, when q=1, the MV of a binary system
is 0.75 mag brighter than the corresponding single star. This usually leads to
a (sometimes considerable) overestimation of the age.
)
of the components and their evolutionary
status. On or near the main sequence, a small q means that the primary
completely dominates the light and there will be no perceptible change in
the observational data. For systems with comparable masses the effects may
be quite large, and in the worst case, when q=1, the MV of a binary system
is 0.75 mag brighter than the corresponding single star. This usually leads to
a (sometimes considerable) overestimation of the age.
To examine the overall statistical effect of unrecognized binaries on the age
determination of a stellar sample we used the synthetic sample from
Sect. 3.7 and added a random secondary to each of the stars. Two
cases were considered for the mass-ratio distribution: in the first case we
assumed a decreasing pdf
f(q) = 1.5 - q, somewhat similar to the empirical
mass-ratio distribution found by Duquennoy & Mayor (1991) for
field F, G and K dwarfs. In the second (worst-case) scenario every star was
given an equal-mass companion. For each system we calculated the total
MV and obtained an effective
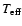 from the luminosity-weighted
mean of
from the luminosity-weighted
mean of
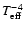 for the two components.
New age estimates were then computed for each system as for a single star.
for the two components.
New age estimates were then computed for each system as for a single star.
The middle and right panels in Figs. 8-9
show the results of the age determinations (using the mode) for the two cases
of a decreasing mass-ratio distribution and equal-mass components.
Figure 10 is a histogram of the shift in the estimated age caused
by the presence of the secondary.
As expected, the addition of secondary components usually causes the ages to
be overestimated, but the overall statistical effect is surprisingly small,
in particular for the decreasing mass-ratio distribution (note the logarithmic scale
of Fig. 10!). This can perhaps
be attributed to the fact that most of the stars for which useful ages can be
determined are located near the main-sequence turn-off point (cf. Fig. 6), where the age estimate is relatively insensitive to
a shift in MV. In fact, for the high-precision sample (
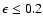 ,
Fig. 9, right panel, and the big dots in Fig. 6)
the binarity even tends to make the ages seem a bit too small.
The bisector slope in the middle and right panels of Fig. 9
is 0.97 and 1.13, respectively.
,
Fig. 9, right panel, and the big dots in Fig. 6)
the binarity even tends to make the ages seem a bit too small.
The bisector slope in the middle and right panels of Fig. 9
is 0.97 and 1.13, respectively.
We conclude that the overall effect of (undetected) binaries in a large
stellar sample is rather modest, compared with the typical statistical
uncertainties of
isochrone ages, unless there is a high fraction of equal-mass binaries in the
sample. However, any one single age determination may be very strongly affected
by the duplicity of that star.
![\begin{figure}
\par\includegraphics[width=16.7cm,clip]{2185f07.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg152.gif) |
Figure 7:
Estimated ages for the synthetic sample of 2968 single stars
(same as in Fig. 5) compared with the true values. From left
to right, the mean, median or mode of the G function was taken as
an estimate of the stellar age. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=16.7cm,clip]{2185f08.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg153.gif) |
Figure 8:
Estimated ages (using the mode of G) for the synthetic
sample of 937 stars with well-defined ages, compared with the true ages.
The left panel is for single stars (same sample as in Fig. 6);
for the middle and right panels secondary components have been added
with two different mass-ratio distributions (see Sect. 3.8
for details). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=16.7cm,clip]{2185f09.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg154.gif) |
Figure 9:
Same as Fig. 8 but for the subsample
with relative uncertainty
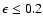 . . |
| Open with DEXTER |
4 Comparison with age estimates from conventional isochrone fitting
In this section we compare the Bayesian method of Sect. 3
with more "conventional'' methods, which are based on a direct comparison
of the observed data with theoretical isochrones. A range of techniques may
be used for the isochrone fitting, from simple visual inspection to highly
elaborated automatic procedures, and we therefore start by describing a
typical such procedure and then discuss how the errors are estimated.
For relevant sections of the HR diagram, stellar ages are conventionally
estimated by some variant of the following procedure. From the set of
isochrones for the 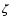 most closely matching the observed [Me/H]
(or two isochrone sets bracketing the observed value), the isochrone
passing through the observed point
most closely matching the observed [Me/H]
(or two isochrone sets bracketing the observed value), the isochrone
passing through the observed point
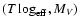 is found by visual or numerical interpolation, and
the corresponding age is assigned to the star. If two isochrone sets are
used to bracket the metallicity, a further interpolation to the observed
[Me/H] is required. The procedure is a simple practical recipe for
computing
is found by visual or numerical interpolation, and
the corresponding age is assigned to the star. If two isochrone sets are
used to bracket the metallicity, a further interpolation to the observed
[Me/H] is required. The procedure is a simple practical recipe for
computing
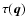 .
As discussed in Sect. 3.2, the
procedure is formally equivalent to minimizing the
.
As discussed in Sect. 3.2, the
procedure is formally equivalent to minimizing the 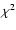 in Eq. (5)
or (under the assumption of Gaussian errors) to ML estimation. If the fitting
is made visually it is sometimes called "chi-by-eye''.
in Eq. (5)
or (under the assumption of Gaussian errors) to ML estimation. If the fitting
is made visually it is sometimes called "chi-by-eye''.
The age ambiguity resulting from overlapping isochrones can be resolved
on the grounds discussed in Sect. 3.2, viz., by selecting the
younger isochrone. For stars with solar-metallicity this occurs roughly
for
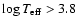 in a band some 1.5-2 mag above the ZAMS; for
low-metallicity stars it occurs at higher temperatures. (We do not consider
here evolutionary stages on and beyond the giant branch, where the
overlapping becomes much more severe.) It is thus possible to define
a unique inverse function
in a band some 1.5-2 mag above the ZAMS; for
low-metallicity stars it occurs at higher temperatures. (We do not consider
here evolutionary stages on and beyond the giant branch, where the
overlapping becomes much more severe.) It is thus possible to define
a unique inverse function
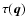 .
A more tricky question is
how to obtain an estimate of the uncertainty of the resulting age.
.
A more tricky question is
how to obtain an estimate of the uncertainty of the resulting age.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{2185f10.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg157.gif) |
Figure 10:
Histogram of the age error for binary systems, when their ages are
determined from the integrated photometry as for single stars. The full line
is for a decreasing mass-ratio distribution (see text), the dotted for
equal-mass binaries. The bin size is 0.25 Gyr. |
| Open with DEXTER |
4.1 Error estimates: The "step method''
If the uncertainties in the observed data are known, it is possible to
derive the uncertainty in the resulting age by examining how sensitive
it is to changes in the observed data. The method used by Ng &
Bertelli (1998, as described in Lachaume et al. 1999)
may be representative: from the observed data point
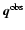 we take a step of one standard deviation in each direction along each
of the three axes; including the original point this gives a set of seven
points in the three-dimensional data space for which ages are obtained
through isochrone fitting. The mean value of the age estimates is adopted
as the final age, and the scatter among the ages is taken to be the
uncertainty of the mean value. (If some of the seven points fall outside
the region covered by the isochrones, the resulting age estimate may be
considered less reliable.)
We refer to this particular method as the "step method''. Superficially it
looks like a reasonable method, but actually it severely underestimates the
uncertainty, since only the error along one axis is considered at a time.
we take a step of one standard deviation in each direction along each
of the three axes; including the original point this gives a set of seven
points in the three-dimensional data space for which ages are obtained
through isochrone fitting. The mean value of the age estimates is adopted
as the final age, and the scatter among the ages is taken to be the
uncertainty of the mean value. (If some of the seven points fall outside
the region covered by the isochrones, the resulting age estimate may be
considered less reliable.)
We refer to this particular method as the "step method''. Superficially it
looks like a reasonable method, but actually it severely underestimates the
uncertainty, since only the error along one axis is considered at a time.
The effect is readily demonstrated by considering
classical error propagation based on the linearization
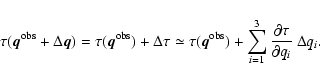 |
(16) |
Assuming uncorrelated, centred errors with standard deviations 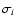 ,
i.e.,
,
i.e.,
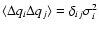 ,
we have
,
we have
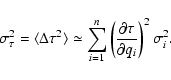 |
(17) |
On the other hand, also from Eq. (16), we have for the seven
selected points
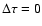 ,
,
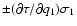 ,
,
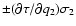 ,
and
,
and
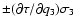 ;
their scatter
(sample standard deviation) is exactly
;
their scatter
(sample standard deviation) is exactly
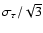 .
Thus, interpreting this scatter as the uncertainty of
.
Thus, interpreting this scatter as the uncertainty of 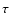 underestimates the standard error by a factor
underestimates the standard error by a factor 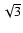 ,
compared with
what is obtained from the classical linear error propagation formula.
(The number 3 comes from the dimensionality of
,
compared with
what is obtained from the classical linear error propagation formula.
(The number 3 comes from the dimensionality of 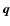 .)
A simple expedient to remedy this effect is to multiply the computed
error by
.)
A simple expedient to remedy this effect is to multiply the computed
error by 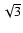 .
We call this the "corrected step method''.
.
We call this the "corrected step method''.
Other factors may however contribute to making the error estimate unreliable.
The strong non-linearity of
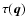 means that there is in general a
neglected contribution to the variance of
means that there is in general a
neglected contribution to the variance of 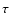 from truncated terms
in the Taylor expansion Eq. (16). Moreover, in the parts of the
HR diagram where the isochrones overlap, the required choice of
from truncated terms
in the Taylor expansion Eq. (16). Moreover, in the parts of the
HR diagram where the isochrones overlap, the required choice of
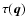 among the multiple possible solutions could statistically lead to an
underestimation of the ages and of their uncertainties.
among the multiple possible solutions could statistically lead to an
underestimation of the ages and of their uncertainties.
4.2 Error estimates: The Monte Carlo method
Monte Carlo (MC) simulation (Press et al. 1992) is often prescribed
as a reliable and robust tool for error estimation. Indeed, it should
effectively remove much of the difficulties caused by local non-linearity
(if not by overlapping isochrones). In the present context the MC technique
can be used as follows. A large number (N) of hypothetical data
points
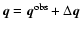 are generated for independent
Gaussian errors
are generated for independent
Gaussian errors
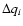 with the assumed standard deviations
with the assumed standard deviations 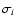 .
An age estimate
.
An age estimate
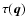 is computed for each point by isochrone
fitting and the sample standard deviation is adopted as the uncertainty
of the mean estimated age. (Alternatively, confidence intervals can
be estimated.) In contrast to the step method, errors in all dimensions
of the data space are considered simultaneously, and non-linearities of
is computed for each point by isochrone
fitting and the sample standard deviation is adopted as the uncertainty
of the mean estimated age. (Alternatively, confidence intervals can
be estimated.) In contrast to the step method, errors in all dimensions
of the data space are considered simultaneously, and non-linearities of
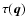 are taken into account because data points several standard
deviations from the observed values are also included in the statistics.
Note that some
are taken into account because data points several standard
deviations from the observed values are also included in the statistics.
Note that some 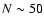 experiments are required for a 10% precision of
the error estimate, and some 5000 experiments if 1% precision is aimed at.
experiments are required for a 10% precision of
the error estimate, and some 5000 experiments if 1% precision is aimed at.
Table 1:
Results of numerical experiments comparing age determination
methods using the step method, the corrected step method, the Monte Carlo
method, and Bayesian estimation. Each line gives summary statistics from
1000 independent sets of synthetic data generated with the uncertainties
specified in the first three columns. All ages are in Gyr.
See Sect. 4.3 for further explanation.
4.3 Numerical examples
To compare the performance of our Bayesian estimation with the
conventional isochrone fitting techniques described above, we have
made extensive numerical simulations for the two representative cases
illustrated in Fig. 1.
In Case 1 we assume the following true stellar model
parameters:
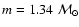 ,
,
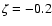 ,
,
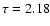 Gyr. The
corresponding true values of the observables are
Gyr. The
corresponding true values of the observables are
![$\mbox{[Me/H]}=-0.2$](/articles/aa/full/2005/22/aa2185-04/img104.gif) ,
,
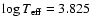 ,
MV=3.0, corresponding to the left point
in Fig. 1. The location of the star near the
turn-off point should make the age determination relatively
straightforward.
,
MV=3.0, corresponding to the left point
in Fig. 1. The location of the star near the
turn-off point should make the age determination relatively
straightforward.
In Case 2 the true parameters are:
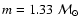 ,
,
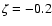 ,
,
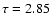 Gyr, corresponding to
Gyr, corresponding to
![$\mbox{[Me/H]}=-0.2$](/articles/aa/full/2005/22/aa2185-04/img104.gif) ,
,
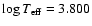 ,
MV=3.0. This is a region in the HR diagram
(right point in Fig. 1) where isochrone overlap may
be a problem.
,
MV=3.0. This is a region in the HR diagram
(right point in Fig. 1) where isochrone overlap may
be a problem.
For each case we generated 1000 synthetic sets of observational data
with the nominal errors (Sect. 2.5). The actual locations
of the data points in the HR diagram are therefore scattered about the
points indicated in Fig. 1 according to the error bars.
An equal number of synthetic data sets were generated with half and
twice the nominal errors. We then applied the various age determination
methods to each data set. Error estimates were obtained as
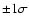 ,
as described in Sects. 4.1 and 4.2, while for the
Bayesian estimate the 68% CI was computed as in Sect. 3.6.
,
as described in Sects. 4.1 and 4.2, while for the
Bayesian estimate the 68% CI was computed as in Sect. 3.6.
Results are summarized in Table 1 in the form of the following
statistics:
- 1.
- The median
![[*]](/icons/foot_motif.gif) of the estimated ages,
of the estimated ages,
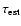 .
This should
ideally equal the true age,
.
This should
ideally equal the true age,
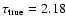 Gyr (Case 1) or
2.85 Gyr (Case 2). The deviation from these values is the bias of
the estimator.
Gyr (Case 1) or
2.85 Gyr (Case 2). The deviation from these values is the bias of
the estimator.
- 2.
- The median of the error estimate
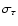 (or error limits
according to the CI), indicating the formal precision of the estimator.
In the table this statistic is indicated by a
(or error limits
according to the CI), indicating the formal precision of the estimator.
In the table this statistic is indicated by a  sign.
sign.
- 3.
- The percentage of data points for which the true age falls within the
computed error limits. This number, which ideally should be 68%,
is given within parentheses in the table. It indicates whether the
preceding error limits are statistically realistic.
- 4.
- The median of the absolute deviation from the true age,
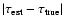 .
This indicates the overall accuracy
of the estimator, including bias, and is given in square brackets.
For unbiased Gaussian errors, the median absolute deviation is
.
This indicates the overall accuracy
of the estimator, including bias, and is given in square brackets.
For unbiased Gaussian errors, the median absolute deviation is
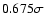 .
.
The results in Table 1 show some interesting trends:
-
From the median
 (item 1) we see that the bias is
predominantly negative in Case 1 for all estimators, although quite
small (at most -6%). This is consistent with the general bias
discussed in Sect. 3.7. In Case 2, however, the step and
MC methods produce a positive bias, generally increasing with the
observational errors (up to +13%), while the Bayesian estimate
goes in the opposite direction (up to -9%).
(item 1) we see that the bias is
predominantly negative in Case 1 for all estimators, although quite
small (at most -6%). This is consistent with the general bias
discussed in Sect. 3.7. In Case 2, however, the step and
MC methods produce a positive bias, generally increasing with the
observational errors (up to +13%), while the Bayesian estimate
goes in the opposite direction (up to -9%).
-
The percentages in parentheses (item 3) show that all the error
estimates are fairly realistic, except for the uncorrected step
method, which (as expected from Sect. 4.1) severly
underestimates the errors.
-
The corrected step method and MC method perform about equally
well, but the Bayesian method nearly always gives smaller formal
(item 2) and actual (item 4) errors. In the limit of vanishing
observational errors the three methods should converge, as they
clearly do at least in Case 1.
Although it may be hazardous to draw general conclusions from
such a limited comparison, the results support our contention,
based on the theoretical arguments in Sect. 3,
that Bayesian estimation provides a more robust and accurate
method for the determination of stellar ages than conventional
isochrone fitting methods. This appears to be the case especially
when the observational uncertainties are relatively large.
5 Application of the Bayesian age estimator
In Sect. 3 we described a general method to estimate
the age of an individual star from the relative posterior probability
density function 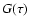 ,
as well as several tests based on simulated
data. In this section we present results obtained by applying the method
to real data, including a limited comparison with other age estimates
obtained by isochrone fitting. The statistical combination of G functions
is briefly discussed in Sect. 5.2, where the method is applied
to the two open clusters IC 4651 and M 67.
,
as well as several tests based on simulated
data. In this section we present results obtained by applying the method
to real data, including a limited comparison with other age estimates
obtained by isochrone fitting. The statistical combination of G functions
is briefly discussed in Sect. 5.2, where the method is applied
to the two open clusters IC 4651 and M 67.
5.1 Ages of individual field stars
5.1.1 The Geneva-Copenhagen survey of the Solar neighbourhood
The most extensive application to date of our method has been for the
Geneva-Copenhagen survey of F and G dwarfs in the Solar
neighbourhood (Nordström et al. 2004). From the
total sample of 16 682 stars, age estimates were obtained for 13 679 stars, of which 11 468 are well-defined according to our criterion
in Sect. 3.6. We refer to that paper for an extensive discussion
of the astrophysical biases that may affect these age determinations,
in addition to the statistical effects addressed above.
It should be
noted that Nordström et al. (2004) found it necessary
to make an empirical adjustment of the temperature scale for the
metal-deficient models (
![$\mbox{[Fe/H]}<-0.3$](/articles/aa/full/2005/22/aa2185-04/img206.gif) ), in order to obtain
agreement with the observed lower main sequence. No such
adjustment has been used in the present paper, which focuses on the
computational techniques.
), in order to obtain
agreement with the observed lower main sequence. No such
adjustment has been used in the present paper, which focuses on the
computational techniques.
As an external check, Nordström et al. (2004) compared
the ages derived by the present method with those by Edvardsson et al. (1993). For the 160 stars in common where our method gives
well-defined ages according to the criterion in Sect. 3.6, the
ages agree well for the oldest stars (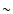 10 Gyr), while for the
younger stars Edvardsson et al. (1993) obtained slightly
higher ages (by about 20% at 2 Gyr). The scatter about the 1:1 line
in a
10 Gyr), while for the
younger stars Edvardsson et al. (1993) obtained slightly
higher ages (by about 20% at 2 Gyr). The scatter about the 1:1 line
in a
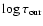 -
-
 diagram (see their
Fig. 8) is 0.12 dex (
diagram (see their
Fig. 8) is 0.12 dex (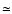 32%), scarcely more than the
32%), scarcely more than the 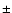 0.1 dex
uncertainty estimated by Edvardsson et al. (1993) for
their data. Given the many improvements in stellar models, calibrations
and distances since the earlier study, the overall agreement is quite
gratifying.
0.1 dex
uncertainty estimated by Edvardsson et al. (1993) for
their data. Given the many improvements in stellar models, calibrations
and distances since the earlier study, the overall agreement is quite
gratifying.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm,clip]{2185f11.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg211.gif) |
Figure 11:
A comparison of our age estimates and confidence intervals
with those of Lachaume et al. (1999) for a sample of
nearby stars. Only the stars with well-defined ages from both
sources have been included. |
| Open with DEXTER |
5.1.2 Comparison with Lachaume et al. (1999)
Apart from the limited comparison with Edvardsson et al. (1993)
described above we have made a more detailed comparison for the small
sample of nearby stars in Table A1 of Lachaume et al. (1999).
These authors explicitly give for each star the observational data
with assumed uncertainties, as well as the resulting ages and confidence
intervals, which makes a comparison relatively straightforward.
Adopting their observational data we find that 44 stars have ages that
are well-defined in both sets. The overall agreement is very good
(Fig. 11) in spite of the fact that Lachaume et al. (1999) used the older isochrone set by Bertelli et al. (1994). An unweighted linear regression gives
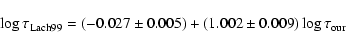 |
(18) |
(where  is in Gyr), with a scatter of 0.028 dex (7%). Thus our ages
are in the mean about 6% higher than those of Lachaume et al. In addition,
we find that our confidence intervals are systematically about 10% narrower.
Both differences can perhaps be
explained by the same effect as was seen for the Monte Carlo estimator in
Case 1 of Table 1, namely a tendency to underestimate the age
and overestimate the uncertainty. Equation (2) in Lachaume et al. (1999) is clearly the analytical equivalent of the Monte Carlo
method of Sect. 4.2, which should therefore give comparable results.
However, the situation is probably more complex, as illustrated by Case 2
in our Table 1, where the biases go in the opposite direction.
In any case the very small scatter shows that the two methods give quite
similar results for this particular sample with rather small observational
uncertainties. This is consistent with the results in Sect. 4.3.
is in Gyr), with a scatter of 0.028 dex (7%). Thus our ages
are in the mean about 6% higher than those of Lachaume et al. In addition,
we find that our confidence intervals are systematically about 10% narrower.
Both differences can perhaps be
explained by the same effect as was seen for the Monte Carlo estimator in
Case 1 of Table 1, namely a tendency to underestimate the age
and overestimate the uncertainty. Equation (2) in Lachaume et al. (1999) is clearly the analytical equivalent of the Monte Carlo
method of Sect. 4.2, which should therefore give comparable results.
However, the situation is probably more complex, as illustrated by Case 2
in our Table 1, where the biases go in the opposite direction.
In any case the very small scatter shows that the two methods give quite
similar results for this particular sample with rather small observational
uncertainties. This is consistent with the results in Sect. 4.3.
5.2 Ages of open clusters: The combination of G functions
In an open cluster the population is coeval and the age estimates of
the individual member stars should all be consistent with a single age.
This can be used to test the consistency of age estimates obtained with
our method. However, the prior information that the stars are coeval can
be used much more powerfully in the Bayesian context, namely to estimate
the age of the cluster. Recall that the relative posterior probability
density for the age of an individual star (i) is given by its G function  .
Assuming that the n stars in a cluster are all single,
members of the cluster, and coeval, and that their observational data are
independent, it follows that the relative posterior probability density for
the cluster age is simply given by the product
.
Assuming that the n stars in a cluster are all single,
members of the cluster, and coeval, and that their observational data are
independent, it follows that the relative posterior probability density for
the cluster age is simply given by the product
 .
The cluster age and a confidence interval can be derived from
this product as for an individual star.
.
The cluster age and a confidence interval can be derived from
this product as for an individual star.
Determining the age of a cluster can be regarded as a special case of the
more general (and much more difficult) problem to determine the star formation
history of a stellar population. In the same sense, taking the product of
the G functions solves a special case of the general integral equation for
the SFR as formulated e.g. in Hernandez et al. (2000).
While the more general problem will be addressed in a future paper, we here
apply the simple multiplication method to determine the ages of IC 4651 and
M 67, using data from the literature. In these applications we neglect
differential reddening (which is small in these clusters) as well as the
radial extent of the clusters (contributing 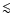 0.03 mag to the scatter in
MV), i.e., we assume that the same reddening and distance modulus apply
to all stars in the cluster.
0.03 mag to the scatter in
MV), i.e., we assume that the same reddening and distance modulus apply
to all stars in the cluster.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm,clip]{2185f12.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg217.gif) |
Figure 12:
HR diagram for 23 stars in IC 4651, together with isochrones at
![$\mbox{[Me/H]}=+0.1$](/articles/aa/full/2005/22/aa2185-04/img216.gif) for the best-fitting age 1.56 Gyr (solid line), and for
1.3 and 1.9 Gyr (dashed). The symbols are: filled circles - well-defined
ages with
for the best-fitting age 1.56 Gyr (solid line), and for
1.3 and 1.9 Gyr (dashed). The symbols are: filled circles - well-defined
ages with
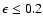 (as in panel c of Fig. 13);
open circles - well-defined ages with
(as in panel c of Fig. 13);
open circles - well-defined ages with
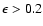 (panel b);
crosses - not well-defined ages (panel a).
(panel b);
crosses - not well-defined ages (panel a). |
| Open with DEXTER |
5.2.1 The age of the open cluster IC 4651
Meibom (2000) and Meibom et al. (2002) studied the
intermediate-age open cluster IC 4651 in great detail, providing
Strömgren photometry from which individual estimates of
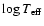 and [Me/H] can be obtained, as well as diagnostics for duplicity [
and [Me/H] can be obtained, as well as diagnostics for duplicity [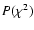 ]
and membership [P(RV)] based on multi-epoch radial velocities. From
Table 1 in Meibom et al. (2002) we found 33 stars with
]
and membership [P(RV)] based on multi-epoch radial velocities. From
Table 1 in Meibom et al. (2002) we found 33 stars with
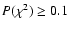 and
and
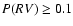 ,
which sample should therefore be relatively
clean from (spectroscopic) binaries and non-members. Using the calibrations
in Nordström et al. (2004), estimates of
,
which sample should therefore be relatively
clean from (spectroscopic) binaries and non-members. Using the calibrations
in Nordström et al. (2004), estimates of
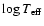 and [Me/H] could be obtained for 23 of these stars (Holmberg, private comm.),
assuming a reddening of
Eb-y=0.071 mag (Meibom et al. 2002).
The mean metallicity was found to be
and [Me/H] could be obtained for 23 of these stars (Holmberg, private comm.),
assuming a reddening of
Eb-y=0.071 mag (Meibom et al. 2002).
The mean metallicity was found to be
![$\mbox{[Me/H]}=0.11\pm 0.05$](/articles/aa/full/2005/22/aa2185-04/img221.gif) ,
in good
agreement with previous determinations, e.g., Meibom et al. (2002)
who find
,
in good
agreement with previous determinations, e.g., Meibom et al. (2002)
who find
![$\mbox{[Fe/H]}=0.13\pm 0.05$](/articles/aa/full/2005/22/aa2185-04/img222.gif) .
.
Meibom et al. (2002) also found a true distance modulus of 10.03 mag
to IC 4651 based on a direct fit to the Hyades main sequence. In comparison with
theoretical isochrones they found however a better fit for an assumed distance
modulus of 9.72-9.80 mag. For calculating MV we assume a true distance
modulus of 9.80 (corresponding to an apparent distance modulus of 10.105 mag),
which we find gives more consistent age estimates than using 10.03 mag.
Figure 12 shows the resulting HR diagram for the final sample
of 23 stars.
Figure 13 shows the G functions for the 23 probable single
members of IC 4651. The dashed line shows the threshold
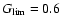 used to compute confidence intervals. The curves are grouped in panels (a)-(c)
according to whether the ages are well-defined and their relative precisions
used to compute confidence intervals. The curves are grouped in panels (a)-(c)
according to whether the ages are well-defined and their relative precisions
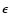 .
In the HR diagram these are marked by different symbols.
The mean value of the 10 best age estimates in panel (c) is
.
In the HR diagram these are marked by different symbols.
The mean value of the 10 best age estimates in panel (c) is
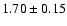 Gyr,
identical to the best estimate for the age of IC 4651 by
Meibom et al. (2002).
Gyr,
identical to the best estimate for the age of IC 4651 by
Meibom et al. (2002).
The fourth panel (d) in Fig. 13 shows the re-normalized product of
all 23 G functions. As previously explained, this product can under certain
assumptions be interpreted as the posterior pdf of the cluster age, and leads
to an estimated cluster age of
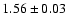 Gyr. However, this result (and
in particular the very small error limits) should not be over-interpreted -
for example, the assumption of independent astrophysical data for the different
stars is clearly violated since we have to assume a common distance modulus
for the cluster. Of the 23 stars, 13 (56%) have confidence intervals for
their individual age estimates that include the value 1.56 Gyr, while the
expected number is 68% or
Gyr. However, this result (and
in particular the very small error limits) should not be over-interpreted -
for example, the assumption of independent astrophysical data for the different
stars is clearly violated since we have to assume a common distance modulus
for the cluster. Of the 23 stars, 13 (56%) have confidence intervals for
their individual age estimates that include the value 1.56 Gyr, while the
expected number is 68% or 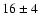 .
The individual age estimates are thus
consistent with the derived cluster age.
.
The individual age estimates are thus
consistent with the derived cluster age.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.7cm,clip]{2185f13.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg226.gif) |
Figure 13:
Panels a)- c) show the G functions for the 23 stars in
Fig. 12, subdivided according to the quality of the age
estimates: a) - not well-defined; b) - well-defined with
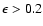 ;
c) - well-defined with ;
c) - well-defined with
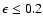 .
Panel d)
shows the product of all 23 G functions, normalized to G=1 at the
mode. This combined G function gives an estimated cluster age of .
Panel d)
shows the product of all 23 G functions, normalized to G=1 at the
mode. This combined G function gives an estimated cluster age of
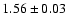 Gyr. Gyr. |
| Open with DEXTER |
In Fig. 12 we also plot the isochrones for 1.30, 1.56 and 1.90 Gyr,
corresponding to a logarithmic uncertainty interval of
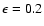 around the
estimated cluster age. As expected, the 10 stars with the best individual age
estimates (filled circles) are mostly located around the turn-off point. However,
one of them (MEI 9745) is conspicuously located
around the
estimated cluster age. As expected, the 10 stars with the best individual age
estimates (filled circles) are mostly located around the turn-off point. However,
one of them (MEI 9745) is conspicuously located  0.7 mag above the main
sequence (a binary?), resulting in the highest individual age estimate
(
0.7 mag above the main
sequence (a binary?), resulting in the highest individual age estimate
(
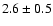 Gyr) in the sub-sample. Eliminating this star gives a mean estimated
age of
Gyr) in the sub-sample. Eliminating this star gives a mean estimated
age of
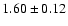 Gyr for the remaining 9 stars. The situation illustrates a
potential source of bias when combining individual age estimates, namely
that the stars with the most precise age estimates tend to be located above
the main sequence (cf. Fig. 6) and therefore often associated
with estimated ages that are too high (viz., if they are scattered from an
actual location closer to the main sequence). The use of G functions
helps to eliminate this effect: for instance, in Fig. 13 the
combined G function rigorously takes into account also the four stars
where the isochrones only give an upper limit to the age (panel (a) and
the crosses in Fig. 12).
Gyr for the remaining 9 stars. The situation illustrates a
potential source of bias when combining individual age estimates, namely
that the stars with the most precise age estimates tend to be located above
the main sequence (cf. Fig. 6) and therefore often associated
with estimated ages that are too high (viz., if they are scattered from an
actual location closer to the main sequence). The use of G functions
helps to eliminate this effect: for instance, in Fig. 13 the
combined G function rigorously takes into account also the four stars
where the isochrones only give an upper limit to the age (panel (a) and
the crosses in Fig. 12).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm,clip]{2185f14.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg231.gif) |
Figure 14:
HR diagram for 412 stars in the M 67 region, together with
isochrones at
![$\mbox{[Me/H]}=0.02$](/articles/aa/full/2005/22/aa2185-04/img230.gif) for 4.05 Gyr (solid line), 3.4 and
4.9 Gyr (dashed line). The symbols are: filled circles - well-defined
ages with
for 4.05 Gyr (solid line), 3.4 and
4.9 Gyr (dashed line). The symbols are: filled circles - well-defined
ages with
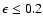 (as in panel c of Fig. 15);
open circles - well-defined ages with
(as in panel c of Fig. 15);
open circles - well-defined ages with
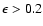 (panel b);
crosses - not well-defined ages (panel a); small dots - no
solution by Eq. (12).
(panel b);
crosses - not well-defined ages (panel a); small dots - no
solution by Eq. (12). |
| Open with DEXTER |
5.2.2 The age of the open cluster M 67
The data used for IC 4651 are unusually clean, and could therefore be
considered an "easy'' test case. A more challenging test is offered by
M 67. This old ( 4 Gyr), well-studied open cluster
(see Sandquist 2004, and references therein) is known to
have a large binary population as well as a number of blue stragglers
(Fan et al. 1996), and is at an age where the morphology of
the isochrones near the turn-off point is particularly complex and
sensitive to model assumptions (e.g., convective core overshooting).
4 Gyr), well-studied open cluster
(see Sandquist 2004, and references therein) is known to
have a large binary population as well as a number of blue stragglers
(Fan et al. 1996), and is at an age where the morphology of
the isochrones near the turn-off point is particularly complex and
sensitive to model assumptions (e.g., convective core overshooting).
Since the Padova isochrones give MI (Cousins) for each theoretical
model, we chose to compute the G functions directly with
q2=(V-I)0 replacing
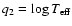 in Eq. (5),
rather than transforming colour indices to effective temperature.
We took V and V-I for 412 stars (some of them probably field
stars) from Laugalys et al. (2004), which appear to be
the most accurate such data currently available for M 67. (That study
gives V in the Vilnius system, which is equivalent to Johnson Vfor the range of colours considered; see Straizys 1973.)
The V-I are on the same scale as in Sandquist (2004),
and we adopt as in that paper the metallicity
in Eq. (5),
rather than transforming colour indices to effective temperature.
We took V and V-I for 412 stars (some of them probably field
stars) from Laugalys et al. (2004), which appear to be
the most accurate such data currently available for M 67. (That study
gives V in the Vilnius system, which is equivalent to Johnson Vfor the range of colours considered; see Straizys 1973.)
The V-I are on the same scale as in Sandquist (2004),
and we adopt as in that paper the metallicity
![$\mbox{[Fe/H]}=0.02$](/articles/aa/full/2005/22/aa2185-04/img233.gif) ,
total interstellar extinction
,
total interstellar extinction
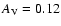 ,
and colour excess
EV-I=0.05. Following Sandquist (see his Fig. 14) we also
apply an empirical correction of -0.05 mag to the synthetic
(V-I)0 in the Padova isochrones. In order to get a good fit
to the main sequence a few magnitudes below the turn-off point, a
distance modulus of
(m-M)0=9.48 mag was assumed. This is intermediate
between the value 9.42 given by Laugalys et al. (2004) and
9.60 from Sandquist (2004), but consistent with both.
Figure 14 shows the HR diagram derived with these
assumptions.
,
and colour excess
EV-I=0.05. Following Sandquist (see his Fig. 14) we also
apply an empirical correction of -0.05 mag to the synthetic
(V-I)0 in the Padova isochrones. In order to get a good fit
to the main sequence a few magnitudes below the turn-off point, a
distance modulus of
(m-M)0=9.48 mag was assumed. This is intermediate
between the value 9.42 given by Laugalys et al. (2004) and
9.60 from Sandquist (2004), but consistent with both.
Figure 14 shows the HR diagram derived with these
assumptions.
G functions could be computed for 364 of the 412 stars (assuming
standard errors of 0.1 dex, 0.01 mag and 0.1 mag in [Me/H], (V-I)0and MV, respectively); a representative selection of them is shown in
Fig. 15. A combined G function was computed by multiplying
together the 364 individual G functions. To avoid numerical underflow and
stabilize the result a constant 0.01 was added to each G function before
multiplication![[*]](/icons/foot_motif.gif) .
The resulting combined G function, shown in panel (d) of Fig. 15,
is very sharp and corresponds to an age estimate of
.
The resulting combined G function, shown in panel (d) of Fig. 15,
is very sharp and corresponds to an age estimate of
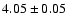 Gyr, in good agreement with Fan et al. (1996),
who find
Gyr, in good agreement with Fan et al. (1996),
who find
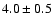 Gyr and Sandquist (2004), who also
find an age around 4 Gyr. The very small formal error in our estimate naturally
does not include the much bigger uncertainties from the colour transformation
and intrinsic model errors, but illustrates the statistical power of
the method. In contrast, many of the individual age estimates are too
small, mainly for the blue straggler population, and as a result the mean
value of the individual high-precision (
Gyr and Sandquist (2004), who also
find an age around 4 Gyr. The very small formal error in our estimate naturally
does not include the much bigger uncertainties from the colour transformation
and intrinsic model errors, but illustrates the statistical power of
the method. In contrast, many of the individual age estimates are too
small, mainly for the blue straggler population, and as a result the mean
value of the individual high-precision (
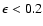 )
age estimates is
only 3.3 Gyr. Clearly the combined G function provides an extremely
robust estimate of the cluster age even in the presence of all these
complications.
)
age estimates is
only 3.3 Gyr. Clearly the combined G function provides an extremely
robust estimate of the cluster age even in the presence of all these
complications.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.7cm,clip]{2185f15.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg237.gif) |
Figure 15:
A random selection of some 50 G functions for the M 67 data,
subdivided according to the quality of the age estimates as in
Fig. 13. The combined G function in panel (d) gives an
estimated cluster age of
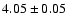 Gyr. Gyr. |
| Open with DEXTER |
6 Discussion
6.1 The Bayesian method in relation to some other
methods described in the literature
There are age determination methods described in the literature that more
or less resemble our method using G functions. Here, we briefly discuss how our
method differs from these. We do not consider the several variants of
isochrone interpolation (including 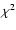 fitting, Sect. 4) used, e.g., by
Twarog (1980),
Edvardsson et al. (1993),
Pols et al. (1997),
Ng & Bertelli (1998),
Chen et al. (2000),
Liu & Chaboyer (2000),
Ibukiyama & Arimoto (2002), and
Lastennet & Valls-Gabaud (2002).
fitting, Sect. 4) used, e.g., by
Twarog (1980),
Edvardsson et al. (1993),
Pols et al. (1997),
Ng & Bertelli (1998),
Chen et al. (2000),
Liu & Chaboyer (2000),
Ibukiyama & Arimoto (2002), and
Lastennet & Valls-Gabaud (2002).
The Lachaume et al. (1999) method is in principle equivalent to
the Monte Carlo (MC) described in Sect. 2.5.
Lachaume et al. (1999) assume, as we have done, uncorrelated
Gaussian errors in the three observed variables
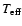 ,
MV, and
[Fe/H], from which they derive the probability density of the age,
,
MV, and
[Fe/H], from which they derive the probability density of the age,
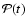 ,
somewhat similar to our G function.
,
somewhat similar to our G function.
Note, however, that
their Eq. (2) gives
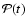 as an integral over the data space
as an integral over the data space
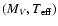 ,
neglecting the uncertainty in [Fe/H], whereas
our Eq. (10) gives G as an integral over the parameter space
,
neglecting the uncertainty in [Fe/H], whereas
our Eq. (10) gives G as an integral over the parameter space
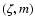 .
The difference is crucial, because it is only in parameter
space that the prior densities (in this case of m and
.
The difference is crucial, because it is only in parameter
space that the prior densities (in this case of m and 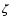 )
can be
properly defined, due to the non-unique inverse transformation from data to
parameters. The presence of the (non-unique) function
)
can be
properly defined, due to the non-unique inverse transformation from data to
parameters. The presence of the (non-unique) function
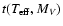 in their Eq. (2) clearly suggests a problem with their choice of
integration variables. Consequently, their
in their Eq. (2) clearly suggests a problem with their choice of
integration variables. Consequently, their
 does not take into
account the different prior probabilities of finding a star at different
locations in the HR diagram as a result of the varying rate of stellar
evolution.
does not take into
account the different prior probabilities of finding a star at different
locations in the HR diagram as a result of the varying rate of stellar
evolution.
The method used by Reddy et al. (2003) to obtain stellar ages
superficially resembles that of Lachaume et al. (1999), although
they use 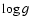 as one of the observables instead of MV. However, in
contrast to Lachaume et al. they perform the integration in the parameter
space (Mi,Z), where Mi (our m) is the initial mass (their Eq. (4)).
They consequently
avoid the non-uniqueness problem and effectively compute the posterior
probability density of the age assuming flat priors for Mi and Z.
However, in this calculation they only include the observed metallicity
by selecting insochrones with a metallicity
within 0.25 dex of the observed value.
as one of the observables instead of MV. However, in
contrast to Lachaume et al. they perform the integration in the parameter
space (Mi,Z), where Mi (our m) is the initial mass (their Eq. (4)).
They consequently
avoid the non-uniqueness problem and effectively compute the posterior
probability density of the age assuming flat priors for Mi and Z.
However, in this calculation they only include the observed metallicity
by selecting insochrones with a metallicity
within 0.25 dex of the observed value.
Hernandez et al. (1999, 2000) developed
a method to reconstruct the star formation history through inversion of
the HR diagram. This is a related, but from a statistical viewpoint quite
separate problem from the determination of individual isochrone ages, and
one that we will consider in a forthcoming paper. However, in their second
paper, the authors introduce an expression (their Eq. (2)) involving a
function Gi(t) of the age (t) of each observed star (i). This is
equivalent to our Eq. (10), except that
the latter is generalized to include any number of observables
(our Eqs. (4) and (5)).
Although Hernandez et al. (2000) do not discuss the
determination of individual stellar ages, the possibility is clearly
implied by their observation that Gi(t) "represents the probability
that a given star, i, was actually formed at time t with any mass'',
and consequently we have adopted our "G'' notation from that paper.
Pont & Eyer (2004) describe a Bayesian approach to the age
determination problem which has much in common with our method. Their
formulation leads to an expression for the posterior pdf of the age,
their Eq. (4), which (apart from minor differences in the choice of
variables) differs from our Eqs. (9) and (10) only in their
inclusion of the Jacobian
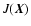 under the double integral.
They motivate this factor by the change of variables in the likelihood
function from the observables to the model parameters.
We believe that is incorrect, since the likelihood is by definition a
function of the model parameters (for given observed data). Nevertheless,
our computation of posterior densities (or G functions) agrees
well with that of Pont & Eyer for selected stars from the Edvardsson
et al. (1993) sample (their Fig. 8), indicating that their
Monte Carlo evaluation leads to results that are practically equivalent
to ours. Pont & Eyer (2004) do not explicitly discuss the choice
of age estimate or the assignment of confidence intervals based on the
posterior density.
under the double integral.
They motivate this factor by the change of variables in the likelihood
function from the observables to the model parameters.
We believe that is incorrect, since the likelihood is by definition a
function of the model parameters (for given observed data). Nevertheless,
our computation of posterior densities (or G functions) agrees
well with that of Pont & Eyer for selected stars from the Edvardsson
et al. (1993) sample (their Fig. 8), indicating that their
Monte Carlo evaluation leads to results that are practically equivalent
to ours. Pont & Eyer (2004) do not explicitly discuss the choice
of age estimate or the assignment of confidence intervals based on the
posterior density.
6.2 Limitations of the method
The calculation of G functions, on which the age estimation rests,
depends on a complex modelling of the observations in several steps,
each with its associated theoretical and practical uncertainties.
In a Bayesian sense, the adoption of a specific grid of theoretical
models - such as the Padova isochrones used in this paper - corresponds
to the a priori choice of a particular hypothesis about the
nature of the observed stars. We attempt to obtain age determinations
that are as good as possible within the framework of that particular
hypothesis, but it is clear that the use of an alternative set of physical
assumptions might have led to significantly different age estimates.
We have chosen to neglect
most of these problems in order to focus on the methodology.
In applications to real observations, however, several such issues
require more careful discussion than has been possible in
this paper. Specifically for the application to the Geneva-Copenhagen
survey (Sect. 5.1.1), we refer to the extensive discussion
in Nordström et al. (2004). Here, we shall only add
some general remarks concerning the various limitations of the method.
In spite of very considerable progress in the theoretical modelling
of stellar interiors and evolution, standard model grids still employ
highly simplified physical descriptions of the transport processes
(convection, overshooting, diffusion, etc.) and mass loss, and suffer
from some uncertainties in element abundances. Although the physical
simplifications are often masked by good formal fits to the observed
data obtained by adjusting ad hoc model parameters (such as the
mixing-length parameter), the uncertainties in the underlying physics
remain. For example, although the importance of convective core
overshooting for the evolution of stars with masses
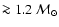 has been known for a long time
(e.g., Maeder & Mermillion 1981), the extent of the
overshooting, e.g. as function of mass, is still quite uncertain
(VandenBerg & Stetson 2004). Diffusive processes, which
affect both the evolutionary course and the surface abundances,
have only recently become possible to treat in a self-consistent way
(Michaud et al. 2004) and are not yet included in standard
model grids. On the upper main sequence, mass loss and rotation add to
the uncertainties;
for example, accounting for the rotation of O- and
early B-type stars could lead to ages larger by about 25% compared with
the use of non-rotating models (Maeder & Meynet 2000).
has been known for a long time
(e.g., Maeder & Mermillion 1981), the extent of the
overshooting, e.g. as function of mass, is still quite uncertain
(VandenBerg & Stetson 2004). Diffusive processes, which
affect both the evolutionary course and the surface abundances,
have only recently become possible to treat in a self-consistent way
(Michaud et al. 2004) and are not yet included in standard
model grids. On the upper main sequence, mass loss and rotation add to
the uncertainties;
for example, accounting for the rotation of O- and
early B-type stars could lead to ages larger by about 25% compared with
the use of non-rotating models (Maeder & Meynet 2000).
As a result of the physical inadequacies normally present even in
solar-type models, Young & Arnett (2005) estimate that the
predictive accuracy of such models is limited to some 5-10% in the
main physical parameters (luminosity, radius and effective temperature)
of stars other than the Sun. In terms of the position of the main sequence
turn-off point, such errors in the effective temperature would translate
into (systematic) age errors of order 25-100%. Of course, the
situation is not quite so bad for stars around
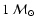 and solar metallicity, since all models are carefully tuned to
agree with the accurately known parameters of the Sun, including
its age. However, for increasingly non-solar masses and metallicities,
or more evolved stars, part of these uncertainties and systematic
errors certainly come into play.
and solar metallicity, since all models are carefully tuned to
agree with the accurately known parameters of the Sun, including
its age. However, for increasingly non-solar masses and metallicities,
or more evolved stars, part of these uncertainties and systematic
errors certainly come into play.
In a similar fashion, inadequacies in
classical (1D, LTE) model atmosphere calculations (which provide both the
outer boundary conditions for stellar interior models and the necessary
transformations from theoretical to observable quantities such as colour
indices) may be masked by semi-empirical corrections to the theoretical
transformations or the use of empirical colour-temperature relations.
The next generation of stellar atmosphere models (see, for example,
Asplund 2003; Hauschildt 2003, and references therein),
will no doubt eliminate some of these uncertainties, but do not yet
cover more than a limited range of the stellar parameters.
In the present context, the most embarrassing discrepancies between
theory and observations concern the location of the subdwarf sequence
(cf. Sect. 5.1.1) and the location and slope of the
red giant branch (cf. Fig. 14).
In Nordström et al. (2004) the theoretical isochrones
for subdwarfs were corrected by up to
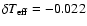 (at
(at
![$\mbox{[Fe/H]}=-1$](/articles/aa/full/2005/22/aa2185-04/img246.gif) ). If left uncorrected, this would translate
into an over-estimation of the ages (in terms of the location of
the turn-off point) by up to 50%. By empirically correcting the
temperature scale, one can hope that the resulting systematic error
in the age determinations is substantially reduced, but this cannot
be further quantified since the reasons for the discrepancy are
largely unknown (Lebreton 2001).
). If left uncorrected, this would translate
into an over-estimation of the ages (in terms of the location of
the turn-off point) by up to 50%. By empirically correcting the
temperature scale, one can hope that the resulting systematic error
in the age determinations is substantially reduced, but this cannot
be further quantified since the reasons for the discrepancy are
largely unknown (Lebreton 2001).
Concerning the location
of the red giant branch (RGB), different models predict differences
in
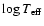 (for the same age, metallicity and luminosity)
by up to
(for the same age, metallicity and luminosity)
by up to 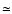 0.015 dex, while uncertainties in the transformation
to V-I (for example) may be
0.015 dex, while uncertainties in the transformation
to V-I (for example) may be 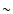 0.05 mag (Salaris 2002);
both correspond to an error in age by up to a factor 2-3 in either
direction. Given these uncertainties, and the sensitivity of its
location to metallicity,
the RGB is mainly useful for relative age
determination.
0.05 mag (Salaris 2002);
both correspond to an error in age by up to a factor 2-3 in either
direction. Given these uncertainties, and the sensitivity of its
location to metallicity,
the RGB is mainly useful for relative age
determination.
Of the many observational effects that influence the age determinations,
in addition to those discussed in previous sections,
we briefly mention photometric variability and interstellar extinction.
Unless repeated measurements are taken, the photometric data on a variable
star may not be representative of its average properties.
A total amplitude exceeding 0.1 mag may add significant
uncertainty to the age determination, especially if the different colour
bands are not observed simultaneously. Based on the survey part of the
Hipparcos and Tycho Catalogues (ESA 1997), we find that about
5% of the bright field stars are variable with a peak-to-valley amplitude
>0.1 mag; about half of these are very red giants (
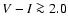 )
for
which reliable ages cannot be estimated anyway. Of the remaining, more than
half are main-sequence or sub-giant stars with
)
for
which reliable ages cannot be estimated anyway. Of the remaining, more than
half are main-sequence or sub-giant stars with
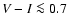 ,
most relevant
for age determination. Thus of the order 2% of the stars may be affected,
including early-type variables (
,
most relevant
for age determination. Thus of the order 2% of the stars may be affected,
including early-type variables (
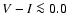 ),
), 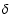 Scuti stars
(
Scuti stars
(
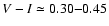 )
and eclipsing binaries (any V-I).
)
and eclipsing binaries (any V-I).
Interstellar reddening has a very direct impact on the ages determined for
stars near the turn-off point.
Moreover, from photometry alone it is difficult to determine an accurate
reddening for individual late-type stars because of its near-degeneracy
with effective temperature. Roughly speaking, an error in V-I of
0.01 mag corresponds to an age error of the order of 10%.
In clusters,
differential reddening and a non-standard extinction law (e.g., R greater
than the standard value 3.1) may contribute to uncertainties in both colour
and absolute magnitude.
In summary, several uncertainties of the theoretical models and
calibrations, as well as observational effects, limit the systematic
accuracy of the age determination, in addition to the statistical
uncertainties and biases discussed in previous sections. Except for
stars that are close to "solar-type'' in all its main parameters,
systematic errors caused by model inadequacies can easily reach
10% and more.
Other limitations of the present age determination method depend on
specific implementation details that could, at least in principle, easily
be modified. For example, as was pointed out in Sect. 2.1,
the use of ([Me/H],
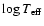 ,
MV) as "observables'' is to
some extent arbitrary and mainly motivated by present uncertainties in
the colour transformations. Given a better understanding of the latter,
which may be achieved with the new generation of stellar atmosphere
models, it will be straightforward to modify the method to use instead
the observed colour indices in any suitable multi-colour system. This
will, in addition, give a better handle on the correlations among the
observables, which can then be explicitly introduced in the likelihood
function by generalization of Eqs. (4) and (5).
In the meantime, the use of different colour systems may help to quantify
the systematic errors introduced by current model inadequacies, since a
correct model should of course give consistent age determinations in the
different systems.
,
MV) as "observables'' is to
some extent arbitrary and mainly motivated by present uncertainties in
the colour transformations. Given a better understanding of the latter,
which may be achieved with the new generation of stellar atmosphere
models, it will be straightforward to modify the method to use instead
the observed colour indices in any suitable multi-colour system. This
will, in addition, give a better handle on the correlations among the
observables, which can then be explicitly introduced in the likelihood
function by generalization of Eqs. (4) and (5).
In the meantime, the use of different colour systems may help to quantify
the systematic errors introduced by current model inadequacies, since a
correct model should of course give consistent age determinations in the
different systems.
Another limitation of the present implementation is the range of
stellar parameters and evolutionary stages covered by the Padova
isochrones. This can be overcome by the use of other (existing or future)
data sets; in principle the modification is straightforward but in
practice each set has its own particularities which require a separate
interface to be coded. Among the several possible extensions, the
inclusion of an additional parameter for the 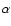 -element enhancement
is very desirable for a better treatment of metal-deficient stars.
To cope with young populations, it may be desirable to include
the pre-main-sequence phase (the Padova isochrones start at the zero-age
main sequence). These limitations are not important for the applications
discussed in this paper, but in a future implementation the incorporation
of, e.g., the Y2 isochrones (Yi et al. 2003) would add that
flexibility to the method.
-element enhancement
is very desirable for a better treatment of metal-deficient stars.
To cope with young populations, it may be desirable to include
the pre-main-sequence phase (the Padova isochrones start at the zero-age
main sequence). These limitations are not important for the applications
discussed in this paper, but in a future implementation the incorporation
of, e.g., the Y2 isochrones (Yi et al. 2003) would add that
flexibility to the method.
7 Conclusions
Conventional methods to determine stellar ages by isochrone interpolation
have a number of weaknesses, most of them related to the strongly non-linear
mapping from stellar model parameters (including age) to the observable data,
and sometimes manifested in severely underestimated (or overestimated) error
limits. Our alternative approach, founded on Bayesian techniques, avoids or
at least takes these weaknesses into account by systematically exploring
the relevant regions of parameter space. In practical terms it leads to
the calculation of a G function summarizing the posterior knowledge of
an individual stellar age, from which age estimates and confidence intervals
can be derived.
While undetected duplicity may lead to drastically wrong ages for
individual objects, we have found that the
statistical effects of binaries are rather modest, compared with the many
other uncertainties of the age determination, when considering a stellar
sample with a realistic binary frequency and mass ratio distribution.
Current and planned large-scale observational programmes in galactic
astrophysics, such as the Gaia mission (Perryman et al. 2001),
require highly automated, efficient and robust methods to classify
and characterize large samples of stars, including the provision of age
estimates. A main conclusion from the present analysis is that the
complex and highly non-linear morphology of isochrones makes
it difficult to assign unique age estimates, or even to define reasonable
confidence intervals, for given observational data except in the most
favourable cases and small observational errors. Moreover, selecting
stars based on the inferred quality of the age estimates will introduce
strong biases towards the more "favourable'' age intervals.
The G functions
are useful to characterize the age information independent of such
considerations, and moreover provide a starting point for estimating
the statistical properties of stellar samples, such as the history of
star formation rate. Simple applications are given in
Sect. 5.2, where the ages of two open clusters
are robustly derived by combining the G functions for the individual stars.
In a subsequent paper we explore a method to derive more generally the
star formation rate of a population from the G functions of a stellar
sample.
Acknowledgements
We are grateful to B. Nordström for giving the impetus to this study
in the context of the Geneva-Copenhagen survey. We thank J. Holmberg for
providing the data for IC 4651, J. Andersen, B. Nordström and S. Feltzing
for many valuable comments on the manuscript, and C. Tout and A. Kucinskas
for stimulating discussions on various aspects of the problem. Comments
by the Editor encouraged us to expand substantially the discussion of
possible errors. This work is supported by the Swedish National Space Board.
- Asplund, M. 2003,
in CNO in the Universe, ed. C. Charbonnel, D. Schaerer, & G.
Meynet, ASP Conf. Ser., 304, 275
(In the text)
- Bertelli, G.,
Bressan, A., Chiosi, C., Fagotto, F., & Nasi, E. 1994,
A&AS, 106, 275 [NASA ADS] (In the text)
- Casella, G.,
& Berger, R. L. 1990, Statistical inference (Belmont: Duxbury
Press)
(In the text)
- Chen, Y. Q., Nissen, P. E.,
Zhao, G., Zhang, H. W., & Benoni, T. 2000, A&AS, 141,
491 [EDP Sciences] [NASA ADS] (In the text)
- Duquennoy, A.,
& Mayor, M. 1991, A&A, 248, 485 [NASA ADS] (In the text)
- Edvardsson, B.,
Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] (In the text)
- ESA 1997, The Hipparcos and
Tycho Catalogues, ESA SP-1200
(In the text)
- Fan, X., Burstein, D., Chen,
J.-S., et al. 1996, AJ, 112, 628 [NASA ADS] [CrossRef] (In the text)
- Feltzing, S.,
Holmberg, J., & Hurley, J. R. 2001, A&A, 377, 911 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Fuhrmann, K. 2004, AN,
325, 3 [NASA ADS] (In the text)
- Girardi, L., Bressan,
A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [EDP Sciences] [NASA ADS] (In the text)
- Gómez, A. E.,
Grenier, S., Udry, S., et al. 1997, Proc. Hipparcos - Venice, ESA
SP-402, 621
(In the text)
- Hauschildt, P. H., Allard,
F., Baron, E., Aufdenberg, J., & Schweitzer, A. 2003, in GAIA
Spectroscopy, Science and Technology, ed. U. Munari, ASP Conf.
Ser., 298, 179
(In the text)
-
Hernandez, X., Valls-Gabaud, D., & Gilmore, G. 1999, MNRAS,
304, 705 [NASA ADS] [CrossRef] (In the text)
-
Hernandez, X., Valls-Gabaud, D., & Gilmore, G. 2000, MNRAS,
316, 605 [NASA ADS] [CrossRef] (In the text)
- Ibukiyama, A.,
& Arimoto, N. 2002, A&A, 394, 927 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Kroupa, P., Tout,
C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] (In the text)
- Lachaume, R.,
Dominik, C., Lanz, T., & Habing, H. J. 1999, A&A, 348,
897 [NASA ADS] (In the text)
- Lastennet, E.,
& Valls-Gabaud, D. 2002, A&A, 396, 551 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Laugalys, V.,
Kazalauskas, A., Boyle, R. P., et al. 2004, Baltic Astron., 13,
1 [NASA ADS] (In the text)
- Laws, C., Gonzalez, G.,
Walker, K. M., et al. 2003, AJ, 125, 2664 [NASA ADS] [CrossRef] (In the text)
- Lebreton, Y. 2001,
ARA&A, 38, 35 [NASA ADS] (In the text)
- Liu, W. H., & Chaboyer,
B. 2000, ApJ, 544, 818 [NASA ADS] [CrossRef] (In the text)
- Maeder, A., & Mermilliod, J.
C. 1981, A&A, 93, 136 [NASA ADS]
- Maeder, A., & Meynet, G.
2000, ARA&A, 38, 143 [NASA ADS]
- Meibom, S. 2000,
A&A, 361, 929 [NASA ADS] (In the text)
- Meibom, S., Andersen,
J., & Nordström, B. 2002, A&A, 386, 187 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Michaud, G., Richard, O.,
Richer, J., & VandenBerg, D. 2004, ApJ, 606, 452 [NASA ADS] [CrossRef]
- Mowlavi, N., Schaerer,
D., Meynet, G., et al. 1998, A&AS, 128, 471 [EDP Sciences] [NASA ADS] (In the text)
- Ng, Y. K., &
Bertelli, G. 1998, A&A, 329, 943 [NASA ADS] (In the text)
- Nordström,
B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Pagel, B. E. J., &
Portinari, L. 1998, MNRAS, 298, 747 [NASA ADS] [CrossRef] (In the text)
- Perryman, M. A. C., de
Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [EDP Sciences] [NASA ADS] (In the text)
- Pols, O. R., Tout, C. A.,
Schröder, K.-P., Eggleton, P. P., & Manners, J. 1997,
MNRAS, 289, 869 [NASA ADS] (In the text)
- Pont, F., & Eyer, L.
2004, MNRAS, 351, 487 [NASA ADS] [CrossRef] (In the text)
- Press, W. H., Teukolsky,
S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical
Recipes, 2nd ed. (Cambridge: Cambridge Univ. Press)
(In the text)
- Reddy, B. E., Tomkin, J.,
Lambert, D. L., & Allende Prieto, C. 2003, MNRAS, 340, 304 [NASA ADS] [CrossRef] (In the text)
- Salaris, M. 2002,
in Observed HR diagrams and stellar evolution, ed. T. Lejeune,
& J. Fernandes, ASP Conf. Ser., 274, 50
(In the text)
- Sandquist, E. L.
2004, MNRAS, 347, 101 [NASA ADS] [CrossRef] (In the text)
- Straizys, V.
1973, A&A, 28, 354 [NASA ADS] (In the text)
- Twarog, B. A. 1980,
ApJ, 242, 242 [NASA ADS] [CrossRef] (In the text)
- VandenBerg, D., & Stetson, P.
B. 2004, PASP, 116, 997 [NASA ADS] [CrossRef]
- Yi, S. K., Kim, Y.-C., &
Demarque, P. 2003, ApJS, 144, 259 [NASA ADS] [CrossRef] (In the text)
- Young, P. A., & Arnett, D.
2005, ApJ, 618, 908 [NASA ADS] [CrossRef]
Copyright ESO 2005
![\begin{displaymath}
\begin{array}{rcl}
\mbox{[Me/H]} &=& \log\left(Z/Z_\odot\rig...
...\zeta - \log\left[1-k\left(10^\zeta-1\right)\right]
\end{array}\end{displaymath}](/articles/aa/full/2005/22/aa2185-04/img44.gif)
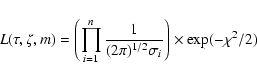
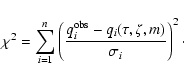
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm,clip]{2185f01.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg73.gif)
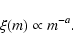
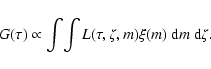
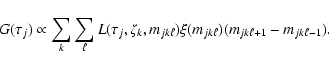
![\begin{figure}
\par\includegraphics[angle=-90,width=8.7cm,clip]{2185f02.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg105.gif)
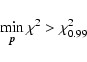
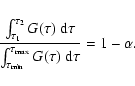
![\begin{displaymath}
1-\alpha = \mbox{Pr}[G(\tau)\ge G_{\rm lim}] \simeq 2\Phi\left(\!\sqrt{-2\ln G_{\rm lim}}\right)-1
\end{displaymath}](/articles/aa/full/2005/22/aa2185-04/img124.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.7cm,clip]{2185f03.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg129.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.7cm,clip]{2185f04.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg138.gif)
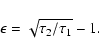
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm,clip]{2185f05.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg146.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm,clip]{2185f06.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg149.gif)
![\begin{figure}
\par\includegraphics[width=16.7cm,clip]{2185f07.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg152.gif)
![\begin{figure}
\par\includegraphics[width=16.7cm,clip]{2185f08.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg153.gif)
![\begin{figure}
\par\includegraphics[width=16.7cm,clip]{2185f09.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg154.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{2185f10.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg157.gif)
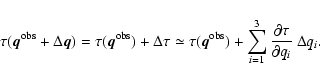
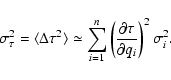
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm,clip]{2185f11.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg211.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm,clip]{2185f12.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg217.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.7cm,clip]{2185f13.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg226.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm,clip]{2185f14.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg231.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.7cm,clip]{2185f15.eps}\end{figure}](/articles/aa/full/2005/22/aa2185-04/Timg237.gif)