A&A 435, 191-199 (2005)
DOI: 10.1051/0004-6361:20041283
V. Suleimanov1,2,4 - M. Revnivtsev2,3 - H. Ritter 2
1 -
Kazan State University, Kremlevskaya
str. 18, 420008 Kazan, Russia
2 -
Max-Planck-Institut für
Astrophysik, Karl-Schwarzschild-Str. 1,
85741 Garching bei München, Germany
3 -
Space Research Institute, Russian Academy of
Sciences, Profsoyuznaya 84/32, 117810 Moscow, Russia
4 -
Astronomy Division, PO Box 3000, 90014 University of Oulu,
Finland
Received 13 May 2004 / Accepted 15 December 2004
Abstract
We present results of an analysis of broadband X-ray
spectra of 14 intermediate polars obtained with the RXTE observatory
(PCA and HEXTE spectrometers, 3-100 keV). For this we have
calculated theoretical models of the structure and the emergent
spectrum of the post-shock region of intermediate polars. By
fitting theoretical model spectra to the observed spectra
we derive estimates for the masses of the white dwarfs.
We compare the resulting masses with masses
obtained by other authors and other methods. The masses obtained by
us are smaller than the masses obtained by using PCA and GINGA
data, and they are in good agreement with the masses
derived from radial velocity studies.
Key words: stars: binaries: close - stars: binaries: spectroscopic - X-ray: binaries - stars: novae, cataclysmic variables
Intermediate polars (IP) form a sub-class of magnetic cataclysmic
variables (mCV) (Warner 1995). A white dwarf (WD) accretes
matter from a companion star (typically a red dwarf) that
fills its Roche lobe. This matter forms an accretion disc inside the
Roche lobe of the WD. The disc, however, is disrupted by
the WD magnetic field at some distance from the WD surface. As a
result the accreting matter freely falls on to the WD surface and
forms a strong shock near its surface. The post-shock matter has a
high temperature (![]() 10-20 keV) and emits X-rays via optical thin
thermal plasma emission (Lamb & Masters 1979).
10-20 keV) and emits X-rays via optical thin
thermal plasma emission (Lamb & Masters 1979).
The temperature of the post-shock matter depends on the WD mass and, therefore, the X-ray spectra of IPs can be used for WD mass determination (Rothschild et al. 1981). Ishida (1991) investigated IPs and polars by using GINGA/LAC observations. He fitted the X-ray spectra with single temperature bremsstrahlung models. Then WD masses were estimated by equaling the resulting best fit bremsstrahlung temperature to the maximal shock temperature. However, a significant part of the post shock region has cooler temperatures due to radiative cooling and, as mentioned by Ishida, WD masses obtained in this way should be considered as lower limits only.
In order to estimate the masses of WDs more precisely using X-ray spectra of IPs one needs to calculate the temperature and emissivity distribution in the post-shock region (PSR). The structure of the PSR was investigated by Aizu (1973), Wu et al. (1994), Woelk & Beuermann (1996), Cropper et al. (1999), see also Frank et al. (2002) and Wu (2000). Wu et al. (1994) and Woelk & Beuermann (1996) took into account cyclotron cooling, which can be important for polars. In these papers it was demonstrated that cyclotron cooling is not important for mCVs with surface magnetic fields less than 10 MG. The model of Wu et al. (1994) was used by Cropper et al. (1998, 1999) and Ramsay (2000) for the fitting of the IPs spectra observed by GINGA/LAC and RXTE/PCA respectively. Beardmore et al. (2000) used a simple analytical model of the PSR (see Frank et al. 2002) to analyse the spectra of V1223 Sgr observed by GINGA/LAC and ASCA. Ezucka and Ishida (1999) estimated the mass of the WD of nine IPs using emission lines ratios from ASCA observations.
The main systematic uncertainty in these works is caused by the fact
that neither the GINGA/LAC nor the RXTE/PCA detectors provide
information at energies ![]() 20 keV. Therefore, it is hard to
get solid estimates for the masses of the WDs if the mass is >0.6
20 keV. Therefore, it is hard to
get solid estimates for the masses of the WDs if the mass is >0.6
![]() ,
because in that case the maximal post-shock temperature
is >20 keV.
,
because in that case the maximal post-shock temperature
is >20 keV.
Moreover, the X-ray continuum of IPs in the range <20 keV is modified by interstellar and intrinsic absorption, and by a possible reflection component. The intrinsic absorption is not yet well understood due to the possible inhomogeneous and complex geometry of the accretion flow (Done & Magdziarz 1998). Usually simple models, such as a partial covering by a cold and a partially ionized absorber are used (see Croper et al. 1999; Beardmore et al. 2000). It is also clear that hard X-rays from the PSR are reflected by Compton scattering from the white dwarf surface which results in an additional continuum component (see Beardmore et al. 2000; Cropper et al. 1998). Therefore, it is difficult to determine the correct intrinsic X-ray continuum of the PSR from the observed spectra of IPs at energies less 20-25 keV and hence to derive reliable estimates for the white dwarf masses. As a result, the white dwarf masses obtained from X-ray continuum fitting are very often inconsistent with masses derived by other methods, e.g. from radial velocity studies (Schwope et al. 2002). All of the above-mentioned problems are less important if spectra which include the harder X-ray energy band (up to 100 keV), for example the total energy band of the RXTE observatory spectrometers (3-250 keV) are used.
On the other hand, WD masses derived from radial velocity studies are often not very reliable because the orbital inclination of a system is well known for eclipsing systems only. If the inclination angle is unknown, additional assumptions have to be made. In most cases this is done by prescribing a mass radius relation for the secondary which, in turn, is equivalent to assuming a secondary mass orbital period relation. However, the use of such assumptions can introduce a significant bias; for example, Belle et al. (2003) have obtained a mass of the WD in EX Hya which is two times larger than that obtained by Beuermann et al. 2003. While Belle et al. (2003) used a main sequence mass radius relation, Beuermann et al. (2003) determined the inclination from X-ray eclipse data. Therefore, it is necessary to compare the WD masses obtained by using X-ray data with WD masses obtained from optical methods. If both methods yield the same result, then this gives us more confidence in the resulting mass.
In this paper we present results of WD mass estimates for 14 bright IPs, obtained from broad-band (3-100 keV) RXTE spectra. Most of the analysed sources have a statistically significant signal at energies >10 keV. The observed spectra have been fitted with PSR model spectra. Details of the model are described in Sect. 2. We compare the WD masses resulting from our best fit parameters with WD masses that were obtained by other authors from X-ray data and by optical methods.
The structure of the stationary post-shock region in a
plane-parallel one-dimensional geometry is described (see e.g. Cropper
et al. 1999) by the mass continuity equation
Equation (1) has the integral
![\begin{figure}
\par\includegraphics[width=6cm,bb=0 166 355 509,clip]{1283fig1.eps}
\end{figure}](/articles/aa/full/2005/19/aa1283/Timg15.gif) |
Figure 1: Geometry of the post-shock region model. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1283fig2.ps}
\end{figure}](/articles/aa/full/2005/19/aa1283/Timg16.gif) |
Figure 2: Temperature and density profiles for one of the PSR models. The dashed lines show a simple analytic solution of the structure of the post shock region (Frank et al. 2002). |
| Open with DEXTER | |
Equations (2) and (3) can be rewritten using
Eq. (6) with the substitution z'=z0-z, where z0 is the
shock coordinate (see Fig. 1):
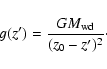 |
(9) |
![\begin{displaymath}R_{\rm wd} = 7.8 \times 10^8 ~{\rm cm }
\left [ \left (\frac...
...\rm wd}}{1.44
~ M_{\odot}} \right )^{2/3} \right ]^{1/2}\cdot
\end{displaymath}](/articles/aa/full/2005/19/aa1283/img25.gif)
In previous investigations (Cropper et al. 1998, 1999; Ramsay 2000; Beardmore et al. 2000) the MEKAL optically thin plasma code (Mewe et al. 1995) was used to calculate both the local continuum and the line emission. But most of the emission lines have energies less than 3 keV (with the exception of a line blend at 6-7 keV). Therefore, most of the emission lines are outside the spectral band (3-100 keV) considered by us.
As the RXTE/PCA detectors have a relatively poor spectral resolution and have adequate sensitivity only at energies higher than 3 keV we limited ourselves to the study of the continuum emission only. The emergent blend of lines at energies 6-7 keV in the resulting spectrum was mimicked by a broad Gaussian line. In the subsequent fitting of the observed spectra, the center and the width of that line were considered as free parameters.
The model of the emergent spectrum is calculated by summing
the local bremsstrahlung spectra:
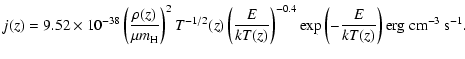 |
In order to compare the results of our model calculations with observations we have chosen data of the RXTE observatory that cover a relatively broad energy band (3-250 keV), where IPs release most of their emission. We limited ourselves only to relatively bright IPs, as we are interested in the hard X-ray (>20 keV) part of the spectra of IPs. The list of IPs consists of V1223 Sgr, FO Aqr, EX Hya, AO Psc, TV Col, GK Per, V709 Cas, PQ Gem, V2400 Oph, BG CMi, V405 Aur, V1062 Tau, DO Dra, and TX Col (see Table 1).
The RXTE/PCA and RXTE/HEXTE data were reduced by means of
standard tasks of the LHEASOFT/FTOOLS 5.2 package. The background
subtraction of the PCA detectors was done with the CMl7_240 model.
The subtraction of the background of the HEXTE detectors is especially
important in our case which concentrates on the hard X-ray part of the
spectrum of IPs. In order to monitor the background of the detectors,
HEXTE rocks by ![]()
![]() with respect to the target. We
analysed the HEXTE spectra of IPs only if the background spectra
obtained at the
with respect to the target. We
analysed the HEXTE spectra of IPs only if the background spectra
obtained at the
![]() and the
and the
![]() offset positions
were statistically compatible, in other words, if there were no
contaminating sources in the vicinity of our targets. The
accuracy of the background subtraction achieved with this method is
shown to be at a level of
offset positions
were statistically compatible, in other words, if there were no
contaminating sources in the vicinity of our targets. The
accuracy of the background subtraction achieved with this method is
shown to be at a level of ![]()
![]() (Rothschild et al.
1998). Practically for all the sources studied, the
systematic uncertainties of the background subtraction
are not important.
(Rothschild et al.
1998). Practically for all the sources studied, the
systematic uncertainties of the background subtraction
are not important.
Table 1: Summary of the RXTE observations used in this paper. PCA count rates represent count rates only from the upper layer of the PCU2 detector. HEXTE count rates are the count rates from one (of the two) clusters of detectors.
The X-ray spectra of the 14 IPs, extracted from the RXTE data are presented in Figs. 3-5.
For the fitting of the observed spectra we used results of our
model calculations described in the previous section with, in
addition, one or two (the latter only in the case of
the very bright IPs GK Per and V1223 Sgr) partial covering components.
We have tabulated the spectra of 51 models with WD masses
ranging from 0.3 to 1.3 ![]() at intervals of
0.02
at intervals of
0.02 ![]() and included them in the XSPEC spectral
fitting package (Arnaud 1996) for the subsequent fitting of
observed spectra of IPs. In contrast to the model used by
Cropper et al. (1998) our model lacks the reflected component.
However, as has been shown by Cropper et al. (1998),
taking into account the reflection changes the best fit white dwarf
mass only slightly. On the other hand, the inclusion of
spectral information at energies higher than
and included them in the XSPEC spectral
fitting package (Arnaud 1996) for the subsequent fitting of
observed spectra of IPs. In contrast to the model used by
Cropper et al. (1998) our model lacks the reflected component.
However, as has been shown by Cropper et al. (1998),
taking into account the reflection changes the best fit white dwarf
mass only slightly. On the other hand, the inclusion of
spectral information at energies higher than ![]() 20 keV helps us
to further reduce the influence of the reflected component on the
shape of the spectral cutoff.
20 keV helps us
to further reduce the influence of the reflected component on the
shape of the spectral cutoff.
The best fit parameters resulting from our models are presented in
Table 2. Using the observed and absorption-corrected fluxes of
the IPs we estimated their luminosities and mass accretion
rates. The best fit model is shown in Figs. 3-5 by a
solid line.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1283fg3a.ps}\hspace*{3mm}
\i...
...fg3e.ps}\hspace*{3mm}
\includegraphics[width=7cm,clip]{1283fg3f.ps}
\end{figure}](/articles/aa/full/2005/19/aa1283/Timg36.gif) |
Figure 3: Spectra of intermediate polars obtained with the RXTE observatory. Crosses denote PCA data, open circles - HEXTE data. The solid lines show the best fit model with parameters presented in Table 1. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1283fg4a.ps}\hspace*{3mm}
\i...
...fg4e.ps}\hspace*{3mm}
\includegraphics[width=7cm,clip]{1283fg4f.ps}
\end{figure}](/articles/aa/full/2005/19/aa1283/Timg37.gif) |
Figure 4: The same as Fig. 3. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1283fg5a.ps}\hspace*{3mm}
\includegraphics[width=7cm,clip]{1283fg5b.ps}
\end{figure}](/articles/aa/full/2005/19/aa1283/Timg38.gif) |
Figure 5: The same as Fig. 3. |
| Open with DEXTER | |
Table 2: Best fit model parameters and inferred physical system parameters. Here CF is the partial covering coefficient, F3-100 the observed X-ray flux in the 3-100 keV band, F0.1-100 the unabsorbed X-ray flux in the 0.1-100 keV band, both in 10-11 erg cm-2 s-1 units. The distances for V405 Aur, V709 Cas, PQ Gem and V2400 Oph are assumed.
Table 3: Comparison of different mass estimates. We present here masses obtained from broad band (3-100 keV) spectral fitting (Col. 2) and narrow band spectral fitting - our model (Cols. 3 and 4), work of Ramsay 2000 (Col. 5), work of Cropper et al. 1999 (Col. 6), and work of Ezucka & Ishida 1999 (Col. 7).
We compare the resulting estimates of the white dwarf masses
with those measured by other methods. In the catalogue of Cataclysmic
Variables (Ritter & Kolb 2003) there are only 5 intermediate
polars that have a spectroscopically measured mass. In
Fig. 6 we present a comparison of our mass estimates with those
given in the catalogue. It is seen that we have a relatively good
agreement, however the error bars of all these estimates are quite
large. The only system in which the WD likely has a higher mass
than we have obtained from our X-ray spectral modelling is GK
Per (during outburst). One possible explanation of this fact could be
the WD's fast rotation (
![]() s = 5.85 min).
s = 5.85 min).
In our model we have implicitly assumed that the
matter freely falls onto white dwarf surface from infinity. But, in
reality, the matter falls freely only from the
magnetospheric radius ![]() (Warner 1995):
(Warner 1995):
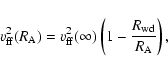
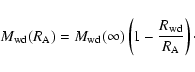
It is well known (e.g. Warner 1995) that accretion onto a
magnetized white dwarf is only possible if
![]() ,
where
,
where
![]() is the corotation radius,
i.e. the radius at which the Keplerian angular velocity equals
the white dwarf rotation angular velocity). Now, for GK Per the
ratio
is the corotation radius,
i.e. the radius at which the Keplerian angular velocity equals
the white dwarf rotation angular velocity). Now, for GK Per the
ratio
Among our targets are also other IPs in which the
white dwarf rotates relatively fast. These are: V709 Cas
(
![]() min), DO Dra (
min), DO Dra (
![]() min), and V405 Aur (
min), and V405 Aur (
![]() min). Because in
all these cases the ratio
min). Because in
all these cases the ratio
![]() and because the
spectra in question have been taken at minimum (see Table 2),
i.e. when
and because the
spectra in question have been taken at minimum (see Table 2),
i.e. when
![]() ,
the degree by which we
underestimate the white dwarf masses in these cases is much smaller
than in the case of GK Per and our mass estimates should be more
accurate.
,
the degree by which we
underestimate the white dwarf masses in these cases is much smaller
than in the case of GK Per and our mass estimates should be more
accurate.
![\begin{figure}
\includegraphics[width=8.1cm,clip]{1283fig6.ps}
\end{figure}](/articles/aa/full/2005/19/aa1283/Timg122.gif) |
Figure 6: Comparison of the masses of the white dwarfs as estimated from RXTE broadband spectra (this work) with estimates obtained by other methods. (1) - Beuermann et al. (2003); (2) - Crampton et al. (1986); (3) - Reinsch (1994); (4) - Haswell et al. (1997); (5) - Mateo et al. (1991); (6) - Friend et al. (1990); (7) - Hellier (1993); (8) - Penning (1985). |
| Open with DEXTER | |
Note that our mass estimates are in better agreement with those
obtained from optical methods than those obtained by Cropper et al.
(1999) from their analysis of GINGA/LAC X-ray spectra
(![]() 2-20 keV) (see Table 3). The masses obtained by Ramsay
(2000) from his analysis of RXTE/PCA (
2-20 keV) (see Table 3). The masses obtained by Ramsay
(2000) from his analysis of RXTE/PCA (![]() 2-20 keV) spectra are
closer to our estimates, but also slightly higher. A possible reason
for this difference could be the lack of the hard X-ray part in the
observed spectrum. We have also fitted our models to the
PCA data only (see Table 3). We thereby obtained results
which are very close to those obtained by Ramsay (2000).
We have also fitted the PCA data with constant
gravity models and obtained results which are practically
identical to those resulting from our models with variable gravity
(see also Table 3).
2-20 keV) spectra are
closer to our estimates, but also slightly higher. A possible reason
for this difference could be the lack of the hard X-ray part in the
observed spectrum. We have also fitted our models to the
PCA data only (see Table 3). We thereby obtained results
which are very close to those obtained by Ramsay (2000).
We have also fitted the PCA data with constant
gravity models and obtained results which are practically
identical to those resulting from our models with variable gravity
(see also Table 3).
It is interesting to note that the parameters listed in
Table 2 show a correlation of the mass accretion rate with the
strength of photoabsorption. That is, in principle, anticipated for
IPs because systems with higher mass accretion rates have higher ![]() values. A similar effect was observed by Ishida et al.
(1992) in the case of GK Per (quiescence and outburst spectra).
values. A similar effect was observed by Ishida et al.
(1992) in the case of GK Per (quiescence and outburst spectra).
Determining the mass of the white dwarf in cataclysmic
variables has been, and still is, a tricky business. Because the
number of known double-lined eclipsing systems which have their radial
velocities reliably measured and for which mass determinations are
straightforward is still very small (see e.g. Ritter & Kolb
2003), the majority of mass determinations which have been
published are based on additional and often not well-founded
assumptions. Consequently, the relaibility of the resulting masses is
difficult to asses. It is therefore important that magnetic
cataclysmic variables offer us an additional possibility
for determining the mass of the white dwarf. Accreted near the
magnetic poles the matter forms a shock wave above the
WD surface. The temperature and the emergent spectrum of
the hot, optically thin post-shock region (PSR) depend in
a first approximation on the mass of the white dwarf
only. Therefore it is possible to estimate WD masses in polars and
intermediate polars by fitting their hard X-ray spectra with
model spectra of the PSR. However, the temperature
of the PSR at the surface of a massive white dwarf
is so high, i.e. (10-30 keV) that a hard X-ray spectrum
emerges, the cutoff energy of which is barely within the
spectral bands of the ASCA, GINGA, and RXTE/PCA
spectrometers (![]() -20 keV) (see Ramsay 2000). Therefore,
to obtain reliable mass estimates for the white dwarf in IPs it is
necessary to take into account the flux distribution of the hard
X-rays emerging from the PSR.
-20 keV) (see Ramsay 2000). Therefore,
to obtain reliable mass estimates for the white dwarf in IPs it is
necessary to take into account the flux distribution of the hard
X-rays emerging from the PSR.
In this paper we present the WD masses of 14 IPs estimated from the fitting of broad band (3-100 keV) RXTE/PCA/HEXTE X-ray spectra with theoretical spectra of the PSR calculated by us. We have not taken into account cyclotron cooling in the PSR and, therefore, did not consider polars, where it can be important. Our estimates give lower WD masses than those obtained from GINGA/LAC (Cropper et al. 1999) and RXTE/PCA (Ramsay 2000) data. We also find satisfactory agreement between our WD mass estimates and those obtained by means of optical spectroscopic methods. In conclusion, this shows that it is absolutely necessary to use the hard X-ray data (E > 20 keV) to obtain reliable WD mass estimates in mCVs.
Acknowledgements
This work was supported by the DAAD Fellowship, Academy of Finland (grant 100488), the Jenny and Antti Wihuri Foundation, Russian Foundation of Fundamental Research (grant 02-02-17174) and by the President's program for support of leading science schools (grant NSh - 1789.2003.2).