W. F. Mahmoudi1 - N. Ben Nessib1 - M. S. Dimitrijevic2,3
1 - Groupe de Recherche en Physique Atomique et
Astrophysique, Faculté des Sciences de Bizerte, 7021 Zarzouna,
Tunisia
2 - Astronomical Observatory, Volgina 7, 11160 Belgrade,
Serbia
3 - Isaac Newton Institute of Chile, Yugoslavia Branch,
Serbia
Received 2 July 2004 / Accepted 8 November 2004
Abstract
Using a modified semiempirical approach, we have
calculated Stark broadening full widths at half maximum for 25 OII
multiplets for temperatures from 5000 K up to 80 000 K using the
needed oscillator strengths from the sophisticated atomic
structure data base TOPbase. Then we compared our results with
experimental data for 41 OII spectral lines and with the available
semi-classical calculations to test the applied method and the
accuracy of the results obtained.
Key words: line: profiles - atomic data
For Stark linewidth determination, Griem (1968)
suggested a simple semiempirical method based on Baranger's
original formulation (Baranger 1958, see also 1962), together with
the use of an effective Gaunt-factor approximation proposed by
Seaton (1962) and Van Regemorter (1962).
For singly ionized atoms, this semiempirical formula agrees on the
average within ![]()
![]() with experiments (Griem
1974). This formula has been modified by
Dimitrijevic & Konjevic (1980) to
minimize the atomic data needed and to extend its validity to
multiply charged ion lines. An effort has been made to obtain new
Stark broadening data with this modified formula (see
Dimitrijevic & Popovic 2001, and
references therein), especially in the case when more
sophisticated methods are not adequately applicable due to the
lack of needed atomic data.
with experiments (Griem
1974). This formula has been modified by
Dimitrijevic & Konjevic (1980) to
minimize the atomic data needed and to extend its validity to
multiply charged ion lines. An effort has been made to obtain new
Stark broadening data with this modified formula (see
Dimitrijevic & Popovic 2001, and
references therein), especially in the case when more
sophisticated methods are not adequately applicable due to the
lack of needed atomic data.
The aim of this paper is twofold: to provide new Stark broadening data for astrophysically important OII lines and to test the modified semiempirical approach (Dimitrijevic & Konjevic 1980). Also, we compared our results to available experimental and other theoretical results for OII.
Within the impact approximation, Baranger (1958) derived a quantum-mechanical expression for the width of an isolated line:
where W is FWHM (Full Width at Half Maximum) in units
of angular frequency and N is the electron concentration. The
symbols
![]() ,
,
![]() represent the inelastic cross sections for collisional transitions
to
represent the inelastic cross sections for collisional transitions
to
![]() ,
,
![]() from the initial (i)and final (f) levels of the optical transition respectively.
from the initial (i)and final (f) levels of the optical transition respectively.
![]() is the line width induced by elastic collisions. The
averaging in Eq. (1) has to be performed over the
electron velocity v distribution.
is the line width induced by elastic collisions. The
averaging in Eq. (1) has to be performed over the
electron velocity v distribution.
Within the framework of the dipole approximation, one may use
Bethe's relation (Bethe 1930)
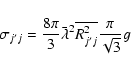 |
(2) |
For higher electron temperatures, Griem (1968) assumed that the contribution of elastic collisions to the line width can be neglected (cf. Eq. (1)) and made an attempt to take elastic collisions into account in the low temperature limit by extrapolating the threshold value of the inelastic cross section below the threshold. The Stark line width can then be calculated from the well-know semiempirical formula (Griem 1968)
Here,
![]() is the energy of the perturbing electron and
is the energy of the perturbing electron and
![]() is
the energy difference between level j and
is
the energy difference between level j and
![]() ( jand
( jand
![]() ,
,
![]() ,
,
![]() where i denotes initial and f final atomic energy level and
where i denotes initial and f final atomic energy level and
![]() ,
,
![]() are their corresponding perturbing levels), g(x)=0.20 for
are their corresponding perturbing levels), g(x)=0.20 for ![]() and
g(x)=0.24, 0.33, 0.56, 0.98, and 1.33 for x=3, 5,
10, 30, and 100. Also
and
g(x)=0.24, 0.33, 0.56, 0.98, and 1.33 for x=3, 5,
10, 30, and 100. Also
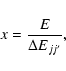 |
(4) |
![]() is the effective principal-, and lj the
orbital angular momentum-quantum numbers, while (Z-1) is the
ionic charge.
is the effective principal-, and lj the
orbital angular momentum-quantum numbers, while (Z-1) is the
ionic charge.
Table 1:
Experimental OII Stark widths ![]() ( FWHM), and
different calculations: the semi-classical values calculated by
Mahmoudi et al. (2004)
( FWHM), and
different calculations: the semi-classical values calculated by
Mahmoudi et al. (2004)
![]() ,
our data obtained
with the modified semiempirical approach (Dimitrijevic & Konjevic 1980)
,
our data obtained
with the modified semiempirical approach (Dimitrijevic & Konjevic 1980)
![]() and semi-classical values of Griem
(1974)
and semi-classical values of Griem
(1974)
![]() .
References: a. Platisa et al. (1975); b. del
Val et al. (1999); c. Djenize et al. (1998); d. Blagojevic
et al. (1999); e. Djenize et al. (1991), with e
.
References: a. Platisa et al. (1975); b. del
Val et al. (1999); c. Djenize et al. (1998); d. Blagojevic
et al. (1999); e. Djenize et al. (1991), with e![]() is
denoted the line where only the shift is reported by Djenize
et al. (1991) and f. Sreckovic et al. (2001). The data
indicated by
is
denoted the line where only the shift is reported by Djenize
et al. (1991) and f. Sreckovic et al. (2001). The data
indicated by ![]() are calculated here and not in the cited
paper. The
are calculated here and not in the cited
paper. The
![]() data for T=60000 K denoted by
data for T=60000 K denoted by ![]() are
extrapolated Griem (1974) values from Djenize et al.
(1991).
are
extrapolated Griem (1974) values from Djenize et al.
(1991).
If one uses Eq. (3) to calculate Stark line widths, we
need the same set of atomic data as for a more sophisticated
semi-classical method, and a lack of atomic data causes the same
difficulties for both methods in the evaluation of necessary
matrix elements. These difficulties are especially serious for
multiply-ionized atoms for which data on higher perturbing levels
are sometimes completely missing in the literature. Moreover for
multiply charged ions the Griem's semiempirical formula becomes
inapplicable. To overcome these problems, Dimitrijevic &
Konjevic (1980) have separated the transitions with
![]() and with
and with
![]() .
In the first case, only two
matrix elements are calculated for the initial state, one for the
transition array
.
In the first case, only two
matrix elements are calculated for the initial state, one for the
transition array
![]()
![]() and the other for
and the other for
![]()
![]() .
Also, only two
matrix elements are needed for the final state. The effective
Gaunt factor
.
Also, only two
matrix elements are needed for the final state. The effective
Gaunt factor
![]() for the transitions with the
principal quantum number n unchanged is taken as
for the transitions with the
principal quantum number n unchanged is taken as
![\begin{displaymath}g_{j^{{\prime }} j}=\frac{\sqrt{3}}{\pi }\left[ \frac{1}{2}+\...
...n_{j}^{\ast{2}}\Delta E_{j^{{\prime }} j}}\right) \right]\cdot
\end{displaymath}](/articles/aa/full/2005/17/aa1574/img55.gif) |
(8) |
For
![]()
where fij is the oscillator strength between levels i and
j, and for
![]()
where li is the orbital quantum number of the valence electron. In such a way Dimitrijevic & Konjevic (1980) extended the validity of the semiempirical method to multiply charged ions, and optimized the needed set of atomic data ensuring that the method is applicable when, due to the lack of atomic data, more sophisticated approaches are not adequately applicable.
When the wavelength of a particular line within the multiplet
differs significantly from the average wavelength
![]() of the whole multiplet, we use the following scaling
(Popovic et al. 2001):
of the whole multiplet, we use the following scaling
(Popovic et al. 2001):
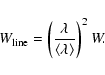 |
(11) |
In the above expression, W and
![]() are
values for the multiplet, and
are
values for the multiplet, and
![]() and
and ![]() refer to
a particular line within the multiplet.
refer to
a particular line within the multiplet.
The atomic energy levels and oscillator strengths for OII
have been taken from TOPbase (Cunto et al. 1993; Zeippen 1995). TOPbase does not provide mean square radii.
Therefore we have calculated them by
using the oscillator strengths (cf. Eq. (9)) and the effective quantum numbers
![]() obtained from the TOPbase (cf. Eq. (10)). By using the modified semiempirical approach
(Dimitrijevic & Konjevic 1980), we
have calculated Stark broadening widths of forty one OII spectral
lines. The obtained Stark FWHM values at various electron
temperatures and electron densities and comparisons with other
experimental and theoretical data are shown in Tables 1 and 2. With
obtained from the TOPbase (cf. Eq. (10)). By using the modified semiempirical approach
(Dimitrijevic & Konjevic 1980), we
have calculated Stark broadening widths of forty one OII spectral
lines. The obtained Stark FWHM values at various electron
temperatures and electron densities and comparisons with other
experimental and theoretical data are shown in Tables 1 and 2. With ![]() are denoted the
measured widths,
are denoted the
measured widths,
![]() is the electron-impact width
calculated by Mahmoudi et al. (2004) on the basis of
the semi-classical approach of Sahal-Bréchot
(1969a,b),
is the electron-impact width
calculated by Mahmoudi et al. (2004) on the basis of
the semi-classical approach of Sahal-Bréchot
(1969a,b),
![]() present calculations with the
modified semiempirical approach of Dimitrijevic and Konjevic (1980) (corresponding to Eqs. (6)-(10)), and
present calculations with the
modified semiempirical approach of Dimitrijevic and Konjevic (1980) (corresponding to Eqs. (6)-(10)), and
![]() the semi-classical approach by Griem (1974).
the semi-classical approach by Griem (1974).
Table 2:
Calculated OII widths for the transition array
![]() :
semi-classical (Griem
1974) values
:
semi-classical (Griem
1974) values ![]() calculated by Dimitrijevic
(1982), semi-classical (Sahal-Bréchot
1969a,b) values
calculated by Dimitrijevic
(1982), semi-classical (Sahal-Bréchot
1969a,b) values
![]() calculated by
Mahmoudi, Ben Nessib and Sahal-Bréchot (2004) and our calculation with
the modified semiempirical approach (Dimitrijevic & Konjevic 1980)
calculated by
Mahmoudi, Ben Nessib and Sahal-Bréchot (2004) and our calculation with
the modified semiempirical approach (Dimitrijevic & Konjevic 1980)
![]() .
.
![]() is the average wavelength for the multiplet.
is the average wavelength for the multiplet.
Calculated
![]() ratios are also
included in the Table 1. This ratio is a measure of the
completeness of the set of perturbing levels with respect to the
sums of dipole matrix elements and it is calculated from the
following relation
ratios are also
included in the Table 1. This ratio is a measure of the
completeness of the set of perturbing levels with respect to the
sums of dipole matrix elements and it is calculated from the
following relation
where in the summation enter terms for
![]() defined by Eq. (9) and terms for
defined by Eq. (9) and terms for
![]() by Eq. (10). For a
complete set of perturbing levels,
by Eq. (10). For a
complete set of perturbing levels,
![]() .
One can see in Table 1 that in all considered
cases
.
One can see in Table 1 that in all considered
cases
![]() is greater than 0, i.e.
the sum in Eq. (12) obtained with the help of Eqs. (9), (10) is larger than the sum (Eq. (5))
within the Coulomb approximation for up to
is greater than 0, i.e.
the sum in Eq. (12) obtained with the help of Eqs. (9), (10) is larger than the sum (Eq. (5))
within the Coulomb approximation for up to ![]() .
This
demonstrates that the introduction of a fictive common energy
level for all perturbing energy levels with
.
This
demonstrates that the introduction of a fictive common energy
level for all perturbing energy levels with
![]() (Eq. (7)) overestimates the theoretical sum rule Eq. (5)
by up to
(Eq. (7)) overestimates the theoretical sum rule Eq. (5)
by up to ![]() ,
but the agreement with experiments indicates that
this is equilibrated by the underestimation of the contribution of
elastic collisions.
,
but the agreement with experiments indicates that
this is equilibrated by the underestimation of the contribution of
elastic collisions.
Table 2 present a comparison of our calculations
(
![]() )
with theoretical results of Dimitrijevic
(1982) (
)
with theoretical results of Dimitrijevic
(1982) (![]() )
obtained using the
semi-classical approach of Griem (1974) and theoretical
data (
)
obtained using the
semi-classical approach of Griem (1974) and theoretical
data (
![]() )
calculated by Mahmoudi et al. (2004)
using the semi-classical method of Sahal-Bréchot
(1969a,b).
)
calculated by Mahmoudi et al. (2004)
using the semi-classical method of Sahal-Bréchot
(1969a,b).
One can see from Tables 1 and 2 that the MSE
results are in good agreement with experiments and more
sophisticated theoretical calculations (Mahmoudi et al.
2004; Griem 1974) for all considered
experimental conditions (T and ![]() ). Indeed the ratio
). Indeed the ratio
![]() and
and
![]() shows on average an agreement within
shows on average an agreement within ![]() and
and ![]() respectively. This is well within the error bars of the
semiempirical and the modified semiempirical methods estimated to
be
respectively. This is well within the error bars of the
semiempirical and the modified semiempirical methods estimated to
be ![]() (Griem 1974; Dimitrijevic & Konjevic 1980) which is a very good agreement
especially taking into account that the needed atomic data set is
much smaller than for more sophisticated semi-classical
calculations (Sahal-Bréchot 1969a,b; Griem
1974; Mahmoudi et al. 2004). The exceptions
are in the multiplets
(Griem 1974; Dimitrijevic & Konjevic 1980) which is a very good agreement
especially taking into account that the needed atomic data set is
much smaller than for more sophisticated semi-classical
calculations (Sahal-Bréchot 1969a,b; Griem
1974; Mahmoudi et al. 2004). The exceptions
are in the multiplets
![]()
![]()
![]() at 18 300 K,
at 18 300 K,
![]()
![]()
![]() at
54 000 K,
at
54 000 K,
![]()
![]()
![]() and
and
![]()
![]()
![]() where the discrepancy between experiment and theoretical
calculations is of the order of
where the discrepancy between experiment and theoretical
calculations is of the order of ![]() which is also within the
error bars of the semi-classical and the modified semiempirical
method.
which is also within the
error bars of the semi-classical and the modified semiempirical
method.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1574fig1.eps}\end{figure}](/articles/aa/full/2005/17/aa1574/Timg91.gif) |
Figure 1:
Theoretical Stark width dependence on electron
temperature for an electron density of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1574fig2.eps}\end{figure}](/articles/aa/full/2005/17/aa1574/Timg92.gif) |
Figure 2:
Theoretical Stark width dependence on electron
temperature for an electron density of 1 |
| Open with DEXTER | |
The results of Table 2 are compared in Figs. 1-3 with available experimental
data but we note that the experimental results are for particular
spectral lines within a multiplet while the theoretical data are
calculated for the multiplet as a whole. One can see that our
results obtained with the modified semiempirical method
(Dimitrijevic & Konjevic 1980) are
in agreement within the error bars with the experimental data and
with more sophisticated semi-classical calculations of
Dimitrijevic (1982) and Mahmoudi et al.
(2004) which demonstrates that this method can be
used especially for large scale calculations and when due to lack
of the needed atomic data more sophisticated methods are not
adequately applicable.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1574fig3.eps}\end{figure}](/articles/aa/full/2005/17/aa1574/Timg93.gif) |
Figure 3:
Theoretical Stark width dependence on electron
temperature for an electron density of 1 |
| Open with DEXTER | |
In Table 3 (available only in electronic form at the CDS) our Stark width
(FWHM) results for 25 OII multiplets calculated for an electron
density of
![]() and temperatures of 5000, 10 000,
20 000, 30 000, 60 000 and 80 000 K are given for the modelling,
analysis and diagnostics of astrophysical plasmas. We note also
that for lower densities a linear scaling is sufficient. For
higher densities, linearity with the electron density may be
assumed if the plasma is ideal. The idealness of the plasma can be
checked by calculating the number of perturbers in the Debye
sphere, i.e.
and temperatures of 5000, 10 000,
20 000, 30 000, 60 000 and 80 000 K are given for the modelling,
analysis and diagnostics of astrophysical plasmas. We note also
that for lower densities a linear scaling is sufficient. For
higher densities, linearity with the electron density may be
assumed if the plasma is ideal. The idealness of the plasma can be
checked by calculating the number of perturbers in the Debye
sphere, i.e.
![]() or
or
![]() cm-3 (Dimitrijevic et al. 1991), where
cm-3 (Dimitrijevic et al. 1991), where ![]() is the Debye
radius. For non-ideal plasmas, the method used here is not
suitable. Stark broadening in a strongly correlated plasma has
been considered recently by Ben Chaouacha et al. (2004). The other
criteria for the applicability of the modified semiempirical
approach have been dicussed in detail in Milovanovic et al.
(2004).
is the Debye
radius. For non-ideal plasmas, the method used here is not
suitable. Stark broadening in a strongly correlated plasma has
been considered recently by Ben Chaouacha et al. (2004). The other
criteria for the applicability of the modified semiempirical
approach have been dicussed in detail in Milovanovic et al.
(2004).
Acknowledgements
This work is a part of the project "Influence of collisional processes on astrophysical plasma line shapes'' (GA 1195), supported by the Ministry of Science and Environment protection of Serbia. Part of this work has been supported by the Ministry of Higher Education, Scientific Research and Technology in Tunisia under the project LMA, FSB, 2001-2004.