A&A 434, 459-467 (2005)
DOI: 10.1051/0004-6361:20041518

Observation of EGRET gamma-ray sources by an Extensive Air Shower experiment

M. Khakian Ghomi - M. Bahmanabadi - J. Samimi

Department of Physics, Sharif university of Technology, PO Box 11365-9161, Tehran, Iran

Received 23 June 2004 / Accepted 3 November 2004

Abstract
Ultra-high-energy (E>100 TeV) Extensive Air Showers (EASs) have been monitored for a period of five years (1997-2003), using a small array of scintillator detectors in Tehran, Iran. The data have been analyzed taking into account the dependence of source counts on zenith angle. During a calendar year different sources come into the field of view of the detector at varying zenith angles. Because of varying thickness of the overlaying atmosphere, the shower count rate is extremely dependent on zenith angle, which has been carefully analyzed over time (2002, Exp. Astron., 13, 39). High energy gamma-ray sources from the EGRET third catalogue where observed and the data were analyzed using an excess method. Upper limits were obtained for a number of EGRET sources, including 6 AGNs or probably AGNs and 4 unidentified sources.

Key words: instrumentation: detectors - methods: data analysis - catalogs - gamma rays: observations

1 Introduction

The EGRET instrument on-board Compton Gamma Ray Observatory (CGRO) has detected both diffuse and discrete gamma-ray emission. The diffuse emission is both Galactic (Hunter et al. 1997) and extra galactic in nature (Sreekumar et al. 1998). EGRET has detected about 271 high energy (>100 MeV) gamma-ray sources (Hartman et al. 1999). Besides AGNs these sources include 170 sources that have not been identified conclusively with unique counterparts at other wavelengths. Two thirds of these EGRET UnIdentified (EUI) sources lie close to the galactic plane; potential counterparts (Bhattacharya et al. 2003) for these include young (radio-active and radio-quiet) pulsars (Torres et al. 2001; D'Amico et al. 2001; Zhang et al. 2000), Wolf Rayet (WR) stars, Of stars, OB associations (Romero et al. 1999), SuperNova Remnants (SNRs) (Combi et al. 2001; Case & Bhattacharya 1998; Sturner & Dermer 1995) and other types of sources.

Some other faint sources are in the mid-latitude region suggested to be associated with the Gould Belt (Gehrels et al. 2000), which underwent an intense star formation period about sixty million years ago (Grainer 2000; Harding & Zhang 2001). High latitude sources, of which there are about 50, might be galactic gamma-ray halo sources (Dixon et al. 1998) or unidentified sources that are thought to be extragalactic. These extragalactic EUI sources comprise Blasars and Active Galactic Nuclei (AGNs), galaxy clusters (Colafrancesco 2002), BL Lacerta objects (Torres et al. 2003) and other types.

Whether the EGRET sources emit at still higher energies, is an interesting question (Lamb & Macomb 1997). Gamma-rays with energies of about 100 TeV and more, entering the earth atmosphere, produce Extensive Air Showers (EASs) (Gaisser 1990) which could be observed by the detection of the secondary particles of the showers on the ground level (Bahmanabadi et al. 1998). Previous attempts have been reported from other EAS arrays (Amenomori et al. 2002, 2000; Borione et al. 1997; Alexandreas et al. 1993; McKay et al. 1993).

This paper reports the results of a small particle detector array located at the Sharif University of Technology in Tehran. This small array is a prototype for a larger EAS array to be built at an altitude of 2600 m ($\equiv$756 g cm-2) at ALBORZ Observatory (AstrophysicaL oBservatory for cOsmic Radiation on alborZ) (http://sina.sharif.edu/~observatory/) near Tehran. The prototype was installed on the roof of the physics department of Sharif University of Technology in Tehran. In this work we present the observational results for 10 EGRET third catalogue sources; we describe the experimental setup in Sect. 2, the data analysis in Sect. 3, the results in Sect. 4. Section 5 is devoted to a discussion of the results.

2 Experimental set-up

The array is constructed of 4 slab plastic scintillators ( $100\times100\times2$ cm3) arranged in a square; at 51$^{\circ}$20'E and 35$^{\circ}$43'N, elevation 1200 m (890 g cm-2); it is shown in Fig. 1. All scintillators are on a flat level surface. Each scintillator is housed in a pyramidal steel box with a height of 15 cm. The interior surface of each box is coated with white paint, (Bahmanabadi et al. 1998) and a 5 cm diameter PMT(EMI 9813KB) is placed at the vertex of the pyramidal box. Figure 1 shows a schematic diagram of the array and its electronic circuit to log each EAS event.
  \begin{figure} \par\includegraphics[width=12.5cm,clip]{1518fig1.eps} \end{figure} Figure 1: Experimental set up and electronic circuits.
Open with DEXTER

If at least one particle hits a detector the PMT creates a signal with a pulse height which is related to the direction, number of particles, and location of the particle tracks in the scintillator. The output signals from the PMTs are amplified in a one stage amplification ($\times$10) with an 8-fold fast amplifier (CAEN N412), and then transferred one by one to an 8-fold fast discriminator (CAEN N413A) which is operated at a fixed level of 20 mV. The threshold of each discriminator is set at the separation point between the signal and background noise levels. Each discriminator has two outputs, one of them connected to a coincidence logic unit (CAEN N455) which acts as a trigger condition. The trigger condition is satisfied when at least one charged particle passes through each of the four detectors within a time window of 150 ns. The other discriminator output is connected to one of three Time to Amplitude Converters (TAC) (EG&G ORTEC 566) which are set to a full scale of 200 ns (maximum acceptable time difference between two scintillators). The output of the No. 4 scintillator is connected to the start input of TAC1 whereas the output of No. 2 is connected to the start inputs of TAC2 and TAC3. The output of No. 3 is connected to the stop input of TAC2 that of No. 1 to stop inputs of TAC1 and TAC3. Then the outputs of these three TACs are fed into a multi-parameter Multi Channel Analyzer (MCA)(KIAN AFROUZ Inc.) via an Analogue to Digital Converter (ADC)(KIAN AFROUZ Inc.) unit.

When all of the scintillators have coincidence pulses, the TACs are trigged by the logic unit and the 3 time lags between the output signals of PMTs (4, 1), (2, 3) and (2, 1) are read out as parameters 1 to 3. So by this procedure an EAS event is logged.

Two different experimental configurations were used in the experimental set up. The first (E1) and the second (E2) experimental configurations were identical except for the size of the array. In E1 the size is 8.75 m $\times$ 8.75 m and in E2the size is 11.30 m $\times$ 11.30 m.

3 Data analysis

The logged time lags between the scintillators and Greenwich Mean Time (GMT) of each EAS event were recorded as raw data. We synchronized our computer to GMT (http://www.timeanddate.com). Our electronic system has a recording capability of 18.2 times per second. If an EAS event occurs, its three time lags will be recorded and if it does not occur "zero'' will be recorded. Therefore the starting time of each experiment and the count of records gives us the GMT of each EAS event. Our detected EAS events are a mixture of cosmic-ray events and gamma-ray events. In E1 the total number of EAS events was 53 907 and the duration of the experiment was 501 460 s. So the mean event rate of the first experiment was 0.1075 events per second. The distribution of the time between successive events is in good agreement with an exponential function, indicating that the event sampling is completely random (Bahmanabadi et al. 2003). In E2 the total number of events was 173 765 and the duration of the second experiment was 2 902 857 s, so its mean event rate was 0.05986 events per seconds.

We refined the data to separate out acceptable events. Events are acceptable if there is good coincidence between the four scintillator pulses. We omitted the events with zenith angles more than 60$^{\circ}$. Therefore after the separation we obtained smaller data sets of 46 334 and 120 331 for E1 and E2respectively. Since we cannot determine the energy of the showers on an event by event basis, we estimate our lower energy threshold by comparing our event rate to a cosmic-ray integral spectrum (Borione et al. 1997)

                                 J(E) = $\displaystyle 2.78\times10^{-5}E^{-2.22} + 9.66\times10^{-6}E^{-1.62}$  
    $\displaystyle - 1.94\times10^{-12} \hspace{3mm} 40\leq E \leq 5000 \hspace{1mm}{\rm TeV}.$ (1)

The obtained lower energy limits were 39 TeV in E1 and 54 TeV in E2. The calculated mean energies were 94 and 132 TeV in E1 and E2 respectively. If the well-known Hillas spectrum (Gaisser 1990)

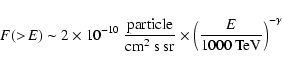\begin{displaymath}F(>\!E) \sim 2\times10^{-10}~\frac{{\rm particle}}{{\rm cm}^2... ...{\rm sr}}\times\left(\frac{E}{1000~{\rm TeV}}\right)^{-\gamma} \end{displaymath} (2)

is used the lower limits will be 40 TeV and 60 TeV. Since the distribution of cosmic-ray events within the array in these energy ranges is homogeneous and isotropic, we used an excess method (Amenomori et al. 2002, 2000) to find signatures of EGRET third catalogue gamma-ray sources. This method was used for both E1 and E2.

The complete analysis procedure is as follows:

3.1 Calculation of local coordinates of each EAS event

The local coordinates are zenith (z) and azimuth $(\phi)$. We used the least-squares method (Mitsui et al. 1990) to calculate z and $\varphi$. It is assumed that the shower front could be approximated by a plane. So we obtain

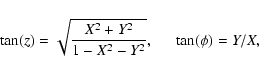\begin{displaymath}\tan(z)=\sqrt{\frac{X^2+Y^2}{1-X^2-Y^2}},\hspace{5mm}\tan(\phi)=Y/X, \end{displaymath} (3)

where
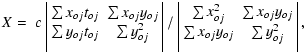$\displaystyle X=\hspace{1mm}c\hspace{1mm}\vline \begin{array}{cc} \sum x_{oj} t... ...& \sum x_{oj} y_{oj} \\ \sum x_{oj} y_{oj} & \sum y^2_{oj} \end{array}\vline~,$     (4)
$\displaystyle Y=\hspace{1mm}c\hspace{1mm}\vline\begin{array}{cc} \sum y_{oj} t_... ...& \sum x_{oj} y_{oj} \\ \sum x_{oj} y_{oj} & \sum y^2_{oj} \end{array}\vline~.$     (5)

$\vec{D}_{oj}=\vec{D}_j-\vec{D}_o=x_{oj}\hat{\vec{i}}$+ $y_{oj}\hat{\vec{j}}$and toj=tj-to are the coordinate vector and the time lag of the jth scintillator with respect to the reference one and c is the velocity of light.

A zenith angle cut off $60^{\circ}$ is implemented to increase the significance.

3.2 Angular distribution of the EAS events

Figure 2a shows the azimuthal angle distribution of the EAS events, which is nearly isotropic. A slight North-South anisotropy is observed which is attributed to the geomagnetic field. We fitted this distribution with a harmonic function as follows: (Bahmanabadi et al. 2002)

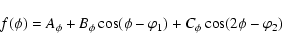\begin{displaymath}f(\phi)=A_{\phi}+B_{\phi}\cos(\phi-\varphi_1)+C_{\phi}\cos(2\phi-\varphi_2) \end{displaymath} (6)

where $A_{\phi}$, $B_{\phi}$ and $C_{\phi}$ are respectively 14516, 1270 and 184. $\varphi_1$ and $\varphi_2$ are phase constants which are respectively 32$^{\circ}$ and 55$^{\circ}$.

Since the thickness of the atmosphere increases quickly with increasing zenith angle z (Gaisser 1990), the number of EAS events is strongly related to z, as shown in Fig. 2b.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{1518fig2.eps} \end{figure} Figure 2: Local coordinate distributions of, a) azimuth "$\phi $'' and b) zenith "z'' angles of logged EAS events.
Open with DEXTER

These distributions were studied separately for the two experimental configurations E1 and E2. The shower rate in E2 is less than in E1 because of the larger size of the array in E2. However, the zenith angle distributions from E1 and E2 are very similar. The differential zenith angle distributions of these data sets are fitted with the function d $N=A_{z}\sin z\cos^n z {\rm d}z$ with a very good agreement for both E1 and E2; in this expression Az=95358 and n=5.85 for 0 $^{\circ}\leq z <50^{\circ}$, and Az=90189 and n=5.00 for 50 $^{\circ}\leq z <60^{\circ}$. For another point of view the mean value of the zenith angle $(\bar{z})$is 26.2746 and 26.4625 in E1 and E2 respectively. Since the results of the two experimental configurations are in a good agreement with one another we have co-added the two data sets to obtain a larger data set with lower energy threshold of E1 which is 39 TeV.

3.3 Calculation of equatorial and galactic coordinates of each EAS event

The equatorial coordinates (RA, Dec) are obtained from the local coordinates ($z,\varphi$), GMT of each EAS event and geographical latitude of the array. In this step the transformation relations (http://aanda.u-strasbg.fr, Roy & Clarke), and the local sidereal time of the starting point of the experiment (http://tycho.usno.navy.mil/sidereal.html) were used.

Then galactic coordinates (l, b) of each EAS event were derived from the equatorial coordinates, for epoch 2000 (http://aanda.u-strasbg.fr). Figure 3 shows the distribution of our data in galactic coordinates.

  \begin{figure} \par\includegraphics[angle=-90,width=13cm,clip]{1518fig3.eps} \end{figure} Figure 3: EAS events map in 1 $^{\circ }\times 1^{\circ }$ bin galactic coordinates.
Open with DEXTER

Table 1: EGRET third catalogue sources observed by our array. ld and bd are displaced galactic coordinates, $\sigma _{E1}$, $\sigma _{E2}$ and $\sigma _{\rm tot}$ are the statistical significances related to the first experiment, the second experiment and the sum of the two, $r_{\rm e}$ is the error angular radius, $\bar{z}$ is the mean value of zenith angles of EASs for source and "Flux'' is the number of EAS events for source. t1: AGN which has been investigated before by CASA-MIA (Catanese et al. 1996), t2: sources with energy >1 GeV (Lamb & Macomb 1997). Sources number 5 and 7 are "Mrk 421'' and "4C +10.45'' respectively.

3.4 Error estimation of investigated sources in galactic coordinates

For the coordinates calculation of each EAS event we have to know estimated errors in these coordinates. These errors are due to experimental error factors, which contain uncertainties in the times and coordinates of each logged EAS event. The defined distance between two scintillators was centre to centre and the size of the scintillators was ( $100\times100\times2$ cm3). The accuracy of the coordinates of each scintillator is determined within a few centimeters. So the error in the measurement of the coordinates of secondary particles of each EAS event is $\Delta d\cong1$ m.

The errors in the time measurement of each EAS event are due to the thickness of front plane of the secondary particles, errors in the electronics and in GMT logging. The error due to the first two factors was $\Delta t\cong2$ ns (Bahmanabadi et al. 2002). The error in the logged time of each EAS event was $\Delta T=0.07$ s which is due to the recording rate and the synchronizing of the computer. These errors cause uncertainties in the coordinates of the investigated sources.

The following quantities were calculated:

From the geometry of Fig. 1 we can derive:
$\displaystyle \sin z \sin\varphi = \frac{c}{d}(t_2 - t_1)$     (7)
$\displaystyle \sin z \cos\varphi =\frac{c}{d}(t_3 - t_2).$     (8)

In these relations tis are the logged times of an EAS event in the $i{\rm th}$ scintillator of the array and d is the side of the square array.

The errors in zenith and azimuth angles were obtained by differentiating from Eqs. (7) and (8):

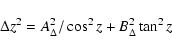\begin{displaymath}\Delta z^2 = A_{\Delta}^2 / \cos^2 z + B_{\Delta}^2 \tan^2 z \end{displaymath} (9)


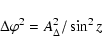\begin{displaymath}\Delta \varphi^2 = A_{\Delta}^2 / \sin^2 z \end{displaymath} (10)

where $A_{\Delta}=2c\Delta t/d$ and $B_{\Delta}=\Delta d/d$. The corresponding errors in equatorial and galactic coordinates were calculated from differentials of Dec( $z,~\varphi$), RA( $z,~\varphi,~T$), b(RA, Dec) and l(RA, Dec).

If y is a generic function of parameters u, v and T, then:

y=y(u,v,T) (11)


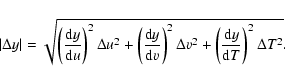\begin{displaymath}\vert\Delta y\vert = \sqrt{\left(\frac{{\rm d}y}{{\rm d}u}\ri... ... v^2 + \left(\frac{{\rm d}y}{{\rm d}T}\right)^2 \Delta T^2}. \end{displaymath} (12)

Where ${\rm d}y/{\rm d}T=2\alpha$ ( $\alpha =1.00273790935$) (http://tycho.usno.navy.mil/sidereal.html) for the calculation of RA(z,  $\varphi,~T$) and ${\rm d}y/{\rm d}T=0$ for the calculation of Dec(z, $\varphi$), b(RA, Dec) and l(RA, Dec).

The error in the observed solid angle of each source is $\Delta \Omega = \cos~b \Delta~b\Delta~l$ and the equivalent error in the angular radius is $r_{\rm e}\cong \sqrt{\Delta\Omega/\pi}$( $r_{\rm e} \ll 1 $)

The above analysis obtains as angular resolution for EAS event individually. But there are many EAS events with different local coordinates which contribute in the signature of each investigated source. Therefore at first angular errors of all of the accumulated EAS events in the galactic coordinates of the source were calculated, then the mean value of these angular errors was chosen as the angular error of the source. Since all of the accumulated EAS events in the angular error region contribute to the source signature, the previous calculations were repeated for all of the accumulated EAS events in a circular region centered on the source and with radius $r_{\rm e}$. Finally the mean value of these EAS angular errors is calculated as the angular error of each source in galactic coordinates. Since the sides distances of the array are different in E1 and E2, the angular errors in these two experiments are different. So for the calculation of the final result for each source these angular errors were calculated separately for E1 and E2 and were weighted with the number of refined EAS events in the related experiment. The final angular errors of the investigated sources ($r_{\rm e}$) are shown in Table 1. Since these angular error radii have a slight fluctuations around a mean value, we sampled over l and b with a steps of 5 degrees from the FOV of the array and calculated these radii to find the mean and standard deviation. Therefore the mean and the standard deviation of the angular error of the experiment were obtained from the angular errors of more than 1000 random points. With these steps we obtained $\bar{r_{\rm e}}=4.35^{\circ}\pm0.82^{\circ}$ as the mean angular error of the experiment.

3.5 Drawing the exposure map, and simulation of the experiment

Because of the variation in sky exposure with time, there is a non-uniform distribution of EAS events in galactic coordinates. The variation in time exposures due to the altitude difference of different sources, and the observation of individual galactic regions during the sub-intervals within the duration of the experiment were simulated. We have 166 665 EAS events in our experiments, so we used the Monte Carlo method for this simulation and we simulated 166 665 random events.
  \begin{figure} \par\includegraphics[angle=-90,width=13cm,clip]{1518fig4.eps} \end{figure} Figure 4: Exposure map of simulated events in 1 $^{\circ }\times 1^{\circ }$ bins base on the general parameters of the total distribution of EAS events in galactic coordinates.
Open with DEXTER

These random numbers were chosen taking the results of Fig. 2 into account. From this figure is seen that the $\phi $ distribution is not isotropic and that thickness effect of the atmosphere is very important; these effects were considered in choosing the random numbers. So in the procedure: With this procedure we obtained 2500 simulated maps, and obtained a map with the mean number of simulated events per ( $1^\circ\times1^\circ $) pixel with an accuracy of 0.001. Figure 4 shows the exposure map of the experiment. The event map in Fig. 3 reflects the uneven exposure of the experiment.

3.6 Investigation of EGRET gamma-ray sources and measurement of their statistical significance

The energy range of the EAS events logged by the array is in the range of 40 to 10 000 TeV. In this energy range the distribution of cosmic rays is completely isotropic and homogeneous in the galaxy. After correcting for the exposure effects, we looked for excess emission that could be from gamma-ray sources. We used the third EGRET catalogue (Hartman et al. 1999) as a reference. But some of EGRET sources do not have acceptable events in the FOV of our array. We counted the number of events, and the number of pixels and then calculated the count per pixel related to each source. We note that the mean count per pixel in the data map is 4.798. Of 151 EGRET sources only 123 have counts per pixel of more than the $\sqrt{4.798}$; of these 98 have counts per pixel of more than 1.5 times the square root of the mean. So we started our investigations with these 98 sources. A method of excess similar to the analysis adopted by the Tibet EAS array, was adopted (Amenomori et al. 2002, 2000). In the first step we divided the data map (Fig. 3) by the exposure map (Fig. 4) pixel by pixel. In the obtained map, most non zero pixels are around 1 except probable source pixels and pixels with higher fluctuations in the data map, which are probably due to the small size of the data set. To eliminate the fluctuating pixels we multiplied the new map by 4.798 to obtained a raw exposure-corrected map. In this step we added counts of all pixels of the raw corrected map. The number must be very near to 166 665 so with this restriction we obtained a lower limit 0.0750 for eliminating pixels with lower count in the exposure map, and the final exposure corrected map was obtained; it is shown in Fig. 5.

  \begin{figure} \par\includegraphics[angle=-90,width=13cm,clip]{1518fig5.eps} \end{figure} Figure 5: Corrected exposure map extracted by pixel-by-pixel division of the data map (Fig. 3) by the exposure map (Fig. 4).
Open with DEXTER

The obtained map was fairly uniform in the FOV of our array in galactic coordinates. Next we investigated the remaining faint inhomogeneity in the corrected map that could be conditionally attributed to the existence of gamma-ray sources. To estimate the significance of an individual source we added all corrected EAS events, ${N}_{\rm on}$, within a radius $\sqrt{2}r_{\rm e}$ from the source position. The number of pixels, $n_{\rm s}$, within this region was also counted. The total number of background counts, $N_{\rm off}$, was found from the pixels that fall within an outer radius of 2$r_{\rm e}$ and an inner radius $\sqrt{2}r_{\rm e}$ from the source position. The number of background pixels, $n_{\rm b}$, was also counted too. The statistical significance of the source was obtained using the Li & Ma method (Li & Ma 1983).

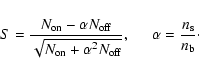\begin{displaymath}S =\frac{N_{\rm on} - \alpha N_{\rm off}}{\sqrt{N _{\rm on}+\... ...off}}} , \hspace{5mm}\alpha = \frac{n_{\rm s}}{n_{\rm b}}\cdot \end{displaymath} (13)

The distribution of the statistical significance of these 98 sources is fitted by a Gaussian function as follows:

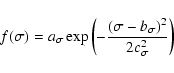\begin{displaymath}f(\sigma)= a_{\sigma}\exp\left(-\frac{(\sigma-b_{\sigma})^2}{2c_{\sigma}^2}\right) \end{displaymath} (14)

which is shown in Fig. 6.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{1518fig6.eps} \end{figure} Figure 6: Distribution of frequency of a) 98 000 virtual random sources and b) 98 EGRET sources in the FOV of our array in galactic coordinates versus their statistical significance. $a_{\sigma }$, $b_{\sigma }$ and $c_{\sigma }$ are described in Eq. (14).
Open with DEXTER

Then for the investigation of the statistical significance distribution we chose 98 000 virtual random sources with similar conditions as 98 EGRET sources. Then we calculated their statistical significance and drew the distribution. Figure 6 shows a normal distribution with mean 0.044 and standard deviation 1.001. The procedure of the significance calculation for virtual sources is like that for the 98 EGRET sources except for the following small difference: basically the virtual sources have no signals so we used another relation for the calculation of their statistical significance (Li & Ma 1983).

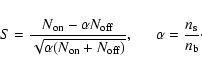\begin{displaymath}S =\frac{N_{\rm on} - \alpha N_{\rm off}}{\sqrt{\alpha(N_{\rm... ...ff})}} , \hspace{5mm}\alpha = \frac{n_{\rm s}}{n_{\rm b}}\cdot \end{displaymath} (15)

3.7 Investigation of a probable displacement of the source signatures

Our exposure-corrected map has not bright source signatures, so we used the third EGRET catalogue as a reference for searching some sources in our energy range. But the EGRET energy range is from 100 MeV to 30 GeV and our energy range is from 40 TeV to 10 000 TeV. So to be detectable in our data these sources should have a spectrum that spreads from at least the EGRET energy range to our energy range, such as blazars, BL Lac objects, Flat-spectrum radio quasars or etc. Since these sources do not usually have exactly the same position in different energy ranges, we searched a position one degree away from these sources. This displaced l and b are shown in Table 1 for each source. It means that around each source with a statistical significance of more than 1 we tried 8 ( $1^\circ\times1^\circ $) pixels and chose the location with the highest statistical significance.

4 Results

4.1 Explanation of the Field of View (FOV) in galactic coordinates

The rotation axis of the Earth passes near the star Polaris; the angular difference between Polaris and the rotation axis is approximately 5 times smaller than our mean angular accuracy ( $\bar{r_{\rm e}}$) in galactic coordinates. So in this analysis Polaris is considered to be on the rotation axis of the Earth. The longitude and latitude of Polaris in galactic coordinates are $123^{\circ}$, 17' and $27^{\circ}$, 28' respectively. The geographical latitude of Tehran is about  $35^{\circ}$ N, so the angle between the zenith of the array and Polaris in Tehran is about $55^{\circ}$. We selected events with zenith angles less than $60^{\circ}$ for the analysis which is deduced from Fig. 2b and therefore, Polaris and regions around it are observable only with High zenith EAS events. From Fig. 2b it can be seen that the best observable region is for zenith angle between  $10^{\circ}$ to  $40^{\circ}$ of zenith angles. In Fig. 3 we show that Galactic longitudes smaller than $l\approx123^{\circ}-(2 \times 60^{\circ} - (60-55)^{\circ})\approx 8^{\circ}$ and larger than $l\approx123^{\circ}+(2 \times 60^{\circ} - 5^{\circ})\approx238^{\circ}$ are less well observable. In other words, given the location of the array there are two different observable regions in galactic coordinates. Galactic latitudes smaller than $b\approx27^{\circ}-(60^{\circ} - 5^{\circ})\approx-38^{\circ}$ and larger than $b\approx27^{\circ}+(60^{\circ}-5^{\circ})\approx82^{\circ}$ are also less suitable to observe regions too.

4.2 Comparison of observed sources of E1 and E2

With the procedure mentioned in Sect. 3.7. we searched for sources with statistical significance >1.5, and we found thirteen sources of which five of them have a significance >2. To avoid possible fluctuations we repeated our search. We searched these displaced sources in E1 and E2 separately. But at this stage, because of the small size of these data sets, specially in E1 we selected sources with a significance >1. Ten sources remained which have a statistical significance >1 in E1 and E2and >1.5 in the sum; these are listed in Table 1. Fortunately five of these sources are AGNs, one is a probable AGN and four are unidentified sources. Note that out of 271 sources of the third EGRET catalogue only 66 are AGNs.

4.3 Distribution of observed shower events around the most significant EGRET sources

It seems that the radial distribution of the number of counts per pixel for each source naturally must be close to a gaussian distribution over a flat back ground. We selected eight regions with approximately the same number of pixels for each source. The first region is a circle with radius $\sqrt{1/2}r_{\rm e}$. The second region is a ring with inner radius $\sqrt{1/2}r_{\rm e}$ and outer radius $\sqrt{2/2}r_{\rm e}$ and so on. The distribution of the mean counts per pixel around 98 000 virtual random sources and 10 most significant EGRET sources is shown in Fig. 7. These distributions fitted a gaussian function over a flat distribution as follows:

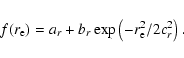\begin{displaymath}f(r_{\rm e})=a_r+b_r \exp\left(-r_{\rm e}^2/2c_r^2\right). \end{displaymath} (16)


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{1518fig7.eps} \end{figure} Figure 7: Distribution of mean count per pixel of a) 98 000 virtual random sources and b) 10 EGRET sources of Table 1 versus error radial distance from the centre of the related sources.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=-90,width=12cm,clip]{1518fig8.eps} \end{figure} Figure 8: Map of EGRET sources with statistical significance more than 1.5 in galactic coordinates. The numbered sources are listed in Table 1.
Open with DEXTER

5 Discussion and concluding remarks

In Table 1 is seen that most significant excesses observed are in the region $10^{\circ} < \bar{z} < 40^{\circ}$. This is reasonable because these angles are in favorable locations in the sky and for this region we have a large amount of data. In addition our data have few counts in some parts of the sky and we had to eliminate some source candidates from our list. To increase the statistical significance of our results and investigate more sources, we should accumulate more data and obtain a map with less fluctuations.

There has been considerable effort worldwide to detect gamma-ray sources via the EAS technique. From a variety of arguments we suspect that some of the EGRET sources would be detectable at very high energies. In this work, we are limited to a discussion of a few sources with relatively small statistical significance. Our values for the statistical significance do not constitute a confident detection limit, our main object was to get an indication of the possibility of detecting some unidentified EGRET sources in the high-TeV range. Of these sources listed in Table 1, we suspect that nine may be extra galactic ( $\vert b\vert> 20^{\circ}$) (Gehrels et al. 2000) and only one is in the galactic region ( $\vert b\vert\leq 20^{\circ}$) and this one is an AGN in the third EGRET catalogue list too. Four of our ten sources were investigated before with CASA-MIA (Catanese et al. 1996) and two of them were GEV EGRET sources (Lamb & Macomb 1997). Therefore we might expect that as many as four of these unidentified sources could indeed be emitters at high energy and might be AGNs.

Some of our observed sources overlap one another (Fig. 8), so a complete and accurate analysis procedure should incorporate the maximum likelihood method (Mattox et al. 1996). We must also emphasize that our experiment cannot distinguish between gamma-ray and cosmic-ray initiated air showers, and so we used the excess method to carry out a search for very high energy gamma-ray emission. After the analysis we understood that the recording rate of our computer is very important and we have to increase it to reduce the angular error radius of observable sources. In our future site at 2600 m above sea level (http://sina.sharif.edu/~observatory), we are constructing underground tunnels which will provide us with ample space to deploy muon detectors. The detection of muons in air showers should be a powerful way to discriminate between cosmic-ray and gamma-ray air showers.

Acknowledgements
This research was supported by a grant from the national research council of Iran for basic sciences. The authors wish to thank Dr. Dipen Bhattacharya at University of California, Riverside and Prof. Rene A. Ong at University of California, Los Angeles for their many constructive comments. The authors wish to thank the anonymous referee for his/her many constructive comments too.

References

 
Copyright ESO 2005