A&A 432, 1137-1150 (2005)
DOI: 10.1051/0004-6361:20041849

Benchmarking atomic data for astrophysics: Fe XXIII

G. Del Zanna - M. C. Chidichimo - H. E. Mason

Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 0WA, UK

Received 16 August 2004 / Accepted 29 November 2004

Abstract
Recent scattering calculations for Fe XXIII are benchmarked against laboratory and astrophysical observations. The collisional data are supplemented by radiative data obtained with empirical adjustments that take into account observed wavelengths. All previous line identifications and energy levels are reviewed and assessed in light of these new calculations. Most of the previous identifications, in particular of the astrophysically-important spectral lines are confirmed. However, some identification are rejected or questioned, and new ones proposed. The agreement between theoretical and experimental data in terms of wavelengths, line intensities and level lifetimes is very good. Observations of Fe XXIII L-shell emission lines provide a great opportunity to directly measure electron temperatures for a wide range of astrophysical sources. Examples from solar (SMM, SOLEX) and stellar (Chandra, EUVE) observations are provided.

Key words: atomic data - line: identification - Sun: corona - techniques: spectroscopic

1 Introduction

This paper is one in a series which aims to provide atomic data for the analysis of astrophysical spectra and assess their accuracy. The approach is practical since it focuses on the lines that are predicted to be the brightest ones in a wide range of astrophysical conditions, and on their potential use for instrument calibrations and plasma diagnostics. For a description of the methods and goals see Paper I (Del Zanna et al. 2004).

In a recent paper, Chidichimo et al. (2005) produced collision strengths for excitations to the n = 2, 3,4 levels in Fe XXIII. These were R-matrix calculations done as part of the IRON Project. The collision strengths within the n=2 complex revise those published by Chidichimo et al. (1999).

Fe XXIII $n=3,4\to 2$ (L-shell) spectral lines fall in the 6-13 Å spectral range, which is densely packed with hundreds of transitions from different ionization stages of Iron. It is no surprise that a large number of lines are either unidentified or have a questionable identification (for solar spectra, see for example the spectral line list in Phillips et al. 1999).

Fe XXIII L-shell lines are prominent in solar flare spectra (see, e.g., Neupert et al. 1967), and in laboratory plasmas (see, e.g., Boiko et al. 1978). In recent years, high-resolution XUV spectroscopic observations by the Chandra and XMM-Newton satellites, have also shown that a vast number of astrophysical sources produce Fe XXIII L-shell emission. An early study by Bhatia & Mason (1981) indicated that some of these lines had a temperature sensitivity.

The main purpose of this work is to re-assess the line identifications and energy levels in light of these new scattering calculations, and to explore the density and temperature diagnostic possibilities. Section 2 describes the experimental data that we adopted for the benchmark. Section 3 describes the procedures we adopt to build our ion model and the benchmark method. Section 4 presents the results, while Sect. 5 draws the conclusions.

   
2 Laboratory, solar and astronomical data

The first observations of Fe XXIII lines in solar flares were made with the OSO-III satellite in the 1.3-20 Å region and were reported by Neupert et al. (1967). They contained $n=3,4\to 2$ L-shell spectral lines. In the following years, a large numbers of papers on further solar observations and on laboratory spectra have been published. Doschek et al. (1972) identified a few Fe XXIV and one Fe XXIII $n=4 \to 2$ transitions at $\lambda \simeq8$ Å from OSO-6 solar spectra, while Doschek et al. (1973) provided a more extended line list including Fe XXIII $n=3 \to 2$ lines also recorded by OSO-6. Neupert et al. (1973) presented OSO-5 spectra of solar flares in the 6-25 Å region, while Kastner et al. (1974) reported the first solar flare spectra containing the ${n=2\to 2}$ L-shell iron emission, in the 66-171 Å range from OSO-5. Fe XXIII L-shell lines are very important for plasma diagnostics because the line ratios depend only on temperature and not on density. The reason for this is that even solar flare densities are significantly lower than the low-density limit (10¹⁴ cm^-3) at which the upper level populations start to become significant compared to the ground level.

Early laboratory spectra containing some Fe XXIII lines were the Iron spark spectra of Feldman & Cohen (1968) and Cohen & Feldman (1970) in the 10-18 Å region, and the vacuum spark spectra of Swartz et al. (1971) in the 8-18 Å region. The spectral resolution of these early instruments was not sufficient to resolve most of the lines, and many identifications of "flare lines'' were very uncertain. Strong blending with lower ionization stages was also a problem.

The breakthrough came with the use of laser spectra. Fawcett & Hayes (1975) used laser spectra to propose the identification of several $n=3 \to 2$ Fe XXIII lines. Many more tentative identifications of $n=3,4\to 2$ lines have been performed using excellent laser spectra by Boiko et al. in a series of papers (see the review in Boiko et al. 1978). These identifications were further revised and extended by Bromage et al. (1978) and Fawcett et al. (1979), also using laser spectra.

The Boiko et al. (1978) laser spectra are still the best in terms of spectral resolution over a large wavelength range, and accuracy of wavelength measurements. We will normally adopt their wavelengths. These spectra were from a plasma obtained using Nd-glass laser emission focused on flat target surfaces with pulses of half-width of $\simeq$2 ns and radiation density $\simeq$10¹⁴ W/cm²(see references in Boiko et al. 1978 for details). The spectrograph contained a bent mica crystal and had an average spectral resolution of $\simeq$0.002 Å. The spectra were recorded on film. Boiko et al. (1978) provided approximate line intensities. The intensities were corrected for the film response and the filter absorption, but not for the reflectivity of the mica crystal, hence only those lines close in wavelength can be directly compared with some reliability. No estimates on the uncertainties were provided. This plasma had typical densities of the order of 10¹⁸-10²⁰ cm^-3 and temperatures up to a few 10⁷ K. The plasma is quickly excited to these high temperatures, and emission from the highest ionization species is dominant. Excitations occur to highly excited states. These, in turn, can increase the lower level populations by radiative cascades. At such high densities, many lower levels become significantly populated and many line ratios become highly density-sensitive, while temperature effects become less important.

All past identifications were largely based on relative gf values and wavelength coincidences. Studies along the isoelectronic sequence help a great deal, but have been limited. Fawcett & Hayes (1975) and Boiko et al. (1978) provided measurements along the Be-I sequence (from K to Ni), but only tentatively identified a few transitions. Bromage et al. (1978) presented additional spectra of V XX while Fawcett et al. (1979) studied Ni XXV. Further studies of Fe XXIII and ions in the Be-I sequence were performed by Spector et al. (1980) and Burkhalter et al. (1985), again using laser spectroscopy, but these measurements were sparse and many line identifications were contradictory.

Further solar flare observations were reported by McKenzie et al. (1985,1980) and recorded by the SOLEX spectrometers. The spectral resolution was much higher than previous solar spectra, but still below the resolution of the laboratory spectra. The wavelength measurements turned out not to be very accurate, and line intensities were only approximately calibrated in the first paper. A further improvement in terms of resolution was achieved with the flat crystal spectrometers (FCS) on-board the Solar Maximum Mission (SMM). Phillips et al. (1982) reported excellent FCS spectra in the 6-19 Å range, containing $n=3 \to 2$ lines. Another excellent SMM/FCS solar flare spectrum, this time with $n=4 \to 2$ calibrated line intensities, was published by Fawcett et al. (1987). The main limitation of all the above-mentioned solar spectra was the fact that the recording of the spectral range was not simultaneous. The wavelength range was scanned as the flare progressed and line intensities were changing. Therefore, only the intensities of lines close in wavelength can reliably be compared.

A tokamak spectrum in the 7-9 Å region of excellent spectral resolution was published by Wargelin et al. (1998), along with a list of identifications. Unfortunately, no line intensities were provided. Recently, Electron Beam Ion Trap (EBIT) spectra containing the few brightest $n=3 \to 2$ lines have been published by Brown et al. (2002). The advantage of the EBIT spectra is the presence of lines formed only at low densities and from a restricted range of ions. The limitation of the EBIT spectra is the poor spectral resolution and signal-to-noise, together with the lack of a radiometric calibration.

In the last few years, the gratings on-board the Chandra and XMM-Newton satellites have shown that a large variety of astrophysical sources emit strong Fe XXIII lines. The Chandra and XMM spectra are of particular relevance because line emission is simultaneously recorded across the entire spectral region. Also, a relatively good radiometric calibration is now becoming available (however, inconsistencies between spectra recorded simultaneously by different instruments are still present). The spectral resolution of the Chandra high-energy transmission grating (HETG) spectra is similar to the best solar ones, and many lines can be resolved. A large number of papers with line lists from various sources have been published. A few examples are selected here.

   
3 The benchmark method

The benchmark method, described in Del Zanna et al. (2004), and also applied in a number of cases (Storey et al. 2005; Del Zanna & Mason 2005), is only summarised here.

We assume steady-state collisionally-ionised optically-thin emission in a plasma with electrons having a Maxwellian distribution. The assumptions on the Maxwellian electron distribution and on the steady-state ion level populations are normally adopted throughout the literature. They are reasonable for the type of plasma we consider, given its high electron density and the very short time-scales for the electron-electron and electron-ion collisional processes (compared to the other relevant processes). For example, the e-e relaxation time (Spitzer 1962) for the laser plasmas considered here is of the order of 10 ps, i.e. more than two orders of magnitude lower than the typical laser pulse width. Also, the lifetimes of the excited states are much shorter than the timescales over which the plasma conditions varied. The characteristic time of the changes in the plasma state can be estimated as the ratio of the radius of the focusing spot ($\simeq$100 $\mu$) to the gas expansion velocity ($\simeq$10⁷ cm/s), i.e. is of the order of 1 ns. The assumptions of steady-state optically-thin emission were used, among others, by Doschek et al. (1975) to interpret emission from a laser beam with a 0.9 ns pulse, and even by Feldman et al. (1976) who considered laser spectra of shorter durations (<0.5 ns).

For faster laser beams, time-dependent effects and non-Maxwellian distributions need to be considered, and indeed have been observed/studied using spatially- and time-resolved spectroscopy (see, e.g., Matte et al. 1994, for an example; there is an extended literature on the subject).

The assumption of optically-thin emission is also often adopted in the literature, however in the laser plasmas the stronger lines (e.g. the resonance transitions of the H I- and He I-like ions) are usually optically thick, and the optical depth needs to be measured/estimated. For solar flare spectra, no clear indications of optical depth effects are normally found.

Another approximation that is often adopted when interpreting both laser and solar flare spectra is that one of ionization equilibrium. The standard assumption is that electron densities are so high that ionization/recombination times are short. At laser plasma densities (10²⁰ cm^-3) the ionization times are, however, much higher than the gas-dynamic and pulse width timescales, and therefore the plasma is not in ionization equilibrium. Indeed diagnostic techniques involving the satellite lines of the H I- and He I-like ions have been used to measure the ionization state of the plasma. In case of solar flares, departures from ionization equilibrium have also been observed. However, results have been somewhat contradicting, and the question as whether ionization equilibrium is a valid assumption (and if the current ionization/recombination rates are correct) remains open (cf. the review of Doschek 1990). It is therefore not appropriate to use e.g. emission measure techniques to infer the temperature distribution of these plasmas.

The benchmark method is composed of four steps (see Paper I for details). The first step is to complement the collisional rates with a set of A-values (spontaneous transition probabilities A_ji from the upper level j to the lower level i), calculated with the SUPERSTRUCTURE program (SS, see Eissner et al. 1974; Nussbaumer & Storey 1978). The program calculates electric dipole and quadrupole (E1, E2), and magnetic dipole and quadrupole (M1, M2) probabilities. The second step is to calculate the fractional population $N_j (N_{\rm e}, T_{\rm e})$ of level j (relative to the total number density of the ion), as a function of electron temperature $T_{\rm e}$ and density $N_{\rm e}$.

The third step is to find which transitions have the brightest theoretical intensities at different density and temperature regimes, to search all the available observations for possible identifications, and to compare calculated and observed $I_{\rm ob}$intensities. The latter is done by plotting the "emissivity ratio values''

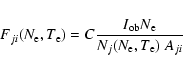$$F_{ji}(N_{\rm e}, T_{\rm e}) = C { I_{\rm ob} N_{\rm e} \over N_j(N_{\rm e}, T_{\rm e}) \;A_{ji}}$$ (1)

calculated at a fixed temperature $T_{\rm e}=T_0$ (or at a fixed density $N_{\rm e}=N_0$) as a function of the electron density $N_{\rm e}$(or temperature $T_{\rm e}$).

With this method we simply consider the ratio of the observed intensities with the theoretical ones, which are proportional to N_j A_ji. The proportionality constant C (which depends on various factors, such as the amount of emitting plasma, the ion abundance, the element abundance, the radiometric calibration or units adopted) is chosen so that the emissivity ratios are close to unity. The constant is fixed for each dataset. In this way, the plots provide a direct measure of the relative uncertainties.

For spectral lines that have the same density (or temperature) dependence, the ratio curves should overlap, if agreement between theory and observation holds. In the case of spectral lines that have different density (or temperature) dependence, the lines will intersect around a value which is the average density (or temperature) of the emitting plasma. We note that in a general case the $F_{ji}(N_{\rm e}, T_{\rm e})$ surfaces for different spectral lines should be considered. However, as discussed below, the two-dimensional approach is a good approximation for the plasmas and the objectives considered here.

We also note that the plasmas considered here are normally multi-thermal and multi-density. Furthermore, that the plasma temperature and density vary not only as a function of space but also of time, so the values obtained are space- and time-averages. In the studies of solar flare plasmas, this is a well-known problem that applies to any measurement, including the most accurate ones that involve the use of the satellite lines (see, e.g. Doschek & Feldman 1987). For laser plasmas, the situation is considerably better, since spatially- and temporally-resolved spectroscopy is available. Detailed studies (see, e.g. Boiko et al. 1975; Boiko et al. 1979) have shown that the temperature is relatively constant across the emitting region, and that the emission from different ions is not strictly co-spatial. In the central core of the focusing spot temperatures are higher, of the order of 10⁷ K. The measured values refer to an average during times of peak radiation and in the region of maximum brightness.

Interestingly, if the F_ji curves do intersect (as they often do, see below), then they provide a strong evidence in favour of the plasma being iso-density (or iso-thermal). In any case, we would like to stress that the present method is applied here not to derive accurate values of densities (or temperatures), but to re-assess the identifications and the presence of blends using line intensities, and not simply gf values. Also, to identify the best lines that can be used for plasma diagnostics.

The fourth step is to identify the blends whenever possible, and define the observed energy levels $E_{\rm obs}$(with their uncertainties, based on uncertainties in the observed wavelengths) using the identified transitions (normally the brightest lines). Then, apply the "term energy correction'' (TEC) procedure (see, e.g. Zeippen et al. 1977; Nussbaumer & Storey 1978) within SUPERSTRUCTURE. Empirical corrections to the LS energies are used to modify the non-relativistic Hamiltonian matrix, which is then used together with the Breit-Pauli relativistic correction to solve the eigenvalue problem and obtain empirically-adjusted fine-structure energies, $E_{\rm SS}$. The adjusted energies $E_{\rm SS}$ are then compared to the observed energies $E_{\rm obs}$. Note that the mixing between fine-structure levels can substantially change once semi-empirical adjustments to the energies are applied.

We then repeat the procedure, in order to identify all the spectral lines that should be observable, and to provide a set of best wavelengths for all the lines in the model ion. At the end of the iterative procedure, a set of best energies $E_{\rm best}$ is provided. These energies are the adopted observed energies, whenever available, and the adjusted $E_{\rm SS}$ values otherwise.

4 Results

Table 1 lists the set of configurations we adopted to calculate the radiative data. All the single and double excitations within n=2,3,4 configurations are included, for a total of 45 configurations, 173 LS levels. We ran various tests, doubling the configurations by also including configurations up to n=7, but noticed only small effects on the lower n=2,3,4 levels. TEC were applied to many levels, using the identifications and the observed energies. For the levels for which no observed energy could firmly be established we applied an energy correction between 7000 and 11 000 cm^-1 based on the corrections applied to levels of the same configuration.

Table 1: The configurations used to calculate the energy levels and the radiative data.

Table 2 presents a summary of our recommended observed energies (or adjusted $E_{\rm SS}$ values), with details about level mixing and comparisons with the energies available from NIST. A few levels have obviously been misidentified. For example, levels 17,18,19 (³D_J) are pure and the energies recommended by NIST are not consistent with the fine-structure splittings of these levels. The same applies to the mixed 2p 3d ³D_Jlevels. The levels 2p 3s are uncertain, but the values in NIST indicate a 50 000 cm^-1 difference compared to the predicted energy, based on the energies of the other configurations.

The gf values (cf. Table 3) of some transitions are very sensitive to the level energies and mixing. Our values are in excellent agreement with those independently obtained by Fawcett (1978,1984,1985) also using semi-empirical adjustments.

Once the energies have been assigned, we have calculated the A values, by using our best energies. These values, as expected, compare well with those available in the literature (cf. Table 3 with comparisons with the values available in NIST).

The lifetimes of a few levels have been measured and these values are in excellent agreement with our predicted values as shown in Table 4. Note that our values are in slightly better agreement with observations, compared to the values obtained by the use of AUTOSTRUCTURE without any semi-empirical adjustments (Chidichimo et al. 2005) and those calculated by Safronova et al. (1999) using relativistic many-body perturbation theory (however they only included n=2 levels).

We have then solved the stationary level balance equations by using our A values and the effective collision strengths of Chidichimo et al. (2005) for excitations up to n=4 levels. Table 5 shows the fractional level populations N_jof the lowest levels. It can be seen that, at laser plasma densities (10¹⁹ cm^-3), some of the lower levels become significantly populated. Knowing the level populations, we have then been able to compare the theoretical line intensities with the experimental ones, to aid the identification process.

In what follows we provide some details about the line identifications. Table 6 provides a summary list of all the lines that we predict to be brightest at low and high densities, with a list of identifications. The second and third columns give the relative intensities of the brightest lines calculated at 10¹², 10¹⁹ cm^-3, i.e. in the low-density limit (astrophysical plasmas) and at the densities typical of laser plasmas. In fourth column we list the wavelengths calculated from our best energies $E_{\rm best}$; in fifth column what we believe to be the best observed wavelengths $\lambda_{\rm obs}$. In the following two columns, we indicate some of the previous identifications and whether or not they are consistent with ours. We note that most published line lists contain a number of incorrect identifications, some of which are discussed here. The complexity of the line identification is obvious by looking at the large number of contradicting identifications found in the literature. Another complication is the fact that the contamination from lines of other ions is almost unique for each observation. Blending of lines is often not taken into account in the literature.

One positive result is that all the brightest lines in the two different density regimes have been observed. All the lines observed in the low-density limit have also been observed in laboratory plasmas, hence we have normally adopted laboratory wavelengths for these lines. We note, however, that wavelength measurements are often not consistent.

Table 2: The details of the most important configurations in Fe XXIII (only the most significant n=4 levels are shown; the full Table is available in electronic form). The percentage of level mixing (>10%) is indicated in second column. $E_{\rm best}$ indicates the best energies (cm^-1) which we propose in this work. The uncertainties in the energies reflect the estimated errors in the wavelength measurements. Levels with uncertain identification are assigned an uncertainty of 5000 cm^-1, an estimate based on the comparisons between the observed energies and the values computed ab initio. The other columns indicate the differences between our $E_{\rm best}$ and the energies from NIST $E_{\rm NIST}$, the collisional calculations $E_{\rm CC}$, and the adjusted SS values $E_{\rm SS}$. Levels are ordered according to the energies $E_{\rm CC}$ from the scattering calculations.

Table 3: Results for the brightest lines in Fe XXIII. The lines are grouped in three ranges (${n=2\to 2}$, $n=3 \to 2$, $n=4 \to 2$), and are displayed in decreasing order of intensity. Columns 2, 3 show the relative line intensities (ergs) $Int=N_{j} A_{ji}/N_{\rm e}$ calculated at different temperatures and at an electron density of 10¹⁰ cm^-3, normalised to the intensity of the 1-15 line at 10⁷ K. Columns 4, 5 show the gf and A values calculated in this work. Column 6 shows, for comparison, the NIST A values. The last two columns show the wavelengths corresponding to the best energies $E_{\rm best}$ of Table 2 and the NIST values. The uncertainties on the proposed wavelengths are derived from the uncertainties assigned to the energies. Note the different temperature sensitivity of the various lines.

4.1 ${n=2\to 2}$ transitions

${n=2\to 2}$ transitions fall in the EUV spectral range. They are very important because accurate measurements of their wavelengths constrain the energies of the levels of the lower 2s 2p and 2p² configurations. In turn, these are important because many $n=3 \to 2$ transitions decay into these levels.

Kastner et al. (1974) were the first to identify in solar flare spectra the 1-5 resonance line observed at 132.83 Å. This line is the dominant one in the EUV spectra of solar flares (and of active stars, see for example the EUVE spectra in Monsignori Fossi et al. 1996), but it is blended with an Fe XX line. However, the contribution from Fe XX can be calculated accurately since other unblended Fe XX lines are observed nearby, at 118.68, 121.84 Å. Various different wavelength measurements of the 1-5 transition exist in the literature. We note that the various solar measurements are inconsistent, when uncertainties are considered. It is well-known that during solar flares, in particular in the impulsive phase, the flare lines become blue-shifted. It is therefore possible that the solar flare measurements were affected. We therefore adopt the laboratory measurement of $132.906\pm0.005$ obtained by Sugar & Rowan (1995), noting that further measurements would be needed to confirm the Sugar & Rowan (1995) value.

Widing (1975) was the first to identify the intercombination line 1-3 in solar flare spectra. Various measurements consistently indicate a wavelength of 263.76 Å. We note that the ratio of the resonance 1-5 and intercombination 1-3 line is an excellent temperature diagnostics (see Table 3).

As far as we know the only solar measurement of both lines is reported in Mason et al. (1984), where OSO-5 spectra of solar flares were presented. The instrument was a scanning spectrometer and the two lines were not recorded simultaneously. This might be one of the reasons why the intensities of the two lines (after blending with Fe XX is taken into account) are not consistent with theory. We recommend that future instruments record the 263.76 Å in first order and the 1-5 in second order (265.81 Å).

The 3-4 transition was first observed in laboratory spectra by Hinnov & Suckewer (1980) at $1079.3\pm0.3$ Å and by Finkenthal et al. (1984) at a wavelength of $1079.1\pm0.5$. Recently, it was also observed in a solar flare spectrum by Feldman et al. (2000) at $1079.41\pm0.03$ Å. We adopt the last and more accurate measurement.

The above three transitions are the only EUV lines observable in astrophysical plasmas. Our model in fact predicts intensities of all the other lines far below the sensitivities of past instruments (e.g. OSO-5).

In high-density laboratory plasmas, other lines become prominent. Unfortunately, there are only few measurements of these lines. Lawson & Peacock (1980) provided the first measurements of these lines, causing Edlén (1981) to revise the energies of the ions in the Be I sequence. These measurements constrain the energies of all the remaining levels, with the exclusion of level 2 (2s 2p ³P $_{0}^{\rm o}$) which is marginally constrained by the 2-17 and 2-53 transitions (here we adopt the Edlén 1981 interpolated value). We note however that there are some inconsistencies in the measurements reported by Lawson & Peacock (1980) and that there are also differences with the measurements reported by Buchet et al. (1982) (see Table 6). New, more accurate measurements would be useful.

4.2 $n=4 \to 2$ transitions

The $n=4 \to 2$ transitions provide an excellent potential for measuring both electron densities in laser plasmas and electron temperatures in tokamak or astrophysical sources. These diagnostics have not previously been explored. Figure 1 shows the F_ji curves relative to the main $n=4 \to 2$ transitions observed in the laser spectra by Boiko et al. (1978). The agreement between theory and observations is exceptionally good, considering the various uncertainties and the simple ion model we adopted. The lines displayed in Fig. 1 belong to the 2s²-2s 4p, 2s 2p-2s 4d, 2s 2p-2s 4s transition arrays, and are excellent density diagnostics at laser plasma temperatures. They consistently indicate log $N_{\rm e}$ = 18-19 cm^-3, consistent with that of the laser plasma.

Table 4: Measured and calculated lifetimes for some of the lower levels in Fe XXIII. SS: calculated with SUPERSTRUCTURE and adjusted energies; AS: calculated with AUTOSTRUCTURE (Chidichimo et al. 2005); S99: calculated by Safronova et al. (1999) using relativistic many-body perturbation theory (including only n=2 levels).

Table 5: The fractional level populations N_j, calculated at different electron densities (cm^-3) and the temperature T= 12.6 MK (log T=7.1) for the lowest (most populated) levels.

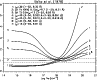Figure 1: The emissivity ratio curves calculated at log $T[{\rm K}]=7.2$ and relative to the $n=4 \to 2$ transitions from singly-excited levels observed in the laser spectra by Boiko et al. (1978). The curves are labelled with increasing numbers. For each line, we indicate: the observed intensities $I_{\rm ob}$; the lower and upper level index corresponding to Table 2; the theoretical wavelength. The dashed lines indicate agreement within $\pm$20%.

Open with DEXTER

The lines from doubly-excited levels (e.g. the 2p²-2p 4d and 2s 2p-2p 4p transition arrays), only visible in laser plasmas, are also well represented (within 50%) by this simple model, at least in a relative sense (see Fig. 2). This allows us to confirm most previous identifications and assess the presence of blends. We note that these doubly-excited levels are not excited from the ground, but mainly from the excited 2s 2p and 2p² levels. The transitions have small collision strengths and therefore have larger uncertainties. Considering that the intensities vary by orders of magnitude over a small density range, and the fact that the intensities are only approximate, the agreement is perfectly reasonable.

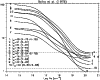	Figure 2: The emissivity ratio curves calculated at log $T[{\rm K}]=7.2$ and relative to the $n=4 \to 2$ transitions from doubly-excited levels observed in the laser spectra by Boiko et al. (1978). The dashed lines indicate relative agreement within $\pm$50%.
Open with DEXTER

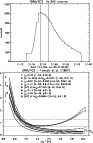Figure 3: Top: total count rates observed by SMM/BCS during the 1985 July 2 flare in the 1.87-1.88 Å range, dominated by Fe XXIII inner-shell lines. The time interval of the region 8.30-8.92 Å scanned by the SMM/FCS is also shown. Line intensities decrease by a maximum 10% during the FCS scan. Bottom: the emissivity ratio curves calculated at 1012 cm-3 and relative to the $n=4 \to 2$ transitions measured in the SMM/FCS solar spectrum by Fawcett et al. (1987). With the exception of the first spectral line (8.30 Å), all other ones intersect within $\pm$30%, indicating an isothermal plasma at $\log~ T \simeq 7.0 \pm 0.1$.

Open with DEXTER

The lines belonging to the 2s²-2s 4p, 2s 2p-2s 4d, 2s 2p-2s 4s transition arrays are also bright in astrophysical plasmas. In this case they provide an excellent temperature diagnostic. The best solar spectrum containing these lines was taken during the peak phase of a flare observed by SMM on 1985 July 2 (Fawcett et al. 1987). Figure 3 (top) shows the light curve in Fe XXIII inner-shell lines during the flare observed by SMM/BCS, and the interval during which SMM/FCS scanned the region 8.30-8.92 Å where the $n=4 \to 2$ lines are. Note that the Fe XXIII line intensities decrease at most by 10% during the FCS scan, hence we can use the FCS line intensities as if they were recorded simultaneously, i.e. to diagnose the plasma state during this interval. Figure 3 (bottom) shows the emissivity ratio curves relative to the $n=4 \to 2$ transitions measured in the SMM/FCS solar spectrum by Fawcett et al. (1987). The agreement between theory and observation is excellent. Notice that: a) we can quantify that the 1-50 transition contributes 30% to the observed line at 8.32 Å , the rest being due to Fe XXIV; b) the lines observed at 8.55, 8.61 Å are both self-blends; c) these two self-blends have a temperature sensitivity markedly different compared to the other nearby lines; this makes them an excellent temperature diagnostic; both lines consistently indicate that the plasma had a temperature log $T[{\rm K}] \simeq 7.0 \pm 0.1$; c) the 6-70 transition appears to contribute by 30% to the line observed at 8.660 Å and listed as unidentified by Fawcett et al. (1987).

4.3 $n=3 \to 2$ transitions

The amount of literature on astrophysical and laboratory observations of $n=3 \to 2$ transitions is extensive. The number of uncertain or contradicting identifications is however disturbing! Ultimately, the difficulty in the line identifications relates to the vast number of L-shell spectral lines of different ionization stages of Iron (and/or other elements) that are present even in the laboratory spectra with the highest spectral resolution.

The number of spectral lines observed in astrophysical plasmas is very small. This is because, up to densities of the order of 10¹⁵ cm^-3 (which are larger than the highest densities measured e.g. in solar flares), most of the ion population is still in the ground state. Hence all the levels are directly excited from the ground level, and the main lines that are emitted are the few strongest dipole-allowed transitions.

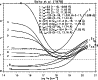	Figure 4: The emissivity ratio curves calculated at log $T[{\rm K}]=7.2$ and relative to the $n=3 \to 2$ transitions from singly-excited levels observed in laser spectra by Boiko et al. (1978).
Open with DEXTER

Lines of the 2s²-2s 3p, 2s 2p-2s 3d, 2s 2p-2s 3s transition arrays are observed both in laboratory and astrophysical spectra. Figure 4 shows the F_ji curves relative to the brightest $n=3 \to 2$ transitions observed in the laser spectra by Boiko et al. (1978). The agreement between theory and observations is again exceptionally good, within 30% (note that a correction factor of 2 has been applied to the normalisation, compared to the value adopted for the $n=4 \to 2$ transitions). The $n=3 \to 2$ transitions indicate the same electron densities as obtained from the $n=4 \to 2$ transitions. The transitions 4-18 (11.46 Å), 3-11 (11.72 Å), and 4-11 (11.85 Å) appear to be blended. The 1-13 (11.018 Å) also appears to be blended, with an Fe XVIII transition according to Boiko et al. (1978). Note that, in low-resolution spectra, this line is further blended with a strong Fe XXIV transition at 11.030 Å. As in the case of the $n=4 \to 2$ transitions, the intensities of the lines from doubly-excited levels are lower than the observed ones, but in relative terms there is good agreement (within a factor of 2), thus allowing us to confirm many of the previous identifications of lines of the 2p²-2p 3d and 2s 2p-2p 3p transition arrays. The laser spectra by Spector et al. (1980) give similar indications, although here the blending of lines appears to be different.

In astrophysical spectra, only a few lines are relatively bright and unblended. Blending varies depending on the source. In the SMM/FCS solar flare spectrum of 1980 August 25 (see Phillips et al. 1982), only the 1-13 (10.98 Å), 5-20 (11.74 Å) and 5-12 (12.16 Å) appear unblended. The 5-12 line (12.16 Å) is in the long-wavelength shoulder of the Ne X, but in high-resolution spectra it can be de-blended (note that Phillips et al. 1982 considered the 12.16 Å line as unidentified). The spectral region 10.98-12.16 Å was scanned during the decay phase in less than 4m, during which the intensities of the Fe XXIII inner-shell lines observed by SMM/BCS in the 1.87-1.88 Å range decreased by at most 25% (cf. Fig. 5). This variation is well within the uncertainty in the measurement of the line intensities, hence for line identification purposes we can use the non-simultaneous line intensities. The Fe XXIII lines during this decay phase were weak. The Phillips et al. (1982) intensities were not calibrated, so we have re-analysed the observation using the standard SolarSoft programs. The 1-13 (11.017 Å) is blended with an unidentified line at 11.012 Å and a strong Fe XVII transition at 11.025 Å (Phillips et al. 1982 reports them at 11.014 and 11.026 Å). The 3-18 (11.333 Å) and 4-19 (11.442 Å), transitions would be an excellent temperature diagnostic, however in this solar spectrum the former is in the wings of a strong 11.324 Å Fe XVIII line, and the latter is blended with a strong Fe XVIII transition.

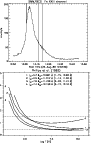	Figure 5: Top: total count rates observed by SMM/BCS during the 1980 August 25 flare in the 1.87-1.88 Å range, dominated by Fe XXIII inner-shell lines. The time interval of the region 10.98-12.16 Å scanned by the SMM/FCS is also shown. Bottom: the emissivity ratio curves calculated at 1012 cm-3 and relative to the $n=3 \to 2$ transitions observed in the SMM/FCS spectrum.
Open with DEXTER

4.4 Combined ${n=2,3,4\to 2}$ transitions

Table 6: Summary of the line identifications for Fe XXIII The columns indicate: 1) the indices corresponding to Tables 2; 2,3) the relative intensities (in photons, scaled to the 1-15 10.980 Å line and calculated at log $T[{\rm K}]=7.2$) typical of astrophysical and laser plasmas (10¹², 10¹⁹ cm^-3); 4) the wavelengths calculated from our best energies $E_{\rm best}$; 5) observed wavelengths $\lambda _{\rm observed}$; some blends are indicated (bl = blend; bl-mr = blend in medium-resolution spectra; bl-w = blend with a weak line); lines with no or a tentative identification have a question mark; 6,7) previous identifications consistent or not with ours (with observed wavelengths in Å; note that observed and calculated wavelengths in the cited literature can differ from the values reported here). Legenda: Bo78: Boiko et al. (1978) (see also original work cited in this review paper); B78: Bromage et al. (1978); B85: Burkhalter et al. (1985); B02: Brown et al. (2002); D72: Doschek et al. (1972); F79: Fawcett et al. (1979); F00: Feldman et al. (2000); H80: Hinnov & Suckewer (1980); K74: Kastner et al. (1974); LP80: Lawson & Peacock (1980); S80: Spector et al. (1980) SF86: Seely & Feldman (1986); SR95: Sugar & Rowan (1995); W75: Widing (1975); W98: Wargelin et al. (1998). The final column indicates weather the lines have only been observed in high-density plasmas (H).

	Figure 6: The emissivity ratio curves calculated at 1012 cm-3 and relative to the $n=3,4\to 2$ transitions observed with the SOLEX A and B spectrometers (McKenzie et al. 1985).
Open with DEXTER

Figure 6 shows the emissivity ratio curves relative to the $n=3,4\to 2$ transitions observed with the SOLEX spectrometers (McKenzie et al. 1985) near the peak of a flare observed on 1981 May 5. The 5.5-12 Å range was observed by scanning the crystals in only 84 s, during which the Fe XXIII 11.737 Å decreased by only 25%, hence in theory all the lines could be directly compared. However, the $n=4 \to 2$ lines were observed with the SOLEX A spectrometer, while the $n=3 \to 2$ lines by SOLEX B. The spectrometers had two different collimators and there is an inconsistency in the two measurements (McKenzie et al. 1985). Indeed a different normalisation has been applied to the lines observed by the two spectrometers and shown in the two plots in Fig. 6. The examination of lines observed by the same spectrometer shows the following: a) the intensity of the 8.32 Å line was assigned by McKenzie et al. (1985) only to Fe XXIV, however $\simeq$20% is due to the 1-50 (8.31 Å) Fe XXIII transition; b) as already pointed out above, the 8.61 Å self-blend (considered as unidentified by the authors) is an excellent temperature diagnostic; c) the 1-13 at 11.02 Å is blended with transitions from other ions; d) also in this case the 3-18 at 11.34 Å is mainly due to Fe XVIII. Finally, we note that the 11.493 Å line was incorrectly assigned by McKenzie et al. (1985) to an Fe XXIII transition.

RS CVn stars produce X-ray spectra quite similar to those of solar flares. Osten et al. (2003) reported a near-simultaneous Chandra and EUVE observation of the $\sigma ^2$ CrB binary. The Chandra gratings recorded the three relatively strong 1-15, 5-20 and 5-12 transitions. The 5-12 line is resolved from Ne X at the Chandra resolution. The strong resonance 1-5 line was observed by the EUVE spectrometers, and its intensity corrected for interstellar H, He absorption by Osten et al. (2003). For most of the observation the stars were in quiescence, hence even though the Chandra and EUVE observations were not strictly simultaneous, the line ratios should be approximately constant. From the intensities of the two Fe XX 118.68, 121.84 Å lines we estimate that 30% of the observed line is due to Fe XX, while the rest is due to the resonance 1-5 line. Figure 7 shows the F_ji curves relative to these lines as measured by the Chandra HETG and EUVE. Notice that the intensities obtained with the Chandra MEG differ from those measured by the HETG. The agreement is excellent, indicating a near-isothermal distribution around a temperature log $T[{\rm K}] \simeq 7.25$, in agreement with a similar analysis using Fe XXIV lines (that will be published elsewhere), and only marginally consistent with the emission measure distributions obtained by Osten et al. (2003).

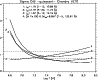	Figure 7: The emissivity ratio curves calculated at 1012 cm-3 and relative to the $n=3 \to 2$, ${n=2\to 2}$ transitions observed in the Chandra HETG and EUVE spectra of $\sigma ^2$ CrB during its quiescent state reported by Osten et al. (2003). The agreement with theory is excellent (within 20%), indicating an electron temperature log $T[{\rm K}] \simeq 7.25$.
Open with DEXTER

The spectral range of the Chandra HETG/MEG instruments allow a simultaneous recording of the Fe XXIII $n=3,4\to 2$ transitions. Note that the combination of $n=3,4\to 2$ transitions is a good temperature diagnostic. We found that in many published papers few spectral lines have been incorrectly identified. Also, that the observed intensities of the $n=4 \to 2$ transitions are often too large, an indication of a possible error in the earlier calibration of the Chandra gratings. As an example, see Fig. 8 where the emissivity ratio curves relative to a Chandra HETG observation of the young star $\Theta ^1$ Ori C (Schulz et al. 2003) are shown (the quoted uncertainties are in the range 20-30%). The $n=3 \to 2$ lines provide a temperature log $T \simeq7.3$ K, in broad agreement with one of the peaks (at log $T \simeq7.4$ K) in the emission measure distribution calculated by Schulz et al. (2003). Finally, we note that Schulz et al. (2003) incorrectly identified the line observed at 8.304 Å with an Fe XXIV transition.

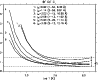	Figure 8: The emissivity ratio curves calculated at 1012 cm-3 and relative to the $n=3,4\to 2$ transitions observed with the Chandra HETG and emitted by the hot young star $\Theta ^1$ Ori C (Schulz et al. 2003). The agreement, when considering the entire spectral range, is only marginal ($\pm$50%).
Open with DEXTER

5 Summary and conclusions

We have reviewed and assessed all previous line identifications for L-shell emission in Fe XXIII, by supplementing recent scattering calculations with new radiative data obtained with empirical adjustments that take into account observed wavelengths. We confirm the previous identifications of the brightest lines. However, many earlier identifications are either revised or questioned.

We have also revised many energy levels, however accurate measurements, in particular of calibrated line intensities, are needed. We have indicated the presence of blends, and which spectral lines are most useful for density or temperature diagnostics. The agreement between theoretical and experimental data in terms of wavelengths, line intensities and level lifetimes is very good, considering the large uncertainties in the experimental data.

In particular, we have shown that $n=3,4\to 2$ transitions are an excellent density diagnostic in laser plasmas. This was previously known, but not applied to specific cases. We found excellent agreement between our simple model and the laser plasma observations of Boiko et al. (1978), for the brightest lines in the 2s²-2s [3,4]p, 2s 2p-2s [3,4]d, 2s 2p-2s [3,4]s transition arrays. They provide densities in agreement with the values obtained using the standard technique involving the He I-like triplets (see, e.g. Aglitskii et al. 1974; Boiko et al. 1979).

We have shown that $n=4 \to 2$ transitions are an excellent temperature diagnostic in astrophysical plasmas, over a wide range. $n=3 \to 2$ transitions are also a good temperature diagnostic, especially if observed in combination with ${n=2\to 2}$ transitions (as shown in the case of Chandra and EUVE spectra of $\sigma ^2$ CrB), or with $n=4 \to 2$ transitions.

The use of the above temperature diagnostics has been suggested in the previous literature. However, this is the first time that they are applied to solar flares and stellar coronae. These diagnostics involve bright lines easily observable by current and future instruments, and offer an independent way of measuring electron temperatures, different from the commonly-used one which involves measurements of the weaker (and often blended) satellites of the H I- and He I-like lines. Well-calibrated and high signal-to-noise observations can provide accurate temperature measurements for "hot'' astrophysical plasmas.

Acknowledgements

Support from PPARC is acknowledged. We warmly thank B. C. Fawcett and G. E. Bromage for useful comments on the manuscript.

References

• Aglitskii, E. V., Boiko, V. A., Vinogradov, A. V., & Iukov, E. A. 1974, Soviet J. Quantum Electronics, 1, 579 [NASA ADS] (In the text)
• Bhatia, A. K., & Mason, H. E. 1981, A&A, 103, 324 [NASA ADS] (In the text)
• Boiko, V. A., Krokhin, O. N., Pikuz, S. A., & Faenov, A. I. 1975, Soviet J. Quantum Electronics, 1, 2178 [NASA ADS] (In the text)
• Boiko, V. A., Faenov, A. I., & Pikuz, S. A. 1978, J. Quantitative Spectroscopy and Radiative Transfer, 19, 11 [NASA ADS] (In the text)
• Boiko, V. A., Pikuz, S. A., & Faenov, A. I. 1979, J. Phys. B Atom. Molec. Phys., 12, 1889 [NASA ADS] [CrossRef] (In the text)
• Bromage, G. E., Fawcett, B. C., Ridgeley, A., & Cowan, R. D. 1978, Opt. Soc. Am. J., 68, 48 [NASA ADS] (In the text)
• Brown, G. V., Beiersdorfer, P., Liedahl, D. A., et al. 2002, ApJS, 140, 589 [NASA ADS] [CrossRef] (In the text)
• Buchet, J. P., Buchet-Poulizac, M. C., Denis, A., et al. 1982, Nucl. Instrum. Methods, 202, 79 [CrossRef] (In the text)
• Buchet, J. P., Buchet-Poulizac, M. C., Denis, A., et al. 1984, Phys. Rev. A, 30, 309 [NASA ADS] [CrossRef]
• Burkhalter, P. G., Newman, D. A., Hailey, C. J., Rockett, P. D., & Charatis, G. 1985, Opt. Soc. Am. J. B Opt. Phys., 2, 1894 [NASA ADS] (In the text)
• Chidichimo, M. C., Zeman, V., Tully, J. A., & Berrington, K. A. 1999, A&AS, 137, 175 [NASA ADS] (In the text)
• Chidichimo, M. C., Del Zanna, G., Mason, H. E., et al. 2005, A&A, 430, 331 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Cohen, L., & Feldman, U. 1970, ApJ, 160, L105 [NASA ADS] [CrossRef] (In the text)
• Del Zanna, G., & Mason, H. E. 2005, A&A, in press (In the text)
• Del Zanna, G., Berrington, K. A., & Mason, H. E. 2004, A&A, 422, 731 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Doschek, G. A. 1990, ApJS, 73, 117 [NASA ADS] [CrossRef] (In the text)
• Doschek, G. A., & Feldman, U. 1987, ApJ, 313, 883 [NASA ADS] [CrossRef] (In the text)
• Doschek, G. A., Meekins, J. F., & Cowan, R. D. 1972, ApJ, 177, 261 [NASA ADS] [CrossRef] (In the text)
• Doschek, G. A., Meekins, J. F., & Cowan, R. D. 1973, Sol. Phys., 29, 125 [NASA ADS] [CrossRef] (In the text)
• Doschek, G. A., Feldman, U., Davis, J., & Cowan, R. D. 1975, Phys. Rev. A, 12, 980 [NASA ADS] [CrossRef] (In the text)
• Edlén, B. 1981, Phys. Scr, 23, 1079 [NASA ADS] (In the text)
• Eissner, W., Jones, M., & Nussbaumer, H. 1974, Computer Phys. Commun., 8, 270 [NASA ADS] [CrossRef] (In the text)
• Fawcett, B. C. 1978, Atomic Data and Nuclear Data Tables, 22, 473 [NASA ADS] [CrossRef]
• Fawcett, B. C. 1984, Atomic Data and Nuclear Data Tables, 30, 1 [NASA ADS] [CrossRef]
• Fawcett, B. C. 1985, Atomic Data and Nuclear Data Tables, 33, 479 [CrossRef]
• Fawcett, B. C., & Hayes, R. W. 1975, MNRAS, 170, 185 [NASA ADS] (In the text)
• Fawcett, B. C., Ridgeley, A., & Hughes, T. P. 1979, MNRAS, 188, 365 [NASA ADS] (In the text)
• Fawcett, B. C., Jordan, C., Lemen, J. R., & Phillips, K. J. H. 1987, MNRAS, 225, 1013 [NASA ADS] (In the text)
• Feldman, U., & Cohen, L. 1968, ApJ, 151, L55 [NASA ADS] [CrossRef] (In the text)
• Feldman, U., Doschek, G. A., Prinz, D. K., & Nagel, D. J. 1976, J. Appl. Phys., 47, 1341 [NASA ADS] [CrossRef] (In the text)
• Feldman, U., Curdt, W., Landi, E., & Wilhelm, K. 2000, ApJ, 544, 508 [NASA ADS] [CrossRef] (In the text)
• Finkenthal, M., Bell, R. E., Moos, H. W., & TFR Group. 1984, J. Appl. Phys., 56, 2012 [NASA ADS] [CrossRef] (In the text)
• Hinnov, E., & Suckewer, S. 1980, Phys. Lett. A, 79, 298 [NASA ADS] [CrossRef] (In the text)
• Hutton, R., Martinson, I., Nyström, B., et al. 1997, Phys. Scr, 55, 431 [NASA ADS]
• Kastner, S. O., Neupert, W. M., & Swartz, M. 1974, ApJ, 191, 261 [NASA ADS] [CrossRef] (In the text)
• Lawson, K. D., & Peacock, N. J. 1980, J. Phys. B Atom. Molec. Phys., 13, 3313 [NASA ADS] [CrossRef] (In the text)
• Mason, H. E., Bhatia, A. K., Neupert, W. M., Swartz, M., & Kastner, S. O. 1984, Sol. Phys., 92, 199 [NASA ADS] [CrossRef] (In the text)
• Matte, J. P., Kieffer, J. C., Ethier, S., Chaker, M., & Peyrusse, O. 1994, Phys. Rev. Lett., 72, 1208 [NASA ADS] [CrossRef] (In the text)
• McKenzie, D. L., Landecker, P. B., Broussard, R. M., et al. 1980, ApJ, 241, 409 [NASA ADS] [CrossRef]
• McKenzie, D. L., Landecker, P. B., Feldman, U., & Doschek, G. A. 1985, ApJ, 289, 849 [NASA ADS] [CrossRef]
• Monsignori Fossi, B. C., Landini, M., Del Zanna, G., & Bowyer, S. 1996, ApJ, 466, 427 [NASA ADS] [CrossRef] (In the text)
• Neupert, W. M., Gates, W., Swartz, M., & Young, R. 1967, ApJ, 149, L79 [NASA ADS] [CrossRef] (In the text)
• Neupert, W. M., Swartz, M., & Kastner, S. O. 1973, Sol. Phys., 31, 171 [NASA ADS] (In the text)
• Nussbaumer, H., & Storey, P. J. 1978, A&A, 64, 139 [NASA ADS] (In the text)
• Osten, R. A., Ayres, T. R., Brown, A., Linsky, J. L., & Krishnamurthi, A. 2003, ApJ, 582, 1073 [NASA ADS] [CrossRef] (In the text)
• Phillips, K. J. H., Fawcett, B. C., Kent, B. J., et al. 1982, ApJ, 256, 774 [NASA ADS] [CrossRef] (In the text)
• Phillips, K. J. H., Mewe, R., Harra-Murnion, L. K., et al. 1999, A&AS, 138, 381 [NASA ADS] (In the text)
• Safronova, U. I., Derevianko, A., Safronova, M. S., & Johnson, W. R. 1999, J. Phys. B Atom. Molec. Phys., 32, 3527 [NASA ADS] (In the text)
• Schulz, N. S., Canizares, C., Huenemoerder, D., & Tibbets, K. 2003, ApJ, 595, 365 [NASA ADS] [CrossRef] (In the text)
• Seely, J. F., & Feldman, U. 1986, Phys. Scr, 33, 110 [NASA ADS] (In the text)
• Spector, N., Zigler, A., Zmora, H., & Schwob, J. L. 1980, Opt. Soc. Am. J., 70, 857 [NASA ADS] (In the text)
• Spitzer, L. 1962, Physics of Fully Ionized Gases, Physics of Fully Ionized Gases (New York: Interscience, 2nd edition) (In the text)
• Storey, P. J., Del Zanna, G., Mason, H. E., & Zeippen, C. 2005, A&A, in press (In the text)
• Sugar, J., & Rowan, W. L. 1995, Opt. Soc. Am. J. B Opt. Phys., 12, 1403 [NASA ADS] (In the text)
• Swartz, M., Kastner, S., Rothe, E., & Neupert, W. 1971, J. Phys. B Atom. Molec. Phys., 4, 1747 [NASA ADS] [CrossRef] (In the text)
• Wargelin, B. J., Beiersdorfer, P., Liedahl, D. A., Kahn, S. M., & von Goeler, S. 1998, ApJ, 496, 1031 [NASA ADS] [CrossRef] (In the text)
• Widing, K. G. 1975, ApJ, 197, L33 [NASA ADS] [CrossRef] (In the text)
• Zeippen, C. J., Seaton, M. J., & Morton, D. C. 1977, MNRAS, 181, 527 [NASA ADS] (In the text)