A&A 431, 477-502 (2005)
DOI: 10.1051/0004-6361:20047021
S. Jester1,![]() - H.-J. Röser1 - K. Meisenheimer1 - R. Perley2
- H.-J. Röser1 - K. Meisenheimer1 - R. Perley2
1 - Max-Planck-Institut für Astronomie, Königstuhl 17,
69117 Heidelberg, Germany
2 - National Radio Astronomy Observatory, PO Box 0, Socorro, NM 87801, USA
Received 6 January 2004 / Accepted 23 October 2004
Abstract
We present deep VLA and HST observations of the large-scale
jet in 3C 273 matched to 0
![]() 3 resolution. The observed spectra
show a significant flattening in the infrared-ultraviolet wavelength
range. The jet's emission cannot therefore be assumed to arise from a
single electron population and requires the presence of an additional
emission component. The observed smooth variations of the spectral
indices along the jet imply that the physical conditions vary
correspondingly smoothly. We determine the maximum particle energy
for the optical jet using synchrotron spectral fits. The slow decline
of the maximum energy along the jet implies particle reacceleration
acting along the entire jet. In addition to the already established
global anti-correlation between maximum particle energy and surface
brightness, we find a weak positive correlation between small-scale
variations in maximum particle energy and surface brightness. The
origin of these conflicting global and local correlations is unclear,
but they provide tight constraints for reacceleration models.
3 resolution. The observed spectra
show a significant flattening in the infrared-ultraviolet wavelength
range. The jet's emission cannot therefore be assumed to arise from a
single electron population and requires the presence of an additional
emission component. The observed smooth variations of the spectral
indices along the jet imply that the physical conditions vary
correspondingly smoothly. We determine the maximum particle energy
for the optical jet using synchrotron spectral fits. The slow decline
of the maximum energy along the jet implies particle reacceleration
acting along the entire jet. In addition to the already established
global anti-correlation between maximum particle energy and surface
brightness, we find a weak positive correlation between small-scale
variations in maximum particle energy and surface brightness. The
origin of these conflicting global and local correlations is unclear,
but they provide tight constraints for reacceleration models.
Key words: galaxies: jets - galaxies: quasars: individual: 3C 273 - radiation mechanisms: non-thermal - acceleration of particles
Jets are collimated outflows, thought to be launched from an accretion disk around a central compact object, which can be a supermassive black hole, a stellar-mass black hole or neutron star, or a young stellar object (YSO). They transport mass, energy, both linear and angular momentum as well as electromagnetic fields outward from the central object. A detailed understanding of the formation of these jets, their connection to the accretion disk from which they are launched, and the physics governing their internal structure and observable properties has not yet been achieved. Here we consider the synchrotron emission from the kiloparsec-scale jet of the quasar 3C 273, which is one of the brightest and largest and therefore an instructive sample case.
Jets became part of the standard model of extragalactic radio sources (Begelman et al. 1984) to link the lobes, which emit the bulk of the synchrotron radio luminosity, with the active galactic nucleus (AGN) of the host galaxy. In this model, jets merely transport energy to feed the lobes. In the most powerful sources, a double shock structure terminates the jets, consisting of an outer bow shock and contact discontinuity separating the jet material from the external medium and an internal shock (Mach disk) at which the relativistic flow is decelerated and bulk kinetic energy is channeled into highly relativistic particles through a shock acceleration mechanism. These particles emit the synchrotron radiation observed from the lobes. The radio hot spot is usually assumed to coincide with the Mach disk. The optical synchrotron emission observed from some hot spots can also be explained by first-order Fermi acceleration at a jet-terminating shock (Heavens & Meisenheimer 1987; Meisenheimer & Heavens 1986; Meisenheimer et al. 1989,1997).
In this model, the electrons responsible for radio synchrotron emission from the jets themselves are accelerated near the black hole and then simply advected with the jet flow. However, observations of high-energy (optical and X-ray) synchrotron radiation from 3C 273 and other jets force us to revise this picture. Electrons with the highly relativistic kinetic energies required for synchrotron emission in the infrared and optical have a very short radiative lifetime. This lifetime is much less than the light-travel time along the jet in 3C 273 (already noted by Greenstein & Schmidt 1964) and other jets. Observations of optical synchrotron emission from such jets (Scarpa & Urry 2002; Röser & Meisenheimer 1991,1999) as well as from the "filament'' near Pictor A's hot spot (Röser & Meisenheimer 1987; Perley et al. 1997) therefore suggest that in addition to a localized, "shock-like'' acceleration process operating in hot spots, there is an extended, "jet-like'' mechanism at work in radio sources in general and 3C 273's jet in particular (Meisenheimer et al. 1997). The extended mechanism may also be at work in the lobes of radio galaxies, where the observed maximum particle energies are above the values implied by the losses within the hot spots (Meisenheimer 1996) and by the dynamical ages of the lobes (Blundell & Rawlings 2000). We therefore make a clear distinction between the emission from the hot spot itself, the lobes and the body of the jet. Although all emit synchrotron radiation, the physical processes accelerating the particles emitting in these regions may be quite different.
The lifetime problem has been exacerbated by observations at even higher frequencies: Einstein and ROSAT observations, for example, showed X-ray emission from the jets in M 87 (Neumann et al. 1997b; Schreier et al. 1982; Biretta et al. 1991) and 3C 273 (Röser et al. 2000; Harris & Stern 1987). More recently, observations with the new X-ray observatory Chandra showed extended X-ray emission from many more jets, like PKS 0637-752 (Schwartz et al. 2000) and Pictor A (Wilson et al. 2001) as well as other jets and hot spots. Chandra also supplied the first high-resolution X-ray images of the jets in 3C 273 and M 87 (Marshall et al. 2001; Sambruna et al. 2001; Marshall et al. 2002). The X-rays from these objects seem to be of non-thermal origin (for an overview, see Harris & Krawczynski 2002): they could at least partially be due to synchrotron emission (Marshall et al. 2001; Röser et al. 2000; Marshall et al. 2002). Alternatively, inverse-Compton scattering could be responsible for the X-rays. The photon seed field can be provided by the synchrotron source itself if it is sufficiently compact, for example in the hot spots of Cygnus A (Wilson et al. 2000; Harris et al. 1994). If the bulk flow of a jet is still highly relativistic on large scales, the boosted energy density of the cosmic microwave background radiation field can lead to the observed X-ray fluxes (Tavecchio et al. 2000; Celotti et al. 2001). In all cases, those electrons producing the radio-optical synchrotron emission suffer additional losses from the inverse-Compton scattering, decreasing their cooling timescale even below the synchrotron cooling scale.
Thus, the fundamental question posed by the observation of optical extragalactic jets is the following: how can we explain high-frequency synchrotron and inverse-Compton emission far from obvious acceleration sites in extragalactic jets? While information on the source's magnetic field structure may be obtained from the polarization structure, the diagnostic tool for the radiating particles is a study of the synchrotron continuum over as broad a range of frequencies as possible, i.e., from radio to UV wavelengths, and with sufficient resolution to discern morphological details. The shape of the synchrotron spectrum gives direct insight into the shape of the electron energy distribution, thus also constraining the emission by the inverse-Compton process at other wavelengths. Here, we consider the shape of the synchrotron spectrum of the jet in 3C 273.
This optical jet was first detected on ground-based images. Like M 87, its optical brightness and length are so unusually large that it was detected even before radio jets were known. It appears to consist of a series of bright knots with fainter emission connecting them (see Fig. 1). Greenstein & Schmidt (1964) described the jet's optical spectrum as "weak, bluish continuum'', suspecting that this was synchrotron radiation. This was confirmed by Röser & Meisenheimer (1991) through optical polarimetry.
3C 273's radio jet extends continuously from the quasar out to a
terminal hot spot at 21
![]() 4 from the core, while optical emission
has been observed only from 12
4 from the core, while optical emission
has been observed only from 12
![]() outward
outward![]() . We concentrate on this "outer'' part of the jet here, and will report observations of optical emission from the inner jet with the VLT in a future publication (see
also Martel et al. 2003). Bahcall et al. (1995) presented the first HST imaging of
this jet, noting the jet resembles a helical structure.
. We concentrate on this "outer'' part of the jet here, and will report observations of optical emission from the inner jet with the VLT in a future publication (see
also Martel et al. 2003). Bahcall et al. (1995) presented the first HST imaging of
this jet, noting the jet resembles a helical structure.
Prior to the present work, synchrotron spectra have been derived for
the hot spot and the brightest knots using ground-based imaging in the
radio (Conway et al. 1993), near-infrared
![]() -band (Neumann et al. 1997a) and
optical I, R, B-bands (Röser & Meisenheimer 1991) at a common resolution of 1
-band (Neumann et al. 1997a) and
optical I, R, B-bands (Röser & Meisenheimer 1991) at a common resolution of 1
![]() 3 (Röser et al. 2000; Meisenheimer et al. 1996a). This radio-to-optical continuum can be explained by a single power-law electron population resulting in a constant radio spectral index
3 (Röser et al. 2000; Meisenheimer et al. 1996a). This radio-to-optical continuum can be explained by a single power-law electron population resulting in a constant radio spectral index![]() of -0.7, but with a high-energy cutoff frequency decreasing from 1017 Hz to 1015 Hz outward along the jet.
of -0.7, but with a high-energy cutoff frequency decreasing from 1017 Hz to 1015 Hz outward along the jet.
Here, we present VLA and HST NICMOS observations (Sect. 2) in
addition to the WFPC2 data already published in Jester et al. (2001).
Together, these constitute a unique data set in terms of resolution
and wavelength coverage for any extragalactic jet - only M 87 is
similarly well-studied (Meisenheimer et al. 1996b; Perlman et al. 1999,2001; Heinz & Begelman 1997; Sparks et al. 1996, and references
therein). Using these observations at
wavelengths 3.6 ![]() ,
2.0
,
2.0 ![]() ,
1.3
,
1.3 ![]() ,
1.6
,
1.6 ![]() m, 620
m, 620 ![]() and 300
and 300 ![]() ,
we
derive spatially resolved (at 0
,
we
derive spatially resolved (at 0
![]() 3) synchrotron spectra for the
jet (Sect. 4). By fitting model spectra according to
Heavens & Meisenheimer (1987), we derive the maximum particle energy everywhere in the
jet in order to identify regions in which particles are either
predominantly accelerated, or predominantly lose energy
(Sect. 5). The model spectra reveal excess near-ultraviolet
emission above a synchrotron cutoff spectrum accounting for the
emission from radio through optical, which implies that a
two-component model is necessary to describe the emission. The
radio-optical-X-ray spectral energy distributions (SEDs) suggest a
common origin for the UV excess and the X-rays from the jet
(Sect. 6.2; see also Jester et al. 2002). By considering just
the optical spectral index, we concluded in Jester et al. (2001) that
particles must be reaccelerated along the entire jet. Here we confirm
this conclusion by using the full spectral information from radio to
near-ultraviolet (Sect. 6.3). We consider whether the observed
changes of cutoff energy and surface brightness along the jet can be
explained solely as effects of changes in the magnetic field and the
Doppler beaming parameter along the jet (Sect. 6.4). We
conclude in Sect. 7.
3) synchrotron spectra for the
jet (Sect. 4). By fitting model spectra according to
Heavens & Meisenheimer (1987), we derive the maximum particle energy everywhere in the
jet in order to identify regions in which particles are either
predominantly accelerated, or predominantly lose energy
(Sect. 5). The model spectra reveal excess near-ultraviolet
emission above a synchrotron cutoff spectrum accounting for the
emission from radio through optical, which implies that a
two-component model is necessary to describe the emission. The
radio-optical-X-ray spectral energy distributions (SEDs) suggest a
common origin for the UV excess and the X-rays from the jet
(Sect. 6.2; see also Jester et al. 2002). By considering just
the optical spectral index, we concluded in Jester et al. (2001) that
particles must be reaccelerated along the entire jet. Here we confirm
this conclusion by using the full spectral information from radio to
near-ultraviolet (Sect. 6.3). We consider whether the observed
changes of cutoff energy and surface brightness along the jet can be
explained solely as effects of changes in the magnetic field and the
Doppler beaming parameter along the jet (Sect. 6.4). We
conclude in Sect. 7.
The jet has been observed at all wavelength bands available at the
NRAO's Very Large Array (VLA), i.e., at 90 cm, 20 cm, 6 cm, 3.6 cm,
2 cm, 1.30 cm and 0.7 cm. Observations were carried out between
July 1995 and November 1997, to obtain data with all array
configurations (thus covering the largest range of spatial
frequencies). Total integration times are of order a few times
10 000 s in each band. At 3.6 cm, the resolution set by the maximum
VLA baseline of just over 32 km is 0
![]() 24, with higher resolution
at shorter wavelengths. However, at 0.7 cm, fewer than half antennas
were equipped with receivers at that time, and the brightness of the
jet is so low relative to the noise that only the hot spot is detected
even at a fairly low resolution of 0
24, with higher resolution
at shorter wavelengths. However, at 0.7 cm, fewer than half antennas
were equipped with receivers at that time, and the brightness of the
jet is so low relative to the noise that only the hot spot is detected
even at a fairly low resolution of 0
![]() 35.
35.
The VLA data were edited, calibrated and CLEANed according to standard
procedures. Table 1 quotes the achieved dynamic
ranges. The present analysis considers the data at 3.6 cm, 2 cm and
1.3 ![]() .
This allows to fix the common resolution for the entire study
at 0
.
This allows to fix the common resolution for the entire study
at 0
![]() 3, slightly inferior to the resolution of the data at 3.6 cm. The remainder of the VLA data set will be discussed in a future publication, which will also contain details about the data processing.
3, slightly inferior to the resolution of the data at 3.6 cm. The remainder of the VLA data set will be discussed in a future publication, which will also contain details about the data processing.
Optical (
![]() )
and near-ultraviolet (
)
and near-ultraviolet (
![]() )
images were obtained under HST proposal #5980, using WFPC2 and
filters F622W (total exposure time 10 000 s) and F300W (exposure time
35 500 s). The data reduction and jet images are described in Jester et al. (2001).
)
images were obtained under HST proposal #5980, using WFPC2 and
filters F622W (total exposure time 10 000 s) and F300W (exposure time
35 500 s). The data reduction and jet images are described in Jester et al. (2001).
Observations were carried out under HST proposal #7848 using NICMOS
camera 2 (NIC2) on board the HST, which has 256 ![]() 256 pixels of
nominal scale 0
256 pixels of
nominal scale 0
![]() 076. Filter F160W was used, with a central
wavelength of
076. Filter F160W was used, with a central
wavelength of
![]() ,
yielding a diffraction limit of 0
,
yielding a diffraction limit of 0
![]() 17.
The total exposure time on the jet was 34 560 s distributed over 30 individual exposures with integer-pixel offsets. Each exposure was read out non-destructively every 256 s. Here we give only an outline of the data reduction; for details, see Jester (2001).
17.
The total exposure time on the jet was 34 560 s distributed over 30 individual exposures with integer-pixel offsets. Each exposure was read out non-destructively every 256 s. Here we give only an outline of the data reduction; for details, see Jester (2001).
Table 1: Dynamic ranges for the VLA images.
Nearly all of the frames reduced using the CALNICA pipeline provided by STScI show an offset in the background level between the detector quadrants as well as an imprint of the flat-field pattern. The quadrant offsets are ascribed to spatial and temporal variations of the detector bias level which have been termed "shading'' and "pedestal'' (NICMOS team 2001a). The recommended use of temperature-dependent dark files (NICMOS team 2001b) did not improve the quality of the reduced images, nor did any of the otherwise available correction tools. We therefore employed a custom reduction routine which initially estimates the sky and dark current by filtering the jet signal from all individual readouts. Any remaining quadrant-to-quadrant variation after subtracting the sky and dark current is ascribed to an additive component. These residual offsets are removed by subtracting the modal value from each quadrant. Finally, cosmic-ray and bad pixels are rejected using a pixelwise median filter.
The resulting images are not perfectly flat individually, suggesting
that there may be a residual problem with the flat-field. However, no
attempt is made to correct this because there is no information on
what the correct flatfield might be. Residual background structures
(including possible large-angle scattering wings from the quasar core)
are removed by modeling the background around the jet using
second-order polynomials along detector rows, whose coefficients are
smoothed in the perpendicular directions (identical to the
method used for the WFPC2 images, see Jester et al. 2001). The photometric
calibration is performed using the appropriate conversion factor from
the synphot package provided by STScI. In the conversion, we
do not correct for variations in the spectral index but always assume
a flat spectrum in ![]() ;
this correction would be at most 2%.
;
this correction would be at most 2%.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{0021f1.eps}\end{figure}](/articles/aa/full/2005/08/aa0021-04/Timg54.gif) |
Figure 1:
Map of near-infrared brightness (
|
| Open with DEXTER | |
Figure 1 shows the reduced and summed images. The
overall appearance of the jet's morphology at 1.6 ![]() m is very
similar to that at visible wavelengths (compare the WFPC2 images
in Jester et al. 2001, and Fig. 2 below). The only
significant difference (apart from the second star St2, see below) is
that the tip of the jet H1 (apparently downstream of the hot spot H2)
is visible on the infrared image, but not at higher frequencies. The
jet appears equally well collimated in the near-infrared as in the
optical. All optical extensions are detected, the southern extension S
here being much weaker than knot A, while they are comparable in the
UV. In1 is clearly brighter than In2, while again their near-UV
brightness is comparable, indicating a marked color difference between
the inner extension's two knots.
m is very
similar to that at visible wavelengths (compare the WFPC2 images
in Jester et al. 2001, and Fig. 2 below). The only
significant difference (apart from the second star St2, see below) is
that the tip of the jet H1 (apparently downstream of the hot spot H2)
is visible on the infrared image, but not at higher frequencies. The
jet appears equally well collimated in the near-infrared as in the
optical. All optical extensions are detected, the southern extension S
here being much weaker than knot A, while they are comparable in the
UV. In1 is clearly brighter than In2, while again their near-UV
brightness is comparable, indicating a marked color difference between
the inner extension's two knots.
There is signal from one of the quasar's diffraction spikes superposed
on the jet emission collected in the first 2/3 of the total exposure
time (Fig. 1). In addition, an IR-bright object St2 is located within the jet, close to the faint star St1 just north of the jet which is also detected on the optical image. We modelled the spike by summing the 10 exposures in which the spike is clear of
the jet (in these, the telescope has been rotated by 4![]() compared
to the previous 20; Fig. 1b). A scaled version
of the model is then subtracted from each individual image. The result
of subtracting the spike model from the "contaminated'' sum frame is
shown in Fig. 1c.
compared
to the previous 20; Fig. 1b). A scaled version
of the model is then subtracted from each individual image. The result
of subtracting the spike model from the "contaminated'' sum frame is
shown in Fig. 1c.
To assess whether the IR-bright object St2 is part of the jet or an
unrelated foreground object, we first checked whether its brightness
profile is consistent with that of a point source. The widths of
Gaussians fitted to 1D cuts along rows and columns of the sum images
are consistent with the known width of the PSF. Secondly, there are
no correlations with total or polarised brightness features of the
radio jet. We are therefore confident that this object is a star
which by chance appears superimposed on the jet image. We modelled
this star on the sum images as a Gaussian sitting on top of a sloping
plane which accounts for the underlying jet flux. An appropriately
scaled version of the star model is subtracted from all 30 individual
frames (for details, see Jester 2001, Sect. 2.2.5). The flux
removed in this manner is
![]() .
The jet flux in an
equivalent aperture (ignoring any possible proper motion) on the F622W image of
.
The jet flux in an
equivalent aperture (ignoring any possible proper motion) on the F622W image of
![]() is an upper limit to this object's flux in this band, giving it an
is an upper limit to this object's flux in this band, giving it an ![]() .
.
In order to determine the synchrotron spectrum over the entire jet, we
perform beam-matching aperture photometry at a grid of positions
covering the jet. The photometry was done by our own MPIAPHOT
software (cf. Röser & Meisenheimer 1991). This uses a weighted summation
scheme, equivalent to a convolution, to match the different point
spread functions to a common beam size. At the same time, it allows an
arbitrary placement of apertures with respect to the pixel grid of
individual images without loss of precision. All images are matched
to a final resolution of 0
![]() 3 FWHM, slightly inferior to that of
the data set with the lowest resolution (the 3.6 cm radio data imaged
with 0
3 FWHM, slightly inferior to that of
the data set with the lowest resolution (the 3.6 cm radio data imaged
with 0
![]() 25 resolution; cf. Sect. 2.1). Following
considerations given in Jester et al. (2001, Appendix A), this requires a
relative image alignment accurate to 0
25 resolution; cf. Sect. 2.1). Following
considerations given in Jester et al. (2001, Appendix A), this requires a
relative image alignment accurate to 0
![]() 03 in order to limit
photometry errors from misalignment to 5% for point sources. The
flanks of point sources have the steepest possible intensity
gradients, the photometry error for extended sources will usually be
an order of magnitude smaller. This accuracy is required to avoid the
introduction of spurious spectral index features.
03 in order to limit
photometry errors from misalignment to 5% for point sources. The
flanks of point sources have the steepest possible intensity
gradients, the photometry error for extended sources will usually be
an order of magnitude smaller. This accuracy is required to avoid the
introduction of spurious spectral index features.
We achieve the desired alignment accuracy by using a grid of
photometry positions, defined as offsets on the sky relative to the
quasar core, which is assumed to coincide at all wavelengths. This
grid is transformed into detector coordinates on each individual data
frame, accounting for telescope offsets and geometric
distortion. There is one frame each for the three VLA wavelengths, 30
for HST-NICMOS, four and 14, respectively, for HST-WFPC2 at 620 ![]() and
300
and
300 ![]() .
Because of 3C 273's location near the celestial equator, and
because all offsets between individual HST frames are small (below 30
.
Because of 3C 273's location near the celestial equator, and
because all offsets between individual HST frames are small (below 30
![]() ), detector and celestial coordinate offsets are related by a simple linear transformation.
), detector and celestial coordinate offsets are related by a simple linear transformation.
The grid transformation is straightforward for the VLA images, which contain both the quasar and the jet and do not suffer from saturation effects. For the HST images, we first obtain the precise location of the quasar core from one short exposure (a few seconds) obtained during each HST "visit''. The telescope offsets between these short exposures and the deep science exposures of the jet are obtained from the engineering ("jitter'') files provided with the data. The aperture pixel position is calculated from the quasar's pixel position, the desired offset on the sky and the telescope offset. We account for geometric distortion by using the wavelength-dependent cubic distortion correction for WFPC2 as determined by Trauger et al. (1995), and the quadratic NICMOS coefficients given in Cox et al. (1997). This procedure also takes care of the slightly differing image scales along the NIC2 detector's x- and y-directions. We stress here that the unsaturated quasar image has been crucial in achieving the necessary alignment accuracy.
![\begin{figure}
\includegraphics[width=13cm,clip]{0021f2.eps}\end{figure}](/articles/aa/full/2005/08/aa0021-04/Timg59.gif) |
Figure 2:
Photometry of the jet in 3C 273 at 0
|
| Open with DEXTER | |
We use a rectangular grid of aperture positions. The grid extends
along position angle 222
![]() 2, starting at a radial distance of
2, starting at a radial distance of
![]() from the quasar and extending to
from the quasar and extending to
![]() .
Perpendicular to the radius vector, the grid extends to
.
Perpendicular to the radius vector, the grid extends to
![]() .
Individual grid points are spaced 0
.
Individual grid points are spaced 0
![]() 1 apart,
yielding a good sampling of the 0
1 apart,
yielding a good sampling of the 0
![]() 3 effective resolution, so that
there are 111 radial grid points and 21 points perpendicular to
the radius vector, i.e., 2331 in total. All points are transferred to
the individual data frames, and the flux per 0
3 effective resolution, so that
there are 111 radial grid points and 21 points perpendicular to
the radius vector, i.e., 2331 in total. All points are transferred to
the individual data frames, and the flux per 0
![]() 3 aperture
centered at each grid position is determined.
3 aperture
centered at each grid position is determined.
The photon shot noise is below 0.5% per beam in all bands. The HST images have a flat-field error of 1% (WFPC2) and 3% (NICMOS) added in quadrature. The uncertainty in the background estimation is
estimated from the scatter in blank sky regions as 0.01 ![]() Jy per
beam for WFPC2, and 0.03
Jy per
beam for WFPC2, and 0.03 ![]() Jy for NICMOS, forming an error floor
significant only for the faintest parts of the jet. An error source
unique to the interferometric radio data is the error from the
deconvolution, i.e., errors in the sense that the inferred brightness
distribution does not correspond to the true distribution on sky, in
particular for the fainter parts of the jet. This error is very hard
to quantify and we use a 3% error to account for this. All these
error sources limit the accuracy of relative photometry within one
waveband. In addition, all wavebands will suffer an error from the
absolute photometric calibration, typically 2%.
Jy for NICMOS, forming an error floor
significant only for the faintest parts of the jet. An error source
unique to the interferometric radio data is the error from the
deconvolution, i.e., errors in the sense that the inferred brightness
distribution does not correspond to the true distribution on sky, in
particular for the fainter parts of the jet. This error is very hard
to quantify and we use a 3% error to account for this. All these
error sources limit the accuracy of relative photometry within one
waveband. In addition, all wavebands will suffer an error from the
absolute photometric calibration, typically 2%.
In order to compare the images at different wavelengths, the photometry results are reassembled into the images shown in Fig. 2. We compare the jet's morphological features at different wavelengths before considering the spectra.
To facilitate a comparison of the jet morphology at different wavelengths beyond a direct inspection of the panels in Fig. 2, we show the flux profile along the jet in Fig. 3 and normalised transverse profiles in Fig. 4. There is a close correspondence of morphological features at all wavelengths, i.e., a coincidence of local brightness maxima and the occurrence of "knots'' across the entire observed wavelength range (cf. Bahcall et al. 1995, who describe the same fact by noting that the jet's features have similar angular sizes at all wavelengths). The sole exception within the jet is region B1, in which the jet's apparently double-stranded nature is most conspicuous. At HST frequencies, B1's northern strand is considerably brighter than the southern, while on the radio images, the situation is exactly the opposite. This is also the only location in the jet which might be classified as edge-brightened (cf. Sect. 4.1.2). Note that the two bright knots of the jet preceding B1 are the sources of the brightest X-ray emission, perhaps with a small offset between the locations of the optical and X-ray peaks (Marshall et al. 2001).
Apart from this discrepancy, only the relative brightness of the knots
changes with wavelength. Relative to knot A at the onset of the
optical jet, the radio peak brightness increases by a factor of about
5-10 for H3, and another factor of two for the radio brightness peak
H2, which has historically been called the radio "hot spot''.
However, in the near-infrared at 1.6 ![]() m, the brightness peaks at H3 and H2 are already fainter than most of the remainder of the jet.
In the near-UV at 300
m, the brightness peaks at H3 and H2 are already fainter than most of the remainder of the jet.
In the near-UV at 300 ![]() ,
H2 is the faintest feature, while A is the
brightest. As already noted above, the tip of the jet H1 is detected
up to the near-infrared, but not at shorter wavelengths (any emission
so far detected at 600
,
H2 is the faintest feature, while A is the
brightest. As already noted above, the tip of the jet H1 is detected
up to the near-infrared, but not at shorter wavelengths (any emission
so far detected at 600 ![]() beyond H2 is related to the nearby galaxy,
not to H1). Thus, the brightness profile tends to invert from radio
to near-ultraviolet. This trend continues up to X-rays: A dominates
the jet's X-ray luminosity (Marshall et al. 2001), while H2 dominates the
radio luminosity. This change in brightness profile with wavelength
is equivalent to a change in the spectrum along the jet, which will be
considered below (Sect. 4.2).
beyond H2 is related to the nearby galaxy,
not to H1). Thus, the brightness profile tends to invert from radio
to near-ultraviolet. This trend continues up to X-rays: A dominates
the jet's X-ray luminosity (Marshall et al. 2001), while H2 dominates the
radio luminosity. This change in brightness profile with wavelength
is equivalent to a change in the spectrum along the jet, which will be
considered below (Sect. 4.2).
The transverse cuts (Fig. 4) confirm the findings of Röser et al. (1996, cf. their Fig. 3#: the width of the radio and optical jet is very similar, but there is extended radio emission without an optical counterpart to the south of the jet. Confirming the findings of Neumann et al. (1997a), there is a tendency for the near-infrared emission to be more extended to the south than the optical and ultraviolet emission. This strengthens their conclusion that the optical jet traces the emission of the jet channel as such. The more extended and fainter low-frequency emission corresponds to a surrounding cocoon of material, interpreted as material which is back-flowing after having passed through the hot spot (Röser et al. 1996).
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0021f3.eps}\end{figure}](/articles/aa/full/2005/08/aa0021-04/Timg64.gif) |
Figure 3: Plot of surface brightness per beam along the jet's ridge line, i.e., showing the brightest point per column from Fig. 2. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=14cm,clip]{0021f4.eps}\end{figure}](/articles/aa/full/2005/08/aa0021-04/Timg66.gif) |
Figure 4:
Normalised cuts through the jet profile at various distances from the quasar at 300 nm (solid line), 620 nm (short dash), 1.6 |
| Open with DEXTER | |
Figures 2 and 3 show a
radial offset of about 0
![]() 2 between the position of H2 at radio
and optical wavelengths. This offset is confirmed by the overlay of
radio and optical data at the respective instrumental resolution in
Fig. 5. The uncertainty of the offset
determination is likely dominated by the systematic pointing
uncertainty of the HST data with respect to the VLA data, which we
kept to better than 0
2 between the position of H2 at radio
and optical wavelengths. This offset is confirmed by the overlay of
radio and optical data at the respective instrumental resolution in
Fig. 5. The uncertainty of the offset
determination is likely dominated by the systematic pointing
uncertainty of the HST data with respect to the VLA data, which we
kept to better than 0
![]() 03 (cf. Sect. 3). We discuss the
interpretation of this offset in Sect. 6.1.
03 (cf. Sect. 3). We discuss the
interpretation of this offset in Sect. 6.1.
It is necessary to know the jet volume to obtain an estimate for the magnetic field by the minimum-energy argument (Sect. 5.2 below). We just noted that the optical jet delineates the jet channel as such, while the radio emission contains contributions from the surrounding material. The geometry of the jet channel is therefore best constrained by considering the optical morphology. We assume the jet has isotropic emissivity which is constant along individual lines of sight through the jet and neglect relativistic beaming effects. (Even in the presence of beaming, the conclusions are unaltered as long as the beaming does not vary significantly along any given line of sight.)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0021f5.eps}\end{figure}](/articles/aa/full/2005/08/aa0021-04/Timg67.gif) |
Figure 5:
Comparison of hotspot position at optical and radio wavelengths. Greyscale shows the 620 nm image at original resolution, contours show the 1.3 cm radio map at 0
|
| Open with DEXTER | |
The jet is center-brightened at all wavelengths on images resolving
its width (the only exception being B1, as noted above in
Sect. 4.1.1). If the emission region was confined to a
cylindrical shell at the jet surface, the resulting brightness
distribution would be edge-brightened, both for uniform emissivity
resulting from a tangled magnetic field geometry, and for an ordered
helical field (Meisenheimer 1990; Laing 1981). To lowest order, the jet is
therefore considered as a cylinder completely filled with emitting
plasma. The small-scale structure seen on the optical images and the
0
![]() 2 optical spectral index map (Jester et al. 2001) suggests that the
true internal structure of the jet is more complicated - so
complicated that a more accurate model than the simple one assumed
here requires a detailed understanding of the internal structure,
composition and flow parameters governing the fluid dynamics of the
jet. However, any model with more free parameters than a filled
cylinder is not constrained by the available data. We therefore assume
that the jet is a cylinder extending along position angle 222
2 optical spectral index map (Jester et al. 2001) suggests that the
true internal structure of the jet is more complicated - so
complicated that a more accurate model than the simple one assumed
here requires a detailed understanding of the internal structure,
composition and flow parameters governing the fluid dynamics of the
jet. However, any model with more free parameters than a filled
cylinder is not constrained by the available data. We therefore assume
that the jet is a cylinder extending along position angle 222
![]() 2
whenever a value of the jet volume is required, and next determine the
appropriate value for the radius of this cylinder.
2
whenever a value of the jet volume is required, and next determine the
appropriate value for the radius of this cylinder.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0021f6.eps}\end{figure}](/articles/aa/full/2005/08/aa0021-04/Timg68.gif) |
Figure 6:
Comparison of jet full-width at half the maximum intensity at different wavelengths. The width is determined column by column on the images in
Fig. 2 as the full width at half the maximum
intensity along the column. The bottom panel shows the optical
( |
| Open with DEXTER | |
Comparing the radio and the optical images (Fig. 2), it appears that the radio emission is widening significantly towards the hot spot, while the optical emission is of smaller and constant width. However, the transverse jet profiles (Fig. 4) show that the radio and optical width are, in fact, comparable throughout. The apparent widening of the radio isophotes is predominantly due to the increasing brightness, and hence and signal-to-noise ratio, as a larger part of the point spread function's (PSF) wings is visible above the background noise. Finite-resolution isophotes should therefore not be used to judge the widths of jets.
With sufficient signal-to-noise, the appropriate comparison would be
using a deconvolution. Here we instead give the run of the jet FWHM in
Fig. 6. As expected from
Fig. 4, the radio jet does not widen in the
way suggested by its isophotal width, but the FWHM remains constant at
roughly 1
![]() (this was first noted by Conway et al. 1993).
(this was first noted by Conway et al. 1993).
One might hope to determine the true extent of the jet on the images
or radio maps with the highest available resolution. While this is
possible on the HST images for the entire jet, the resolution of
![]()
![]() for the optical and
for the optical and ![]()
![]() for the
infrared is not reached by the VLA with sufficient signal-to-noise for
most part of the jet. This is a consequence of the large dynamic range
of over 30 000 between the fainter parts of the jet and the radio
core. Therefore, the current radio data do not permit a comparison of
the jet width at the resolution reached by HST. The dynamic range of
these radio images actually fell short of expectations for reasons we
are currently trying to understand.
for the
infrared is not reached by the VLA with sufficient signal-to-noise for
most part of the jet. This is a consequence of the large dynamic range
of over 30 000 between the fainter parts of the jet and the radio
core. Therefore, the current radio data do not permit a comparison of
the jet width at the resolution reached by HST. The dynamic range of
these radio images actually fell short of expectations for reasons we
are currently trying to understand.
Since the optical jet has fairly sharp boundaries on the WFPC2
R-band image at original resolution, we use the average width of the
![]() isophote of 0
isophote of 0
![]() 7 as the width of the jet channel
(this is identical to the value reported by Bahcall et al. 1995). Thus,
the jet channel is described as a cylinder of constant radius
7 as the width of the jet channel
(this is identical to the value reported by Bahcall et al. 1995). Thus,
the jet channel is described as a cylinder of constant radius
![]() for regions A1-D2/H3
(r=
for regions A1-D2/H3
(r=
![]() -
-
![]() ). This width agrees with the hot spot
diameter given by Meisenheimer et al. (1997), so to lowest order, we can extend the
cylindrical model to cover the entire jet out to the tip of the jet H1.
). This width agrees with the hot spot
diameter given by Meisenheimer et al. (1997), so to lowest order, we can extend the
cylindrical model to cover the entire jet out to the tip of the jet H1.
As the cocoon emission (cf. Fig. 4) is much
fainter than the jet's, its morphology is much more difficult to
establish. To assess any likely contribution of the cocoon emission to
the flux observed from the jet, the radio emission surrounding the
optical jet channel is described as a cylindrical shell with inner
radius 0
![]() 35 (enclosing the optical jet channel without a gap) and
outer radius 0
35 (enclosing the optical jet channel without a gap) and
outer radius 0
![]() 8, close to the isophotal width of the radio jet
there and roughly twice that of the optical jet.
8, close to the isophotal width of the radio jet
there and roughly twice that of the optical jet.
The volume belonging to each photometry aperture (or pixel in
Fig. 2), i.e., the effective jet volume sampled by
each photometry aperture, is calculated by explicitly convolving the
model assumed for the jet (a filled cylinder of radius 0
![]() 35) with
the observing beam of 0
35) with
the observing beam of 0
![]() 3 FWHM at the location of each aperture,
assuming that the symmetry axis of the cylinder lies along the radius
vector at position angle 222
3 FWHM at the location of each aperture,
assuming that the symmetry axis of the cylinder lies along the radius
vector at position angle 222
![]() 2. The obtained values are tabulated
in Table 2. We use them here to assess the
likely relative volume emissivity of the jet and the cocoon. The jet
volume sampled by each aperture will be used in the calculation of the
minimum-energy field in Sect. 5.2, where we also consider the
effect of the inclination of the jet to the line of sight.
2. The obtained values are tabulated
in Table 2. We use them here to assess the
likely relative volume emissivity of the jet and the cocoon. The jet
volume sampled by each aperture will be used in the calculation of the
minimum-energy field in Sect. 5.2, where we also consider the
effect of the inclination of the jet to the line of sight.
Table 2:
Effective volume of the jet sampled by photometry apertures at distance
![]() from
the symmetry axis of the model. Jet volume, contribution from
the jet channel visible in the optical, assumed as filled cylinder
extending from
from
the symmetry axis of the model. Jet volume, contribution from
the jet channel visible in the optical, assumed as filled cylinder
extending from
![]() to
to
![]() .
Cocoon volume, contribution
from the cocoon, modelled as hollow cylinder wrapped extending from
.
Cocoon volume, contribution
from the cocoon, modelled as hollow cylinder wrapped extending from
![]() to
to
![]() around
the jet channel. These values assume a fully side-on view.
around
the jet channel. These values assume a fully side-on view.
![\begin{figure*}
\par\hspace*{2.45cm}\parbox[c]{0.1\hsize}{\hspace*{0.1\hsize}}\p...
...0.79\hsize}{\includegraphics[width=0.79\hsize,clip]{0021f7m.eps}}
\end{figure*}](/articles/aa/full/2005/08/aa0021-04/Timg78.gif) |
Figure 7:
Spectral index maps at 0
|
| Open with DEXTER | |
Using Table 2, we can now also estimate the
contribution of the cocoon or backflow material along the line of
sight to the central part of the jet. The effective volume contributed
by the cocoon volume is much larger than that of the jet
channel. Therefore, the cocoon's volume emissivity can be no more
than about 1% of the jet's volume emissivity (the exact ratio depends
on the azimuthal extent of the cocoon). Otherwise, the cocoon
emission would completely dominate the jet emission and the profile
would not appear centrally peaked, or fall off more slowly than
observed. In the central part of the jet, the cocoon will then also
contribute only about 1% of the jet emission. The same constraint
from the observed brightness profile implies that the contribution of
the cocoon to the central jet flux cannot be appreciable even if the
true width of the cocoon is different from the assumed 0
![]() 8.
8.
In summary, the overall morphology of the jet is similar at all
observed wavelengths from 3.6 cm to 300 nm. The exceptions to this
are the radio-quiet "extensions'' (In1, In2, S;
Fig. 1 and Jester et al. 2001) to the optical jet, and region B1, in which the SED of the southern strand of emission peaks in the radio, but that of the northern strand peaks at optical wavelengths. All of the emission blueward of 1.6 ![]() m and the bulk of the radio
emission at the wavelengths of 3.6
m and the bulk of the radio
emission at the wavelengths of 3.6 ![]() and shorter considered here
are emission from the jet itself, while the steep-spectrum radio
cocoon (or "backflow'') south of the jet makes a negligible
contribution along the line of sight to the jet channel
(cf. Conway & Davis 1994; Conway et al. 1993). We therefore use the full data set from
3.6
and shorter considered here
are emission from the jet itself, while the steep-spectrum radio
cocoon (or "backflow'') south of the jet makes a negligible
contribution along the line of sight to the jet channel
(cf. Conway & Davis 1994; Conway et al. 1993). We therefore use the full data set from
3.6 ![]() to 300
to 300 ![]() to analyse the spectrum of the jet emission here.
to analyse the spectrum of the jet emission here.
![\begin{figure}
\par\includegraphics[origin=rB,angle=270,width=12cm,clip]{0021f8.eps} \end{figure}](/articles/aa/full/2005/08/aa0021-04/Timg79.gif) |
Figure 8:
Run of the spectral indices along the jet at 0
|
| Open with DEXTER | |
From the photometry results shown in Fig. 2, we
compute pairwise spectral indices ![]() .
The spectral index maps
are shown in Fig. 7. Their run along the jet's
centre line is shown in Fig. 8 (Fig. 1 in
Jester et al. 2002). The error bars in Fig. 8 have
been calculated from the total random error. There is an additional
systematic error from flux calibration uncertainties (typically 2%,
Sect. 3). These change all flux measurements through one
filter by the same factor. Its effect on the spectral index
determination is to offset a given spectral index by a constant amount
for the entire jet. The magnitude of the effect is smaller than any of
features which we detect at high statistical significance. Our
conclusions are, therefore, unaffected by this residual systematic
uncertainty.
.
The spectral index maps
are shown in Fig. 7. Their run along the jet's
centre line is shown in Fig. 8 (Fig. 1 in
Jester et al. 2002). The error bars in Fig. 8 have
been calculated from the total random error. There is an additional
systematic error from flux calibration uncertainties (typically 2%,
Sect. 3). These change all flux measurements through one
filter by the same factor. Its effect on the spectral index
determination is to offset a given spectral index by a constant amount
for the entire jet. The magnitude of the effect is smaller than any of
features which we detect at high statistical significance. Our
conclusions are, therefore, unaffected by this residual systematic
uncertainty.
The two radio spectral indices (between 3.6 ![]() and 2
and 2 ![]() ,
and between
2
,
and between
2 ![]() and 1.3
and 1.3 ![]() )
behave erratically out to a radius of about 19
)
behave erratically out to a radius of about 19
![]() .
These variations are not significant: the radio jet is detected at low signal-to-noise ratio at the inner end, and the
deconvolution involved in the reconstruction of the brightness
distribution on the sky from the observed interferometric data is only
accurate (in the sense of achieving an image representing the true
brightness distribution) for high signal-to-noise. We therefore show
an overall radio spectral index in Fig. 8 which
has been determined by a least-squares straight-line fit to the three
radio data points. For the outer part of the jet, the radio spectral
index shows a steepening of the hot spot (H2) spectrum compared to the
remainder of the jet. The run of the spectral index between 6
.
These variations are not significant: the radio jet is detected at low signal-to-noise ratio at the inner end, and the
deconvolution involved in the reconstruction of the brightness
distribution on the sky from the observed interferometric data is only
accurate (in the sense of achieving an image representing the true
brightness distribution) for high signal-to-noise. We therefore show
an overall radio spectral index in Fig. 8 which
has been determined by a least-squares straight-line fit to the three
radio data points. For the outer part of the jet, the radio spectral
index shows a steepening of the hot spot (H2) spectrum compared to the
remainder of the jet. The run of the spectral index between 6 ![]() and
3.6
and
3.6 ![]() ,
for which only lower-resolution data at 0
,
for which only lower-resolution data at 0
![]() 5 are available,
agrees with the spectral index run determined at the wavelengths
considered here (cf. Conway et al. 1993).
5 are available,
agrees with the spectral index run determined at the wavelengths
considered here (cf. Conway et al. 1993).
The infrared-radio spectral index (Fig. 7c) is
nearly constant at
![]() along the centre of the
optical jet, with some flattening in optically bright regions and a
pronounced steepening in the transition from D2
(
along the centre of the
optical jet, with some flattening in optically bright regions and a
pronounced steepening in the transition from D2
(
![]() )
to the radio hot spot H2. It steepens markedly
to
)
to the radio hot spot H2. It steepens markedly
to ![]() -1.2 away from the centre line. These features are
identical to those identified by Neumann et al. (1997a) on a spectral index map
at 1
-1.2 away from the centre line. These features are
identical to those identified by Neumann et al. (1997a) on a spectral index map
at 1
![]() 3 resolution generated from observations at 73
3 resolution generated from observations at 73 ![]() and 2.1
and 2.1 ![]() m. There is no spectral index feature uniquely corresponding to the hot spot H2, as is the case on the radio spectral index map. On the other hand, the tip of the jet H1 is identifiable as region with
radio-infrared spectral index slightly flatter than H2.
m. There is no spectral index feature uniquely corresponding to the hot spot H2, as is the case on the radio spectral index map. On the other hand, the tip of the jet H1 is identifiable as region with
radio-infrared spectral index slightly flatter than H2.
We use the term "high-frequency'' to refer to the infrared-optical
and optical-ultraviolet spectral indices. As already noted by
considering the spectral index map derived from the optical and
near-ultraviolet imaging at 0
![]() 2 resolution (Jester et al. 2001), there
are none but smooth changes in the optical-UV spectral index along the
jet. The same is true for the infrared-optical spectral index. Both
these spectral indices decline globally along the jet. At the onset
of the optical jet at A and at B1, both have a value of -0.7, i.e., the optical-UV spectrum there is flatter than the radio and
radio-infrared. Both high-frequency indices decrease to about -1.7at C2. The optical-ultraviolet
2 resolution (Jester et al. 2001), there
are none but smooth changes in the optical-UV spectral index along the
jet. The same is true for the infrared-optical spectral index. Both
these spectral indices decline globally along the jet. At the onset
of the optical jet at A and at B1, both have a value of -0.7, i.e., the optical-UV spectrum there is flatter than the radio and
radio-infrared. Both high-frequency indices decrease to about -1.7at C2. The optical-ultraviolet
![]() remains near this value for the
reminder of the jet, while the infrared-optical
remains near this value for the
reminder of the jet, while the infrared-optical
![]() steepens
further, reaching a minimum near -2 between D1 and D2, and
flattening back to -1.7 at D2.
steepens
further, reaching a minimum near -2 between D1 and D2, and
flattening back to -1.7 at D2.
Thus, as already reported in Jester et al. (2002), the spectrum does not steepen everywhere towards higher frequencies, but flattens between the near-infrared and optical in nearly all parts of the jet. We will consider the implications of this finding in Sects. 5 and 6.2.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0021f9.eps}\end{figure}](/articles/aa/full/2005/08/aa0021-04/Timg82.gif) |
Figure 9:
Comparison of high-frequency spectral indices with previous observations at 1
|
| Open with DEXTER | |
The general outward steepening of the high-frequency spectral indices
is in agreement with previous determinations of the knots' synchrotron
spectrum which showed a decrease of the cutoff frequency outward
(Röser et al. 2000; Meisenheimer et al. 1996a). There is an excellent correspondence of the run
of the optical-infrared spectral index
![]() along the jet with the
spectral index
along the jet with the
spectral index
![]() between
between ![]() m and the
optical as determined by Neumann et al. (1997a) at 1
m and the
optical as determined by Neumann et al. (1997a) at 1
![]() 3 resolution
(Fig. 9). As has been noted in
Jester et al. (2001), the overall run of the optical-ultraviolet spectral
index
3 resolution
(Fig. 9). As has been noted in
Jester et al. (2001), the overall run of the optical-ultraviolet spectral
index
![]() at 0
at 0
![]() 3 agrees overall with the run of the optical
spectral index
3 agrees overall with the run of the optical
spectral index
![]() at 1
at 1
![]() 3, with discrepancies in a few
regions: a comparison of Figs. 8 and 9 shows that these discrepancies arise precisely in those regions in which the spectrum flattens at high
frequencies. The discrepancies can thus be ascribed to the different
wavelength of the bluest HST and ground-based images (300 nm compared
to 400 nm) and the fact that the flattening occurs just in this
wavelength region (between 600 to 300 nm).
3, with discrepancies in a few
regions: a comparison of Figs. 8 and 9 shows that these discrepancies arise precisely in those regions in which the spectrum flattens at high
frequencies. The discrepancies can thus be ascribed to the different
wavelength of the bluest HST and ground-based images (300 nm compared
to 400 nm) and the fact that the flattening occurs just in this
wavelength region (between 600 to 300 nm).
Optical spectral index variations are not strongly correlated with
brightness variations. Some local peaks of
![]() coincide with
brightness maxima, while others coincide with minima. In contrast,
there is a correlation between the optical-infrared spectral index
coincide with
brightness maxima, while others coincide with minima. In contrast,
there is a correlation between the optical-infrared spectral index
![]() and the jet's surface brightness, in the sense that brighter
regions show a flatter spectrum (smaller
and the jet's surface brightness, in the sense that brighter
regions show a flatter spectrum (smaller
![]() ,
see
Figs. 7b and 8). This
correlation is most clearly visible on the spectral index map for the
outer end of the jet. The bright regions D2/H3 together with the hot
spot H2 appear as an island of
,
see
Figs. 7b and 8). This
correlation is most clearly visible on the spectral index map for the
outer end of the jet. The bright regions D2/H3 together with the hot
spot H2 appear as an island of
![]() surrounded by
regions with steeper spectrum. The correlation between local maxima
in surface brightness and
surrounded by
regions with steeper spectrum. The correlation between local maxima
in surface brightness and
![]() is also present in the inner part of
the jet, although the spectral index maxima are displaced sideways
from the brightness peaks due to a transverse spectral index gradient.
is also present in the inner part of
the jet, although the spectral index maxima are displaced sideways
from the brightness peaks due to a transverse spectral index gradient.
This spectral index gradient is suggestive of a residual misalignment between
the optical and infrared images, e.g., a rotation between the two about
a point close to D2/H3. It could also have been caused by an
overestimation of the diffraction spike signal which has been modelled
and subtracted (see Sect. 2.3.2). Since Neumann et al. (1997a) did
not detect a significant change of the infrared-optical spectral index
transversely to the jet at 1
![]() 3, and although the alignment
procedures described above (Sect. 3) should have ensured that
such an error should not have occurred, we reconsidered this
possibility to avoid the introduction of spurious gradients. After a
detailed investigation (details are contained in Jester 2001),
we concluded that the misalignment necessary to produce such a
gradient was far greater than compatible with the alignment precision
established previously. Neither can the gradient firmly be linked to
the diffraction spike subtraction or any obviously detectable
misalignment. In the given situation, we rely on the data with the
offsets established to the best of our knowledge. The clarification of
this matter has to await new observational data.
3, and although the alignment
procedures described above (Sect. 3) should have ensured that
such an error should not have occurred, we reconsidered this
possibility to avoid the introduction of spurious gradients. After a
detailed investigation (details are contained in Jester 2001),
we concluded that the misalignment necessary to produce such a
gradient was far greater than compatible with the alignment precision
established previously. Neither can the gradient firmly be linked to
the diffraction spike subtraction or any obviously detectable
misalignment. In the given situation, we rely on the data with the
offsets established to the best of our knowledge. The clarification of
this matter has to await new observational data.
In summary, there are two surprising findings regarding the spectral
indices. Firstly, the knots, i.e., the local brightness peaks occurring
at nearly the same position at all wavelengths, have a flatter
infrared-optical spectrum than the regions separating them. Thus,
there is a local positive correlation between the jet brightness at
any wavelength and the infrared-optical spectral index. This contrasts
with the global anti-correlation between energy output and spectral
index: the radio surface brightness increases while the high-frequency
spectrum steepens considerably. Secondly, the spectrum flattens in
the optical-UV wavelength region. In fact, the optical-ultraviolet
![]() spectral index is nowhere significantly below the
infrared-optical
spectral index is nowhere significantly below the
infrared-optical
![]() ,
in contrast to the expectation of a
synchrotron spectrum which steepens at higher frequencies. We will
consider the implications in Sect. 6.4 and first turn to the
determination of the maximum particle energy from the observations.
,
in contrast to the expectation of a
synchrotron spectrum which steepens at higher frequencies. We will
consider the implications in Sect. 6.4 and first turn to the
determination of the maximum particle energy from the observations.
The present observations have been obtained to study the behaviour of
the maximum particle energy along the jet in 3C 273, with the aim of
identifying acceleration and/or loss sites within the jet. In order
to determine the maximum particle energy from the observed spectral
energy distributions, we need to determine both the cutoff frequency
![]() which is the characteristic synchrotron frequency corresponding
to the highest particle energy, and the magnetic field in the jet,
assumed to be uniform along lines of sight. We first consider the
determination of the cutoff frequency and then estimate the magnetic
field strength using the minimum-energy argument in
Sect. 5.2.
which is the characteristic synchrotron frequency corresponding
to the highest particle energy, and the magnetic field in the jet,
assumed to be uniform along lines of sight. We first consider the
determination of the cutoff frequency and then estimate the magnetic
field strength using the minimum-energy argument in
Sect. 5.2.
The cutoff frequency is to be determined from the observed spectral
energy distributions by fitting them with model synchrotron spectra.
All previous studies have used single-population models to describe
the jet's synchrotron spectrum (Neumann et al. 1997a; Meisenheimer et al. 1996a; Röser et al. 2000; Meisenheimer et al. 1997). We
noted above that there is a flattening of the observed spectrum
towards the ultraviolet (Fig. 8 in
Sect. 4.2). This means that a description using a single
electron population is, in fact, inadequate: any non-idealised
power-law electron population (i.e., with finite maximum
particle energy and rapid pitch-angle scattering) always gives rise to
a synchrotron spectrum with steepening slope in the
![]() -
-![]() plane. The observed high-frequency flattening
implies that a second high-frequency emission component must be
present, which contributes either predominantly to the jet's
near-infrared or near-ultraviolet flux to produce the observed
high-frequency flattening. The discrepancy can be explained by
assuming that one of the two spectral indices reflects the true
synchrotron spectrum, while the other is contaminated by flux not due
to the same population as the remainder of the jet. To assess the
likely reason for this discrepancy between the observations and the
expectations from synchrotron theory, we perform two separate fits
which differ in the determination of the cutoff frequency
(Fig. 10): either the cutoff is described by the
optical-ultraviolet spectral index leading to an infrared excess
(model A), or conversely, the true cutoff is described by the
infrared-optical spectrum and there is additional flux in the
ultraviolet (model B; see Jester et al. 2002). This allows us to perform
the fits using a single-population model.
plane. The observed high-frequency flattening
implies that a second high-frequency emission component must be
present, which contributes either predominantly to the jet's
near-infrared or near-ultraviolet flux to produce the observed
high-frequency flattening. The discrepancy can be explained by
assuming that one of the two spectral indices reflects the true
synchrotron spectrum, while the other is contaminated by flux not due
to the same population as the remainder of the jet. To assess the
likely reason for this discrepancy between the observations and the
expectations from synchrotron theory, we perform two separate fits
which differ in the determination of the cutoff frequency
(Fig. 10): either the cutoff is described by the
optical-ultraviolet spectral index leading to an infrared excess
(model A), or conversely, the true cutoff is described by the
infrared-optical spectrum and there is additional flux in the
ultraviolet (model B; see Jester et al. 2002). This allows us to perform
the fits using a single-population model.
Following previous studies, we use the method of computing synchrotron
spectra with a smooth cutoff from Heavens & Meisenheimer (1987) to determine the cutoff
frequency from the observed spectral energy distribution. They model
the synchrotron source as a region of constant magnetic field into
which a power-law distribution of electrons extending up to a maximum
electron Lorentz factor
![]() is continuously injected. The
resulting spectrum has a low-frequency power law part with spectral
index
is continuously injected. The
resulting spectrum has a low-frequency power law part with spectral
index
![]() ,
which steepens by one-half power at a
break frequency
,
which steepens by one-half power at a
break frequency
![]() and cuts off exponentially above the cutoff
frequency
and cuts off exponentially above the cutoff
frequency
![]() .
The break is produced by adding up the
contributions from the electron population observed at increasing times
since acceleration, i.e., with different cutoff frequencies. The
magnitude of the break of 1/2 is fixed by the cooling mechanism.
Although the model was originally devised to describe the spectra of
hot spots, the use of such a continuous-injection model is justified
by the fact that optically emitting electrons must be accelerated
within the jet: our calculation in Jester et al. (2001) showed that
relativistic beaming and/or sub-equipartition magnetic fields cannot
remove the discrepancy between light-travel time along 3C 273's jet
and the lifetime of electrons emitting optical synchrotron radiation.
.
The break is produced by adding up the
contributions from the electron population observed at increasing times
since acceleration, i.e., with different cutoff frequencies. The
magnitude of the break of 1/2 is fixed by the cooling mechanism.
Although the model was originally devised to describe the spectra of
hot spots, the use of such a continuous-injection model is justified
by the fact that optically emitting electrons must be accelerated
within the jet: our calculation in Jester et al. (2001) showed that
relativistic beaming and/or sub-equipartition magnetic fields cannot
remove the discrepancy between light-travel time along 3C 273's jet
and the lifetime of electrons emitting optical synchrotron radiation.
The model spectrum has four free parameters: the low-frequency
spectral index
![]() ,
the ratio of cutoff energy to
break energy of the emitting electron population =
,
the ratio of cutoff energy to
break energy of the emitting electron population =
![]() ,
the observed cutoff frequency
,
the observed cutoff frequency
![]() ,
and a flux normalisation. Since
we only observe the spectrum at six frequencies, we introduce
additional constraints to obtain meaningful fits. First, we restrict
,
and a flux normalisation. Since
we only observe the spectrum at six frequencies, we introduce
additional constraints to obtain meaningful fits. First, we restrict
![]() so that the break is in the range
109 Hz-1012 Hz, i.e., within the range of the observed
radio data. Secondly, we artificially fix
so that the break is in the range
109 Hz-1012 Hz, i.e., within the range of the observed
radio data. Secondly, we artificially fix
![]() ,
so that the observed radio-infrared spectral index of about -0.9 (Fig. 8) corresponds to
,
so that the observed radio-infrared spectral index of about -0.9 (Fig. 8) corresponds to
![]() .
In effect, only the cutoff frequency
.
In effect, only the cutoff frequency
![]() is determined by this fitting procedure. The fit is performed
using a
is determined by this fitting procedure. The fit is performed
using a ![]() minimisation technique; the detailed steps can be
found in Jester (2001, Sect. 4.2 and references therein). We
discuss the implications of these constraints on the interpretation of
the fit results in Sect. 5.3 below.
minimisation technique; the detailed steps can be
found in Jester (2001, Sect. 4.2 and references therein). We
discuss the implications of these constraints on the interpretation of
the fit results in Sect. 5.3 below.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0021f10.eps}\end{figure}](/articles/aa/full/2005/08/aa0021-04/Timg95.gif) |
Figure 10: Illustration of the two different spectral fits performed. Model A assumes infrared emission in excess of the cutoff given by the optical-ultraviolet spectral index, while model B assumes an ultraviolet excess above the infrared-optical cutoff. |
| Open with DEXTER | |
Model A assigns a low weight to the near-infrared flux point in the
data set. This is motivated by the indication that the radio cocoon
(possibly a "backflow'') around the jet (Röser et al. 1996) may also be
detectable at 2.1 ![]() m (Neumann et al. 1997a), suggesting that the flux from
the jet at 1.6
m (Neumann et al. 1997a), suggesting that the flux from
the jet at 1.6 ![]() m may be contaminated by emission from the
cocoon as well. Hence, the cutoff in model A is determined by the
optical and near-ultraviolet points at 620
m may be contaminated by emission from the
cocoon as well. Hence, the cutoff in model A is determined by the
optical and near-ultraviolet points at 620 ![]() and 300
and 300 ![]() ,
respectively. Conversely, in model B, the location of the cutoff is
dominated by the infrared and optical points at 1.6
,
respectively. Conversely, in model B, the location of the cutoff is
dominated by the infrared and optical points at 1.6 ![]() m and 620
m and 620 ![]() ,
respectively.
,
respectively.
In contrast to the remainder of the jet, the hot spot shows an offset
between optical and radio hot spot position
(Fig. 5) and a change of the radio-infrared
spectral index (Sect. 4.2). Therefore, the spectra from the
hot spot regions H2 and H1 at radii beyond
![]() are fitted
differently by allowing
are fitted
differently by allowing
![]() to vary between -0.8and -0.3. This model is referred to as model HS.
to vary between -0.8and -0.3. This model is referred to as model HS.
Table 3: Fit parameters describing the shape of the spectra (low-frequency spectral index, break frequency, cutoff frequency) shown in Fig. 12.
In the bright peaks of A, B1 and B2, there is no cutoff within the
observed frequency range (the high-frequency spectral indices are
flatter than -1 there (Fig. 8), so that the
spectral energy density continues to rise towards higher frequencies).
Where this is the case, an artificial high-frequency data point is
introduced to allow the fit to proceed, which assumes the presence of
a local maximum in the data set. The artificial point is chosen so
that it has a spectral index relative to the observed UV point of -1.2 and is introduced at a frequency 1018 Hz, 1000 times higher than the frequency of UV emission. It is assigned a large error so that it does not influence the goodness-of-fit. The results
obtained for
![]() for these points are then only lower limits to the
true cutoff frequency as it would be inferred from observations at
higher frequencies. On the other hand, it is possible that the
optical/UV emission in these regions has a substantial contribution
from the second, high-energy emission component (Sect. 6.2).
In this case, there may be a cutoff to the "low-energy''
radio-optical synchrotron component at lower energies than
obtained here. Observations in additional wavebands, in particular at
longer infrared wavelengths, or a comparison of the radio and optical
polarisation of these regions at high resolution may shed light on
this issue. However, given the similarity of radio and optical
polarisation at low resolution, it appears unlikely that the emission
is dominated by the high-energy component, although its
contribution may be significant.
for these points are then only lower limits to the
true cutoff frequency as it would be inferred from observations at
higher frequencies. On the other hand, it is possible that the
optical/UV emission in these regions has a substantial contribution
from the second, high-energy emission component (Sect. 6.2).
In this case, there may be a cutoff to the "low-energy''
radio-optical synchrotron component at lower energies than
obtained here. Observations in additional wavebands, in particular at
longer infrared wavelengths, or a comparison of the radio and optical
polarisation of these regions at high resolution may shed light on
this issue. However, given the similarity of radio and optical
polarisation at low resolution, it appears unlikely that the emission
is dominated by the high-energy component, although its
contribution may be significant.
At the chosen resolution of 0
![]() 3, the inter-knot regions are
fairly well-resolved from the knots themselves, so that we obtain
meaningful values for the cutoff frequency for the entire jet. For the
following discussion, we have chosen 16 locations corresponding to
distinct features, the inter-knot regions and the brightness peaks.
These locations are indicated in Fig. 11.
Figure 12 shows the corresponding spectra, Table 3 shows the fit parameters describing the shape of the spectrum (low-frequency spectral index, break frequency, cutoff frequency).
3, the inter-knot regions are
fairly well-resolved from the knots themselves, so that we obtain
meaningful values for the cutoff frequency for the entire jet. For the
following discussion, we have chosen 16 locations corresponding to
distinct features, the inter-knot regions and the brightness peaks.
These locations are indicated in Fig. 11.
Figure 12 shows the corresponding spectra, Table 3 shows the fit parameters describing the shape of the spectrum (low-frequency spectral index, break frequency, cutoff frequency).
The fit results for the models A and B are very similar in most cases. As described in detail in Jester et al. (2002, Sect. 3), we reject the large near-infrared residuals obtained with Model A as implausible and prefer model B, which has a significant excess in the near-UV. This implies that the jet emission consists of a "low-frequency'' component responsible for emission from radio through optical, and at least one "high-energy'' component, responsible for the near-UV emission, and possibly the X-rays at well. We will nevertheless show all results for both models to illustrate that the quantities derived from either model do not differ significantly.
| |
Figure 11: Location of apertures for which spectra are shown in Fig. 12. Locations at local peaks ("knots'') are marked by a line below the image, while locations in inter-knot regions are marked by a line above. |
| Open with DEXTER | |
Figure 12 highlights the development of the spectra along the jet: a global increase in luminosity coupled with a decrease in cutoff frequency. As expected from the brightness profiles, the spectral energy distribution peaks at lower frequencies at larger radii from the core. Simultaneously, the peak flux density increases.
![\begin{figure}
\par\includegraphics[width=7.05cm,clip]{0021f12a.eps}\hspace*{3mm...
....eps}\hspace*{3mm}
\includegraphics[width=7.05cm,clip]{0021f12f.eps}\end{figure}](/articles/aa/full/2005/08/aa0021-04/Timg153.gif) |
Figure 12:
Observed data points with fitted spectra for the points shown in
Fig. 11. To account for the observed
flattening of the spectrum towards the ultraviolet, model A assumes a
contamination in the infrared, so that the cutoff is determined by the
optical-ultraviolet spectral index there, while the cutoff in model B
is determined by the infrared-optical spectral index. Those spectra
which require an artificial high-frequency data point to obtain a fit
result are labelled "cut''; for these, models A and B are
identical, and the artificially obtained value for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.05cm,clip]{0021f13a.eps}\hspace*{3mm...
....eps}\hspace*{3mm}
\includegraphics[width=7.05cm,clip]{0021f13f.eps}\end{figure}](/articles/aa/full/2005/08/aa0021-04/Timg154.gif) |
Figure 12: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.05cm,clip]{0021f14a.eps}\hspace*{3mm...
....eps}\hspace*{3mm}
\includegraphics[width=7.05cm,clip]{0021f14d.eps}\end{figure}](/articles/aa/full/2005/08/aa0021-04/Timg155.gif) |
Figure 12: continued. |
| Open with DEXTER | |
Compared to earlier studies at lower resolution (Röser et al. 2000; Meisenheimer et al. 1996a; Neumann 1995), the contributions from individual knots are now clearly separated from each other. While previously only knot A showed a spectrum without a cutoff, it is now seen that there is no cutoff at the brightness peaks in B1 and B2, either. Not only is there no cutoff, but the infrared-optical-UV spectrum is harder than the radio-infrared spectrum in these locations, as already inferred from the spectral indices (compare Fig. 8). There is, however, a cutoff in the transition A-B1, between these peaks. The presence of a cutoff in the southern part of B1 can already be inferred from the fact that it is optically much fainter than the northern part, while it is brighter in the radio (cf. Fig. 2). The differences between the spectra fitted at the brightness peaks and the regions connecting them are nowhere else as drastic. However, for the first time we see that there is an increase of the cutoff frequency in the knots, compared to inter-knot regions, corresponding to the slightly flatter spectrum there (cf. Sect. 4.2). This local increase is a modulation of the global outward decrease of the cutoff frequency.
The synchrotron radiation at the cutoff frequency is emitted by those
particles with the highest energy. The maximum particle energy can
therefore be computed from the cutoff frequency through the
synchrotron characteristic frequency, the frequency around
which most of the synchrotron emission of an electron of energy
![]() in a magnetic field of flux density B is emitted:
in a magnetic field of flux density B is emitted:
In the absence of any other reliable method, the magnetic field for the jet can only be estimated by making use of the minimum-energy assumption. We therefore present the derivation of the value of the minimum-energy magnetic field for the type of spectra described here.
There is a firm minimum value for the total energy density (in relativistic particles and magnetic field) necessary to generate a given synchrotron luminosity. This energy density can be deduced from observations with the help of assumptions about the source geometry and the range of frequencies over which synchrotron emission is emitted. Pacholczyk (1970) presents a clear derivation of the minimum energy density of a synchrotron source for the assumption of a power-law electron energy distribution in the source.
The minimum-energy field is that value of the source's magnetic field corresponding to the minimum total energy sufficient to give rise to the observed emission. Due to the lack of other diagnostic tools, this minimum-energy magnetic field is often used as estimate for the true magnetic field. Doing so, one introduces a local correlation between the magnetic field strength and the energy density in particles. This correlation provides the most efficient way to produce a given synchrotron luminosity. One may imagine magneto-hydrodynamical processes causing this correlation, because the particles are both tied to magnetic field lines and create them by their motion. However, no detailed microphysical feedback process has been identified which maintains this correlation on all scales, and it appears dangerous to us to draw conclusions deriving from this correlation until it is is established that it is a natural, not an artificial one. Nevertheless, it seems reasonable to assume that the minimum-energy magnetic field is a good indicator of the order of magnitude of the source's magnetic field (Meisenheimer et al. 1989).
With this caveat in mind, we use the minimum-energy magnetic field as
a measure of the jet's magnetic field, calculating it following
Pacholczyk (1970, p. 168 ff.) but explicitly assuming a broken power
law. To account for the break in the electron spectrum at Lorentz
factor
![]() leading to a break in the model spectrum at
leading to a break in the model spectrum at
![]() ,
we write the electron density as
,
we write the electron density as
The calculation of the minimum energy density involves integrating
both the electron energy over the electron distribution, and the
observed flux density over the corresponding frequency range. We use
a fixed low-frequency limit of
![]() Hz. While a
choice of a fixed lower electron energy limit would have been more
physical, it turns out that the value of
Hz. While a
choice of a fixed lower electron energy limit would have been more
physical, it turns out that the value of
![]() has little
influence on the result for
has little
influence on the result for
![]() because terms
in
because terms
in
![]() enter logarithmically or can be
neglected altogether. Similarly, for the observed cutoff in the optical
range, a term in
enter logarithmically or can be
neglected altogether. Similarly, for the observed cutoff in the optical
range, a term in
![]() can be neglected.
With these approximations, we obtain the following expressions for the
total energy in electrons, the luminosity following from the electron
energy distribution, and the observed luminosity, respectively:
can be neglected.
With these approximations, we obtain the following expressions for the
total energy in electrons, the luminosity following from the electron
energy distribution, and the observed luminosity, respectively:
We next discuss the impact of the jet orientation the assumptions we have made about the shape of the spectrum before discussing the behaviour of the minimum-energy field and hence the maximum particle energy along the jet.
If the jet does not lie in the plane of the sky but is inclined to the
line of sight by an angle i, all lines of sight passing through the
jet, and hence the total jet volume, are longer by a factor ![]() compared to the side view (ignoring edge effects at the end of the
jet). The minimum-energy field is influenced by the variation in
volume V as
compared to the side view (ignoring edge effects at the end of the
jet). The minimum-energy field is influenced by the variation in
volume V as
![]() .
A line-of-sight angle
.
A line-of-sight angle
![]() has been inferred for the flow into the hot spot from
independent considerations of the jet's polarisation change there and
the hot spot's morphology (Meisenheimer et al. 1997; Conway & Davis 1994). If the jet is at the
same angle, the values in Table 2 need to be
scaled up by
has been inferred for the flow into the hot spot from
independent considerations of the jet's polarisation change there and
the hot spot's morphology (Meisenheimer et al. 1997; Conway & Davis 1994). If the jet is at the
same angle, the values in Table 2 need to be
scaled up by
![]() .
Hence, the minimum-energy
field needs to be scaled down by about 10%, and correspondingly the
maximum energy up by 10%. Since we do not expect the minimum energy
to be accurate to this level, we simply assume the jet is in the plane
of the sky. Even if the jet flow is relativistic, the value of
.
Hence, the minimum-energy
field needs to be scaled down by about 10%, and correspondingly the
maximum energy up by 10%. Since we do not expect the minimum energy
to be accurate to this level, we simply assume the jet is in the plane
of the sky. Even if the jet flow is relativistic, the value of
![]() inferred from the minimum-energy field and the observed
inferred from the minimum-energy field and the observed
![]() is
nearly independent of the value of the Doppler factor since both
is
nearly independent of the value of the Doppler factor since both
![]() and
and
![]() are modified by the beaming in nearly
the same way (Meisenheimer et al. 1996a; Neumann 1995).
are modified by the beaming in nearly
the same way (Meisenheimer et al. 1996a; Neumann 1995).
Our fits of the observed spectra with theoretical models
(Sect. 5.1) constrained the spectral shape to have a low-frequency spectral index of
![]() or flatter and a break
of
or flatter and a break
of
![]() in the frequency range of the VLA observations, leaving the cutoff frequency as the only "shape parameter'' to be determined by the observations. This is an
appropriate model of the observations since all radio observations
show a nearly constant radio spectral index
in the frequency range of the VLA observations, leaving the cutoff frequency as the only "shape parameter'' to be determined by the observations. This is an
appropriate model of the observations since all radio observations
show a nearly constant radio spectral index
![]() everywhere in the jet, while there are variations in the spectral
indices only in the infrared/optical/UV wavelength range
(Sect. 4.2; and Conway et al. 1993). We are primarily interested
in the value of the cutoff frequency, but also in the behaviour of the
bolometric luminosity of the radio-optical emission component. We
show now that the impact of the assumptions about the spectral shape
on these quantities only has negligible impact on our conclusions.
everywhere in the jet, while there are variations in the spectral
indices only in the infrared/optical/UV wavelength range
(Sect. 4.2; and Conway et al. 1993). We are primarily interested
in the value of the cutoff frequency, but also in the behaviour of the
bolometric luminosity of the radio-optical emission component. We
show now that the impact of the assumptions about the spectral shape
on these quantities only has negligible impact on our conclusions.
To check the impact of our assumptions, we repeated the minimum-energy
argument for a simple power law with spectral index
![]() (approximating the radio observations). For spectral indices
(approximating the radio observations). For spectral indices
![]() and for
and for
![]() ,
the only spectral shape
parameters that remain in the expression for the minimum-energy field
are the spectral index itself and the assumed minimum frequency. The
value of the cutoff frequency has negligible impact on the
minimum-energy field. The spectral index only appears in a
slowly-varying function, so that small changes in the assumed
,
the only spectral shape
parameters that remain in the expression for the minimum-energy field
are the spectral index itself and the assumed minimum frequency. The
value of the cutoff frequency has negligible impact on the
minimum-energy field. The spectral index only appears in a
slowly-varying function, so that small changes in the assumed ![]() do not have a large impact on the result. Changing the break
frequency
do not have a large impact on the result. Changing the break
frequency
![]() ,
which could in principle lie in the unobserved gap
between the VLA and HST data, by as much as a factor of 104 only
changes the derived minimum-energy field by a factor of about two.
Similar changes will be produced by much more modest variations in the
assumed values of the filling factor
,
which could in principle lie in the unobserved gap
between the VLA and HST data, by as much as a factor of 104 only
changes the derived minimum-energy field by a factor of about two.
Similar changes will be produced by much more modest variations in the
assumed values of the filling factor ![]() and the ratio k of
energy in other relativistic particles to energy in relativistic
electrons. Thus, our lack of knowledge about
and the ratio k of
energy in other relativistic particles to energy in relativistic
electrons. Thus, our lack of knowledge about ![]() and kconstitutes the dominant systematic uncertainty. Even these
uncertainties do not have a strong impact on our results because the
inferred maximum particle energy scales as
and kconstitutes the dominant systematic uncertainty. Even these
uncertainties do not have a strong impact on our results because the
inferred maximum particle energy scales as
![]() so that
so that
![]() depends at most on the
7
depends at most on the
7
![]() root of any quantity of interest. The results
presented in the following section are therefore very robust with
respect to changing any of the underlying assumptions, at least for
the low-energy emission component responsible for the radio-optical
synchrotron emission (cf. Sect. 6.2).
root of any quantity of interest. The results
presented in the following section are therefore very robust with
respect to changing any of the underlying assumptions, at least for
the low-energy emission component responsible for the radio-optical
synchrotron emission (cf. Sect. 6.2).
| |
Figure 13: Maps of the cutoff frequency. Grey levels run from 1013 Hz (white) to 1017 Hz (black) with a pseudo-logarithmic stretch as indicated by the greyscale bar. The values fitted in A and B2 are lower limits. As expected, model A bears a closer resemblance to the optical-ultraviolet spectral index map, while model B is dominated by the infrared-optical spectral index map (cf. Fig. 7). Regions H2 and H1 are fitted with a different model HS. |
| Open with DEXTER | |
For each photometry aperture (or pixel in
Fig. 2), the values for
![]() and
and
![]() from the fitted spectra together with the
appropriate volume from Table 2 and the
assumed value of
from the fitted spectra together with the
appropriate volume from Table 2 and the
assumed value of
![]() are used to calculate
are used to calculate
![]() .
With this knowledge, the maximum particle energy
.
With this knowledge, the maximum particle energy
![]() can be inferred from the fitted value of
can be inferred from the fitted value of
![]() by Eq. (1).
by Eq. (1).
We consider the determined values of the cutoff frequency, minimum-energy field and hence maximum particle energy and their relation to the jet morphology. In particular, we will be interested whether it is possible to identify localised acceleration regions in the jet.
![\begin{figure}
\par\includegraphics[width=7.85cm,clip]{0021f16.eps} \end{figure}](/articles/aa/full/2005/08/aa0021-04/Timg208.gif) |
Figure 14:
Run of the fitted cutoff frequency
|
| Open with DEXTER | |
We present maps of the fitted cutoff frequency
![]() for the three
different fits in Fig. 13, and its run along the
radius vector at position angle 222
for the three
different fits in Fig. 13, and its run along the
radius vector at position angle 222
![]() 2 in
Fig. 14. No cutoff is observed in the regions at
2 in
Fig. 14. No cutoff is observed in the regions at
![]() (A1) and at 15
(A1) and at 15
![]() (B2) (cf. Sect. 4.2),
so the fitted values there are only lower limits to the true cutoff
frequency. The overall trend is a decrease in
(B2) (cf. Sect. 4.2),
so the fitted values there are only lower limits to the true cutoff
frequency. The overall trend is a decrease in
![]() with increasing
distance from the core. The lowest value of
with increasing
distance from the core. The lowest value of
![]() is reached at the
hot spot, which is characterised by a sharp drop in
is reached at the
hot spot, which is characterised by a sharp drop in
![]() from
1015 Hz at 21
from
1015 Hz at 21
![]() 2 (optical hot spot position) to
1014 Hz at
2 (optical hot spot position) to
1014 Hz at
![]() .
As expected from the overall
similarity of the spectral indices determined at 0
.
As expected from the overall
similarity of the spectral indices determined at 0
![]() 3 resolution
and in earlier work at 1
3 resolution
and in earlier work at 1
![]() 3 resolution
(Fig. 9), the cutoff frequency determined
here agrees well with the run of the cutoff frequency
3 resolution
(Fig. 9), the cutoff frequency determined
here agrees well with the run of the cutoff frequency
![]() determined by
Meisenheimer et al. (1996a).
determined by
Meisenheimer et al. (1996a).
All variations are rather smooth. Any sharp jumps are due to the uncertainties introduced into the fitting by the fact that there are only three high-frequency data points which cannot constrain the cutoff frequency and the UV excess well simultaneously. Therefore, only those local peaks are significant which correspond to significant peaks in the high-frequency spectral indices (Fig. 8). In fact, local peaks in the cutoff frequency are not as pronounced as expected from the peaks in the infrared-optical spectral index, e.g. at C2 and D2. Considering the fits in these locations (Fig. 12), it is apparent that the cutoff frequency is likely overestimated in those locations. In any case, there is a tendency for the cutoff frequency to be slightly higher in the brighter regions than in the immediate surroundings. However, the variation in cutoff frequency is less pronounced than the corresponding variation in the jet's surface brightness at all wavelengths. Thus, there is a local positive correlation between brightness and cutoff frequency, while globally, the cutoff frequency decreases along the jet as the (radio) surface brightness increases.
Only small discrepancies arise in the value of the cutoff frequency
between models A and B for most of the jet (for a discussion, see
Sect. 6.2 below). Between r=17.5 and r=19.5, where the
spectral hardening is most pronounced, the value of
![]() in model A, in which the cutoff is determined mainly by the optical-UV
spectral index, is a factor of 3-10 larger than in the preferred
model B, in which the steeper (by
in model A, in which the cutoff is determined mainly by the optical-UV
spectral index, is a factor of 3-10 larger than in the preferred
model B, in which the steeper (by
![]() )
infrared-optical spectral index determines the cutoff frequency.
Before we discuss the variation of the particles' maximum energy along
the jet, we consider the derived minimum-energy field.
)
infrared-optical spectral index determines the cutoff frequency.
Before we discuss the variation of the particles' maximum energy along
the jet, we consider the derived minimum-energy field.
![\begin{figure}
\par\includegraphics[angle=270,width=7.8cm,clip]{0021f17.eps} \end{figure}](/articles/aa/full/2005/08/aa0021-04/Timg212.gif) |
Figure 15:
Run of the minimum-energy field
|
| Open with DEXTER | |
| |
Figure 16:
Map of the bolometric surface brightness assuming isotropic
emissivity. Values range from 1.5 |
| Open with DEXTER | |
The variation of the derived minimum-energy field perpendicular to the
jet axis is dominated by the assumed geometry. We therefore present
only its run along the assumed jet axis in
Fig. 15. It starts at just below 10 nT at the
onset of the optical jet, increasing to 20-25 nT in the hot
spot. The corresponding value of the electron number density ranges
from about 1-5 m-3. The evolution of the minimum-energy field
along the jet corresponds qualitatively to the run of the bolometric
surface brightness (Fig. 16). This is expected
because for the constant spectral shape assumed here (justified by the
constant radio spectral index) and for a constant emitting volume, the
minimum-energy field scales with the surface brightness ![]() (at
any frequency
(at
any frequency ![]() significantly below the cutoff frequency) as S2/7. As already noted in Sects. 5.2 and 5.3.2 above, the cutoff frequency has negligible
influence on the minimum-energy field for spectra with
significantly below the cutoff frequency) as S2/7. As already noted in Sects. 5.2 and 5.3.2 above, the cutoff frequency has negligible
influence on the minimum-energy field for spectra with
![]() .
Therefore, the possibility that the synchrotron spectrum extends
up to X-rays in regions A, B1 and B2 has no influence on the minimum-energy estimate.
.
Therefore, the possibility that the synchrotron spectrum extends
up to X-rays in regions A, B1 and B2 has no influence on the minimum-energy estimate.
The minimum-energy field of ![]() 25 nT determined for the hot
spot seems to be low compared to the magnetic field value determined
by Meisenheimer et al. (1997), both from spectral fits (
(39+24-10) nT) and
from the minimum-energy argument (
(35+8-4) nT; cf. Fig. 15). This difference is entirely due to
the different values assumed for the ratio k in Eq. (7),
chosen as k=1 here but k=10 in Meisenheimer et al. (1997). Thus, our
determination of the minimum-energy field agrees with previous
spectral fits at lower resolution.
25 nT determined for the hot
spot seems to be low compared to the magnetic field value determined
by Meisenheimer et al. (1997), both from spectral fits (
(39+24-10) nT) and
from the minimum-energy argument (
(35+8-4) nT; cf. Fig. 15). This difference is entirely due to
the different values assumed for the ratio k in Eq. (7),
chosen as k=1 here but k=10 in Meisenheimer et al. (1997). Thus, our
determination of the minimum-energy field agrees with previous
spectral fits at lower resolution.
As discussed below, only the order of magnitude of the minimum-energy field matters in the considerations here. We therefore do not discuss its behaviour in detail.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0021f19.eps} \end{figure}](/articles/aa/full/2005/08/aa0021-04/Timg219.gif) |
Figure 17:
Run of the maximum particle Lorentz factor
|
| Open with DEXTER | |
The run of the maximum particle energy inferred from the
minimum-energy field and the cutoff frequency is shown in
Fig. 17. This run is very similar to the run of
the cutoff frequency in Fig. 14; this arises
from the relation used to derive the maximum particle energy
(Eq. (1)):
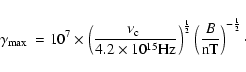
![\begin{figure*}
\par\parbox[c]{.15\hsize}{image\\ 620~\mbox{${\rm nm}$ }}\parbox...
...hsize}{!}{\includegraphics[clip,width=.9\hsize]{0021f20c.eps}}}\\
\end{figure*}](/articles/aa/full/2005/08/aa0021-04/Timg222.gif) |
Figure 18:
Map of the maximum particle Lorentz factor
|
| Open with DEXTER | |
As expected from the run of the spectral indices from previous
studies, the global trend is a decrease of
![]() from >107down to 105-106. Simultaneously, there is a strong increase
of the jet's luminosity, i.e., luminosity and maximum energy are
anti-correlated. We consider the local variations next. As we noted
above, local extrema of the infrared-optical spectral indices
correspond to extrema of
from >107down to 105-106. Simultaneously, there is a strong increase
of the jet's luminosity, i.e., luminosity and maximum energy are
anti-correlated. We consider the local variations next. As we noted
above, local extrema of the infrared-optical spectral indices
correspond to extrema of
![]() and hence of
and hence of
![]() because
the minimum-energy field does not change much along the jet.
Significant local extrema of
because
the minimum-energy field does not change much along the jet.
Significant local extrema of
![]() are found in the following regions:
are found in the following regions:
Meisenheimer & Heavens (1986) presented a model for particle acceleration in the hot spot of 3C 273. They showed that the hot spot spectrum can be understood by modelling the hot spot as a planar shock at which
first-order Fermi acceleration of particles takes place (details of
the spectral modelling are contained in Heavens & Meisenheimer (1987), while further
observations of this and other hot spots have been presented by
Meisenheimer et al. (1989,1997)). This model predicts an offset between the
peaks of the radio and optical emission of 0
![]() 2, arising from the
vastly different synchrotron loss scales of electrons being advected
downstream from the shock itself: "radio'' electrons lose a
negligible fraction of their total energy, while "optical'' electrons
quickly lose their entire energy as they move away from the
acceleration region. Recall that the strong compression at the shock
leads to an increased magnetic field compared to the jet flow, and
hence to stronger losses.
2, arising from the
vastly different synchrotron loss scales of electrons being advected
downstream from the shock itself: "radio'' electrons lose a
negligible fraction of their total energy, while "optical'' electrons
quickly lose their entire energy as they move away from the
acceleration region. Recall that the strong compression at the shock
leads to an increased magnetic field compared to the jet flow, and
hence to stronger losses.
Figure 5 clearly shows the predicted offset in the position of the hot spot (H2) between radio and optical wavelengths. This strengthens the identification of H2 with a planar shock with strongly localised particle acceleration.
We note that again the minimum-energy magnetic field determined for the hot spot agrees with the magnetic field determined from the hot spot spectrum by Meisenheimer et al. (1997, the only difference arises due to different values of the parameter k in the minimum-energy field determination).
Thus, at 0
![]() 3 resolution, the Heavens & Meisenheimer (1987) hot spot model is
consistent with all observations. Moreover, our new observations have
confirmed the predicted offset in the hot spot's position. However,
it is remarkable that even the hot spot shows a UV excess, indicating
that the hot spot, too, has a more complicated internal structure than
previously assumed. In addition, the presence of emission from the
tip of the jet H1 (which has been called a "precursor'' inthe
literature; see Foley & Davis 1985, e.g.) and its relation to the hot spot must be
explained. The next tests of this model will involve a detailed
analysis of the hot spot's radio morphology at the highest available
resolution, which we defer to a future paper.
3 resolution, the Heavens & Meisenheimer (1987) hot spot model is
consistent with all observations. Moreover, our new observations have
confirmed the predicted offset in the hot spot's position. However,
it is remarkable that even the hot spot shows a UV excess, indicating
that the hot spot, too, has a more complicated internal structure than
previously assumed. In addition, the presence of emission from the
tip of the jet H1 (which has been called a "precursor'' inthe
literature; see Foley & Davis 1985, e.g.) and its relation to the hot spot must be
explained. The next tests of this model will involve a detailed
analysis of the hot spot's radio morphology at the highest available
resolution, which we defer to a future paper.
When describing synchrotron spectra as power laws, the underlying
assumption is a power-law electron energy distribution. As noted
above, a non-idealised spectrum with finite maximum particle energy
and rapid pitch-angle scattering will furthermore exhibit a
quasi-exponential cutoff at some frequency
![]() ,
the synchrotron
frequency corresponding to the highest electron energies. This cutoff
implies that the spectrum has a convex shape, so that the spectrum
steepens progressively towards higher frequencies. Any high-frequency
flux must therefore lie below a power-law extrapolation from lower
frequencies.
,
the synchrotron
frequency corresponding to the highest electron energies. This cutoff
implies that the spectrum has a convex shape, so that the spectrum
steepens progressively towards higher frequencies. Any high-frequency
flux must therefore lie below a power-law extrapolation from lower
frequencies.
In employing broken power laws, the only physical break is a
steepening of the spectrum from
![]() to
to
![]() near some break
frequency
near some break
frequency
![]() .
This break arises in a model of the
synchrotron source as a loss region into which a power-law
distribution of electrons with approximately constant number density
and maximum energy is continuously injected. The break is produced by
adding up the contributions from the electron population observed at
different times since acceleration, i.e., with different cutoff
frequencies. The magnitude of the break of 1/2 is fixed by the
cooling mechanism
.
This break arises in a model of the
synchrotron source as a loss region into which a power-law
distribution of electrons with approximately constant number density
and maximum energy is continuously injected. The break is produced by
adding up the contributions from the electron population observed at
different times since acceleration, i.e., with different cutoff
frequencies. The magnitude of the break of 1/2 is fixed by the
cooling mechanism![]() . Describing synchrotron
spectra with arbitrary breaks is therefore inconsistent with any
physically motivated model; in violation of our reasoning above, one
could then even invent breaks to flatter spectra.
. Describing synchrotron
spectra with arbitrary breaks is therefore inconsistent with any
physically motivated model; in violation of our reasoning above, one
could then even invent breaks to flatter spectra.
We used the detailed shape of cutoff spectra as computed by Heavens & Meisenheimer (1987). The spectral shape is the result of observing a mixture of electron populations, and the appearance of the entire source can be understood in terms of the temporal evolution of the initially accelerated population. As long as the spectral shape is determined only by radiation losses, not even homogeneous source conditions are required. The resulting spectrum rarely will follow a power law over many decades in frequency, but will be curved and in any case exhibit a convex shape.
In contrast, a more complex electron distribution could be produced if different parts of a source accelerate electrons to different maximum energies, and contain different numbers of electrons. Such a source could be a jet with an inhomogeneous distribution of particles and magnetic fields. This source must be described by more than one electron population (or equivalently, as the sum of the emission from more than one source). This corresponds precisely to the situation encountered in 3C 273's jet: the observed flattening of the spectrum implies that a description using a single electron population is inadequate. This implies unambiguously that there are at least two components to the observed spectrum: one is the "low-frequency'' synchrotron spectrum from radio through optical wavelengths. In addition, there is a "high-frequency'' component responsible for the UV excess, and hence the observed flattening. We have suggested that this second component is the same as that responsible for the jet's X-rays (Jester et al. 2002), which could be a second synchrotron component (Marshall et al. 2001; Röser et al. 2000) or beamed inverse Compton emission (cf. Sambruna et al. 2001). In any case, our spectra prove that 3C 273's jet is not a homogeneous synchrotron source.
It is notable that besides 3C 273, the spectral energy distributions (SEDs) of M 87's jet shows the same upward curvature: Marshall et al. (2002) have presented SEDs for that jet from radio through X-rays (their Fig. 3). They fitted two different single-population models, a Jaffe-Perola model assuming a randomly tangled magnetic field structure and pitch-angle scattering, and a Kardashev-Pacholczyk model, also assuming a tangled field but no pitch angle scattering. Only the latter provides an acceptable fit to the observed SEDs, but it is unclear how pitch-angle scattering could be avoided in a tangled field geometry. Moreover, the spectra for knots HST-1 and D clearly show a steeper downturn near 1015 Hz (already hinted at by the ground-based spectra obtained by Meisenheimer et al. 1996b, their Figs. 7 and 8) than the Kardashev-Pacholczyk spectrum, which is therefore inadequate. Instead, again a second spectral component must be invoked to account for the X-ray flux lying above the cutoff observed in the near-infrared-optical region. Marshall et al. (2002) viewed this as evidence in favour of the spatially stratified model for M 87's jet presented by Perlman et al. (1999).
Our determination of the maximum energy of synchrotron-emitting
electrons shows a lower limit for the Lorentz factors of
![]() at the onset of the optical jet, 12
at the onset of the optical jet, 12
![]() from the quasar core
(Fig. 17). The maximum Lorentz factor first
drops outward along the jet, and then stays nearly constant at a
Lorentz factor of a few times 106 at radii >
from the quasar core
(Fig. 17). The maximum Lorentz factor first
drops outward along the jet, and then stays nearly constant at a
Lorentz factor of a few times 106 at radii >
![]() .
It drops
again by factor of 3 within the hot spot. This drop most likely is caused by the
stronger magnetic field there. In any case, the Lorentz factor of the
particles emitting optical synchrotron radiation cannot be much lower
than 105 anywhere in the jet. Electrons with such high energies can
only be observed close to their acceleration sites: as noted in all
previous studies, synchrotron cooling timescales for these particles
are of the order of a few hundred or thousand years (see Guthrie & Napier 1975; Meisenheimer et al. 1996a; Röser & Meisenheimer 1991,
e.g.). The corresponding loss scales are a
few hundred parsec for the case of electrons freely streaming at
the speed of light, which is unrealistic since they will have to follow
tangled field lines.
.
It drops
again by factor of 3 within the hot spot. This drop most likely is caused by the
stronger magnetic field there. In any case, the Lorentz factor of the
particles emitting optical synchrotron radiation cannot be much lower
than 105 anywhere in the jet. Electrons with such high energies can
only be observed close to their acceleration sites: as noted in all
previous studies, synchrotron cooling timescales for these particles
are of the order of a few hundred or thousand years (see Guthrie & Napier 1975; Meisenheimer et al. 1996a; Röser & Meisenheimer 1991,
e.g.). The corresponding loss scales are a
few hundred parsec for the case of electrons freely streaming at
the speed of light, which is unrealistic since they will have to follow
tangled field lines.
The development of the maximum particle energy along the jet is therefore consistent with the absence of any synchrotron cooling. The same conclusion can already be drawn from the smooth changes of just the optical spectral index, which should most strongly reflect the synchrotron losses the particles undergo, and from the mere presence of optical synchrotron radiation along the entire jet (Jester et al. 2001). The apparent absence of cooling in the presence of synchrotron radiation can only be explained by a distributed acceleration mechanism.
The smooth changes of the spectral features along the jet indicate a correspondingly smooth variation of the physical conditions along the jet. The present detailed high-resolution study of the jet in 3C 273 set out with the aim to map those regions in which particles are preferentially accelerated. Since the observed cooling is much less drastic than expected, the conclusion is that the entire jet is the particle acceleration region. The fact that the jet has a much higher emissivity than the radio cocoon around it (see Sect. 4.1.3) also implies a difference in physical conditions between the jet and the surrounding material. Furthermore, the jet's X-ray emission is a further sink of energy (whatever the emission process) which needs to be filled by the re-acceleration mechanism. Note that this does not preclude the possibility that the knots in the jet are due to shocks, at which particle acceleration can also take place. But even in this case, particles must be accelerated between the shocks as well.
This corresponds to the "jet-like'' acceleration mechanism proposed by Meisenheimer et al. (1997). The detailed physics of this distributed acceleration mechanisms are unknown, but several theoretical suggestions have been made. Magnetic reconnection is one way to tap the energy stored in the jet fluid and convert it continuously into relativistic particles (Litvinenko 1999). Another possible energy source is the velocity shear between the surface of the jet and the surrounding medium (Stawarz & Ostrowski 2002). This latter mechanism would be limited to particle acceleration within a thin surface layer. Since it appears that the jet emission is not edge-brightened, as would be expected for emission from a surface layer (Sect. 4.1.2), surface velocity shear is unlikely to be the acceleration mechanism providing optical electrons along the entire jet. It may, however, be appropriate to explain the second higher-energy emission component identified above (Sect. 6.2), provided this turns out to be edge-brightened. A similar mechanism has recently been proposed by Rieger & Mannheim (2002): these authors suggest that velocity shear and centrifugal forces in a rotating jet flow may provide efficient particle acceleration.
The global energy budget of the jet is a related question. If the entire jet operates at the minimum energy condition, and if there is no strong, variable beaming, the increase in the minimum-energy field along the jet (linked to the increase in synchrotron luminosity) corresponds to an increase of the energy density stored in magnetic fields and relativistic particles by about one order of magnitude. This raises interesting questions about the energy budget of the jet: if the total energy flux in magnetic fields and relativistic particles is to be conserved, the jet would need to slow down (cf. Georganopoulos & Kazanas 2003). The necessity to account for the kinetic energy and momentum flux imposes further constraints. On the other hand, it may be possible to convert jet kinetic energy into magnetic and particle energy, as in some of the acceleration mechanisms just mentioned, leading to a different mutual dependence of jet speed and magnetic energy density than in the pure energy conservation case. A detailed examination of the jet's energy budget addressing these issues is certainly a worthy exercise, but beyond the scope of the present publication.
As described in Sect. 5.4.3, there is a local positive correlation between surface brightness and maximum particle energy, although these quantities are anti-correlated globally. The opposite correlations must be caused by two different physical mechanisms. Although the cutoff frequency is the direct observable, the underlying physical parameters are the maximum particle energy and the jet's magnetic field. In 3C 273, the global run of the maximum particle energy is practically identical to that of the cutoff frequency, and the local variations in cutoff frequency are much smaller than those in surface brightness (see Figs. 14 and 17).
We have established above (Sect. 6.3) that particles must be
accelerated continuously within the jet. In this case, the value of
the maximum particle energy is obtained by equating the acceleration
timescale
![]() ,
which is the time during which a
particle's energy is increased by a factor of two, with the
synchrotron loss timescale
,
which is the time during which a
particle's energy is increased by a factor of two, with the
synchrotron loss timescale
![]() (e.g., Longair 1994):
(e.g., Longair 1994):
We have taken the jet Doppler factor to be
![]() in all
calculations up to here, which is justified because the value of the
maximum particle energy as inferred from the jet's surface brightness
and minimum-energy magnetic field only depends very weakly on the true
value of the Doppler factor (cf. Sect. 5.2; and Meisenheimer et al. 1996a; Neumann 1995). The observed surface brightness S and
cutoff frequency
in all
calculations up to here, which is justified because the value of the
maximum particle energy as inferred from the jet's surface brightness
and minimum-energy magnetic field only depends very weakly on the true
value of the Doppler factor (cf. Sect. 5.2; and Meisenheimer et al. 1996a; Neumann 1995). The observed surface brightness S and
cutoff frequency
![]() have the following scalings with B and
have the following scalings with B and
![]() for a continuous jet (see Begelman et al. 1984, e.g.):
for a continuous jet (see Begelman et al. 1984, e.g.):
The only other jet which has been studied similarly well is that in
M 87. There are key differences between the behaviour of the maximum
particle energy between these two jets. Meisenheimer et al. (1996b) showed that M 87
shows a strong correlation between surface brightness and cutoff
frequency, while the maximum particle energy remains practically
unchanged. This correlation can be understood purely in terms of
variations of the magnetic field strength, while the constancy of the
maximum particle energy is explained by invoking acceleration in
shocks (e.g. Sparks et al. 1996), by an extended acceleration mechanism
(Meisenheimer et al. 1996b), or by assuming a sub-equipartition magnetic field and
relativistic time dilation which both lower the loss times
sufficiently even without particle acceleration (Heinz & Begelman 1997).
Meisenheimer et al. (1996b) conclude that re-acceleration is responsible, and that
the mechanism in M 87's jet obeys the scaling
![]() to achieve a constant maximum particle energy
(cf. Eq. (9)). It is useful to consider whether this
acceleration mechanism proposed for M 87 could be identical to the one
at work in 3C 273, i.e., whether it is universal.
to achieve a constant maximum particle energy
(cf. Eq. (9)). It is useful to consider whether this
acceleration mechanism proposed for M 87 could be identical to the one
at work in 3C 273, i.e., whether it is universal.
Since the maximum particle energy changes significantly along
3C 273's jet, the acceleration mechanism invoked by Meisenheimer et al. (1996b) for
M 87 must be different from the one acting in 3C 273's jet. To
produce a local correlation between brightness and maximum particle
energy via magnetic field variations, the acceleration time scale in
3C 273 would need to follow a scaling
![]() with s>2 so that both
with s>2 so that both
![]() and S correlate with B(Eqs. (9) and (10)). In that case, local
magnetic field variations could explain the observed
correlations. However, since the brightness changes are larger than
the changes in the maximum particle energy and cutoff frequency, it
seems more likely that small-scale variations in the Doppler factor
and S correlate with B(Eqs. (9) and (10)). In that case, local
magnetic field variations could explain the observed
correlations. However, since the brightness changes are larger than
the changes in the maximum particle energy and cutoff frequency, it
seems more likely that small-scale variations in the Doppler factor
![]() are responsible because S varies more strongly with
are responsible because S varies more strongly with
![]() than with B. But variations in
than with B. But variations in
![]() by themselves are insufficient for 3C 273 because they do not produce a
correlation between brightness and maximum particle energy. To
clarify the origin of this correlation, it will be necessary to
disentangle the UV excess from the remainder of the jet emission to
remove any uncertainty about the true value of the cutoff frequency,
and ideally to obtain a measurement of the jet's magnetic field other
than the minimum-energy estimate.
by themselves are insufficient for 3C 273 because they do not produce a
correlation between brightness and maximum particle energy. To
clarify the origin of this correlation, it will be necessary to
disentangle the UV excess from the remainder of the jet emission to
remove any uncertainty about the true value of the cutoff frequency,
and ideally to obtain a measurement of the jet's magnetic field other
than the minimum-energy estimate.
The global anti-correlation of brightness and maximum energy appears
intuitive for synchrotron radiation: stronger synchrotron emission
implies larger energy losses, and hence a lower maximum energy.
However, as noted above, the actual behaviour of the maximum particle
energy in the presence of particle acceleration depends on the details
of the acceleration mechanism. If the local correlation of brightness
and
![]() can be explained by the nature of the acceleration
mechanism, the global anticorrelation must be due to an entirely
different effect which reverses the local correlation. It may be
possible that the local correlations are produced by a "shock-like''
acceleration mechanism acting only in the brighter regions (e.g. if the
bright regions are shocks), while electrons elsewhere are
accelerated by the "jet-like'' mechanism (Meisenheimer et al. 1997). However,
such a scenario is somewhat unappealing because there would need to be
a certain fine-tuning to explain the overall smoothness of the
spectral index changes. Furthermore, although this may explain the
different global and local behaviour within 3C 273 as well as the
presence of two distinct emission components (Sect. 6.2), the
difference to M 87 remains, in which the "jet-like'' mechanism is
assumed to produce the positive correlation. We therefore need to
appeal to further differences. Meisenheimer (1996) suggested that the
observations of M 87 and 3C 273 could be unified if there was a link
between the maximum particle energy and the velocity gradient along
the jet, and the jet velocity was relativistic, so that changes in the
velocity would lead both to changes in the maximum particle energy and
in the Doppler factor and hence the apparent brightness. We will
discuss this idea elsewhere.
can be explained by the nature of the acceleration
mechanism, the global anticorrelation must be due to an entirely
different effect which reverses the local correlation. It may be
possible that the local correlations are produced by a "shock-like''
acceleration mechanism acting only in the brighter regions (e.g. if the
bright regions are shocks), while electrons elsewhere are
accelerated by the "jet-like'' mechanism (Meisenheimer et al. 1997). However,
such a scenario is somewhat unappealing because there would need to be
a certain fine-tuning to explain the overall smoothness of the
spectral index changes. Furthermore, although this may explain the
different global and local behaviour within 3C 273 as well as the
presence of two distinct emission components (Sect. 6.2), the
difference to M 87 remains, in which the "jet-like'' mechanism is
assumed to produce the positive correlation. We therefore need to
appeal to further differences. Meisenheimer (1996) suggested that the
observations of M 87 and 3C 273 could be unified if there was a link
between the maximum particle energy and the velocity gradient along
the jet, and the jet velocity was relativistic, so that changes in the
velocity would lead both to changes in the maximum particle energy and
in the Doppler factor and hence the apparent brightness. We will
discuss this idea elsewhere.
One of the main unsolved questions in the study of extragalactic jets is posed by the observations of optical synchrotron radiation over scales much larger than typical synchrotron loss scales and far from the "working surfaces'' of the standard model (Blandford & Rees 1974). Another puzzle has been posed by the recent Chandra observations of X-rays from extragalactic jets, whose emission mechanism remains debated and which form a further sink of energy that has to be filled within the jet. The study of the physical conditions giving rise to the observed emission by keeping up the particle energy against strong synchrotron losses at optical wavelength and supplying the energy observed in X-rays can only be performed via a study of the synchrotron continuum, at the highest possible spatial resolution and covering the largest possible wavelength range.
We present new HST and VLA images of the jet at
![]() 3.6
3.6 ![]() ,
2.0
,
2.0 ![]() ,
1.3
,
1.3 ![]() ,
1.6
,
1.6 ![]() m, 620
m, 620 ![]() and 300
and 300 ![]() matched to a
common resolution of 0
matched to a
common resolution of 0
![]() 3 (Fig. 2). We
combine the data to obtain spectral energy distributions which we fit
with theoretical synchrotron spectra (Fig. 12).
Contrary to expectations for synchrotron emission, the observed
spectra show a significant flattening in the infrared-ultraviolet
wavelength range, implying that the emission cannot be modelled as
synchrotron emission due to a single electron population, as has been
assumed in previous studies of this jet's emission
(Meisenheimer et al. 1996a). Instead, additional emission must be present which can
lead to the observed flattening. The most likely explanation is an
additional flat-spectrum component in the ultraviolet. The same
component may simultaneously be responsible for the jet's X-ray
emission (for details, see Jester et al. 2002).
3 (Fig. 2). We
combine the data to obtain spectral energy distributions which we fit
with theoretical synchrotron spectra (Fig. 12).
Contrary to expectations for synchrotron emission, the observed
spectra show a significant flattening in the infrared-ultraviolet
wavelength range, implying that the emission cannot be modelled as
synchrotron emission due to a single electron population, as has been
assumed in previous studies of this jet's emission
(Meisenheimer et al. 1996a). Instead, additional emission must be present which can
lead to the observed flattening. The most likely explanation is an
additional flat-spectrum component in the ultraviolet. The same
component may simultaneously be responsible for the jet's X-ray
emission (for details, see Jester et al. 2002).
The optical-ultraviolet spectral index map generated at 0
![]() 3 resolution (Fig. 7a) shows no strong
correlation between local spectral index and surface brightness
variations. There is, however, such a correlation on the
radio-infrared and infrared-optical spectral index maps. Even these
correlations are less pronounced than those found in the jet of M 87
(Perlman et al. 2002,2001), where they are taken as evidence of localised
particle acceleration in the knots of this jet (but see
Meisenheimer 1996 for an alternative explanation). As confirmed by our
spectral fits (see below), the spectral index variations reflect
variations of the maximum particle energy along the jet.
3 resolution (Fig. 7a) shows no strong
correlation between local spectral index and surface brightness
variations. There is, however, such a correlation on the
radio-infrared and infrared-optical spectral index maps. Even these
correlations are less pronounced than those found in the jet of M 87
(Perlman et al. 2002,2001), where they are taken as evidence of localised
particle acceleration in the knots of this jet (but see
Meisenheimer 1996 for an alternative explanation). As confirmed by our
spectral fits (see below), the spectral index variations reflect
variations of the maximum particle energy along the jet.
We find an offset between the radio and optical images of the hotspot that is consistent with the prediction by Heavens & Meisenheimer (1987). This adds further to the confidence that the assumed hot spot model is correct (Meisenheimer et al. 1997). However, the role of the tip of the jet H1 and its relation to the hot spot remains to be clarified, perhaps in a model fully describing the hot spot flow in three dimensions, instead of just one. If the jet flow is still highly relativistic just upstream of the hot spot, the details of the flow's deceleration in the hot spot may also change its appearance (Georganopoulos & Kazanas 2003).
We fitted the observed spectra with model synchrotron spectra to extract physical information, in particular the maximum particle energy and its variation along the jet.
Model synchrotron spectra according to Heavens & Meisenheimer (1987) have been used to
determine the cutoff frequency
![]() .
It is mainly determined by the
infrared-optical spectral index. We infer the maximum particle energy
from the fitted cutoff frequency by assuming an equipartition magnetic
field
.
It is mainly determined by the
infrared-optical spectral index. We infer the maximum particle energy
from the fitted cutoff frequency by assuming an equipartition magnetic
field
![]() .
It is a general result that the value of
.
It is a general result that the value of
![]() is very robust with respect to assumptions about the details of the spectral shape, as long as the spectrum has a power law index that is steeper than
is very robust with respect to assumptions about the details of the spectral shape, as long as the spectrum has a power law index that is steeper than
![]() .
.
The cutoff frequency decreases from above
![]() in region A at
in region A at
![]() and settles to a plateau of order 106 at
and settles to a plateau of order 106 at
![]() .
A further decrease to
.
A further decrease to
![]()
![]() 105 is only
observed at the position of the radio hot spot, beyond which there is
no optical, but still infrared emission. This global run corresponds
to the findings of previous studies at 1
105 is only
observed at the position of the radio hot spot, beyond which there is
no optical, but still infrared emission. This global run corresponds
to the findings of previous studies at 1
![]() 3 resolution, which
showed that the maximum particle energy decreases as the radio jet
brightness increases. As expected from the spectral index variations,
there is an additional weak correlation between local variations of
maximum particle energy and surface brightness.
3 resolution, which
showed that the maximum particle energy decreases as the radio jet
brightness increases. As expected from the spectral index variations,
there is an additional weak correlation between local variations of
maximum particle energy and surface brightness.
An earlier examination of the effect of relativistic beaming on the
inferred synchrotron lifetime had shown that the overall slow decrease
of
![]() cannot be explained by an enhancement of the true
synchrotron lifetime by beaming effects (Jester et al. 2001). We concluded
that particle acceleration must take place distributed across the
entire jet. This conclusion is strengthened by the X-ray observations,
whatever the X-ray emission mechanism: The radiative lifetimes of
X-ray synchrotron electrons in an equipartition field of 20 nT are a
few tens of years, those of UV-emitting electrons are a few hundreds
of years. In the inverse Compton scenario, the combined effects of
relativistic beaming and lower magnetic fields lead to lifetimes of a
few times 104 years for UV-emitting electrons. In both cases,
particles must therefore be accelerated continuously within the entire
jet ("jet-like'' acceleration, Meisenheimer et al. 1997). The same conclusion
is drawn from the fact that the physical conditions within the jet of
3C 273 vary very smoothly down to the spatial scales of
cannot be explained by an enhancement of the true
synchrotron lifetime by beaming effects (Jester et al. 2001). We concluded
that particle acceleration must take place distributed across the
entire jet. This conclusion is strengthened by the X-ray observations,
whatever the X-ray emission mechanism: The radiative lifetimes of
X-ray synchrotron electrons in an equipartition field of 20 nT are a
few tens of years, those of UV-emitting electrons are a few hundreds
of years. In the inverse Compton scenario, the combined effects of
relativistic beaming and lower magnetic fields lead to lifetimes of a
few times 104 years for UV-emitting electrons. In both cases,
particles must therefore be accelerated continuously within the entire
jet ("jet-like'' acceleration, Meisenheimer et al. 1997). The same conclusion
is drawn from the fact that the physical conditions within the jet of
3C 273 vary very smoothly down to the spatial scales of
![]() resolved here. This does not preclude the
possibility that the enhanced-brightness regions are shocks at which
particles are accelerated - but even if they are, re-acceleration
between them is necessary to explain the observed spectral features.
resolved here. This does not preclude the
possibility that the enhanced-brightness regions are shocks at which
particles are accelerated - but even if they are, re-acceleration
between them is necessary to explain the observed spectral features.
The details of the acceleration mechanism determine the scaling of the maximum particle energy with changes in the magnetic field. The interplay between the "jet-like'' and "shock-like'' acceleration mechanisms might explain the conflicting global and local behaviour of the maximum particle energy in 3C 273. However, both mechanisms must be different from the one invoked by Meisenheimer et al. (1996b) for M 87's jet (Sect. 6.4).
We stress again the observed flattening of the high-frequency spectrum, which implies that the jet's emission cannot be assumed to arise from a single electron population, but requires the presence of an additional emission component. In particular, the spectrum of knot A cannot be considered as a single power law from radio through X-rays, as concluded from lower-resolution data (Marshall et al. 2001; Röser et al. 2000). Instead of considering the jet as a homogeneous synchrotron source filled with a simple electron population, we must realise that jets have an internal energetic structure (cf. Perlman et al. 1999,2001). Future work to investigate the acceleration mechanism at work in this and other jets must be based on these results.
With the present radio-optical data, it has only been possible to detect the high-frequency hardening of the jet emission, and thus the presence of a second emission component. No statements can be made about the spectral shape of this "high-energy'' component beyond the approximate match of the X-ray extrapolation and the UV excess. We have been awarded HST time to extend the wavelength coverage into the far-ultraviolet (150 nm). Using these data, we will be able to constrain the run of the optical synchrotron cutoff more accurately, and to characterise the spectrum of the UV excess. This will achieve a separation of the two spectral components from each other. Particular insight can be expected by considering the high-frequency spectra in those regions of the jet showing the strongest difference between radio, optical and X-ray morphology (Sect. 4.1.1).
In order to test theories for extended particle acceleration, we require detailed predictions both from theoretical work and from magneto-hydrodynamical simulations of the jet flow, in particular regarding the spatial distribution of relativistic particles. The most sensitive observational tool is multi-wavelength polarimetry resolving the jet width. This allows not only a study the particles' energy distribution, but also an assessment whether particles at different energies probe the same underlying magnetic field, that is, whether they actually occupy the same emitting volume. Thus, multi-wavelength polarimetry is the natural followup programme for our detection of multiple emission components. We will use our guaranteed time for the adaptive optics camera CONICA/NAOS at the VLT to obtain near-infrared polarimetry at a resolution comparable to the data presented here. However, optical polarimetry of 3C 273's jet making full use of the HST's capabilities is still missing.
Exciting new facts about the jet in 3C 273 have been revealed by each advance in optical and radio observing technology. From the surprising observational facts encountered here, more surprises are yet to be expected en route to an understanding of the physics of this object. Current advances in numerical work are also expected to shed further light on the structure and dynamics of jets. As an extreme object of its kind, 3C 273 will remain high on the agenda of astrophysicists studying jet phenomena.
Acknowledgements
S.J. was supported in part by the US Department of Energy under contract No. DE-AC02-76CH03000. This research has made use of NASA's Astrophysics Data System. We are grateful to the referees, Herman Marshal, Eric Perlman and Markos Georganopoulos, for their thorough review and constructive comments.