A&A 430, 751-759 (2005)
DOI: 10.1051/0004-6361:20041162

A catalog of LEDA galaxies with DENIS measurements[*]

G. Paturel1 - I. Vauglin1 - C. Petit1 - J. Borsenberger 2 - N. Epchtein3 - P. Fouqué 4 - G. Mamon5


1 - CRAL - Observatoire de Lyon, 69561 Saint-Genis Laval Cedex, France
2 - Observatoire de Paris-Meudon, 5, place Jules-Janssen, 92195 Meudon, France
3 - LUAN, Université de Nice Sophia-Antipolis, CNRS - UMR 6525, Parc Valrose, Nice, France
4 - Observatoire Midi-Pyrénées, 14 avenue Edouard-Belin, 31400 Toulouse, France
5 - Institut d'Astrophysique de Paris, 98B Bd. Arago, 75014 Paris, France

Received 26 April 2004 / Accepted 17 September 2004

Abstract
We present a catalog of near-infrared properties of LEDA galaxies, using the full resolution images from the DENIS survey. The fluxes are integrated in eight homothetic ellipses defined by their proper axis ratio, position angle and major axis (up to twice the blue diameter at the isophote 25 mag arcsec-2) extracted from the LEDA database. From the curves of growth in I, J and $K_{\rm s}$ photometric bands, we estimated different apparent magnitudes and diameters ("total'', "Kron'' and "isophotal''). Isophotal parameters refer to the limiting surface brightnesses: 22.5 I mag arcsec-2, 21.0 J mag arcsec-2 and 20.0 $K_{\rm s}$ mag arcsec-2 for the three photometric bands, respectively. The result is a catalog of $753\ 153$ objects (among which there are $508\ 224$ galaxies, $34\ 449$ probable galaxies and $210\ 480$ galaxies to be confirmed). The catalog gives about (the figures vary, depending on the considered magnitude or diameter): $668 \ 000$ I-band magnitudes, $576 \ 000$ J-band magnitudes, $357 \ 000$ $K_{\rm s}$-band magnitudes and $452 \ 000$ I-band diameters, $299 \ 000$ J-band diameters, $114 \ 000$ $K_{\rm s}$-band diameters.

The typical standard deviations for I, J and $K_{\rm s}$ magnitudes are 0.14, 0.15 and 0.25, respectively, for magnitudes limited at I=16, J=15 and $K_{\rm s}=14$. The contamination by superimposed objects probably remains the major source of problems and could require future improvement. The completeness limits in magnitude are about: 15.5, 14.5 and 13 in I, J and $K_{\rm s}$, respectively.

Key words: galaxies: general - catalogs

1 Introduction

DENIS was the first attempt to carry out a very large near infrared survey from a direct electronic acquisition on the sky. The project was first presented by Epchtein (1997). The result of seven years of measurements, conducted under the control of P. Fouqué, has lead to an impressive amount of data: about $900 \ 000$ images in Gunn- I band at $0.8 ~\mu$m, in J band at $1.25~ \mu$m and $K_{\rm s}$ band at $2.12 ~ \mu$m. Each elementary image is $12' \times 12'$ with a pixel size of $1\hbox{$^{\prime\prime}$ }$ (for J and $K_{\rm s}$ this spatial resolution is obtained by microscanning). The integration time is 10 s. The sequence of observation is made at a given right ascension for a wide range of declination ( $30^{\circ}$). This arrangement is called a strip. It contains 180 elementary images with 1' overlap on each side.

Today many such large surveys have been undertaken in different wavelength bands (2MASS, SLOAN, HIPASS, FIRST). The 2MASS project was conducted on the whole sky with similar purposes: a very large sky infrared survey. It uses J, H and $K_{\rm s}$ bands (Jarrett et al. 2000) with two dedicated telescopes. DENIS was conducted in a more difficult way, using a telescope rented to ESO. For the extragalactic domain we produced preliminary catalogs using low resolution images (Vauglin et al. 1999; Paturel et al. 2003b; Rousseau et al. 2000; Vauglin et al. 2002).

In this paper we present an exploitation of the DENIS survey using full resolution images. This leads to a catalog of $753\ 153$ galaxies with I, J, $K_{\rm s}$ magnitudes. This is still a provisional catalog because the final DENIS catalog (Mamon et al. 2004, in preparation) will not be restricted to LEDA objects[*]. It will be deeper, more accurate and more homogeneous. Nevertheless, the present catalog should be useful for preliminary studies, especially when I-band data is required. The present catalog is about ten times larger than the one we produced, for I-band only, with low resolution images (Paturel et al. 2003b).

2 First reduction process and checking

The data reduction was conducted by Borsenberger (1997). The data received from the observational site of La Silla are first sent to the Paris Data Analysis Center where they are pre-processed. They are flat-fielded and the sky background is subtracted. The original coordinate system given in the header is replaced by a calibrated one obtained by a cross-identification of stellar sources with the USNO-A2.0 astrometric catalog (Monet et al. 1998). Despite this improvement some coordinates are still uncertain. We will see below how this problem is solved.

Many primary or secondary photometric standards were measured at least twice every 180 images (strip). From this analysis one of us (JB) derived the I, J and $K_{\rm s}$ zero points needed to transform intensities to absolute fluxes. The adopted zero points are given for each night (the strips from the same night have thus the same zero-point). The variations along the survey are shown in Fig. 1. Some abrupt changes correspond to cleaning of mirrors or modifications of the camera. When it was not possible to measure zero-points, we adopt the mean between the previous and next values, instead of using a default value. In such cases a flag is put on the corresponding data. This flag is designated as  $f_{\rm zp}$. The statistics of flagged objects is given in Table 1.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{1162fi01.eps} \end{figure} Figure 1: Variation of adopted zero-points with strip number (i.e. with time) for I, J and $K_{\rm s}$ photometric bands.
Open with DEXTER

Table 1: Statistics of the different flags, for I, J and $K_{\rm s}$ photometric bands.

During the DENIS survey there was no automatic monitoring to check the quality of the sky. So, we use the stability of the sky background to test the reliability as showed in a previous paper (Vauglin et al. 2002). The sky background may vary along a strip, e.g. when the strip crosses the Milky Way. However, the standard deviation of the sky background calculated for an elementary image should be more stable along a strip if the sky is clear. On the contrary, if clouds cross the field, the pixel intensities will vary at random and the standard deviation of the sky background will increase. Of course, one cannot exclude that unresolved stars also affect the standard deviation of the sky background in crowed fields, but this will also produce poorer data[*]. Thus, the fluctuations of the standard deviation of the sky background along a strip is used to estimate the quality q of the strip. The definition is thus:

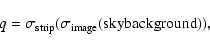\begin{displaymath}q= \sigma _{\rm strip} (\sigma _{\rm image} ({\rm sky background})), \end{displaymath} (1)

where $\sigma _{\rm domain}({\rm quantity})$ is the standard deviation of "quantity'' calculated over "domain". As an example we show the quality q for the I-band for all strips of the survey (Fig. 2). When q is higher than 0.3 mag (in I) or 0.2 mag (in J or $K_{\rm s}$) a flag is put on the measurement. This flag is designated as  $f_{\rm qlt}$. The statistics of flagged objects are given in Table 1.
  \begin{figure} \par\includegraphics[width=8.6cm,clip]{1162fi02.eps} \end{figure} Figure 2: Variation of quality estimated from the fluctuations of the sky background along a strip as a function of strip number for the I photometric band.
Open with DEXTER

3 Recognition and photometry of galaxies

Our previous experience (Vauglin et al. 1999; Paturel et al. 2000) showed us that it is difficult to have full reliability with automatic recognition of galaxies. So, we made use of our LEDA database containing about 2 million galaxies from which about 1 million galaxies have been confirmed either by redshift measurements or by visual inspection up to the $18{\rm th}$ B-magnitude. By selecting objects in the DENIS survey area, 921 340 galaxies are kept (of which 565 000 are considered as confirmed galaxies).

Further, because the coordinates in LEDA are relatively good (the standard deviation is typically a few arcseconds according to Paturel et al. 1999) this solves the remaining problem of DENIS coordinates. We will keep only objects for which a good agreement exists between both coordinate determinations.

From LEDA we also extracted the diameter D25, axis ratio R25 and position angle $\beta$ for all selected galaxies. The dimensions refer, on average, to the blue limiting surface brightness 25 mag arcsec-2. Diameters and position angle are used to integrate the flux in eight homothetic ellipses having diameters regularly distributed between D25/4 and 2D25 (i.e., 2D25/i, i down from eight to one).

During this integration process we searched for the maximum of the pixel intensity within the ellipse of diameter 2D25/5. This defines the adopted center of the galaxy. The central flux and the surface area of the corresponding ellipse is used to estimate the object type (star or galaxy) when it is not confirmed from LEDA (see Sect. 4). We calculate the DENIS coordinates for the pixel of maximum central intensity. When the discrepancy with the LEDA coordinates exceeds twice the minor axis or is greater than  $30\hbox{$^{\prime\prime}$ }$, a flag is put on the measurement. Objects having a problem of coordinates are rare (a few percent). They are simply removed.

In order to remove superimposed stars we use the following procedure: when a pixel intensity is higher than the maximum found at the center of the galaxy, we replace the surface area corresponding to the Point Spread Function (PSF) around this pixel by a constant intensity. This constant intensity is chosen in the vicinity of the considered pixel (typically at a distance corresponding to the PSF radius). When the total correction exceeds 0.3 mag a flag is put on the measurement. This flag will be designated as f*. The statistics of flagged objects are given in Table 1. As expected, the number of objects that have this flag increases towards low galactic latitude (Fig. 3). Note that the presence of a flag does not mean that the magnitude should be rejected. It simply means that a correction for superimposed stars has been applied.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{1162fi03.eps} \end{figure} Figure 3: Fraction of objects having a flag f* as a function of absolute value of the galactic latitude. The dashed line represents the mean fraction.
Open with DEXTER

The eight fluxes within the eight homothetic ellipses are transformed into magnitudes using proper zero points (previous section) and constant atmospheric extinction coefficients: 0.02 in I, 0.08 in J and 0.11 in $K_{\rm s}$. Because the sky background has been reduced to zero, on average, the magnitudes do not need, in principle, a sky background subtraction. In practice, the local sky background is estimated from external ellipses. We give an example of a curve of growth (magnitude vs. surface area) for a typical galaxy arbitrarily chosen (Fig. 4). In the next section, we use the surface brightness profile for each galaxy.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{1162fi04.eps} \end{figure} Figure 4: The curve of growth of a typical galaxy (NGC 7808). The points (filled circles) and dashed line represent the raw measurements obtained by integrating within the eight homothetic ellipses defined in the text. The open circles and solid line represent the measurements corrected for the local sky-background calculated from the two largest ellipses. The error bars are obtained from the standard deviation of the curve of growth.
Open with DEXTER

The final test of quality is made by flagging galaxies that are near the edge of the frame. If the marginal projections of the largest ellipse have more than five percent length outside the limit of the frame, a flag  $f_{\rm edge}$ is put on the measurements for this object. Table 1 summarizes the statistics of all flags.

After this first step we obtain three catalogs. They contain: $1\ 562\ 677$ measurements for $724 \ 973$ objects in I, $1\ 315\ 302$ measurements for $633 \ 049$ objects in J and $934\ 816$ measurements for $416 \ 234$ objects in $K_{\rm s}$. Many objects are measured several times because of the overlap of the images along a strip and the overlap of adjacent strips. Thus, we have to calculate the mean curve of growth for each object.

4 Mean of different determinations

To calculate the weighted mean of different measurements we have first to estimate the standard deviation of each of them. Because the standard error on magnitudes is the same as the standard error on surface brightness (assuming there is no uncertainty on the calculation on the surface area), this standard error is estimated through a fit of a parametric Sersic profile (surface brightness SB vs. r1/n, as shown for instance in Fig. 5). Different values of the parameter n are used over the range 1 to 4 in order to reproduce either the exponential law or the de Vaucouleurs' law. The standard deviation of the best fit is attached to a given curve of growth.

The galaxy profile is calculated as follows: Let fi ( fi = 10-0.4 mi, i=1 to 8) be the fluxes within the eight ellipses of surface $s_i=\pi a_i b_i$. The surface brightness Bi at an equivalent radius[*]

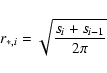\begin{displaymath}r_{*,i}=\sqrt{\frac {s_i + s_{i-1}}{2 \pi}} \end{displaymath} (2)

is expressed as:

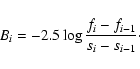\begin{displaymath}B_i=-2.5 \log \frac {f_i - f_{i-1}} {s_i - s_{i-1}} \cdot \end{displaymath} (3)

We limited the calculation to realistic values of the surface brightness; i.e., up to 24, 23 and 22 mag arcsec-2 for I, J and $K_{\rm s}$, respectively.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{1162fi05.eps} \end{figure} Figure 5: Fit of a Sersic function to the brightness profile of a typical galaxy (NGC 7808). The error bars result from the standard deviation of the fit.
Open with DEXTER

Using the standard deviation (rms residuals) of the fit, we calculated the weight of each individual magnitude as the inverse of the square of the standard deviation ( $w=1/\sigma^2$). Then, we calculated the weighted mean magnitudes within the eight homothetic ellipses and their actual error (Paturel et al. 1997). This actual error takes into account both the internal uncertainty given by the standard deviation of the fit and the external uncertainty resulting from the comparison of independent measurements. An object is rejected if, at a given level, the magnitude cannot be calculated. Further, when the standard deviation of the fit is larger than a given limit, all measurements are also rejected. The adopted limits are: 0.6, 0.8 and 1.0 mag for I, J and $K_{\rm s}$, respectively.

We calculated the mean of each flag. The integer division gives the final flags, each being 0 or 1. We also calculated the confidence in the recognition of an object as a galaxy. Many objects are confirmed galaxies. Hence, this parameter is useful only for objects not yet confirmed. This parameter is defined in magnitude as:

\begin{displaymath}G=-2.5 \log{ f_{\rm maxi}} + 2.5 \log{S_{\rm central}}, \end{displaymath} (4)

the higher the parameter, the more secure the acceptation as galaxy. This parameter was used in our first attempt to extract galaxies from binned DENIS images (Vauglin et al. 1999). $f_{\rm maxi}$ is the central peak flux (calibrated and corrected for extinction) and $S_{\rm central}$ is the surface area of the central region (see previous section). The justification is that, unlike to a galaxy, a star has a small surface area and a high central intensity. Then, a typical star correspond to a small "G''. On the contrary, a galaxy has a high "G''. In order to test the significance of this parameter we show its distribution for two classes of objects (Fig. 6): confirmed and not confirmed galaxies, the latter ones being chosen near the galactic plane ( $\vert b\vert < 10^{\circ}$) to increase the chance of having non extragalactic objects. For confirmed galaxies G may be as low as 21, 20 or 18.5 in I, Jand $K_{\rm s}$, respectively. Below these values the classification as "galaxy'' is uncertain. To be more conservative, it is better to accept unconfirmed object as galaxies when Gis larger than 22.5, 21.0 or 19.6 in I, J and $K_{\rm s}$, respectively. In our catalog, the object type will be noted "G'' for confirmed galaxies, "g'' for not confirmed galaxies with high "G'' and "?'' for objects that should be confirmed either by a visual inspection or by redshift measurement because G is too small (i.e. below the adopted limit). For such a classification only I and J are considered because $K_{\rm s}$is clearly not discriminant (see Fig. 6).
  \begin{figure} \par\includegraphics[width=5.7cm,clip]{1162fi06.eps}\hspace*{2mm}... ....eps}\hspace*{2mm} \includegraphics[width=5.7cm,clip]{1162fi08.eps} \end{figure} Figure 6: Parameter G for two populations: confirmed galaxies (full line) or unconfirmed objects near the galactic plane (dashed line). Below the limits drawn with a vertical doted line an unconfirmed object should not be considered as a galaxy without verification.
Open with DEXTER

We plot (Fig. 7) the fraction of not confirmed galaxies versus the default magnitude in I-band. The fraction is almost constant up to the completeness limit ( $I_{\rm lim} \approx 15.5$ mag) found in Sect. 8, but rises quickly above this limit. This shows that much work is still needed to confirm the extragalactic nature of many objects in LEDA. Nevertheless, the DENIS magnitudes will be available from this paper, when these objects will be confirmed.

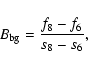5 Magnitudes and diameters

The largest ellipses used for flux integration are very large (up to twice the D25 blue diameter). They are used to correct for the local variations of the sky background. The local brightness of the sky background is estimated as:

\begin{displaymath}B_{\rm bg}=\frac {f_8-f_6}{s_8-s_6}, \end{displaymath} (5)

where fi is the flux within the ith homothetic ellipse (i.e., 10-0.4 mi) and si its corresponding surface area. The corrected magnitude within the ith ellipse is calculated as:

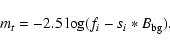\begin{displaymath}m_t=-2.5 \log (f_i - s_i*B_{\rm bg}). \end{displaymath} (6)

Actually, the corrected flux is calculated up to 6/8 of twice the D25 blue diameter (i.e., 1.5 times D25). For the $K_{\rm s}$-band we integrated up to D25 only and used the last four elliptical rings to estimate the local sky background. Now, we will consider only the corrected magnitudes.

We calculated four kinds of magnitude for each band:

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{1162fi09.eps} \end{figure} Figure 7: Fraction (in percentage of the total number) of not confirmed galaxies versus the default magnitude, $I_{\rm d}$. The dashed line shows the completeness limit (dashed line) found in Sect. 8. Above this limit the fraction of not confirmed galaxies raises rapidly.
Open with DEXTER

1-
Default magnitudes $I_{\rm d}$, $J_{\rm d}$ and $K_{\rm d}$. They are simply the integration of corrected flux up to the last ellipse ( $1.5 \ D_{25}$ for I and J, D25 for $K_{\rm s}$).

2-
Total asymptotic magnitudes It, Jt and Kt. They result from the extrapolation where the curve of growth becomes flat (i.e., where the derivative of the polynomial representation of the curve of growth is zero).

3-
Kron magnitudes (Kron 1980) $I_{\rm k}$, $J_{\rm k}$ and $K_{\rm k}$. They result from the integration of corrected flux up to the adaptive equivalent Kron radius :

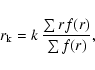\begin{displaymath}r_{\rm k}= k \ \frac{\sum r f(r)}{\sum f(r)}, \end{displaymath} (7)

where f(r) is the flux up to the equivalent radius r. The calculation of rk is made up to the last ellipse. The balance between systematic and random errors is achieved for k=2 (Bertin & Arnouts 1996).

4-
Isophotal magnitudes $I_{\rm s}$, $J_{\rm s}$ and $K_{\rm s}$. They result from the integration of corrected flux up to the isophotal ellipse at 22.5 I mag arcsec-2, 21.0 J mag arcsec-2and 20.0 $K_{\rm s}$ mag arcsec-2, respectively.
The uncertainty on these magnitudes is calculated as the quadratic sum of the actual error on the surface brightness (calculated in previous section) and of the error on the surface area calculated as $1.086 \ \Delta s /s$, where $\Delta s$ is the uncertainty on the surface area, i.e. on the number of pixels. We estimated roughly this error as $\sqrt{s}$. So, the total error on total magnitudes is calculated as:

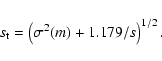\begin{displaymath}s_{\rm t}=\left(\sigma^2 (m) + 1.179/s\right)^{1/2}. \end{displaymath} (8)

In order to remove exceedingly faint objects (in LEDA some galaxies reach 20th B-magnitude) we consider only objects for which the total magnitude is smaller than: 18, 17 or 16 for I, J and $K_{\rm s}$, respectively. With the calculation of magnitudes, we calculated "total'', "Kron'' and "isophotal'' diameters for I, J and $K_{\rm s}$.

We calculated also the colours I-J, $I-K_{\rm s}$ and $J-K_{\rm s}$ from K-magnitudes to reveal discrepant magnitudes. Indeed, when a magnitude is involved in two discrepant colors (differing from the mean at the 3$\sigma$ level) it is removed because it results from an uncertain measurement. The mean values are the following:

\begin{displaymath}\langle I-J \rangle = 1.12 \ \ \ \sigma= 0.41 \end{displaymath}


\begin{displaymath}\langle I-K_{\rm s} \rangle = 2.25 \ \ \ \sigma= 0.62\end{displaymath}


\begin{displaymath}\langle J-K_{\rm s} \rangle = 1.10 \ \ \ \sigma= 0.61.\end{displaymath}

The distributions are shown in Fig. 8. Note that a better estimate of colors can be deduced from the difference of magnitudes within a same ellipse. The study of colors will be conducted in a separate paper.
  \begin{figure} \par\includegraphics[width=5.7cm,clip]{1162fi10.eps}\hspace*{2mm}... ....eps}\hspace*{2mm} \includegraphics[width=5.7cm,clip]{1162fi12.eps} \end{figure} Figure 8: Colours I-J, $I-K_{\rm s}$ and $J-K_{\rm s}$, calculated from total magnitudes.
Open with DEXTER

6 Comparison with independent surveys

We first make an internal comparison of our ``default'', ``Kron'' and ``isophotal'' magnitudes with our ``total'' magnitude (Table 2). The scales agree very well and we will consider zero point shifts only. Except for the isophotal magnitude, they do not differ from total magnitude by more than a few percent.

In order to have an external estimate of the standard deviation of our DENIS magnitudes, we make a comparison of our I magnitudes with the I-band ones of the survey by Mathewson et al. (1992). Our J and $K_{\rm s}$ magnitudes are compared with the J and $K_{\rm s}$ magnitudes of the 2MASS survey (Jarrett et al. 2002). For 2MASS we use the "total'' magnitudes (Cols. 41, 44 and 47 in the 2MASS extended source catalog).

We first made a cross-identification with these surveys. Each galaxy of our catalog is searched in other catalogs within a radius of $r=10\hbox{$^{\prime\prime}$ }$. The cross-identification is accepted when there is only one candidate within r and when the agreement between coordinates is better than  $5\hbox{$^{\prime\prime}$ }$.

A cut at a limiting magnitude (16, 15 and 14 for I, J and $K_{\rm s}$, respectively) avoids the classical bias that distorts the relationship (Paturel et al. 1991) when the catalogs involved in the comparison have different depths. The effect of the choice of these limits is studied below (Table 4). Further, in order to obtain the nominal standard deviation, we first made the comparison for confirmed galaxies, with no flags and with an internal actual error less than 0.2 mag. This last limitation practically does not affect the results. Indeed, we repeated the calculation with an internal error as large as 0.9 mag without having a significant change in the final standard deviation (see Table 5). The case of less accurate objects (those with a flag) is studied in next section.

Table 2: Comparison of zero-points of different kinds of apparent magnitude ("default'', "Kron'' and "isophotal'') with the "total'' magnitude.

The different results of the two-by-two comparisons are summarized in Table 3. Examples of the comparison are given in Fig. 9 for the default magnitudes: $I_{\rm d}$, $J_{\rm d}$ and $K_{\rm d}$.

For the comparison with Mathewson's sample, we considered the direct regression (because Mathewson's magnitudes are assumed to be much more accurate than our magnitudes), while for the comparison with 2MASS we used the mean regression, because we assume that both systems have nearly the same accuracy (this is a first estimate, probably leading to an underestimation of our standard deviations). The slopes for I-band magnitudes are not significantly different from one. For J and $K_{\rm s}$-bands, the small departure from one, always leads to a shift in magnitude smaller than half the standard deviation, over a range of 10 mag. Thus, we will provisionaly consider only the zero-point differences.

The zero-point shift (Table 3) is reasonably small (less than a few percents) when considering "default'' magnitudes. Our total magnitudes are brighter than those from other surveys, but the zero-point shifts never exceed 0.1 mag. In another paper we will make more detailed comparisons, in order to convert magnitudes to homogeneous systems.

To estimate the standard errors of our magnitudes we assumed that all the error in I-band comes from our own I-magnitudes and that the errors in J and $K_{\rm s}$ are the same than those of 2MASS J and $K_{\rm s}$ magnitudes. In other words, the standard deviation of the I-band regression gives directly the standard error on our I-magnitudes while the standard error on J- and $K_{\rm s}$-magnitudes is obtained by dividing the standard deviation of the regression by $\sqrt{2}$ (same error on both axes). The results for different limiting magnitudes are summarized in Table 4. Let us note again that the standard errors on J and $K_{\rm s}$ magnitudes of 2MASS are probably smaller than ours. Thus our standard errors may be underestimated.

Table 3: Comparison of zero-points of our DENIS magnitudes, with those of other samples ("Mathewson'' and "2MASS'').

Table 4: Standard error on our magnitudes as a function of the limiting magnitudes.

A comparison of our I magnitudes with J ones from 2MASS gives a standard deviation $\sigma \approx 0.21$. Assuming again that the error on both axes is the same, one deduces that the uncertainty on our I-band magnitude is about $0.21/\sqrt{2}$, i.e., $\sigma(I)\approx 0.15$. This is in good agreement with the value estimated from the comparison with Mathewson's sample around the same limit (0.14 at $15{\rm th}$ mag). These results are obtained after one cycle of $2\sigma$ rejection. Without any rejection, they give larger standard errors. For instance, for limiting magnitudes 16, 15 and 14 in I, J and $K_{\rm s}$ respectively, we obtain 0.20 (instead of 0.14), 0.18 (instead of 0.14) and 0.28 (instead of 0.25).

We compared our I-band diameters at the isophote 22.5 I-mag arcsec-2 with those measured by Mathewson at the isophote 23.5 I-mag arcsec-2. The comparison is shown in Fig. 10. The shift between both diameter systems is 0.066 with a standard deviation $\sigma=0.052$. This shows that, on average, the accuracy of these diameters is as good as, e.g. Nilson's diameters ( $\sigma=0.06$ according to Paturel et al. 1991).

We estimate the quantity $\partial \log D / \partial \mu \approx 0.07$ for the I-band around the brightness $\mu= 23$ mag arcsec-2. For comparison, in B-band, around 25 mag arcsec-2, this quantity is 0.09, for a typical spiral galaxy (Fouqué & Paturel 1985).

7 Influence of flags

Some measurements have a flag to say that they can be affected by a problem. Four flags are used: $f_{\rm zp}$ quality of the zero-point, $f_{\rm qlt}$ quality of the night, $f_{\rm edge}$ object near the edge of the frame and f* contamination by superimposed object. The flag indicating that the coordinates do not agree with original ones is not considered because the corresponding objects have been removed.

The standard deviations, calculated as previously, are given in Table 5. The calculation is made for the limiting magnitudes 16, 15 and 14 for I, J and $K_{\rm s}$, respectively. The most severe influence comes from f* (star contamination).

Table 5: Standard error on total magnitudes as a function of the flag. The first two lines give the result when there is no flag but for actual error limited to either 0.2 mag or 0.9 mag.

Table 6: Description of the structure of the catalog for each galaxy. In the electronic form available at CDS, only the numerical data are given (the designation of columns are given here only for clearness). Further, the four lines are all written on a single line to make the reading easier. The catalog is sorted in Right Ascension for the Equinox 2000.


  \begin{figure} \par\includegraphics[width=5.7cm,clip]{1162fi13.eps}\hspace*{2mm}... ....eps}\hspace*{2mm} \includegraphics[width=5.7cm,clip]{1162fi15.eps} \end{figure} Figure 9: Comparison of DENIS I-, J-, $K_{\rm s}$-bands "default'' magnitudes with respectively the I-band magnitudes from Mathewson's sample and the J and $K_{\rm s}$ magnitudes from the 2MASS survey.
Open with DEXTER

8 The catalog of raw data

The three catalogs for I-, J- and $K_{\rm s}$-band have been merged in one catalog arranged as follows. Four lines are given for each galaxy. The first line gives the parameters common to the three photometric bands; the next three lines give diameters and magnitudes for each photometric band. The detailed description is given below with an example in Table 6.

8.1 First line: Identification and common parameters

Column 1: right ascension and declination for the equinox 2000 in hours, minutes, seconds and tenths, and in degrees, arcminutes and arcseconds respectively. These coordinates are those calculated from the I-band images;
Col. 2: the Principal Galaxy Catalog numbering (Paturel et al. 2003a);
Col. 3: alternate names following our previous hierarchy (Paturel et al. 2003a). Names that correspond to a multiple system are written in parenthesis. Names that do not agree with NED identification have been written with a question mark (?). Names that have been moved from one galaxy to another since the first PGC(1989) catalog have been written with an exclamation point (!);
Col. 4: label indicating that the object is present in the 2MASS extended source catalog;
Col. 5: apparent blue diameter $\log D_{25}$ in log scale (D25 in 0.1 arcmin) at the isophote 25 B-mag arcsec-2;
Col. 6: axis ratio in log scale (log of major axis to minor axis) at the isophote 25 B-mag arcsec-2;
Col. 7: adopted position angle in degrees measured from the North to the East. Its value covers the range $0^{\circ}{-}180^{\circ}$;
Col. 8: object nature: confirmed galaxies (G), possible galaxies (g) or object to be confirmed (?).

8.2 Next three lines: Global parameters

Column 1: photometric band designation (I, J or $K_{\rm s}$);
Col. 2: right ascension and declination for the equinox 2000 in decimal hours and degrees;
Col. 3: discrepancy d of the coordinates with respect to the LEDA coordinates. d is measured in arcseconds;
Col. 4: parameter G (see text) to characterize the nature of the object for not confirmed galaxies;
Col. 5: flags of quality. Each flag has a value 0 when there is no problem or 1 when one can suspect the data to be affected. The flags characterize the following features (in this order from the left to the right): flag 1 for quality of zero point, flag 2 for quality of the night, flag 3 for quality of the position of the object within the frame (edge effect), flag 4 for superimposed sources;
Col. 6: number of independent measurements;
Col. 7: decimal logarithm of apparent total diameter $\log D_{\rm t}$ ($D_{\rm t}$ in 0.1');
Col. 8: decimal logarithm of apparent Kron diameter $\log D_{\rm k}$ ($D_{\rm k}$ in 0.1');
Col. 9: decimal logarithm of apparent isophotal diameter $\log D_{\rm s}$ ($D_{\rm s}$ in 0.1'), at isophote 22.5, 21.0 or 20.0 mag arcsec-2 for I, J or $K_{\rm s}$, respectively;
Col. 10: standard deviation attached to the logarithms of diameters;
Col. 11: default apparent magnitude $m_{\rm d}$ integrated up to the last ellipse (see text);
Col. 12: apparent total magnitude $m_{\rm t}$, integrated up to the ellipse of major axis $D_{\rm t}$;
Col. 13: apparent Kron magnitude $m_{\rm k}$, integrated up to the ellipse of major axis $D_{\rm k}$;
Col. 14: apparent isophotal magnitude $m_{\rm s}$, integrated up to the ellipse of major axis $D_{\rm s}$;
Col. 15: standard deviation attached to the apparent magnitudes.
  \begin{figure} \par\includegraphics[width=8.3cm,clip]{1162fi16.eps} \end{figure} Figure 10: Comparison of DENIS I-band diameter at the isophote 22.5 I-mag arcsec-2 with those measured by Mathewson at the isophote 23.5 I-mag arcsec-2.
Open with DEXTER

8.3 Completeness of the catalog

The catalog gives data for $753\ 153$ galaxies (among which there are $508\ 224$ galaxies, $34\ 449$ probable galaxies and $210\ 480$ galaxies to be confirmed). The catalog gives about (the figures may vary, depending on the considered magnitude or diameter): $668 \ 000$ total I-band magnitudes, $576 \ 000$ total J-band magnitudes, $357 \ 000$ total $K_{\rm s}$-band magnitudes and $452 \ 000$ total I-band diameters, $299 \ 000$ total J-band diameters, $114 \ 000$ total $K_{\rm s}$-band diameters.

The typical standard deviations on total magnitudes are 0.14, 0.15 and 0.25, for I-, J- and $K_{\rm s}$-band and limits in magnitude of 16, 15 and 14, respectively.

In order to estimate the mean completeness limit for each band, we plotted the $\log N(m<m_{\rm lim})$ vs. $m_{\rm lim}$ (Fig. 11), for the three bands. The slopes differ significantly from the canonical value 0.6, expected for a uniform distribution of galaxies. The slopes are: 0.52, 0.54 and 0.58, for I-, J- and $K_{\rm s}$-band respectively. This variation seems to be correlated with the uncertainty: the higher the uncertainty on magnitude, the closer to the canonical value 0.6. This could be an illustration of the Eddington effect recently analyzed by Teerikorpi (2004).

  \begin{figure} \par\includegraphics[width=5.7cm,clip]{1162fi17.eps}\hspace*{2mm}... ....eps}\hspace*{2mm} \includegraphics[width=5.7cm,clip]{1162fi19.eps} \end{figure} Figure 11: Completeness curves for I, J and $K_{\rm s}$ magnitudes. Black circles and solid line represent the completeness curves for the present DENIS catalog. Open circles and dashed line represent the completeness curves for the 2MASS extended source catalog.
Open with DEXTER

From Fig. 11 one sees that the completeness limits are about : 15.5, 14.5 and 13.5 in I, J and $K_{\rm s}$, respectively. For comparison we give the same plot for J and $K_{\rm s}$ of the 2MASS extended source catalog (open circles), limited to the southern hemisphere. 2MASS is deeper in $K_{\rm s}$ ($\approx$14 mag instead of 13.5). In J, the deepness is almost the same for both survey. The 2MASS catalog has more objects than the DENIS one but it presents an excess of bright objects, while DENIS presents a lack of bright objects (in J). On the other hand, due to the selection of our objects from LEDA (essentially built from blue plates), our catalog is probably biased towards blue objects.

In conclusion, we want to warn any potential user that the contamination by superimposed objects (stars or companion galaxies) remains the major cause of problems. In using of individual measurements it is advisable to check that there is no contamination within $2 \ D_{25}$. This could be a way to improve the database in the future.

Acknowledgements
We thank all astronomers and technicians who participated to the measurements in La Silla. A part of the calculation (I-band) was made on a computer managed by Ph. Prugniel; we thank him for that. We thank the referee, T. H. Jarrett, for very good suggestions that helped us to improve the paper.

References

 
Copyright ESO 2005