A&A 430, 319-325 (2005)
DOI: 10.1051/0004-6361:20035872

Determination of the mass of (4) Vesta based on new close approaches

A. Kovacevic

Department of Astronomy, Faculty of Mathematics, University of Belgrade, Studentski trg 16, 11000 Belgrade, Serbia and Montenegro

Received 16 February 2004 / Accepted 2 September 2004

Abstract
Here I present a new attempt to determine the mass of (4) Vesta, based on its close approaches with relatively well observed minor planets: (3057) Malaren, (5205) 1988CU7, (8331) Dawkins and (21225) 1995GQ1. The obtained values for the mass of (4) Vesta are comparable with earlier determined ones.

Key words: celestial mechanics - astrometry

1 Introduction

The masses for nearly 30 asteroids have been determined during the last 40 years although the history of asteroid observations is about two centuries long.

The knowledge of the masses and densities of asteroids is important in determining their composition, understanding the evolution of small bodies and of the Solar system itself, and for more precise modelling of asteroid perturbations of the high accuracy planetary ephemerides (Standish 2000).

As is well known, the method of minor planet mass determination that considers gravitational perturbations produced by a asteroid on other bodies (major planets, minor planets or spacecraft) during a mutual close encounter was developed first. However, this method is affected by significant formal errors of mass derivation. For example, adopted masses of only five asteroids: (1) Ceres; (2) Pallas; (4) Vesta; (11) Parthenope and (253) Mathilde were determined with formal errors smaller than $5 \%$. This may be a consequence of inhomogeneous distribution of observations of perturbed bodies, their insufficient number and accuracy or low gravitational effects. Nevertheless, the majority of asteroid mass determination was based on single asteroid close encounters.

As can be seen in Table 1, Hertz (Hertz 1966) discussed 59 observations of (197) Arete and determined the first value of an asteroid mass. Enlarged collections of observations allowed Hertz (1968) to recalculate and improve the mass of (4) Vesta. Working on an extended and partly corrected set of observations of (197) Arete, Schubart & Matson (1979) obtained for the mass of (4) Vesta a value increased by $15 \%$. Analyzing Viking lander radar ranging data, collected over short time span (1976-1981), Standish & Hellings (1989) obtained for the mass of (4) Vesta a greater value than the one adopted nowadays. Later, the mass of (4) Vesta was obtained as a solution of the JPL ephemerides DE403 (Standish et al. 1995) and DE405 (Standish et al. 1998) where 300 asteroids are included in the dynamical model. Hilton (1999) determined the mass of (4) Vesta by using the largest asteroid (1) Ceres as a perturbed body (the closest approach between these two bodies occured in 1893). In spite of the huge number of observations used (9354) and very careful data processing, the obtained value is far from the adopted one and the formal error is about $10 \%$ of the determined mass. An investigation of gravitational effects, caused by mass of (4) Vesta on the motion of (1) Ceres, can explain such a result. Using backward integration, differences in right ascension and declination are only $1.5~ {\rm arcsec}$ and $0.5~ {\rm arcsec}$ respectively, which are within the range of accuracy of observations. On the other hand, the gravitational influence of the mass of Vesta calculated using forward integration (starting from the epoch JD 2 397 000.5) reached $2.5~ {\rm arcsec}$ in right ascension and $-1.0~ {\rm arcsec}$ in declination at the instances of newly collected observations.

In order to avoid problems of reliability of asteroid mass determination, Sitarski & Todorovic-Juchniewicz (1992) used the method of asteroid gravitational perturbations on the orbits of many other perturbed bodies. A simplified method was applied to mass determination of (4) Vesta by using 22 (Kuznetsov 1999) and 26 (Michalak 2000) suitable close encounters. In these cases, it could be seen that the standard deviation of the weighted mean value of the mass of (4) Vesta is strongly influenced by the number of individual determinations. Viateau & Rapaport (1997) noticed a strong perturbation of the orbit of asteroid (17) Thetis caused by two large minor planets, (4) Vesta and (11) Parthenope. These gravitational perturbations allowed Viateau & Rapaport (2001) to determine both the mass of (4) Vesta and the mass of (11) Parthenope. It was the first time that asteroid (17) Thetis had been used to determine the mass of Vesta. The authors emphasized the importance of a reliable level of accuracy of the mass of (4) Vesta, since this asteroid is the second most massive body in the main belt having a important gravitational influence on the orbits of many other solar system objects.

The mentioned reasons imply that new asteroid mass determinations (especially based on new recorded close encounters) are needed.

Table 1: Values for the mass of (4) Vesta determined by other authors.

2 Procedure of mass determination

The list of close encounters suitable for mass determination of 17 large main belt asteroids was published by Galad & Gray (2002). There are five strongly perturbed asteroids ((17) Thetis, (3057) Malaren, (5205) 1988CU7, (8331) Dawkins and (21225) 1995GQ1) due to gravitational influence of the mass of (4) Vesta, which were relatively well observed before and after a close encounter. Due to the fact that a close encounter with (17) Thetis had been successfully used for mass determination of (4) Vesta (Viateau & Rapaport 2001), it is not included in this study.

Geometrical and kinematical parameters (Table 2) as well as expected gravitational effects (Fig. 1) revealed the potential high efficiency of these close approaches. The influence of the mass of (4) Vesta on the trajectory of perturbed bodies has been determined by two separate computations of the orbits of perturbed bodies. The first one took into account perturbation by the adopted mass of (4) Vesta, whereas the second did not.

Bearing in mind that some other minor planets could perturb the motion of the chosen perturbed asteroids, the 9 largest asteroids have been included in the dynamical model, as well as all major planets. The mass values of perturbing asteroids used are given in Table 3. The gravitational influence of the perturbed asteroids on the perturber is negligible due to their small diameters.

Table 2: Geometrical and kinematical parameters of close encounters: $\rho $ is minimum distance, $V_{\rm r}$ is relative velocity and $\theta $ is angle of deflection of perturbed asteroid.

Table 3: Masses of perturbing minor planets.

The numerical integration of differential equations of motion of perturbed bodies is carried out by Addams-Bashforth-Moulton predictor-corrector method (Moshier 1992). The initial osculating orbital elements for the epoch JD 2 452 600.5 were taken from the Edward Bowell database (http://www.lowell.edu/users/elgb/).

In order to analyze the motion of perturbed asteroids, sets of observational data were downloaded from the public database AstDys (http://hamilton.dm.unipi.it/astdys). The classical least-squares method was applied for the mass determination of (4) Vesta. Corrections of six orbital elements of the perturbed asteroid and correction of the mass of (4) Vesta are computed simultaneously. According to this method, the system of linear equations could be expressed in the matrix space as:

\begin{displaymath}L\Delta E=R ~, \end{displaymath} (1)

where the matrix L depends on the partial derivatives of the coordinates (right ascensions and declinations) of the perturbed asteroid with respect to 7 parameters (six osculating elements of the perturbed body and the perturbing mass). Further, ${\Delta E}=(\Delta E_{1},...,\Delta E_{6},\Delta E_{7})$ is a $7\times1$ matrix belonging to the space of system solutions, which contains the corrections of six orbital elements of the perturbed body and correction of the mass of the perturbing body. Finally, R is the matrix depending on (O-C) residuals in coordinates of the perturbed body. Elements of matrices L, R were computed for each epoch of observation. As it is well known, the procedure of solving the system (1) is an iterative one. At the first iteration, elements of matrices L and R were calculated using previously selected observations of perturbed bodies (based on $3\sigma$ criterion described later in this section). Obtained corrections, the matrix $\Delta E$, produced a new solution which was used as the initial condition for the next iteration. Only two iterations were performed until convergence. This technique, applied on Keplerian orbital elements, produces a correlation matrix with a large correlation between the mass of the perturbing body and the mean motion (or the semimajor axis) of the perturbed one (see Table 5). On the other hand, if the calculation is performed using Cartesian coordinates (initial position and velocity) such a characteristic is not common. A metric which could parameterize the uncertainty in the mass of the perturbing asteroid (Bowell et al. 1994) depends on the rms of orbital residuals, semimajor axis and eccentricity of perturbed asteroid orbit, mass of perturbing asteroid, number of pre and post encounter observations used, length of corresponding orbital arcs covered by them, as well as the impact parameter and relative velocity of the close encounter. It could be considered that close encounters examined here are kinematically well conditioned, pre- and post- encounter arcs of perturbed orbits are long enough and the number of postencounter observations is large enough (greater than 100 in each case) for mass determination of Vesta. The presumption that formal errors could be small was confirmed during the determination of the mass of (4) Vesta. The calculated formal errors (Table 5) are comparable with those obtained recently (Table 1). Michalak (2002) obtained formal errors of the order of $10^{-12}~M_{\odot}$ for the mass of (4) Vesta in only three individual mass determination of (4) Vesta. The complete set of available observations of perturbed bodies was used in the procedure of mass determination of (4) Vesta. The distribution of discarded and used pre(post)encounter observations is given in Table 4. Generally, the distribution of observations is inhomogeneous. The number of preencounter observations used (in almost all cases) is 10 times (or more) less that of the postencounter ones (Table 4). Also, only in the case of (5205) 1988CU7, O-C residuals of only one preencounter observation are very large ( $-135~ {\rm arcsec}$ in right ascension and $62~ {\rm arcsec}$ in declination). Preencounter observations of (3057) Malaren, (8331) Dawkins and (21225) 1995GQ1 do not exhibit such a specific characteristic. For example, the ranges of O-C residuals of the discarded observations, based on the $3\sigma$ criterion, are ( $0.5~ {\rm arcsec}$- $4.6~ {\rm arcsec}$) in right ascension and ( $0.1~ {\rm arcsec}$- $2.2~ {\rm arcsec}$) in declination. From this point of view, sets of observations of these four perturbed asteroids compared to sets of observations of brighter perturbed asteroids used in previous studies, do not exhibit any specific characteristics. Concerning the accuracy of observations, it could be concluded that calculations of perturbed orbits are strongly influenced by newly collected observations (within the last few years). During the process of calculation of perturbed orbits, both coordinates (right ascension and declination) were discarded if one of them gave a residual above $3\sigma$.

During the process of mass determination, it was noticed that, integrating backward and using Eq. (1), partial derivatives of the coordinates (right ascension and declination) of the perturbed body with respect to the perturbing mass (coefficients of $\Delta E_{7}$), calculated at the instants of postencounter observations are practically zero and vice versa, coefficients computed at the moments of preencounter observations in forward integration. Having in mind that the number of preencounter observational equations is 10 times less than the number of postencounter observational equations in each case, different results were expected for the mass and its formal error. However, this did not affect the obtained results for the mass of (4) Vesta and corresponding formal errors.


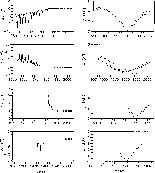  \begin{figure} \par\includegraphics{11395f1.eps} \end{figure} Figure 1: Differences of the geocentric right ascensions of perturbed bodies caused by (4) Vesta ( left) and mutual distances between perturbed asteroids and (4) Vesta ( right). Differences of the geocentric right ascensions of perturbed bodies calculated at the instances of available sets of observations are denoted by asterisks. Pairs of plots from the top to the bottom correspond to close encounters with: (3057) Malaren, (5205) 1988CU7, (8331) Dawkins and (21225) 1995GQ1, respectively.
Open with DEXTER

3 Results and discussion

Table 4: The distribution of observations of perturbed asteroids. In the columns N1, N2, N3, N4, N5 are given number of observations, number of discarded preenc. observations, number of used preenc. observations, number of discarded postenc. observations and number of used postenc. observations. T1 and T2 are time intervals covered by preencounter and postencounter observations. The standard deviations of orbital residuals are given in the last column.

The close encounters that occurred between the second largest perturber in the main belt and (3057) Malaren, (8331) Dawkins, (5205) 1988CU7 and (21225) 1995GQ1 have some common characteristics. The relative velocities are particularly low (Table 2) implying that these close encounters are long lasting. The evolution of the distance between (4) Vesta and the perturbed asteroids over time is given in Fig. 1. As can be seen from Table 2, the minimum distances between (4) Vesta and four perturbed asteroids are small. These close encounters of (4) Vesta are also characterized by the almost 3 year long $0.5~ {\rm AU}$ limitation of their mutual distance. Consequently, the gravitational influence of (4) Vesta on these four perturbed asteroids is significant and could be compared with those seen in the cases of close encounters with (17) Thetis, (67) Asia and (197) Arete which are the most effective close encounters with Vesta (Fig. 2).

Besides the geometry of the mutual approaches, the quality of asteroid mass determination depends on the number and distribution of the observations. The time spans covered by pre and postencounter observations of perturbed asteroids (3057) Malaren and (5205) 1988CU7 are the largest, as it can be seen from Table 4. Inspection of Table 5 shows that the best comparable masses of (4) Vesta with the adopted one have been calculated from its close approaches with these two mentioned asteroids. Prior to a more detailed analysis of the sensitivity of individual solutions for the mass of (4) Vesta to the observation distribution and precision, a global solution of the mass of Vesta was obtained: $(1.28\pm0.01) \times 10^{-10}~M_{\odot}$. According to the method proposed by Sitarski & Todorovic-Juchniewicz (1992) the set of 25 normal equations corresponding to 2194 observational equations of four perturbed asteroids was created. Compared to the previous mass determinations of (4) Vesta (Table 1), it could be noticed that the formal error thus obtained is the smallest one.

  \begin{figure} \par\includegraphics{11395f2.eps} \end{figure} Figure 2: Differences of the geocentric right ascensions of (17) Thetis (curve on lowest position), (67) Asia (curve on medium position) and (197) Arete (curve on highest position) caused by (4) Vesta.
Open with DEXTER

Analyzing the gravitational effects in the case of the close encounter with (3057) Malaren, it can be noticed that they are significant (Fig. 1). Especially if we have in mind that among the most effective single close encounters with (4) Vesta, only (17) Thetis exhibits greater gravitational influence ( $36~ {\rm arcsec}$ in right ascension (Fig. 2)) within a equal time span of 31 years before the close approach. On the other hand, the gravitational effects expressed during the same period prior to the latest close encounter with (197) Arete reached only $5~ {\rm arcsec}$ in right ascension (Fig. 2). Further, the symmetry in the calculated gravitational effects by using backward ( $-13~ {\rm arcsec}$ in right ascension) and forward integration ( $-10~ {\rm arcsec}$ in right ascension) could be noted. Therefore, the mass of (4) Vesta was calculated by using backward (initial epoch of osculating elements was JD 2 453 200.5) and forward (JD 2 434 300.5) integration. The differences between the obtained values were negligible as in the case of calculation of the mass of (16) Psyche from its close approach with (13206) 1997GC22 (Kuzmanoski & Kovacevic 2002). Thus, the mass value of (4) Vesta ( $1.32\pm0.08) \times 10^{-10}~M_{\odot}$ obtained by using 254 observations collected until October 2003 is affected by large gravitational effects as well as by suitable distribution of preencounter and postencounter observations. It could be noted that the corresponding time spans are well balanced and long enough to provide a well calculated perturbed orbit and perturbing mass. The calculated formal error is in good agreement with formal errors obtained by other authors (as can be seen from Table 1). On the other hand, using a widened set of observations collected until April 2004 (307), the obtained mass of Vesta was ( $1.29\pm0.08) \times 10^{-10}~M_{\odot}$. As it can be seen from this case, the calculated correction of the mass of Vesta could be sensitive to the addition newly collected observations in the future.

As already mentioned, the closest encounter occurred with (5205) 1988CU7. Almost 24 years had elapsed from the first observation of (5205) 1988CU7 to the long lasting closest approach with (4) Vesta. During this period gravitational effects reached $47~ {\rm arcsec}$ in right ascension (Fig. 1). Considering the time span of equal length relative to the close approach of the most effective single close encounters that occurred with (17) Thetis (Viateau & Rapaport 1997) and (67) Asia (Michalak 2000), it was noticed that they reached $24~ {\rm arcsec}$ and $6~ {\rm arcsec}$ in right ascension, respectively. In the case of the latest close encounter with (197) Arete corresponding gravitational effects are less than $4~ {\rm arcsec}$ in right ascension within the same time interval (Fig. 2).

Table 5: Results of the mass determinations for (4) Vesta. Mean densities based on a IRAS diameter of $501~ {\rm km}$ are given in the third column. In the last column are presented correlation coefficients between the mass of Vesta and the mean motions of the perturbed asteroids.

Even though the length of time spans covered by pre(post)encounter observations are similar, their distribution is uneven. There are only three preencounter observations; two of them were made in 1954 during a 1 day interval. In spite of the fact that the distribution of observations is uneven, preencounter observations were made long enough before the close encounter, providing the possibility of taking into account such significant gravitational effects. Also, gravitational effects calculated using backward integration (Fig. 1) are comparable with those calculated by forward integration ( $47~ {\rm arcsec}$ in right ascension). The values for the mass of (4) Vesta calculated by forward (starting from the epoch JD 2 434 500.5) and backward integration are almost equal. The obtained mass of (4) Vesta $(1.31\pm0.02) \times 10^{-10}~M_{\odot}$ is very near to the result derived from observations of (3057) Malaren. As it can be seen, the difference between them is within the range of standard deviation of both results. However, the value of the formal error is among the smallest ones; actually, it is comparable to the formal error of the derived mass of Vesta from observations of (17) Thetis (Table 1). It could be the consequence of significant gravitational effects as well as of the large number of good postencounter observations. In order to investigate the influence of the postencounter data set on the correction of the mass of Vesta in more detail, additional calculations were performed. A data set of 288 observations collected until 2002 gave identical result to the previous one: $(1.31\pm 0.025) \times 10^{-10}~M_{\odot}$. However, as we shall see later, in the case of (8331) Dawkins and (21225) 1995GQ1 the correction of the mass of Vesta varied if the postencounter data set was reduced by 1 year. Further, if the set of 316 postencounter observations was restricted to the most recent 216 observations from the period 2000-2003 while 100 observations from period 1986-1999 were discarded, the calculated value of the mass of Vesta was $(1.50\pm0.13) \times 10^{-10}~M_{\odot}$.

Similar distribution characteristics of observations is seen in the case of the close approach with (8331) Dawkins. There are only five preencounter observations made during the 12 day interval, whereas there are 345 postencounter observations covering a 13 year period. These five preencounter observations were made in May 1982, only six years before the close approach. The maximum variation in right ascension of (8331) Dawkins due to the gravitational influence of (4) Vesta is $11~ {\rm arcsec}$ within the six year period before the closest approach. Considering the equal time span prior to the closest encounters of the most effective close approaches with (4) Vesta, it was noticed that greater gravitational effects were seen on the orbit of (17) Thetis ( $17~ {\rm arcsec}$) (Fig. 2). On the other hand, the gravitational effects calculated by using backward integration (Fig. 1) are almost two times lower than those calculated by forward integration (JD 2 434 500). Keeping this in mind, the mass of (4) Vesta was determined by using both forward and backward integration. There was no significant difference between obtained values. The short time span of preencounter observations too near to the epoch of close approach, unequal length of time spans covered by pre and postencounter observations and gravitational effect asymmetry influenced the derived mass of (4) Vesta. Also, the high sensitivity of the obtained correction of the mass of Vesta to the preencounter observations as well as to the newly collected postencounter observations was noticed. Collecting new observations provides a extension of the time interval covered by postencounter observations in such a way that the mass of (4) Vesta could be successfully determined. For example, the value of $(1.08\pm0.06) \times 10^{-10}~M_{\odot}$ for the mass of (4) Vesta is calculated by using 281 postencounter observations collected from 1990 to 2002. Now, using a widened set of postencounter observations (340) collected until October 2003, the value of $(1.11\pm0.05) \times 10^{-10}~M_{\odot}$ is obtained. Adding eight observations collected in October and November 2003 led to $ (1.12\pm0.05) \times 10^{-10}~M_{\odot}$ for the mass of Vesta. Also, if it is possible to find preencounter observations that were made far enough from the close approach, a more reliable mass determination of (4) Vesta could be expected. As mentioned before, the total number and high accuracy of new observations could affect the mass determination of (4) Vesta based on this close encounter.

In the case of the mutual approach with (21225) 1995GQ1, the maximum variation of the right ascension, as a consequence of gravitational perturbation of its orbit due to (4) Vesta, is $-8~ {\rm arcsec}$ after backward integration whereas it is three times greater after forward integration (Fig. 1). The gravitational effects recorded in the preencounter time interval are greater than those seen within the equal time spans of closest approaches with (67) Asia and (197) Arete, whereas in the case of (17) Thetis the gravitational influence is almost equal (Fig. 2). As in the previous cases, calculated values of the mass of (4) Vesta by using backward and forward integration (JD 2 434 300.5) do not show significant discrepancies. As mentioned in the case of the close encounter with (8331) Dawkins, the correction of the mass is sensitive to the preencounter observations used as well as to the newly collected postencounter observations. Therefore, the result obtained by using the set of postencounter observations collected until June 2002 was $(1.23\pm0.17) \times 10^{-10}~M_{\odot}$, whereas after adding 72 observations collected until the end of November 2003 the obtained value of the mass of (4) Vesta is $(1.12\pm0.17) \times 10^{-10}~M_{\odot}$. It is possible that the uneven distribution of observations and differences in gravitational effects affect the obtained value of the mass of (4) Vesta (see Table 4). 100 postencounter observations cover the time span 1995-2003, while only 4 preencounter positions of the perturbed body were observed in 1972 during a very short 1 day interval. The maximum variation of right ascension of (21225) 1995GQ1 was $-6~ {\rm arcsec}$ during the period when preencounter observations were made. The available set of observations of (21225) 1995GQ1 covers only seven oppositions, i.e. too small an arc of the orbit. Much more reliable calculation of corrections of elements of the perturbed orbit and perturbing mass could be expected after a widening of the postencounter set of observations. All previous attempts of determination of the mass of (4) Vesta were based on close approaches with asteroids numbered less than 5000.

4 Conclusion

Three of the four considered perturbed asteroids are relatively faint objects. Despite this, the obtained results are in agreement with previous determinations of the mass of Vesta and are of comparable precision. Using faint objects will provide an enlargement of the number of close encounters and perturbed asteroids suitable for asteroid mass determination. Concerning the adopted value of the mass of (4) Vesta the best results are obtained from the close encounters with (3057) Malaren and (5205) 1988CU7 (see Table 5), where strongly expressed gravitational effects, as well as distribution of observations on the post-encounter and pre-encouter part of the orbit, are well balanced.

However, the values of the mass of (4) Vesta obtained from its close approaches with (8331) Dawkins and (21225) 1995GQ1 (Table 5) are influenced by very different gravitational effects on the pre and postencounter part of orbit as well as by different length of time spans covered by preencounter and postencounter sets of observations and their number. In spite of the fact that these two results are too far from the adopted value, it can be seen that these deviations are comparable with deviations of the masses of Vesta obtained by some other authors using single close encounters.

Having in mind that gravitational effects are strong in all four cases of close encounters, we could expect that collection of new observations of (21225) 1995GQ1 and (8331) Dawkins will provide better postencounter coverage in such a way that a more reliable mass of (4) Vesta could be determined within the next few years.

The planned launch of the Dawn Discovery Mission (Russel et al. 2002) emphasizes the importance of new attempts of mass determination of the two largest perturbers in the main belt.

Acknowledgements
The author would like to thank M. Kuzmanoski, O. Atanackovic-Vukmanovic and D. Mirkovic for help. Also, the author is grateful to the referee for his/her invaluable suggestions and remarks. This research was supported by the Ministry of Science, Technologies and Development of Serbia through No. 1238 "Positions and motion of minor bodies of the solar system."

References

 
Copyright ESO 2005